Numerical Calculation and Analysis of Water Dump Distribution Out of the Belly Tanks of Firefighting Helicopters
Abstract
1. Introduction
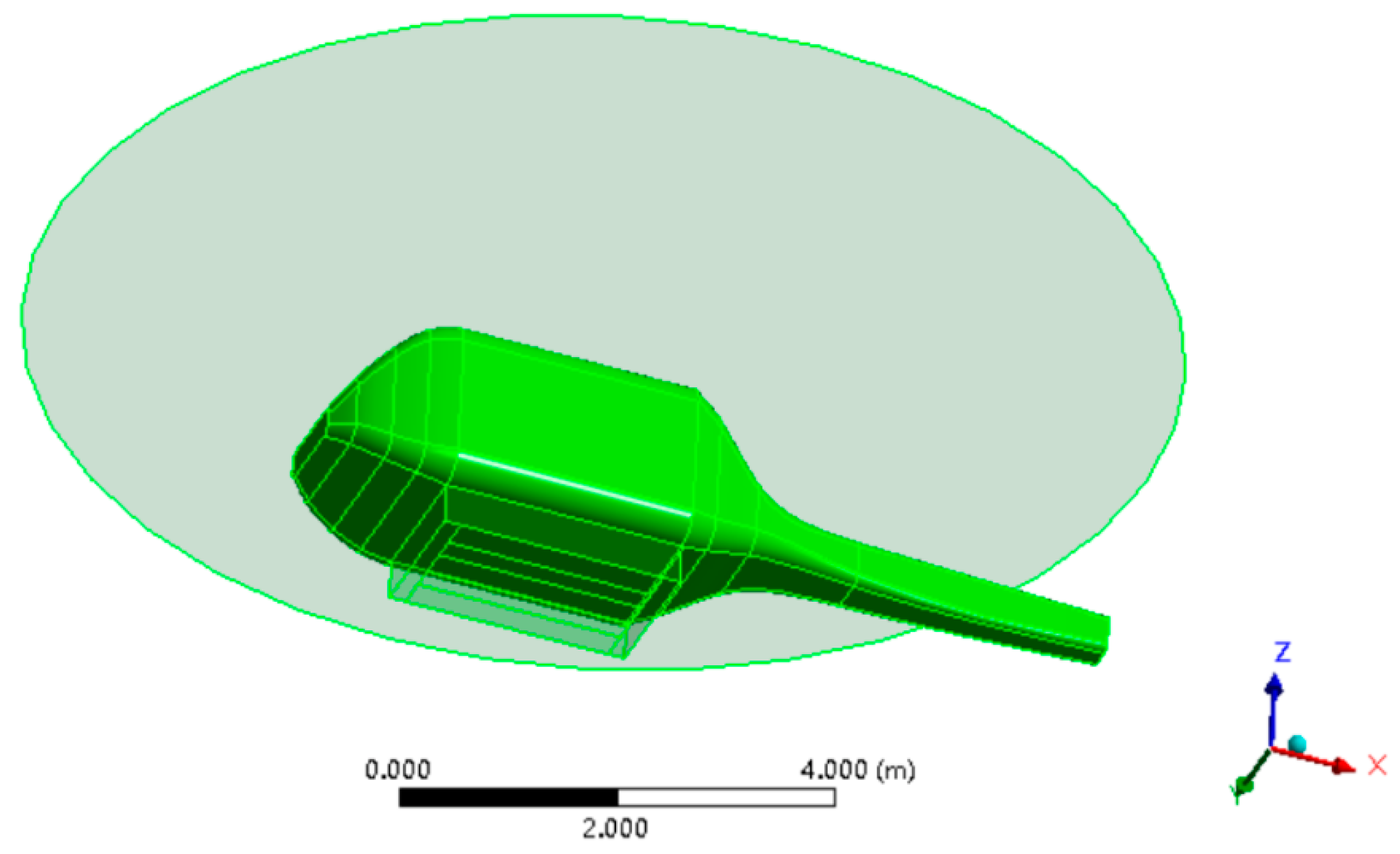
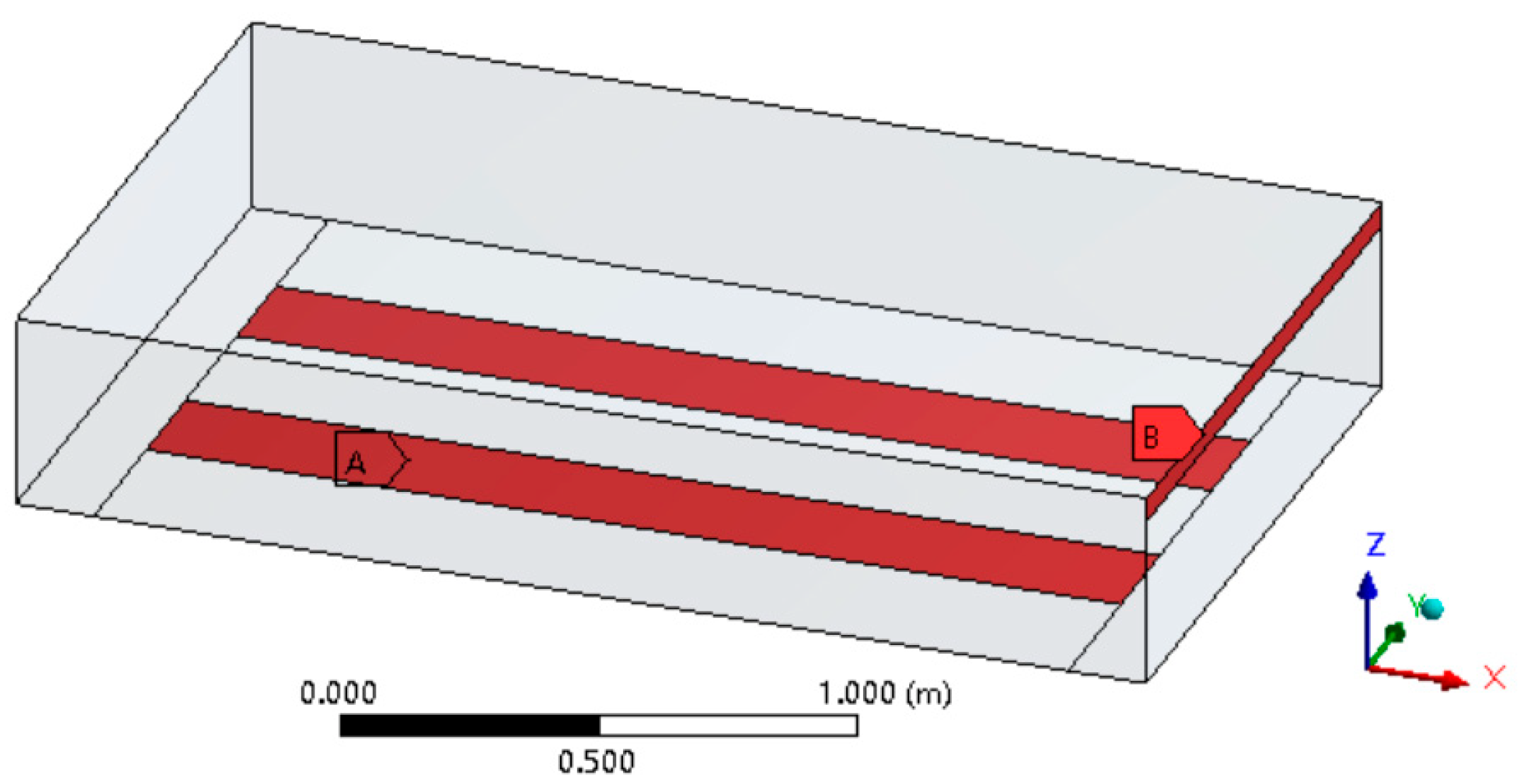
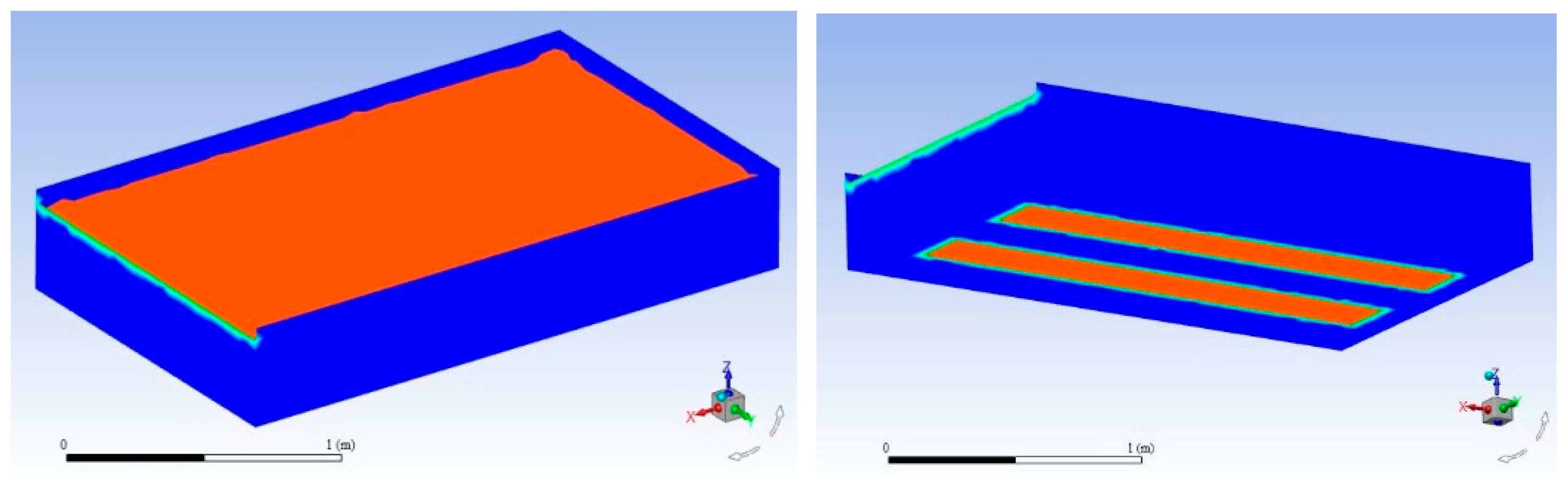
2. Helicopter and Tank Models
3. Water Dump Simulation Model of Helicopter Belly Firefighting Tank
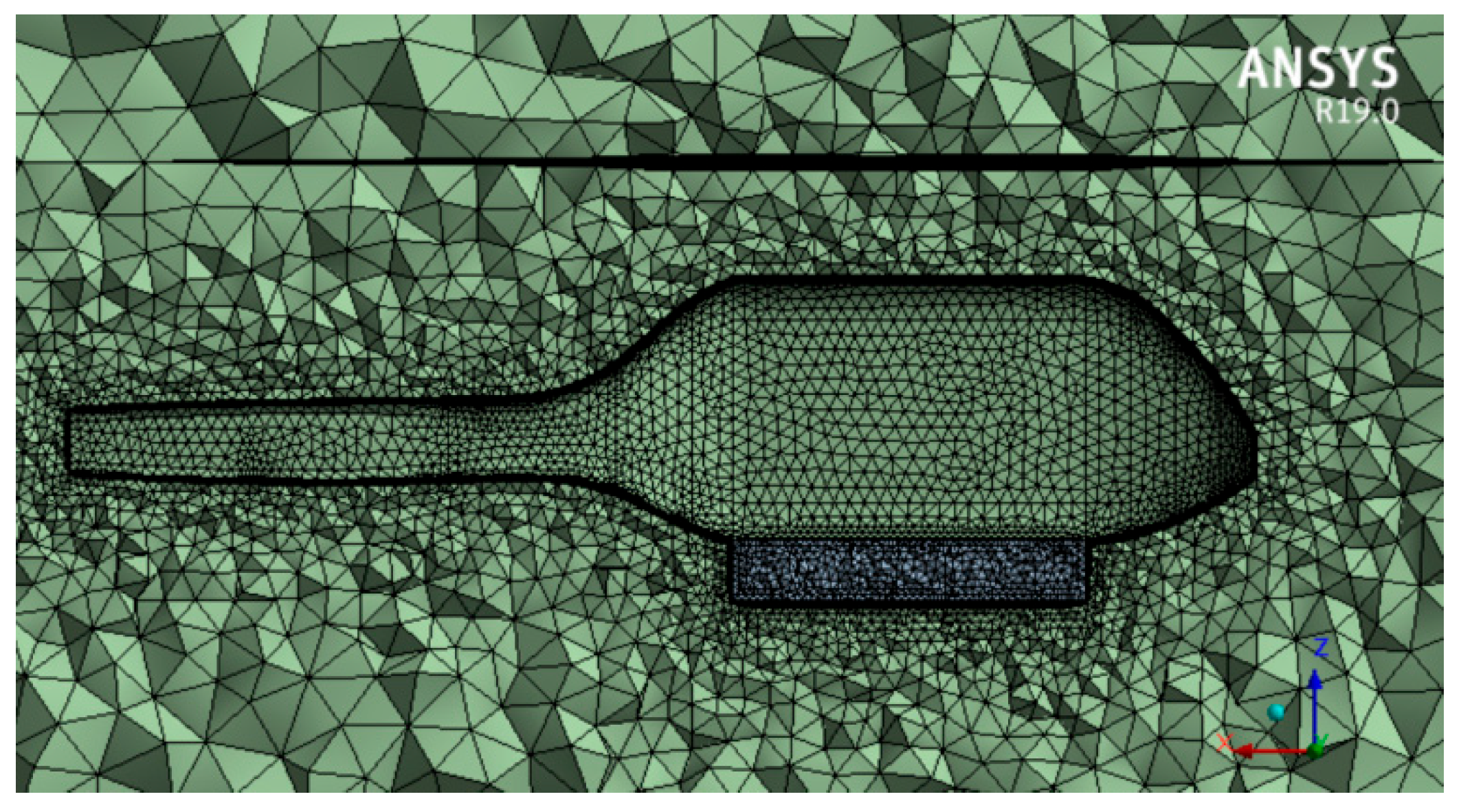
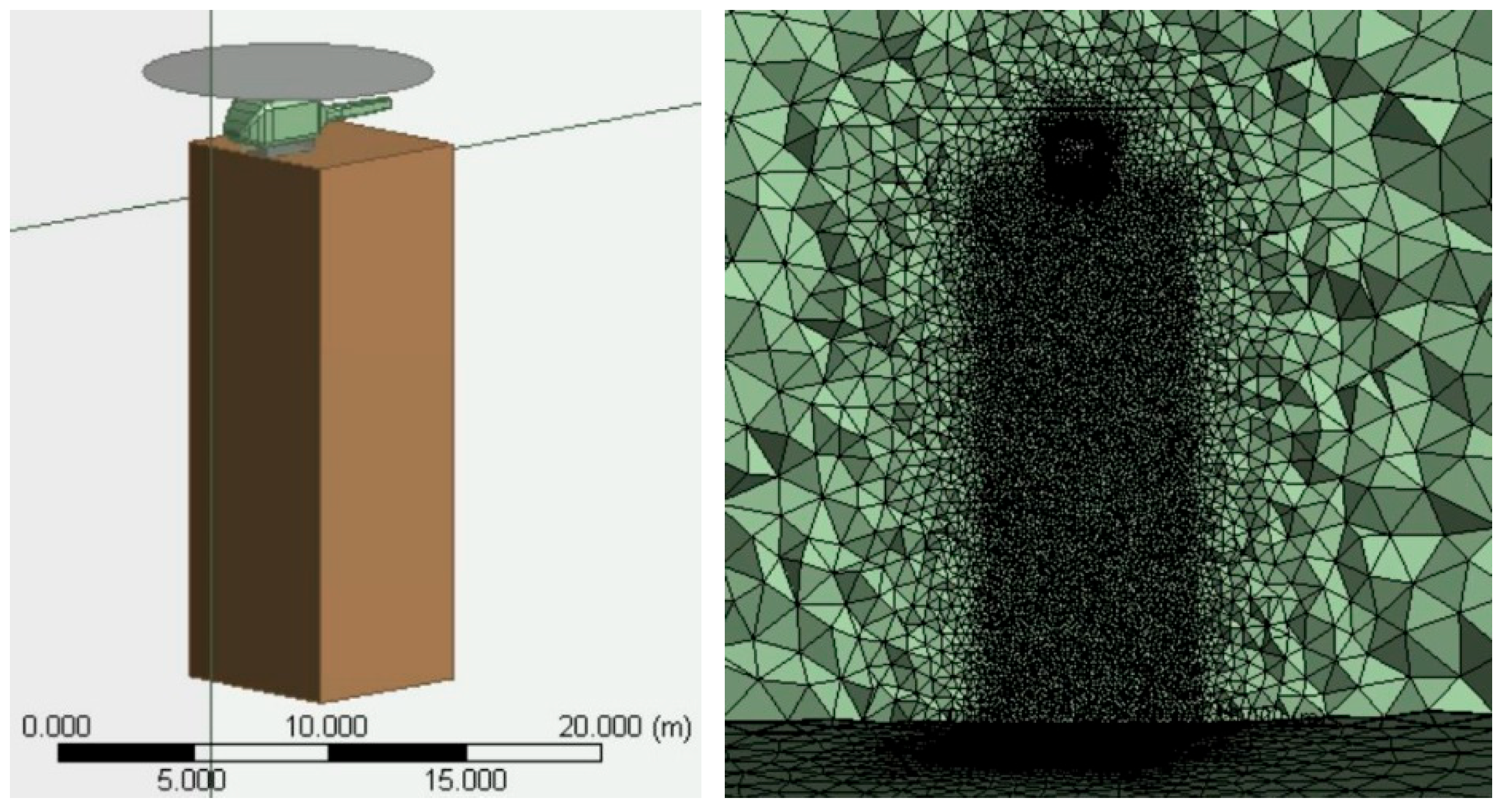
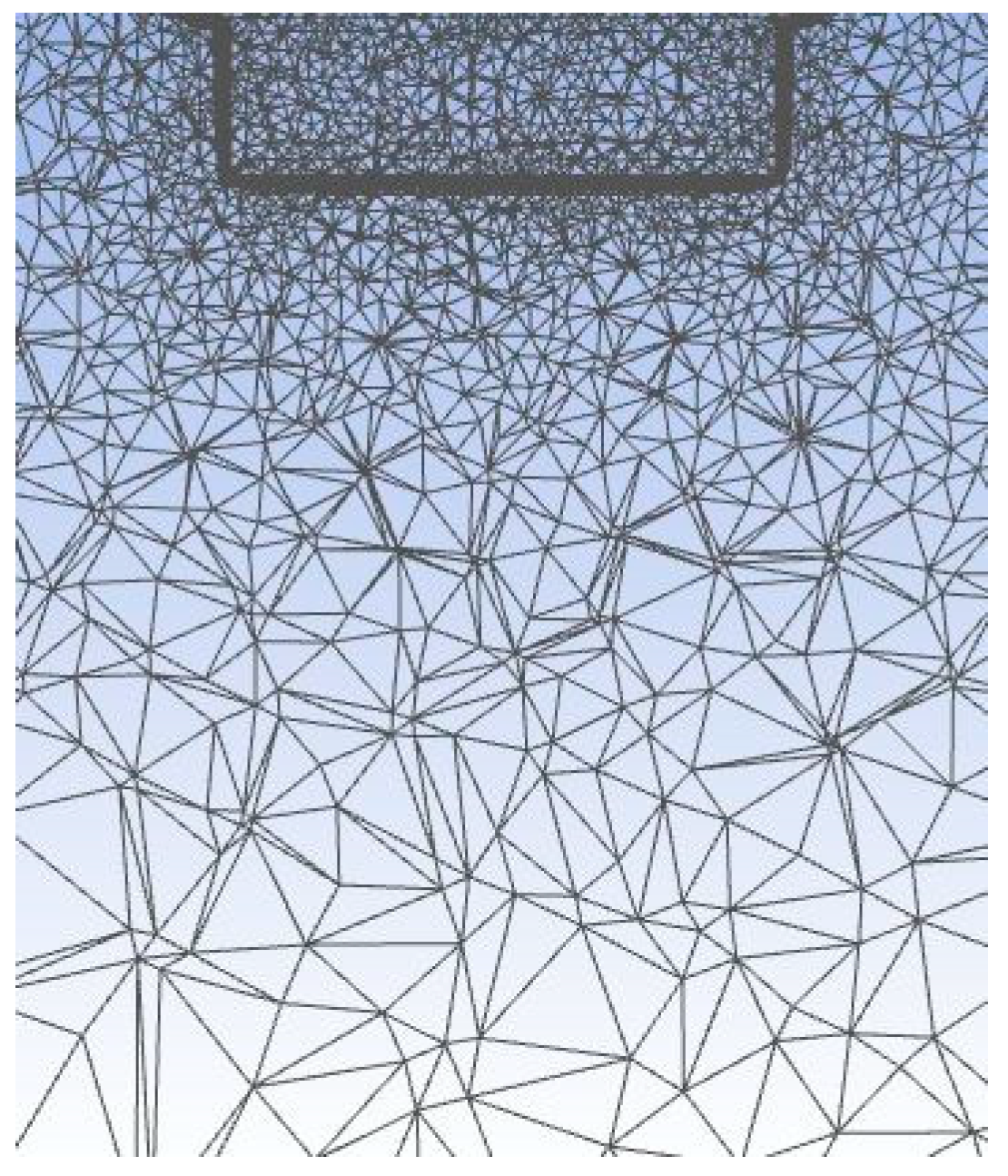
3.1. Mesh Independence Verification
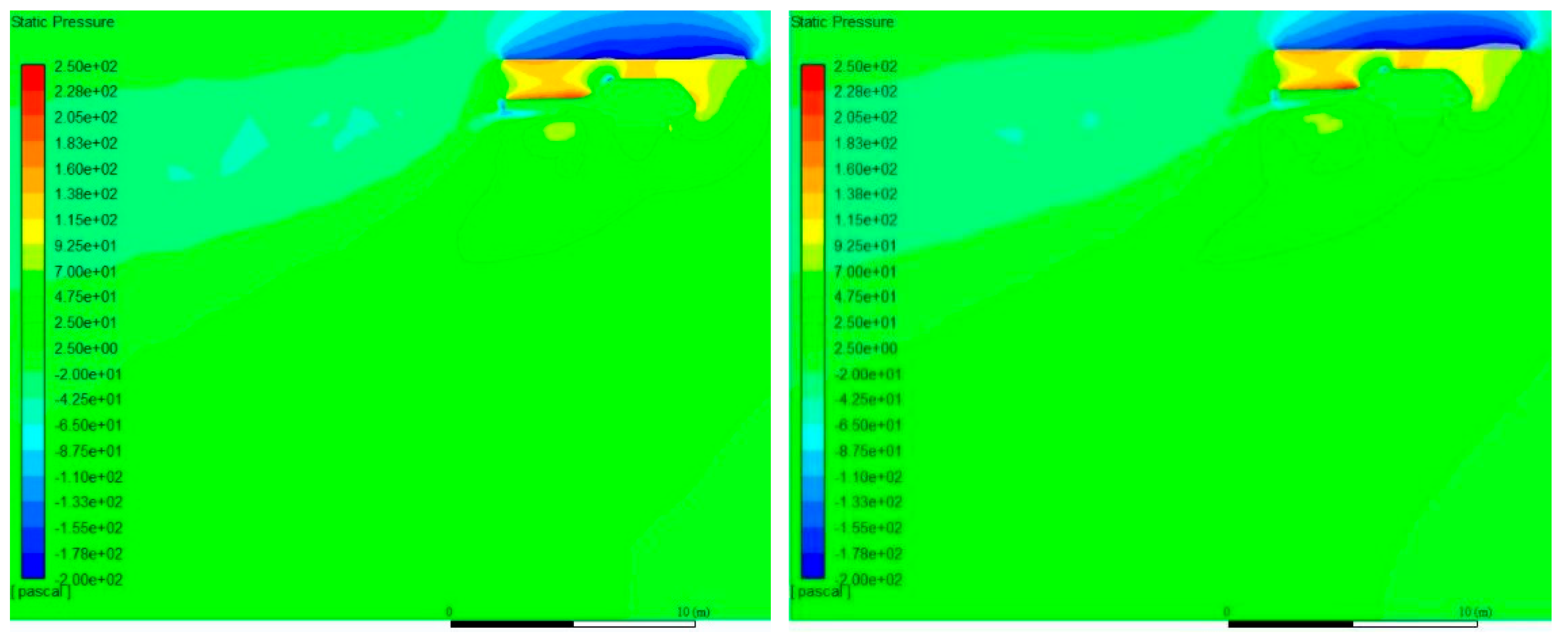
3.2. Analysis of Initial Scenario Results before Water Dump
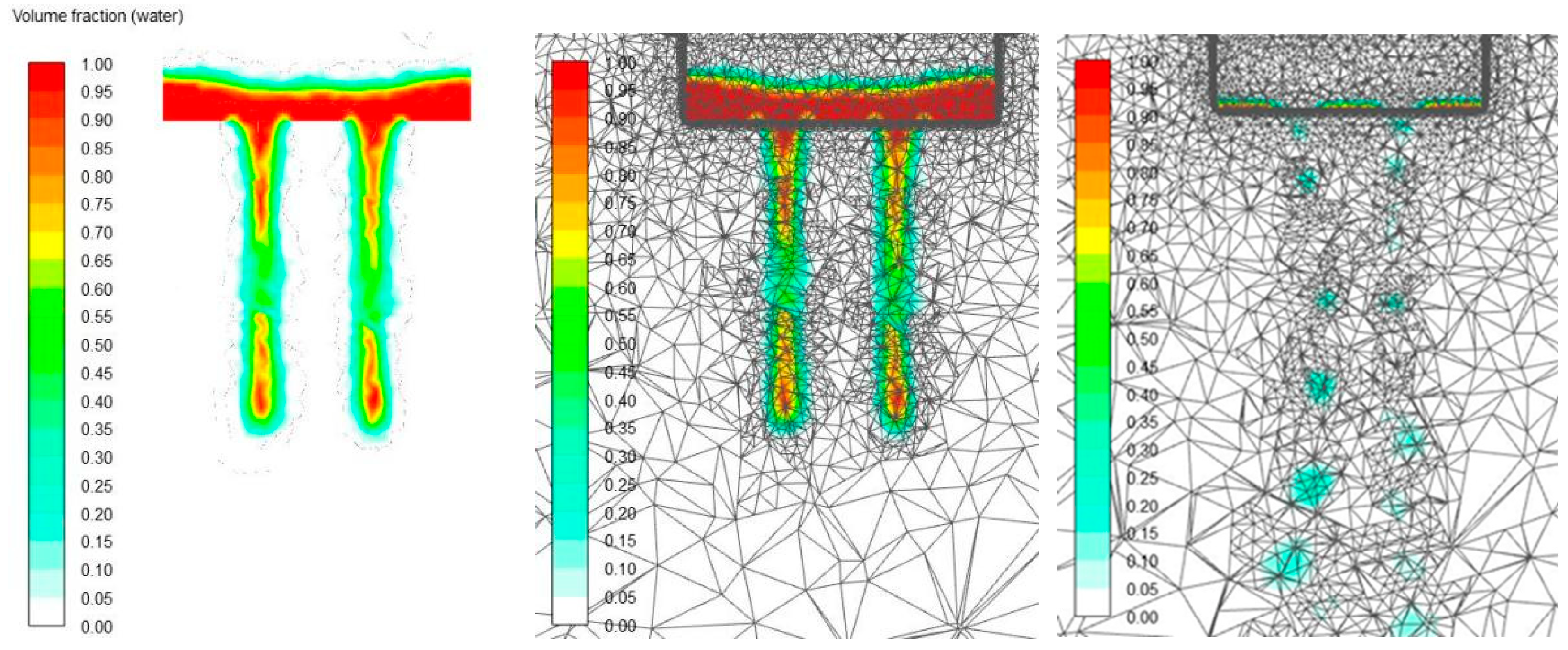
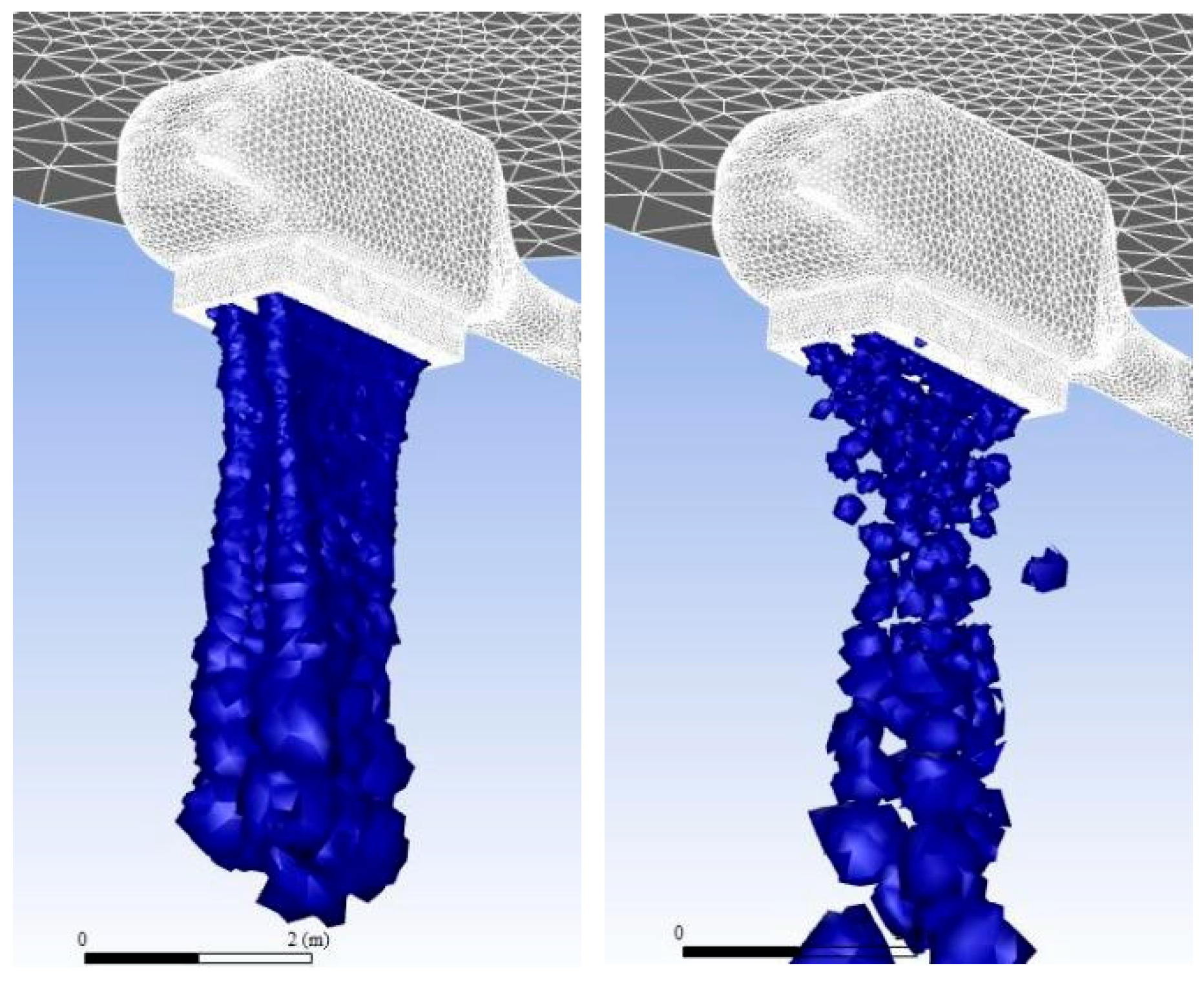
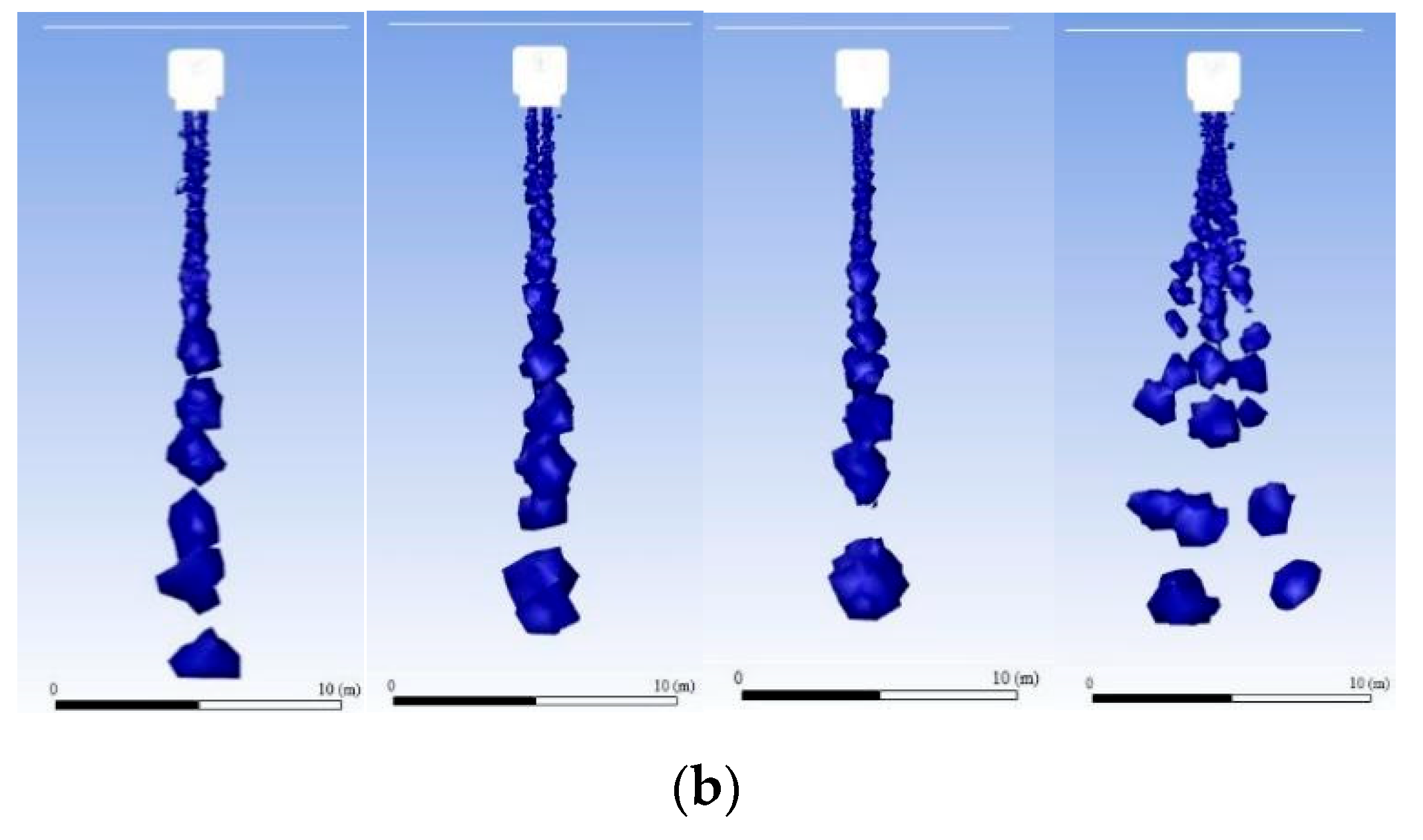
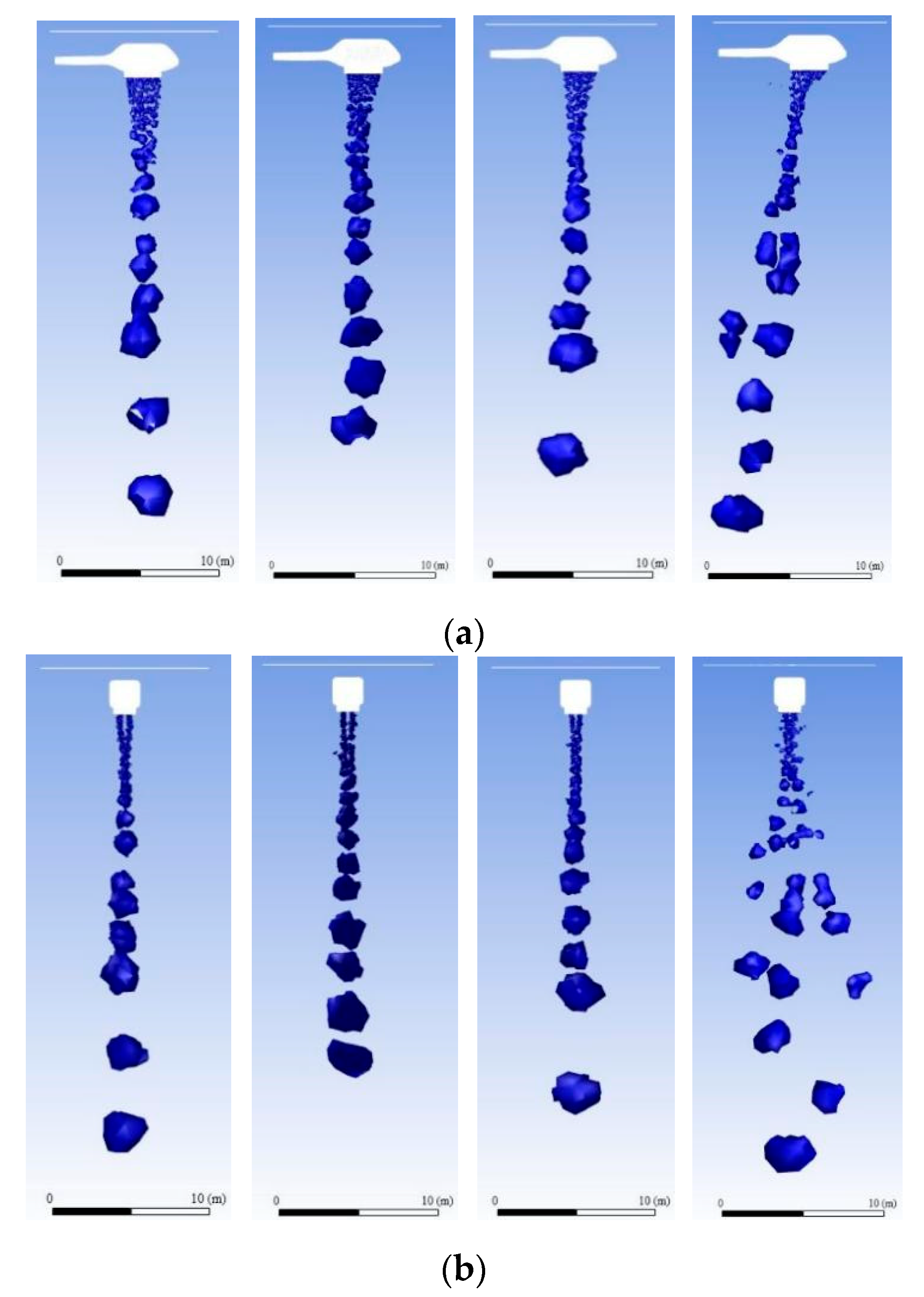
3.3. Transient Result Analysis of Water Dump
4. Simulation Conclusion Analysis and Rule of Water Dumping Out of Helicopter Belly Firefighting Tank
4.1. Result Analysis and Summary of Initial Scenario before Water Dump
4.2. Transient Result Analysis and Summary of Water Dump
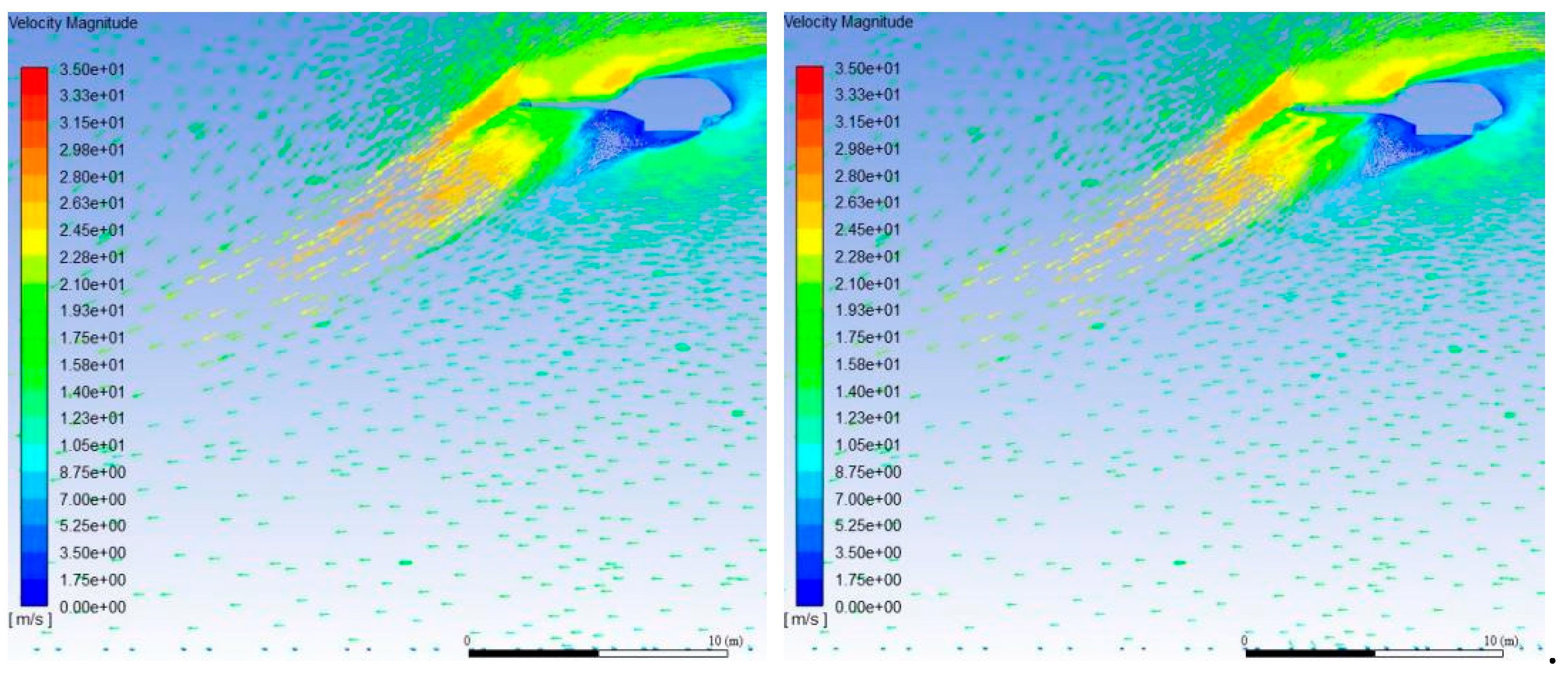
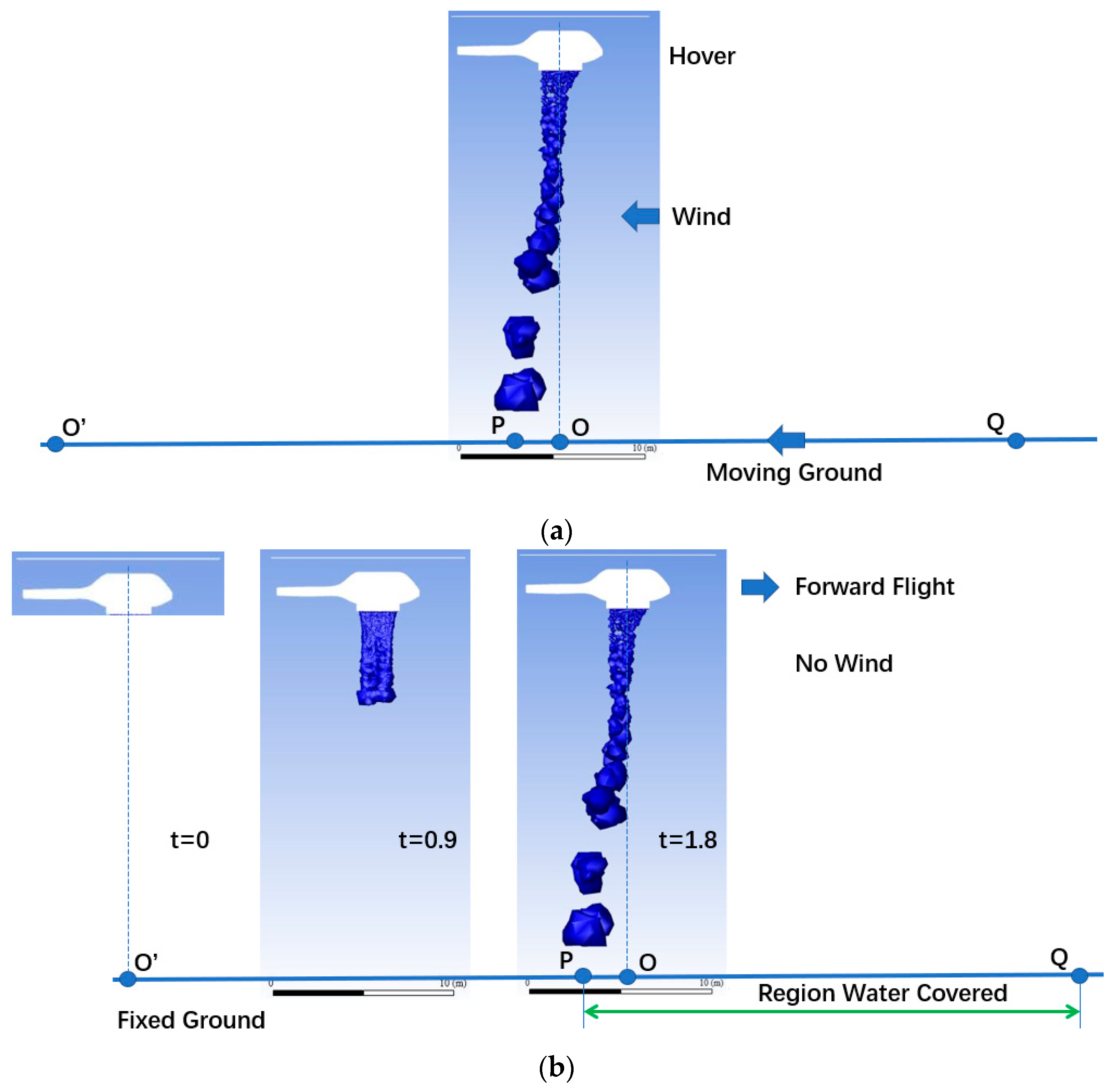
4.3. Forward Helicopter Flight
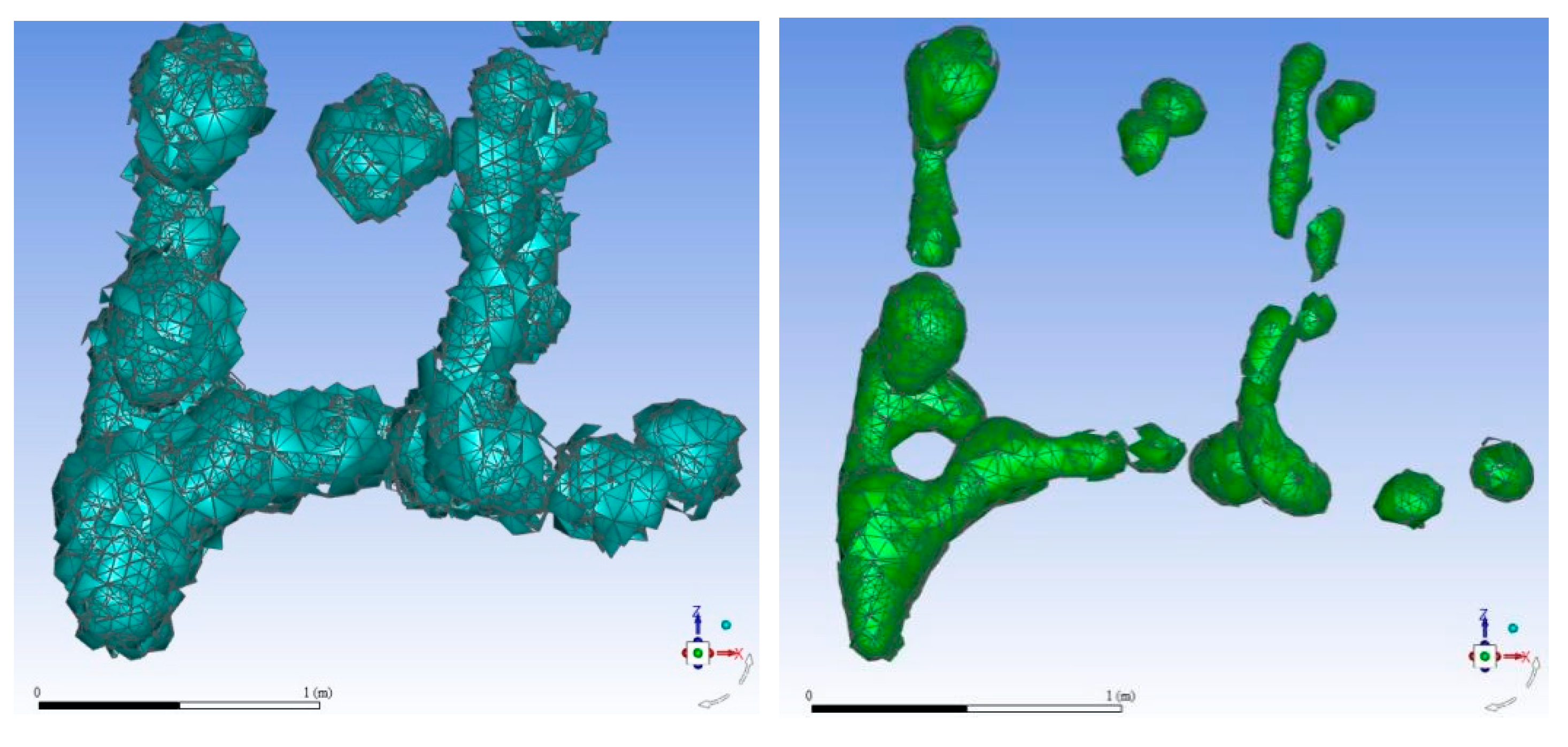
4.4. Rule of Water Distribution on the Ground
5. Conclusions
- (1)
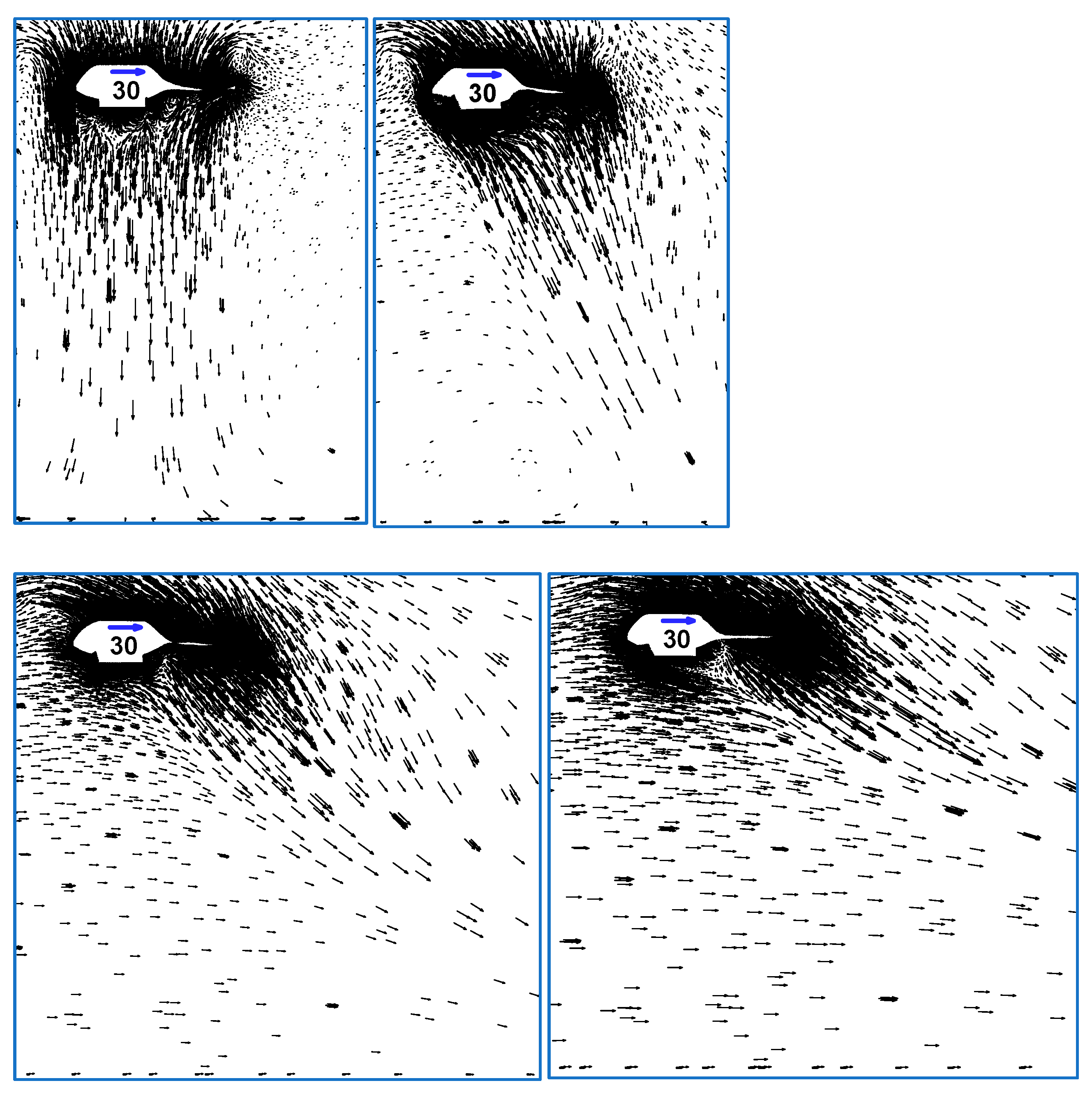
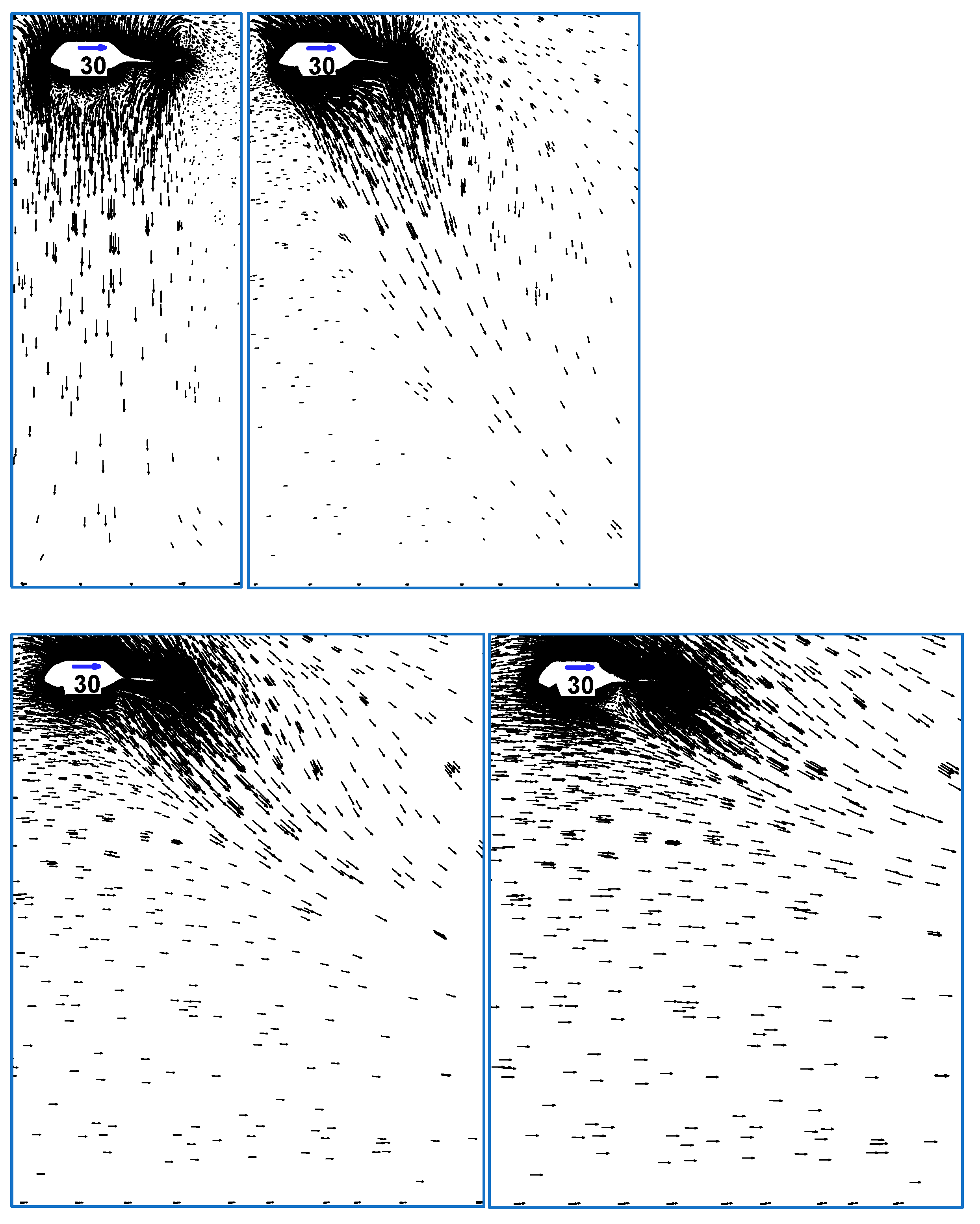
- Wind speed had a significant influence on the direction of wake flow when the helicopter was hovering. The wake flow could by deviated by nearly 30, 45, and 60 degrees by wind speeds of 5 m/s, 10 m/s, and 15 m/s, respectively;
- (2)
- The height above the ground also influenced the wake flow speed. The higher the helicopter was above the ground, the lower the wake flow speed near the ground. When the H125 helicopter hovered 30 m above the ground, the wake flow speed near the ground was about 8 m/s;
- (3)
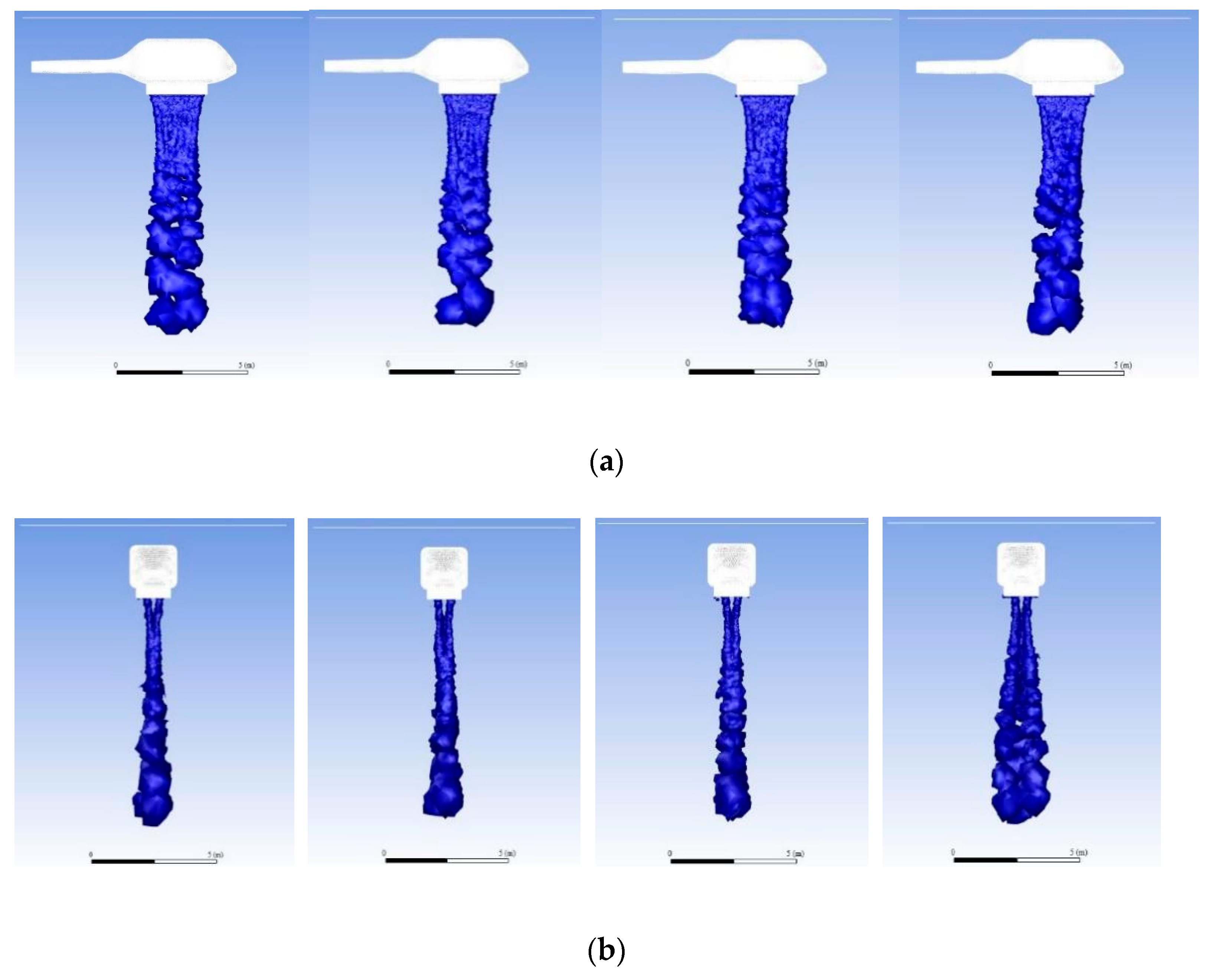
- There was no significant change in water mass distribution at wind speeds below 10 m/s, but when the wind speed rose to 15 m/s, the water masses deviated significantly in the wind direction and expanded significantly in the horizontal direction. Hence, the area covered by water on the ground increased significantly, and the average depth of water accumulated per unit area decreased significantly;
- (4)
- The higher the tank was above the ground, the greater the area covered by water on the ground, and the less the average depth of water accumulated per unit area. However, the results at a height of 10 m are significantly less pronounced than those at 20 m and 30 m, although the results at the latter two heights are relatively close to each other;
- (5)
- For forward flight, the higher the forward flight speed, the less the average depth of water on the ground; a similar relation held for flight height. The average depth of water was one order of magnitude less than in the cases of the corresponding hovering helicopter and the various wind speeds.
6. Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tymstra, C.; Stocks, B.J.; Cai, X.; Flannigan, M.D. Wildfire management in Canada: Review, challenges and opportunities. Prog. Disaster Sci. 2020, 5, 100045. [Google Scholar] [CrossRef]
- McWethy, D.B.; Schoennagel, T.; Higuera, P.E.; Krawchuk, M.; Harvey, B.J.; Metcalf, E.C.; Schultz, C.; Miller, C.; Metcalf, A.L.; Buma, B.; et al. Rethinking resilience to wildfire. Nat. Sustain. 2019, 2, 797–804. [Google Scholar] [CrossRef]
- Hessburg, P.F.; Prichard, S.J.; Hagmann, R.K.; Povak, N.A.; Lake, F.K. Wildfire and climate change adaptation of western North American forests: A case for intentional management. Ecol. Appl. 2021, 31, e02432. [Google Scholar] [CrossRef] [PubMed]
- Marchi, E.; Neri, F.; Tesi, E.; Fabiano, F.; Brachetti Montorselli, N. Analysis of helicopter activities in forest fire-fighting. Croat. J. For. Eng. J. Theory Appl. For. Eng. 2014, 35, 233–243. [Google Scholar]
- Kal’avský, P.; Petríček, P.; Kelemen, M.; Rozenberg, R.; Jevčák, J.; Tomaško, R.; Mikula, B. The efficiency of aerial firefighting in varying flying conditions. In Proceedings of the 2019 International Conference on Military Technologies (ICMT), Brno, Czech Republic, 30–31 May 2019; pp. 1–5. [Google Scholar]
- Hnilica, R.; Ťavodová, M.; Hnilicová, M.; Matej, J.; Messingerová, V. The Innovative Design of the Fire-Fighting Adapter for Forest Machinery. Forests 2020, 11, 843. [Google Scholar] [CrossRef]
- Legendre, D.; Becker, R.; Alméras, E.; Chassagne, A. Air tanker drop patterns. Int. J. Wildland Fire 2014, 23, 272–280. [Google Scholar] [CrossRef]
- Wu, Z.; Zhou, Y.; Zhen, X.; Li, X.; Zhang, Z.; Liu, J.; Jiang, X.; Wang, Z.; Guo, T.; Wu, Y.; et al. Research on efficiency of bucket water dump firefighting—Take K-32 helicopter for instance. Forest Fire Prev. 2017, 1, 4. (In Chinese) [Google Scholar]
- Ma, Y.; Ma, D. Application analysis of helicopter bucket firefighting in China forests. For. Labor Saf. 2013, 26, 4. (In Chinese) [Google Scholar]
- Chen, Z.; Wu, T. Comparison empirical analysis of helicopter forest firefighting methods. In Proceedings of the 2010 Transportation Graduate Academic Forum & Science and Technology Innovation Proceedings, Tianjin, China, 21 May 2010. [Google Scholar]
- Zhou, W. Applicability analysis of MI-26T helicopter in fighting against forest fire in southwest forest region. For. Fire Prev. 2007, 1. (In Chinese) [Google Scholar]
- Xie, Y.; Zhang, H.; Hu, M. Significance of introduction of K-32A helicopter and its application in forest fire prevention. For. Fire Prev. 2009, 1, 56–59. (In Chinese) [Google Scholar]
- Zhou, T.; Lu, J.; Wu, C.; Li, B.; Tan, Y.; Liu, L. Test and application of helicopter water dump firefighting of mountain fires on power transmission lines. High Volt. Eng. 2021, 47, 2811–2819. (In Chinese) [Google Scholar] [CrossRef]
- Solarz, P.; Jordan, C. Ground Pattern Performance of the LA County Bell S205 Helicopter with Sheetcraft Fixed Tank; United States Department of Agriculture Forest Service, Technology & Development Program, USDA Forest Service Missoula Technology and Development Center: Missoula, MT, USA, 2000; 0057-2863-MTDC.
- Biggs, H. An Evaluation of the Performance of the Simplex 304 Helicopter Belly-Tank; Research Report no. 71; Fire Management Division Department of Sustainability and Environment: Melbourne, Australia, 2004. [Google Scholar]
- Zhao, X.; Zhou, P.; Yan, X.; Weng, Y.; Yang, X.L. Numerical simulation of the aerial drop of water for fixed wing airtankers. In Proceedings of the 31st Congress of the International Council of the Aeronautic Sciences, Belo Horizonte, Brazil, 9–14 September 2018. [Google Scholar]
- Satoh, K.; Maeda, I.; Kuwahara, K.; Yang, K.T. A numerical study of water dump in aerial fire fighting. Fire Saf. Sci. 2005, 8, 777–787. [Google Scholar] [CrossRef]
- Borisov, I.V.; Tsipenko, A.V. Computing simulation for firefighting helicopter operation analysis. In Proceedings of the 29th Congress of the International Council of the Aeronautical Sciences, St. Petersburg, Russia, 7–12 September 2014. [Google Scholar]
- Kim, Y.-H.; Park, S.-O. Navier-Stokes simulation of unsteady rotor-airframe interaction with momentum source method. Int. J. Aeronaut. Space Sci. 2009, 10, 125–133. [Google Scholar] [CrossRef]
- Lacombe, F.; Pelletier, D.; Garon, A. Compatible wall functions and adaptive remeshing for the k-omega SST model. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019; p. 2329, AIAA 2020-2284. [Google Scholar]
- Balasubramanian, A.K.; Kumar, V.; Nakod, P.; Schütze, J.; Rajan, A. Multiscale modelling of a doublet injector using hybrid VOF-DPM method. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar]
- Sullivan, P.P.; McWilliams, J.C. Frontogenesis and frontal arrest of a dense filament in the oceanic surface boundary layer. J. Fluid Mech. 2018, 837, 341–380. [Google Scholar] [CrossRef]
- Eggers, J. Nonlinear dynamics and breakup of free-surface flows. Rev. Mod. Phys. 1997, 69, 865–930. [Google Scholar] [CrossRef]
- Sula, C.; Grosshans, H.; Papalexandris, M.V. Assessment of droplet breakup models for spray flow simulations. Flow Turbul. Combust. 2020, 105, 889–914. [Google Scholar] [CrossRef]
- Sazhin, S.S. Droplets and Sprays; Springer: London, UK, 2014. [Google Scholar]


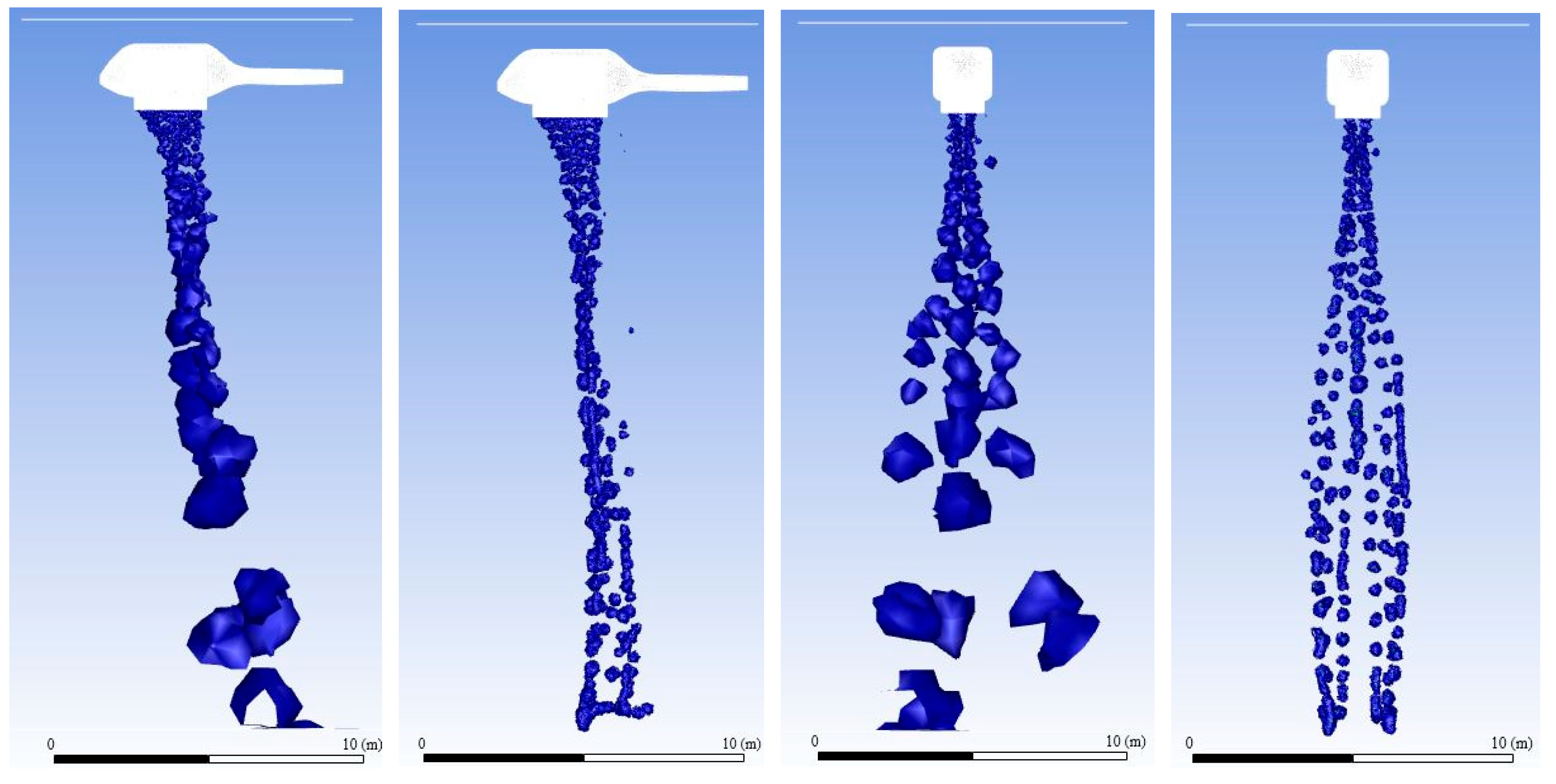







| Height of Tank bottom above the Ground/Wind Speed | 0 m/s | 5 m/s | 10 m/s | 15 m/s |
|---|---|---|---|---|
| 10 m | 2.4 m × 1.6 m = 3.84 m2 0.29 m water depth/m2 | 2.2 m × 1.7 m = 3.74 m2 0.30 m water depth/m2 | 2.1 m × 1.7 m = 3.57 m2 0.31 m water depth/m2 | 2.1 m × 2.5 m = 5.25 m2 0.21 m water depth/m2 |
| 20 m | 3.4 m × 3.0 m = 10.2 m2 0.11 m water depth/m2 | 3.2 m × 3.0 m = 9.6 m2 0.12 m water depth/m2 | 3.2 m × 3.2 m = 10.24 m2 0.11 m water depth/m2 | 4.0 m × 7.0 m = 28.0 m2 0.04 m water depth/m2 |
| 30 m | 2.9 m × 2.9 m = 8.41 m2 0.13 m water depth/m2 | 3.0 m × 3.0 m = 9.0 m2 0.12 m water depth/m2 | 3.0 m × 3.0 m = 9.0 m2 0.12 m water depth/m2 | 5.0 m × 9.0 m = 45.0 m2 0.025 m water depth/m2 |
| Height of the Tank bottom above the Ground/Forward Flight Speed | 5 m/s | 10 m/s | 15 m/s |
|---|---|---|---|
| 10 m | 5 × 1.2 × 1.7 = 10.2 m2 0.11 m water depth/m2 | 10 × 1.2 × 1.7 = 20.4 m2 0.055 m water depth/m2 | 15 × 1.2 × 2.5 = 45 m2 0.025 m water depth/m2 |
| 20 m | 5 × 2.0 × 3.0 = 30 m2 0.037 m water depth/m2 | 10 × 2.0 × 3.2 = 64 m2 0.0175 m water depth/m2 | 15 × 2.0 × 7.0 = 210 m2 0.005 m water depth/m2 |
| 30 m | 5 × 2.5 × 3.0 = 37.5 m2 0.03 m water depth/m2 | 10 × 2.5 × 3.2 = 80 m2 0.014 m water depth/m2 | 15 × 2.5 × 9.0 = 337.5 m2 0.003 m water depth/m2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, T.; Lu, J.; Wu, C.; Lan, S. Numerical Calculation and Analysis of Water Dump Distribution Out of the Belly Tanks of Firefighting Helicopters. Safety 2022, 8, 69. https://doi.org/10.3390/safety8040069
Zhou T, Lu J, Wu C, Lan S. Numerical Calculation and Analysis of Water Dump Distribution Out of the Belly Tanks of Firefighting Helicopters. Safety. 2022; 8(4):69. https://doi.org/10.3390/safety8040069
Chicago/Turabian StyleZhou, Tejun, Jiazheng Lu, Chuanping Wu, and Shilong Lan. 2022. "Numerical Calculation and Analysis of Water Dump Distribution Out of the Belly Tanks of Firefighting Helicopters" Safety 8, no. 4: 69. https://doi.org/10.3390/safety8040069
APA StyleZhou, T., Lu, J., Wu, C., & Lan, S. (2022). Numerical Calculation and Analysis of Water Dump Distribution Out of the Belly Tanks of Firefighting Helicopters. Safety, 8(4), 69. https://doi.org/10.3390/safety8040069






