Decision-Making Processes Underlying Pedestrian Behaviors at Signalized Crossings: Part 2. Do Pedestrians Show Cultural Herding Behavior?
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Sites
2.2. Data Scoring
2.3. Research Ethics
2.4. Data Analysis
- —
- The light color when crossing (red or green).
- —
- The departure time, ΔTj, i.e., the period between the previous light color change and the moment the pedestrian j starts crossing the road. This variable is positive for pedestrians crossing after the light (for pedestrians) has turned red but negative for pedestrians crossing before the light turns red.
- —
- The departure latency ΔTj,j−1, i.e., the time elapsed between the departure of pedestrian j and previous pedestrian j−1.
- —
- The departure order of pedestrians, where the first pedestrian to leave the kerb is ranked as 1, the second as 2, and so on. Here, we then focused on pedestrians of ranks 2 to n, n being the number of following pedestrians in a crossing event, with a maximum threshold set at n = 10.
- —
- The gender (male or female).
- —
- The age, estimated at 10-year intervals from 0–9, 10–19, …, to 80–89. However, given the number of data and the analyses we carried out, it was not possible to analyze the effect of age (per interval) on the decision-making processes. Indeed, the number of pedestrians below 20 and above 60 years old was not sufficient to calculate mean departure latencies per pedestrian crossing rank (less than about 3 data per age category per rank).
- —
- The country (France or Japan).
- —
- The waiting time, i.e., the time between the moment a pedestrian stops at the light and the moment he/she starts crossing the road.
2.5. Mathematical Analyses
2.6. Modelling
- i.
- Independence hypothesis
- ii.
- Mimetic process hypothesis
2.7. Statistical Analyses
3. Results
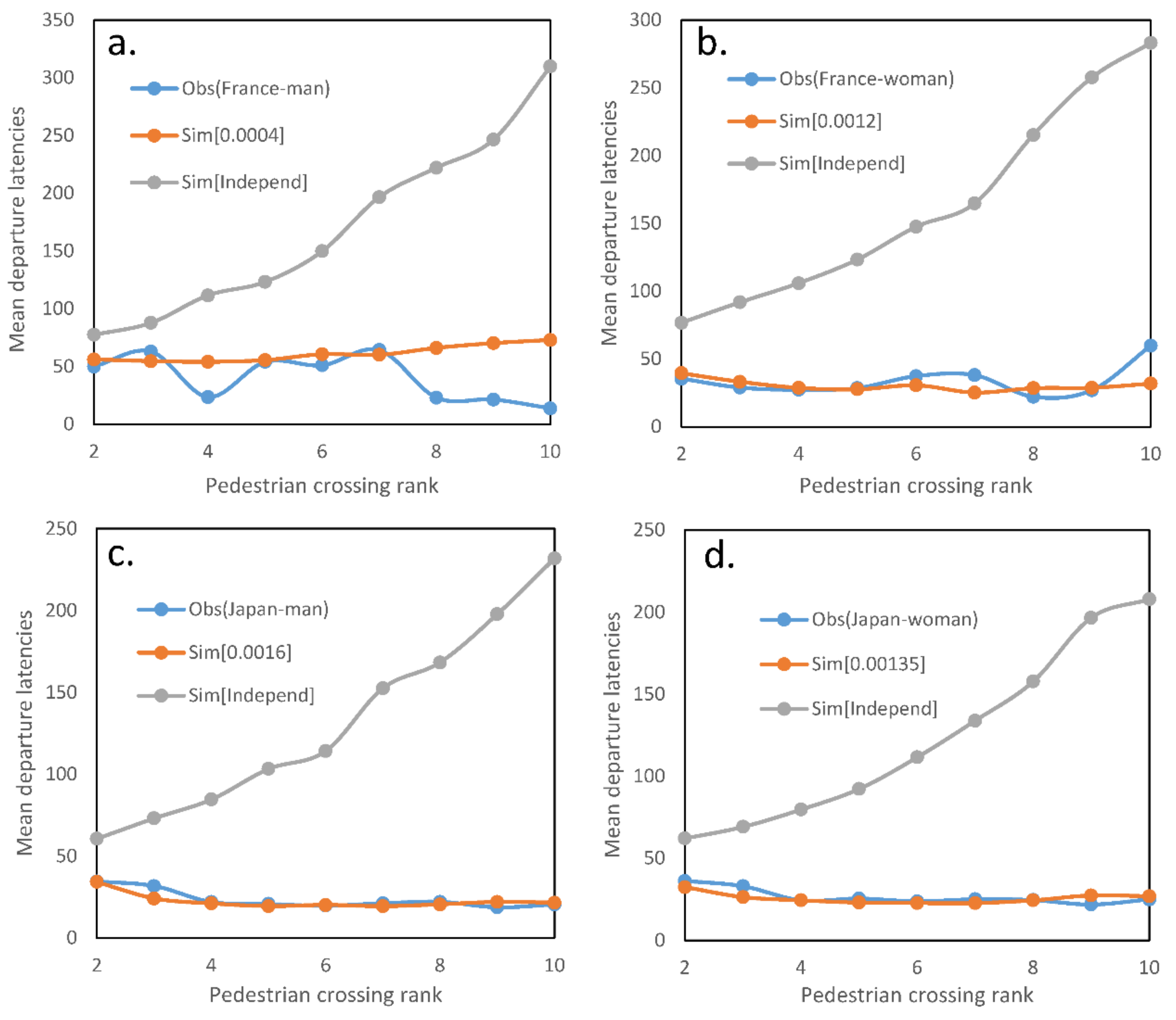
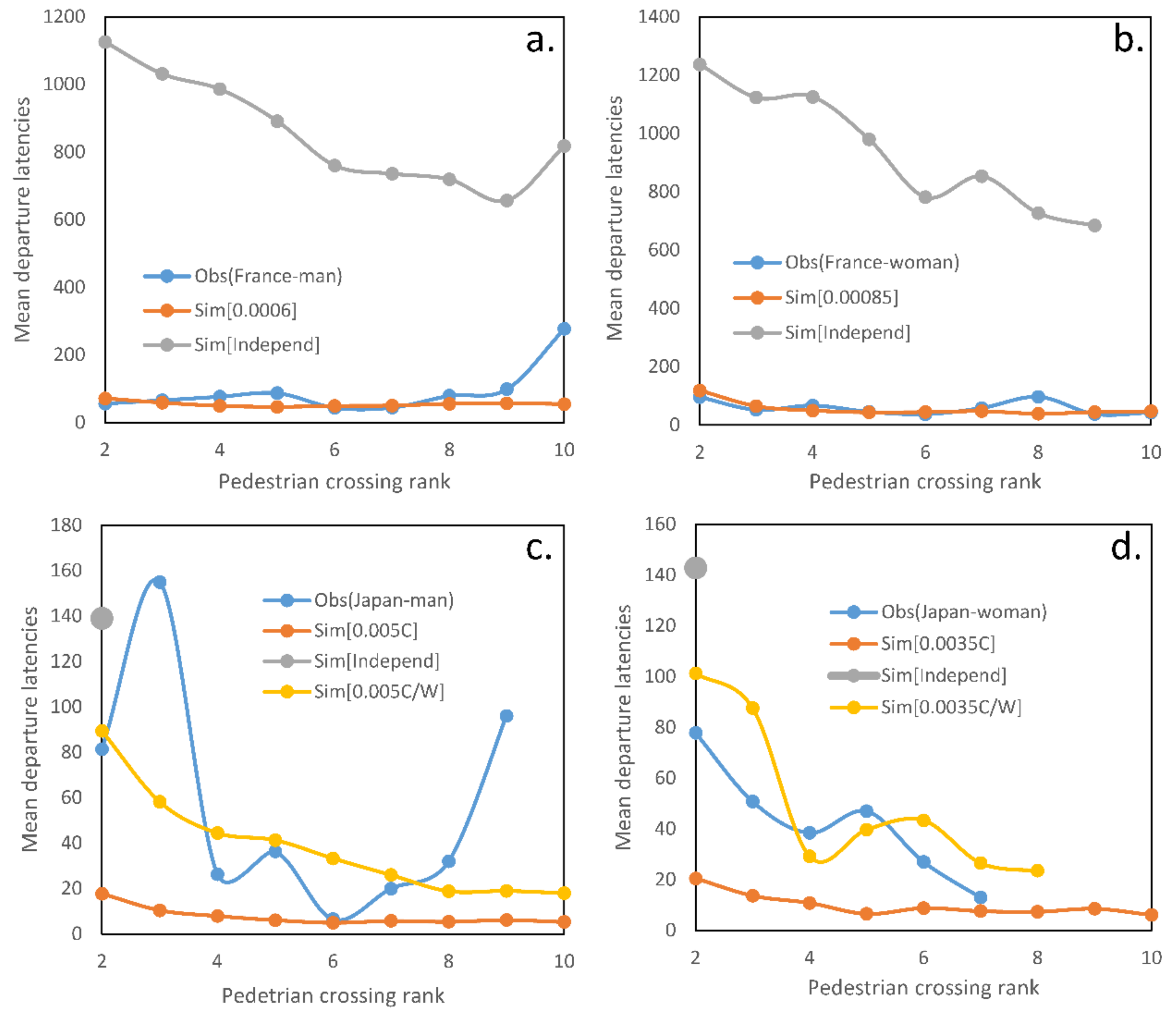
3.1. Analyses of Departure Latencies According to Pedestrian Departure Rank
3.2. Comparison between Observed Crossing and Simulated Crossing
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Twain, M. What is Man? And Other Philosophical Writings; University of California Press: London, UK, 1973; p. 62. [Google Scholar]
- Haghani, M.; Sarvi, M. Following the crowd or avoiding it? Empirical investigation of imitative behaviour in emergency escape of human crowds. Anim. Behav. 2017, 124, 47–56. [Google Scholar] [CrossRef]
- Helbing, D.; Farkas, I.; Vicsek, T. Simulating dynamical features of escape panic. Nature 2000, 407, 487–490. [Google Scholar] [CrossRef] [PubMed]
- Helbing, D.; Schweitzer, F.; Keltsch, J.; Molnár, P. Active walker model for the formation of human and animal trail systems. Phys. Rev. E 1997, 56, 2527. [Google Scholar] [CrossRef]
- Mawson, A.R. Understanding Mass Panic and Other Collective Responses to Threat and Disaster. Psychiatry Interpers. Biol. Process. 2005, 68, 95–113. [Google Scholar] [CrossRef] [PubMed]
- Dyer, J.R.G.; Johansson, A.; Helbing, D.; Couzin, I.D.; Krause, J. Leadership, consensus decision making and collective behaviour in humans. Philos. Trans. R. Soc. B Biol. Sci. 2009, 364, 781–789. [Google Scholar] [CrossRef] [PubMed]
- Kurvers, R.H.J.M.; Wolf, M.; Naguib, M.; Krause, J. Self-organized flexible leadership promotes collective intelligence in human groups. Open Sci. 2015, 2, 150222. [Google Scholar] [CrossRef] [PubMed]
- King, A.J.; Johnson, D.D.P.; Van Vugt, M. The Origins and Evolution of Leadership. Curr. Biol. 2009, 19, R911–R916. [Google Scholar] [CrossRef] [PubMed]
- Van Vugt, M.; Hogan, R.; Kaiser, R.B. Leadership, followership, and evolution: Some lessons from the past. Am. Psychol. 2008, 63, 182–196. [Google Scholar] [CrossRef] [PubMed]
- Faralla, V.; Innocenti, A.; Venturini, E. Risk Taking and Social Exposure; Social Science Research Network: Rochester, NY, USA, 2013. [Google Scholar]
- Sueur, C.; Class, B.; Hamm, C.; Meyer, X.; Pelé, M. Different risk thresholds in pedestrian road crossing behaviour: A comparison of French and Japanese approaches. Accid. Anal. Prev. 2013, 58, 59–63. [Google Scholar] [CrossRef] [PubMed]
- Faria, J.J.; Krause, S.; Krause, J. Collective behavior in road crossing pedestrians: The role of social information. Behav. Ecol. 2010, 21, 1236–1242. [Google Scholar] [CrossRef]
- Gould, J.P. Risk, stochastic preference, and the value of information. J. Econ. Theory 1974, 8, 64–84. [Google Scholar] [CrossRef]
- Lipovac, K.; Vujanic, M.; Maric, B.; Nesic, M. The influence of a pedestrian countdown display on pedestrian behavior at signalized pedestrian crossings. Transp. Res. Part F Traffic Psychol. Behav. 2013, 20, 121–134. [Google Scholar] [CrossRef]
- Pelé, M.; Bellut, C.; Debergue, E.; Gauvin, C.; Jeanneret, A.; Leclere, T.; Nicolas, L.; Pontier, F.; Zausa, D.; Sueur, C. Cultural influence of social information use in pedestrian road-crossing behaviours. Open Sci. 2017, 4, 160739. [Google Scholar] [CrossRef] [PubMed]
- Boos, M.; Pritz, J.; Lange, S.; Belz, M. Leadership in Moving Human Groups. PLoS Comput. Biol. 2014, 10, e1003541. [Google Scholar] [CrossRef]
- Faria, J.J.; Dyer, J.R.G.; Tosh, C.R.; Krause, J. Leadership and social information use in human crowds. Anim. Behav. 2010, 79, 895–901. [Google Scholar] [CrossRef]
- Katsikopoulos, K.V.; King, A.J. Swarm Intelligence in Animal Groups: When Can a Collective Out-Perform an Expert? PLoS ONE 2010, 5, e15505. [Google Scholar] [CrossRef] [PubMed]
- Lewis, J.; Wartzok, D.; Heithaus, M. Individuals as information sources: Could followers benefit from leaders’ knowledge? Behaviour 2013, 150, 635–657. [Google Scholar] [CrossRef]
- Rosenbloom, T. Crossing at a red light: Behaviour of individuals and groups. Transp. Res. Part F Traffic Psychol. Behav. 2009, 12, 389–394. [Google Scholar] [CrossRef]
- Camazine, S.; Deneubourg, J.-L.; Franks, N.R.; Sneyd, J.; Theraula, G.; Bonabeau, E. Self-Organization in Biological Systems; Princeton University Press: Princeton, NJ, USA, 2003; ISBN 978-0-691-11624-2. [Google Scholar]
- Sueur, C.; Deneubourg, J.-L. Self-Organization in Primates: Understanding the Rules Underlying Collective Movements. Int. J. Primatol. 2011, 32, 1413–1432. [Google Scholar] [CrossRef]
- Hung, A.A.; Plott, C.R. Information cascades: Replication and an extension to majority rule and conformity-rewarding institutions. Am. Econ. Rev. 2001, 91, 1508–1520. [Google Scholar] [CrossRef]
- Osman, L.M. Conformity or compliance? A study of sex differences in pedestrian behaviour. Br. J. Soc. Psychol. 1982, 21, 19–21. [Google Scholar] [CrossRef]
- Powell, M.; Ansic, D. Gender differences in risk behaviour in financial decision-making: An experimental analysis. J. Econ. Psychol. 1997, 18, 605–628. [Google Scholar] [CrossRef]
- Tom, A.; Granié, M.-A. Gender differences in pedestrian rule compliance and visual search at signalized and unsignalized crossroads. Accid. Anal. Prev. 2011, 43, 1794–1801. [Google Scholar] [CrossRef] [PubMed]
- Centola, D.; Baronchelli, A. The spontaneous emergence of conventions: An experimental study of cultural evolution. Proc. Natl. Acad. Sci. USA 2015, 7. [Google Scholar] [CrossRef] [PubMed]
- Ito, Y. Socio-cultural backgrounds of Japanese interpersonal communication style. Civilisations 1989, 39, 101–128. [Google Scholar] [CrossRef]
- Lee, S.M.; Lim, S.; Pathak, R.D. Culture and entrepreneurial orientation: A multi-country study. Int. Entrep. Manag. J. 2011, 7, 1–15. [Google Scholar] [CrossRef]
- Mihet, R. Effects of Culture on Firm Risk-Taking: A Cross-Country and Cross-Industry Analysis; International Monetary Fund: Washington, DC, USA, 2012. [Google Scholar]
- Czaczkes, T.J.; Czaczkes, B.; Iglhaut, C.; Heinze, J. Composite collective decision-making. Proc. R. Soc. B 2015, 282. [Google Scholar] [CrossRef] [PubMed]
- Pelé, M.; Sueur, C. Decision-making theories: Linking the disparate research areas of individual and collective cognition. Anim. Cogn. 2013, 16, 543–556. [Google Scholar] [CrossRef] [PubMed]
- Miller, R.G.; Gong, G.; Muñoz, A. Survival Analysis; John Wiley & Sons: Hoboken, NJ, USA, 1981. [Google Scholar]
- Aoyagi, S.; Hayashi, R.; Nagai, M. Modeling of Pedestrian Behavior in Crossing Urban Road for Risk Prediction Driving Assistance System; SAE International: Warrendale, PA, USA, 2011. [Google Scholar]
- Papadimitriou, E. Theory and models of pedestrian crossing behaviour along urban trips. Transp. Res. Part F Traffic Psychol. Behav. 2012, 15, 75–94. [Google Scholar] [CrossRef]
- Sueur, C.; Perony, N.; Amblard, F.; Guillaume, J.-L. Modélisation des réseaux sociaux. In Analyse des Réseaux Sociaux Appliquée à l’Ethologie et à l’Ecologie; Editions Matériologiques: Paris, France, 2015; pp. 423–444. [Google Scholar]
- Epstein, J.M. Why Model? Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Sueur, C.; Petit, O.; Deneubourg, J. Selective mimetism at departure in collective movements of Macaca tonkeana: An experimental and theoretical approach. Anim. Behav. 2009, 78, 1087–1095. [Google Scholar] [CrossRef]
- Brewer, M.; Fitzpatrick, K.; Whitacre, J.; Lord, D. Exploration of Pedestrian Gap-Acceptance Behavior at Selected Locations. Transp. Res. Rec. J. Transp. Res. Board 2006, 1982, 132–140. [Google Scholar] [CrossRef]
- Jiang, N.; Shi, M.; Xiao, Y.; Shi, K.; Watson, B. Factors Affecting Pedestrian Crossing Behaviors at Signalized Crosswalks in Urban Areas in Beijing and Singapore; ASCE Library: Reston, VA, USA, 2011; pp. 1090–1097. [Google Scholar]
- King, M.J.; Soole, D.; Ghafourian, A. Illegal pedestrian crossing at signalised intersections: Incidence and relative risk. Accid. Anal. Prev. 2009, 41, 485–490. [Google Scholar] [CrossRef] [PubMed]
- Sueur, C. Viability of decision-making systems in human and animal groups. J. Theor. Biol. 2012, 306, 93–103. [Google Scholar] [CrossRef] [PubMed]
- Pillot, M.-H.; Gautrais, J.; Arrufat, P.; Couzin, I.D.; Bon, R.; Deneubourg, J.-L. Scalable Rules for Coherent Group Motion in a Gregarious Vertebrate. PLoS ONE 2011, 6, e14487. [Google Scholar] [CrossRef] [PubMed]
- Pillot, M.-H.; Deneubourg, J.-L. Collective movements, initiation and stops: Diversity of situations and law of parsimony. Behav. Process. 2010, 84, 657–661. [Google Scholar] [CrossRef] [PubMed]
- Yannis, G.; Papadimitriou, E.; Theofilatos, A. Pedestrian gap acceptance for mid-block street crossing. Transp. Plan. Technol. 2013, 36, 450–462. [Google Scholar] [CrossRef]
- Pelé, M.; Deneubourg, J.-L.; Sueur, C. Decision-Making Processes Underlying Pedestrian Behaviors at Signalized Crossing: Part the First to Step off the Kerb. Safety 2019, 5, 79. [Google Scholar] [CrossRef]
- Fernandez, A.A.; Deneubourg, J.L. On following behaviour as a mechanism for collective movement. J. Theor. Biol. 2011, 284, 7–15. [Google Scholar] [CrossRef] [PubMed]
- King, A.J.; Cowlishaw, G. Leaders, followers and group decision-making. Integr. Commun. Biol. 2009, 2, 147–150. [Google Scholar] [CrossRef] [PubMed]
- Klein, J.P.; Goel, P.K. Survival Analysis: State of the Art; Springer: Berlin/Heidelberg, Germany, 1992; ISBN 978-0-7923-1634-3. [Google Scholar]
- Gautrais, J.; Michelena, P.; Sibbald, A.; Bon, R.; Deneubourg, J.-L. Allelomimetic synchronization in Merino sheep. Anim. Behav. 2007, 74, 1443–1454. [Google Scholar] [CrossRef]
- Amé, J.-M.; Halloy, J.; Rivault, C.; Detrain, C.; Deneubourg, J.L. Collegial decision making based on social amplification leads to optimal group formation. Proc. Natl. Acad. Sci. USA 2006, 103, 5835–5840. [Google Scholar] [CrossRef] [PubMed]
- Sober, E. The Principle of Parsimony. Br. J. Philos. Sci. 1981, 32, 145–156. [Google Scholar] [CrossRef]
- Sklar, E. NetLogo, a Multi-agent Simulation Environment. Artif. Life 2007, 13, 303–311. [Google Scholar] [CrossRef] [PubMed]
- Cioffi-Revilla, C. Invariance and universality in social agent-based simulations. Proc. Natl. Acad. Sci. USA 2002, 99, 7314–7316. [Google Scholar] [CrossRef] [PubMed]
- Wilensky, U.; Rand, W. An Introduction to Agent-Based Modeling: Modeling Natural, Social, and Engineered Complex Systems with NetLogo; MIT Press: Cambridge, MA, USA, 2015; ISBN 978-0-262-73189-8. [Google Scholar]
- Lachapelle, U.; Cloutier, M.-S. On the complexity of finishing a crossing on time: Elderly pedestrians, timing and cycling infrastructure. Transp. Res. Part Policy Pract. 2017, 96, 54–63. [Google Scholar] [CrossRef]
- Holland, C.; Hill, R. The effect of age, gender and driver status on pedestrians’ intentions to cross the road in risky situations. Accid. Anal. Prev. 2007, 39, 224–237. [Google Scholar] [CrossRef] [PubMed]
- Banerjee, A.V. A Simple Model of Herd Behavior. Q. J. Econ. 1992, 107, 797–817. [Google Scholar] [CrossRef]
- Bikhchandani, S.; Hirshleifer, D.; Welch, I. A Theory of Fads, Fashion, Custom, and Cultural Change as Informational Cascades. J. Polit. Econ. 1992, 100, 992–1026. [Google Scholar] [CrossRef]
- Chen, Y.-F. Herd behavior in purchasing books online. Comput. Hum. Behav. 2008, 24, 1977–1992. [Google Scholar] [CrossRef]
- Hirshleifer, D.; Hong Teoh, S. Herd Behaviour and Cascading in Capital Markets: A Review and Synthesis. Eur. Financ. Manag. 2003, 9, 25–66. [Google Scholar] [CrossRef]
- Raafat, R.M.; Chater, N.; Frith, C. Herding in humans. Trends Cogn. Sci. 2009, 13, 420–428. [Google Scholar] [CrossRef] [PubMed]
- Couzin, I.D.; Krause, J. Self-Organization and Collective Behavior in Vertebrates; Academic Press: Cambridge, MA, USA, 2003; Volume 32, pp. 1–75. ISBN 0065-3454. [Google Scholar]
- King, A.J.; Sueur, C. Where Next? Group Coordination and Collective Decision Making by Primates. Int. J. Primatol. 2011, 32, 1245–1267. [Google Scholar] [CrossRef]
- Krause, J.; Ruxton, G.D. Living in Groups; Oxford University Press: Oxford, UK, 2002; ISBN 978-0-19-850818-2. [Google Scholar]
- Benedict, R. The Chrysanthemum and the Sword: Patterns of Japanese Culture; Houghton Mifflin Harcourt: Boston, MA, USA, 2005; ISBN 978-0-618-61959-7. [Google Scholar]
- Lebra, T.S.; Lebra, W.P. Japanese Culture and Behavior: Selected Readings; University of Hawaii Press: Honolulu, HI, USA, 1986; ISBN 978-0-8248-1055-9. [Google Scholar]
- Chinese “Jaywalker Catcher” Sprays Unruly Pedestrians with WATER. Available online: http://www.dailymail.co.uk/news/article-5635117/Chinas-latest-jaywalker-catcher-humiliates-pedestrians-spray-WATER-road-crossings.html (accessed on 5 November 2019).
| Information Type | France-Strasbourg | |||
| Sites | Train Station | Pont des Corbeaux | Place Broglie | |
| Coordinates | 48.584474, 7.736135 | 48.579509, 7.750745 | 48.584559, 7.748628 | |
| Lanes | 2 * 1 | 2 * 2 | 2 * 1 | |
| Mean pedestrian flow per h | 667 | 612 | 850 | |
| Mean road-crossing speed (m.s−1) | 0.96 ± 0.05 | 1.11 ± 0.29 | 1.01 ± 0.16 | |
| Data collection dates | 2–7 July 2014 | 1–25 October 2014 | 15 February–9 March 2015 | |
| Information Type | Japan-Nagoya | |||
| Sites | Train Station | Maruei | Excelco | Osu-Kannon |
| Coordinates | 35.170824, 136.884328 | 35.168638, 136.905740 | 35.166891, 136.907284 | 35.159316, 136.901697 |
| Lanes | 2 * 3 | 1 * 1 | 2 * 1 | 2 * 1 |
| Mean pedestrian flow per h | 480 | 645 | 869 | 814 |
| Mean road-crossing speed (m.s−1) | 1.10 ± 0.22 | 1.15 ± 0.21 | 0.98 ± 0.21 | 1.07 ± 0.18 |
| Data collection dates | 13 June–5 July 2011 | 27 January–5 February 2015 | ||
| Light Color | Country | Gender | D | ψ01 | Range of Calculated C | Best C | Crossing Rule |
|---|---|---|---|---|---|---|---|
| Green | France | Man | 98 | 0.013 | 0.0001–0.0026 | 0.0006 | Crossing |
| Green | France | Woman | 130 | 0.013 | 0.0005–0.0031 | 0.0012 | Crossing |
| Green | Japan | Man | 638 | 0.016 | 0.0006–0.0026 | 0.0016 | Crossing |
| Green | Japan | Woman | 972 | 0.017 | 0.0004–0.0031 | 0.00135 | Crossing |
| Red | France | Man | 290 | 0.0008 | 0.00047–0.0006 | 0.0005 | Crossing |
| Red | France | Woman | 384 | 0.0006 | 0.00083–0.0002 | 0.0008 | Crossing |
| Red | Japan | Man | 35 | 0.0003 | 0.0056–0.011 | 0.005 | Crossing/Waiting |
| Red | Japan | Woman | 22 | 0.0003 | 0.0021–0.0032 | 0.005 | Crossing/Waiting |
| Country | Gender | Green Light | Red Light | ||||
|---|---|---|---|---|---|---|---|
| df | F | p | df | F | p | ||
| France | Man | 7 | 2.79 | 0.139 | 7 | 15.37 | 0.006 |
| France | Woman | 7 | 4.01 | 0.08 | 7 | 1.448 | 0.268 |
| Japan | Man | 7 | 42.02 | 0.0003 | 7 | 5.93 | 0.026 |
| Japan | Woman | 7 | 40.1 | 0.0004 | 4 | 7.81 | 0.039 |
| Hypotheses | France | Japan | ||
|---|---|---|---|---|
| men | women | men | women | |
| Observed | 0.46 | 0.38 | 0.02 | 0.02 |
| Independence hyp. | 0.24 | 0.19 | 0.0006 | 0.001 |
| Mimetic hyp. (C) | 0.50 | 0.50 | 0.12 | 0.04 |
| Mimetic hyp. (C/W) | NA | NA | 0.02 | 0.02 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pelé, M.; Deneubourg, J.-L.; Sueur, C. Decision-Making Processes Underlying Pedestrian Behaviors at Signalized Crossings: Part 2. Do Pedestrians Show Cultural Herding Behavior? Safety 2019, 5, 82. https://doi.org/10.3390/safety5040082
Pelé M, Deneubourg J-L, Sueur C. Decision-Making Processes Underlying Pedestrian Behaviors at Signalized Crossings: Part 2. Do Pedestrians Show Cultural Herding Behavior? Safety. 2019; 5(4):82. https://doi.org/10.3390/safety5040082
Chicago/Turabian StylePelé, Marie, Jean-Louis Deneubourg, and Cédric Sueur. 2019. "Decision-Making Processes Underlying Pedestrian Behaviors at Signalized Crossings: Part 2. Do Pedestrians Show Cultural Herding Behavior?" Safety 5, no. 4: 82. https://doi.org/10.3390/safety5040082
APA StylePelé, M., Deneubourg, J.-L., & Sueur, C. (2019). Decision-Making Processes Underlying Pedestrian Behaviors at Signalized Crossings: Part 2. Do Pedestrians Show Cultural Herding Behavior? Safety, 5(4), 82. https://doi.org/10.3390/safety5040082






