Reducing Data Uncertainties: Fuzzy Real-Time Safety Level Methodology for Socio-Technical Systems
Abstract
1. Introduction
2. Related Work
3. Methods
3.1. STAMP/STPA
3.2. EWaSAP
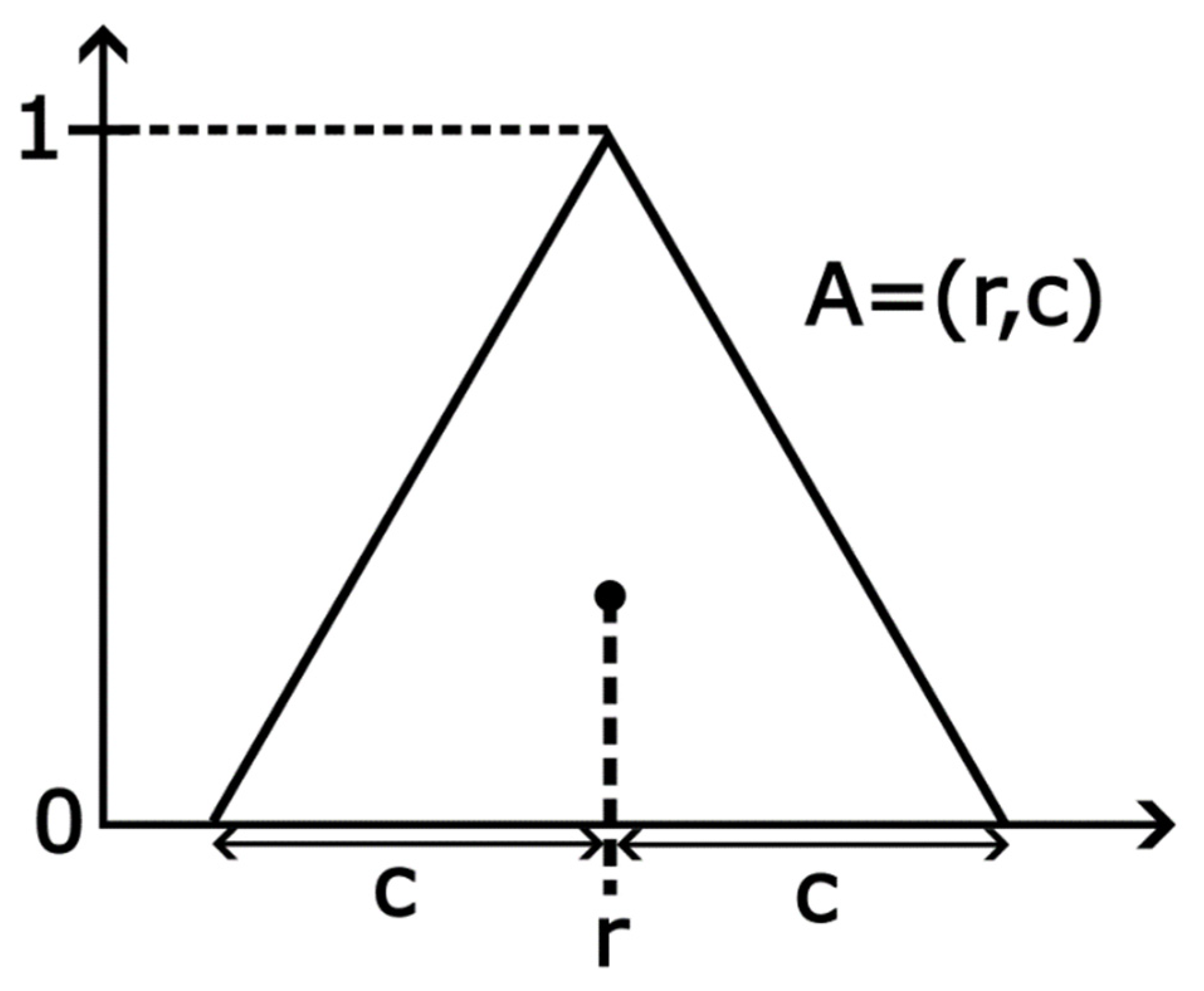
3.3. Fuzzy Logic
- Handling linguistic variables. Fuzzy logic allows for the representation and manipulation of linguistic variables, which are subjective and qualitative in nature. This enables experts to express and reason with imprecise concepts and knowledge that cannot be modelled effectively with probabilistic quantification.
- Dealing with imprecision. Fuzzy logic provides a framework for managing imprecision and vagueness in data and knowledge. Instead of requiring precise numerical values, fuzzy logic assigns degrees of membership to fuzzy sets, accommodating gradual transitions and overlapping boundaries.
- Robustness to noise and incomplete data. Fuzzy logic can effectively handle noisy or incomplete data by providing a smooth and flexible representation. It can accommodate uncertain or missing information, making it suitable for real-world applications where data may be limited or unreliable.
- Intuitive reasoning. Fuzzy logic offers intuitive reasoning capabilities by allowing the use of linguistic rules and fuzzy inference. This makes it easier for humans to understand, interpret, and contribute to decision-making processes.
- Integration with expert knowledge. Fuzzy logic allows for the incorporation of expert knowledge and heuristics into the system. Experts can contribute their domain expertise by defining fuzzy sets, membership functions, and rules, enhancing the system’s performance and adaptability.
4. RealTSL and Fuzzy RealTSL
4.1. RealTSL
4.1.1. RealTSL Mathematical Model
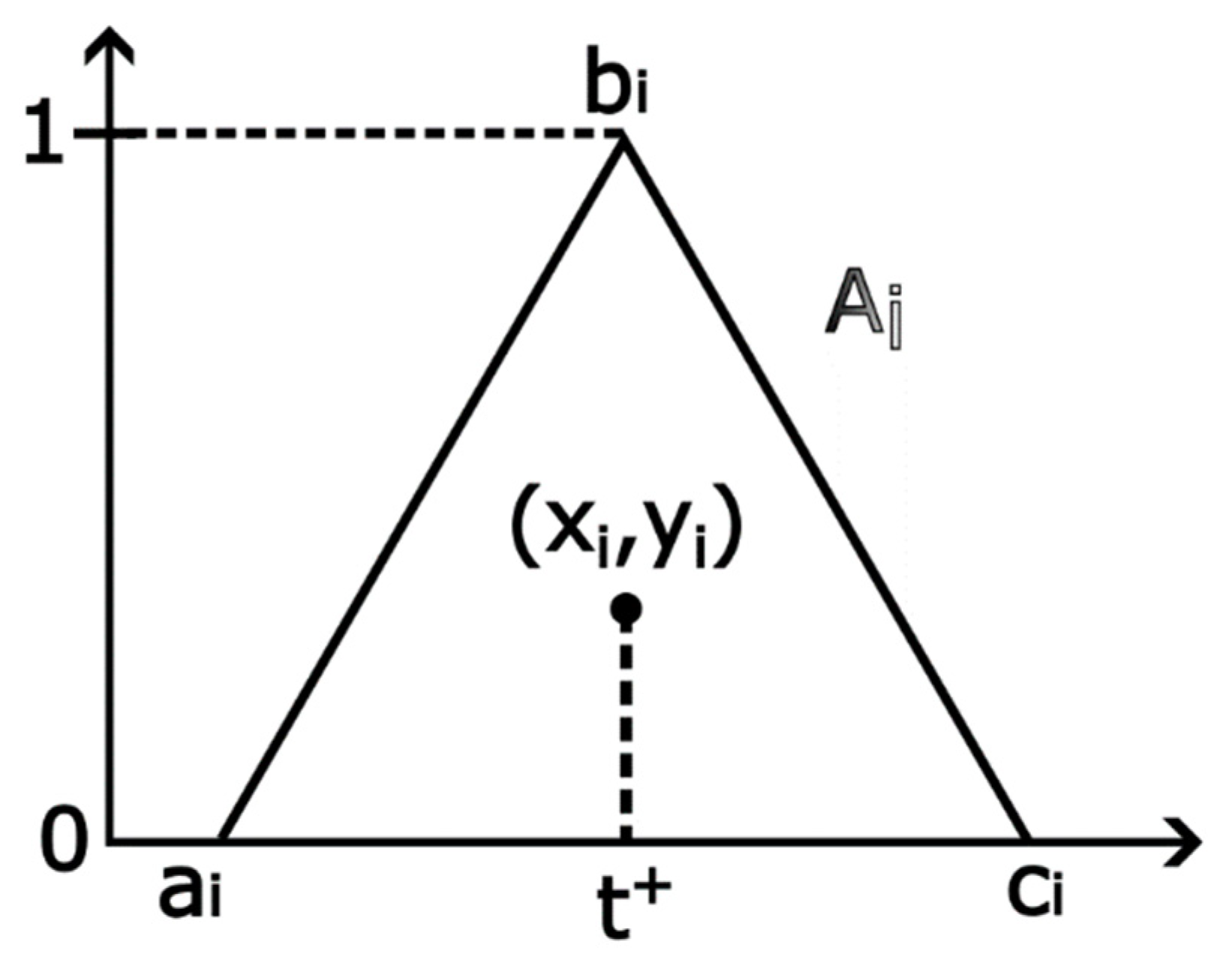
4.2. Fuzzy RealTSL
5. Case Study
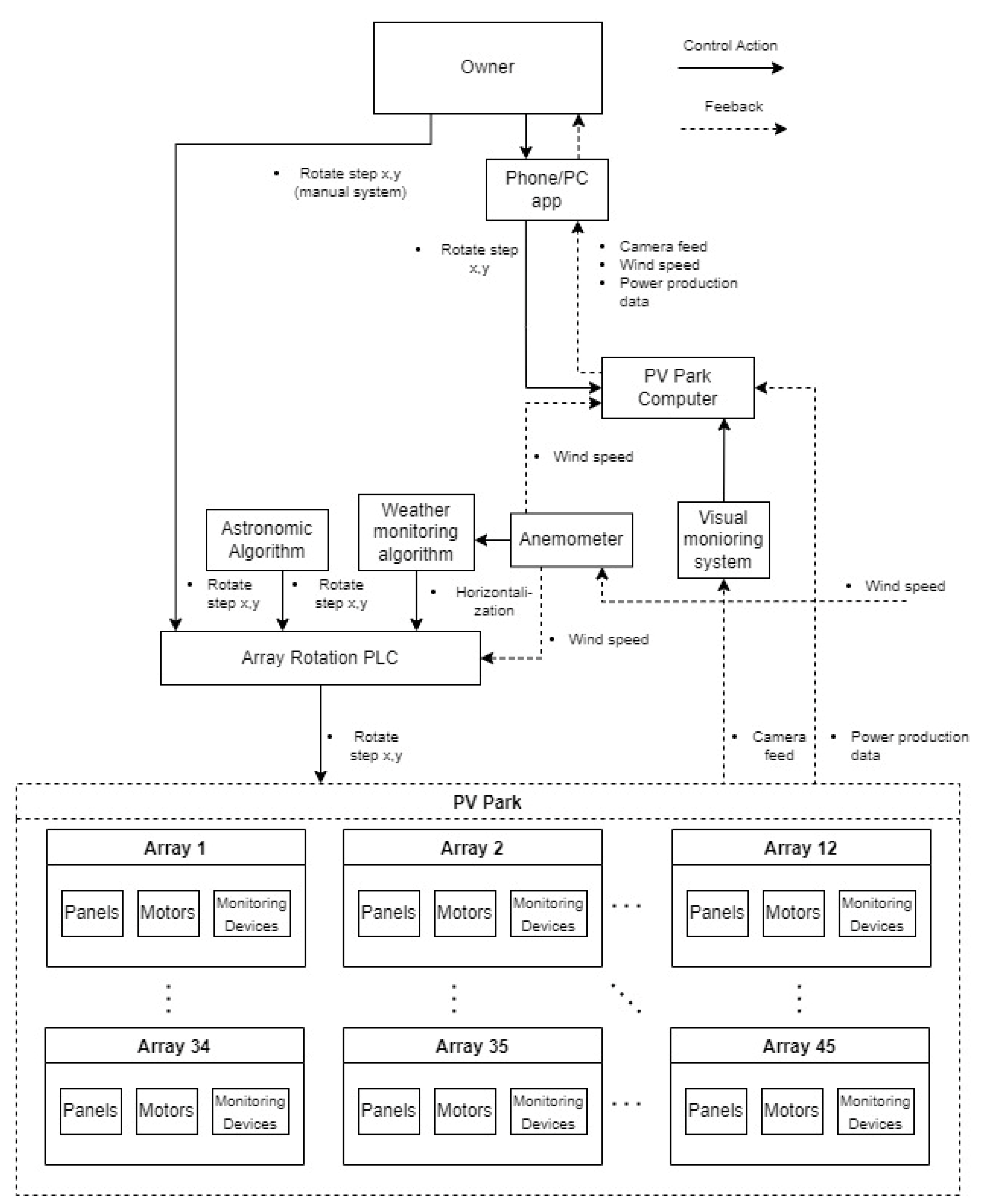
5.1. System Description
- It has 45 arrays, each one containing: ≃18 PV panels;
- It has two electric motors for lateral and longitudinal movement in each array;
- One programmable logic controller that houses the astronomical and weather monitoring algorithms.
- There is one switch box that limits each array’s movement individually to obtain the optimal position against the sun and avoid potentially rotating arrays in unexpected ways. This is achieved without software, as the switch box just cuts power to the motors of each array in case one tries to rotate in an unwanted position.
- One sensor data recorder that records the data from the various sensors positioned on the array.
- Fire detection and suppression system.
- Surveillance system with cameras that have a complete view of the park.
- Power transformer that inverts the direct current generated by the array to alternating current to be transported through the power grid.
- An anemometer for weather measurements.
- A storage room for housing the park’s main computer, manual array alignment controller and other electrical systems as well as storing maintenance equipment and extra components.
5.2. STPA
5.2.1. First Step
5.2.2. Second Step of STPA
5.2.3. Third Step of STPA
- SC-5-UCA-1: Sequence of “Rotate step x,y” CAs should be provided by the owner when one or more arrays are not positioned with proper alignment.
- SC-10-UCA-6: When the array is positioned with proper alignment “Rotate step x,y” CAs should not be provided by the owner and the astronomical algorithm.
- SC-19-UCA-19: “Rotate step x,y” CAs should not be provided by the astronomical algorithm too late after the sun has moved too far such that one time step movement would not place the array in the position at which the PV panels generate electricity optimally.
5.2.4. Fourth Step of STPA
- LS 5 (loss scenario) for UCA-1: The owner does not have access to the phone/pc app and is in a remote location.
- LS 7 for UCA-1: The owner does not have access to the phone/pc app and the temperature of the computer room, or the surrounding area is too hot; it may not be safe for the owner to manually adjust the arrays.
- LS 13 for UCA-1: The owner is in a remote location and their phone or pc are receiving software updates.
- LS 16 for UCA-6: The camera feed is stuck showing the park in a previous time and the owner believes that the arrays are out of proper alignment.
- LS 18 for UCA-19: The clock used by the astronomical algorithm runs out of battery, causing the astronomical algorithm to provide erratic control actions.
- LS 19 for UCA-19: The clock used by the astronomical algorithm malfunctions, causing the astronomical algorithm to provide erratic control actions.
- SC-28-S5-UCA-1: The owner should be near a phone or pc with the app installed at all times.
- SC-32-S7-UCA-1: The park’s computer room should have adequate cooling (through large windows, fans, or an AC unit).
- SC-41-S13-UCA-1: The owner should check if updates are available for their phone and PC. They should also update their devices after they have checked into the park or while at the park.
- SC-46-S16-UCA-6: The camera feed should have a time stamp so the owner will be able to check if the time on the visual feed matches the current time.
- SC-47-S16-UCA-6: The owner should also check the power production data for discrepancies when checking the park’s camera feeds.
- SC-48-S18-UCA-19: A notification system should be in place to notify the owner, technician, and park maintenance staff when the clock battery used by the astronomical algorithm reaches 10 percent.
- SC-49-S19-UCA-19: A system should be in place that checks whether the clock used by the astronomical algorithm is working properly and notifies the owner, technician, and park maintenance staff if it is not.
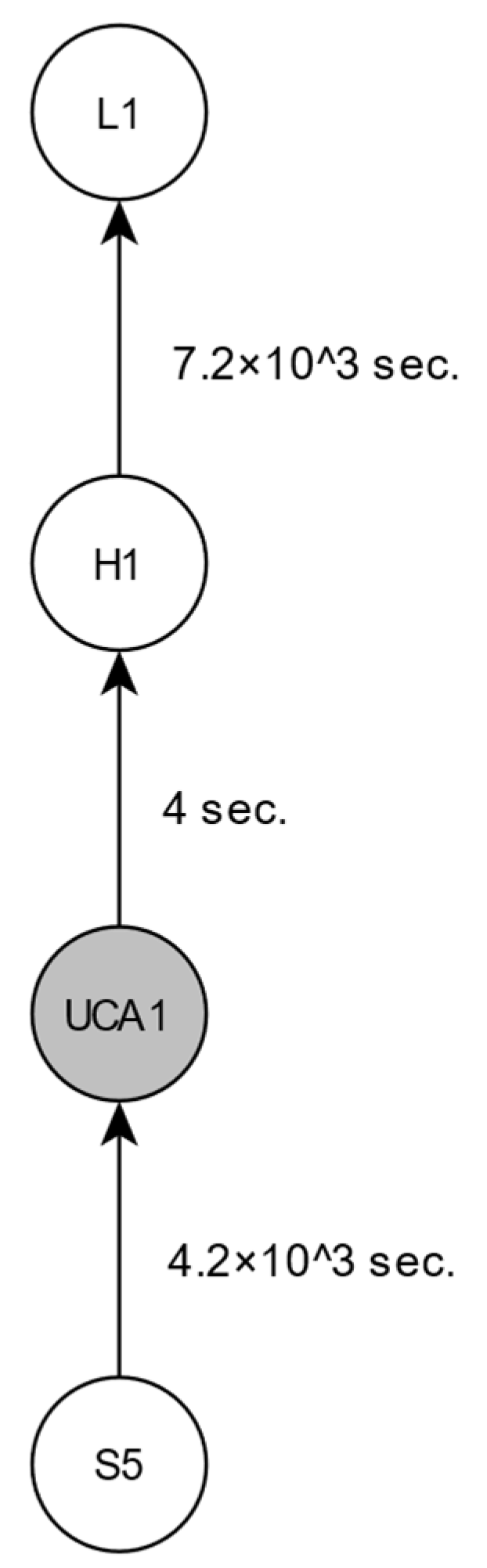
5.3. Determining Time Values and Calculating the Safety Level
- LS-5 -> UCA-1: This time value was determined to be equal to two times between “Rotate step x,y” control actions due to the sun movement of Table 4 This is the case because if the owner monitors the solar park right before a rotation of the arrays takes place, then it would take two consecutive movements of the arrays for someone to identify the discrepancy through the phone or PC app. So, the time value is t_(LS5 → UCA1) = 2.2 × 103 = 4.2 × 103 s.
- UCA-1 -> H-1: This value is considered the same as the execution time for the “Rotate step x,y” control action time constant of Table 4. So, the value is t_(UCA1→H1) = 4 s.
- H-1 -> L-1: This time value was taken directly from the time constant of Table 4. The time between panels not being aligned perfectly with the sun and having a significant loss of production. So, it is t_(H1→L1) = 7.2 × 103 s.
5.4. EWaSAP
- SC-63-EWaSAP-H-2: An array position sensor should be integrated into every array of the system.
- SC-64-EWaSAP-H-2: A rotate step x,y CA listener should be integrated into the system’s PLC controller.
- SC-65-EWaSAP-H-2: An alert awareness action should be provided when an array is rotated to its maximum angle and a rotate step x,y is provided.
- SC-66-EWaSAP-H-3: An array position sensor should be integrated into every array of the system.
- SC-67-EWaSAP-H-3: An anemometer should be integrated into the system.
- SC-68-EWaSAP-H-3: An alert awareness action should be provided when all array positions are not horizontal while the anemometer registers strong winds (strong as referred to by the engineers)
- SC-69-EWaSAP-UCA-1: The energy production graph should be shown in the app.
- SC-70-EWaSAP-UCA-1: An accelerometer should be integrated into every array of the system.
- SC-71-EWaSAP-UCA-1: An AI visual pattern recognition system using the feed from the security systems cameras should be integrated into the system.
- SC-72-EWaSAP-UCA-1: A solar tracking sensor should be integrated into the system.
- SC-73-EWaSAP-UCA-1: A rotate step x,y CA listener should be integrated into the PLC controller of the system.
- SC-74-EWaSAP-UCA-1: A warning awareness action should be provided when the production graph declines over time.
- SC-75-EWaSAP-UCA-1: A warning awareness action should be provided when one or more arrays are out of alignment with the rest of the arrays.
- SC-76-EWaSAP-UCA-1: When all arrays are out of alignment with the sun’s position, a warning awareness action should be provided (visual check or solar tracking sensor).
- SC-77-EWaSAP-UCA-1: When the accelerometer indicates that an array has not moved in a while, a warning awareness action should be provided.
- SC-78-EWaSAP-UCA-1: A warning awareness action should be provided when the rotate step x,y CA is not provided for some time.
- SC-79-EWaSAP-UCA-6: A rotate step x,y CA listener should be integrated into the system’s PLC controller.
- SC-80-EWaSAP-UCA-6: The energy production graph should be shown in the app.
- SC-81-EWaSAP-UCA-6: An AI visual pattern recognition system using the feed from the security systems cameras should be integrated into the system.
- SC-82-EWaSAP-UCA-6: A array position sensor should be integrated into every array in the system.
- SC-83-EWaSAP-UCA-6: A warning awareness action should be provided when the rotate step x,y CA is provided (the arrays are in alignment with the sun’s position (visual check)), or the production graph shows no discrepancies or that all arrays are in sync (position sensor).
5.5. Calculations in Real-Time
- SC-1-H-1, this constraint is not in place (SC-1-H-1 = 0).
- SC-54-EWaSAP-H-1, this constraint is not in place (SC-54-EWaSAP-H1 = 0).
- SC-55-EWaSAP-H-1, this constraint is not in place (SC-55-EWaSAP-H1 = 0).
- SC-56-EWaSAP-H-1, this constraint is not in place (SC-56-EWaSAP-H1 = 0).
- SC-57-EWaSAP-H-1, this constraint is not in place (SC-57-EWaSAP-H1 = 0).
- SC-58-EWaSAP-H-1, this constraint is not in place (SC-58-EWaSAP-H1 = 0).
- SC-59-EWaSAP-H-1, this constraint is not in place (SC-59-EWaSAP-H1 = 0).
- SC-60-EWaSAP-H-1, this constraint is in place (SC-60-EWaSAP-H1 = 1).
- SC-61-EWaSAP-H-1, this constraint is not in place (SC-61-EWaSAP-H1 = 0).
- SC-62-EWaSAP-H-1, this constraint is not in place (SC-62-EWaSAP-H1 = 0).
- SC-5-UCA-1, this constraint is not in place (SC-1-UCA-1 = 0).
- SC-69-EWaSAP-UCA-1, this constraint is in place (SC-69-EWaSAP-UCA-1 = 1).
- SC-70-EWaSAP-UCA-1, this constraint is not in place (SC-70-EWaSAP-UCA-1 = 0).
- SC-71-EWaSAP-UCA-1, this constraint is not in place (SC-71-EWaSAP-UCA-1 = 0).
- SC-72-EWaSAP-UCA-1, this constraint is not in place (SC-72-EWaSAP-UCA-1 = 0).
- SC-73-EWaSAP-UCA-1, this constraint is not in place (SC-73-EWaSAP-UCA-1 = 0).
- SC-74-EWaSAP-UCA-1, this constraint is not in place (SC-74-EWaSAP-UCA-1 = 0).
- SC-75-EWaSAP-UCA-1, this constraint is not in place (SC-75-EWaSAP-UCA-1 = 0).
- SC-76-EWaSAP-UCA-1, this constraint is not in place (SC-76-EWaSAP-UCA-1 = 0).
- SC-77-EWaSAP-UCA-1, this constraint is not in place (SC-77-EWaSAP-UCA-1 = 0).
- SC-78-EWaSAP-UCA-1, this constraint is not in place (SC-78-EWaSAP-UCA-1 = 0).
- SC-28-S5-UCA-1, this constraint is not in place (SC-28-S5-UCA-1 = 0).
- SC-84-EWaSAP-LS-5, this constraint is not in place (SC-84-EWaSAP-LS-5 = 0).
- SC-85-EWaSAP-LS-5, this constraint is not in place (SC-85-EWaSAP-LS-5 = 0).
6. Concluding Remarks and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Knegtering, B.; Pasman, H. The safety barometer: How safe is my plant today? Is instantaneously measuring safety level utopia or realizable? J. Loss Prev. Process Ind. 2013, 26, 821–829. [Google Scholar] [CrossRef]
- Asgari, A.; Beauregard, Y. Using a Brain-Inspired Decision-Making System to Model a Real-Time Responsive Risk Assessment of the Dynamic Tasks Involved with Hazardous Materials. Safety 2022, 8, 45. [Google Scholar] [CrossRef]
- Zeleskidis, A.; Dokas, I.; Papadopoulos, B. Knowing the safety level of a system in real-time: An extended mathematical model of the STAMP-based RealTSL methodology. Saf. Sci. 2022, 152, 105739. [Google Scholar] [CrossRef]
- Leveson, N.G.; Thomas, J.P. STPA Handbook, 1st ed.; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Dokas, I.M.; Feehan, J.; Syed, I. EWaSAP: An Early Warning Identification Approach Based on a Systemic Hazard Analysis. Saf. Sci. 2013, 58, 11–26. [Google Scholar] [CrossRef]
- Pelz, P.F.; Pfetsch, M.E.; Kersting, S.; Kohler, M.; Matei, A.; Melz, T.; Platz, R.; Schaeffner, M.; Ulbrich, S.; Kersting, S.; et al. Types of uncertainty. In Mastering Uncertainty in Mechanical Engineering; Springer International Publishing: Cham, Switzerland, 2021; pp. 25–42. [Google Scholar]
- Patriarca, R.; De Carlo, F.; Leoni, L. A System-Theoretic Fuzzy Analysis (STheFA) for systemic safety assessment. Process Saf. Environ. Prot. 2023, 177, 1181–1196. [Google Scholar]
- Bu, Y.; Wu, Y.; Li, X.; Pei, Y. Operational risk analysis of a containerized lithium-ion battery energy storage system based on STPA and fuzzy evaluation. Process Saf. Environ. Prot. 2023, 176, 627–640. [Google Scholar] [CrossRef]
- Pavlovic, B. Automated Control Flaw Generation Procedure: Cheakamus Dam Case Study. Master’s Thesis, The University of Western Ontario, London, ON, Canada, 2016. [Google Scholar]
- Borges, S.; Belderrain, M.; Junior, M.; Castilho, D. Integration of STPA and TOPSIS fuzzy methods for risk analysis in aerospace projects. Int. J. Decis. Sci. Risk Manag. 2022, 10, 212–226. [Google Scholar]
- Qiao, W.; Huang, E.; Guo, H.; Lian, C.; Chen, H.; Ma, X. On the causation analysis for hazards involved in the engine room fire-fighting system by integrating STPA and BN. Ocean. Eng. 2023, 288. [Google Scholar] [CrossRef]
- Zeleskidis, A.; Dokas, I. A fuzzy extension to the risk situation awareness provision indicator (RiskSOAP). Risk Anal. Based Data Crisis Response Beyond Knowl. 2019, 417–423. [Google Scholar] [CrossRef]
- Ross, T. Fuzzy Logic with Engineering Applications, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Zadeh, L. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Leveson, N. Engineering a Safer World: Systems Thinking Applied to Safety, 1st ed.; MIT PRESS: Cambridge, MA, USA, 2011. [Google Scholar]
- Bakar, A.S.A.; Gegov, A. Ranking of fuzzy numbers based on centroid point and spread. J. Intell. Fuzzy Syst. 2014, 27, 1179–1186. [Google Scholar] [CrossRef]

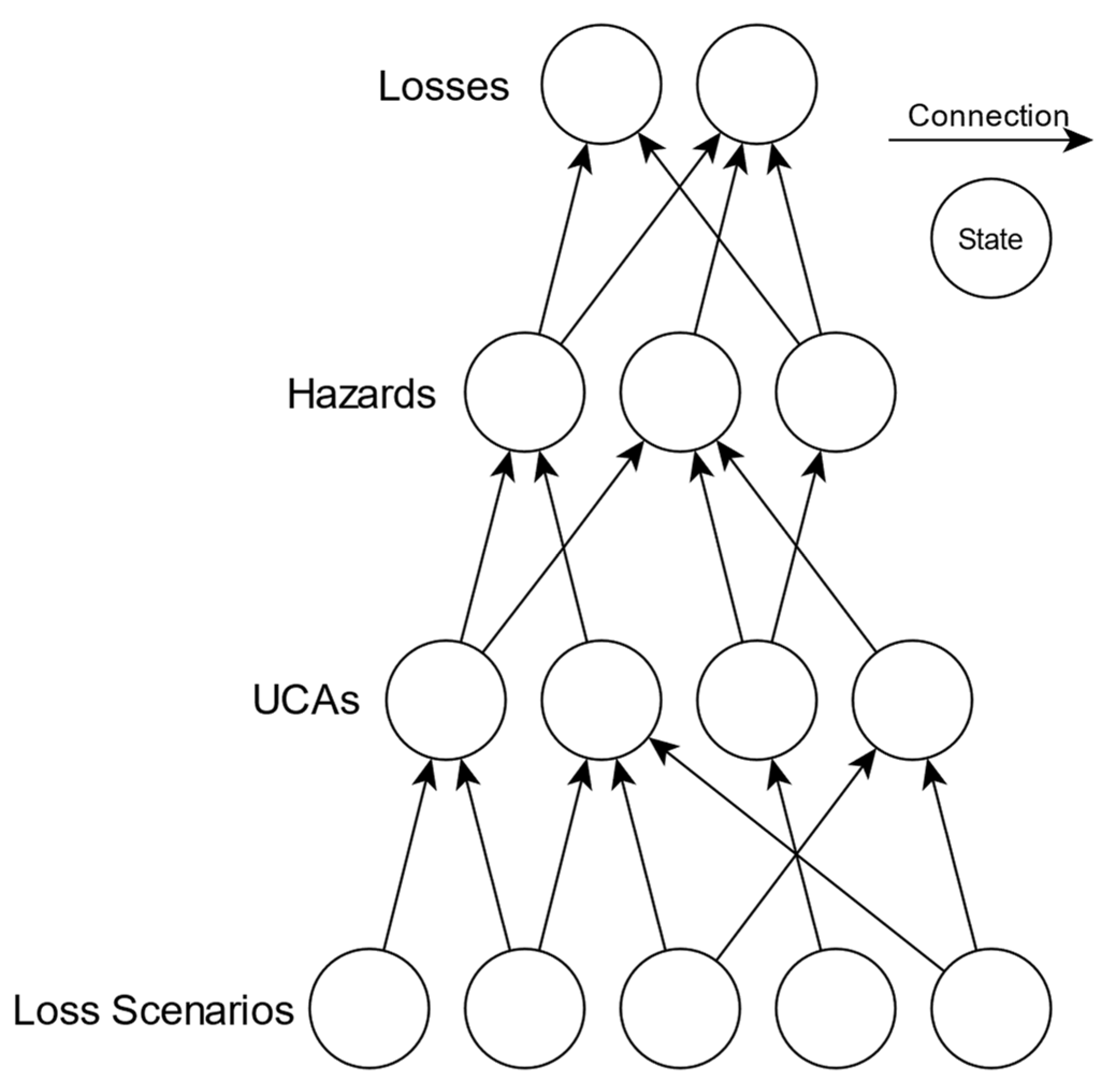
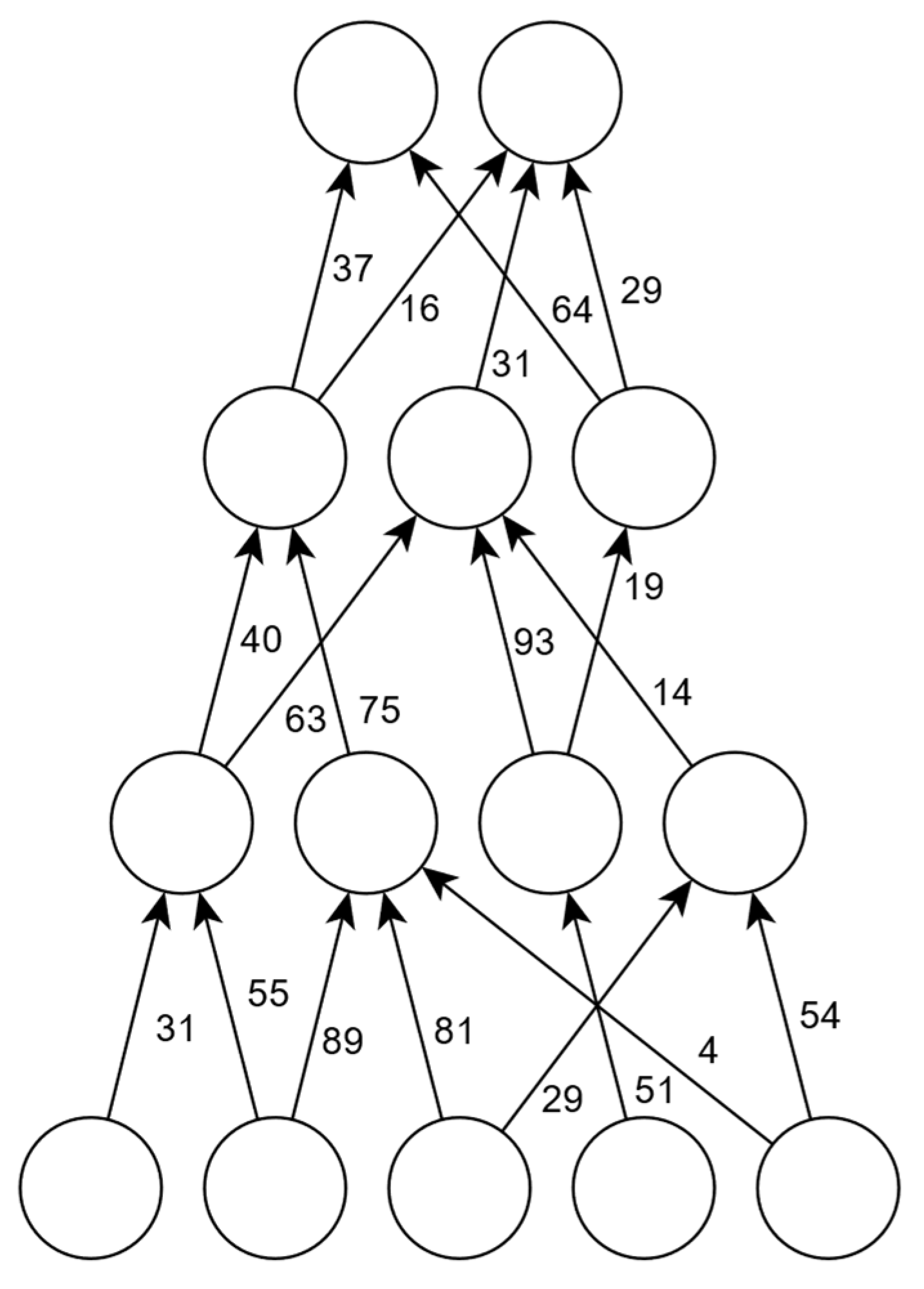
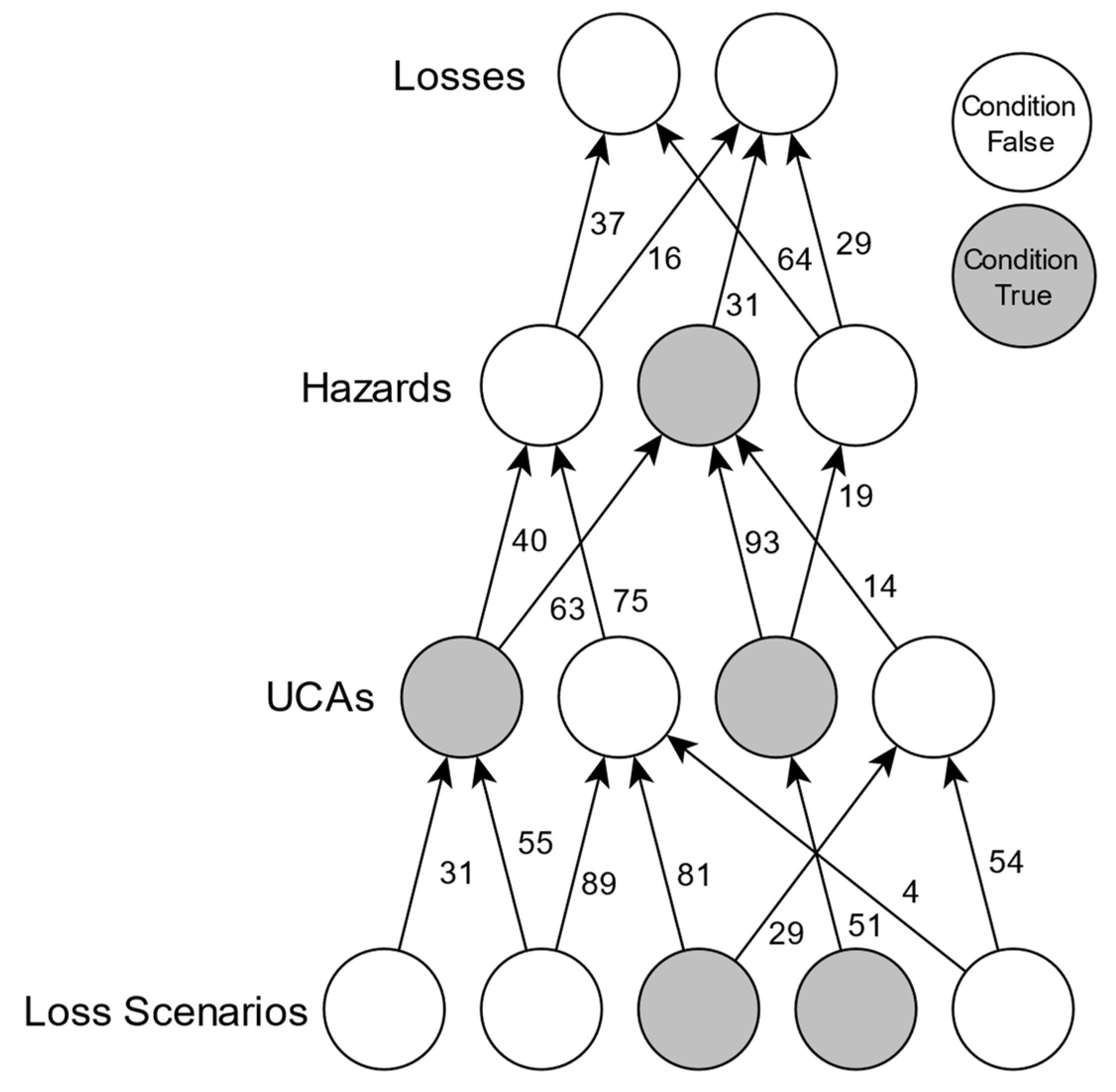
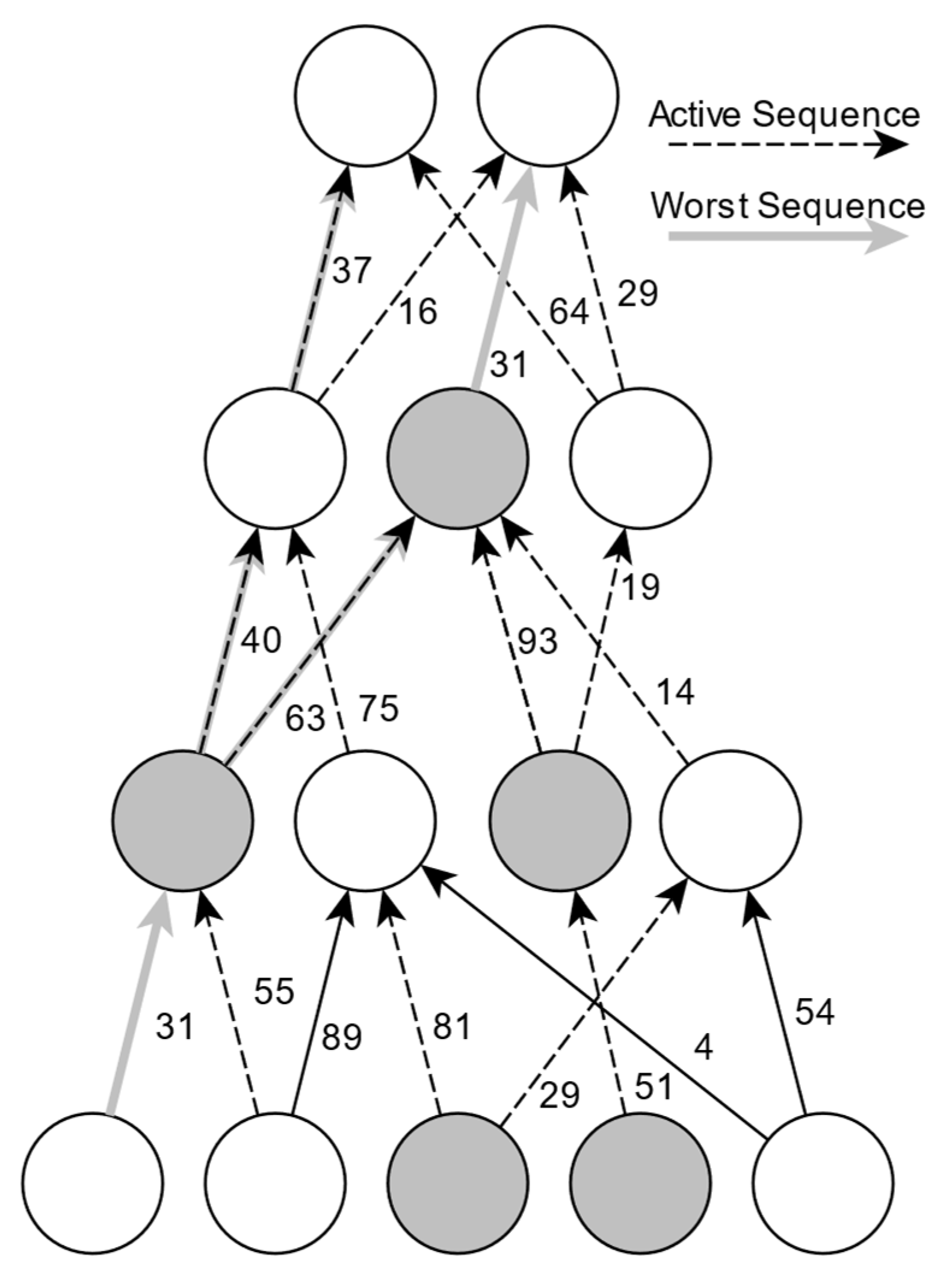

| A/A | Description | Leads to |
|---|---|---|
| L-1 | Loss of production. | N/A |
| L-2 | Loss of equipment or damages | N/A |
| L-3 | Loss of life or injury. | N/A |
| H-1 | One or multiple arrays out of proper alignment. | L-1 |
| H-2 | Array rotating past component tolerance angle. | L-2 |
| H-3 | Minimum safe distance violation from the array by people, objects, or animals. | L-2, L-3 |
| H-4 | Non-horizontal array position during adverse weather conditions. | L-2, L-3 |
| SC-1-H-1 | All arrays should be simultaneously at the proper alignment at which the PV panels are producing maximum electric power at all times. | H-1 |
| SC-2-H-2 | The array motors should be unable to provide motion to the array when it has reached the limit of its possible rotation | H-2 |
| SC-3-H-3 | The array should be unable to rotate when the minimum safe distance between it and people, objects or animals has been violated. | H-3 |
| SC-4-H-4 | All arrays should be maintained simultaneously at the horizontal position when adverse weather conditions are taking place. | H-4 |
| Control Action | Providing CA Causes Hazard | Not Providing CA Causes Hazard | Wrong Timing/Order of CA Causes Hazard | CA Stopped Too Soon/Applied Too Long |
|---|---|---|---|---|
| Rotate step x,y (PV park computer) | UCA-6: When the array is positioned with proper alignment. [H-1, H-2, H-3, H-4] | UCA-1: When the array is not positioned with proper alignment. [H-1] | UCA-16: When it is provided after sunset leading to discrepancy at sunrise. [H-1] | - |
| UCA-7: When maintenance staff are close to the array. [H-3] | UCA-2: When maintenance on the arrays is taking place or is about to occur. [H-3] | UCA-18: When it is provided simultaneously by two different controllers (either the astronomical algorithm and the PV park computer or by the owner and the phone/PC app). [H-1, H-2, H-3, H-4] | ||
| UCA-8: When cleaning of the PV panels is taking place on the array. [H-3] | UCA-3: When a number of arrays are out of sync with the rest of the park. [H-1] | |||
| UCA-9: When the array is in the horizontal position and adverse environmental conditions occur. [H-3] | ||||
| Rotate step x,y (astronomical algorithm) | UCA-10: When the array is positioned with proper alignment. [H-1, H-2, H-3, H-4] | UCA-4: When the sun has moved enough for the PV panels to not generate electricity optimally. [H-1] | UCA-19: When it is provided too soon before the sun moves an adequate amount. [H-1] | - |
| UCA-11: When maintenance staff are close to the array. [H-3] | UCA-20: When it is provided too late after the sun has moved too far. [H-1] | |||
| UCA-12: When cleaning of PV panels is taking place on the array. [H-3] | ||||
| UCA-13: When the array is in the horizontal position and adverse environmental conditions occur. [H-4] | ||||
| Horizontalization | UCA-14: When maintenance is taking place or is about to take place. [H-3] | UCA-5: When adverse weather conditions are taking place. [H-4] | UCA-21: When provided simultaneously as the Rotate step x,y CA. [H-1, H-4] | UCA-22: Applied too long when adverse weather conditions stopped taking place. [H-1] |
| UCA-15: When adverse weather conditions are not taking place. [H-1] |
| Time Constant | Time Value |
|---|---|
| Execution time for the “Rotate step x,y” control action. | 4 s |
| Time between “Rotate step x,y” control actions due to sun movement. According to the developers, the astronomical algorithm is designed to provide 20 “Rotate step x,y” control actions each day. Due to the change in daytime between winter and summer solstice, 2 time-values were derived for this time constant: 43 min and 18 s during summer solstice and 28 min and 18 s for winter solstice. For simplicity in this paper, the average between these two is used 35 min and 48 s, rounded to 35 min. | 35 min = 2.1 × 103 s |
| Daytime similar to the time between “Rotate step x,y”; there are two time values for summer and winter solstice in the year 2023: 14 h 30 min, 9 h and 30 min. | 11 h and 40 min = 4.2 × 104 s |
| Time between mandatory checks of the park by an individual. Through discussion with the system owner, it became apparent that there is a standard procedure in place that states that some individuals should check up on the system every 48 h at dawn. This was used in the same calculations accordingly. | 48 h = 1.72 × 105 s |
| Time between panels not being aligned perfectly with the sun and having a significant loss of production. To quantify this parameter, a time value of 2 h was chosen. This means that one array would have to be out of optimal alignment with the sun’s position for 2 h for that to be considered a significant loss of production. | 2 h = 7.2 × 103 s |
| Astronomical algorithm clock battery capacity. These values were taken from the battery’s specification documentation. | 70 years = 2.2 × 109 s |
| Symbols | Description | Sensory System | Identifying Signs |
|---|---|---|---|
| H-2 | Tracker rotating past component tolerance angle. | Tracker position sensor. Rotate step x,y CA listener. | The tracker is rotated at its maximum angle and a rotate step x,y is provided. |
| H-3 | Non-horizontal array position during adverse weather conditions | Tracker position sensor. Anemometer. | All array positions are not horizontal while the anemometer registers strong winds (strong referred to by the engineers). |
| UCA-1 | The owner does not provide rotate step x,y when the array is not positioned properly. | Visual check via video feed and AI recognition system. Accelerometer. Energy production graph. Solar tracking sensor. Rotate step x,y CA listener. | Production graph declines over time. One or more arrays are out of alignment with the rest of the arrays. All arrays are out of alignment with the sun’s position (visual check or solar tracking sensor). The accelerometer informs that an array has not moved in a while. Rotate step x,y CA is not provided. |
| UCA-6 | Rotate step x,y is provided by the owner when the array is positioned with proper alignment. | Rotate step x,y CA listener. Visual check via video feed and AI recognition system. Energy production tracker position sensor. | Rotate step x,y CA is provided. Trackers are in alignment with the sun’s position (visual check). Production graph shows no discrepancies. All arrays are in sync (position sensor). |
| UCA-19 | Rotate step x,y is unsafely provided by the astronomical algorithm when it is provided too soon before the sun moves an adequate amount. | Rotate step x,y CA listener. Tracker position sensor. Solar tracking sensor. | Rotate step x,y CA is provided. Trackers were in alignment with the sun’s position and have not moved in the pre-set amount of time that it takes the sun to move to the position for a “rotate step x,y” CA to put it in the proper position. |
| UCA-1: Rotate step x,y is provided by the astronomical algorithm when the array is in the horizontal position and adverse environmental conditions are taking place. [H-1] | |||
| LS-5 | The owner does not have access to the phone/pc app and is in a remote location. | Application listener for if the owner has checked the park. | The owner has not checked the park through the app in a significant amount of time. |
| LS-7 | The owner does not have access to the phone/pc app and the temperature of the computer room, or the surrounding area is too hot; it may not be safe for the owner to manually adjust the arrays. | Computer room and surrounding area thermometer, application listener for if the owner has checked the park. | The owner has not checked the park through the app in a significant amount of time and the thermometer is showing dangerous temperatures. |
| UCA-6: Rotate step x,y is provided by the owner when the array is positioned with proper alignment. [H-1, H-2, H-3, H-4] | |||
| LS-16 | The camera is stuck showing the park in a previous time and the owner believes that the arrays are out of proper alignment. | Camera feed timestamp cross check | Camera feed timestamp discrepancy with actual time. |
| UCA-19: Rotate step x,y is unsafely provided by the astronomical algorithm when it is provided too soon before the sun moves an adequate amount. [H-1] | |||
| The clock used by the astronomical algorithm runs out of battery causing the astronomical algorithm to provide erratic control actions. | Astronomical algorithm clock battery sensor | The astronomical algorithm clock battery is empty | |
| LS-19 | The clock used by the astronomical algorithm malfunctions causing the astronomical algorithm to provide erratic control actions. | Astronomical algorithm clock operability cross check | The astronomical algorithm clock is experiencing technical issues. |
| Node | Description of System State | Safety and Awareness Constraints |
|---|---|---|
| L-1 | Loss of production. | N/A |
| H-1 | One or multiple arrays out of proper alignment. | SC-1-H-1, SC-54-EWaSAP-H-1, SC-55-EWaSAP-H-1, SC-56-EWaSAP-H-1, SC-57-EWaSAP-H-1, SC-58-EWaSAP-H-1, SC-59-EWaSAP-H-1, SC-60-EWaSAP-H-1, SC-61-EWaSAP-H-1, SC-62-EWaSAP-H-1 |
| UCA1 | Rotate step x,y is provided by the astronomical algorithm when the array is in the horizontal position and adverse environmental conditions are taking place. | SC-5-UCA-1, SC-69-EWaSAP-UCA-1, SC-70-EWaSAP-UCA-1, SC-71-EWaSAP-UCA-1, SC-72-EWaSAP-UCA-1, SC-73-EWaSAP-UCA-1, SC-74-EWaSAP-UCA-1, SC-75-EWaSAP-UCA-1, SC-76-EWaSAP-UCA-1, SC-77-EWaSAP-UCA-1, SC-78-EWaSAP-UCA-1 |
| S5 | The owner does not have access to the phone/pc app and is in a remote location. | SC-28-S5-UCA-1, SC-84-EWaSAP-LS-5, SC-85-EWaSAP-LS-5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeleskidis, A.; Charalampidou, S.; Dokas, I.M. Reducing Data Uncertainties: Fuzzy Real-Time Safety Level Methodology for Socio-Technical Systems. Safety 2024, 10, 85. https://doi.org/10.3390/safety10040085
Zeleskidis A, Charalampidou S, Dokas IM. Reducing Data Uncertainties: Fuzzy Real-Time Safety Level Methodology for Socio-Technical Systems. Safety. 2024; 10(4):85. https://doi.org/10.3390/safety10040085
Chicago/Turabian StyleZeleskidis, Apostolos, Stavroula Charalampidou, and Ioannis M. Dokas. 2024. "Reducing Data Uncertainties: Fuzzy Real-Time Safety Level Methodology for Socio-Technical Systems" Safety 10, no. 4: 85. https://doi.org/10.3390/safety10040085
APA StyleZeleskidis, A., Charalampidou, S., & Dokas, I. M. (2024). Reducing Data Uncertainties: Fuzzy Real-Time Safety Level Methodology for Socio-Technical Systems. Safety, 10(4), 85. https://doi.org/10.3390/safety10040085







