A Low-Rate Video Approach to Hyperspectral Imaging of Dynamic Scenes
Abstract
1. Introduction
2. Approach
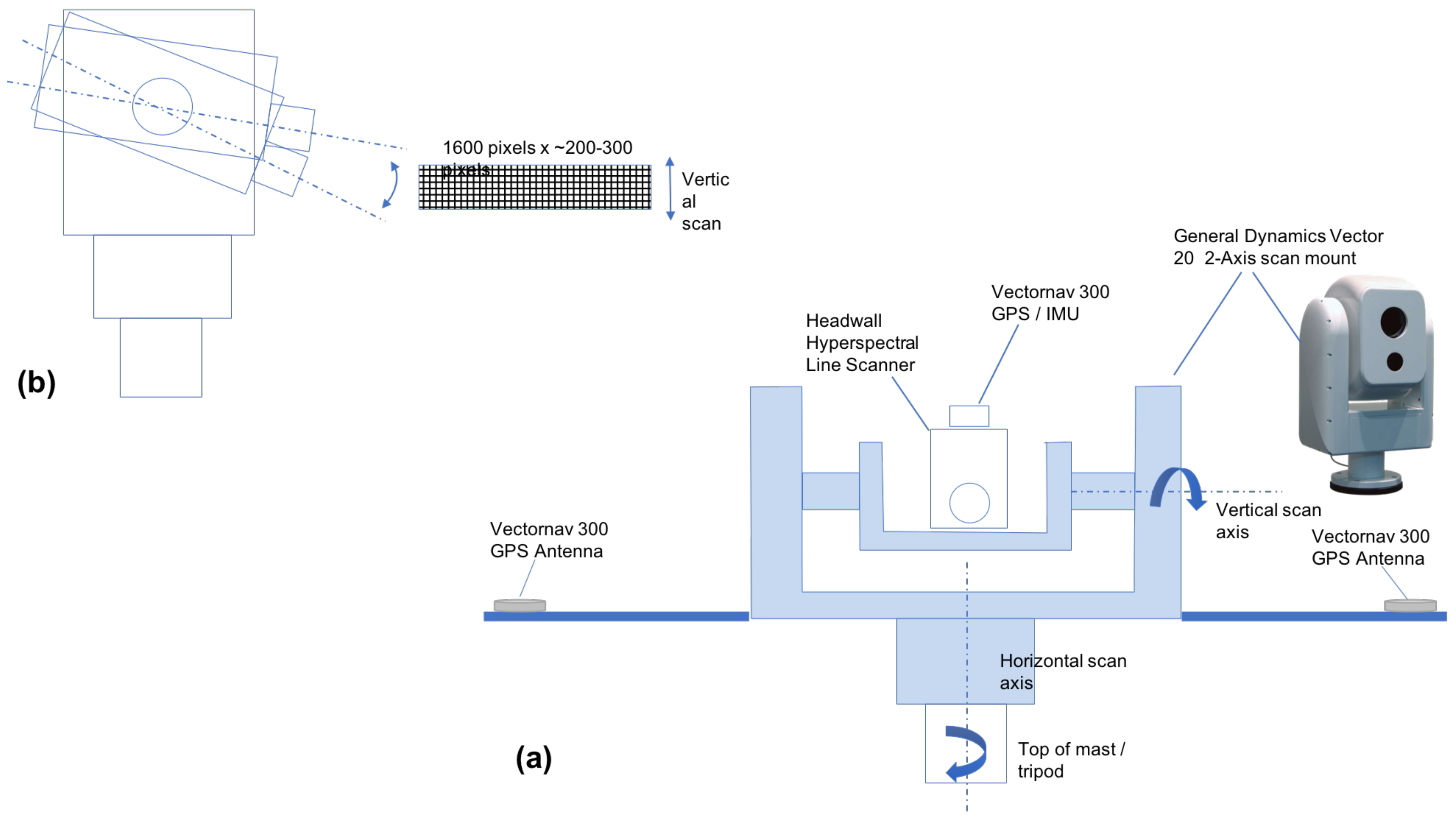
2.1. Low-Rate Hyperspectral Video System
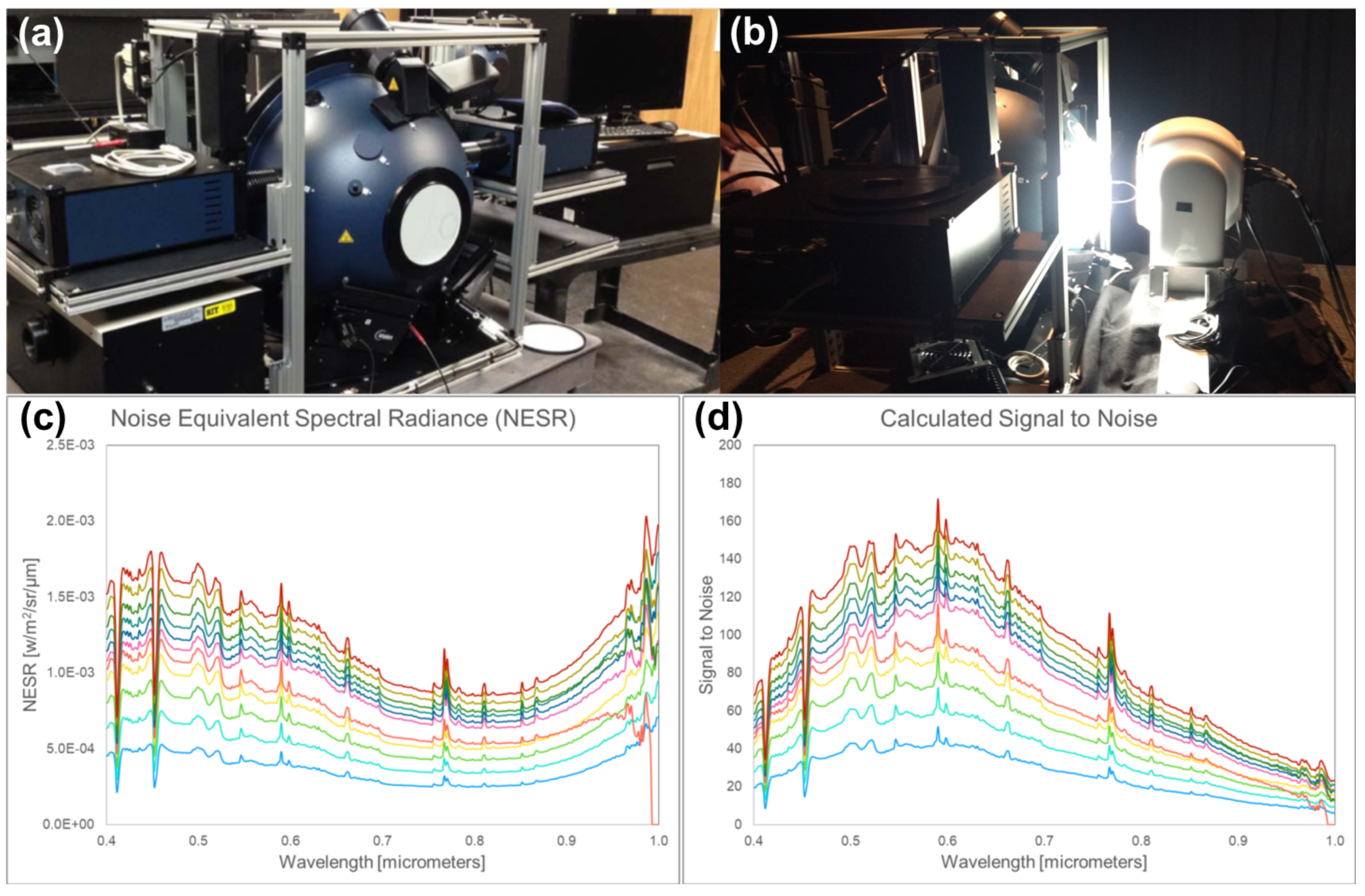
2.2. System Calibration
2.3. Imaging the Dynamics of the Surf Zone
2.4. Real-Time Vehicle Tracking Using Hyperspectral Imagery
3. Results
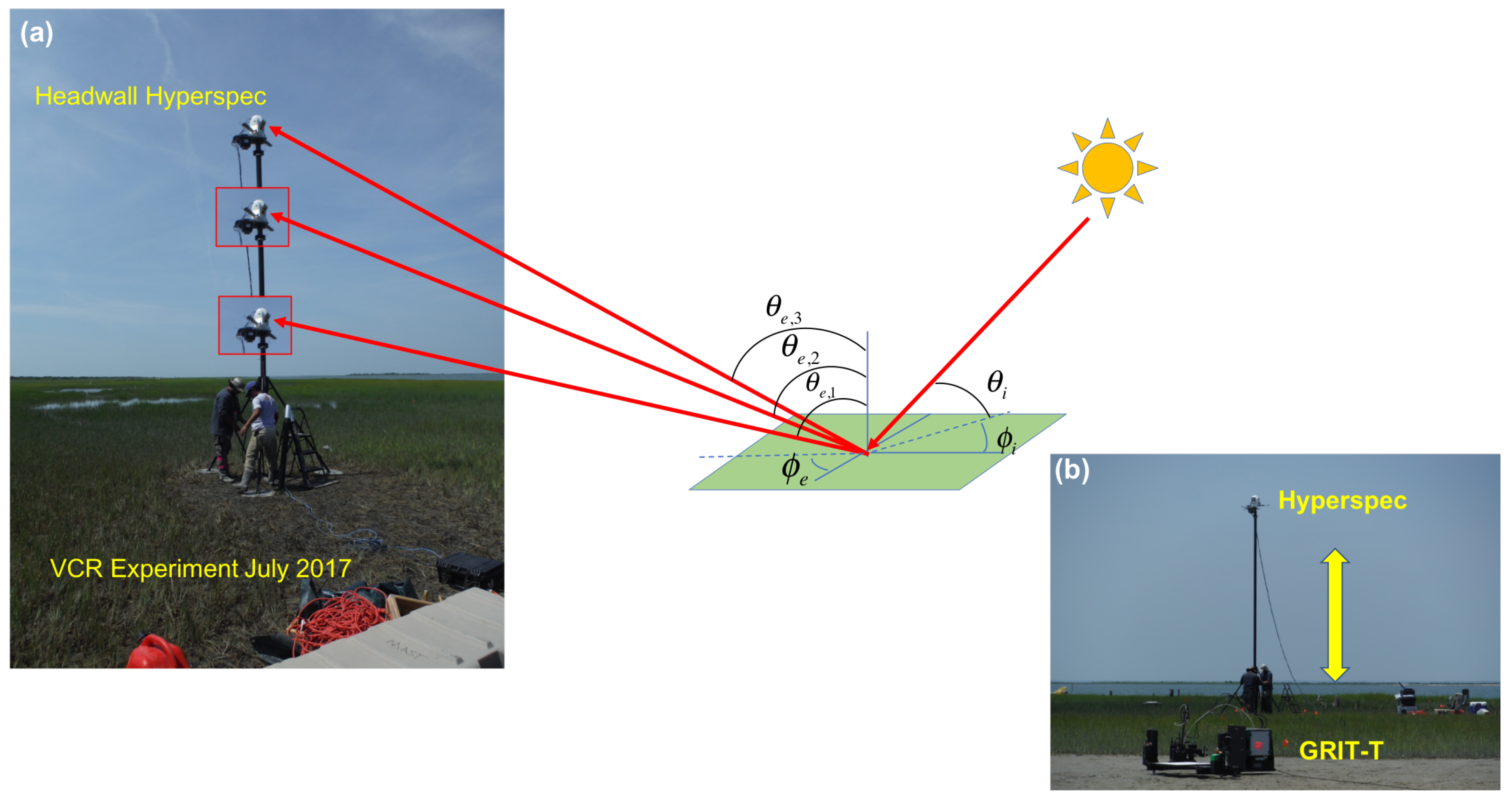
3.1. Hyperspectral Data Collection Experiment
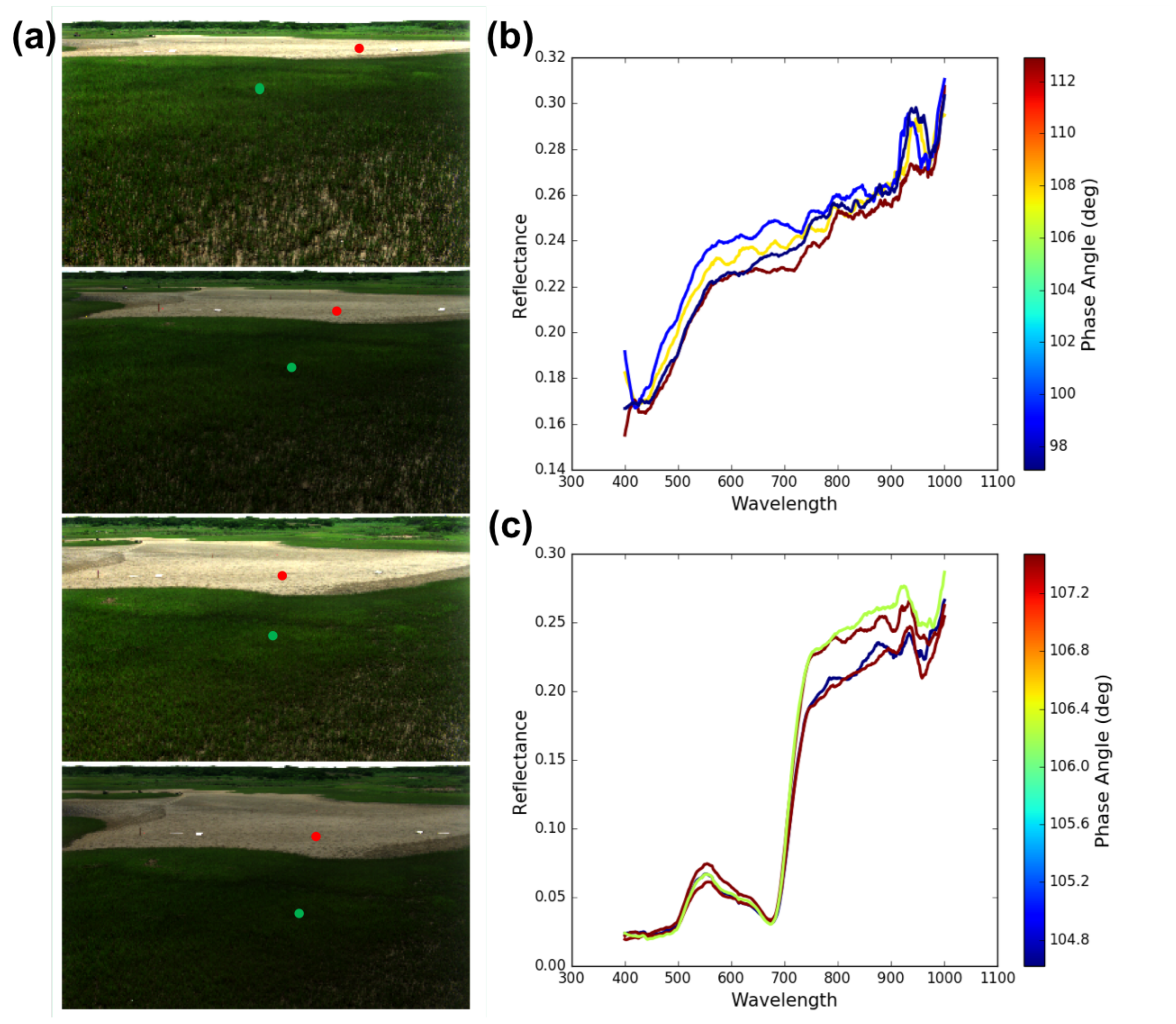
3.2. Digital Elevation Model and HCRF from Hyperspectral Stereo Imagery
3.3. Low-Rate Hyperspectral Video Image Sequence of the Surf Zone
3.4. Time Series Hyperspectral Imagery of Moving Vehicles
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Dutta, D.; Goodwell, A.E.; Kumar, P.; Garvey, J.E.; Darmody, R.G.; Berretta, D.P.; Greenberg, J.A. On the feasibility of characterizing soil properties from aviris data. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5133–5147. [Google Scholar] [CrossRef]
- Huesca, M.; García, M.; Roth, K.L.; Casas, A.; Ustin, S.L. Canopy structural attributes derived from AVIRIS imaging spectroscopy data in a mixed broadleaf/conifer forest. Remote Sens. Environ. 2016, 182, 208–226. [Google Scholar] [CrossRef]
- Schlerf, M.; Atzberger, C.; Hill, J. Remote sensing of forest biophysical variables using HyMap imaging spectrometer data. Remote Sens. Environ. 2005, 95, 177–194. [Google Scholar] [CrossRef]
- Giardino, C.; Brando, V.E.; Dekker, A.G.; Strömbeck, N.; Candiani, G. Assessment of water quality in Lake Garda (Italy) using Hyperion. Remote Sens. Environ. 2007, 109, 183–195. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Pattey, E.; Zarco-Tejada, P.J.; Strachan, I.B. Hyperspectral vegetation indices and novel algorithms for predicting green LAI of crop canopies: Modeling and validation in the context of precision agriculture. Remote Sens. Environ. 2004, 90, 337–352. [Google Scholar] [CrossRef]
- Garcia, R.A.; Lee, Z.; Hochberg, E.J. Hyperspectral Shallow-Water Remote Sensing with an Enhanced Benthic Classifier. Remote Sens. 2018, 10, 147. [Google Scholar] [CrossRef]
- Mobley, C.D.; Sundman, L.K.; Davis, C.O.; Bowles, J.H.; Downes, T.V.; Leathers, R.A.; Montes, M.J.; Bissett, W.P.; Kohler, D.D.; Reid, R.P.; et al. Interpretation of hyperspectral remote-sensing imagery by spectrum matching and look-up tables. Appl. Opt. 2005, 44, 3576–3592. [Google Scholar] [CrossRef]
- Liu, Y.; Gao, G.; Gu, Y. Tensor matched subspace detector for hyperspectral target detection. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1967–1974. [Google Scholar] [CrossRef]
- Prasad, S.; Bruce, L.M. Decision fusion with confidence-based weight assignment for hyperspectral target recognition. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1448–1456. [Google Scholar] [CrossRef]
- Chang, C.I.; Jiao, X.; Wu, C.C.; Du, Y.; Chang, M.L. A review of unsupervised spectral target analysis for hyperspectral imagery. EURASIP J. Adv. Signal Process. 2010, 2010, 503752. [Google Scholar] [CrossRef]
- Power, H.; Holman, R.; Baldock, T. Swash zone boundary conditions derived from optical remote sensing of swash zone flow patterns. J. Geophys. Res. Oceans 2011. [Google Scholar] [CrossRef]
- Lu, J.; Chen, X.; Zhang, P.; Huang, J. Evaluation of spatiotemporal differences in suspended sediment concentration derived from remote sensing and numerical simulation for coastal waters. J. Coast. Conserv. 2017, 21, 197–207. [Google Scholar] [CrossRef]
- Dorji, P.; Fearns, P. Impact of the spatial resolution of satellite remote sensing sensors in the quantification of total suspended sediment concentration: A case study in turbid waters of Northern Western Australia. PLoS ONE 2017, 12, e0175042. [Google Scholar] [CrossRef] [PubMed]
- Kamel, A.; El Serafy, G.; Bhattacharya, B.; Van Kessel, T.; Solomatine, D. Using remote sensing to enhance modelling of fine sediment dynamics in the Dutch coastal zone. J. Hydroinform. 2014, 16, 458–476. [Google Scholar] [CrossRef]
- Puleo, J.A.; Holland, K.T. Estimating swash zone friction coefficients on a sandy beach. Coast. Eng. 2001, 43, 25–40. [Google Scholar] [CrossRef]
- Concha, J.A.; Schott, J.R. Retrieval of color producing agents in Case 2 waters using Landsat 8. Remote Sens. Environ. 2016, 185, 95–107. [Google Scholar] [CrossRef]
- Puleo, J.A.; Farquharson, G.; Frasier, S.J.; Holland, K.T. Comparison of optical and radar measurements of surf and swash zone velocity fields. J. Geophys. Res. Oceans 2003. [Google Scholar] [CrossRef]
- Muste, M.; Fujita, I.; Hauet, A. Large-scale particle image velocimetry for measurements in riverine environments. Water Resour. Res. 2008. [Google Scholar] [CrossRef]
- Puleo, J.A.; McKenna, T.E.; Holland, K.T.; Calantoni, J. Quantifying riverine surface currents from time sequences of thermal infrared imagery. Water Resour. Res. 2012. [Google Scholar] [CrossRef]
- Gao, L.; Wang, L.V. A review of snapshot multidimensional optical imaging: Measuring photon tags in parallel. Phys. Rep. 2016, 616, 1–37. [Google Scholar] [CrossRef]
- Hagen, N.A.; Gao, L.S.; Tkaczyk, T.S.; Kester, R.T. Snapshot advantage: A review of the light collection improvement for parallel high-dimensional measurement systems. Opt. Eng. 2012, 51, 111702. [Google Scholar] [CrossRef] [PubMed]
- Saari, H.; Aallos, V.V.; Akujärvi, A.; Antila, T.; Holmlund, C.; Kantojärvi, U.; Mäkynen, J.; Ollila, J. Novel miniaturized hyperspectral sensor for UAV and space applications. In Proceedings of the International Society for Optics and Photonics, Sensors, Systems, and Next-Generation Satellites XIII, Berlin, Germany, 31 August–3 September 2009; Volume 7474, p. 74741M. [Google Scholar]
- Pichette, J.; Charle, W.; Lambrechts, A. Fast and compact internal scanning CMOS-based hyperspectral camera: The Snapscan. In Proceedings of the International Society for Optics and Photonics, Instrumentation Engineering IV, San Francisco, CA, USA, 28 January–2 February 2017; Volume 10110, p. 1011014. [Google Scholar]
- De Oliveira, R.A.; Tommaselli, A.M.; Honkavaara, E. Geometric calibration of a hyperspectral frame camera. Photogramm. Rec. 2016, 31, 325–347. [Google Scholar] [CrossRef]
- Aasen, H.; Burkart, A.; Bolten, A.; Bareth, G. Generating 3D hyperspectral information with lightweight UAV snapshot cameras for vegetation monitoring: From camera calibration to quality assurance. ISPRS J. Photogramm. Remote Sens. 2015, 108, 245–259. [Google Scholar] [CrossRef]
- Honkavaara, E.; Rosnell, T.; Oliveira, R.; Tommaselli, A. Band registration of tuneable frame format hyperspectral UAV imagers in complex scenes. ISPRS J. Photogramm. Remote Sens. 2017, 134, 96–109. [Google Scholar] [CrossRef]
- Aasen, H.; Bendig, J.; Bolten, A.; Bennertz, S.; Willkomm, M.; Bareth, G. Introduction and Preliminary Results of a Calibration for Full-Frame Hyperspectral Cameras to Monitor Agricultural Crops with UAVs; ISPRS Technical Commission VII Symposium; Copernicus GmbH: Istanbul, Turkey, 29 September–2 October 2014; Volume 40, pp. 1–8.
- Hill, S.L.; Clemens, P. Miniaturization of high spectral spatial resolution hyperspectral imagers on unmanned aerial systems. In Proceedings of the International Society for Optics and Photonics, Next-Generation Spectroscopic Technologies VIII, Baltimore, MD, USA, 3 June 2015; Volume 9482, p. 94821E. [Google Scholar]
- Warren, C.P.; Even, D.M.; Pfister, W.R.; Nakanishi, K.; Velasco, A.; Breitwieser, D.S.; Yee, S.M.; Naungayan, J. Miniaturized visible near-infrared hyperspectral imager for remote-sensing applications. Opt. Eng. 2012, 51, 111720. [Google Scholar] [CrossRef]
- Headwall E-Series Specifications. Available online: https://cdn2.hubspot.net/hubfs/145999/June%202018%20Collateral/MicroHyperspec0418.pdf (accessed on 28 December 2018).
- Greeg, R.O.; Eastwood, M.L.; Sarture, C.M.; Chrien, T.G.; Aronsson, M.; Chippendale, B.J.; Faust, J.A.; Pavri, B.E.; Chovit, C.J.; Solis, M.; et al. Imaging Spectroscopy and the Airborne Visible/Infrared Imaging Spectrometer (AVIRIS). Remote Sens. Environ. 2013, 65, 227–248. [Google Scholar]
- Pearlman, J.S.; Barry, P.S.; Segal, C.C.; Shepanski, J.; Beiso, D.; Carman, S.L. Hyperion, a space-based imaging spectrometer. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1160–1173. [Google Scholar] [CrossRef]
- Diner, D.J.; Beckert, J.C.; Reilly, T.H.; Bruegge, C.J.; Conel, J.E.; Kahn, R.A.; Martonchik, J.V.; Ackerman, T.P.; Davies, R.; Gerstl, S.A.; et al. Multi-angle Imaging SpectroRadiometer (MISR) instrument description and experiment overview. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1072–1087. [Google Scholar] [CrossRef]
- Guanter, L.; Kaufmann, H.; Segl, K.; Foerster, S.; Rogass, C.; Chabrillat, S.; Kuester, T.; Hollstein, A.; Rossner, G.; Chlebek, C.; et al. The EnMAP spaceborne imaging spectroscopy mission for earth observation. Remote Sens. 2015, 7, 8830–8857. [Google Scholar] [CrossRef]
- Babey, S.; Anger, C. A compact airborne spectrographic imager (CASI). In Proceedings of the IGARSS ’89 and Canadian Symposium on Remote Sensing: Quantitative Remote Sensing: An Economic Tool for the Nineties, Vancouver, BC, Canada, 10–14 July 1989; Volume 1, pp. 1028–1031. [Google Scholar]
- Johnson, W.R.; Hook, S.J.; Mouroulis, P.; Wilson, D.W.; Gunapala, S.D.; Realmuto, V.; Lamborn, A.; Paine, C.; Mumolo, J.M.; Eng, B.T. HyTES: Thermal imaging spectrometer development. In Proceedings of the 2011 IEEE Aerospace Conference, Big Sky, MT, USA, 5–12 March 2011; pp. 1–8. [Google Scholar]
- Rickard, L.J.; Basedow, R.W.; Zalewski, E.F.; Silverglate, P.R.; Landers, M. HYDICE: An airborne system for hyperspectral imaging. In Proceedings of the International Society for Optics and Photonics, Imaging Spectrometry of the Terrestrial Environment, Orlando, FL, USA, 11–16 April 1993; Volume 1937, pp. 173–180. [Google Scholar]
- Lucieer, A.; Malenovskỳ, Z.; Veness, T.; Wallace, L. HyperUAS—Imaging spectroscopy from a multirotor unmanned aircraft system. J. Field Robot. 2014, 31, 571–590. [Google Scholar] [CrossRef]
- Cocks, T.; Jenssen, R.; Stewart, A.; Wilson, I.; Shields, T. The HyMapTM airborne hyperspectral sensor: The system, calibration and performance. In Proceedings of the 1st EARSeL Workshop on Imaging Spectroscopy, EARSeL, Zurich, Switzerland, 6–8 October 1998; pp. 37–42. [Google Scholar]
- Eon, R.; Bachmann, C.; Gerace, A. Retrieval of Sediment Fill Factor by Inversion of a Modified Hapke Model Applied to Sampled HCRF from Airborne and Satellite Imagery. Remote Sens. 2018, 10, 1758. [Google Scholar] [CrossRef]
- Uzkent, B.; Rangnekar, A.; Hoffman, M.J. Aerial vehicle tracking by adaptive fusion of hyperspectral likelihood maps. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Honolulu, HI, USA, 21–26 July 2017; pp. 233–242. [Google Scholar]
- Bhattacharya, S.; Idrees, H.; Saleemi, I.; Ali, S.; Shah, M. Moving object detection and tracking in forward looking infra-red aerial imagery. In Machine Vision beyond Visible Spectrum; Springer: New York, NY, USA, 2011; pp. 221–252. [Google Scholar]
- Cao, Y.; Wang, G.; Yan, D.; Zhao, Z. Two algorithms for the detection and tracking of moving vehicle targets in aerial infrared image sequences. Remote Sens. 2015, 8, 28. [Google Scholar] [CrossRef]
- Teutsch, M.; Grinberg, M. Robust detection of moving vehicles in wide area motion imagery. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 27–35. [Google Scholar]
- Cormier, M.; Sommer, L.W.; Teutsch, M. Low resolution vehicle re-identification based on appearance features for wide area motion imagery. In Proceedings of the 2016 IEEE Applications of Computer Vision Workshops (WACVW), Lake Placid, NY, USA, 10 March 2016; pp. 1–7. [Google Scholar]
- Tuermer, S.; Kurz, F.; Reinartz, P.; Stilla, U. Airborne vehicle detection in dense urban areas using HoG features and disparity maps. IEEE J. Sel. To. Appl. Earth Obs. Remote Sens. 2013, 6, 2327–2337. [Google Scholar] [CrossRef]
- Vodacek, A.; Kerekes, J.P.; Hoffman, M.J. Adaptive Optical Sensing in an Object Tracking DDDAS. Procedia Comput. Sci. 2012, 9, 1159–1166. [Google Scholar] [CrossRef]
- General Dynamics Vector 20 Maritime Pan Tilt. Available online: https://www.gd-ots.com/wp-content/uploads/2017/11/Vector-20-Stabilized-Maritime-Pan-Tilt-System-1.pdf (accessed on 8 October 2018).
- Vectornav VN-300 GPS IMU. Available online: https://www.vectornav.com/products/vn-300 (accessed on 8 October 2018).
- BlueSky AL-3 (15m) Telescopic Mast. Available online: http://blueskymast.com/product/bsm3-w-l315-al3-000/ (accessed on 9 October 2018).
- Labsphere Helios 0.5 m Diameter Integrating Sphere. Available online: https://www.labsphere.com/labsphere-products-solutions/remote-sensing/helios/ (accessed on 9 October 2018).
- Mobley, C.D. Light and Water: Radiative Transfer in Natural Waters; Academic Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Coifman, B.; Beymer, D.; McLauchlan, P.; Malik, J. A real-time computer vision system for vehicle tracking and traffic surveillance. Transp. Res. Part C Emerg. Technol. 1998, 6, 271–288. [Google Scholar] [CrossRef]
- Hsieh, J.W.; Yu, S.H.; Chen, Y.S.; Hu, W.F. Automatic traffic surveillance system for vehicle tracking and classification. IEEE Trans. Intell. Transp. Syst. 2006, 7, 175–187. [Google Scholar] [CrossRef]
- Kim, Z.; Malik, J. Fast vehicle detection with probabilistic feature grouping and its application to vehicle tracking. In Proceedings of the Ninth IEEE International Conference on Computer Vision, Nice, France, 13–16 October 2003; p. 524. [Google Scholar]
- Uzkent, B.; Hoffman, M.J.; Vodacek, A. Real-time vehicle tracking in aerial video using hyperspectral features. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 36–44. [Google Scholar]
- Virginia Coast Reserve Long Term Ecological Research. Available online: https://www.vcrlter.virginia.edu/home2/ (accessed on 10 November 2018).
- National Science Foundation Long Term Ecological Research Network. Available online: https://lternet.edu/ (accessed on 10 November 2018).
- Nicodemus, F.E.; Richmond, J.; Hsia, J.J. Geometrical Considerations and Nomenclature for Reflectance; US Department of Commerce, National Bureau of Standards: Washington, DC, USA, 1977; Volume 160. [Google Scholar]
- Schaepman-Strub, G.; Schaepman, M.; Painter, T.H.; Dangel, S.; Martonchik, J.V. Reflectance quantities in optical remote sensing—Definitions and case studies. Remote Sens. Environ. 2006, 103, 27–42. [Google Scholar] [CrossRef]
- Bachmann, C.M.; Abelev, A.; Montes, M.J.; Philpot, W.; Gray, D.; Doctor, K.Z.; Fusina, R.A.; Mattis, G.; Chen, W.; Noble, S.D.; et al. Flexible field goniometer system: The goniometer for outdoor portable hyperspectral earth reflectance. J. Appl. Remote Sens. 2016, 10, 036012. [Google Scholar] [CrossRef]
- Harms, J.D.; Bachmann, C.M.; Ambeau, B.L.; Faulring, J.W.; Torres, A.J.R.; Badura, G.; Myers, E. Fully automated laboratory and field-portable goniometer used for performing accurate and precise multiangular reflectance measurements. J. Appl. Remote Sens. 2017, 11, 046014. [Google Scholar] [CrossRef]
- Bachmann, C.M.; Eon, R.S.; Ambeau, B.; Harms, J.; Badura, G.; Griffo, C. Modeling and intercomparison of field and laboratory hyperspectral goniometer measurements with G-LiHT imagery of the Algodones Dunes. J. Appl. Remote Sens. 2017, 12, 012005. [Google Scholar] [CrossRef]
- AgiSoft PhotoScan Professional (Version 1.2.6) (Software). 2016. Available online: http://www.agisoft.com/downloads/installer/ (accessed on 10 November 2018).
- Lorenz, S.; Salehi, S.; Kirsch, M.; Zimmermann, R.; Unger, G.; Vest Sørensen, E.; Gloaguen, R. Radiometric correction and 3D integration of long-range ground-based hyperspectral imagery for mineral exploration of vertical outcrops. Remote Sens. 2018, 10, 176. [Google Scholar] [CrossRef]
- Curcio, J.A.; Petty, C.C. The near infrared absorption spectrum of liquid water. JOSA 1951, 41, 302–304. [Google Scholar] [CrossRef]
- Bachmann, C.M.; Montes, M.J.; Fusina, R.A.; Parrish, C.; Sellars, J.; Weidemann, A.; Goode, W.; Nichols, C.R.; Woodward, P.; McIlhany, K.; Hill, V.; Zimmerman, R.; Korwan, D.; Truitt, B.; Schwarzschild, A. Bathymetry retrieval from hyperspectral imagery in the very shallow water limit: A case study from the 2007 virginia coast reserve (VCR’07) multi-sensor campaign. Marine Geodesy 2010, 33, 53–75. [Google Scholar] [CrossRef]
- Pacheco, A.; Horta, J.; Loureiro, C.; Ferreira, Ó. Retrieval of nearshore bathymetry from Landsat 8 images: A tool for coastal monitoring in shallow waters. Remote Sens. Environ. 2015, 159, 102–116. [Google Scholar] [CrossRef]
- Lyzenga, D.R.; Malinas, N.P.; Tanis, F.J. Multispectral bathymetry using a simple physically based algorithm. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2251–2259. [Google Scholar] [CrossRef]
- Brando, V.E.; Anstee, J.M.; Wettle, M.; Dekker, A.G.; Phinn, S.R.; Roelfsema, C. A physics based retrieval and quality assessment of bathymetry from suboptimal hyperspectral data. Remote Sens. Environ. 2009, 113, 755–770. [Google Scholar] [CrossRef]
- Lee, Z.; Weidemann, A.; Arnone, R. Combined Effect of reduced band number and increased bandwidth on shallow water remote sensing: The case of worldview 2. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2577–2586. [Google Scholar] [CrossRef]


| Height of Camera (m) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Distance from Mast (m) | |||||||||||
| 1 | 0.0008 | 0.0012 | 0.0017 | 0.0022 | 0.0028 | 0.0033 | 0.0038 | 0.0044 | 0.0049 | 0.0054 | 0.0081 |
| 2 | 0.0012 | 0.0015 | 0.0020 | 0.0024 | 0.0029 | 0.0034 | 0.0039 | 0.0045 | 0.0050 | 0.0055 | 0.0082 |
| 5 | 0.0028 | 0.0029 | 0.0032 | 0.0035 | 0.0038 | 0.0042 | 0.0047 | 0.0051 | 0.0056 | 0.0061 | 0.0086 |
| 10 | 0.0054 | 0.0055 | 0.0057 | 0.0058 | 0.0061 | 0.0063 | 0.0066 | 0.0069 | 0.0073 | 0.0077 | 0.0098 |
| 15 | 0.0081 | 0.0082 | 0.0083 | 0.0084 | 0.0086 | 0.0088 | 0.0090 | 0.0092 | 0.0095 | 0.0098 | 0.0115 |
| 20 | 0.0109 | 0.0109 | 0.0110 | 0.0111 | 0.0112 | 0.0113 | 0.0115 | 0.0117 | 0.0119 | 0.0121 | 0.0136 |
| 25 | 0.0136 | 0.0136 | 0.0136 | 0.0137 | 0.0138 | 0.0139 | 0.0141 | 0.0142 | 0.0144 | 0.0146 | 0.0158 |
| 30 | 0.0163 | 0.0163 | 0.0163 | 0.0164 | 0.0165 | 0.0166 | 0.0167 | 0.0168 | 0.0170 | 0.0171 | 0.0182 |
| 35 | 0.0190 | 0.0190 | 0.0190 | 0.0191 | 0.0192 | 0.0192 | 0.0193 | 0.0195 | 0.0196 | 0.0197 | 0.0206 |
| 40 | 0.0217 | 0.0217 | 0.0217 | 0.0218 | 0.0218 | 0.0219 | 0.0220 | 0.0221 | 0.0222 | 0.0223 | 0.0232 |
| 45 | 0.0244 | 0.0244 | 0.0244 | 0.0245 | 0.0245 | 0.0246 | 0.0247 | 0.0248 | 0.0249 | 0.0250 | 0.0257 |
| 50 | 0.0271 | 0.0271 | 0.0271 | 0.0272 | 0.0272 | 0.0273 | 0.0274 | 0.0274 | 0.0275 | 0.0276 | 0.0283 |
| 55 | 0.0298 | 0.0298 | 0.0299 | 0.0299 | 0.0299 | 0.0300 | 0.0301 | 0.0301 | 0.0302 | 0.0303 | 0.0309 |
| 60 | 0.0325 | 0.0325 | 0.0326 | 0.0326 | 0.0326 | 0.0327 | 0.0327 | 0.0328 | 0.0329 | 0.0330 | 0.0335 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bachmann, C.M.; Eon, R.S.; Lapszynski, C.S.; Badura, G.P.; Vodacek, A.; Hoffman, M.J.; McKeown, D.; Kremens, R.L.; Richardson, M.; Bauch, T.; et al. A Low-Rate Video Approach to Hyperspectral Imaging of Dynamic Scenes. J. Imaging 2019, 5, 6. https://doi.org/10.3390/jimaging5010006
Bachmann CM, Eon RS, Lapszynski CS, Badura GP, Vodacek A, Hoffman MJ, McKeown D, Kremens RL, Richardson M, Bauch T, et al. A Low-Rate Video Approach to Hyperspectral Imaging of Dynamic Scenes. Journal of Imaging. 2019; 5(1):6. https://doi.org/10.3390/jimaging5010006
Chicago/Turabian StyleBachmann, Charles M., Rehman S. Eon, Christopher S. Lapszynski, Gregory P. Badura, Anthony Vodacek, Matthew J. Hoffman, Donald McKeown, Robert L. Kremens, Michael Richardson, Timothy Bauch, and et al. 2019. "A Low-Rate Video Approach to Hyperspectral Imaging of Dynamic Scenes" Journal of Imaging 5, no. 1: 6. https://doi.org/10.3390/jimaging5010006
APA StyleBachmann, C. M., Eon, R. S., Lapszynski, C. S., Badura, G. P., Vodacek, A., Hoffman, M. J., McKeown, D., Kremens, R. L., Richardson, M., Bauch, T., & Foote, M. (2019). A Low-Rate Video Approach to Hyperspectral Imaging of Dynamic Scenes. Journal of Imaging, 5(1), 6. https://doi.org/10.3390/jimaging5010006





