Abstract
Background Estimation is a common computer vision task, used for segmenting moving objects in video streams. This can be useful as a pre-processing step, isolating regions of interest for more complicated algorithms performing detection, recognition, and identification tasks, in order to reduce overall computation time. This is especially important in the context of embedded systems like smart cameras, which may need to process images with constrained computational resources. This work focuses on accelerating SuperBE, a superpixel-based background estimation algorithm that was designed for simplicity and reducing computational complexity while maintaining state-of-the-art levels of accuracy. We explore both software and hardware acceleration opportunities, converting the original algorithm into a greyscale, integer-only version, and using Hardware/Software Co-design to develop hardware acceleration components on FPGA fabric that assist a software processor. We achieved a 4.4× speed improvement with the software optimisations alone, and a 2× speed improvement with the hardware optimisations alone. When combined, these led to a 9× speed improvement on a Cyclone V System-on-Chip, delivering almost 38 fps on 320 × 240 resolution images.
1. Introduction
Many computer vision applications rely on scanning an image by applying a sliding window across the image, whether it is a simple filter operation or a more complex object detection and recognition task. The use of multi-scale image pyramids may mean that the entire image is effectively scanned multiple times. In many scenarios, this is wasteful because the regions or objects of interest only occupy some of the image space, while the majority of the camera view yields negative results. Background estimation (also known as background subtraction, background modelling, or foreground detection) is a popular method of segmenting images in order to isolate foreground regions of interest. This allows for further analysis with subsequent algorithms, saving computation time by processing a smaller image and therefore iterating over fewer window positions.
However, using background estimation has two limitations. Firstly, sequential frames in a video are usually required in order to compare frames to each other and classify similar parts of the images as background, and there is a general assumption that objects of interest are moving between frames. This eliminates the applicability of background estimation in some offline image processing applications where the images contain no notion of time or may be entirely independent, but for most real-world applications there is some continuous monitoring where multiple frames of the same view are captured. Secondly, background estimation is not free; it still requires some computation time, and that computation time must be sufficiently low to justify introducing background estimation before running more complex algorithms.
While computation time is a critical factor for justifying background estimation, most of the literature focuses on incrementally improving accuracy with new algorithms at any cost. Popular pixel-level models such as the Gaussian Mixture Model (GMM) [1] have been around for decades, but recent approaches have included applying adaptive weights and parameters [2,3], deep convolutional neural networks [4,5,6], and ensemble models with stochastic model optimisation [7], all of which significantly increase computation time while only marginally improving accuracy, failing to address the challenges of real-world implementation.
Instead of blindly pursuing gains in accuracy, once a sufficient level of accuracy has been reached we should focus on accelerating those approaches, in order to minimise the impact of background estimation in more complex image processing pipelines with multiple stages. In our previous work, we applied superpixels to ViBE [8], a popular background estimation algorithm, and incorporated further optimisations of computation time to develop an algorithm called SuperBE [9]. We were able to achieve real-time processing with speeds of approximately 135 fps on 320 × 240 resolution images on a standard desktop PC while maintaining comparable accuracy to other state-of-the-art algorithms. In this work, we make two contributions by exploring further acceleration in two directions. Firstly, since the original SuperBE algorithm used RGB images with floating-point mathematics, we target software acceleration by investigating the effect of reducing the amount of information being processed by using greyscale and integer-only versions of SuperBE. Secondly, we developed an embedded system implementation of the algorithm with constrained computational resources for a real-world use case, targeting hardware acceleration by using Hardware/Software Co-design techniques [10] to partition the algorithm on a System-on-Chip (SoC) with an ARM processor and connected Field Programmable Gate Array (FPGA) fabric. In both cases, we present quantitative results justifying our acceleration strategies, while also detailing the effects on accuracy. The primary intention of the paper is to show how an algorithm like SuperBE can be accelerated in a variety of ways, in detail, without requiring software developers to spend excessive amounts of time on learning how to develop hardware.
In Section 2, we present some related works in the area of real-time background estimation and acceleration of background estimation algorithms, including a summary of the SuperBE algorithm to provide full context for this paper. In Section 3 and Section 4, we provide a detailed description of the software and hardware acceleration procedures explored in this work, as well as full experimental results demonstrating the effectiveness of these acceleration strategies in Section 3.1 and Section 4.1. We present our conclusions and ideas for future work in Section 5.
2. Literature Review and Background
2.1. Fast Background Estimation
While basic background estimation algorithms such as frame differences, running averages, and median filters are very fast, they tend to suffer from an inability to deal with high-frequency salt and pepper noise as well as low-frequency environmental changes such as lighting variations over time [11]. First popularised by Stauffer and Grimson [1] in 1999 and improved upon by others including [12,13,14], the Gaussian Mixture Model (GMM) remains one of the most popular background estimation algorithms today, primarily because of its simplicity and wide availability as one of the default algorithms available in most image processing libraries. In many applications, a GMM approach is “good enough” for background estimation, even though it still produces a substantial amount of noise from false positives and negatives. For applications where false positives or negatives are costly, such as safety-critical systems, acceptable error rates will depend on the requirements of the specific application and may need to be further reduced. This can somewhat be alleviated through the use of post-processing filters, but this adds further computation time. On the challenging CDW2014 [15] dataset, the Zivkovic GMM [12] misclassifies just under 4% of all pixels across the 11 categories and 53 video sequences. The error rate is also known as the Percentage of Wrong Classifications (PWC). However, it is important to note that this is an average. Figure 1 shows the difference in segmentation quality between different levels of PWC on different video sequences. The figure shows that even a 4% PWC can appear to be poorly segmented, while a 1.3% PWC is perhaps sufficiently accurate, but this will strongly depend on the end application.

Figure 1.
Examples of background estimation with different levels of PWC. In each row, the leftmost image is the raw image, the middle image is the ground truth, and the right image is the output of the Zivkovic GMM algorithm [12], with the approximate PWC and name of the sequence from the CDW2014 [15] dataset on the right.
Current state-of-the-art methods are able to reduce that error rate to less than 2%, but this has come with a heavy computation cost. Whereas the Zivkovic GMM can achieve around 49 fps on this dataset on a standard desktop computer, Ref. [6] requires a high-end Graphics Processing Unit (GPU) to achieve 18 fps, Ref. [16] achieves 8–9 fps on a desktop computer, and Ref. [3] only achieves 2 fps for 320 × 240 video on a high-end i5 CPU. While improving accuracy is important, the trade-off between accuracy and speed needs to be more carefully considered, as more accurate algorithms are unlikely to be adopted in the real world if they cannot justify slow computation times. Comprehensive background estimation survey papers are available in [17,18,19].
In most background estimation methods, the algorithm works at the pixel level. This means that for every pixel in the image, a background model is maintained and compared against pixels from newer frames to determine whether that pixel should be classified as background or foreground for the current frame. Colour is generally the feature that is used to describe the pixels and ascertain differences, although depth/range can also sometimes be used [20]. We also generally include a model update step to allow the model to adapt over time to changes in environmental conditions. The computation time is therefore strongly dependent on the number of pixels in the image, which presents an issue in terms of scalability as imaging technology continues to improve and image resolutions increase. SuperBE [9] addressed this by incorporating the use of superpixels (groups of pixels clustered together for colour and spatial coherency) into the popular background estimation algorithm ViBe [8]. Superpixels have been used in background estimation in the literature before [21,22,23,24], but most works in the literature still have very high computation times, particularly because superpixel segmentation is relatively expensive.
2.2. SuperBE
Using the SLICO [25] algorithm to generate superpixels, SuperBE essentially reduces the number of elements that need to be classified in background estimation, based on the assumption that all of the pixels within a superpixel cluster are very likely to have the same foreground or background classification. Reducing the number of elements means that fewer background models need to be maintained, compared against, and updated, decreasing both memory requirements and computation time. SuperBE is shown in Figure 2, and it can be seen how the superpixels form the main shape of the output background mask that can then be post-processed to form a contiguous region of interest.

Figure 2.
SuperBE on the CDW2014 backdoor sequence, showing the superpixel segmentation (top-left), the output mask without (top-right) and with (bottom-left) post-processing, and then with the mask applied to the original image (bottom-right).
As shown in Figure 3, SuperBE is comprised of two main processes. The first process is model initialisation, where a single frame is provided to the algorithm so that the background model can be created for the first time. After pre-processing, we apply superpixel clustering to group the pixels in the image, identifying the bounds of background objects and grouping similarly coloured areas together. It is important to note that superpixel clustering is only performed once in the entire algorithm, during initialisation, and not performed again for each subsequent frame, leading to significant speed increases in comparison to other superpixel-based algorithms as clustering can be computationally expensive. This is generally suitable in static surveillance cases, although in scenarios with panning cameras or dynamically changing backgrounds it may be necessary to re-initialise the algorithm more regularly. Then, we use the clusters to initialise the background model based on the colour means and colour covariance matrices of each superpixel. For each superpixel, we store multiple background samples to maintain robustness over time, although initially they are set to be identical. This helps compensate for only performing superpixel clustering once at initialisation by allowing for some variation in the background model when matching.
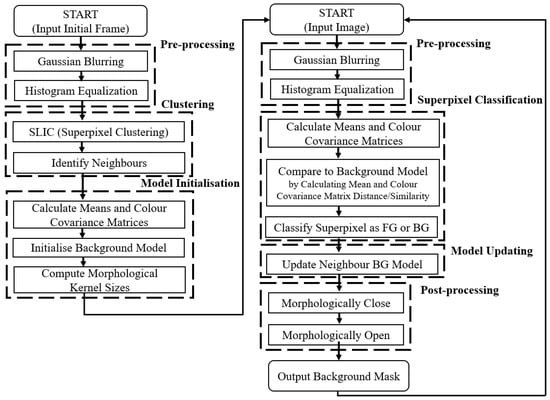
Figure 3.
Flowcharts showing the background model initialisation (left) and frame masking (right) processes of SuperBE [9].
The second process is frame masking, where subsequent frames in the video sequence are presented to the algorithm and an output background mask is produced. For each frame, SuperBE applies the same superpixel segmentation obtained in the initialisation process, and then classifies each superpixel as background or foreground based on its similarity to the background model samples in terms of colour means and covariance. For each superpixel, the algorithm iterates through the background model samples, and checks if the similarity is below a parameterised threshold. Once enough background model samples have been found to be similar enough to the current superpixel (based on another parameter), then the algorithm exits that superpixel and classifies it as background. This is done to reduce time spent unnecessarily checking excess background model samples when only a few are required to accurately classify the superpixel as background.
While computing the mean and colour covariance matrix is relatively fast, computing the similarity of two colour covariance matrices is challenging. In SuperBE, the Jensen-Bregman LogDet Divergence was used for its computational efficiency, but that computational efficiency only holds true for complex processors that can compute logarithm operations quickly, making it less suitable for simpler processors or pure hardware implementation.
If the current superpixel values are sufficiently similar to those in the background model, then the content of the superpixel has not changed substantially and is probably also background. In this case, we also conduct a model update step by randomly replacing one of the background model samples with the values from the current superpixel, so that over time the background model incorporates minor variation in the background pixels in order to remain robust against low-frequency environmental changes. The algorithm also updates the background model for a random neighbouring superpixel with the values from the current superpixel. This helps improve robustness against small spatial shifts and allows neighbouring superpixels to “invade” each others models in order to erode false positives over time. These update procedures are relatively computationally light, as they are mostly comprised of control flow operations and memory reads/writes. The random selection of samples to be replaced is challenging to emulate in hardware, but it appears that the algorithm does not need true randomness, and some pseudorandom approach with a relatively uniform distribution should be sufficient. An optional post-processing step using morphological closing and opening can help reduce the amount of false positive noise patches and false negative holes in the resultant output mask. However, these morphological operations are very computationally expensive, as they tend to require multiple passes across the entire image and need to store multiple copies of the image in order to perform accurately.
The resulting algorithm is both fast and sufficiently accurate for most applications, reaching 135 fps on 320 × 240 images on an i7 CPU using only one core, while achieving an error rate of between 0.4–3% depending on the type of video. However, it is important to investigate how to make the algorithm even less computationally expensive so that it can still achieve good speeds on resource constrained systems with less powerful processing capabilities. This is especially important for enabling the development of useful smart cameras: imaging devices with embedded processing hardware, that either partially or fully process video streams at the point of image capture. In the subsequent acceleration, we mostly focus on the frame masking process (on the right of Figure 3), since the model initialisation process is only executed once and is therefore not an important factor in the long-run execution time. The key reason to focus on SuperBE is that it is more accurate that algorithms like GMM without introducing the significant computation costs of more modern background estimation approaches.
2.3. Hardware Implementations
Some literature does exist for describing systems that implement various background estimation algorithms on hardware platforms with the goal of achieving real-time speeds. Ref. [26] implements a GMM algorithm on a high-end GPU device, achieving speeds of over 50 fps for high-definition video. A separate work, Ref. [27], reports that a GPU implementation of GMM has a 5× speed-up over CPU implementations, reaching 58.1 fps for 352 × 288 resolution images. A competing FPGA implementation of GMM reported 20 fps at a 1920 × 1080 resolution [28], while a FPGA implemenation of ViBe achieved 60fps on 640 × 480 resolution images [29]. Alternatively, instead of taking an existing background estimation algorithm and merely porting it to a hardware device, algorithm designers could take the hardware architecture into account to leverage memory structures and parallelism. A method that is highly optimised for hardware using a codebook implementation on an FPGA achieved 50 fps on 768 × 576 resolution images [30]. Using a simple convolutional filter as the main processing step in their algorithm, Ref. [31] reports 60 fps on 800 × 480 images, although the simplicity of their approach is likely to lead to low accuracy on large images.
Unfortunately, the largest challenge with hardware design has generally been the high level of skill needed, and the associated high development time and cost required for well-optimised designs. While pure hardware designs can be very fast, this continuing challenge impedes adoption of faster hardware systems. This can partly be addressed through the use of Hardware/Software Co-Design. In these systems, the algorithm is still predominantly software-based and controlled on a standard CPU, but parts of the processing are offloaded to specialised hardware accelerator components that can decrease the computation time significantly. Ref. [32] leverages shared memory resources to compute multi-modal background masks based on a GMM approach on a FPGA, achieving 38 fps on 1024 × 1024 resolution images. In [33], a kernel based tracking system is implemented on an FPGA with a soft processor, reporting hundreds of frames per second based on a window size of 64 × 64 pixels with pipelining to process multiple frames at the same time. Ref. [34] implemented the Mixture of Gaussians (MoG) algorithm using many pipeline stages in hardware with an ARM processor to achieve real-time background estimation on Full-HD images. Nevertheless, there are relatively few HW/SW Co-design systems for background estimation published in the literature, and even fewer using modern background estimation techniques. In a bid to balance higher levels of accuracy with acceptably fast computation times, we propose to implement SuperBE on an embedded platform. While SuperBE as an algorithm is more complex and therefore slower than GMM or similar methods previously accelerated, it has an average PWC of 1.75%, much better than the 4% error rate expected from GMM (both scores measured on the CDW2014 dataset). In our work, we target a hard CPU with attached FPGA fabric, using a similar strategy from [10] to partition SuperBE into software and hardware components with the intention of accelerating computation on an embedded system. This improves upon the existing literature by accelerating a new algorithm that achieves better accuracy than most of the existing hardware implementations of background estimation algorithms, with real-time speeds on an embedded system.
3. Software Acceleration
Our main strategy for reducing computation time is to reduce the amount of information that needs to be processed while maintaining a sufficiently high accuracy. We produced three new versions of the algorithm: greyscale-only, integer-only, and a combined greyscale + integer version. In [8], it is reported that a greyscale variant of their background estimation algorithm is approximately 15% faster than the RGB version, with a less than one percentage point increase in the error rate. In the context of SuperBE, each superpixel is described by its colour means and colour covariance matrices. Since there are three colour channels, this results in three mean values and a 3 × 3 matrix for each superpixel. In a greyscale version, we still need to describe the superpixel in terms of its mean and variance, but this becomes much simpler as there is only one channel. While reducing the colour means from three to one would not have a large impact, replacing the colour covariance matrix calculation and the covariance matrix similarity calculation with a simple single-variable variance leads to a much lower computational complexity. By removing the covariance matrix similarity calculation, we also remove a number of logarithm operators that produce odd results at extreme values, which could lead to a positive effect on the accuracy. In addition to this, histogram equalisation tends to have less of an impact on greyscale images than colour images, so we removed this step from greyscale versions of SuperBE to further reduce computation time.
Since we will eventually target a hardware device, it is also worth considering the effect of casting/rounding all numbers in an integer-only version of the algorithm. For a standard desktop CPU, floating-point mathematics is well optimised, so there may not be a large speed improvement. On many smaller processors used in embedded devices, simpler processor architectures may not include specialised hardware for floating-point operations, causing these operations to be extremely costly. Implementing floating-point mathematics on hardware is also much more resource-intensive than fixed-point mathematics, restricting most designs to fixed-point or integer-based arithmetic [35]. We should expect there to be some increase in error as a result of losing precision, but it is likely to be small since background estimation is generally looking for relatively large changes in features. However, casting or rounding of the numbers is not the only effect of moving towards an integer-only version of the algorithm; operators such as log and square root also need to be approximated with integers, which could potentially lead to larger errors in output.
3.1. Software Evaluation
To test the effect of these optimisations, we used the Change Detection Workshop CDW2014 dataset [15], excluding the three categories PTZ, intermittent object motion, and thermal, which were also omitted in the original SuperBE paper as it is unsuitable for these video types. The tested video sequences included low framerates, shaky cameras, poor image quality, and a variety of image resolutions ranging from 320 × 240 to 720 × 576. As shown in Table 1, experiments were conducted both with and without post-processing, where the reference algorithm was the one provided in the original SuperBE paper [9]. The main metric that we used for accuracy was the Percentage of Wrong Classifications (PWC), which is equivalent to the error rate, calculated by dividing the number of incorrectly classified pixels by the total number of pixels and converting to a percentage. The speeds given in FPS are normalised for a 320 × 240 resolution image, meaning that we take all of the speeds from the different image resolutions, and then scale them based on the number of pixels to a 320 × 240 resolution image in order to make a fair comparison between methods. The relative speed for each version is given relative to the reference version. All experiments were conducted on the same laptop computer, with a 2.4 GHz i7-4700HQ CPU, 16GB of RAM, running Linux Kubuntu 17.04. The algorithms are implemented in C++, compiled with -O3.

Table 1.
Software Acceleration Results.
As expected, the software optimisations significantly increased the speed of the algorithm. In the integer-only case, there is an unexpected improvement to the accuracy as well—this was identified to be due to the approximated log function in the integer version, which was clamped to not return negative values, whereas the reference version included a log function that would sometimes give very negative values that could cause misclassification of superpixels. The grayscale version does increase the error rate, but this is still low enough to be suitable for many applications. It appears that the grayscale optimisation has a much larger impact on speed than the integer optimisation, which makes sense since there is substantially less data being processed in the grayscale version, while the integer version relies on the differences between integer processing units and floating-point processing units being significant.
It should be noted that with post-processing, the grayscale and grayscale + integer cases have very similar error rates and speeds, performing far worse than without post-processing. This would suggest that the current post-processing scheme of morphologically closing and then opening the background mask may not be as suitable when applied to an output derived from grayscale data. This is further supported by the fact that the grayscale and grayscale + integer versions have worse accuracy with post-processing than without. It appears that this post-processing method also does not justify itself in terms of computation time, as in the reference and integer-only cases it only reduces the error rate by about 0.1–0.2% but slows down the algorithm by 45–55%.
For a standard case where SuperBE is being used on a desktop PC or in the cloud, the grayscale version without post-processing is likely to be sufficient in terms of accuracy while delivering very fast speeds. If it is desirable to add the integer optimisation on top for hardware implementation, then the effect on accuracy is relatively limited and likely to be acceptable in exchange for the further improvement in speed. Based on these results, we targeted the grayscale + integer version without post-processing for embedded implementation and hardware acceleration. A flowchart of the resultant simplified algorithm is shown in Figure 4.
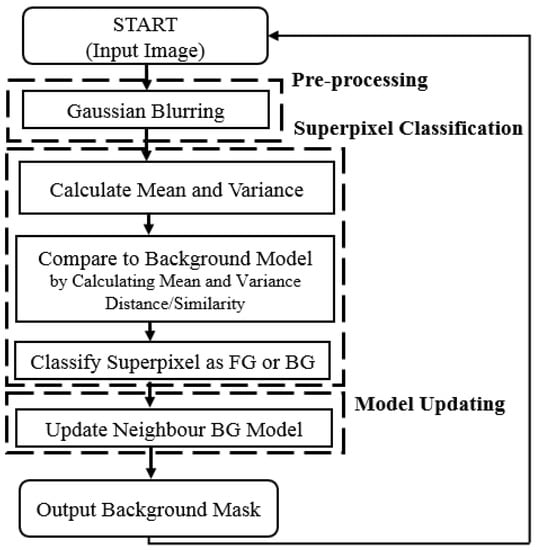
Figure 4.
Flowchart of the simplified Greyscale + Integer algorithm for embedded implementation.
4. Hardware Acceleration
It is theoretically possible that SuperBE could be entirely implemented in hardware, for example by describing the algorithm through components in a Hardware Description Language (HDL) and then synthesising onto a FPGA. However, this is a very time consuming and high-skill task, and some of the components might not deliver any better performance than if the same functionality was implemented in software on a CPU. In our approach, we use HW/SW Co-design to achieve the maximum improvement in speed for the least amount of development time, while maintaining sufficient accuracy. This involves combining a Hard Processor System (HPS) which executes the software, with hardware circuits on FPGA fabric. The most important step in partitioning an algorithm between hardware and software is therefore determining which parts of the algorithm are the most computationally expensive, so that if accelerated, would have the largest effect on the computation time. In our case, we used Valgrind with Callgrind to perform execution profiling on the algorithm across a few thousand frames. The results are shown in Table 2. Note that the values in this table do not sum to 100% because we have not included steps that cannot be easily accelerated in our system, such as reading the image in from memory or initialising matrices and vectors.

Table 2.
Runtime Analysis of SuperBE.
In addition to a timing analysis, the communication requirements need to be taken into consideration. In a HW/SW Co-design system, some data communication has to occur between the Hardware (HW) component and the Software (SW) component, which requires a non-zero amount of time. In [10], we identified that the communication channels can become the bottleneck that prevents faster speeds from being achieved. If multiple non-sequential tasks are partitioned onto the hardware, then data needs to be passed between the HW and SW units multiple times. Therefore, it is desirable, where possible, to complete a contiguous block of the algorithm together on the HW accelerator, and then pass the data to the SW processor for completion. Taking the computation and communication times into account, we decided to accelerate the two earliest stages of the algorithm, Gaussian blurring and the mean/variance calculation. It makes sense that these are the stages that may require the most computation time because they process the largest amount of data—after the mean/variance calculation, the algorithm represents each superpixels with two numbers, rather than all of the pixel values within the superpixel, essentially reducing the amount of data that needs to be processed in subsequent steps. We did not accelerate the similarity calculation step because there would be significant communication and memory overheads, as the background model values would need to be either transferred between the HPS and FPGA regularly or duplicated and updated on the FPGA side as well as the HPS side. A high-level block diagram of the hardware partition is shown in Figure 5, showing the data flow between the HPS and FPGA as well as the different hardware components. The buffers shown are modular Scatter Gather DMA (mSGDMA) IP blocks from Intel (Altera) that provide interfacing between the HPS and FPGA, allowing the memory-mapped interface of the HPS to feed into a streaming First-In-First-Out (FIFO) buffer on the FPGA. Control signals are omitted, since the only control signal comes from the HPS to the FPGA to tell the components to reset and start again when a new image is being transferred across.
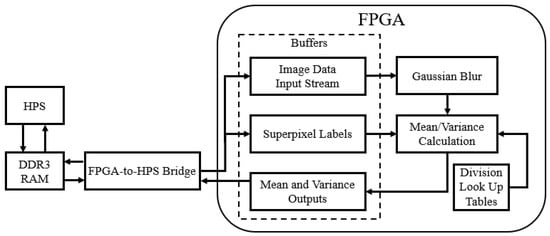
Figure 5.
Top-level architectural diagram of the hardware partition, with arrows representing data flow.
Our target execution platform is the DE1-SoC development board, which has an Altera Cyclone V 5CSEMA5F31C6 System-on-Chip (SOC) device. This device includes a dual-core ARM Cortex A9 (which we refer to as the hard processor system or HPS) and FPGA logic cells, Digital Signal Processing (DSP) blocks, and memory resources. A conceptual diagram of the HPS-FPGA system is shown in Figure 6, where the AMBA AXI bridges between the HPS and FPGA are shown in bold arrows. These bridges allow two-way communication, so that the master side can send an instruction to request data and have the result returned on the same bridge. Therefore, communication between the HPS and FPGA is not single-cycle, creating an overhead for each transaction. We do save some transfer time by interfacing the FPGA with the external memory (RAM) module so that image data can be read directly, rather than transferring the data from the RAM to the HPS and then through the HPS-to-FPGA bridge. We described our hardware components in VHDL, and then synthesised onto the FPGA fabric.
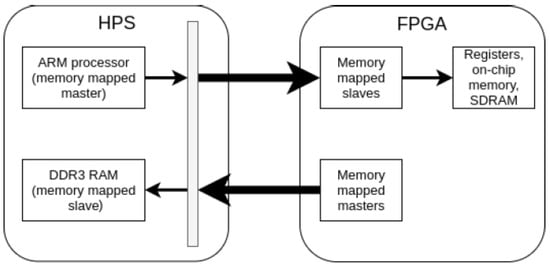
Figure 6.
Block diagram showing the software (HPS) and hardware (FPGA) partitions of the Cyclone V SOC device.
The Gaussian blur was implemented using a sliding window approach based on [10,36], shown in Figure 7. Essentially, the filter operation is parallelised so that the convolution operator can be applied to pixels simultaneously, with a Gaussian kernel to create a blurring effect. To further reduce hardware resource consumption, instead of implementing floating-point multipliers (since a standard Gaussian kernel has floating-point values), the kernel was approximated with powers of two so that the appropriate right shifts could be applied to the binary values instead using combinational logic. While this is not a perfect Gaussian blur, it should sufficiently filter out high frequency noise, while remaining a single-cycle operation with a small hardware footprint.
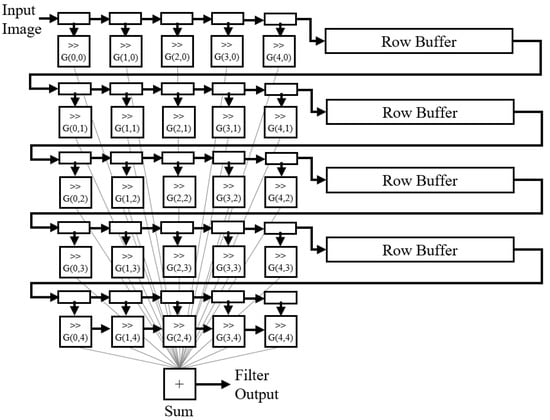
Figure 7.
A block diagram showing a 5 × 5 Gaussian blur operator in hardware, where indicates a right shift and G is a matrix representing the Gaussian kernel.
The mean and variance calculation was more challenging to implement in hardware, as it needs to iterate through all of the pixel values within each superpixel. Traditionally, a two-pass method is used, where the first pass calculates the mean, and then the second pass uses the previously computed mean to determine the variance. This has a critical drawback in that either we have to transfer the pixels between the SW and HW subsystems twice (once for each pass) to stream the data through, or we need a substantial amount of memory on the HW side to store an entire image’s worth of pixels. Instead, we used the modified Welford algorithm [37,38], shown in Algorithm 1, which can compute mean and variance in a single pass but may introduce some small error.
This method does require the use of division, which normally requires multiple cycles and is relatively computationally expensive in comparison to addition or multiplication operations. To simplify the division operator, we used a multiply-shift approach and a Look Up Table (LUT) for all possible division values, since we know that the operation is limited to integer values between 1 and 255. Empirically we found that for the image resolutions we were working with, the largest superpixel contained 165 pixels, so we set a safe upper bound of 255 for the denominator, allowing us to store a finite number of multiply-shift parameters. Using the LUT, we can approximate any division operation by multiplying the numbers together and then shifting right, which is the same as dividing by a power of two. While this method does introduce some error since it is an integer approximation, it can be completed in a single pass of all the pixels and is much faster than a standard division operation.
| Algorithm 1 Modified Welford algorithm for calculating mean and variance in a single pass |
|
To summarise the communication requirements between the FPGA and HPS shown in Figure 5, for each image being processed, the image data input stream receives one value per pixel (the greyscale intensity of that pixel), the superpixel labels register receives one value per pixel (representing the superpixel number for that pixel), and the mean and variance outputs register returns two numbers per superpixel (a mean and a variance). In order to make full use of the communication buses between the FPGA fabric and HPS, we use the full-size 128-bit bridge, with data packing to concatenate as much data together before transmission in order to minimise the number of transactions and therefore the communication overheads. The FPGA was clocked at 50 MHz during testing, with interconnect logic clocked at 150 MHz, although it could potentially be run at a higher clock frequency depending on the device.
4.1. Hardware Evaluation
As shown in Table 3, running SuperBE in software alone (using the HPS only) is much slower than on a Desktop PC. This is predominantly caused by the fact that the embedded processor is much slower, running at 800 MHz with a Reduced Instruction Set Computer (RISC) architecture in comparison to the 2.4 GHz+ CPU on a laptop or desktop. We use the HPS-only version as the reference embedded benchmark against which hardware accelerated versions should be compared. Firstly, parallelising the Gaussian blur operator has a negligible effect on speed, as the speed gain through parallelisation in hardware barely covers the added communication overheads. It is theoretically possible to increase the throughput of the Gaussian blur component further by instantiating multiple copies of the component and dividing the image into blocks for processing in parallel [39], but this further increases the hardware cost and is likely to still be constrained by the communication bandwidth between the HPS and FPGA.

Table 3.
Hardware Acceleration Results.
The hardware versions of the mean and variance operations add speed to the system, although this is at the cost of also introducing significant error, which should be expected since we are using multiple approximations in that calculation. This is an approximate computing trade-off, where we could have a higher level of accuracy, but this would require more hardware resources and likely reduce the speed. The final HW/SW Co-design version with both Gaussian blurring and the mean/variance calculation accelerated on FPGA in one contiguous block yields a speed of 37.91 fps (normalised for 320 × 240 resolution images), a 2× increase from the HPS-only Grayscale + Integer version. This comes at the cost of approximately 1% extra error introduced into the system, which is likely to be acceptable for most purposes. More importantly, we can compare the final version to the original colour SuperBE algorithm being run on the HPS to find the overall improvement from both the software and hardware optimisations on the same test platform. The overall 9x speed improvement more than justifies the 1.4% higher error.
In all previous results in this paper, the computation times have been normalised for a 320 × 240 image size. In the first part of Table 4, we show how that time varies as the image resolution becomes larger, reaching 720p. As the image becomes larger, the computation time will increase, which is due to the fact that there are more pixels to process when calculating the mean and variance of each superpixel. As the modified Welford algorithm allows this to be done in one pass, the increase in computation time is linear, or in other words, this part of the algorithm is O(n) complex. Since this algorithm is superpixel-based, the classification and model update steps do not increase based on the image resolution, since the number of superpixels remains relatively similar. However, the resolution is not the only factor that influences the computation time; the more dominating factor is how much of the image is foreground, since SuperBE has to spend more time comparing superpixel values to past model values to confirm that the superpixel is foreground. This is reflected in the second part of Table 4, where the sequences with a grey background are from the lowFramerate and nightVideos categories, where the processing time per frame is considerably slower for the same image resolutions as the first part of the table. This is the primary reason that the normalised 320 × 240 speed is so much lower than the computation time for the backdoor sequence even though it is also 320 × 240—the more computationally expensive sequences pull the average computation time up (and therefore push the fps down).

Table 4.
Average Computation Times on Selected Sequences from CDW2014.
5. Conclusions and Future Work
This work presents the acceleration of a background estimation algorithm, SuperBE, in both the software and hardware worlds, through a systematic approach towards improving speed while maintaining acceptable levels of accuracy. In software, the main optimisations focused on reducing the amount of data to be processed by converting the algorithm into greyscale and integer-only versions, yielding a 4.38× speed improvement over the original algorithm (without post-processing) at the cost of a 0.6% higher error rate. In hardware, the main optimisations focused on accelerating the Gaussian blur and mean/variance calculation steps, parallelising these steps and adding more specialised computation units. This resulted in a further 2× speed improvement within the embedded implementation. When combined, there is a 9× speed improvement over the original SuperBE algorithm when executed on an embedded processor. This work shows that Hardware/Software Co-design is a valid approach for improving the performance of algorithms, without needing to invest significant resources to develop a pure hardware design. This work also provides evidence that SuperBE can be accelerated sufficiently to be used in embedded real-time processing contexts, especially where background estimation is used as a first step in an image processing pipeline to reduce the workload of subsequent algorithms.
In future work, there is opportunity for improvements to be made to both speed and accuracy if needed. One of the major challenges with Hardware/Software Co-design is always the introduction of increase communication time between the hardware and software platforms, which is often assumed by developed to be free but is actually non-zero and can contribute to a significant portion of the overall computation time. Further reducing the usage of the HPS-FPGA bridges would decrease the communication time, which could be done by directly loading images onto the FPGA and completing preliminary processing there, and then only sending the mean and variance values for each superpixel back across to the CPU for model comparison and updating. This may be challenging, as the first frame still needs to be provided to the CPU for model initialisation, as it would be very difficult to implement superpixel segmentation in hardware. Additionally, the value of doing so would be limited since it is only executed once, during initialisation. Alternatively, a device with wider or faster communication buses between the HPS and FPGA systems would reduce the communication and co-ordination costs. There is also potential for further parallelisation—the SOC CPU has more than one core, and multiple copies of the hardware components could be made to allow independent superpixels to be processed simultaneously if more hardware resourcing was available on a larger device. It is important to consider that most modern cameras provide HD 1080p image resolutions, so some further acceleration may be necessary to achieve real-time processing of high resolution imagery and video. Lastly, accuracy could be improved by further investigating the effect of different data widths in the hardware components; increasing the bit widths of the mean/variance component would likely make the results more accurate, but would also consume more hardware resources. Investigating more suitable post-processing schemes that clean up the output background masks, particularly in hardware, would also improve accuracy but introduce additional computational complexity.
Author Contributions
Conceptualization, A.T.-Y.C. and K.I.-K.W.; Methodology, A.T.-Y.C., R.G. and A.B.; Project administration, K.I.-K.W. and M.B.-A.; Development/Software, R.G. and A.B.; Supervision, A.T.-Y.C. and K.I.-K.W.; Validation, R.G. and A.B.; Writing—original draft, A.T.-Y.C.; Writing—review & editing, A.T.-Y.C., K.I.-K.W. and M.B.-A.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Stauffer, C.; Grimson, E. Adaptive Background Mixture Models for Real-time Tracking. In Proceedings of the 1999 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Collins, CO, USA, 23–25 June 1999; pp. 246–252. [Google Scholar]
- Hofmann, M.; Tiefenbacher, P.; Rigoll, G. Background segmentation with feedback: The Pixel-Based Adaptive Segmenter. In Proceedings of the 2012 IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops, Providence, RI, USA, 16–21 June 2012; pp. 38–43. [Google Scholar]
- Jiang, S.; Lu, X. WeSamBE: A Weight-Sample-Based Method for Background Subtraction. IEEE Trans. Circuits Syst. Video Technol. 2017, 28, 2105–2115. [Google Scholar] [CrossRef]
- Babaee, M.; Dinh, D.T.; Rigoll, G. A deep convolutional neural network for video sequence background subtraction. Pattern Recognit. 2018, 76, 635–649. [Google Scholar] [CrossRef]
- Wang, Y.; Luo, Z.; Jodoin, P.M. Interactive deep learning method for segmenting moving objects. Pattern Recognit. Lett. 2017, 96, 66–75. [Google Scholar] [CrossRef]
- Lim, L.A.; Keles, H.Y. Foreground Segmentation Using a Triplet Convolutional Neural Network for Multiscale Feature Encoding. arXiv, 2018; arXiv:1801.02225. [Google Scholar]
- Bianco, S.; Ciocca, G.; Schettini, R. Combination of Video Change Detection Algorithms by Genetic Programming. IEEE Trans. Evol. Comput. 2017, 21, 914–928. [Google Scholar] [CrossRef]
- Barnich, O.; van Droogenbroeck, M. ViBe: A Universal Background Subtraction Algorithm for Video Sequences. IEEE Trans. Image Process. 2011, 20, 1709–1724. [Google Scholar] [CrossRef] [PubMed]
- Chen, A.T.Y.; Biglari-Abhari, M.; Wang, K.I.K. SuperBE: Computationally-Light Background Estimation with Superpixels. J. Real-Time Image Process. 2018, 11, 1–17. [Google Scholar] [CrossRef]
- Chen, A.T.Y.; Biglari-Abhari, M.; Wang, K.I.K.; Bouzerdoum, A.; Tivive, F.H.C. Convolutional Neural Network Acceleration with Hardware/Software Co-design. Appl. Intell. 2017, 1–14. [Google Scholar] [CrossRef]
- Horprasert, T.; Harwood, D.; Davis, L.S. A statistical approach for real-time robust background subtraction and shadow detection. In Proceedings of the International Conference on Computer Vision, Kerkyra, Greece, 20–27 September 1999; pp. 1–19. [Google Scholar]
- Zivkovic, Z. Improved Adaptive Gaussian Mixture Model for Background Subtraction. In Proceedings of the 17th International Conference on Pattern Recognition, Cambridge, UK, 26 August 2004; Volume 2, pp. 28–31. [Google Scholar]
- KaewTraKulPong, P.; Bowden, R. An improved adaptive background mixture model for real-time tracking with shadow detection. Video-Based Surveill. Syst. 2002, 1, 135–144. [Google Scholar]
- Tian, Y.L.; Lu, M.; Hampapur, A. Robust and efficient foreground analysis for real-time video surveillance. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; Volume 1, pp. 1182–1187. [Google Scholar]
- Wang, Y.; Jodoin, P.; Porikli, F.M.; Konrad, J.; Benezeth, Y.; Ishwar, P. CDnet 2014: An Expanded Change Detection Benchmark Dataset. In Proceedings of the Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 24–27 June 2014; pp. 393–400. [Google Scholar]
- Sajid, H.; Cheung, S.C.S. Universal Multimode Background Subtraction. IEEE Trans. Image Process. 2017, 26, 3249–3260. [Google Scholar] [CrossRef] [PubMed]
- Brutzer, S.; Höferlin, B.; Heidemann, G. Evaluation of background subtraction techniques for video surveillance. In Proceedings of the Conference on Computer Vision and Pattern Recognition, Colorado Springs, CO, USA, 20–25 June 2011; pp. 1937–1944. [Google Scholar]
- Bouwmans, T. Traditional and recent approaches in background modeling for foreground detection: An overview. Comput. Sci. Rev. 2014, 11, 31–66. [Google Scholar] [CrossRef]
- Sobral, A.; Vacavant, A. A comprehensive review of background subtraction algorithms evaluated with synthetic and real videos. Comput. Vis. Image Underst. 2014, 122, 4–21. [Google Scholar] [CrossRef]
- Gordon, G.; Darrell, T.; Harville, M.; Woodfill, J. Background estimation and removal based on range and color. In Proceedings of the 1999 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Fort Collins, CO, USA, 23–25 June 1999; Volume 2, pp. 459–464. [Google Scholar]
- Giordano, D.; Murabito, F.; Palazzo, S.; Spampinato, C. Superpixel-based video object segmentation using perceptual organization and location prior. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 4814–4822. [Google Scholar]
- Lim, J.; Han, B. Generalized Background Subtraction Using Superpixels with Label Integrated Motion Estimation. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 173–187. [Google Scholar]
- Schick, A.; Bäuml, M.; Stiefelhagen, R. Improving foreground segmentations with probabilistic superpixel Markov random fields. In Proceedings of the 2012 IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops, Providence, RI, USA, 16–21 June 2012; pp. 27–31. [Google Scholar]
- Shu, G.; Dehghan, A.; Shah, M. Improving an Object Detector and Extracting Regions Using Superpixels. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 3721–3727. [Google Scholar]
- Achanta, R.; Shaji, A.; Smith, K.; Lucchi, A.; Fua, P.; Süsstrunk, S. SLIC Superpixels Compared to State-of-the-Art Superpixel Methods. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 2274–2282. [Google Scholar] [CrossRef] [PubMed]
- Pham, V.; Vo, P.; Hung, V.T. GPU Implementation of Extended Gaussian Mixture Model for Background Subtraction. In Proceedings of the 2010 IEEE RIVF International Conference on Computing & Communication Technologies, Research, Innovation, and Vision for the Future, Hanoi, Vietnam, 1–4 November 2010; pp. 1–4. [Google Scholar]
- Carr, P. GPU Accelerated Multimodal Background Subtraction. In Proceedings of the International Conference on Digital Image Computing: Techniques and Applications, Canberra, Australia, 1–3 December 2008; pp. 279–286. [Google Scholar]
- Genovese, M.; Napoli, E. FPGA-based architecture for real time segmentation and denoising of HD video. J. Real-Time Image Process. 2013, 8, 389–401. [Google Scholar] [CrossRef]
- Kryjak, T.; Gorgon, M. Real-time implementation of the ViBe foreground object segmentation algorithm. In Proceedings of the 2013 Federated Conference on Computer Science and Information Systems, Krakow, Poland, 8–11 September 2013; pp. 591–596. [Google Scholar]
- Rodriguez-Gomez, R.; Fernandez-Sanchez, E.J.; Diaz, J.; Ros, E. Codebook hardware implementation on FPGA for background subtraction. J. Real-Time Image Process. 2015, 10, 43–57. [Google Scholar] [CrossRef]
- Sánchez-Ferreira, C.; Mori, J.Y.; Llanos, C.H. Background subtraction algorithm for moving object detection in FPGA. In Proceedings of the 2012 Southern Conference on Programmable Logic, Bento Goncalves, Spain, 20–23 March 2012; pp. 1–6. [Google Scholar]
- Jiang, H.; Ardo, H.; Owall, V. Hardware accelerator design for video segmentation with multi-modal background modelling. In Proceedings of the 2005 IEEE International Symposium on Circuits and Systems, Kobe, Japan, 23–26 May 2005; Volume 2, pp. 1142–1145. [Google Scholar]
- Ali, U.; Malik, M.B. Hardware/software co-design of a real-time kernel based tracking system. J. Syst. Archit. 2010, 56, 317–326. [Google Scholar] [CrossRef]
- Tabkhi, H.; Sabbagh, M.; Schirner, G. An Efficient Architecture Solution for Low-Power Real-Time Background Subtraction. In Proceedings of the 2015 IEEE 26th International Conference on Application- specific Systems, Architectures and Processors, Toronto, ON, Canada, 27–29 July 2015; pp. 218–225. [Google Scholar]
- MacLean, W.J. An Evaluation of the Suitability of FPGAs for Embedded Vision Systems. In Proceedings of the Conference on Computer Vision and Pattern Recognition Workshops, San Diego, CA, USA, 20–26 June 2005; pp. 131–137. [Google Scholar]
- Bailey, D.G. Design for Embedded Image Processing on FPGAs; Wiley: Singapore, 2011. [Google Scholar]
- Ling, R.F. Comparison of Several Algorithms for Computing Sample Means and Variances. J. Am. Stat. Assoc. 1974, 69, 859–866. [Google Scholar] [CrossRef]
- Welford, B.P. Note on a Method for Calculating Corrected Sums of Squares and Products. Technometrics 1962, 4, 419–420. [Google Scholar] [CrossRef]
- Draper, B.A.; Beveridge, J.R.; Bohm, A.P.W.; Ross, C.; Chawathe, M. Accelerated image processing on FPGAs. IEEE Trans. Image Process. 2003, 12, 1543–1551. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).