Unsupervised Local Binary Pattern Histogram Selection Scores for Color Texture Classification
Abstract
:1. Introduction
2. Feature Selection Scores
2.1. Unsupervised Feature Selection Scores
2.1.1. Variance Score
2.1.2. Laplacian Score
- is the squared Euclidean distance between the rth feature of two images and ,
- is the similarity measure between and using all the input feature space composed by the D features. It is defined by: , where represents the squared Euclidean distance between and in the D-dimensional initial feature space [30,31]. The parameter t has to be tuned in order to represent the local dispersion of the data [32],
- represents a local density measure defined by: ,
- and is the weighted feature average: .
3. Histogram Selection Scores
3.1. Adapted Variance Score
3.2. Adapted Laplacian Score
4. LBP Histogram Selection for Color Texture Classification
4.1. Candidate Color Texture Descriptors
4.2. Histogram Selection
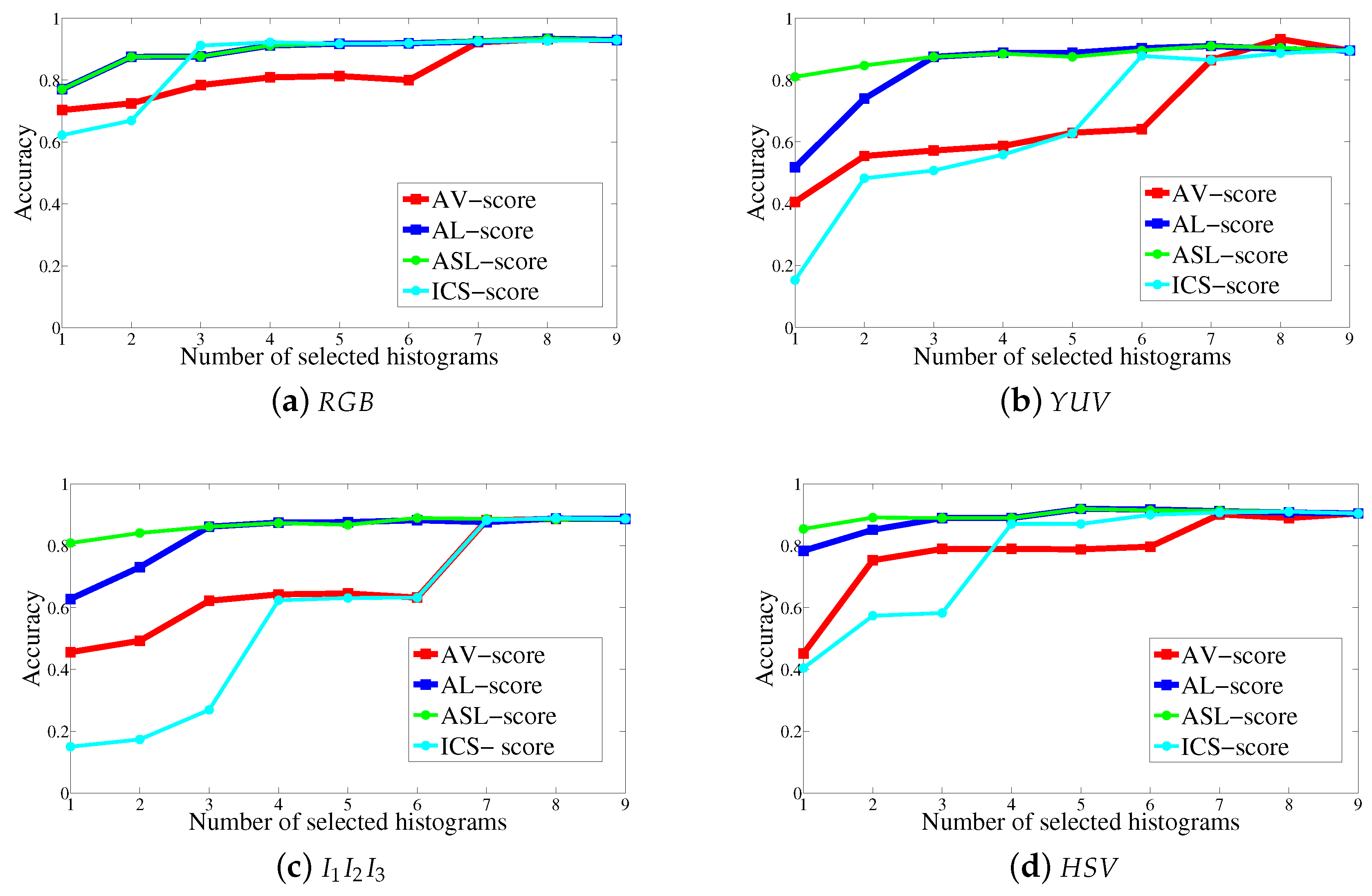
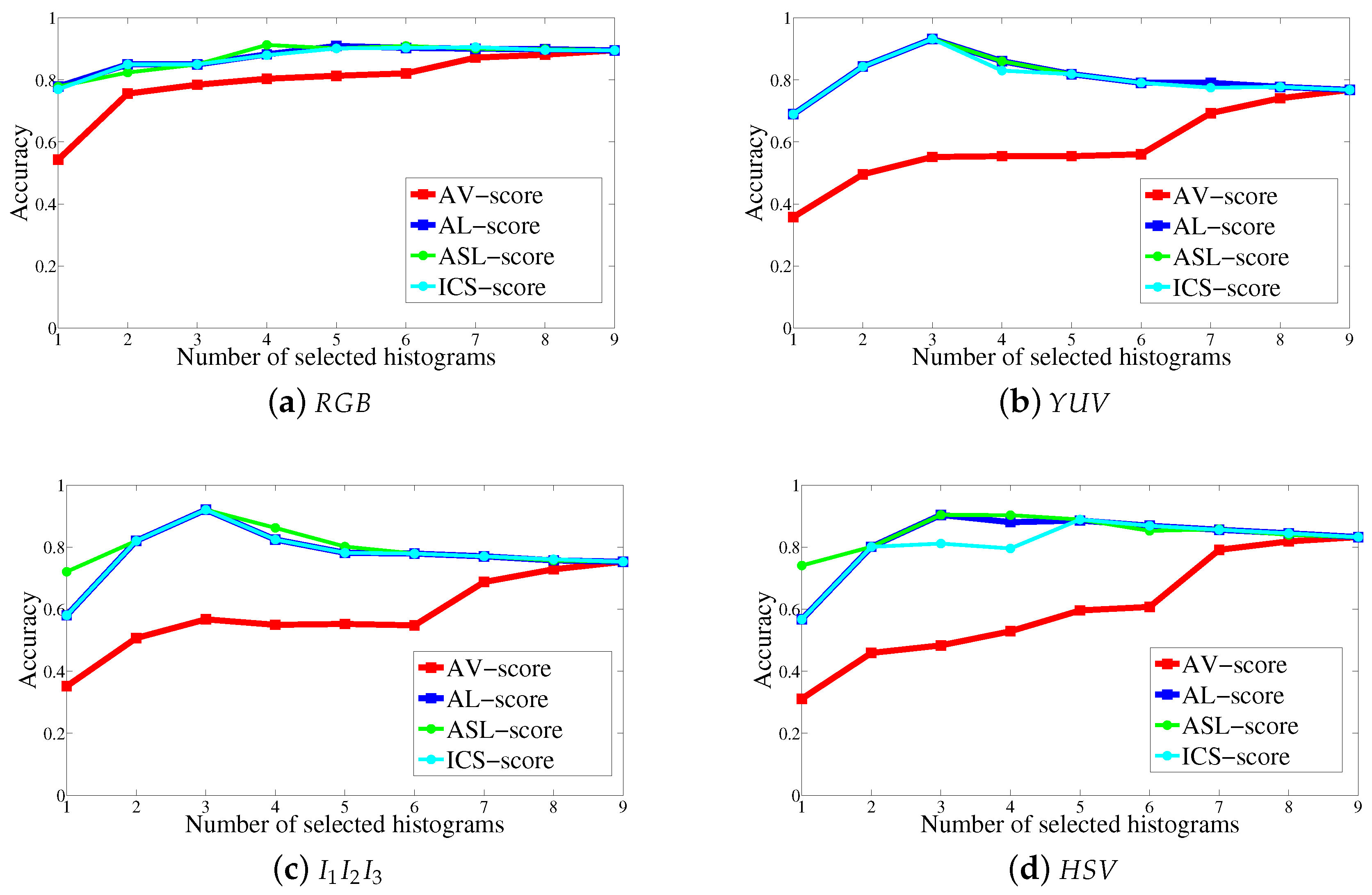
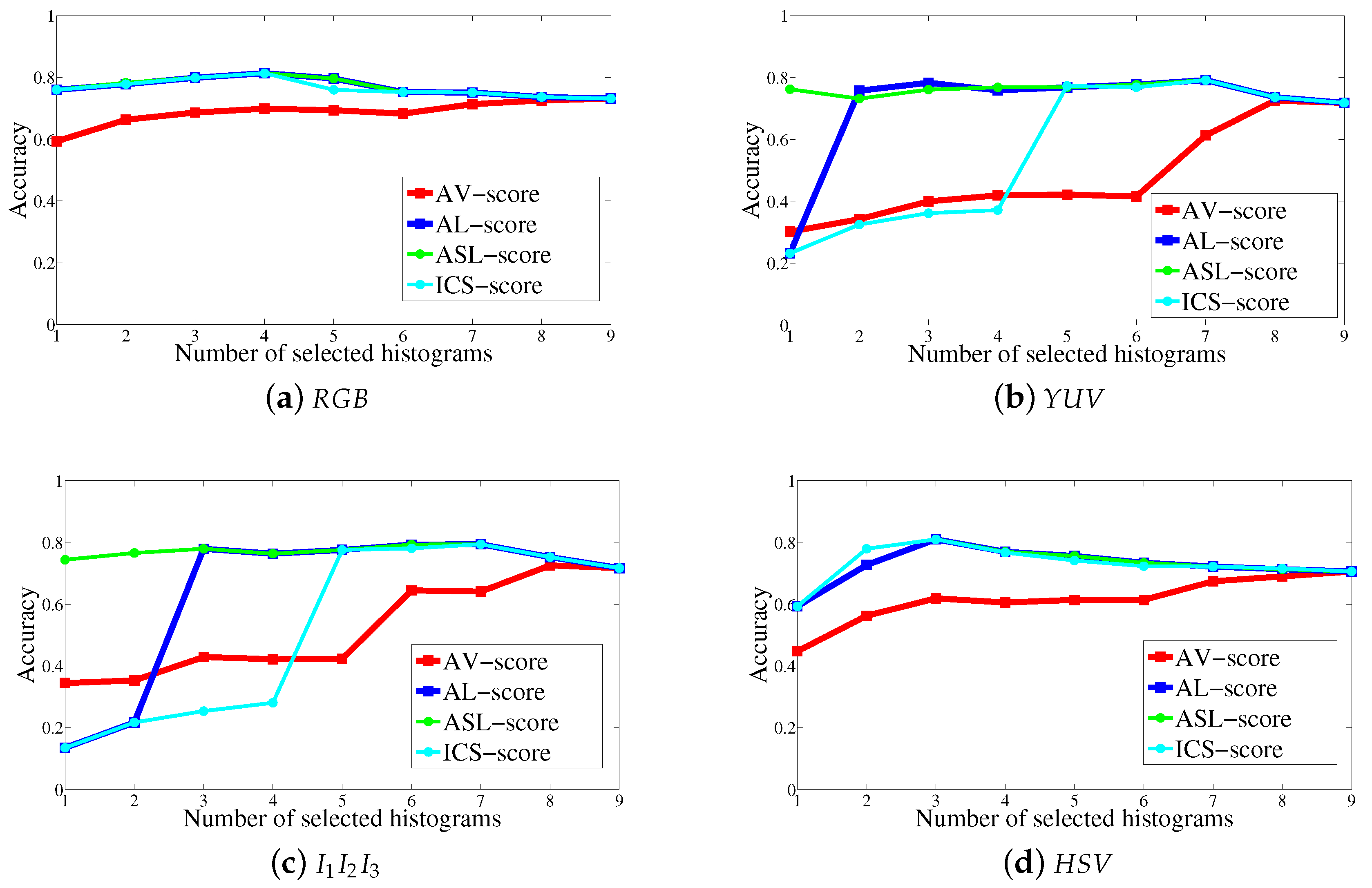
5. Experiments
5.1. Comparison of the Histogram Selection Scores
5.2. Comparison of the Histogram Ranks
5.3. Comparison with the State of the Art
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Tuceryan, M.; Jain, A.K. Texture analysis. In Handbook of Pattern Recognition and Computer Vision; Chen, C.H., Pau, L.F., Wang, P.S.P., Eds.; World Scientific Publishing Co.: Singapore, 1998; pp. 207–248. [Google Scholar]
- Bianconi, F.; Harvey, R.; Southam, P.; Fernandez, A. Theoretical and experimental comparison of different approaches for color texture classification. J. Electron. Imaging 2011, 20, 043006. [Google Scholar] [CrossRef]
- De Wouwer, G.V.; Scheunders, P.; Livens, S.; van Dyck, D. Wavelet correlation signatures for color texture characterization. Pattern Recognit. 1999, 32, 443–451. [Google Scholar] [CrossRef] [Green Version]
- Porebski, A.; Vandenbroucke, N.; Macaire, L. Supervised texture classification: Color space or texture feature selection? Pattern Anal. Appl. J. 2013, 16, 1–18. [Google Scholar] [CrossRef]
- Arvis, V.; Debain, C.; Berducat, M.; Benassi, A. Generalization of the cooccurrence matrix for colour images: Application to colour texture classification. Image Anal. Stereol. 2004, 23, 63–72. [Google Scholar] [CrossRef]
- Tang, J.; Alelyani, S.; Liu, H. Feature selection for classification: A review. In Data Classification Algorithms and Applications; Aggarwal, C., Ed.; CRC Press: Boca Raton, FL, USA, 2014; pp. 37–64. [Google Scholar]
- He, X.; Cai, D.; Niyogi, P. Laplacian Score for Feature Selection. In Advances in Neural Information Processing Systems; MIT Press: Vancouver, Canada, December 2005; pp. 507–514. [Google Scholar]
- Kalakech, M.; Biela, P.; Macaire, L.; Hamad, D. Constraint scores for semi-supervised feature selection: A comparative study. Pattern Recognit. Lett. 2011, 32, 656–665. [Google Scholar] [CrossRef]
- Sandid, F.; Douik, A. Robust color texture descriptor for material recognition. Pattern Recognit. Lett. 2016, 80, 15–23. [Google Scholar] [CrossRef]
- Fernandez, A.; Alvarez, M.X.; Bianconi, F. Texture Description Through Histograms of Equivalent Patterns. J. Math. Imaging Vis. 2012, 45, 76–102. [Google Scholar] [CrossRef] [Green Version]
- Alvarez, S.; Vanrell, M. Texton theory revisited: A bag-of-words approach to combine textons. Pattern Recognit. 2012, 45, 4312–4325. [Google Scholar] [CrossRef]
- Liu, L.; Fieguth, P.; Guo, Y.; Wang, X.; Pietikäinen, M. Local binary features for texture classification: Taxonomy and experimental study. Pattern Recognit. 2017, 62, 135–160. [Google Scholar] [CrossRef]
- Pietikäinen, M.; Hadid, A.; Zhao, G.; Ahonen, T. Computer Vision Using Local Binary Patterns; Springer: Berlin, Germany; London, UK, 2011. [Google Scholar]
- Ojala, T.; Pietikäinen, M.; Mäenpää, T. Multiresolution gray-scale and rotation invariant texture classification with local binary patterns. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 7, 971–987. [Google Scholar] [CrossRef]
- Mäenpää, T.; Ojala, T.; Pietikäinen, M.; Soriano, M. Robust texture classification by subsets of local binary patterns. In Proceedings of the 15th International Conference on Pattern Recognition, Barcelona, Spain, 3–7 September 2000; pp. 947–950. [Google Scholar]
- Liao, S.; Law, M.; Chung, C. Dominant local binary patterns for texture classification. IEEE Trans. Image Process. 2009, 18, 1107–1118. [Google Scholar] [CrossRef] [PubMed]
- Bianconi, F.; González, E.; Fernández, A. Dominant local binary patterns for texture classification: Labelled or unlabelled? Pattern Recognit. Lett. 2015, 65, 8–14. [Google Scholar] [CrossRef]
- Fu, X.; Shi, M.; Wei, H.; Chen, H. Fabric defect detection based on adaptive local binary patterns. In Proceedings of the IEEE International Conference on Robotics and Biomimetics (ROBIO2009), Guilin, China, 19–23 December 2009; pp. 1336–1340. [Google Scholar]
- Nanni, L.; Brahnam, S.; Lumini, A. Selecting the best performing rotation invariant patterns in local binary/ternary patterns. In Proceedings of the International Conference on Image Processing, Computer Vision, and Pattern Recognition, Las Vegas, NV, USA, 12–15 July 2010; pp. 369–375. [Google Scholar]
- Doshi, N.P.; Schaefer, G. Dominant multi-dimensional local binary patterns. In Proceedings of the IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC2013), Kunming, China, 5–8 August 2013. [Google Scholar]
- Guo, Y.; Zhao, G.; Pietikäinen, M.; Xu, Z. Descriptor learning based on fisher separation criterion for texture classification. In Asian Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2010; pp. 1491–1500. [Google Scholar]
- Guo, Y.; Zhao, G.; Pietikäinen, M. Discriminative features for texture description. Pattern Recognit. 2012, 45, 3834–3843. [Google Scholar] [CrossRef]
- Chan, C.; Kittler, J.; Messer, K. Multispectral local binary pattern histogram for component-based color face verification. In Proceedings of the IEEE Conference on Biometrics: Theory, Applications and Systems, Crystal City, VA, USA, 27–29 September 2007; pp. 1–7. [Google Scholar]
- Dalal, N.; Triggs, B. Histograms of oriented gradients for human detection. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Diego, CA, USA, 20–25 June 2005; pp. 886–893. [Google Scholar]
- Tan, X.; Triggs, B. Enhanced local texture feature sets for face recognition under difficult lighting conditions. IEEE Trans. Image Process. 2010, 19, 1635–1650. [Google Scholar] [PubMed]
- Hussain, S.; Triggs, B. Feature sets and dimensionality reduction for visual object detection. In British Machine Vision Conference; BMVA Press: London, UK, 2010; pp. 112.1–112.10. [Google Scholar]
- Porebski, A.; Vandenbroucke, N.; Hamad, D. LBP histogram selection for supervised color texture classification. In Proceedings of the 20th IEEE International Conference on Image Processing, Melbourne, Australia, 15–18 September 2013; pp. 3239–3243. [Google Scholar]
- Kalakech, M.; Porebski, A.; Vandenbroucke, N.; Hamad, D. A new LBP histogram selection score for color texture classification. In Proceedings of the 5th IEEE international Workshops on Image Processing Theory, Tools and Applications, Orleans, France, 10–13 November 2015. [Google Scholar]
- Porebski, A.; Hoang, V.T.; Vandenbroucke, N.; Hamad, D. Multi-color space local binary pattern-based feature selection for texture classification. J. Electron. Imaging 2018, 27, 011010. [Google Scholar]
- Luxburg, U.V. A tutorial on spectral clustering statistics and computing. Stat. Comput. 2007, 17, 395–416. [Google Scholar] [CrossRef]
- Ng, A.Y.; Jordan, M.; Weiss, Y. On spectral clustering: analysis and an algorithm. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, Canada, 3–8 December 2001; pp. 849–856. [Google Scholar]
- Zelink-Manor, L.; Perona, P. Self-tuning spectral clustering. In Proceedings of the Advances in Neural Information Processing Systems, Cambridge, MA, USA, 5 May 2005; pp. 1601–1608. [Google Scholar]
- Rubner, Y.; Puzich, J.; Tomasi, C.; Buhmann, J.M. Empirical evaluation of dissimilarity measures for color and texture. Comput. Vis. Image Underst. 2001, 84, 25–43. [Google Scholar] [CrossRef]
- Bianconi, F.; Bello-Cerezo, R.; Napoletano, P. Improved opponent color local binary patterns: An effective local image descriptor for color texture classification. J. Electron. Imaging 2017, 27, 011002. [Google Scholar] [CrossRef]
- Liu, L.; Lao, S.; Fieguth, P.; Guo, Y.; Wang, X.; Pietikainen, M. Median robust extended local binary pattern for texture classification. IEEE Trans. Image Process. 2016, 25, 1368–1381. [Google Scholar] [CrossRef] [PubMed]
- Jain, A.; Zongker, D. Feature selection: Evaluation, application and small sample performance. IEEE Trans. Pattern Anal. Mach. Intell. 1997, 19, 153–158. [Google Scholar] [CrossRef]
- Dash, M.; Liu, H. Feature selection for classification. Intell. Data Anal. 1997, 1, 131–156. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Yu, L. Toward integrating feature selection algorithms for classification and clustering. IEEE Trans. Knowl. Data Eng. 2005, 17, 491–502. [Google Scholar] [Green Version]
- Ojala, T.; Mäenpää, T.; Pietikäinen, M.; Viertola, J.; Kyllönen, J.; Huovinen, S. Outex new framework for empirical evaluation of texture analysis algorithms. In Proceedings of the 16th International Conference on Pattern Recognition, Quebec City, QC, Canada, 11–15 August 2002; pp. 701–706. [Google Scholar]
- Backes, A.R.; Casanova, D.; Bruno, O.M. Color texture analysis based on fractal descriptors. Pattern Recognit. 2012, 45, 1984–1992. [Google Scholar] [CrossRef] [Green Version]
- Lakmann, R. Barktex Benchmark Database of Color Textured Images. Koblenz-Landau University. Available online: ftp://ftphost.uni-koblenz.de/outgoing/vision/Lakmann/BarkTex (accessed on 28 September 2018).
- Porebski, A.; Vandenbroucke, N.; Macaire, L.; Hamad, D. A new benchmark image test suite for evaluating color texture classification schemes. Multimed. Tools Appl. J. 2013, 70, 543–556. [Google Scholar] [CrossRef]
- Mäenpää, T.; Pietikäinen, M. Classification with color and texture: jointly or separately? Pattern Recognit. Lett. 2004, 37, 1629–1640. [Google Scholar] [CrossRef] [Green Version]
- Casanova, D.; Florindo, J.; Falvo, M.; Bruno, O.M. Texture analysis using fractal descriptors estimated by the mutual interference of color channels. Inf. Sci. 2016, 346, 58–72. [Google Scholar] [CrossRef]
- Pietikäinen, M.; Mäenpää, T.; Viertola, J. Color texture classification with color histograms and local binary patterns. In Proceedings of the 2nd International Workshop on Texture Analysis and Synthesis, Copenhagen, Denmark, 1 June 2002; pp. 109–112. [Google Scholar]
- Qazi, I.; Alata, O.; Burie, J.C.; Moussa, A.; Fernandez, C. Choice of a pertinent color space for color texture characterization using parametric spectral analysis. Pattern Recognit. 2011, 44, 16–31. [Google Scholar] [CrossRef]
- Iakovidis, D.; Maroulis, D.; Karkanis, S. A comparative study of color-texture image features. In Proceedings of the 12th International Workshop on Systems, Signals & Image Processing (IWSSIP’05), Chalkida, Greece, 22–24 September 2005; pp. 203–207. [Google Scholar]
- Liu, P.; Guo, J.; Chamnongthai, K.; Prasetyo, H. Fusion of color histogram and lbp-based features for texture image retrieval and classification. Inf. Sci. 2017, 390, 95–111. [Google Scholar] [CrossRef]
- Maliani, A.D.E.; Hassouni, M.E.; Berthoumieu, Y.; Aboutajdine, D. Color texture classification method based on a statistical multi-model and geodesic distance. J. Vis. Commun. Image Represent. 2014, 25, 1717–1725. [Google Scholar] [CrossRef]
- Guo, J.-M.; Prasetyo, H.; Lee, H.; Yao, C.C. Image retrieval using indexed histogram of void-and-cluster block truncation coding. Signal Process. 2016, 123, 143–156. [Google Scholar] [CrossRef]
- Ledoux, A.; Losson, O.; Macaire, L. Color local binary patterns: compact descriptors for texture classification. J. Electron. Imaging 2016, 25, 1–12. [Google Scholar] [CrossRef]
- Xu, Q.; Yang, J.; Ding, S. Color texture analysis using the wavelet-based hidden markov model. Pattern Recognit. Lett. 2005, 26, 1710–1719. [Google Scholar] [CrossRef]
- Martínez, R.A.; Richard, N.; Fernandez, C. Alternative to colour feature classification using colour contrast ocurrence matrix. In Proceedings of the 12th International Conference on Quality Control by Artificial Vision SPIE, Le Creusot, France, 3–5 June 2015; pp. 1–9. [Google Scholar]
- Hammouche, K.; Losson, O.; Macaire, L. Fuzzy aura matrices for texture classification. Pattern Recognit. 2016, 53, 212–228. [Google Scholar] [CrossRef] [Green Version]
- Oliveira, M.W.D.; da Silva, N.R.; Manzanera, A.; Bruno, O.M. Feature extraction on local jet space for texture classification. Phys. A Stat. Mech. Appl. 2015, 439, 160–170. [Google Scholar] [CrossRef]
- Florindo, J.; Bruno, O. Texture analysis by fractal descriptors over the wavelet domain using a best basis decomposition. Phys. A Stat. Mech. Appl. 2016, 444, 415–427. [Google Scholar] [CrossRef]
- Sandid, F.; Douik, A. Dominant and minor sum and difference histograms for texture description. In Proceedings of the 2016 International Image Processing, Applications and Systems (IPAS), Hammamet, Tunisia, 5–7 November 2016; pp. 1–5. [Google Scholar]
- Wang, J.; Fan, Y.; Li, N. Combining fine texture and coarse color features for color texture classification. J. Electron. Imaging 2017, 26, 9. [Google Scholar]
| Feature Selection | Histogram Selection | |
|---|---|---|
| Dataset | Dataset of N color texture images defined in a D-dimensional feature space | Dataset of N color texture images defined in a -dimensional histogram space |
| Data matrix | ; ; is the rth feature value of the ith image | ; ; is the rth histogram extracted from the ith image |
| Row | with | |
| Column | ||
| Selection | The most discriminant features among the D available ones | The most discriminant histograms among the D available ones |
| Distance | is the squared Euclidean distance between the two images and using the considered feature | is the squared Jeffrey distance between the two images and using the considered histogram |
| Similarity | evaluates the similarity between the images and in the D-dimensional input space | evaluates the similarity between the images and in the -dimensional input space using the histogram intersection |
| Mean | with | |
| Variance Score | ||
| Degree | ||
| Weighted average | with | |
| Laplacian Score |
| Without | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Score | Score | Score | Score | Selection | |||||
| 93.25% | 8 | 8 | 8 | 92.94% | 9 | 92.94% | |||
| 89.56% | 9 | 91.03% | 7 | 91.03% | 7 | 89.56% | 9 | 89.56% | |
| 88.67% | 8 | 88.82% | 8 | 88.97% | 6 | 88.97% | 8 | 88.68% | |
| 90.44% | 9 | 91.91% | 5 | 91.91% | 5 | 91.03% | 8 | 90.44% | |
| Without | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Score | Score | Score | Score | Selection | |||||
| 89.53% | 9 | 90.92% | 5 | 91.27% | 4 | 90.58% | 7 | 89.53% | |
| 76.79% | 9 | 3 | 3 | 3 | 76.79% | ||||
| 75.31% | 9 | 92.06% | 3 | 92.06% | 3 | 92.06% | 3 | 75.31% | |
| 83.25% | 9 | 90.40% | 3 | 90.40% | 3 | 88.92% | 5 | 83.35% | |
| Without | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Score | Score | Score | Score | Selection | |||||
| 73.16% | 9 | 4 | 4 | 4 | 73.16% | ||||
| 71.81% | 9 | 79.17% | 7 | 79.17% | 7 | 79.17% | 7 | 71.81% | |
| 71.68% | 9 | 79.41% | 7 | 79.41% | 7 | 79.41% | 7 | 71.69% | |
| 70.59% | 9 | 81% | 3 | 81% | 3 | 81% | 3 | 70.59% | |
| OuTex | USPTex | BarkTex | ||
|---|---|---|---|---|
| -score | 2 4 3 6 8 7 1 5 9 | 5 4 6 8 7 9 2 3 1 | 3 7 6 8 4 2 5 1 9 | |
| -score | 9 1 5 8 7 6 3 4 2 | 1 3 2 9 7 8 6 4 5 | 9 1 5 2 4 8 6 7 3 | |
| -score | 9 1 5 8 7 6 4 3 2 | 1 2 3 7 4 9 6 8 5 | 9 5 1 2 4 8 6 7 3 | |
| -score | 8 7 1 9 5 3 4 2 6 | 3 1 2 8 7 9 4 5 6 | 9 1 5 2 8 4 6 7 3 | |
| -score | 8 4 6 2 7 3 1 9 5 | 8 7 9 4 5 6 1 3 2 | 8 6 4 7 2 3 9 5 1 | |
| -score | 5 9 1 3 7 6 2 4 8 | 3 2 1 4 5 6 7 9 8 | 3 1 2 5 9 7 4 6 8 | |
| -score | 1 9 5 6 8 3 7 2 4 | 3 2 1 4 5 6 9 7 8 | 3 2 7 4 1 5 9 6 8 | |
| -score | 3 6 7 8 2 1 4 9 5 | 3 2 1 5 4 6 9 7 8 | 3 2 7 4 1 5 9 6 8 | |
| -score | 8 6 7 4 3 2 1 5 9 | 8 7 9 5 6 4 1 2 3 | 8 6 4 7 2 5 3 9 1 | |
| -score | 9 5 1 2 4 3 7 6 8 | 3 1 2 5 4 6 9 7 8 | 3 2 1 5 9 7 4 6 8 | |
| -score | 1 9 5 6 8 2 3 4 7 | 2 3 1 6 4 5 9 7 8 | 1 3 2 5 9 7 4 6 8 | |
| -score | 2 4 3 6 7 8 1 9 5 | 3 2 1 5 4 6 9 8 7 | 3 2 7 4 1 5 9 6 8 | |
| -score | 3 2 6 8 7 4 1 5 9 | 6 4 7 9 5 8 1 2 3 | 8 7 2 4 6 3 1 9 5 | |
| -score | 9 5 1 7 4 3 2 8 6 | 3 2 1 8 7 4 5 9 6 | 5 9 1 4 2 3 6 7 8 | |
| -score | 1 5 9 8 6 7 4 3 2 | 2 3 1 7 4 9 8 6 5 | 5 1 9 4 2 3 6 7 8 | |
| -score | 7 8 6 1 3 4 9 5 2 | 3 2 7 4 1 8 5 9 6 | 5 1 9 6 2 4 3 8 7 | |
| Features | Color Space | Classifier | R (%) |
|---|---|---|---|
| 3D-adaptive sum and difference histograms [9] | SVM | 95.8 | |
| 3D color histogram [43] | 1-NN | 95.4 | |
| Fractal descriptors [44] | LDA | 95.0 | |
| EOCLBP with selection thanks to the -score | SVM | 94.9 | |
| Haralick features [5] | 5-NN | 94.9 | |
| 3D color histogram [45] | 3-NN | 94.7 | |
| 3D color histogram [46] | I- | 1-NN | 94.5 |
| Haralick features [11] | 1-NN | 94.1 | |
| EOCLBP/C [47] | SVM | 93.5 | |
| EOCLBP with selection thanks to the -score | 1-NN | 93.4 | |
| EOCLBP with selection thanks to the -score [28] | 1-NN | 93.4 | |
| EOCLBP [27] | 1-NN | 92.9 | |
| Reduced Size Chromatic Co-occurrence Matrices [4] | 1-NN | 92.5 | |
| Between color component LBP histogram [43] | 1-NN | 92.5 | |
| Color histogram + LBP-based features [48] | 1-NN | 90.3 | |
| Wavelet coefficients [49] | BDC | 89.7 | |
| Autoregressive models + 3D color histogram [46] | I- | 1-NN | 88.9 |
| Halftoning local derivative pattern + Color histogram [50] | 1-NN | 88.2 | |
| Autoregressive models [46] | 1-NN | 88.0 | |
| Within color component LBP histogram [43] | 1-NN | 87.8 | |
| Mixed color order LBP [51] | 1-NN | 87.1 | |
| Features from wavelet transform [52] | 7-NN | 85.2 | |
| Color contrast occurrence matrix [53] | 1-NN | 82.6 | |
| Fuzzy aura matrices [54] | 1-NN | 80.2 |
| Features | Color Space | Classifier | R (%) |
|---|---|---|---|
| Color histogram + LBP-based features [48] | 1-NN | 95.9 | |
| Local jet + LBP [55] | Luminance | LDA | 94.3 |
| Halftoning local derivative pattern + Color histogram [50] | 1-NN | 93.9 | |
| EOCLBP with selection thanks to the -score | 1-NN | 93.2 | |
| EOCLBP with selection thanks to the -score | SVM | 87.9 | |
| Fractal descriptors [56] | Luminance | LDA | 85.6 |
| Mixed color order LBP [51] | 1-NN | 84.2 |
| Features | Color space | Classifier | R (%) |
|---|---|---|---|
| Dominant and minor sum and difference histograms [57] | SVM | 89.6 | |
| EOCLBP with selection thanks to the -score | SVM | 84.9 | |
| Fine Texture and Coarse Color Features [58] | NSC | 84.3 | |
| 3D-adaptive sum and difference histograms [9] | SVM | 82.1 | |
| EOCLBP with selection thanks to the -score | 1-NN | 81.4 | |
| EOCLBP with selection thanks to the -score [27] | 1-NN | 81.4 | |
| EOCLBP with selection thanks to the -score [28] | 1-NN | 81.4 | |
| Mixed color order LBP [51] | 1-NN | 77.7 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kalakech, M.; Porebski, A.; Vandenbroucke, N.; Hamad, D. Unsupervised Local Binary Pattern Histogram Selection Scores for Color Texture Classification. J. Imaging 2018, 4, 112. https://doi.org/10.3390/jimaging4100112
Kalakech M, Porebski A, Vandenbroucke N, Hamad D. Unsupervised Local Binary Pattern Histogram Selection Scores for Color Texture Classification. Journal of Imaging. 2018; 4(10):112. https://doi.org/10.3390/jimaging4100112
Chicago/Turabian StyleKalakech, Mariam, Alice Porebski, Nicolas Vandenbroucke, and Denis Hamad. 2018. "Unsupervised Local Binary Pattern Histogram Selection Scores for Color Texture Classification" Journal of Imaging 4, no. 10: 112. https://doi.org/10.3390/jimaging4100112
APA StyleKalakech, M., Porebski, A., Vandenbroucke, N., & Hamad, D. (2018). Unsupervised Local Binary Pattern Histogram Selection Scores for Color Texture Classification. Journal of Imaging, 4(10), 112. https://doi.org/10.3390/jimaging4100112






