Stochastic Capsule Endoscopy Image Enhancement
Abstract
1. Introduction
2. Background
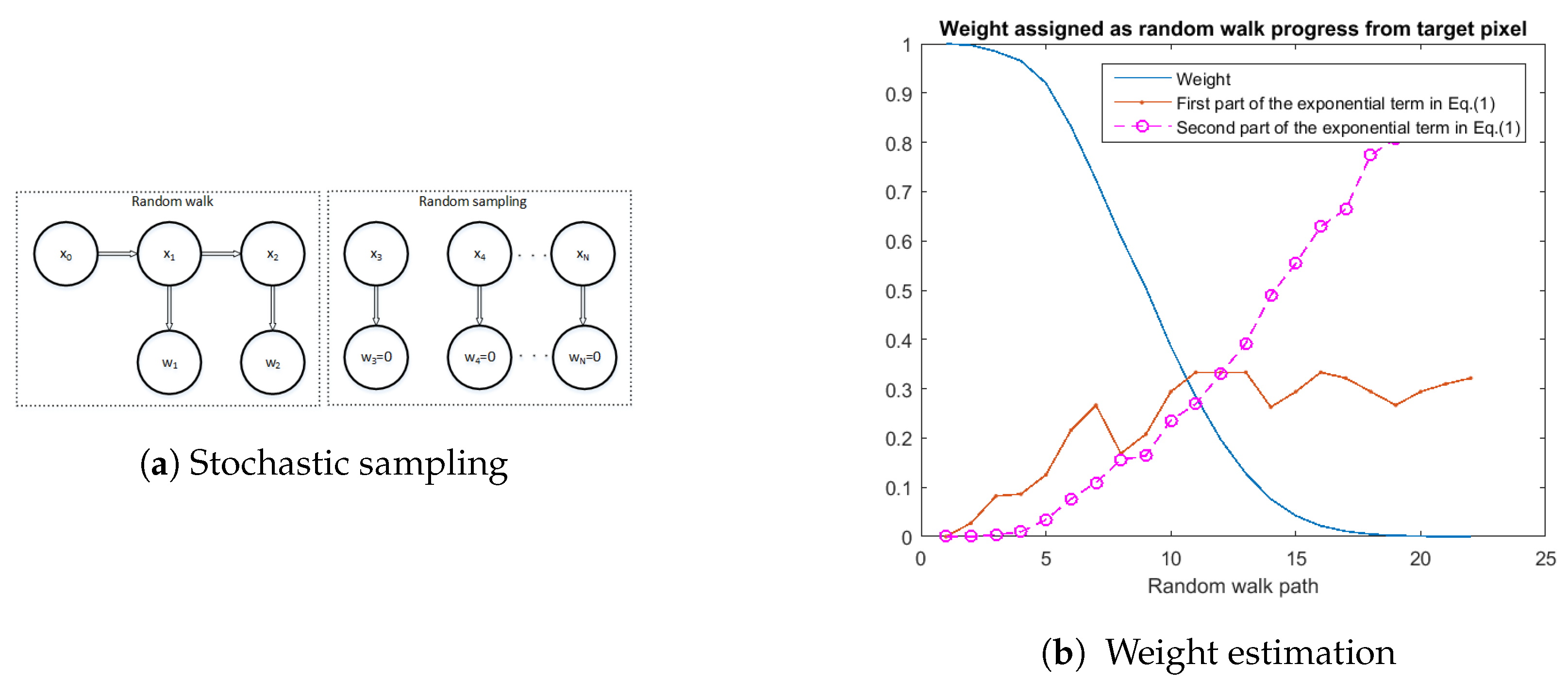
2.1. Edge-Aware Smoothing and Random Walks
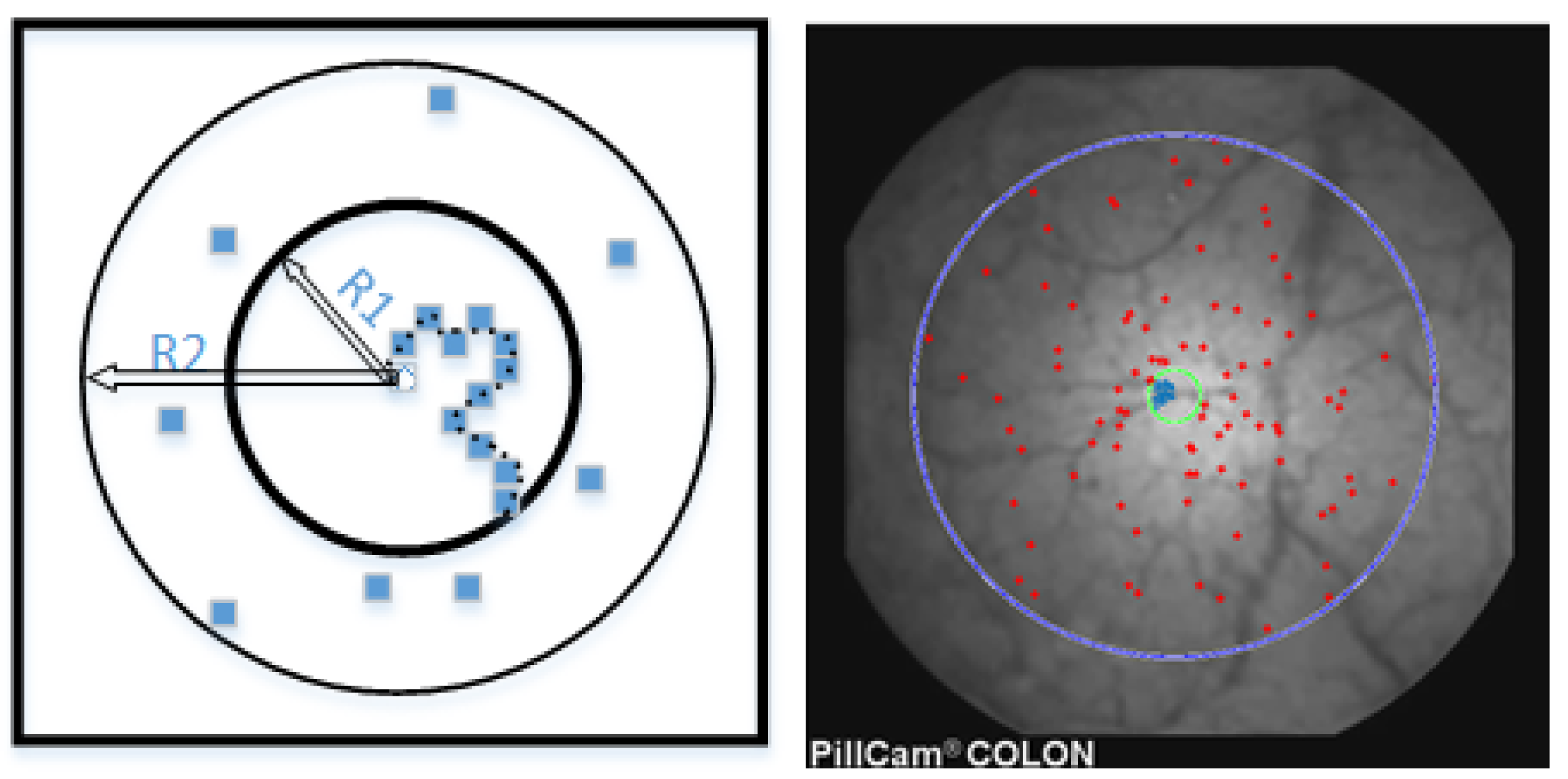
2.2. Retinex-Inspired Envelope with Stochastic Sampling
3. Stochastic Cve Image Enhancement
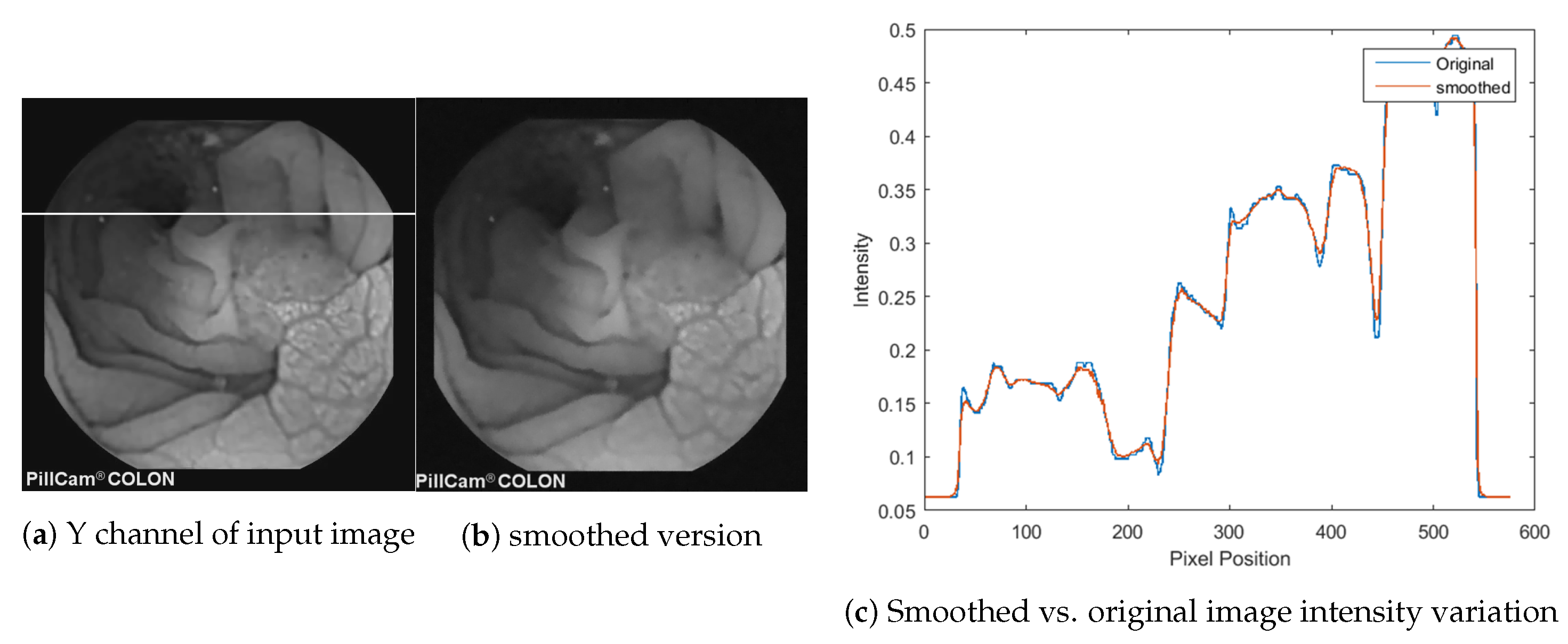
3.1. Smoothing
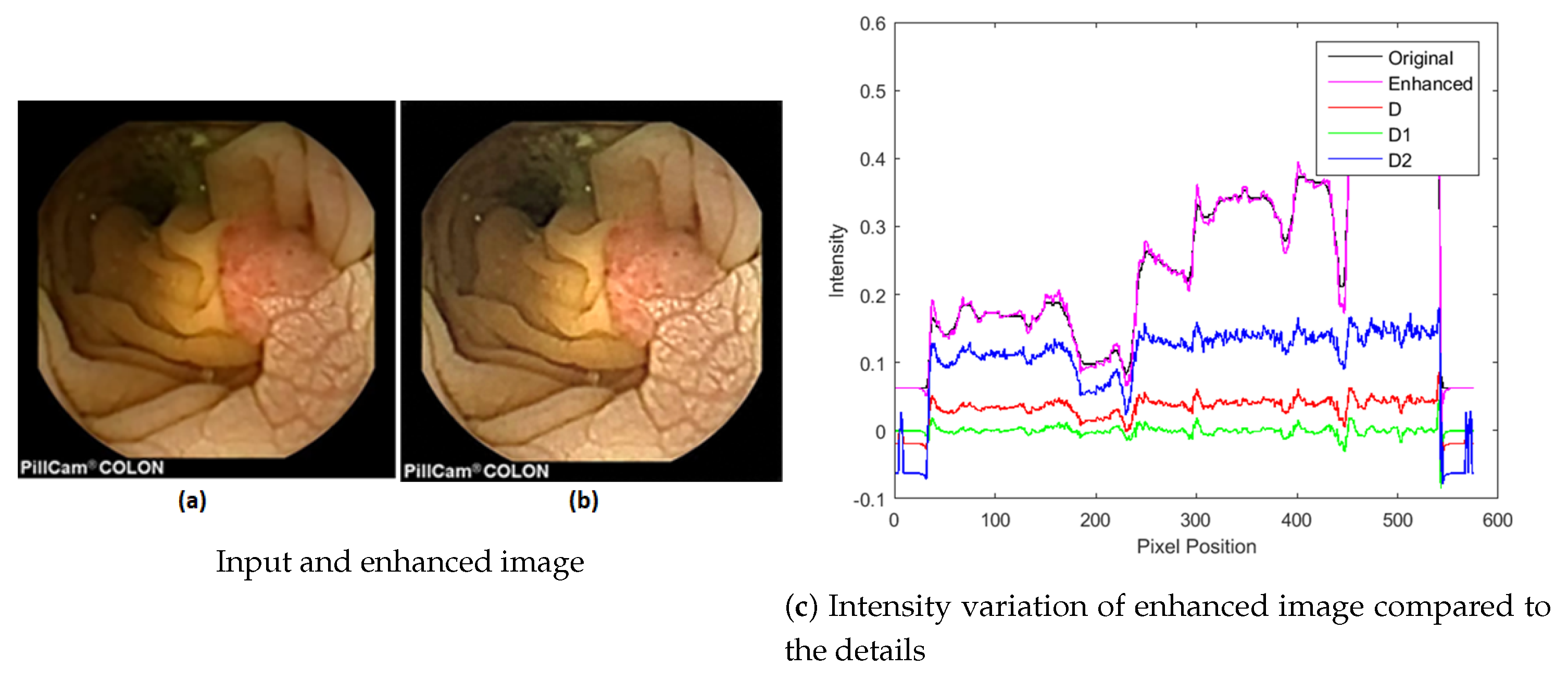
3.2. Local Contrast Enhancement
3.3. Image Decomposition
4. Implementation
| Algorithm A1: Stochastic CVE image enhancement |
Data:
PROCEDURE: G = color gradient Equation (4) foreachpixeldo  |
5. Result and Evaluation
5.1. Experimental Setup and Procedure
5.2. Dataset
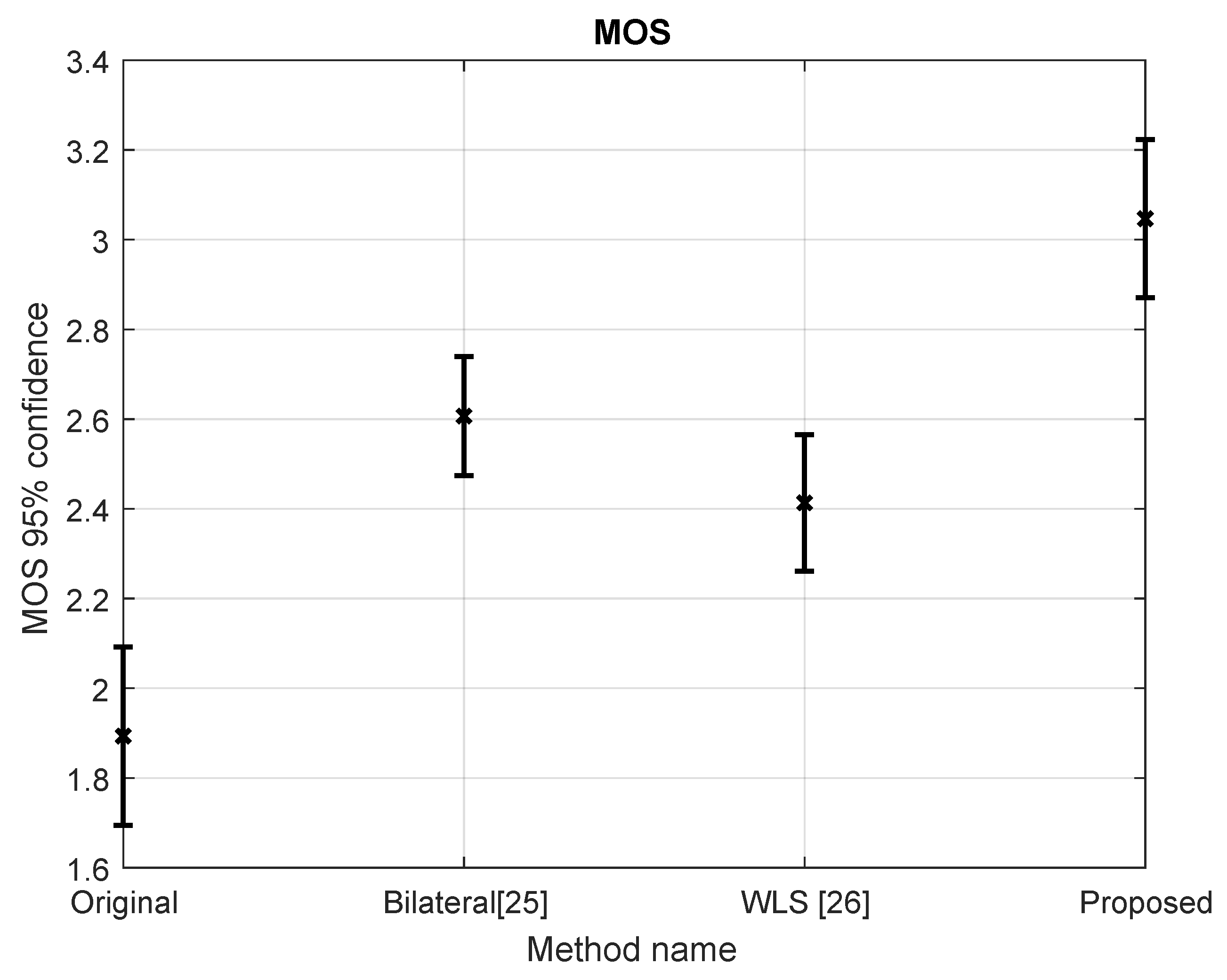
5.3. Subjective Evaluation
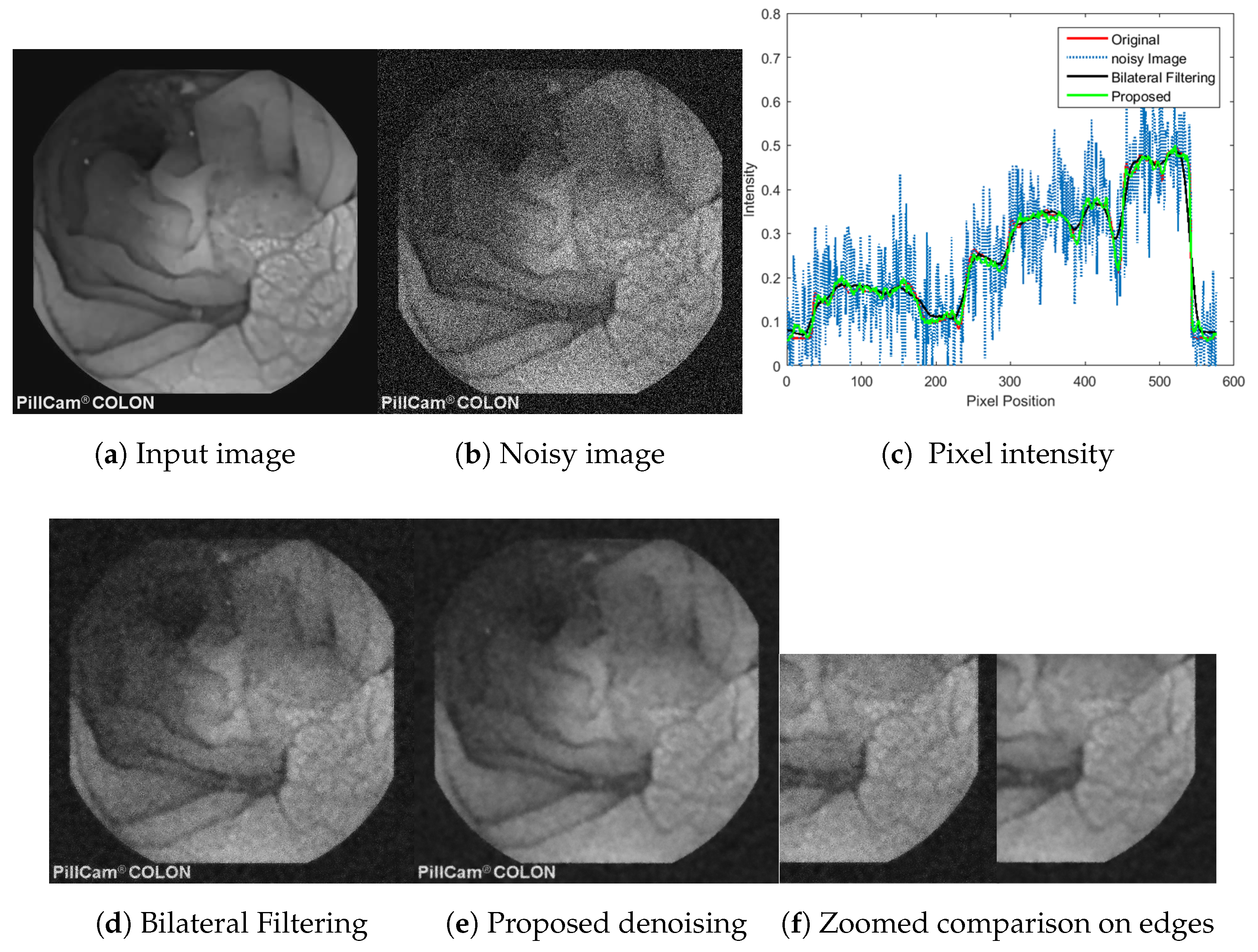
5.4. Objective Evaluation and Comparison
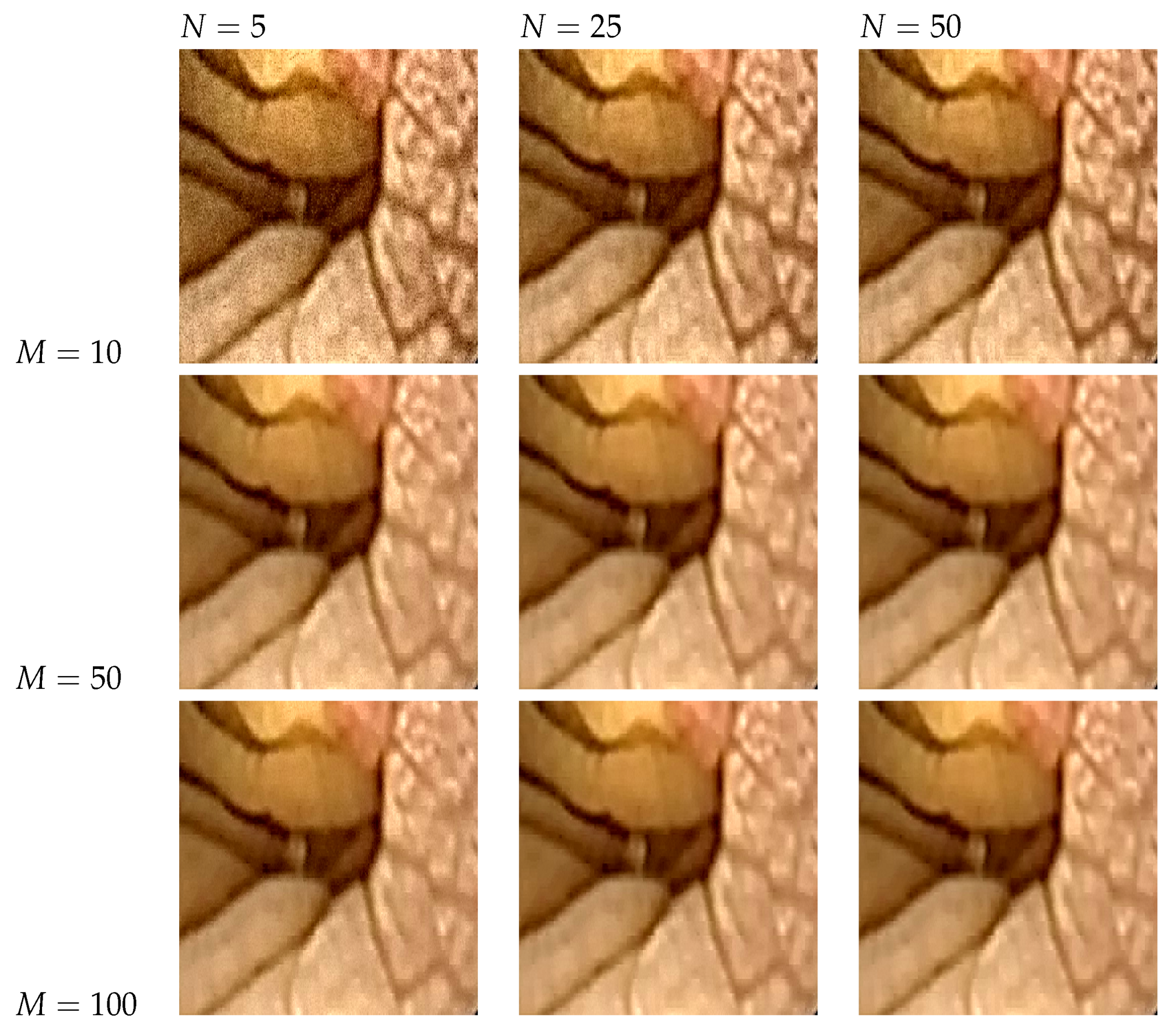
5.5. The Effect of Parameter Selection
5.6. Base Layer Estimation
5.7. Applicability the Proposed Method and Computational Cost
6. Conclusions and Future Work
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| CVE | Capsule video endoscopy |
| CCE | Colon capsule endoscopy |
| CLAHE | Contrast limited adaptive histogram equalization |
| CMOS | Complementary metal-oxide semiconductor) |
| DFT | Discrete Fourier transform |
| FICE | Flexible spectral imaging color enhancement |
| HVS | Human Visual System |
| JND | Just noticeable difference |
| NBI | Narrow Band Imaging |
| SSIM | Structural similarity index |
| WLF | Weighted-level framework |
| WLS | weighted least square |
References
- Rimbaş, M.; Negreanu, L.; Ciobanu, L.; Benguş, A.; Spada, C.; Băicuş, C.R.; Costamagna, G. Is virtual chromoendoscopy useful in the evaluation of subtle ulcerative small-bowel lesions detected by video capsule endoscopy? Endosc. Int. Open 2015, 3, E615. [Google Scholar] [CrossRef] [PubMed]
- Sakai, E.; Endo, H.; Kato, S.; Matsuura, T.; Tomeno, W.; Taniguchi, L.; Uchiyama, T.; Hata, Y.; Yamada, E.; Ohkubo, H.; et al. Capsule endoscopy with flexible spectral imaging color enhancement reduces the bile pigment effect and improves the detectability of small bowel lesions. BMC Gastroenterol. 2012, 12, 83. [Google Scholar] [CrossRef] [PubMed]
- Lambert, R.; Kuznetsov, K.; Rey, J. Narrow-band imaging in digestive endoscopy. Sci. World J. 2007, 7, 449–465. [Google Scholar] [CrossRef] [PubMed]
- Ramaraj, M.; Raghavan, S.; Khan, W.A. Homomorphic filtering techniques for WCE image enhancement. In Proceedings of the 2013 Computational Intelligence and Computing Research (ICCIC), Enathi, India, 26–28 December 2013; pp. 1–5. [Google Scholar]
- Ibrahim, H.; Kong, N.S.P. Brightness preserving dynamic histogram equalization for image contrast enhancement. IEEE Trans. Consum. Electr. 2007, 53, 1752–1758. [Google Scholar] [CrossRef]
- Okuhata, H.; Nakamura, H.; Hara, S.; Tsutsui, H.; Onoye, T. Application of the real-time Retinex image enhancement for endoscopic images. In Proceedings of the 35th Annual International Conference of the Engineering in Medicine and Biology Society (EMBC), Osaka, Japan, 3–7 July 2013; pp. 3407–3410. [Google Scholar]
- Provenzi, E. Computational Color Science: Variational Retinex-Like Methods; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Gopi, V.P.; Palanisamy, P.; Niwas, S.I. Capsule endoscopic colour image denoising using complex wavelet transform. In Wireless Networks and Computational Intelligence; Springer: Heidelberg/Berlin, Germany, 2012; pp. 220–229. [Google Scholar]
- Liu, H.; Lu, W.S.; Meng, M.Q.H. De-blurring wireless capsule endoscopy images by total variation minimization. In Proceedings of the 2011 IEEE Pacific Rim Conference on Communications, Computers and Signal Processing (PacRim), Victoria, BC, Canada, 23–26 August 2011; pp. 102–106. [Google Scholar]
- Beck, A.; Teboulle, M. Fast gradient-based algorithms for constrained total variation image denoising and deblurring problems. IEEE Trans. Image Process. 2009, 18, 2419–2434. [Google Scholar] [CrossRef] [PubMed]
- Vu, H.; Echigo, T.; Yagi, K.; Okazaki, H.; Fujiwara, Y.; Yagi, Y.; Arakawa, T. Image-Enhanced capsule endoscopy preserving the original color tones. In Proceedings of the International MICCAI Workshop on Computational and Clinical Challenges in Abdominal Imaging, Cambridge, MA, USA, 14 September 2011; Springer: Heidelberg/Berlin, Germany, 2011; pp. 35–43. [Google Scholar]
- Imtiaz, M.S.; Wahid, K.A. Color enhancement in endoscopic images using adaptive sigmoid function and space variant color reproduction. Comput. Math. Methods Med. 2015, 2015, 3905–3908. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Meng, M.Q.H. Wireless capsule endoscopy images enhancement via adaptive contrast diffusion. J. Vis. Commun. Image Represent. 2012, 23, 222–228. [Google Scholar] [CrossRef]
- Attar, A.; Xie, X.; Zhang, C.; Wang, Z.; Yue, S. Wireless Micro-Ball endoscopic image enhancement using histogram information. In Proceedings of the 2014 36th Annual International Conference of the Engineering in Medicine and Biology Society (EMBC), Chicago, IL, USA, 26–30 August 2014; pp. 3337–3340. [Google Scholar]
- Srivastava, R.; Gupta, J.; Parthasarthy, H.; Srivastava, S. PDE based unsharp masking, crispening and high boost filtering of digital images. In Proceedings of the International Conference on Contemporary Computing, Aachen, Germany, 19–21 August 2009; Springer: Heidelberg/Berlin, Germany, 2009; pp. 8–13. [Google Scholar]
- Sheet, D.; Garud, H.; Suveer, A.; Mahadevappa, M.; Chatterjee, J. Brightness preserving dynamic fuzzy histogram equalization. IEEE Trans. Consum. Electr. 2010, 56, 2475–2480. [Google Scholar] [CrossRef]
- Rukundo, O.; Pedersen, M.; Hovde, Ø. Advanced Image Enhancement Method for Distant Vessels and Structures in Capsule Endoscopy. Comput. Math. Methods Med. 2017, 2017. [Google Scholar] [CrossRef] [PubMed]
- Kolås, Ø.; Farup, I.; Rizzi, A. Spatio-temporal Retinex-inspired envelope with stochastic sampling: A framework for spatial color algorithms. J. Imag. Sci. Technol. 2011, 55, 40503-1–40503-10. [Google Scholar]
- Black, M.J.; Sapiro, G.; Marimont, D.H.; Heeger, D. Robust anisotropic diffusion. IEEE Trans. Image Process. 1998, 7, 421–432. [Google Scholar] [CrossRef] [PubMed]
- Estrada, F.J.; Fleet, D.J.; Jepson, A.D. Stochastic Image Denoising. In Proceedings of the British Machine Vision Conference, London, UK, 7–10 September 2009; pp. 1–11. [Google Scholar]
- Azzabou, N.; Paragios, N.; Guichard, F. Random Walks, Constrained Multiple Hypothesis Testing and Image Enhancement; Springer: Heidelberg/Berlin, Germany, 2006; pp. 379–390. [Google Scholar]
- Subr, K.; Soler, C.; Durand, F. Edge-preserving multiscale image decomposition based on local extrema. ACM Trans. Graph. 2009, 28, 147. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, H.; Sun, X.; Zheng, X. An Image Enhancement Method Based on Edge Preserving Random Walk Filter; Springer: Heidelberg/Berlin, Germany, 2015; pp. 433–442. [Google Scholar]
- Perona, P.; Malik, J. Scale-space and edge detection using anisotropic diffusion. IEEE Trans. Patt. Anal. Mach. Intell. 1990, 12, 629–639. [Google Scholar] [CrossRef]
- Easley, G.R.; Labate, D.; Colonna, F. Shearlet-based total variation diffusion for denoising. IEEE Trans. Image Process. 2009, 18, 260–268. [Google Scholar] [CrossRef] [PubMed]
- Shih, A.C.; Liao, H.Y.; Lu, C.S. A new iterated two-band diffusion equation: theory and its application. IEEE Trans. Image Process. 2003, 12, 466–476. [Google Scholar] [CrossRef] [PubMed]
- Rajpoot, K.; Rajpoot, N.; Noble, J.A. Discrete Wavelet Diffusion for Image Denoising; Springer: Heidelberg/Berlin, Germany, 2008; pp. 20–28. [Google Scholar]
- Fattal, R.; Agrawala, M.; Rusinkiewicz, S. Multiscale shape and detail enhancement from multi-light image collections. ACM Trans. Graph. 2007, 26, 51. [Google Scholar] [CrossRef]
- Farbman, Z.; Fattal, R.; Lischinski, D.; Szeliski, R. Edge-preserving decompositions for multi-scale tone and detail manipulation. ACM Trans. Graph. 2008, 27, 67. [Google Scholar] [CrossRef]
- Holm, J.; Tastl, I.; Johnson, T. Definition & use of the ISO 12640-3 reference color gamut. In Proceedings of the Color and Imaging Conference Society for Imaging Science and Technology, Scottsdale, AZ, USA, 6–10 November 2006; Volume 2006, pp. 62–68. [Google Scholar]
- Koulaouzidis, A.; Iakovidis, D. KID: Towards a Reference Database for Intelligent Capsule Endoscopy. In Proceedings of the IEEE Engineering in Medicine and Biology Conference (EMBC), Milan, Italy, 25–29 August 2015; pp. 1–2. [Google Scholar]
- Montag, E.D. Empirical formula for creating error bars for the method of paired comparison. J. Electr. Imag. 2006, 15, 010502. [Google Scholar] [CrossRef]
- Simone, G.; Pedersen, M.; Hardeberg, J.Y. Measuring perceptual contrast in digital images. J. Vis. Commun. Image Represent. 2012, 23, 491–506. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: from error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Zhang, L.; Mou, X.; Zhang, D. FSIM: A feature similarity index for image quality assessment. IEEE Trans. Image Proces. 2011, 20, 2378–2386. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Li, Q. Information content weighting for perceptual image quality assessment. IEEE Trans. Image Process. 2011, 20, 1185–1198. [Google Scholar] [CrossRef] [PubMed]
- Zuiderveld, K. Contrast limited adaptive histogram equalization. In Graphics Gems; Academic Press Inc.: Cambridge, UK, 1994; pp. 474–485. [Google Scholar]
- Xu, L.; Lu, C.; Xu, Y.; Jia, J. Image smoothing via L 0 gradient minimization. ACM Trans. Graph. 2011, 30, 174. [Google Scholar] [CrossRef]
- Tomasi, C.; Manduchi, R. Bilateral filtering for gray and color images. In Proceedings of the Sixth International Conference on Computer Vision, Bombay, India, 7 Januray 1998; pp. 839–846. [Google Scholar]
- Shim, K.N.; Jeon, S.R.; Jang, H.J.; Kim, J.; Lim, Y.J.; Kim, K.O.; Song, H.J.; Lee, H.S.; Park, J.J.; Kim, J.H.; et al. Quality indicators for small bowel capsule endoscopy. Clin. Endosc. 2017, 50, 148. [Google Scholar] [CrossRef] [PubMed]
- Imagawa, H.; Oka, S.; Tanaka, S.; Noda, I.; Higashiyama, M.; Sanomura, Y.; Shishido, T.; Yoshida, S.; Chayama, K. Improved detectability of small-bowel lesions via capsule endoscopy with computed virtual chromoendoscopy: a pilot study. Scand. J. Gastroenterol. 2011, 46, 1133–1137. [Google Scholar] [CrossRef] [PubMed]
- Hatogai, K.; Hosoe, N.; Imaeda, H.; Rey, J.F.; Okada, S.; Ishibashi, Y.; Kimura, K.; Yoneno, K.; Usui, S.; Ida, Y.; et al. Role of enhanced visibility in evaluating polyposis syndromes using a newly developed contrast image capsule endoscope. Gut liver 2012, 6, 218. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Ren, J.; Yan, Q.; Liao, R.; Jia, J. Deep edge-aware filters. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 1669–1678. [Google Scholar]
- Wang, Z.; Wang, H. Image smoothing with generalized random walks: Algorithm and applications. Appl. Soft Comput. 2016, 46, 792–804. [Google Scholar] [CrossRef]
- Grady, L. Random walks for image segmentation. IEEE Trans. Patt. Anal. Mach. Intell. 2006, 28, 1768–1783. [Google Scholar] [CrossRef] [PubMed]



| Average Performance of Enhancement Methods Based on Objective Quality Metrics | |||||
|---|---|---|---|---|---|
| Methods | WLF Ratio | SSIM | CIE2000 | FSIM | IW-SSIM |
| Bilateral [28] | 1.06 | 0.92 | 3.03 | 0.95 | 0.93 |
| WLS [29] | 1.28 | 0.92 | 3.29 | 0.94 | 0.92 |
| CLAHE [37] | 2.65 | 0.82 | 3.60 | 0.89 | 0.83 |
| Proposed | 1.48 | 0.90 | 3.45 | 0.92 | 0.93 |
| Denoising | |||
|---|---|---|---|
| Value | Bilateral Filter | Anisotropic Diffusion | Random Walks |
| = 0.03 | 36.08 | 27.59 | 35.17 |
| = 0.09 | 33.40 | 27.29 | 32.45 |
| = 0.27 | 19.41 | 32.45 | 23.85 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohammed, A.; Farup, I.; Pedersen, M.; Hovde, Ø.; Yildirim Yayilgan, S. Stochastic Capsule Endoscopy Image Enhancement. J. Imaging 2018, 4, 75. https://doi.org/10.3390/jimaging4060075
Mohammed A, Farup I, Pedersen M, Hovde Ø, Yildirim Yayilgan S. Stochastic Capsule Endoscopy Image Enhancement. Journal of Imaging. 2018; 4(6):75. https://doi.org/10.3390/jimaging4060075
Chicago/Turabian StyleMohammed, Ahmed, Ivar Farup, Marius Pedersen, Øistein Hovde, and Sule Yildirim Yayilgan. 2018. "Stochastic Capsule Endoscopy Image Enhancement" Journal of Imaging 4, no. 6: 75. https://doi.org/10.3390/jimaging4060075
APA StyleMohammed, A., Farup, I., Pedersen, M., Hovde, Ø., & Yildirim Yayilgan, S. (2018). Stochastic Capsule Endoscopy Image Enhancement. Journal of Imaging, 4(6), 75. https://doi.org/10.3390/jimaging4060075







