Characterization of Crystallographic Structures Using Bragg-Edge Neutron Imaging at the Spallation Neutron Source †
Abstract
:1. Introduction
2. Materials and Methods
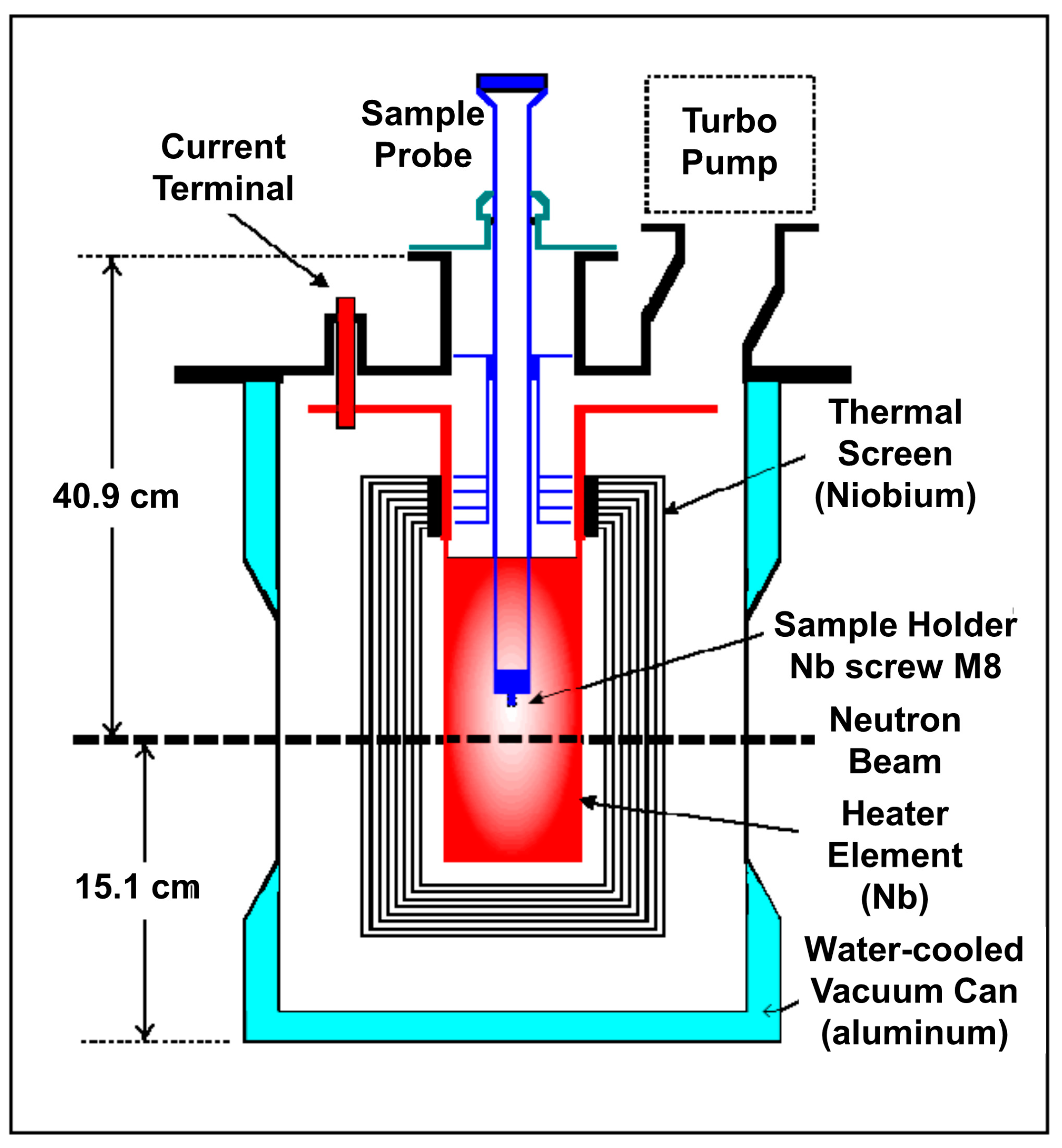
2.1. Bragg-Edge Neutron Radiography at SNS SNAP and Neutron Diffraction at SNS VULCAN Beamlines
2.2. Powder Samples
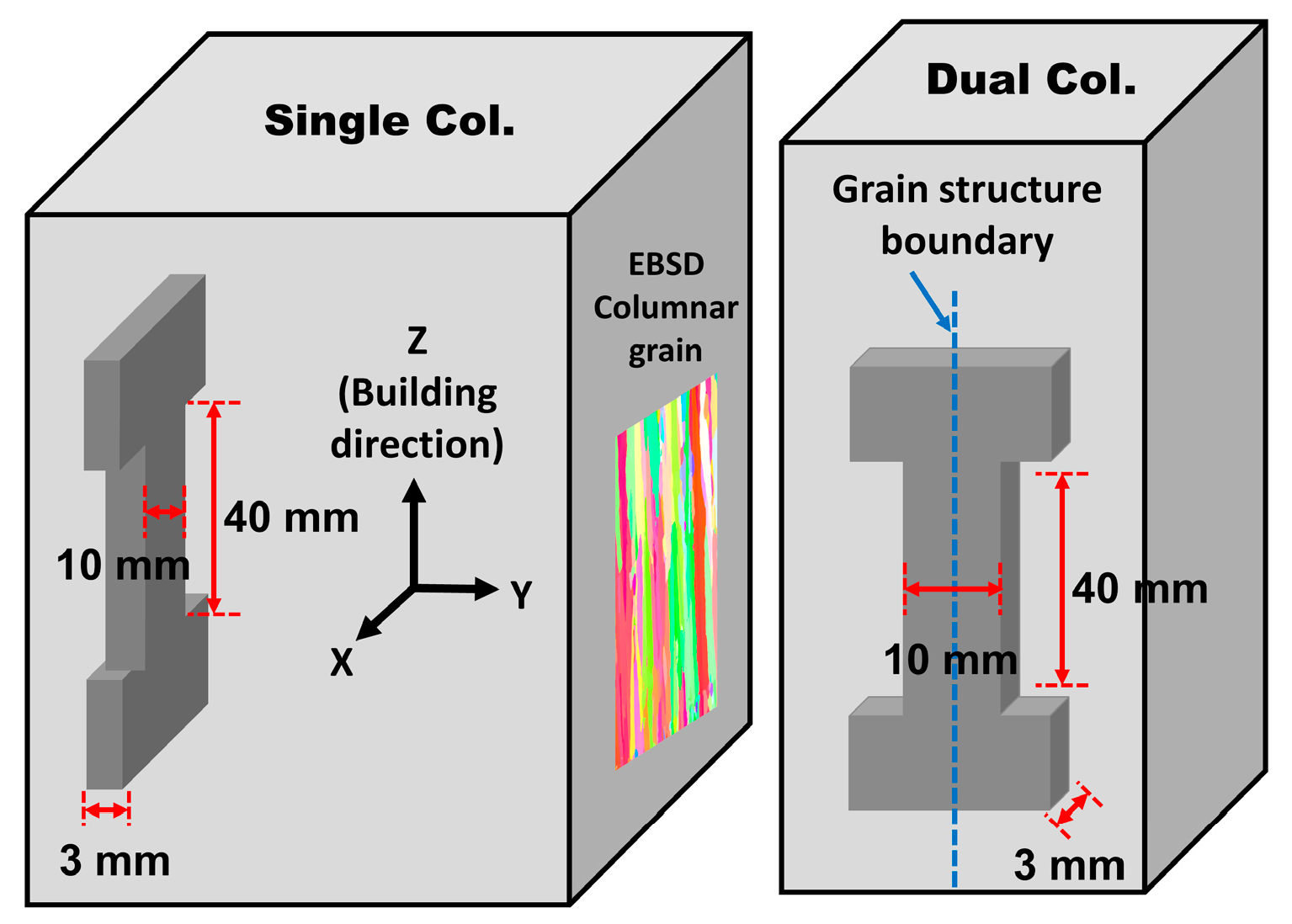
2.3. AM Inconel 718 Block
3. Quantitative Data Analysis of Bragg Edges
3.1. Phenomenological Bragg-Edge Analysis (iBeatles)
3.2. Theoretical Model Based on Materials Properties, Scattering Properties, and Instrument Characteristics
4. Results and Discussion
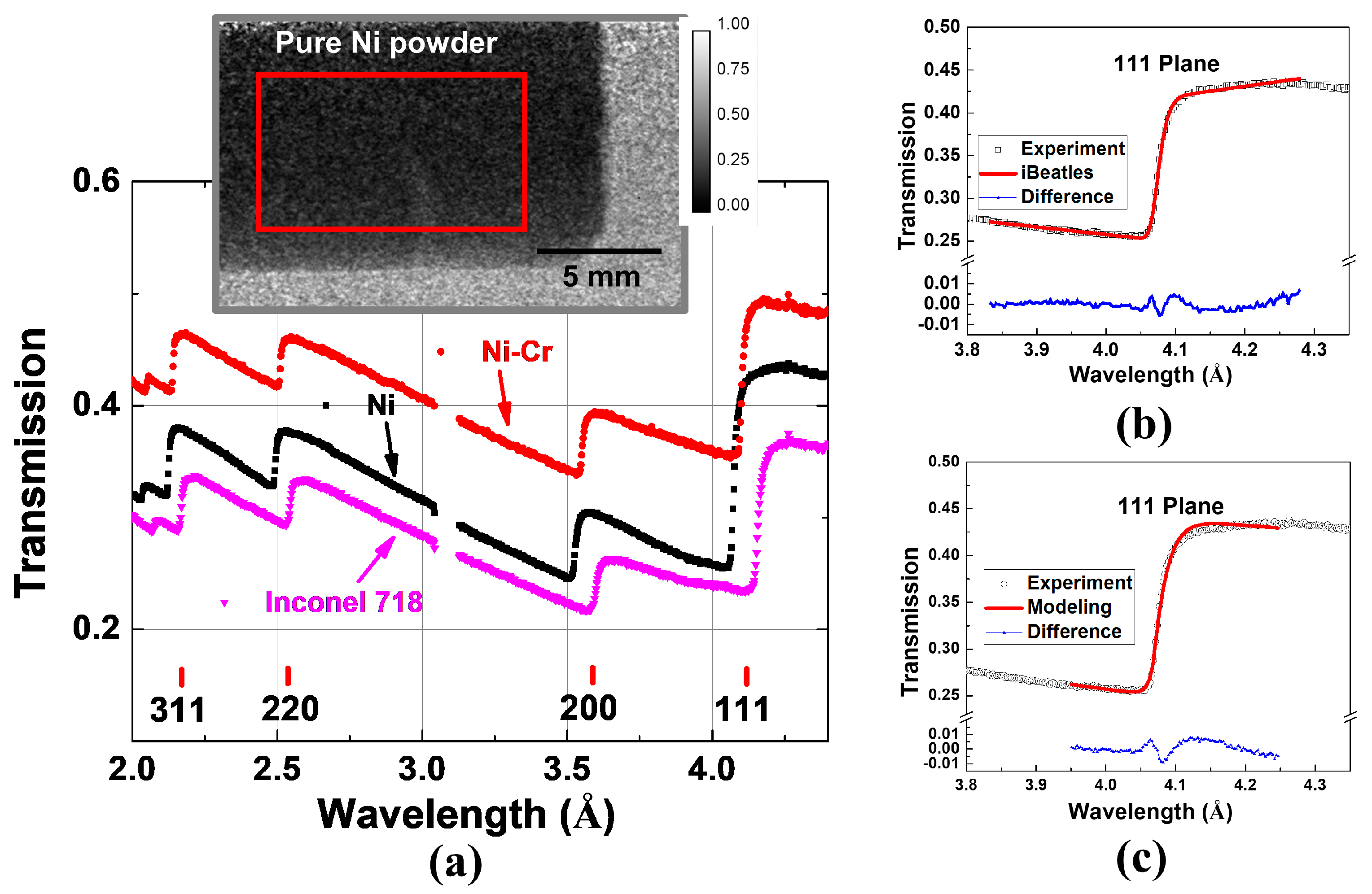
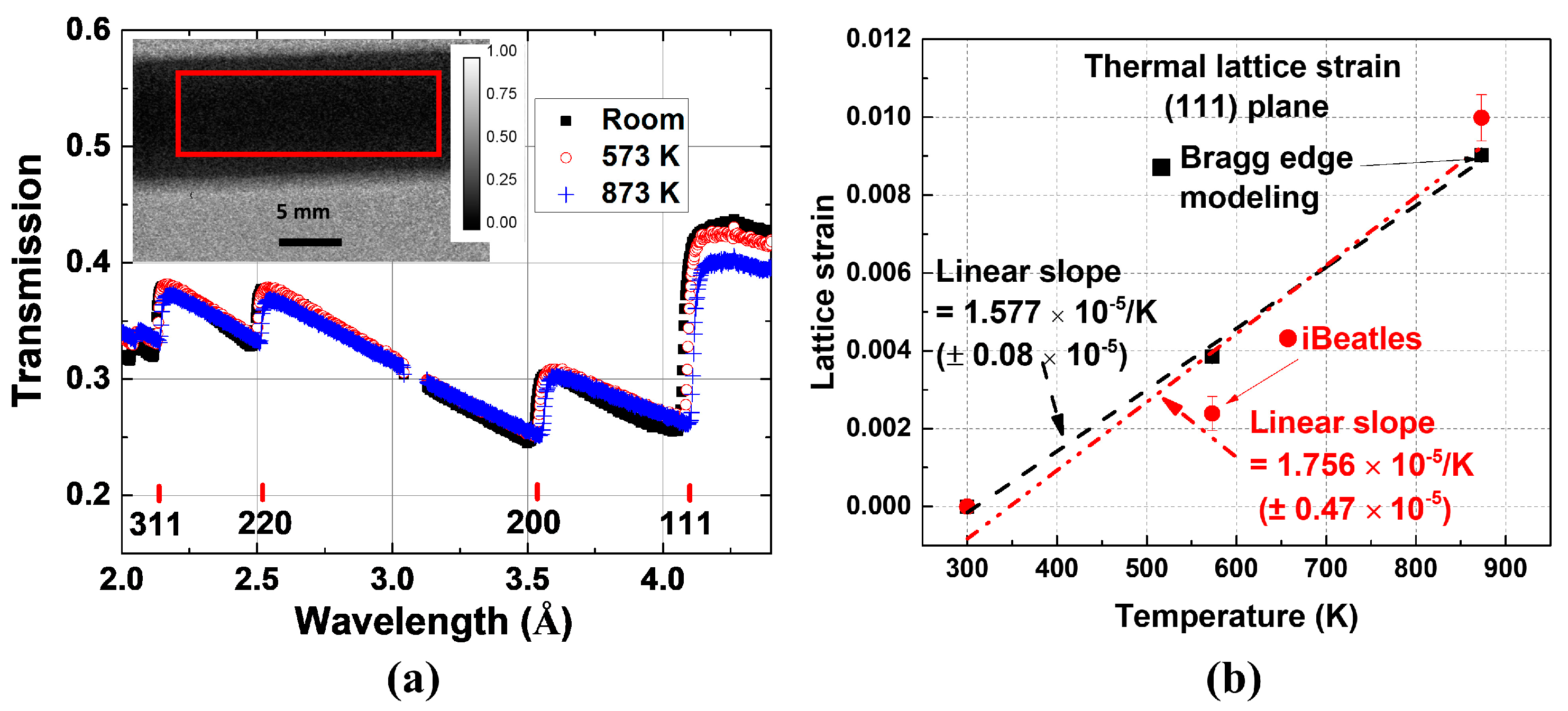
4.1. Powder Sample Measurements
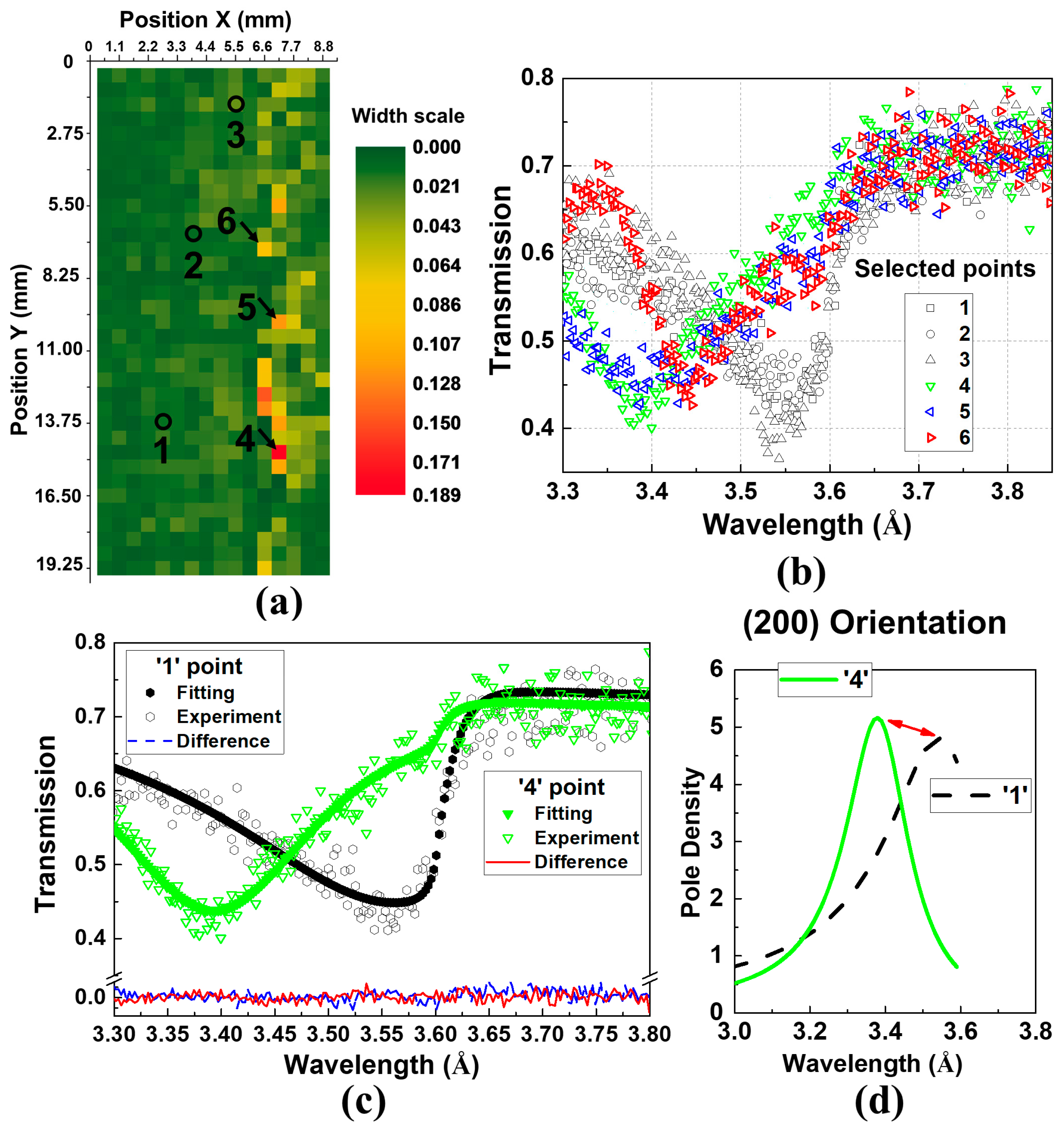
4.2. Microstructural Characterization of AM Inconel 718 Components
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Cekanova, M.; Donnell, R.; Bilheux, H.; Bilheux, J. 2014 Annual oak ridge national laboratory biomedical science and engineering center conference. In Proceedings of the Biomedical Science and Engineering Center Conference (BSEC), Oak Ridge, TN, USA, 6–8 May 2014; pp. 1–4. [Google Scholar]
- Jorgensen, S.W.; Johnson, T.A.; Payzant, E.A.; Bilheux, H.Z. Anisotropic storage medium development in a full-scale, sodium alanate-based, hydrogen storage system. Int. J. Hydrogen Energy 2016, 41, 13557–13574. [Google Scholar] [CrossRef]
- Chen, Y.; Cheng, Y.; Li, J.; Feygenson, M.; Heller, W.T.; Liang, C.; An, K. Lattice-cell orientation disorder in complex spinel oxides. Adv. Energy Mater. 2017, 7, 1601950. [Google Scholar] [CrossRef]
- Huang, H.; Wu, Y.; He, J.; Wang, H.; Liu, X.; An, K.; Wu, W.; Lu, Z. Phase-transformation ductilization of brittle high-entropy alloys via metastability engineering. Adv. Mater. 2017, 29, 1701678. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.D.; Tian, H.; Stoica, A.D.; Wang, X.L.; Liaw, P.K.; Richardson, J.W. The development of grain-orientation-dependent residual stressess in a cyclically deformed alloy. Nat. Mater. 2003, 2, 101–106. [Google Scholar] [CrossRef] [PubMed]
- Santodonato, L.J.; Zhang, Y.; Feygenson, M.; Parish, C.M.; Gao, M.C.; Weber, R.J.K.; Neuefeind, J.C.; Tang, Z.; Liaw, P.K. Deviation from high-entropy configurations in the atomic distributions of a multi-principal-element alloy. Nat. Commun. 2015, 6, 5964. [Google Scholar] [CrossRef] [PubMed]
- Stoica, G.M.; Stoica, A.D.; Miller, M.K.; Ma, D. Temperature-dependent elastic anisotropy and mesoscale deformation in a nanostructured ferritic alloy. Nat. Commun. 2014, 5, 5178. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.; Liaw, P.K.; An, K. Unraveling cyclic deformation mechanisms of a rolled magnesium alloy using in situ neutron diffraction. Acta Mater. 2015, 85, 343–353. [Google Scholar] [CrossRef]
- Song, G.; Sun, Z.; Li, L.; Xu, X.; Rawlings, M.; Liebscher, C.H.; Clausen, B.; Poplawsky, J.; Leonard, D.N.; Huang, S.; et al. Ferritic alloy with extreme creep resistance via coherent hierarchical precipitates. Sci. Rep. 2015, 5, 16327. [Google Scholar] [CrossRef] [PubMed]
- Song, G.; Sun, Z.; Li, L.; Clausen, B.; Zhang, S.Y.; Gao, Y.; Liaw, P.K. High temperature deformation mechanism in hierarchical and single precipitate strengthened ferritic alloys by in situ neutron diffraction studies. Sci. Rep. 2017, 7, 45965. [Google Scholar] [CrossRef] [PubMed]
- Garlea, E.; King, M.O.; Galloway, E.C.; Boyd, T.L.; Smyrl, N.R.; Bilheux, H.Z.; Santodonato, L.J.; Morrell, J.S.; Leckey, J.H. Identification of lithium hydride and its hydrolysis products with neutron imaging. J. Nucl. Mater. 2017, 485, 147–153. [Google Scholar] [CrossRef]
- Zhou, H.; An, K.; Allu, S.; Pannala, S.; Li, J.; Bilheux, H.Z.; Martha, S.K.; Nanda, J. Probing multiscale transport and inhomogeneity in a lithium-ion pouch cell using in situ neutron methods. ACS Energy Lett. 2016, 1, 981–986. [Google Scholar] [CrossRef]
- Nanda, J.; Bilheux, H.; Voisin, S.; Veith, G.M.; Archibald, R.; Walker, L.; Allu, S.; Dudney, N.J.; Pannala, S. Anomalous discharge product distribution in lithium-air cathodes. J. Phys. Chem. C. 2012, 116, 8401–8408. [Google Scholar] [CrossRef]
- Perfect, E.; Cheng, C.L.; Kang, M.; Bilheux, H.Z.; Lamanna, J.M.; Gragg, M.J.; Wright, D.M. Neutron imaging of hydrogen-rich fluids in geomaterials and engineered porous media: A review. Earth Sci. Rev. 2014, 129, 120–135. [Google Scholar] [CrossRef]
- Warren, J.M.; Bilheux, H.; Kang, M.; Voisin, S.; Cheng, C.; Horita, J.; Perfect, E. Neutron imaging reveals internal plant water dynamics. Plant Soil 2013, 366, 683–693. [Google Scholar] [CrossRef]
- Ossler, F.; Santodonato, L.J.; Bilheux, H.Z. In-situ neutron imaging of hydrogenous fuels in combustion generated porous carbons under dynamic and steady state pressure conditions. Carbon 2017, 116, 766–776. [Google Scholar] [CrossRef]
- Kardjilov, N.; Manke, I.; Hilger, A.; Strobl, M.; Banhart, J. Neutron imaging in materials science. Mater. Today 2011, 14, 248–256. [Google Scholar] [CrossRef]
- Kockelmann, W.; Frei, G.; Lehmann, E.H.; Vontobel, P.; Santisteban, J.R. Energy-selective neutron transmission imaging at a pulsed source. Nucl. Instrum. Methods Phys. Res. Sect. A 2007, 578, 421–434. [Google Scholar] [CrossRef]
- Tremsin, A.S.; McPhate, J.B.; Kockelmann, W.; Vallerga, J.V.; Siegmund, O.H.W.; Feller, W.B. High resolution Bragg-edge transmission spectroscopy at pulsed neutron sources: Proof of principle experiments with a neutron counting MCP detector. Nucl. Instrum. Methods Phys. Res. Sect. A 2011, 633, S235–S238. [Google Scholar] [CrossRef]
- Tremsin, A.; Vallerga, J.; McPhate, J.; Siegmund, O. Optimization of high count rate event counting detector with Microchannel Plates and quad Timepix readout. Nucl. Instrum. Methods Phys. Res. Sect. A 2015, 787, 20–25. [Google Scholar] [CrossRef]
- Parker, J.D.; Harada, M.; Hattori, K.; Iwaki, S.; Kabuki, S.; Kishimoto, Y.; Kubo, H.; Kurosawa, S.; Matsuoka, Y.; Miuchi, K.; et al. Applications of a micro-pixel chamber (μPIC) based, time-resolved neutron imaging detector at pulsed neutron beams. J. Phys. Conf. Ser. 2014, 502, 012048. [Google Scholar] [CrossRef]
- Kiyanagi, Y.; Kamiyama, T.; Kino, K.; Sato, H.; Sato, S.; Uno, S. Pulsed neutron imaging using 2-dimensional position sensitive detectors. J. Inst. 2014, 9, C07012. [Google Scholar] [CrossRef]
- Tremsin, A.S.; McPhate, J.B.; Vallerga, J.V.; Siegmund, O.H.; Feller, W.B.; Bilheux, H.Z.; Molaison, J.J.; Tulk, C.A.; Crow, L.; Cooper, R.G.; et al. Transmission Bragg-edge spectroscopy measurements at ORNL Spallation Neutron Source. J. Phys. Conf. Ser. 2010, 251, 012069. [Google Scholar] [CrossRef]
- Woracek, R.; Penumadu, D.; Kardjilov, N.; Hilger, A.; Strobl, M.; Wimpory, R.C.; Manke, I.; Banhart, J. Neutron Bragg-edge-imaging for strain mapping under in situ tensile loading. J. Appl. Phys. 2011, 109, 093506. [Google Scholar] [CrossRef]
- Santisteban, J.R.; Vicente-Alvarez, M.A.; Vizcaino, P.; Banchik, A.D.; Vogel, S.C.; Tremsin, A.S.; Vallerga, J.V.; McPhate, J.B.; Lehmann, E.; Kockelmann, W. Texture imaging of zirconium based components by total neutron cross-section experiments. J. Nucl. Mater. 2012, 425, 218–227. [Google Scholar] [CrossRef]
- Boin, M.; Hilger, A.; Kardjilov, N.; Zhang, S.Y.; Oliver, E.C.; James, J.A.; Randau, C.; Wimpory, R.C. Validation of Bragg-edge experiments by Monte Carlo simulations for quantitative texture analysis. J. Appl. Crystallogr. 2011, 44, 1040–1046. [Google Scholar] [CrossRef]
- Boin, M.; Wimpory, R.C.; Hilger, A.; Kardjilov, N.; Zhang, S.Y.; Strobl, M. Monte Carlo simulations for the analysis of texture and strain measured with Bragg-edge neutron transmission. J. Phys. Conf. Ser. 2012, 340, 012022. [Google Scholar] [CrossRef]
- Woracek, R.; Penumadu, D.; Kardjilov, N.; Hilger, A.; Boin, M.; Banhart, J.; Manke, I. 3D mapping of crystallographic phase distribution using energy-selective neutron tomography. Adv. Mater. 2014, 26, 4069–4073. [Google Scholar] [CrossRef] [PubMed]
- Wensrich, C.; Hendriks, J.; Meylan, M. Bragg-edge neutron transmission strain tomography in granular systems. Strain. 2016, 52, 80–87. [Google Scholar] [CrossRef]
- Tremsin, A.S.; Kockelmann, W.; Paradowska, A.M.; Shu, Y.Z.; Korsunsky, A.M.; Shinohara, T.; Feller, W.B.; Lehmann, E.H. Investigation of microstructure within metal welds by energy resolved neutron imaging. J. Phys. Conf. Ser. 2016, 746, 012040. [Google Scholar] [CrossRef]
- Sato, H.; Sato, T.; Shiota, Y.; Kamiyama, T.; Tremsin, A.S.; Ohnuma, M.; Kiyanagi, Y. Relation between vickers hardness and Bragg-edge broadening in quenched steel rods observed by pulsed neutron transmission imaging. Mater. Trans. 2015, 56, 1147–1152. [Google Scholar] [CrossRef]
- Tremsin, A.; McPhate, J.; Steuwer, A.; Kockelmann, W.; Paradowska, A.M.; Kelleher, J.; Vallerga, J.; Siegmund, O.; Feller, W. High-Resolution strain mapping through time-of-flight neutron transmission diffraction with a microchannel plate neutron counting detector. Strain 2012, 48, 296–305. [Google Scholar] [CrossRef]
- Iwase, K.; Sato, H.; Harjo, S.; Kamiyama, T.; Ito, T.; Takata, S.; Aizawa, K.; Kiyanagi, Y. In situ lattice strain mapping during tensile loading using the neutron transmission and diffraction methods. J. Appl. Crystallogr. 2012, 45, 113–118. [Google Scholar] [CrossRef]
- Wang, X.L.; Holden, T.; Rennich, G.Q.; Stoica, A.; Liaw, P.K.; Choo, H.; Hubbard, C.R. VULCAN—The engineering diffractometer at the SNS. Physica B Condens. Matter. 2006, 385, 673–675. [Google Scholar] [CrossRef]
- Bilheux, H. Neutron characterization of additively manufactured Inconel 718. Adv. Mater. Processes. 2016, 175, 16–20. [Google Scholar]
- Kirka, M.; Lee, Y.; Greeley, D.; Okello, A.; Goin, M.; Pearce, M.; Dehoff, R. Strategy for texture management in metals additive manufacturing. JOM 2017, 69, 523–531. [Google Scholar] [CrossRef]
- Dehoff, R.; Kirka, M.; Sames, W.; Bilheux, H.; Tremsin, A.; Lowe, L.; Babu, S. Site specific control of crystallographic grain orientation through electron beam additive manufacturing. Mater. Sci. Technol. 2015, 31, 931–938. [Google Scholar] [CrossRef]
- An, K. VDRIVE-Data Reduction and Interactive Visualization Software for Event Mode Neutron Diffraction; ORNL Report No. ORNL-TM-2012-621; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 2012. [Google Scholar]
- Steuwer, A.; Santisteban, J.R.; Withers, P.J.; Edwards, L.; Fitzpatrick, M.E.; Daymond, M.R.; Bruno, G. Bragg-edge determination for accurate lattice parameter and elastic strain measurement. Phys. Stat. Sol.(a). 2001, 185, 221–230. [Google Scholar] [CrossRef]
- Kropff, F.; Granada, J.R.; Mayer, R.E. The bragg lineshapes in time-of-flight neutron powder spectroscopy. Nucl. Instrum. Methods Phys. Res. 1982, 198, 515–521. [Google Scholar] [CrossRef]
- Von Dreele, R.B.; Jorgensen, J.D.; Windsor, C.G. Rietveld refinement with spallation neutron powder diffraction data. J. Appl. Crystallogr. 1982, 15, 581–589. [Google Scholar] [CrossRef]
- Tremsin, A.S.; Gao, Y.; Dial, L.C.; Grazzi, F.; Shinohara, T. Investigation of microstructure in additive manufactured Inconel 625 by spatially resolved neutron transmission spectroscopy. Sci. Technol. Adv. Mater. 2016, 17, 324–336. [Google Scholar] [CrossRef] [PubMed]
- Github Library for iBeatles. Available online: https://github.com/ornlneutronimaging/iBeatles (accessed on 6 April 2017).
- Binder, K. Total Coherent Cross sections for the scattering of Neutrons from Crystals. Phys. Stat. Sol. 1970, 41, 767–779. [Google Scholar] [CrossRef]
- Granada, J.R. Total Scattering Cross Section of Solids for Cold and Epithermal Neutrons. Z. Naturforsch. A 1984, 39, 1160. [Google Scholar] [CrossRef]
- Vogel, S. A Rietveld-Approach for the Analysis of Neutron Time-of-Flight Transmission data. Ph.D. Thesis, Christian-Albrechts Universität Kiel, Kiel, Germany, 2000. [Google Scholar]
- Sabine, T. A reconciliation of extinction theories. Acta Crystallogr. Sect. A Found. Crystallogr. 1988, 44, 368–374. [Google Scholar] [CrossRef]
- Sabine, T.M.; von Dreele, R.B.; Jorgensen, J.E. Extinction in time-of-flight neutron powder diffractometry. Acta Crystallogr. Sect. A Found. Crystallogr. 1988, 44, 374–379. [Google Scholar] [CrossRef]
- Chaturvedi, M.C.; Han, Y. Strengthening mechanisms in Inconel 718 superalloy. Metal Sci. 1983, 17, 145–149. [Google Scholar] [CrossRef]
- Han, Y.F.; Deb, P.; Chaturvedi, M.C. Coarsening behaviour of γ″- and γ′-particles in Inconel alloy 718. Met. Sci. 1982, 16, 555–562. [Google Scholar] [CrossRef]
- Cao, W.D. Solidification and solid state phase transformation of Allvac® 718Plus™ alloy. Superalloys 2005, 718, 165–177. [Google Scholar]
- Hidnert, P. Thermal expansion of some nickel alloys. J. Res. Natl. Bur. Stand. 1957, 58, 89. [Google Scholar] [CrossRef]
- Santisteban, J.R.; Edwards, L.; Steuwer, A.; Withers, P.J. Time-of-flight neutron transmission diffraction. J. Appl. Crystallogr. 2001, 34, 289–297. [Google Scholar] [CrossRef]
- Santisteban, J.R.; Edwards, L.; Stelmukh, V. Characterization of textured materials by TOF transmission. Phys. B Condens. Matter 2006, 385–386, 636–638. [Google Scholar] [CrossRef]
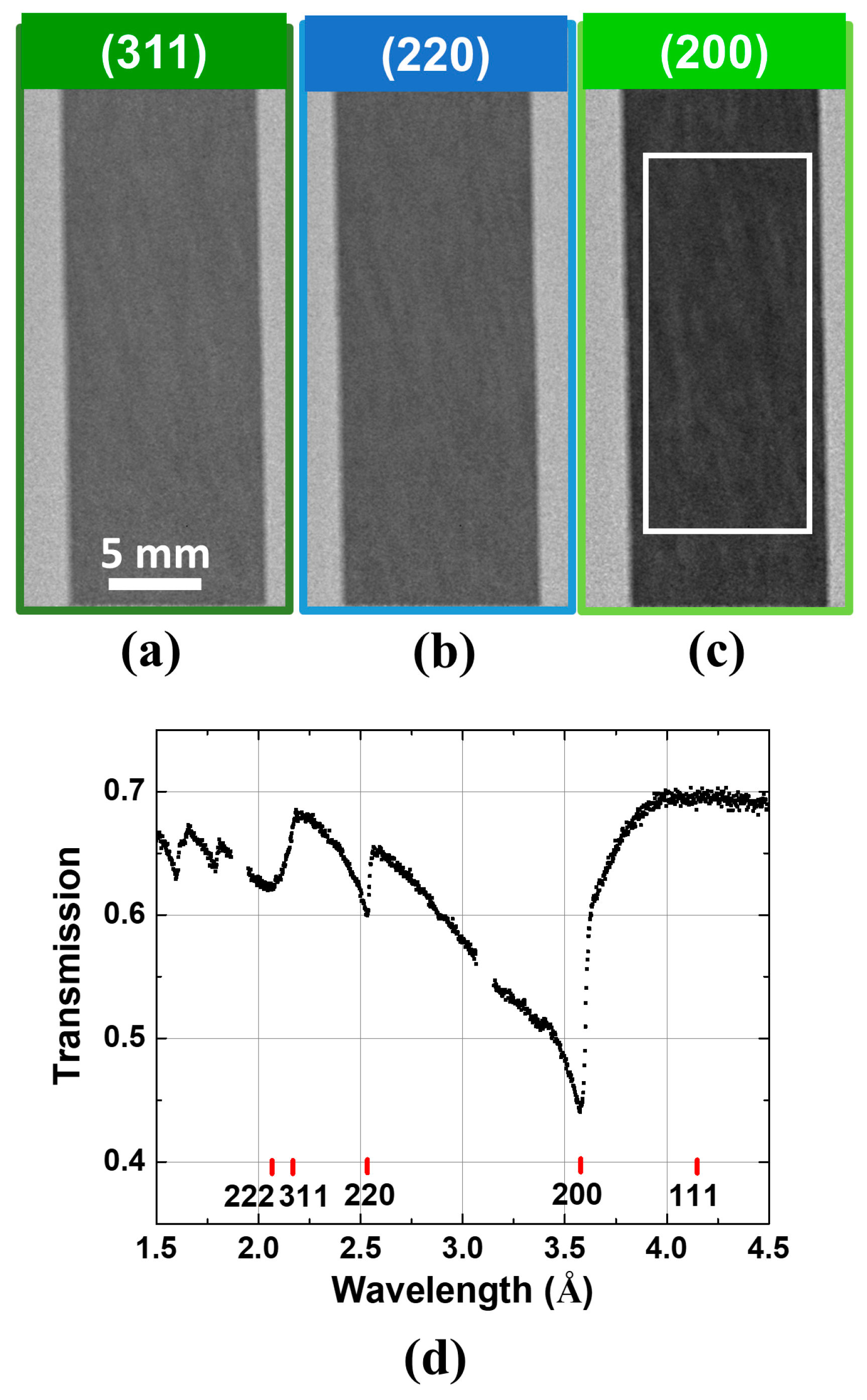
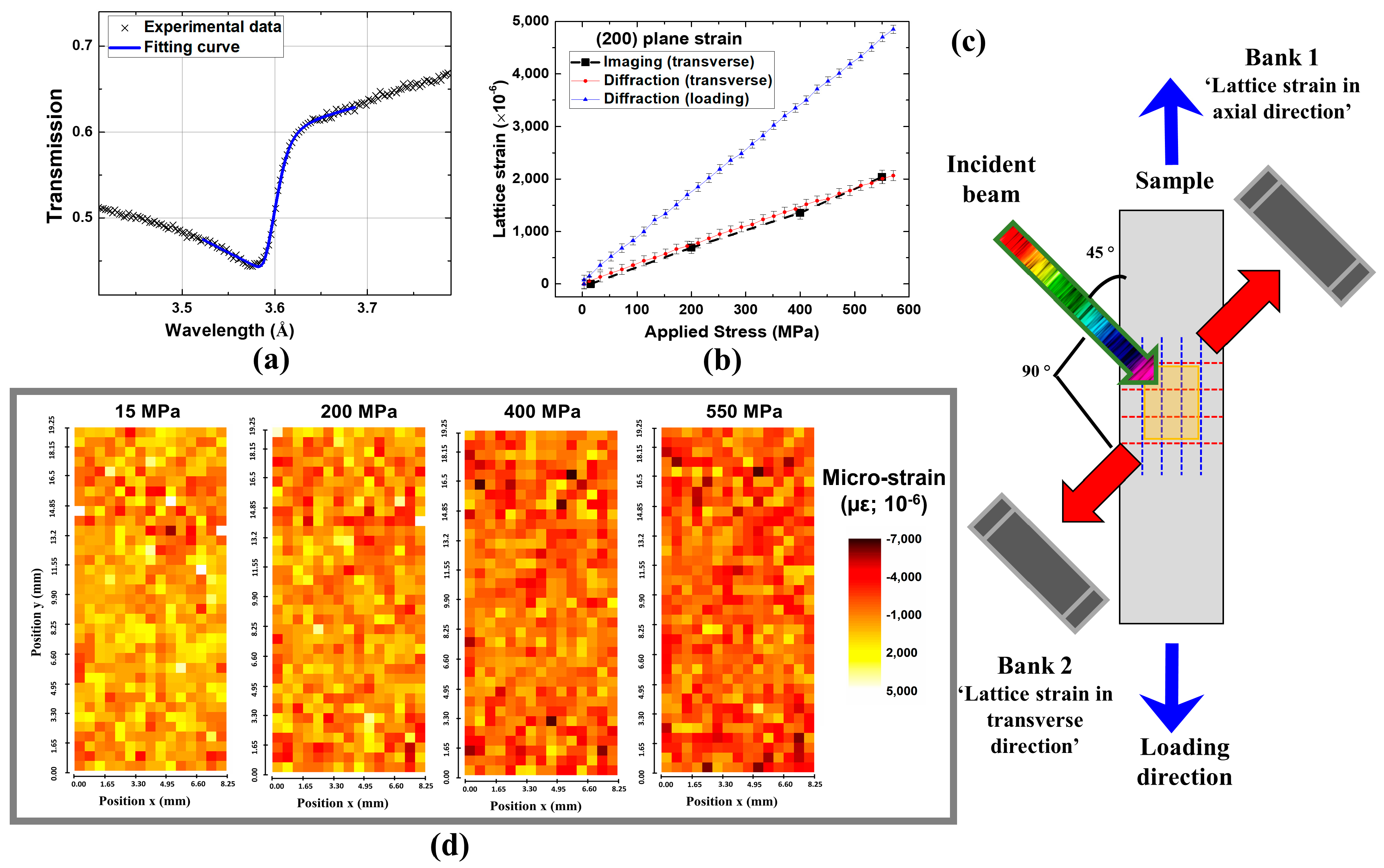
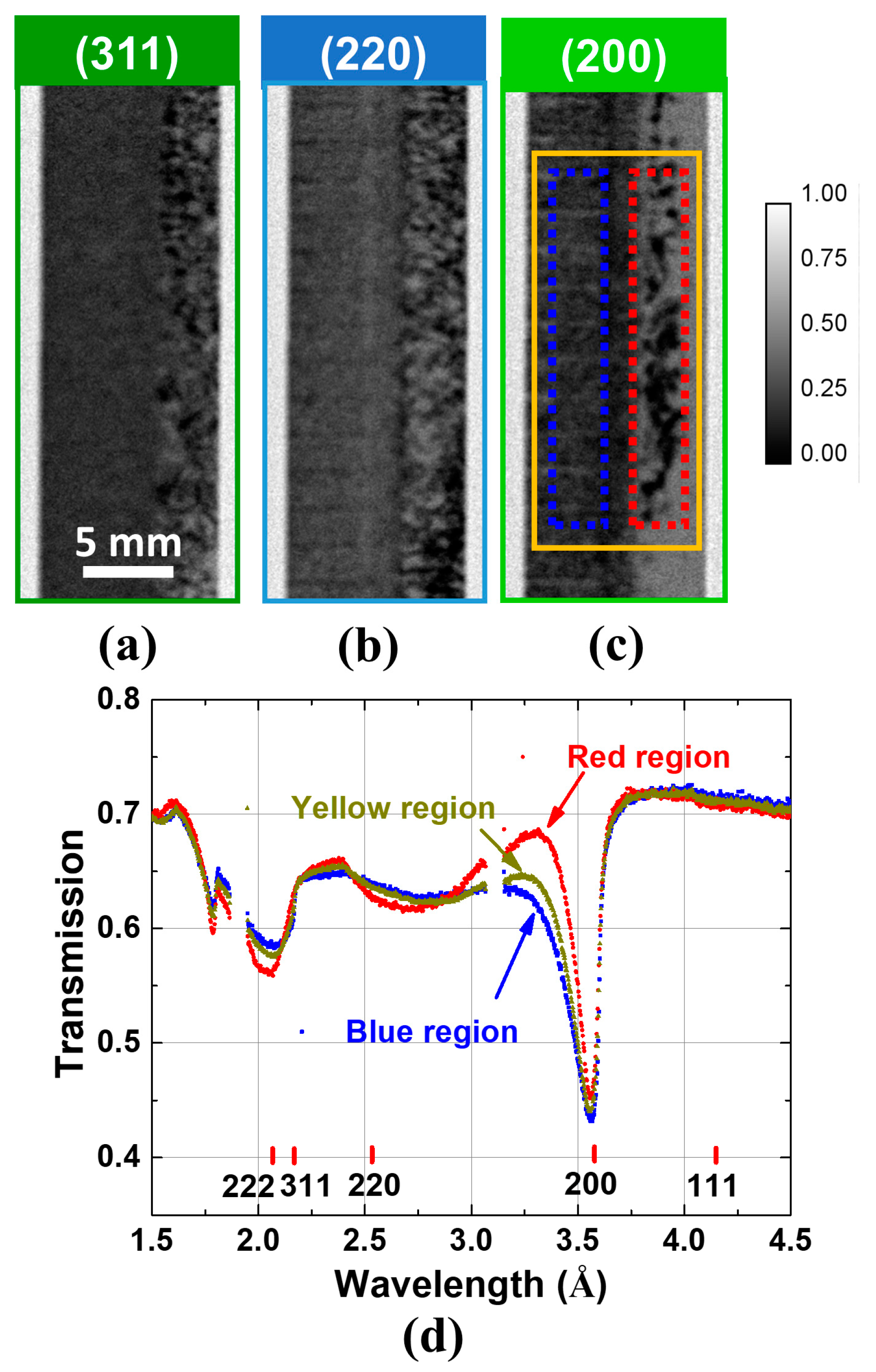
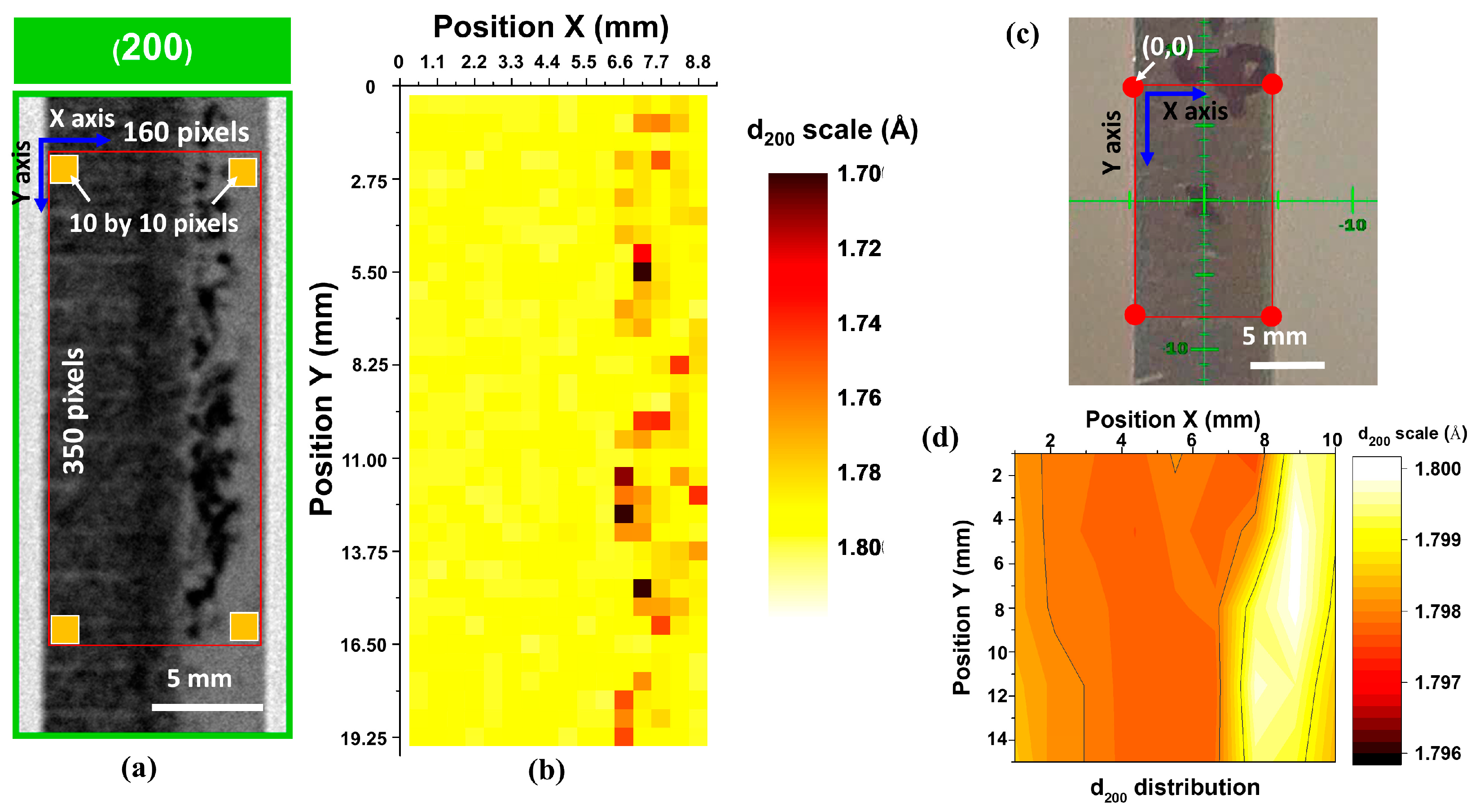
| Element | Ni | Fe | Cr | Mo | Nb | Cu | Al | Ti | C |
|---|---|---|---|---|---|---|---|---|---|
| wt. % | Balance | 18.5 | 18.5 | 3.0 | 5.0 | 0.15 | 0.5 | 1.0 | 0.05 |
| Plane | Technique | Pure Ni | Ni39Cr11 | Inconel 718 |
|---|---|---|---|---|
| 111 | Diffraction | 2.03376 (0.00003) | 2.04896 (0.00004) | 2.07573 (0.00008) |
| iBeatles | 2.03683 (0.00062) | 2.05091 (0.00069) | 2.07839 (0.00450) | |
| Bragg-edge modeling | 2.03258 (0.00003) | 2.05009 (0.00003) | 2.07629 (0.00002) | |
| 200 | Diffraction | 1.761392 (0.00004) | 1.77440 (0.00003) | 1.79766 (0.00006) |
| iBeatles | 1.76392 (0.00420) | 1.77497 (0.00082) | 1.79474 (0.00057) | |
| Bragg-edge modeling | 1.76180 (0.00007) | 1.77441 (0.00006) | 1.79719 (0.00005) |
| Plane | Technique | Room | 573 K | 873 K |
|---|---|---|---|---|
| 111 | iBeatles | 2.03701 (0.00067) | 2.04188 (0.00060) | 2.05736 (0.00100) |
| Bragg-edge modeling | 2.03569 (0.00001) | 2.04354 (0.00002) | 2.05406 (0.00002) | |
| 200 | iBeatles | 1.76368 (0.00185) | 1.77218 (0.00535) | 1.78153 (0.00126) |
| Bragg-edge modeling | 1.76311 (0.00003) | 1.77098 (0.00005) | 1.77916 (0.00005) |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, G.; Lin, J.Y.Y.; Bilheux, J.C.; Xie, Q.; Santodonato, L.J.; Molaison, J.J.; Skorpenske, H.D.; M. Dos Santos, A.; Tulk, C.A.; An, K.; et al. Characterization of Crystallographic Structures Using Bragg-Edge Neutron Imaging at the Spallation Neutron Source. J. Imaging 2017, 3, 65. https://doi.org/10.3390/jimaging3040065
Song G, Lin JYY, Bilheux JC, Xie Q, Santodonato LJ, Molaison JJ, Skorpenske HD, M. Dos Santos A, Tulk CA, An K, et al. Characterization of Crystallographic Structures Using Bragg-Edge Neutron Imaging at the Spallation Neutron Source. Journal of Imaging. 2017; 3(4):65. https://doi.org/10.3390/jimaging3040065
Chicago/Turabian StyleSong, Gian, Jiao Y. Y. Lin, Jean C. Bilheux, Qingge Xie, Louis J. Santodonato, Jamie J. Molaison, Harley D. Skorpenske, Antonio M. Dos Santos, Chris A. Tulk, Ke An, and et al. 2017. "Characterization of Crystallographic Structures Using Bragg-Edge Neutron Imaging at the Spallation Neutron Source" Journal of Imaging 3, no. 4: 65. https://doi.org/10.3390/jimaging3040065
APA StyleSong, G., Lin, J. Y. Y., Bilheux, J. C., Xie, Q., Santodonato, L. J., Molaison, J. J., Skorpenske, H. D., M. Dos Santos, A., Tulk, C. A., An, K., Stoica, A. D., Kirka, M. M., Dehoff, R. R., Tremsin, A. S., Bunn, J., Sochalski-Kolbus, L. M., & Bilheux, H. Z. (2017). Characterization of Crystallographic Structures Using Bragg-Edge Neutron Imaging at the Spallation Neutron Source. Journal of Imaging, 3(4), 65. https://doi.org/10.3390/jimaging3040065









