Integrated Model of Image Protection Techniques

Abstract

We propose an integrated model of Block-Permutation-Based Encryption (BPBE) and Reversible Data Hiding (RDH). The BPBE scheme involves four processes for encryption, namely block scrambling, block-rotation/inversion, negative-positive transformation and the color component shuffling. A Histogram Shifting (HS) method is adopted for RDH in our model. The proposed scheme can be well suitable for the hierarchical access control system, where the data can be accessed with the different access rights. This scheme encrypts R, G and B components independently. Therefore, we can generate similar output images from different input images. Additionally, the key derivation scheme also provides the security according to the different access rights. Our scheme is also resilient against brute-force attacks and Jigsaw Puzzle Solvers (JPSs). Furthermore, the compression performance is also not severely degraded using a standard lossless compression method.

1. Introduction

Due to the development of digital communication technologies, there are more services such as E-learning, digital diagnosis and web conferences. Therefore, digital content needs to be secured properly, as it can be easily manipulated and have problems with copyright, data security, authentication, etc.

Generally, data hiding can be classified into two categories, namely Irreversible Data Hiding (IDH) [1,2,3] and Reversible Data Hiding (RDH) [4,5,6,7,8,9]. In IDH, the host signal cannot be completely recovered. On the other hand, RDH is also referred to as invertible or lossless data hiding, which has been extensively studied to embed secret message bits into a cover object such as an image/video or audio to generate the marked one. In RDH, not only the embedded message needs to be restored precisely, but also the cover image should be losslessly recovered. Therefore, RDH techniques are desirable in some special scenarios such as remote sensing, medical imagery, military communications and law forensics where no permanent change is permitted. Most of the RDH methods aim to provide a good performance on the data hiding rate, the quality of the marked image, the level of security and the computational complexity.

One of the popular methods for RDH is the Histogram Shifting (HS) method. The algorithm proposed by Ni et al. [9] is based on an HS method, in which the data are embedded to the peak of the histogram of an image.

Block-Permutation-Based Encryption (BPBE) schemes [10,11,12,13] comprise one of the perceptual encryption techniques. In BPBE schemes, first, an original image is divided into definite block size, and the four processes of encryption, namely block scrambling, block rotation/inversion, negative-positive transformation and color component shuffling, are processed. The main feature of BPBE schemes is that the compression efficiency of the encrypted images is compatible with JPEG compression [11]. Similarly, the BPBE schemes have been proposed for encryption-then-compression (ETC) technique [14,15,16,17,18,19,20], in which a user securely transmits images via a Social Network Service (SNS) provider.

Recently, the encryption-based RDH method using adaptive code embedding has been proposed [19]. It is a pixel-based scrambling method. This method has the advantage of a maximum embedding rate of 1.72 bpp and allows the severe distortion of the final encrypted image by embedding more data. However, the disadvantage of this method is that the decryption process is not possible without the extraction of embedded data. Similarly, the access rights cannot be controlled according to various permission levels. In addition, there is no consideration for the compatibility on compression efficiency using international standards. Therefore, we propose an integrated model of BPBE and RDH in this paper. The proposed scheme has the advantage of decryption of the image without extraction of data. Our scheme can also control the quality of the embedded image. Similarly, the access rights can be controlled according to various permission levels. This scheme also considers standard lossless compression methods such as JPEG-LS [21]. The proposed scheme can be attractive in scenarios such as the doctor-nurse relation in a hospital, large organizations and hierarchical file systems, where there is a hierarchical access control according to the various access rights. In some organizations, there is a complex hierarchy between the CEO and front line employees. Different employees have to access different types of information as per their requirements. For example, the CEO is the only user with full permission. A manager may have partial permission to know the salary of the employees, but not personal information such as telephone numbers. Furthermore, we also propose an efficient key derivation scheme to manage the multiple keys, which has been utilized in BPBE and RDH. The experimental results and analysis demonstrate the effectiveness of the proposed scheme.

2. Preliminaries

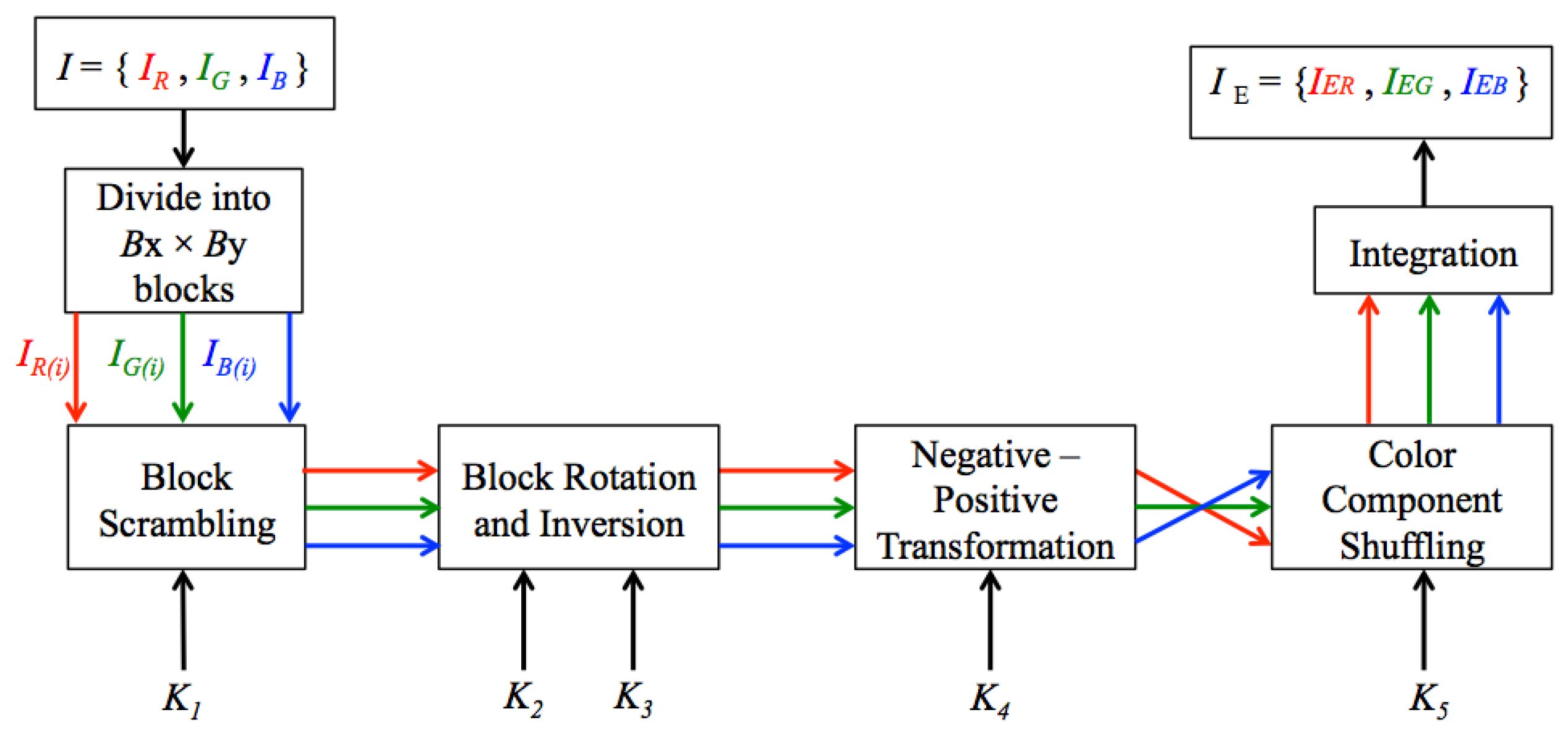
2.1. BPBE Scheme

In the BPBE scheme [13], an original image with $M\times N$ pixels is divided into different non-overlapping blocks of $B_x\times B_y$ pixels. As illustrated in Figure 1, this scheme has four processes, i.e., block scrambling, block rotation/inversion, negative-positive transformation and color component shuffling, respectively. The procedures for the above-mentioned four processes are elaborated as follows.

Step 1

Divide each color component of a color image $I=\{I_R,I_G,I_B\}$ into multiple blocks with $B_x\times B_y$ size.

Step 2

Permute the positions of the divided blocks randomly using a key $K_1$.

Step 3

Rotate and invert each of the divided blocks using keys $K_2$ and $K_3$.

Step 4

Apply a negative-positive transformation to the blocks using a key $K_4$.

Step 5

Shuffle each color components in each block using a key $K_5$.

In this scheme, the keys $K_1$, $K_2$, $K_3$ and $K_4$ are commonly used for the Red (R), Green (G) and Blue (B) color components.

2.2. RDH

For RDH, we have applied the conventional RDH algorithm, which is employed in the spatial domain and is based on HS [9], to our work as one of the examples. This algorithm is chosen to maintain the quality of an image. However, the other RDH algorithms can also be employed in our scheme.

3. Proposed Scheme

We propose an integrated model of BPBE and RDH that can be well applied to the hierarchical access control system. The major purposes of using a hierarchical system are that the embedded data can be extracted and also the encrypted image can be decrypted according to the various permission levels. Similarly, the level of security can be controlled by embedding more confidential data at a higher level and less confidential data at a lower level in the hierarchical system. Therefore, the users with a higher permission level are allowed to extract more confidential data than the users with a low permission level. On the other hand, for decryption-only permission, the users are able to decrypt the image, but are not allowed to extract the embedded data. In this manner, the access control can be made flexible for the various users who are accessing the confidential data from different levels in the hierarchy.

Here, we use three independent keys for the R, G and B components [10] for the encryption and embedding process. In the case that we use JPEG-LS [21], which processes the images in the RGB color space without conversion to any other color spaces for the final encrypted images, we can maintain the compression efficiency.

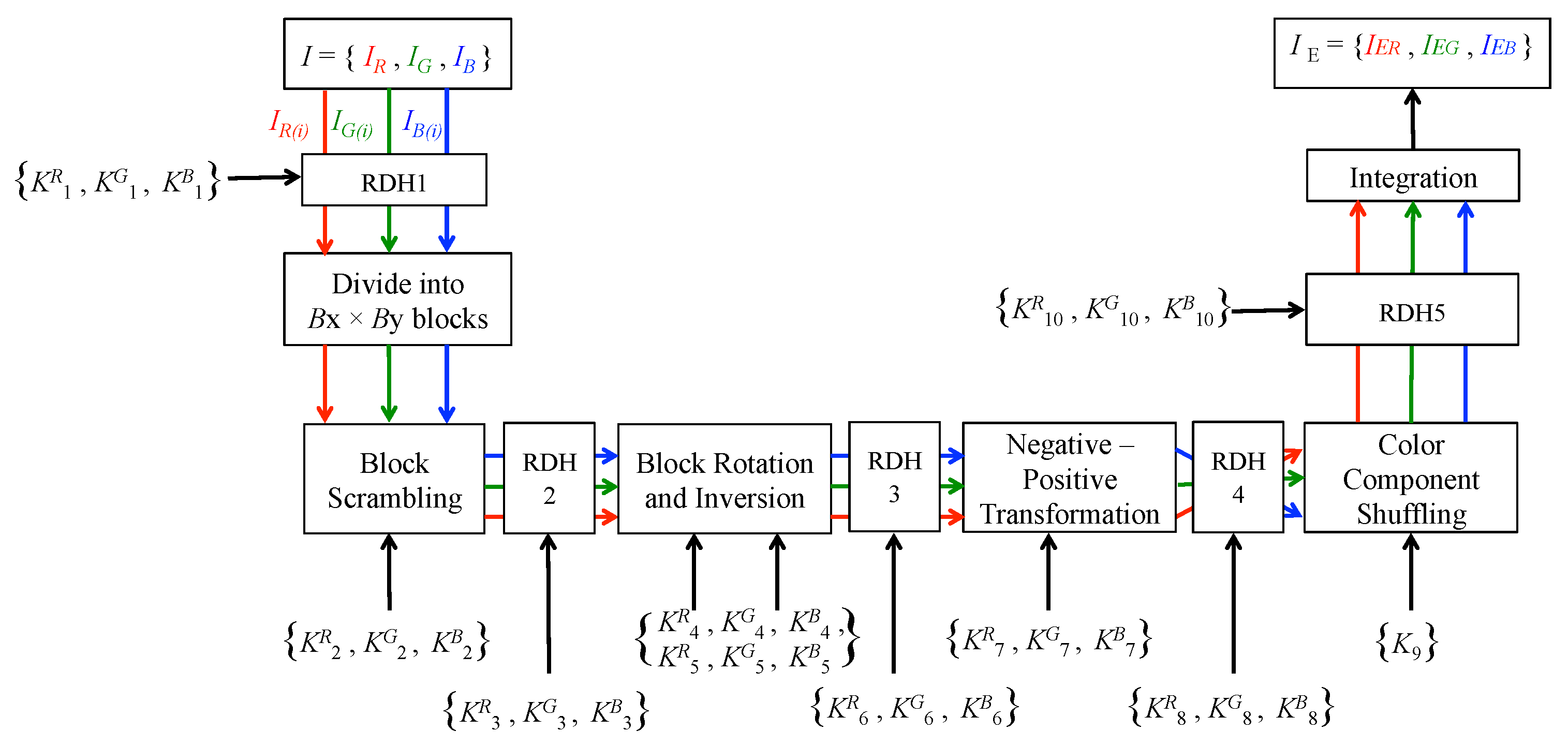
3.1. Encryption and Embedding Process

In this section, we elaborate the encryption and embedding process as shown in Figure 2. For the simulation, we have employed a hundred different test images with $768\times 512$ (70) and $512\times 768$ pixels (30) from the image database “Content-based image retrieval database” [22]. The divided block size is selected as $16\times 16$ pixels for encryption to maintain JPEG compression efficiency [11].

Step 1

Apply RDH to an original image $I=\{I_R,I_G,I_B\}$ of $M\times N$ pixels using keys $K_1^R$, $K_1^G$ and $K_1^B$.

Step 2

Divide each color component of an original image into multiple blocks with $B_x\times B_y$ pixels.

Step 3

Permute the positions of the divided blocks randomly using keys $K_2^R$, $K_2^G$ and $K_2^B$.

Step 4

Apply RDH using keys $K_3^R$, $K_3^G$ and $K_3^B$.

Step 5

Rotate and invert each block randomly using keys $K_4^R$, $K_4^G$, $K_4^B$, $K_5^R$, $K_5^G$ and $K_5^B$.

Step 6

Apply RDH using keys $K_6^R$, $K_6^G$ and $K_6^B$.

Step 7

Apply the negative-positive transformation for each block using keys $K_7^R$, $K_7^G$ and $K_7^B$.

Step 8

Apply RDH using keys $K_8^R$, $K_8^G$ and $K_8^B$.

Step 9

Shuffle the three color components, i.e., R, G, and B in each block by using a key $K_9$.

Step 10

Apply RDH using keys $K_{10}^R$, $K_{10}^G$ and $K_{10}^B$.

Step 11

Generate the encrypted image $I_E=\{I_{ER},I_{EG},I_{EB}\}$ by integrating all the transformed blocks.

3.2. Key Derivation

A large amount of keys would be generated in the proposed scheme due to the use of independent keys $K_1^i$, $K_2^i$, …, $K_8^i$, $K_{10}^i$ ($i=R,G,B$) for three components. Therefore, the management of those multiple keys is an important issue. Hence, we also consider deriving an efficient key management scheme with the use of hash chains [23] and decrease the number of managed keys. With the use of hash chains, we assign the derived keys to each step of encryption and embedding. The number of managed keys is diminished to one, that is key $K_M$. Keys $K_x$ can be given by:

$$K_x=H^x(K_M),$$

(1)

where $x=1,2,\dots ,10$ and $H(·)$ is a one-way hash function.

An efficient key derivation scheme is as shown in Figure 3. The keys $K_{\mathrm{e}(u)}^i$ are the representation for the embedding process, whereas the keys $K_{\mathrm{c}(u)}^i$ are the representation for the encryption process. Here, $u(u=1,2,\dots ,5)$ indicates the number of the encryption or the embedding process. In the embedding process, a key $K_{\mathrm{e}(1)}^R$ can be derived by performing a one-way hash chain to the result obtained by XOR (exclusive or) operation between key $K_M$ and its associated random numbers $a_{\mathrm{e}}^R$. Similarly, $K_{\mathrm{e}(1)}^G$ can be achieved by a one-way hash function to the result of XOR operation between $K_{\mathrm{e}(1)}^R$ and $a_{\mathrm{e}}^G$. A key $K_{\mathrm{e}(1)}^B$ can be derived by performing a one-way hash function to the result obtained by XOR operation between $K_{\mathrm{e}(1)}^G$ and $a_{\mathrm{e}}^B$. The key derivation can be given as follows.

$$K_{\mathrm{e}(1)}^R=H(K_M\oplus a_{\mathrm{e}}^R),$$

(2)

$$K_{\mathrm{e}(1)}^G=H(K_{\mathrm{e}(1)}^R\oplus a_{\mathrm{e}}^G),$$

(3)

$$K_{\mathrm{e}(1)}^B=H(K_{\mathrm{e}(1)}^G\oplus a_{\mathrm{e}}^B),$$

(4)

where ⊕ represents a bitwise XOR operation.

In addition, by using hash chains, all other keys $K_{\mathrm{e}(1)}^i$, $K_{\mathrm{e}(2)}^i$, …, $K_{\mathrm{e}(5)}^i$, $(i=R,G,B)$ can be obtained as follows.

$$K_{\mathrm{e}(u)}^R=H^{u-1}(K_{\mathrm{e}(1)}^R),$$

(5)

$$K_{\mathrm{e}(u)}^G=H^{u-1}(K_{\mathrm{e}(1)}^G),$$

(6)

$$K_{\mathrm{e}(u)}^B=H^{u-1}(K_{\mathrm{e}(1)}^B),$$

(7)

where $u=2,3,4,5$.

In encryption process, $K_{\mathrm{c}(1)}^R$ can be obtained by the result of the XOR operation between $K_{\mathrm{e}(1)}^R$ and $a_{\mathrm{c}}^R$. The key derivation process is described as follows.

$$K_{\mathrm{c}(1)}^R=H(K_{\mathrm{e}(1)}^R\oplus a_{\mathrm{c}}^R),$$

(8)

$$K_{\mathrm{c}(1)}^G=H(K_{\mathrm{c}(1)}^R\oplus a_{\mathrm{c}}^G),$$

(9)

$$K_{\mathrm{c}(1)}^B=H(K_{\mathrm{c}(1)}^G\oplus a_{\mathrm{c}}^B),$$

(10)

Similarly,

$$K_{\mathrm{c}(u)}^R=H^{u-1}(K_{\mathrm{c}(1)}^R),$$

(11)

$$K_{\mathrm{c}(u)}^G=H^{u-1}(K_{\mathrm{c}(1)}^G),$$

(12)

$$K_{\mathrm{c}(u)}^B=H^{u-1}(K_{\mathrm{c}(1)}^B),$$

(13)

where $u=2,3,4$. Regarding the key for the color component shuffling, it is single for each image. Therefore, it is derived by:

$$K_{\mathrm{c}(5)}^B=H(K_{\mathrm{c}(4)}^B).$$

(14)

3.3. Decryption and Extraction Process

As shown in Figure 3, there are different hierarchical levels. Therefore, the access rights for each hierarchical level can be easily controlled for the decryption and extraction. The user with high permission is able to extract and decrypt more confidential data and images, respectively, than the user with low permission.

Table 1. Embedding capacity at each level of Japan Image32.

Level	Embedding Capacity (bits)
	Single Embedding	Double Embedding
Data 1	18,709	37,233
Data 2	18,524	36,866
Data 3	18,476	36,090
Data 4	16,827	31,934
Data 5	15,297	27,396
Total	87,833	169,519

shows the total embedding capacity of Japan Image32 at each level for single embedding (one time) and double embedding (two times).

Table 2. Total embedding capacity (bits) and Peak Signal-to-Noise Ratio (PSNR) values for single embedding.

Image	Single Embedding
(768 × 512 pixels)	Total Embedding Capacity (bits)	PSNR
Japan Image22	41,576	38.34
Japan Image27	78,682	43.93 (max)
Japan Image32	87,833	40.41
Australia Image01	75,360	43.80
Australia Image03	86,720	41.69
Australia Image05	41,965	38.75
Indonesia Image01	285,821	37.91
Indonesia Image35	240,071	37.42 (min)
Iran Image13	525,427 (max)	38.29
Iran Image49	132,792	38.41
(512 × 768 pixels)	Total Embedding Capacity (bits)	PSNR
Japan Image26	38,418 (min)	38.81
Japan Image31	55,594	39.61
Australia Image02	41,212	42.77
Australia Image06	65,859	40.55
Indonesia Image20	89,424	40.98
Indonesia Image26	112,831	39.69
Iran Image10	218,532	42.29
Iran Image15	62,670	41.94

and

Table 3. Total embedding capacity (bits) and PSNR values for double embedding (Japan).

Image (768 × 512 pixels)	Double Embedding
	Total Embedding Capacity (bits)	PSNR
Japan Image01	131,529	37.44
Japan Image13	85,156	34.64
Japan Image32	169,519	34.65
Japan Image17	165,832	35.55
Japan Image15	88,180	32.93
Japan Image22	79,477	32.43
Japan Image27	142,136	39.68
Japan Image08	90,016	34.53
Japan Image20	101,275	35.66
Japan Image02	111,144	37.65

illustrate the total embedding capacity and the Peak Signal-to-Noise Ratio (PSNR) values of test images for single embedding and double embedding, respectively. Figure 4 and Figure 5 show the simulation results of Japan Image32 and Japan Image22 obtained by different permissions in the case of single embedding. The following sections describe the decryption and extraction process for different permissions.

3.3.1. Full Permission

Let us consider that a user has the full access right to extract all the embedded data and to entirely decrypt the images. Therefore, the user has the full permission to get a managed key $K_M$ as given in Figure 3a. If a user were to obtain a key $K_M$, the user would be able to derive all twenty eight keys, retrieve the original image from the final encrypted image as shown in Figure 4b and Figure 5b and also extract all the embedded data, as shown in Table 1.

3.3.2. Partial Permission

In this case, let us assume that another user is only permitted to extract Data 3, 4 and 5, as shown in Figure 3b. The user would obtain six keys, i.e., $K_{\mathrm{e}(3)}^R$, $K_{\mathrm{e}(3)}^G$, $K_{\mathrm{e}(3)}^B$, $K_{\mathrm{c}(4)}^R$, $K_{\mathrm{c}(4)}^G$ and $K_{\mathrm{c}(4)}^B$. Hence, the user is able to derive the seven keys, i.e., $K_{\mathrm{e}(4)}^R$, $K_{\mathrm{e}(5)}^R$, $K_{\mathrm{e}(4)}^G$, $K_{\mathrm{e}(5)}^G$, $K_{\mathrm{e}(4)}^B$, $K_{\mathrm{e}(5)}^B$, $K_{\mathrm{c}(5)}^B$, extract Data 3, 4, and 5 and obtain the half encrypted image as given in Figure 4c and Figure 5c.

3.3.3. Decryption-Only Permission

Let us assume that a user is only allowed to decrypt the image, but is restricted in extracting the embedded data. If a user were to obtain a key, i.e., $K_{\mathrm{c}(1)}^R$, then he/she would be able to derive the twelve keys, i.e., $K_{\mathrm{c}(1)}^G$, $K_{\mathrm{c}(1)}^B$, $K_{\mathrm{c}(2)}^R$, $K_{\mathrm{c}(2)}^G$, $K_{\mathrm{c}(2)}^B$, $K_{\mathrm{c}(3)}^R$, $K_{\mathrm{c}(3)}^G$, $K_{\mathrm{c}(3)}^B$, $K_{\mathrm{c}(4)}^R$, $K_{\mathrm{c}(4)}^G$, $K_{\mathrm{c}(4)}^B$ and $K_{\mathrm{c}(5)}^B$. Figure 4d and Figure 5d show the simulation results for decryption-only permission. From the experimental results of 100 images, the maximum and minimum values of PSNR are 43.93 (Japan Image27) and 37.42 (Indonesia Image35), respectively, as shown in Table 2. Hence, there is approximately only 6.51 dB of variation in PSNR values. The maximum embedding capacity for ‘Iran Image13’ is 525,427 bits with its corresponding PSNR value as 38.29 dB. Similarly, the minimum embedding capacity for ‘Japan Image26’ is 38,418 bits with its corresponding PSNR value as 38.81 dB. In this case, our scheme is effective for ‘Iran Image13’, as it has comparatively higher embedding capacity than ‘Japan Image26’.

4. Experimental Results and Analysis

4.1. Key Space

Generally, there are various types of attacks on encryption such as differential attacks, brute-force attacks, statistical attacks, and so on. A brute-force attack is a kind of a trial-and-error method that is used to obtain the possible combination. Here, we evaluate the size of key space assuming the brute-force attacks. The conventional BPBE scheme [13] has four encryption processes, namely block scrambling, block rotation/inversion, negative-positive transformation and color component shuffling, respectively. It performs the encryption with the identical keys for all color components. The key space can be determined by the number of the divided blocks n. The four encryption processes are independent of each other. Therefore, the total key space is calculated by multiplying the key spaces of each encryption process as described below.

If an original image with $M\times N$ pixels is divided into n blocks with $B_x\times B_y$ pixels, n is calculated by:

$$n={\displaystyle \frac{M\times N}{B_x\times B_y}}.$$

(15)

In block scrambling, the key space $N_B$ is the number of permutations of n blocks, which is given by:

$$N_B=n!.$$

(16)

Similarly, while combining each of the four processes of rotation and inversion, there are some similar patterns generated. Therefore, the maximum possible patterns generated due to the rotation and the inversions are eight, respectively. The key space of the block rotation and inversion $N_R$ is given as:

$$N_R=8^n.$$

(17)

The number of patterns for the negative-positive transformation $N_N$ and color component shuffling $N_C$ is two and six, respectively. Hence, the total key spaces can be calculated by:

$$N_N=2^n,$$

(18)

$$N_C=6^n.$$

(19)

The total key space of the encrypted images $N_A$ can be calculated by:

$$\begin{array}{cc}\hfill N_A& =N_B\times N_R\times N_N\times N_C\hfill \\ & =n!\times 8^n\times 2^n\times 6^n\hfill \\ & =n!\times 2^{5n}\times 3^n.\hfill \end{array}$$

(20)

On the other hand, the proposed scheme performs the encryption with the independent keys for all color components. Hence, the key spaces $N_B^{{}^{\prime }}$, $N_R^{{}^{\prime }}$ and $N_N^{{}^{\prime }}$ are given by:

$$N_B^{{}^{\prime }}=(n){!}^3.$$

(21)

$$N_R^{{}^{\prime }}={(8^n)}^3.$$

(22)

$$N_N^{{}^{\prime }}={(2^n)}^3,$$

(23)

Therefore, the total key space of the encrypted image $N_A^{{}^{\prime }}$ can be calculated by:

$$\begin{array}{cc}\hfill N_A^{{}^{\prime }}& =N_B^{{}^{\prime }}\times N_R^{{}^{\prime }}\times N_N^{{}^{\prime }}\times N_C\hfill \\ & =(n){!}^3\times {(8^n)}^3\times {(2^n)}^3\times 6^n\hfill \\ & =(n){!}^3\times 2^{13n}\times 3^n.\hfill \end{array}$$

(24)

From the above-mentioned analysis, the proposed scheme has a larger key space than the conventional scheme [13] due to the use of independent keys for R, G and B components in the encryption. Although the conventional scheme [10] utilizes the independent keys for encryption, the key space of the proposed scheme is more complex because of the embedding process. Therefore, the proposed scheme is more secured by confirming its large key space. Hence, the resilience against brute-force attacks can be improved.

4.2. Resilience Against Jigsaw Puzzle Solvers

JPS is a kind of attack that uses the correlation between the large numbers of pieces to obtain an original image. In an encrypted image, each block has a strong correlation to that of an original image. Hence, it is required to analyze the security of the proposed scheme with JPSs. According to [24,25], direct comparison $D_c$ is the ratio of number of the pieces that are in correct position. Neighbor comparison $N_c$ represents the ratio of the number of correctly joined blocks. Similarly, the largest component that is denoted as $L_c$ is the ratio of the number of largest joined blocks that have correct adjacencies. As shown in

Table 4. Evaluation of Jigsaw Puzzle Solvers (JPSs) using standard images of $512\times 512$ pixels.

Component	BPBE Scheme $(32\times 32)$
	Identical	Independent
$D_c$(Avg)	0.102	0.002
$N_c$(Avg)	0.152	0.006
$L_c$(Avg)	0.197	0.008

, we have calculated the average scores of $D_c$, $N_c$ and $L_c$ of seven different standard images, i.e., Lena, Mandrill, Milkdrop, Pepper, Girl, Lake and Airplane of $512\times 512$ pixels from the Signal and Image Processing Institute (SIPI) database [26]. The original images of $512\times 512$ pixels are trimmed to $512\times 480$ pixels to make a rectangular shape in the JPSs analysis. It is noted that a block size of $32\times 32$ is chosen for the encryption. The scores of $D_c$, $N_c$ and $L_c$ are ${}^{\prime }1{}^{\prime }$s if the image is completely assembled by JPSs, whereas these scores are ${}^{\prime }0{}^{\prime }$s when the puzzles are not assembled at all. Hence, it is confirmed that the use of independent keys for encryption makes puzzle solvers almost impossible even when the number of blocks is 240.

4.3. Compression Efficiency

The compression efficiency is evaluated by calculating the bitrates, which is given by:

$$Bitrate(bpp)={\displaystyle \frac{Sizeofimagefile}{No.ofpixelsinoriginalimage}}.$$

(25)

JPEG is a lossy compression algorithm. Therefore, if we use lossy compression in our scheme, the embedded data will be broken, and we cannot extract the embedded data. However, the lossless compression methods such as JPEG-LS can be applied for our scheme. As shown in

Table 5. Calculation of bitrate after JPEG-LS compression (Iran Image13).

Image	Bitrate (bpp)
Original	13.10
Proposed scheme (independent)	13.73
Proposed scheme (identical)	13.70

, the compression performance of the proposed scheme is not severely degraded as compared to the original image. Hence, our scheme is somehow compatible with the JPEG-LS compression method.

5. Conclusions

In this paper, we proposed an integrated model of image protection techniques. The proposed scheme allows the hierarchical process for the encryption and the data embedding. Therefore, our scheme is suitable for the hierarchical access control system, where the permission is granted according to the various access rights. The compression performance is also not severely degraded as compared to the original image. In addition, we also posit an efficient key derivation scheme for managing the large amount of keys generated in the encryption and data embedding process. The size of the key space in the proposed scheme is larger than the conventional schemes due to the use of independent keys and the embedding process. Hence, our scheme is resilient against brute-force attacks. Similarly, we also assure that the proposed scheme is almost impossible for JPSs attacks. Our future work involves embedding the data that are related to the original image. For example, it may be possible to control the visibility of Regions of Interest (ROIs) via embedded data in a hierarchical manner.