Experimental and Numerical Investigations of a Thermal Management System Using Phase-Change Materials and Forced-Air Cooling for High-Power Li-Ion Battery Packs
Abstract
1. Introduction
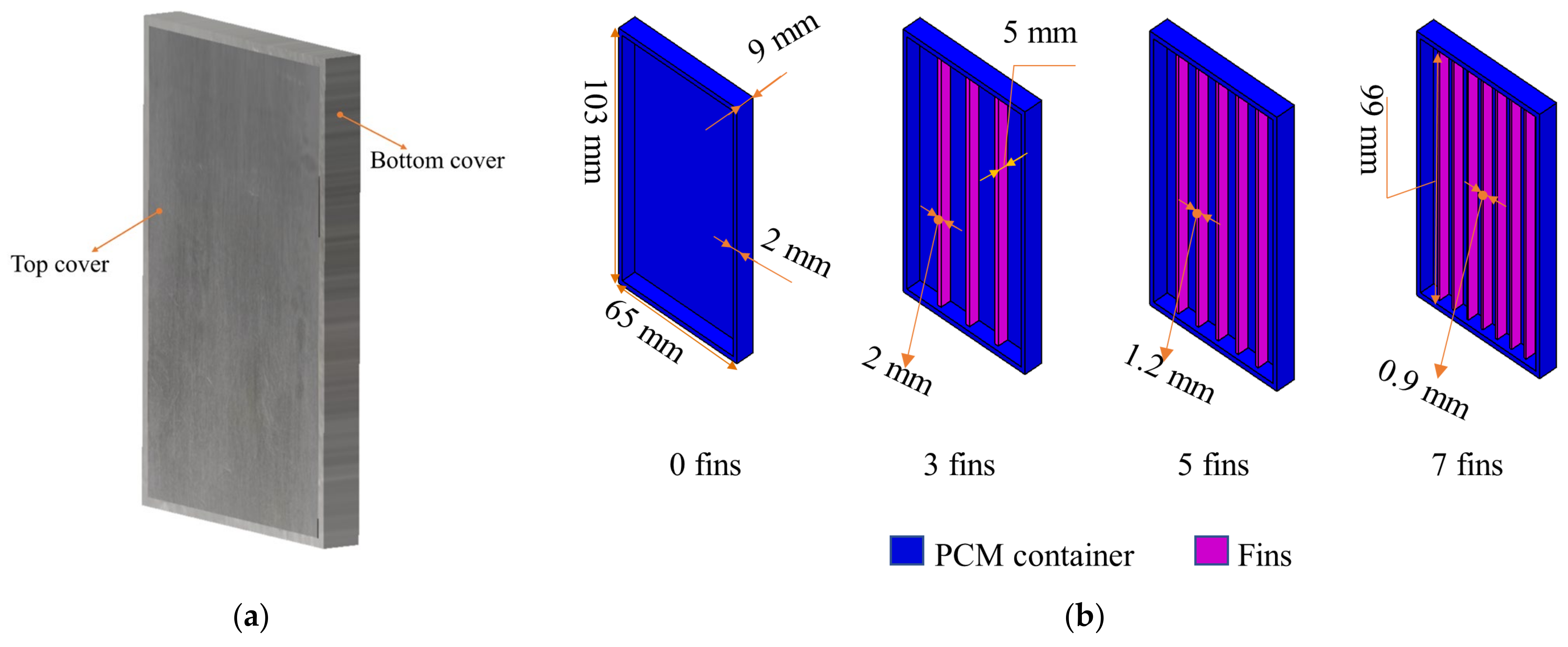
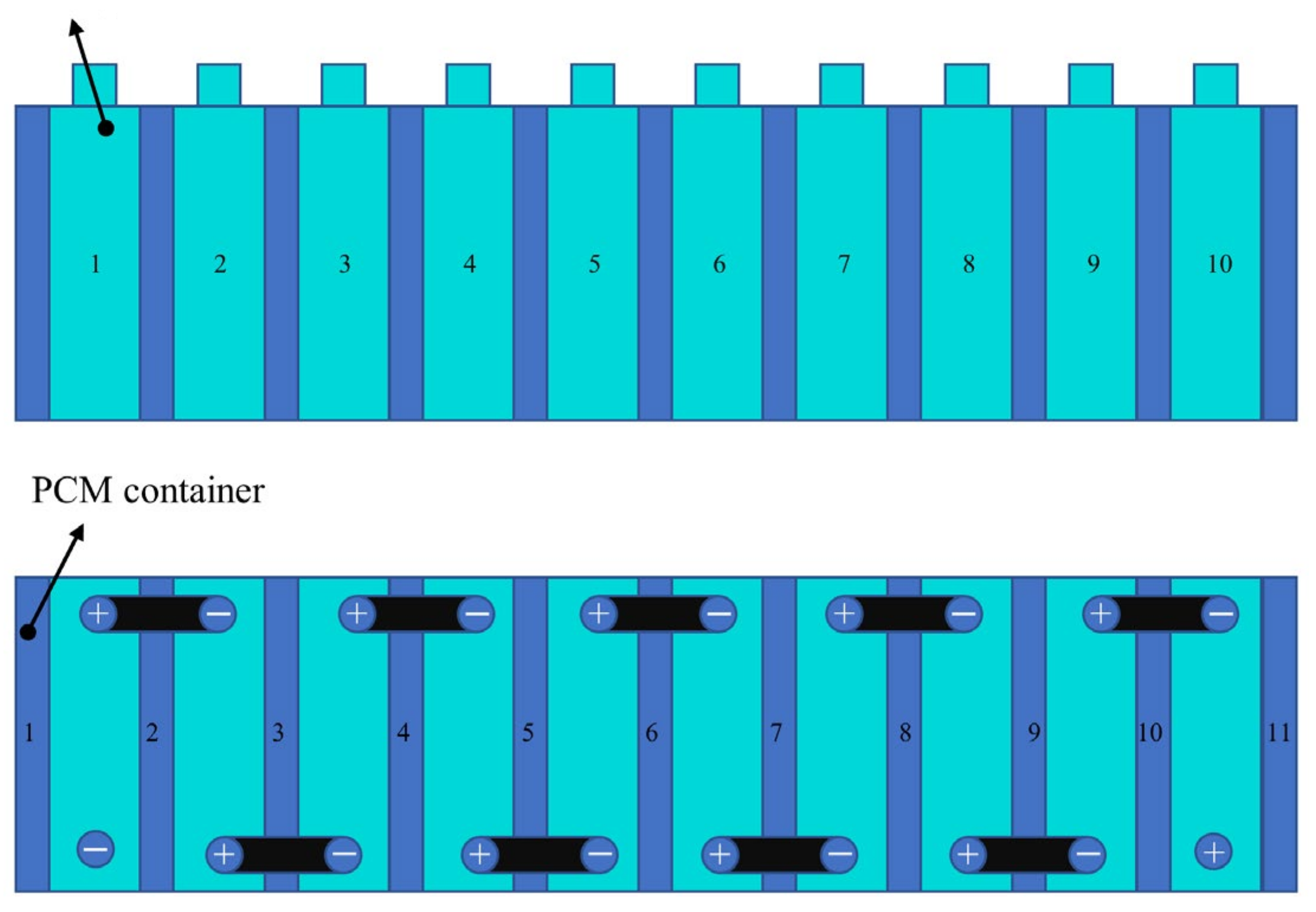
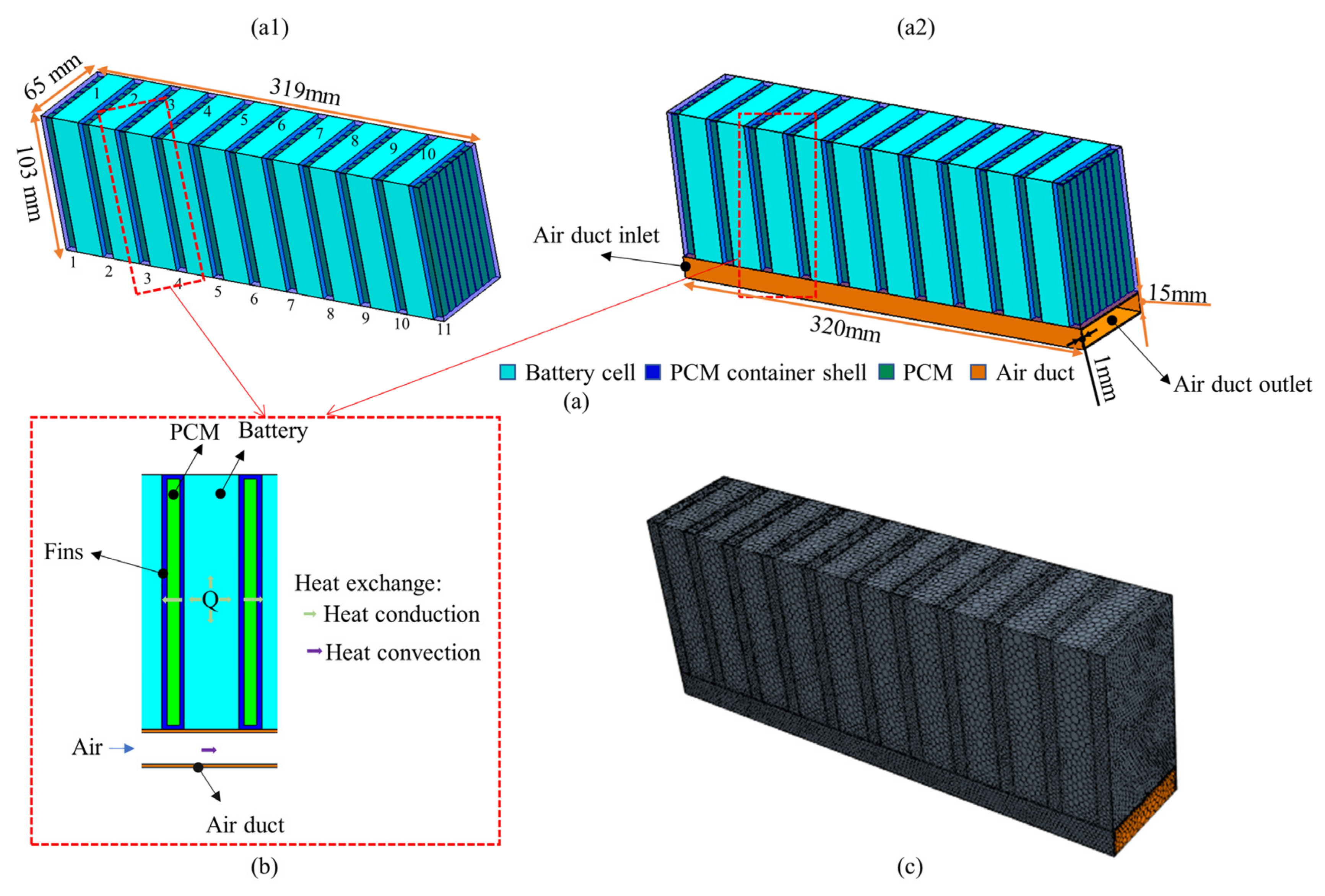
2. Experimental Setup
3. Mathematical Modeling
3.1. Model Establishment
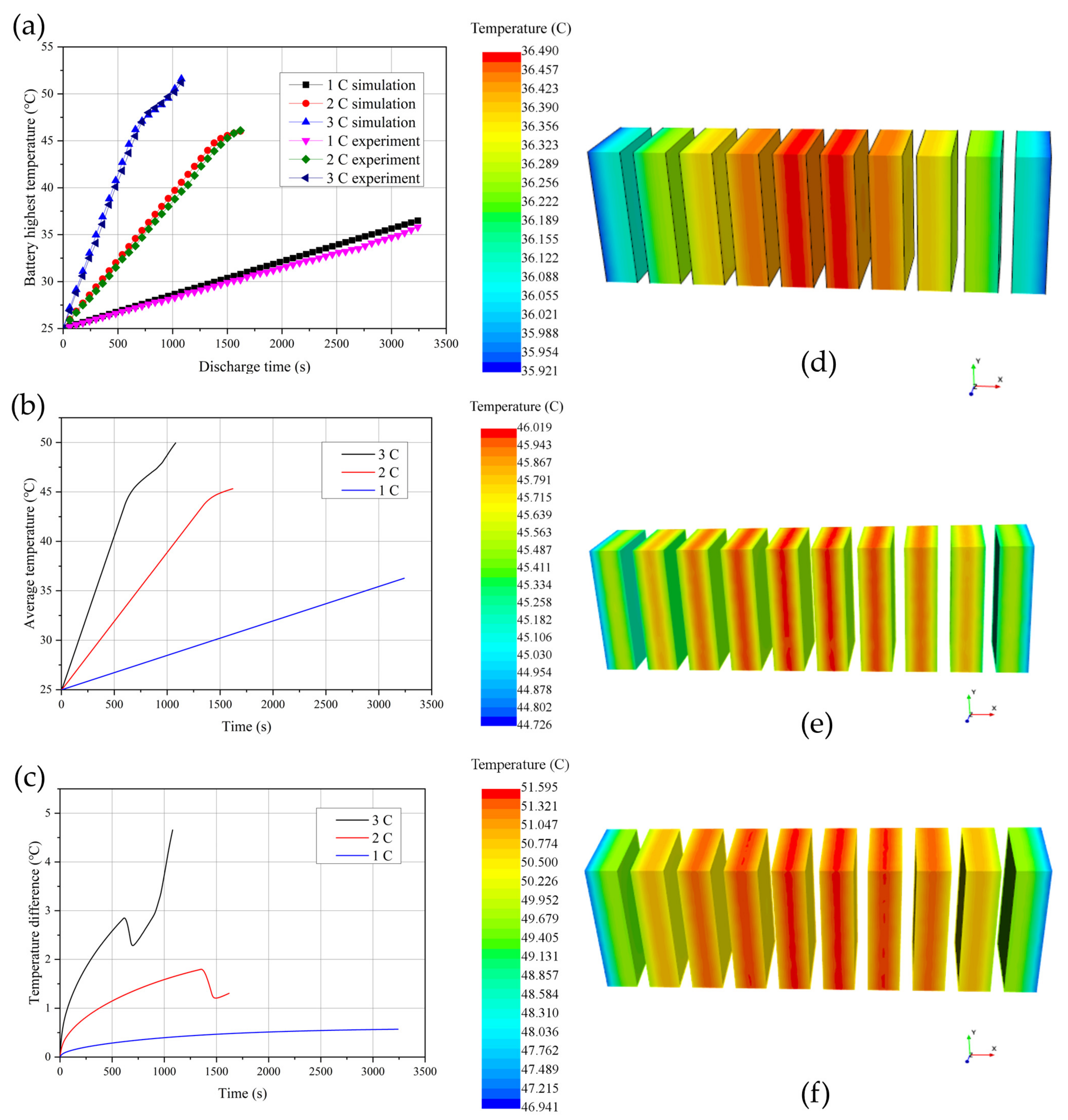
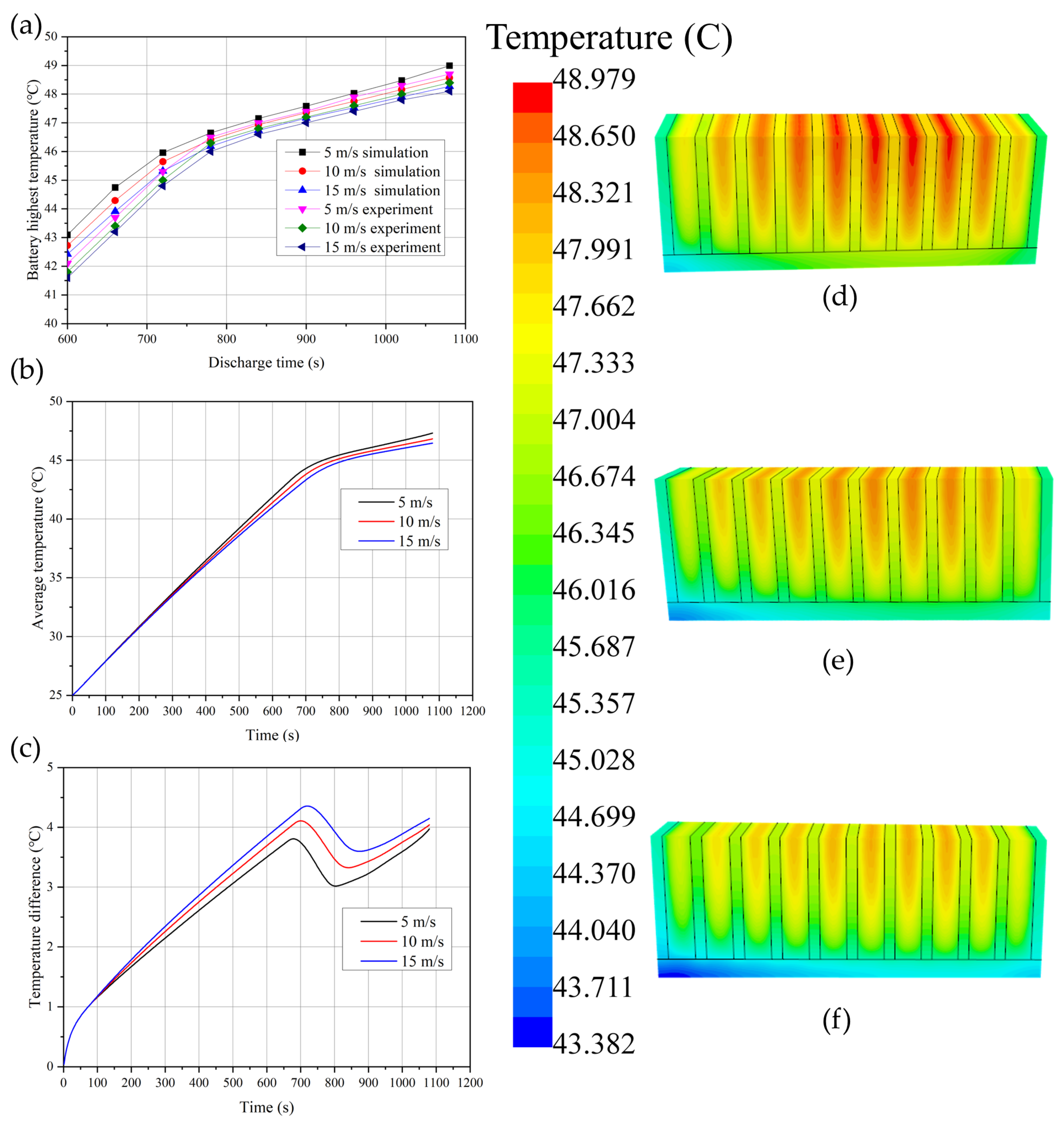
3.2. Model Validation and Uncertainty Analysis
4. Results and Discussion
4.1. The Thermal Performance at Different Discharge Rates
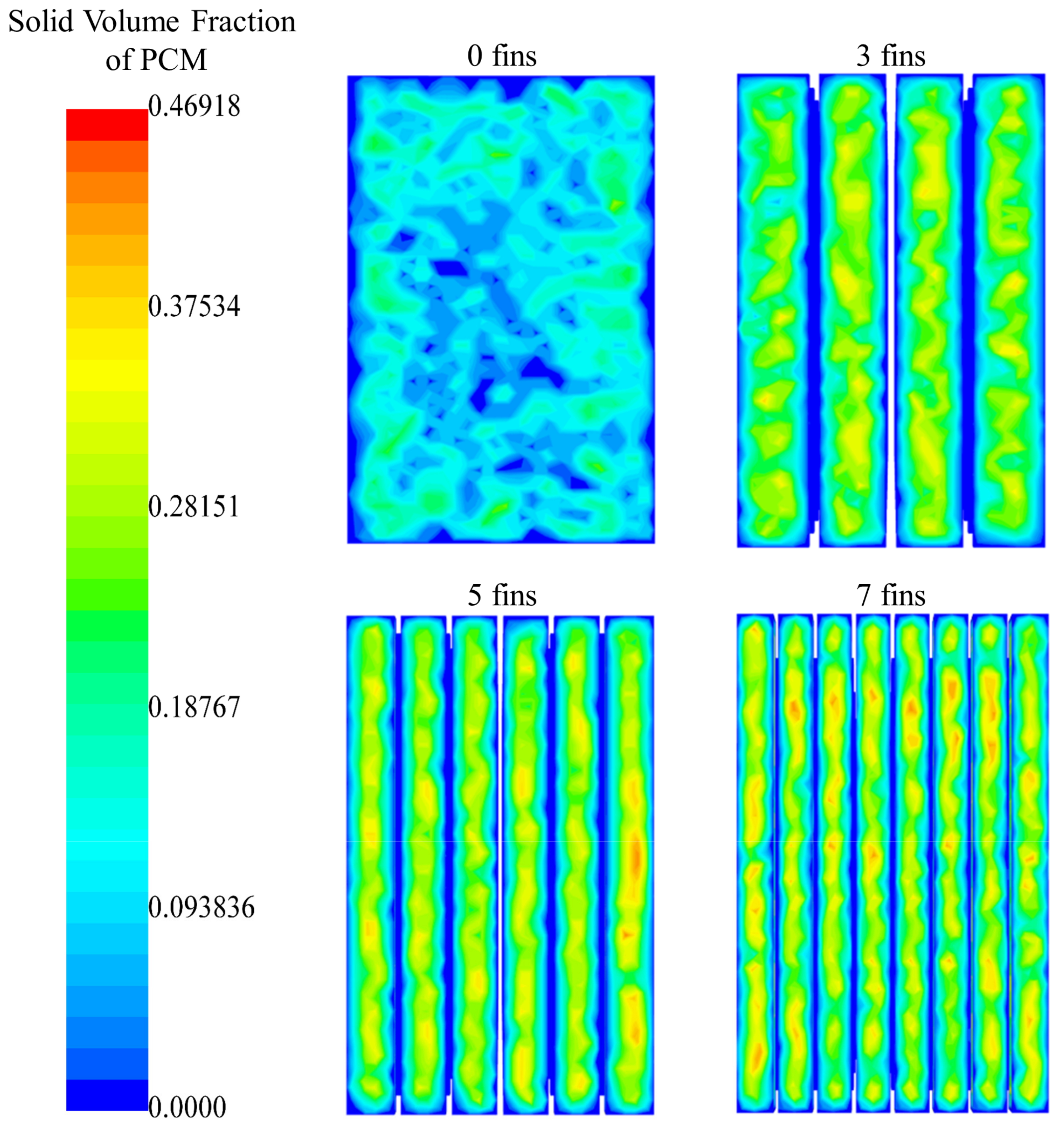
4.2. Fin Effect on Cooling System
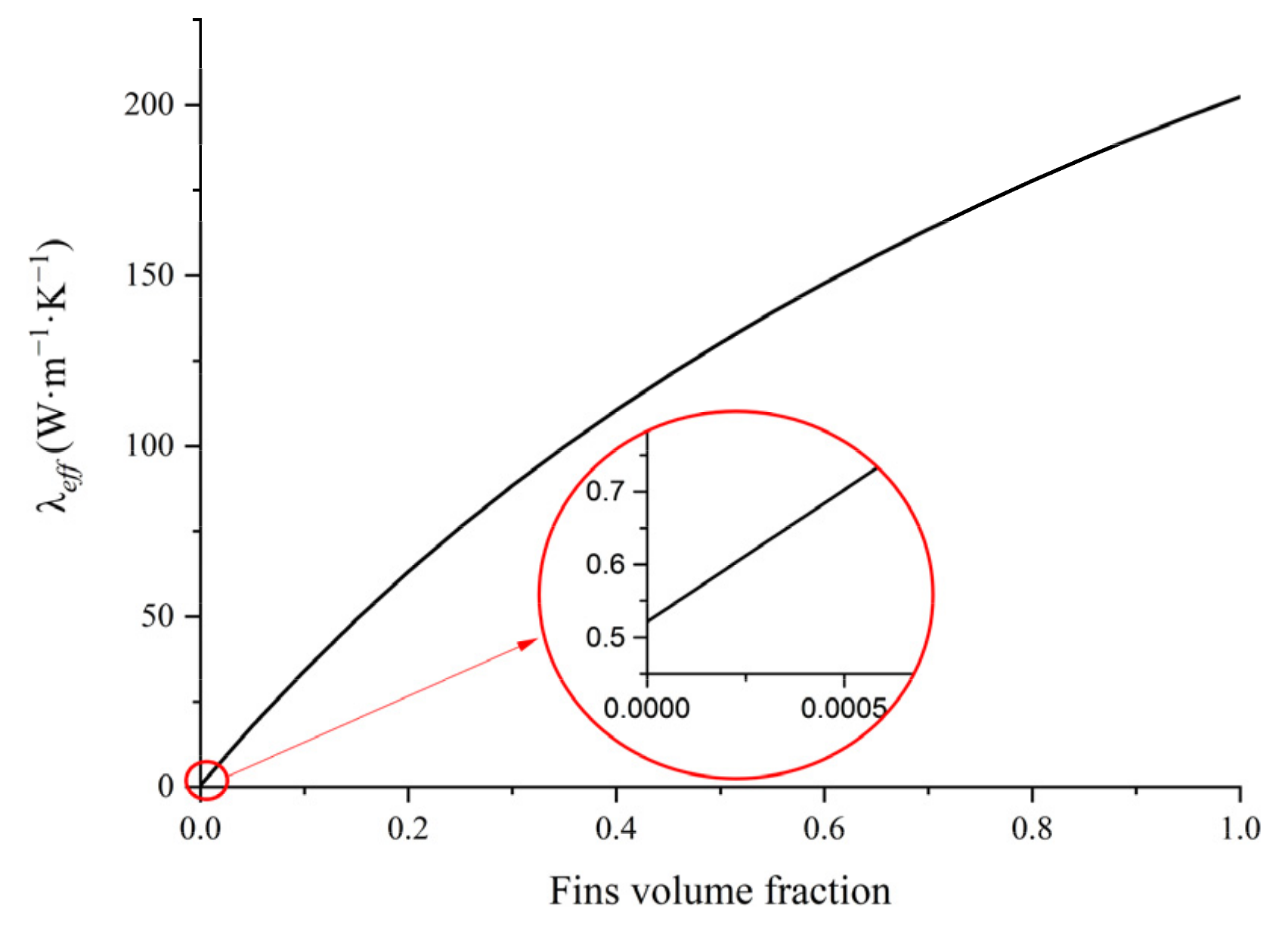
4.3. PCM Container Heat Transfer Analysis
4.4. Phase-Change Materials PCM Container Coupled with Forced-Air Cooling
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jiang, X.; Chen, Y.; Meng, X.; Cao, W.; Liu, C.; Huang, Q.; Naik, N.; Murugadoss, V.; Huang, M.; Guo, Z. The Impact of Electrode with Carbon Materials on Safety Performance of Lithium-Ion Batteries: A Review. Carbon N. Y. 2022, 191, 448–470. [Google Scholar] [CrossRef]
- Xu, H.; Zhang, X.; Xiang, G.; Li, H. Optimization of Liquid Cooling and Heat Dissipation System of Lithium-Ion Battery Packs of Automobile. Case Stud. Therm. Eng. 2021, 26, 101012. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, L.; Yang, L.; Du, X. Numerical Study of Combined Air and Phase Change Cooling for Lithium-Ion Battery during Dynamic Cycles. Int. J. Therm. Sci. 2021, 165, 106968. [Google Scholar] [CrossRef]
- Luo, J.; Zou, D.; Wang, Y.; Wang, S.; Huang, L. Battery Thermal Management Systems (BTMs) Based on Phase Change Material (PCM): A Comprehensive Review. Chem. Eng. J. 2022, 430, 132741. [Google Scholar] [CrossRef]
- Alipour, M.; Esen, E.; Varzeghani, A.R.; Kizilel, R. Performance of High Capacity Li-Ion Pouch Cells over Wide Range of Operating Temperatures and Discharge Rates. J. Electroanal. Chem. 2020, 860, 113903. [Google Scholar] [CrossRef]
- Wang, H.; Wang, S.; Feng, X.; Zhang, X.; Dai, K.; Sheng, J.; Zhao, Z.; Du, Z.; Zhang, Z.; Shen, K.; et al. An Experimental Study on the Thermal Characteristics of the Cell-To-Pack System. Energy 2021, 227, 120338. [Google Scholar] [CrossRef]
- Jaliliantabar, F.; Mamat, R.; Kumarasamy, S. Prediction of Lithium-Ion Battery Temperature in Different Operating Conditions Equipped with Passive Battery Thermal Management System by Artificial Neural Networks. Mater. Today Proc. 2022, 48, 1796–1804. [Google Scholar] [CrossRef]
- Zichen, W.; Changqing, D. A Comprehensive Review on Thermal Management Systems for Power Lithium-Ion Batteries. Renew. Sustain. Energy Rev. 2021, 139, 110685. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Z.; Luo, L.; Fan, Y.; Du, Z. A Review on Thermal Management of Lithium-Ion Batteries for Electric Vehicles. Energy 2022, 238, 121652. [Google Scholar] [CrossRef]
- Wang, N.; Li, C.; Li, W.; Chen, X.; Li, Y.; Qi, D. Heat Dissipation Optimization for a Serpentine Liquid Cooling Battery Thermal Management System: An Application of Surrogate Assisted Approach. J. Energy Storage 2021, 40, 102771. [Google Scholar] [CrossRef]
- Zhang, J.; Shao, D.; Jiang, L.; Zhang, G.; Wu, H.; Day, R.; Jiang, W. Advanced Thermal Management System Driven by Phase Change Materials for Power Lithium-Ion Batteries: A Review. Renew. Sustain. Energy Rev. 2022, 159, 112207. [Google Scholar] [CrossRef]
- Galazutdinova, Y.; Al-Hallaj, S.; Grágeda, M.; Ushak, S. Development of the Inorganic Composite Phase Change Materials for Passive Thermal Management of Li-Ion Batteries: Material Characterization. Int. J. Energy Res. 2020, 44, 2011–2022. [Google Scholar] [CrossRef]
- Hassan, F.; Jamil, F.; Hussain, A.; Ali, H.M.; Janjua, M.M.; Khushnood, S.; Farhan, M.; Altaf, K.; Said, Z.; Li, C. Recent Advancements in Latent Heat Phase Change Materials and Their Applications for Thermal Energy Storage and Buildings: A State of the Art Review. Sustain. Energy Technol. Assess. 2022, 49, 101646. [Google Scholar] [CrossRef]
- Mohammed, A.G.; Elfeky, K.E.; Wang, Q. Thermal Management Evaluation of Li-Ion Battery Employing Multiple Phase Change Materials Integrated Thin Heat Sinks for Hybrid Electric Vehicles. J. Power Sources 2021, 516, 230680. [Google Scholar] [CrossRef]
- Zheng, Q.; Hao, M.; Miao, R.; Schaadt, J.; Dames, C. Advances in Thermal Conductivity for Energy Applications: A Review. Prog. Energy 2021, 3, 12002. [Google Scholar] [CrossRef]
- Kant, K.; Biwole, P.H.; Shamseddine, I.; Tlaiji, G.; Pennec, F.; Fardoun, F. Recent Advances in Thermophysical Properties Enhancement of Phase Change Materials for Thermal Energy Storage. Sol. Energy Mater. Sol. Cells 2021, 231, 111309. [Google Scholar] [CrossRef]
- Cheng, P.; Chen, X.; Gao, H.; Zhang, X.; Tang, Z.; Li, A.; Wang, G. Different Dimensional Nanoadditives for Thermal Conductivity Enhancement of Phase Change Materials: Fundamentals and Applications. Nano Energy 2021, 85, 105948. [Google Scholar] [CrossRef]
- Babu Sanker, S.; Baby, R. Phase Change Material Based Thermal Management of Lithium Ion Batteries: A Review on Thermal Performance of Various Thermal Conductivity Enhancers. J. Energy Storage 2022, 50, 104606. [Google Scholar] [CrossRef]
- Sanchez, P.S.; Ezquerro, J.M.; Porter, J.; Fernandez, J.J. The Effect of Thermocapillary Convection on PCM Melting in Microgravity: Results and Expectations. In Proceedings of the International Astronautical Congress, Paris, France, 18–22 September 2020. [Google Scholar]
- Jain, A.; Parhizi, M. Theoretical Analysis of Phase Change Heat Transfer and Energy Storage in a Spherical Phase Change Material with Encapsulation. Int. J. Heat Mass Transf. 2022, 185, 122348. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Z.; Min, H.; Li, H.; Li, Q. Performance Investigation of a Passive Battery Thermal Management System Applied with Phase Change Material. J. Energy Storage 2021, 35, 102279. [Google Scholar] [CrossRef]
- El Idi, M.M.; Karkri, M.; Abdou Tankari, M. A Passive Thermal Management System of Li-Ion Batteries Using PCM Composites: Experimental and Numerical Investigations. Int. J. Heat Mass Transf. 2021, 169, 120894. [Google Scholar] [CrossRef]
- Qian, Z.; Li, Y.; Rao, Z. Thermal Performance of Lithium-Ion Battery Thermal Management System by Using Mini-Channel Cooling. Energy Convers. Manag. 2016, 126, 622–631. [Google Scholar] [CrossRef]
- Hu, Y.; Choe, S.-Y.; Garrick, T.R. Measurement of Heat Generation Rate and Heat Sources of Pouch Type Li-Ion Cells. Appl. Therm. Eng. 2021, 189, 116709. [Google Scholar] [CrossRef]
- Bernardi, D.; Pawlikowski, E.; Newman, J. A General Energy Balance for Battery Systems. J. Electrochem. Soc. 1985, 132, 5–12. [Google Scholar] [CrossRef]
- Wu, W.; Wu, W.; Wang, S. Thermal Management Optimization of a Prismatic Battery with Shape-Stabilized Phase Change Material. Int. J. Heat Mass Transf. 2018, 121, 967–977. [Google Scholar] [CrossRef]
- Cheng, J.; Shuai, S.; Tang, Z.; changfa, T. Thermal Performance of a Lithium-Ion Battery Thermal Management System with Vapor Chamber and Minichannel Cold Plate. Appl. Therm. Eng. 2023, 222, 119694. [Google Scholar] [CrossRef]





| Parameters | Value |
|---|---|
| Battery type | Lithium iron phosphate |
| Voltage (V) | 3.2 |
| Capacity (Ah) | 16 |
| Size (mm) Density (kg·m−3) | 103 × 65 × 22 2000 |
| Specific heat capacity(J·kg−1·K−1) | 1030 |
| Thermal conductivity (x, y, z) (W·m−1·K−1) | 0.37/24/24 |
| Equivalent internal resistance (mΩ) | 6 |
| Maximum sustained discharge rate | 3 C |
| Parameters | Value |
|---|---|
| Paraffin type | 44# |
| Supplier | Sheng bang (China) |
| Chemical formula | C22H46 |
| Thermal conductivity (solid/liquid) (W·m−1·K−1) | 0.29/0.21 |
| Melting point (°C) | 44–46 |
| Latent heat (J·kg−1) | 189,000 |
| Specific heat capacity (J·kg−1·K−1) | 1770 |
| Density (kg·m−3) | 910 |
| Errors | Discharge Rates | TMP1 | TMP3 |
|---|---|---|---|
| MAE | 1 C | 0.44 | 0.46 |
| 2 C | 0.43 | 0.45 | |
| 3 C | 0.38 | 0.40 | |
| RMSE | 1 C | 0.51 | 0.52 |
| 2 C | 0.50 | 0.50 | |
| 3 C | 0.44 | 0.41 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Zhao, S.; Zhou, T.; Wang, H.; Li, S.; Yuan, Y.; Ma, Z.; Wei, J.; Zhao, X. Experimental and Numerical Investigations of a Thermal Management System Using Phase-Change Materials and Forced-Air Cooling for High-Power Li-Ion Battery Packs. Batteries 2023, 9, 153. https://doi.org/10.3390/batteries9030153
Zhang Y, Zhao S, Zhou T, Wang H, Li S, Yuan Y, Ma Z, Wei J, Zhao X. Experimental and Numerical Investigations of a Thermal Management System Using Phase-Change Materials and Forced-Air Cooling for High-Power Li-Ion Battery Packs. Batteries. 2023; 9(3):153. https://doi.org/10.3390/batteries9030153
Chicago/Turabian StyleZhang, Yulong, Shupeng Zhao, Tingbo Zhou, Huizhi Wang, Shen Li, Yongwei Yuan, Zhikai Ma, Jiameng Wei, and Xu Zhao. 2023. "Experimental and Numerical Investigations of a Thermal Management System Using Phase-Change Materials and Forced-Air Cooling for High-Power Li-Ion Battery Packs" Batteries 9, no. 3: 153. https://doi.org/10.3390/batteries9030153
APA StyleZhang, Y., Zhao, S., Zhou, T., Wang, H., Li, S., Yuan, Y., Ma, Z., Wei, J., & Zhao, X. (2023). Experimental and Numerical Investigations of a Thermal Management System Using Phase-Change Materials and Forced-Air Cooling for High-Power Li-Ion Battery Packs. Batteries, 9(3), 153. https://doi.org/10.3390/batteries9030153






