Introducing the Loewner Method as a Data-Driven and Regularization-Free Approach for the Distribution of Relaxation Times Analysis of Lithium-Ion Batteries
Abstract
:1. Introduction
- Analysis of the LM through different ECMs with known time constants and gains;
- Detailed discussion of the correlation between model order, error, and distribution of gains for synthetic data;
- Investigation of the effects of noise on the distribution of gains;
- Application of the LM for process identification of LIB;
- Comparison of LM and gDRT.
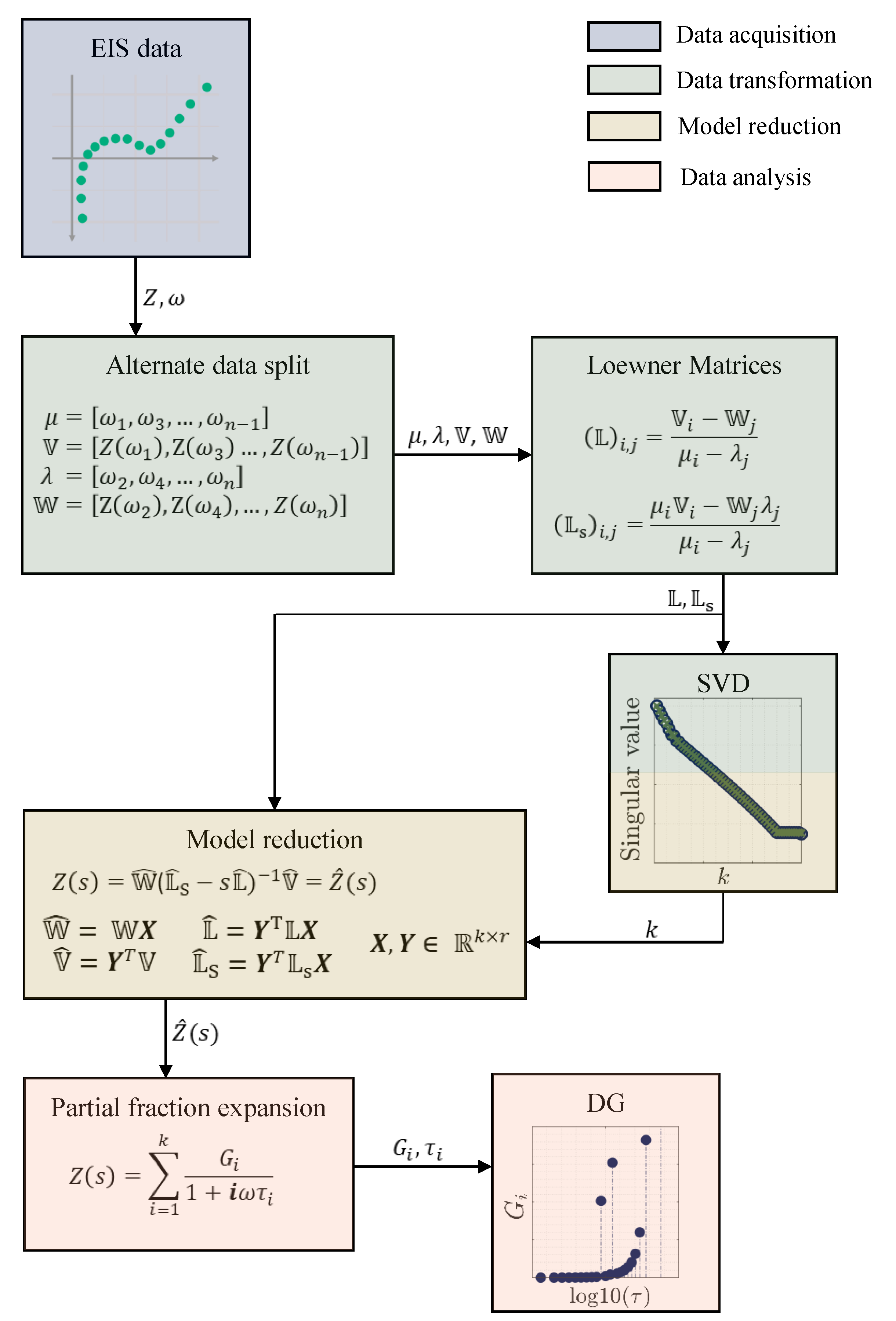
2. Loewner Method
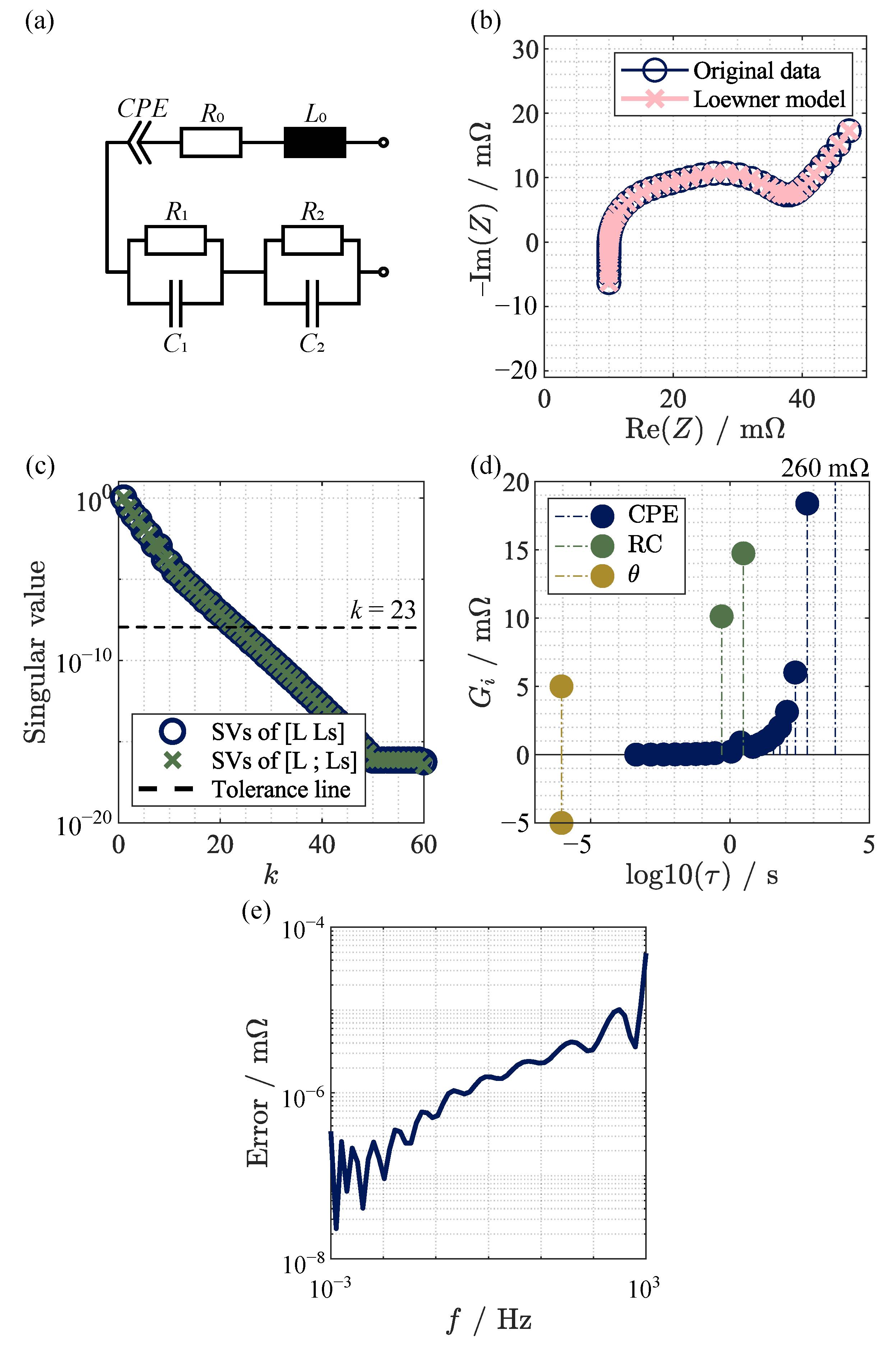
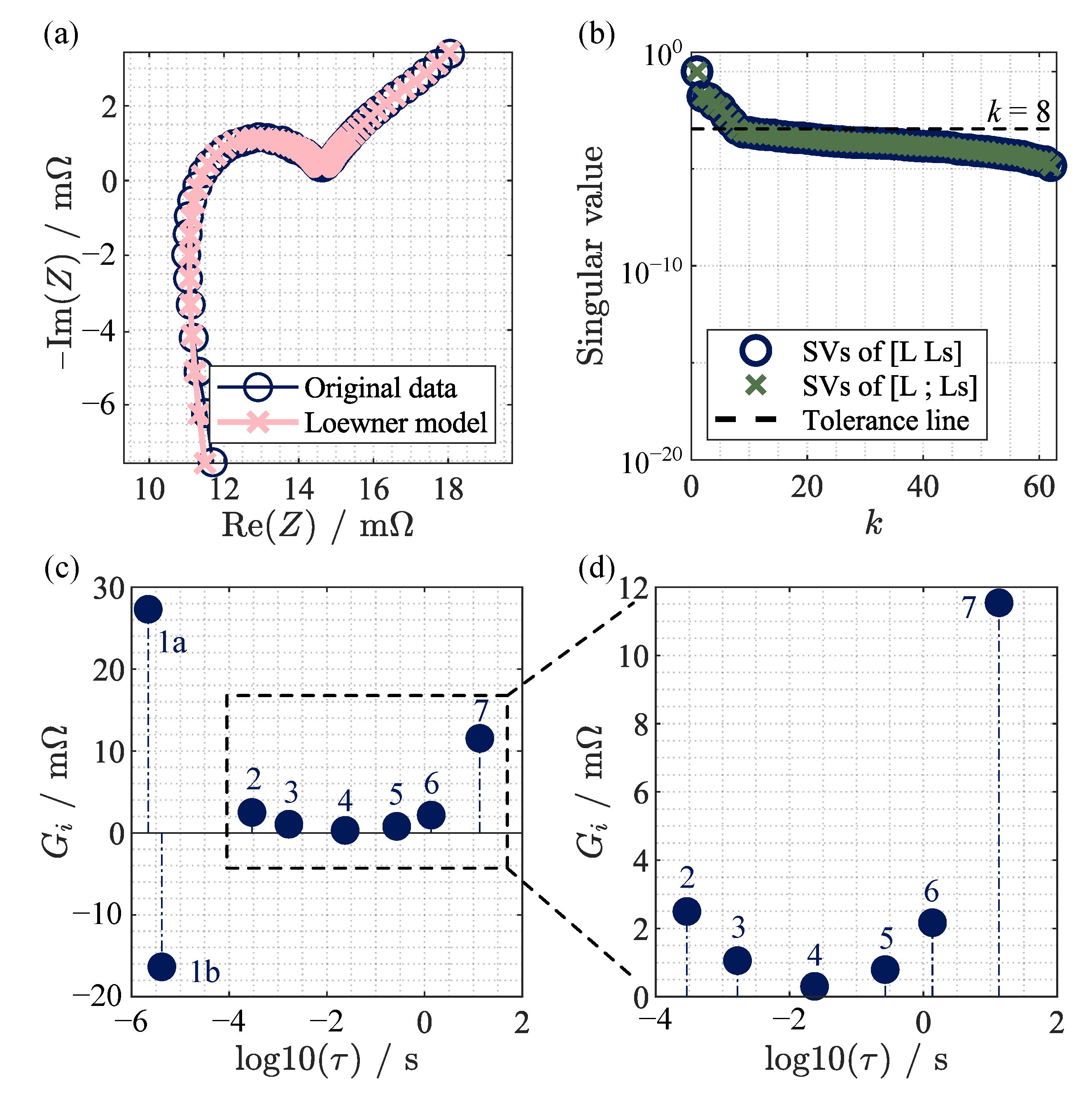
3. Application of Loewner Method for Process Identification
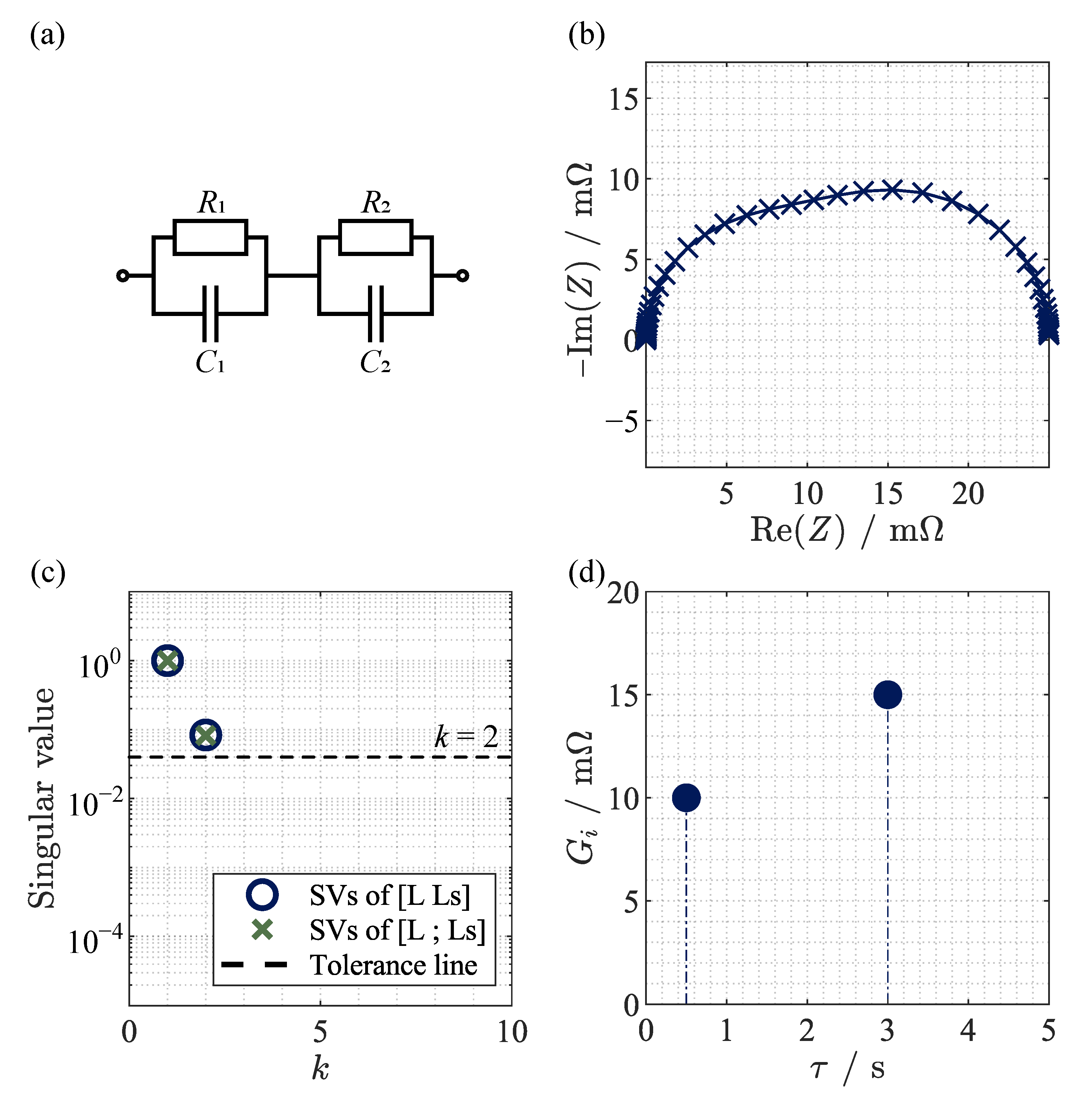
3.1. Analysis of Different Equivalent Circuit Models
- Using the bend point of the singular value curve, considering all values with the highest gradient, leading to ;
- Introducing a tolerance limit, here exemplary leading to ;
- Choosing the first model order in which the singular values are (nearly) zero.
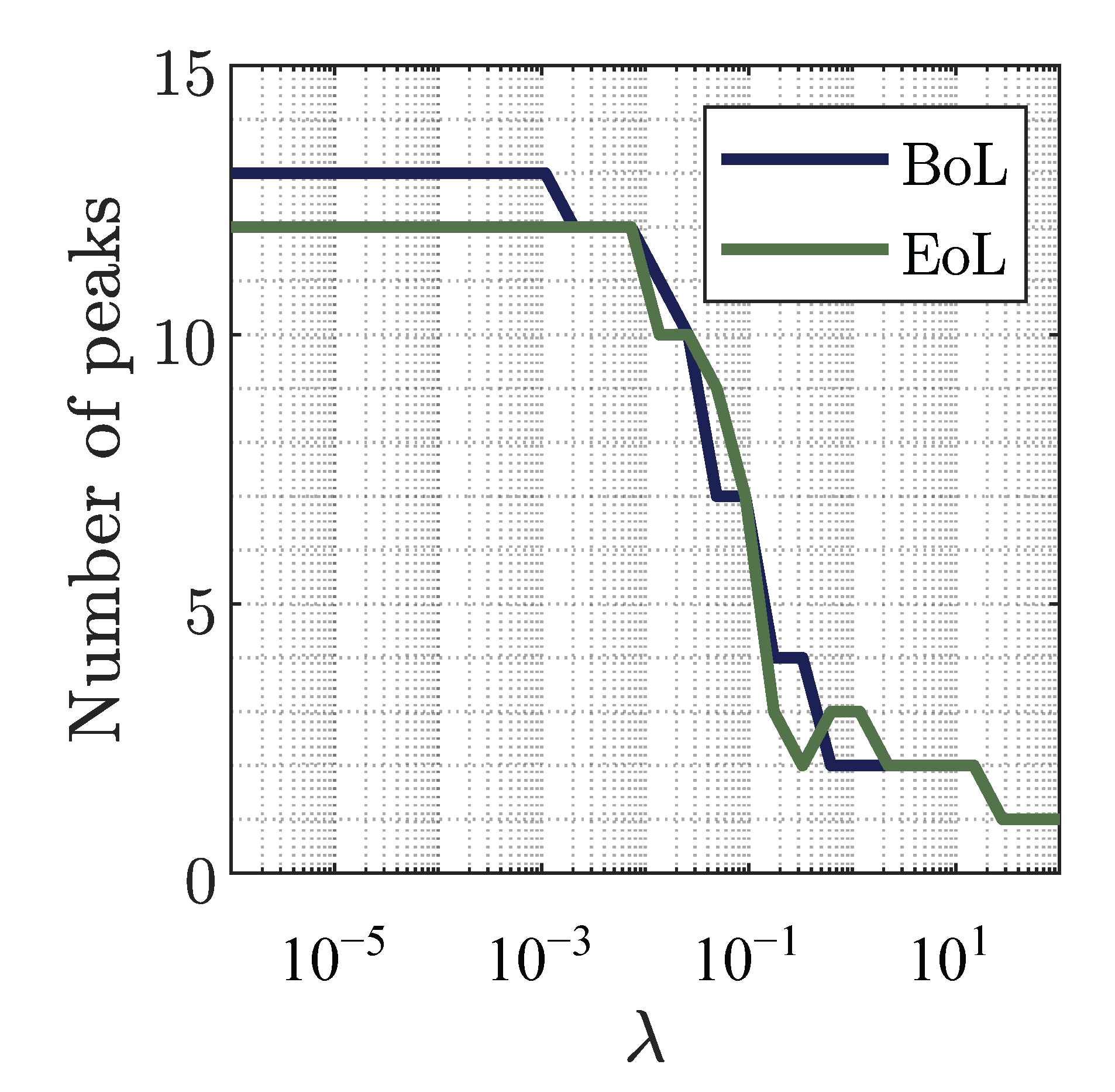
3.2. Analysis of Noise
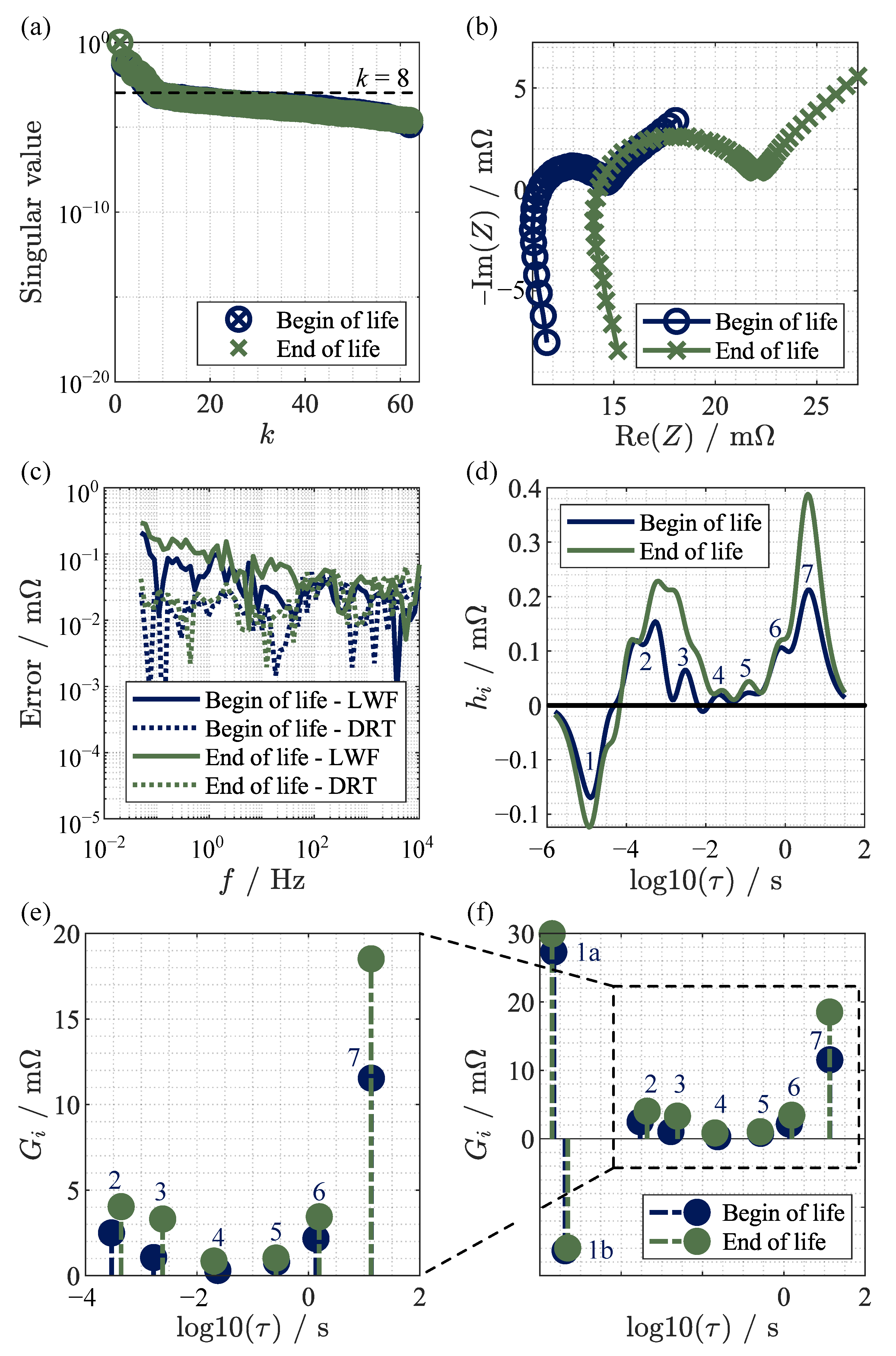
3.3. Measured Impedance Data
4. Comparison of Loewner Method and Generalized Distribution of Relaxation Times
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| BOL | Begin of life |
| CPE | Constant phase element |
| DRT | Distribution of relaxation times |
| ECM | Equivalent circuit model |
| EIS | Electrochemical impedance spectroscopy |
| EOL | End of life |
| gDRT | Generalized distribution of relaxation times |
| LIB | Lithium-ion battery |
| LM | Loewner method |
| LWF | Loewner framework |
| PEMFC | Polymer electrolyte membrane fuel cell |
| SEI | Solid electrolyte interphase |
| SNR | Signal-to-noise ratio |
| SOC | State of charge |
| SVD | Singular value decomposition |
Appendix A
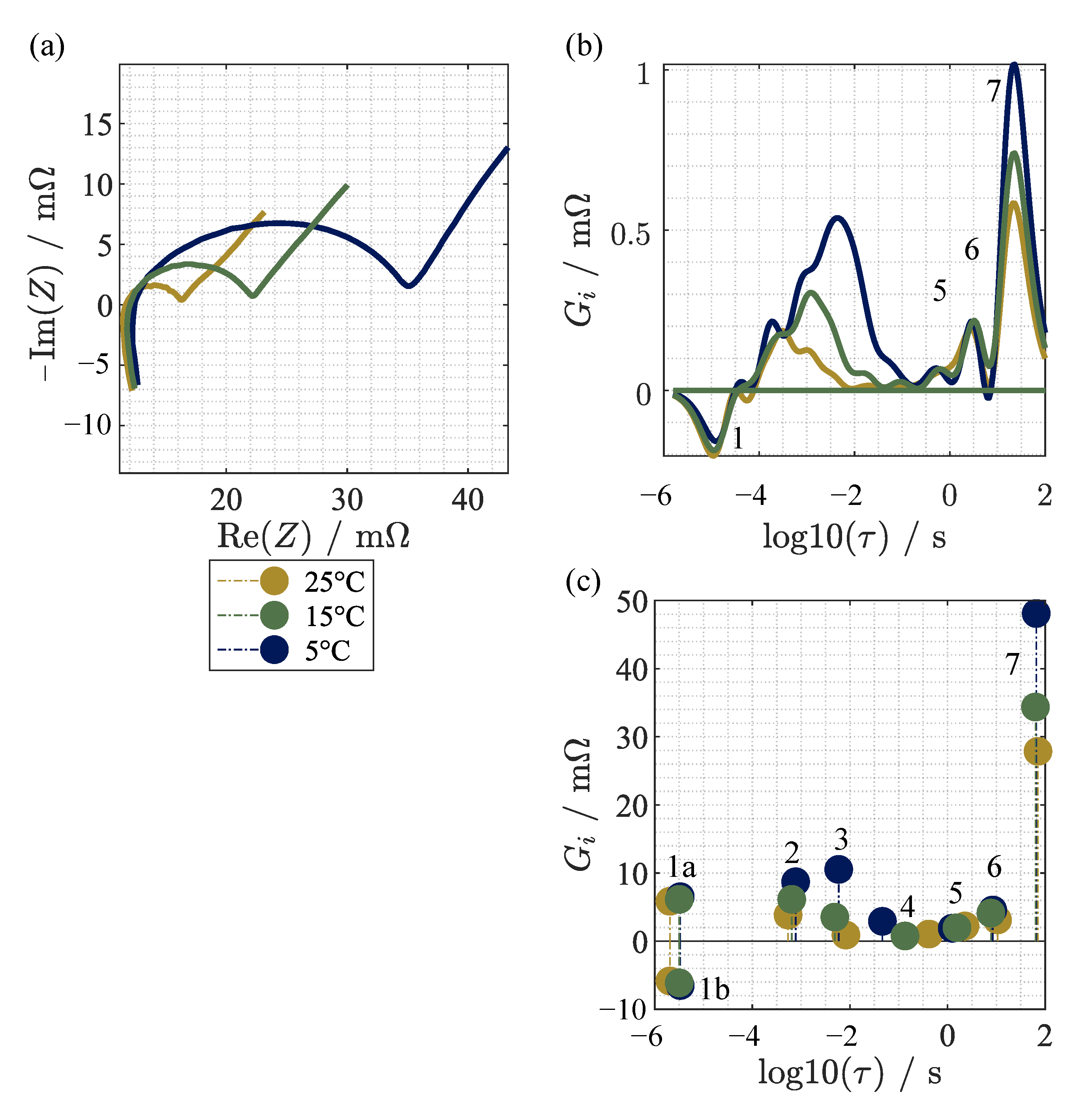
| 1a | 1b | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|---|
| BOL | ||||||||
| EOL |
| I | II | III | IV | V | VI | VII | |
|---|---|---|---|---|---|---|---|
| 0.08 | |||||||
| 0.11 | |||||||
| 0.14 |
References
- Rodat, S.; Sailler, S.; Druart, F.; Thivel, P.X.; Bultel, Y.; Ozil, P. EIS measurements in the diagnosis of the environment within a PEMFC stack. J. Appl. Electrochem. 2009, 40, 911–920. [Google Scholar] [CrossRef]
- Fang, Q.; de Haart, U.; Schäfer, D.; Thaler, F.; Rangel-Hernandez, V.; Peters, R.; Blum, L. Degradation Analysis of an SOFC Short Stack Subject to 10,000 h of Operation. J. Electrochem. Soc. 2020, 167, 144508. [Google Scholar] [CrossRef]
- Middlemiss, L.A.; Rennie, A.J.; Sayers, R.; West, A.R. Characterisation of batteries by electrochemical impedance spectroscopy. Energy Rep. 2020, 6, 232–241. [Google Scholar] [CrossRef]
- Maheshwari, A.; Heck, M.; Santarelli, M. Cycle aging studies of lithium nickel manganese cobalt oxide-based batteries using electrochemical impedance spectroscopy. Electrochim. Acta 2018, 273, 335–348. [Google Scholar] [CrossRef]
- Katzer, F.; Rüther, T.; Plank, C.; Roth, F.; Danzer, M.A. Analyses of polarisation effects and operando detection of lithium deposition in experimental half- and commercial full-cells. Electrochim. Acta 2022, 436, 141401. [Google Scholar] [CrossRef]
- Danzer, M.A. Generalized Distribution of Relaxation Times Analysis for the Characterization of Impedance Spectra. Batteries 2019, 5, 53. [Google Scholar] [CrossRef]
- Yoo, H.D.; Jang, J.H.; Ryu, J.H.; Park, Y.; Oh, S.M. Impedance analysis of porous carbon electrodes to predict rate capability of electric double-layer capacitors. J. Power Sources 2014, 267, 411–420. [Google Scholar] [CrossRef]
- Schmidt, J.P.; Arnold, S.; Loges, A.; Werner, D.; Wetzel, T.; Ivers-Tiffée, E. Measurement of the internal cell temperature via impedance: Evaluation and application of a new method. J. Power Sources 2013, 243, 110–117. [Google Scholar] [CrossRef]
- McGrogan, F.P.; Bishop, S.R.; Chiang, Y.M.; van Vliet, K.J. Connecting Particle Fracture with Electrochemical Impedance in LiXMn2O4. J. Electrochem. Soc. 2017, 164, A3709–A3717. [Google Scholar] [CrossRef]
- Meddings, N.; Heinrich, M.; Overney, F.; Lee, J.S.; Ruiz, V.; Napolitano, E.; Seitz, S.; Hinds, G.; Raccichini, R.; Gaberšček, M.; et al. Application of electrochemical impedance spectroscopy to commercial Li-ion cells: A review. J. Power Sources 2020, 480, 228742. [Google Scholar] [CrossRef]
- Rüther, T.; Plank, C.; Schamel, M.; Danzer, M.A. Detection of inhomogeneities in serially connected lithium-ion batteries. Appl. Energy 2023, 332, 120514. [Google Scholar] [CrossRef]
- Carthy, K.M.; Gullapalli, H.; Ryan, K.M.; Kennedy, T. Review—Use of Impedance Spectroscopy for the Estimation of Li-ion Battery State of Charge, State of Health and Internal Temperature. J. Electrochem. Soc. 2021, 168, 080517. [Google Scholar] [CrossRef]
- Rivera-Barrera, J.; Muñoz-Galeano, N.; Sarmiento-Maldonado, H. SoC Estimation for Lithium-ion Batteries: Review and Future Challenges. Electronics 2017, 6, 102. [Google Scholar] [CrossRef]
- Galeotti, M.; Cinà, L.; Giammanco, C.; Cordiner, S.; Carlo, A.D. Performance analysis and SOH (state of health) evaluation of lithium polymer batteries through electrochemical impedance spectroscopy. Energy 2015, 89, 678–686. [Google Scholar] [CrossRef]
- Pan, Y.; Ren, D.; Han, X.; Lu, L.; Ouyang, M. Lithium Plating Detection Based on Electrochemical Impedance and Internal Resistance Analyses. Batteries 2022, 8, 206. [Google Scholar] [CrossRef]
- Schmidt, J.P.; Adam, A.; Wandt, J. Time-Resolved and Robust Lithium Plating Detection for Automotive Lithium-Ion Cells with the Potential for Vehicle Application. Batteries 2023, 9, 97. [Google Scholar] [CrossRef]
- Koseoglou, M.; Tsioumas, E.; Ferentinou, D.; Jabbour, N.; Papagiannis, D.; Mademlis, C. Lithium plating detection using dynamic electrochemical impedance spectroscopy in lithium-ion batteries. J. Power Sources 2021, 512, 230508. [Google Scholar] [CrossRef]
- Gaddam, R.R.; Katzenmeier, L.; Lamprecht, X.; Bandarenka, A.S. Review on physical impedance models in modern battery research. Phys. Chem. Chem. Phys. 2021, 23, 12926–12944. [Google Scholar] [CrossRef]
- Hahn, M.; Schindler, S.; Triebs, L.C.; Danzer, M.A. Optimized Process Parameters for a Reproducible Distribution of Relaxation Times Analysis of Electrochemical Systems. Batteries 2019, 5, 43. [Google Scholar] [CrossRef]
- Zhao, Y.; Kücher, S.; Jossen, A. Investigation of the diffusion phenomena in lithium-ion batteries with distribution of relaxation times. Electrochim. Acta 2022, 432, 141174. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, D.; Schaltz, E.; Stroe, D.I.; Gismero, A.; Yang, B. Degradation mechanism analysis and State-of-Health estimation for lithium-ion batteries based on distribution of relaxation times. J. Energy Storage 2022, 55, 105386. [Google Scholar] [CrossRef]
- Iurilli, P.; Brivio, C.; Wood, V. Detection of Lithium-Ion Cells’ Degradation through Deconvolution of Electrochemical Impedance Spectroscopy with Distribution of Relaxation Time. Energy Technol. 2022, 10, 2200547. [Google Scholar] [CrossRef]
- He, R.; He, Y.; Xie, W.; Guo, B.; Yang, S. Comparative analysis for commercial li-ion batteries degradation using the distribution of relaxation time method based on electrochemical impedance spectroscopy. Energy 2023, 263, 125972. [Google Scholar] [CrossRef]
- Illig, J.; Ender, M.; Weber, A.; Ivers-Tiffée, E. Modeling graphite anodes with serial and transmission line models. J. Power Sources 2015, 282, 335–347. [Google Scholar] [CrossRef]
- Chen, X.; Li, L.; Liu, M.; Huang, T.; Yu, A. Detection of lithium plating in lithium-ion batteries by distribution of relaxation times. J. Power Sources 2021, 496, 229867. [Google Scholar] [CrossRef]
- Brown, D.E.; McShane, E.J.; Konz, Z.M.; Knudsen, K.B.; McCloskey, B.D. Detecting onset of lithium plating during fast charging of Li-ion batteries using operando electrochemical impedance spectroscopy. Cell Rep. Phys. Sci. 2021, 2, 100589. [Google Scholar] [CrossRef]
- Bergmann, T.G.; Schlüter, N. Introducing Alternative Algorithms for the Determination of the Distribution of Relaxation Times. ChemPhysChem 2022, 23, e202200012. [Google Scholar] [CrossRef]
- Mayo, A.J.; Antoulas, A.C. A framework for the solution of the generalized realization problem. Linear Algebra Its Appl. 2007, 425, 634–662. [Google Scholar] [CrossRef]
- Patel, B. Application of Loewner Framework for Data-Driven Modeling and Diagnosis of Polymer Electrolyte Membrane Fuel Cells. Master’s Thesis, Otto von Guericke-University, Magdeburg, Germany, 2021. [Google Scholar]
- Sorrentino, A.; Gosea, I.V.; Patel, B.; Antoulas, A.C.; Vidakovic-Koch, T. Loewner Framework and Distribution of Relaxation Times of Electrochemical Systems: Solving Issues Through a Data-Driven Modeling Approach. SSRN Electron. J. 2022. [Google Scholar] [CrossRef]
- Gosea, I.V.; Zivkovic, L.; Karachalios, D.S.; Antoulas, A.C.; Vidakovic-Koch, T. A data-based nonlinear frequency response approach based on the Loewner framework: Preliminary analysis. In Proceedings of the 12th IFAC Symposium on Nonlinear Control Systems, Canberra, Australia, 4–6 January 2023; Elsevier: Amsterdam, The Netherlands, 2023. [Google Scholar]
- Sorrentino, A.; Gosea, I.V.; Patel, B.; Antoulas, A.C.; Vidakovic-Koch, T. The Loewner Framework for Data-Driven Identification of Electrochemical Systems; MPI: Magdeburg, Germany, 2022. [Google Scholar]
- Antoulas, A.C.; Lefteriu, S.; Ionita, A.C. A tutorial introduction to the Loewner framework for model reduction; Computational Science & Engineering, Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2017. [Google Scholar]
- Gosea, I.V.; Poussot-Vassal, C.; Antoulas, A.C. Chapter 15: Data-driven modeling and control of large-scale dynamical systems in the Loewner framework: Methodology and applications. In Handbook of Numerical Analysis, Numerical Control: Part A; Trélat, E., Zuazua, E., Eds.; Elsevier: Amsterdam, The Netherlands, 2022; Volume 23, pp. 499–530. [Google Scholar] [CrossRef]
- Antoulas, A.C.; Beattie, C.A.; Gugercin, S. Interpolatory Methods for Model Reduction; Computational Science & Engineering, Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2020. [Google Scholar]
- Embree, M.; Ionita, A.C. Pseudospectra of Loewner matrix pencils. In Realization and Model Reduction of Dynamical Systems; Springer: Berlin/Heidelberg, Germany, 2022; pp. 59–78. [Google Scholar] [CrossRef]
- Drmač, Z.; Peherstorfer, B. Learning low-dimensional dynamical-system models from noisy frequency-response data with Loewner rational interpolation. In Realization and Model Reduction of Dynamical Systems; Springer: Berlin/Heidelberg, Germany, 2022; pp. 39–57. [Google Scholar]
- Gosea, I.V.; Zhang, Q.; Antoulas, A.C. Preserving the DAE structure in the Loewner model reduction and identification framework. Adv. Comput. Math. 2020, 46, 1–32. [Google Scholar] [CrossRef]
- Wang, X.; Wei, X.; Zhu, J.; Dai, H.; Zheng, Y.; Xu, X.; Chen, Q. A review of modeling, acquisition, and application of lithium-ion battery impedance for onboard battery management. eTransportation 2021, 7, 100093. [Google Scholar] [CrossRef]
- Deng, Z.; Zhang, Z.; Lai, Y.; Liu, J.; Li, J.; Liu, Y. Electrochemical Impedance Spectroscopy Study of a Lithium/Sulfur Battery: Modeling and Analysis of Capacity Fading. J. Electrochem. Soc. 2013, 160, A553–A558. [Google Scholar] [CrossRef]
- Golub, G.H.; Van Loan, C.F. Matrix Computations, 3rd ed.; Johns Hopkins University Press: Baltimore, MD, USA, 1996. [Google Scholar]
- Plank, C.; Ruther, T.; Danzer, M.A. Detection of Non-Linearity and Non-Stationarity in Impedance Spectra using an Extended Kramers-Kronig Test without Overfitting. In Proceedings of the 2022 International Workshop on Impedance Spectroscopy (IWIS), Chemnitz, Germany, 27–30 September 2022. [Google Scholar] [CrossRef]
- Shafiei Sabet, P.; Sauer, D.U. Separation of predominant processes in electrochemical impedance spectra of lithium-ion batteries with nickel-manganese-cobalt cathodes. J. Power Sources 2019, 425, 121–129. [Google Scholar] [CrossRef]
- Manikandan, B.; Ramar, V.; Yap, C.; Balaya, P. Investigation of physico-chemical processes in lithium-ion batteries by deconvolution of electrochemical impedance spectra. J. Power Sources 2017, 361, 300–309. [Google Scholar] [CrossRef]
- Schlüter, N.; Ernst, S.; Schröder, U. Finding the Optimal Regularization Parameter in Distribution of Relaxation Times Analysis. ChemElectroChem 2019, 6, 6027–6037. [Google Scholar] [CrossRef]
- Schlüter, N.; Ernst, S.; Schröder, U. Direct Access to the Optimal Regularization Parameter in Distribution of Relaxation Times Analysis. ChemElectroChem 2020, 7, 3445–3458. [Google Scholar] [CrossRef]
- Paul, T.; Chi, P.W.; Wu, P.M.; Wu, M.K. Computation of distribution of relaxation times by Tikhonov regularization for Li ion batteries: Usage of L-curve method. Sci. Rep. 2021, 11, 12624. [Google Scholar] [CrossRef]
- Hu, D.; Chen, L.; Tian, J.; Su, Y.; Li, N.; Chen, G.; Hu, Y.; Dou, Y.; Chen, S.; Wu, F. Research Progress of Lithium Plating on Graphite Anode in Lithium–Ion Batteries. Chin. J. Chem. 2020, 39, 165–173. [Google Scholar] [CrossRef]
- Wang, C.; Appleby, A.J.; Little, F.E. Low-Temperature Characterization of Lithium-Ion Carbon Anodes via Microperturbation Measurement. J. Electrochem. Soc. 2002, 149, A754–A760. [Google Scholar] [CrossRef]
- Zhang, S.; Xu, K.; Jow, T. Low temperature performance of graphite electrode in Li-ion cells. Electrochim. Acta 2002, 48, 241–246. [Google Scholar] [CrossRef]
- Jow, T.R.; Delp, S.A.; Allen, J.L.; Jones, J.P.; Smart, M.C. Factors Limiting Li+ Charge Transfer Kinetics in Li-Ion Batteries. J. Electrochem. Soc. 2018, 165, A361–A367. [Google Scholar] [CrossRef]


| Lowener Method | Generalized DRT |
|---|---|
| − Meta parameter needed (k) | − Meta parameter needed () |
| + Simple process identification | − Difficult process identification |
| − Interpretation of resistive, capacitive, and resistive–inductive processes is challenging | + Interpretation of resistive, inductive, and resistive–inductive behavior possible |
| + Smaller polarization contributions interpretable | − Partial merging of peaks due to regularization |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rüther, T.; Gosea, I.V.; Jahn, L.; Antoulas, A.C.; Danzer, M.A. Introducing the Loewner Method as a Data-Driven and Regularization-Free Approach for the Distribution of Relaxation Times Analysis of Lithium-Ion Batteries. Batteries 2023, 9, 132. https://doi.org/10.3390/batteries9020132
Rüther T, Gosea IV, Jahn L, Antoulas AC, Danzer MA. Introducing the Loewner Method as a Data-Driven and Regularization-Free Approach for the Distribution of Relaxation Times Analysis of Lithium-Ion Batteries. Batteries. 2023; 9(2):132. https://doi.org/10.3390/batteries9020132
Chicago/Turabian StyleRüther, Tom, Ion Victor Gosea, Leonard Jahn, Athanasios C. Antoulas, and Michael A. Danzer. 2023. "Introducing the Loewner Method as a Data-Driven and Regularization-Free Approach for the Distribution of Relaxation Times Analysis of Lithium-Ion Batteries" Batteries 9, no. 2: 132. https://doi.org/10.3390/batteries9020132
APA StyleRüther, T., Gosea, I. V., Jahn, L., Antoulas, A. C., & Danzer, M. A. (2023). Introducing the Loewner Method as a Data-Driven and Regularization-Free Approach for the Distribution of Relaxation Times Analysis of Lithium-Ion Batteries. Batteries, 9(2), 132. https://doi.org/10.3390/batteries9020132









