A Novel Evaluation Criterion for the Rapid Estimation of the Overcharge and Deep Discharge of Lithium-Ion Batteries Using Differential Capacity
Abstract
:1. Introduction
1.1. Incremental Data Analysis
1.2. Scope of This Study
2. Materials and Methods
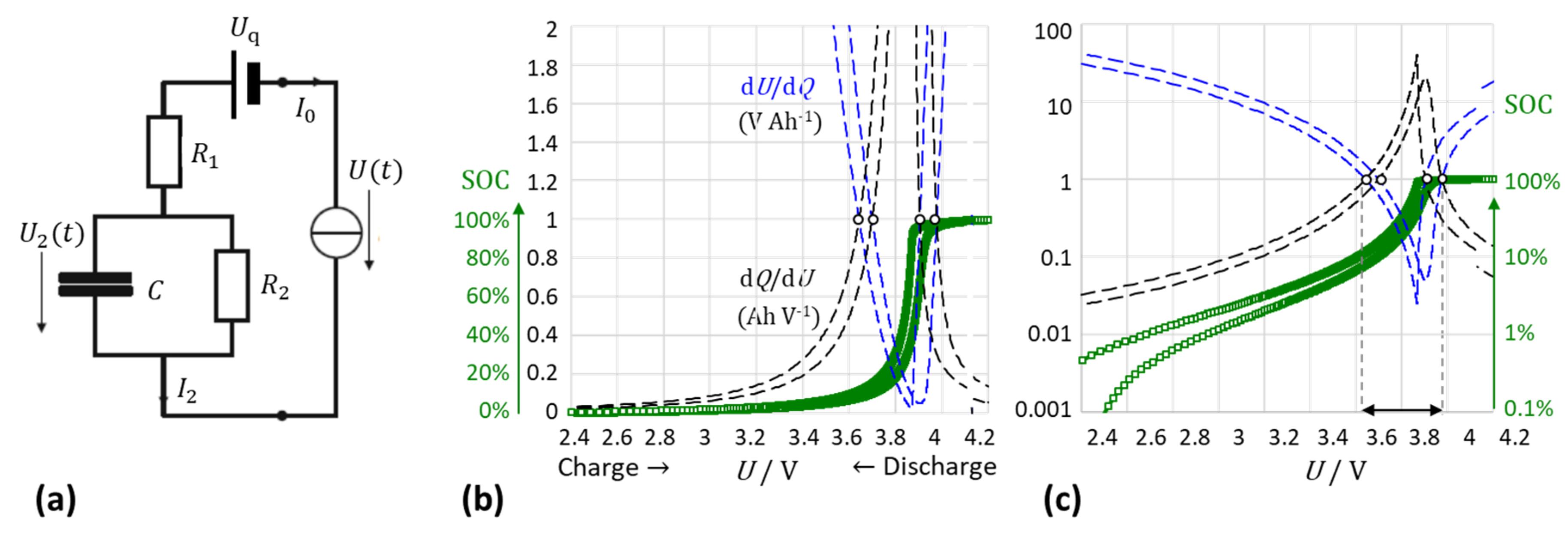
2.1. Differential Capacity and Resistance
2.2. The Intersection Method: A New Approch
2.3. Theoretical Background of the Intersection Criterion
3. Results and Discussion
3.1. Battery Monitoring Using the Intersection Method
- (a)
- Differential capacity
- (b)
- Incremental voltage
- (c)
- Intersection method
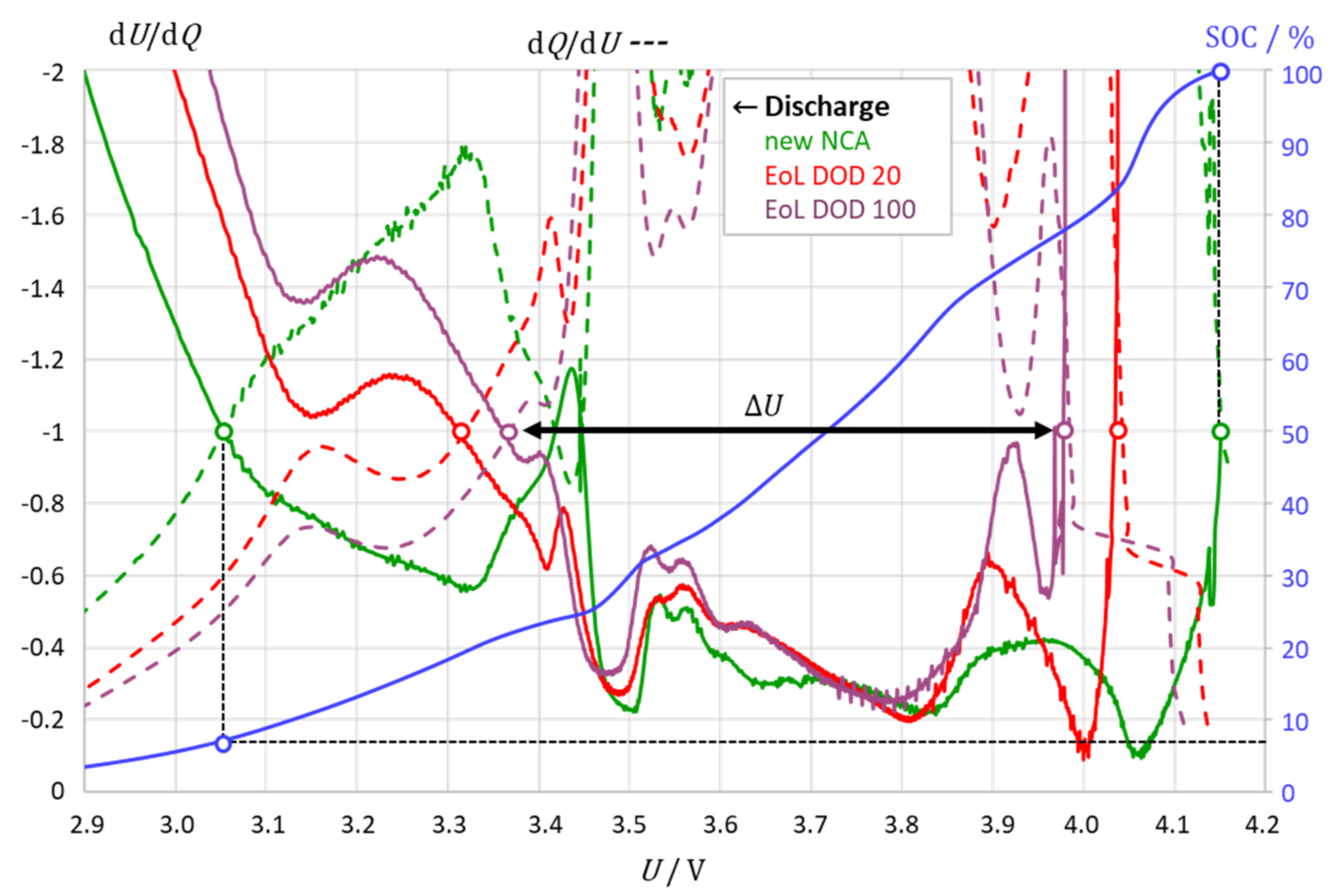
3.2. The Intersection Method Indicates the Degree of Aging
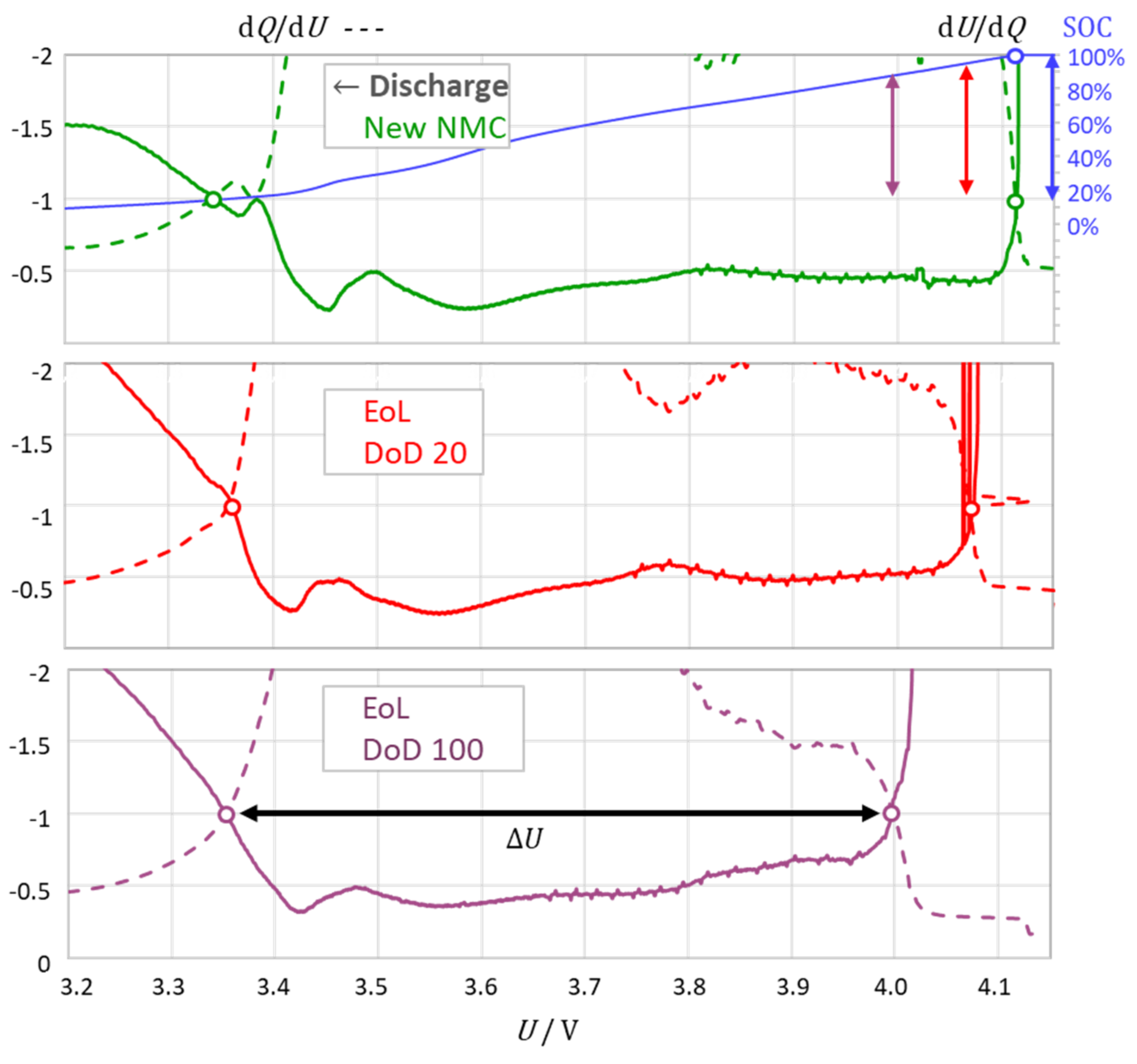
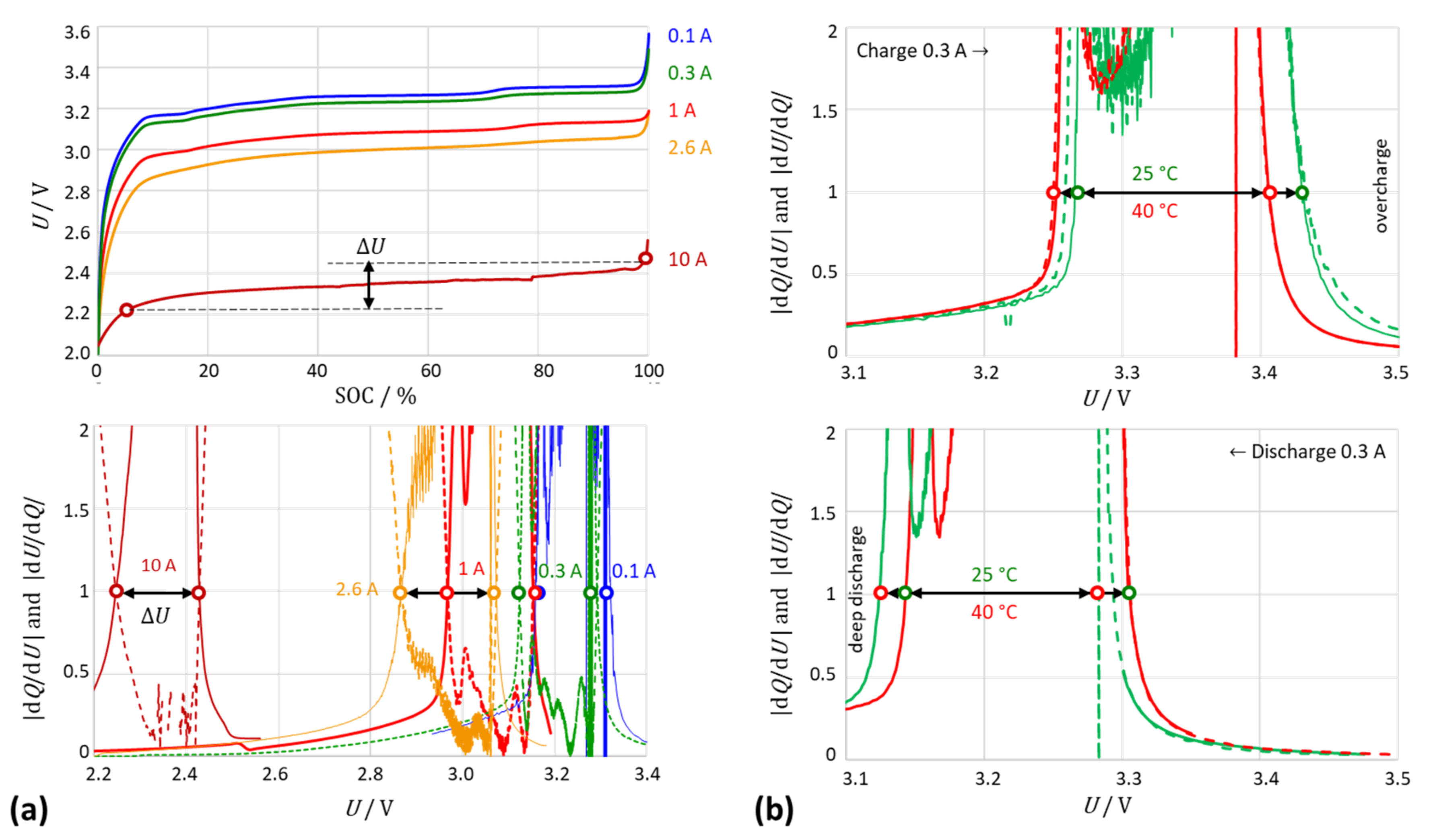
3.3. The Intersection Criterion Reflects Kinetic Inhibitions
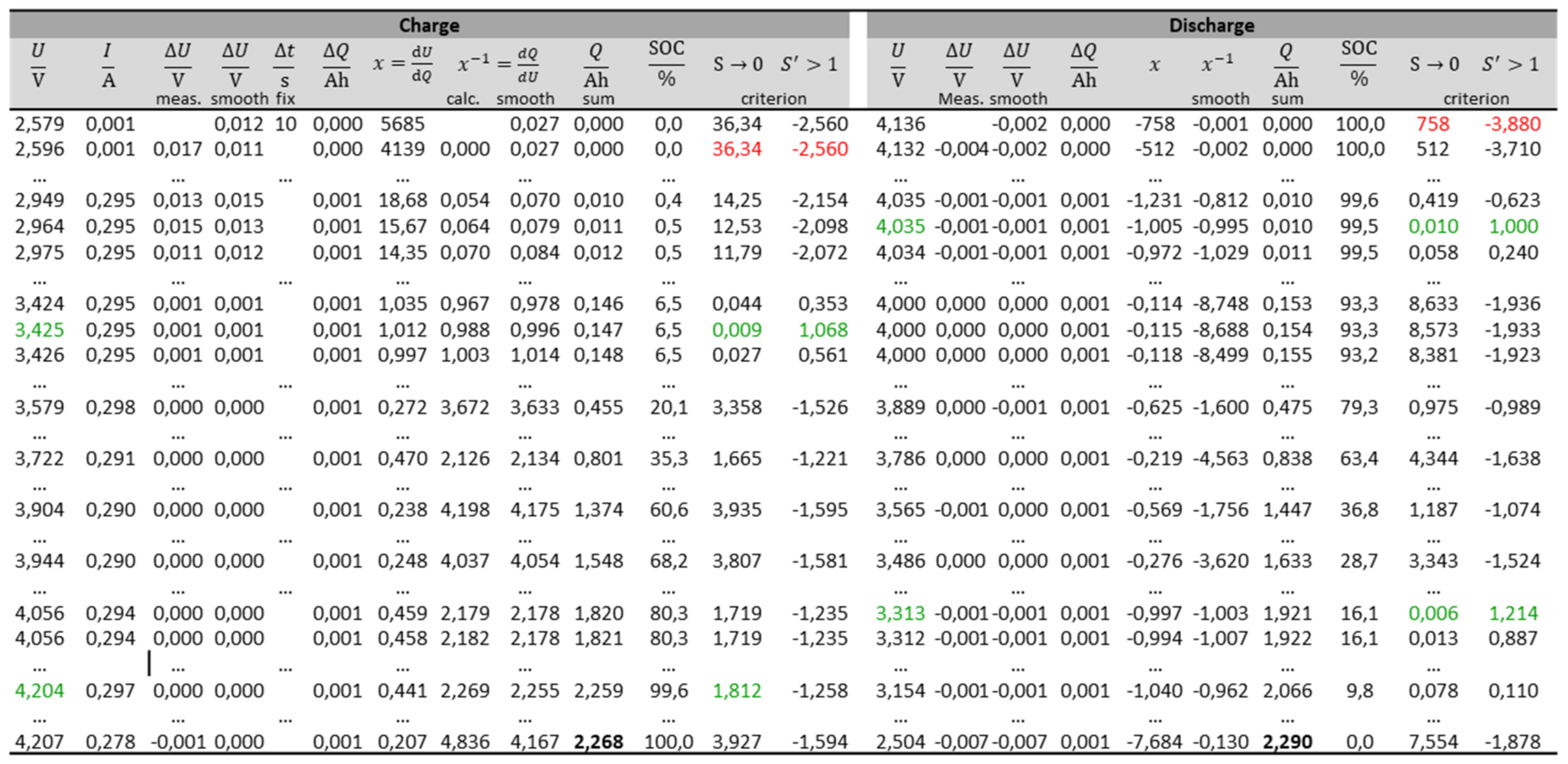
3.4. Practical Implementation
- Measurement of voltage U and electric current I during charging and discharging, e.g., every 10 s;
- Calculation of the differences for all voltage values (;
- Calculation of charge differences using the average value of constant current I and time interval Δt. Informatively, SOC = Q/Qmax can be added for each voltage point;
- Smoothing of voltage differences by averaging over 15 data points (total curve has 3000 data points);
- Calculation of incremental voltage (“DV”), dU/dQ ≈ ΔU/ΔQ, using the smoothed voltage vector;
- Calculation of the reciprocal dQ/dU ≈ (ΔU/ΔQ)−1;
- Smoothing of dQ/dU by averaging over 17 data points.
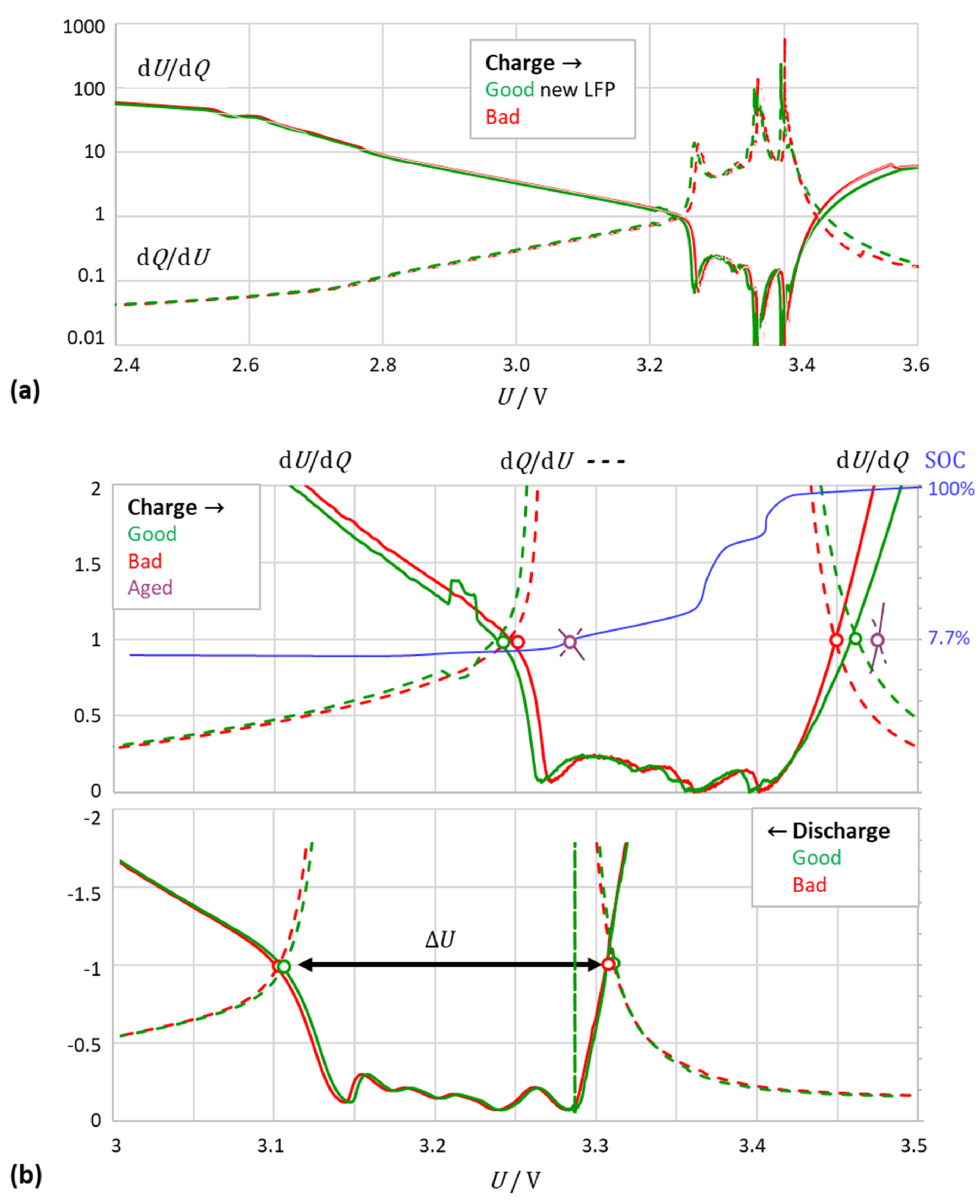
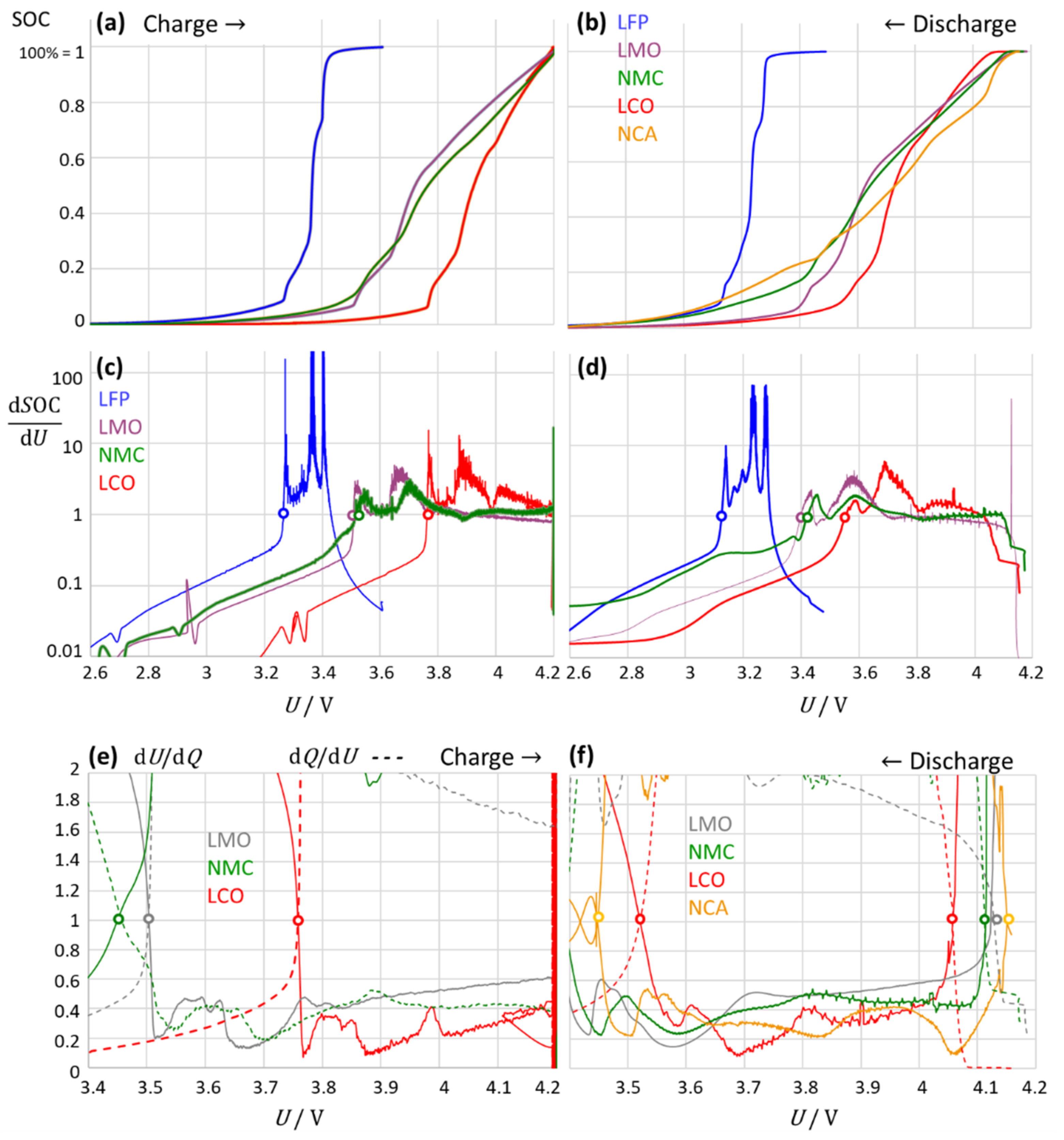
3.5. Limitations of the Method: Application to Different Cell Chemistries
- (a)
- Lithium–iron phosphate (LFP)
- (b)
- Lithium–cobalt oxide (LCO)
- (c)
- Lithium–manganese oxide (LMO)
- (d)
- Lithium nickel manganese cobalt oxide (NMC)
- (e)
- Lithium nickel cobalt aluminum oxide (NCA)
3.6. Verification of the Intersection Criterion Using Synthetic Data
4. Conclusions
- The intersection points corresponded to the kink points in the charge–voltage curve. At the upper intersection, the battery was “virtually full” and was considered a warning of impending overcharge or phase change. The small deviation to full charge depended on the cell chemistry;
- At the lower intersection point, the battery was “virtually empty” with a small amount of residual charge remaining in the battery; this was considered as a warning of impending deep discharge or phase change. For “completely empty”, including deep discharge, the criterion diverged from one: dQ/dU → 0 and dU/dQ → −∞;
- With an increasing current, the intersection points shifted to higher voltages (charging) or lower voltages (discharging); the distance between the intersections slightly increased with the current due to the voltage drop across the internal resistance of the cell.
Relevance to Battery Management Systems
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
List of Symbols and Abbreviations
| C | Capacitance, dQ/dU = 1/x (F) | LCO | lithium cobalt oxide |
| Q | electric charge, battery capacity (Ah) | LMO | lithium manganese spinel |
| Q0 | capacity of a fully charged battery (Ah) | LFP | lithium iron phosphate |
| R | ohmic resistance, real part of impedance (Ω) | NCA | nickel cobalt aluminum |
| Re | electrolyte resistance (Ω) | NMC | nickel manganese cobalt |
| U | cell voltage (V) | SOC | state-of-charge |
| x | incremental voltage: dU/dQ (Ω/s) | SOH | state-of-health |
References
- Waag, W.; Sauer, D.U. State-of-Charge/Health. In Encyclopedia of Electrochemical Power Sources; Garche, J., Dyer, C., Moseley, P.T., Ogumi, Z., Rand, D., Scrosati, B., Eds.; Elsevier: Amsterdam, The Netherlands, 2009; Volume 4, pp. 793–804. [Google Scholar]
- Piller, S.; Perrin, M.; Jossen, A. Methods for state-of-charge determination and their applications. J. Power Sources 2001, 96, 113–120. [Google Scholar] [CrossRef]
- Xiong, R.; Pan, Y.; Shen, W.; Li, H.; Sun, F. Lithium-ion battery aging mechanisms and diagnosis method for automotive applications: Recent advances and perspectives. Renew. Sustain. Energy Rev. 2020, 131, 110048. [Google Scholar] [CrossRef]
- Gauthier, R.; Luscombe, A.; Bond, T.; Bauer, M.; Johnson, M.; Harlow, J.; Louli, A.J.; Dahn, J.R. How do Depth of Discharge, C-rate and Calendar Age Affect Capacity Retention, Impedance Growth, the Electrodes, and the Electrolyte in Li-Ion Cells? J. Electrochem. Soc. 2022, 169, 020518. [Google Scholar] [CrossRef]
- Tran, M.-K.; Fowler, M. A Review of Lithium-Ion Battery Fault Diagnostic Algorithms: Current Progress and Future Challenges. Algorithms 2020, 13, 62. [Google Scholar] [CrossRef] [Green Version]
- Bloom, I.; Jansen, A.N.; Abraham, D.P.; Knuth, J.; Jones, S.A.; Battaglia, V.S.; Henriksen, G.L. Differential voltage analyses of high-power, lithium-ion cells: 1. Technique and application. J. Power Sources 2005, 139, 295–303. [Google Scholar] [CrossRef]
- Barai, A.; Uddin, K.; Dubarry, M.; Somerville, L.; McGordon, A.; Jennings, P.; Bloom, I. A comparison of methodologies for the non-invasive characterization of commercial Li-ion cells. Prog. Energy Combust. Sci. 2019, 72, 1–31. [Google Scholar] [CrossRef]
- Hatzikraniotis, E.; Mitsas, C.L.; Siapkas, D.I. Differential Capacity Analysis, a Tool to Examine the Performance of Graphites for Li-Ion Cells. In Materials for Lithium-Ion Batteries; NATO Science Series; Julien, C., Stoynov, Z., Eds.; Springer: Dordrecht, The Netherlands, 2020; Volume 85. [Google Scholar] [CrossRef]
- Dubarry, M.; Svoboda, V.; Hwu, R.; Liaw, B.Y. Incremental capacity analysis and close-to-equilibrium OCV measurements to quantify capacity fade in commercial rechargeable lithium batteries. Electrochem. Solid State Lett. 2006, 9, A454. [Google Scholar] [CrossRef]
- Dahn, H.M.; Smith, A.J.; Burns, J.C.; Stevens, D.A.; Dahn, J.R. User-Friendly Differential Voltage Analysis Freeware for the Analysis of Degradation Mechanisms in Li-Ion Batteries. J. Electrochem. Soc. 2012, 159, A1405. [Google Scholar] [CrossRef]
- Smith, A.J.; Burns, J.C.; Dahn, J.R. High-Precision Differential Capacity Analysis of LiMn2O4/graphite Cells. Electrochem. Solid-State Lett. 2011, 14, A39. [Google Scholar] [CrossRef]
- Smith, A.J.; Dahn, J.R. Delta Differential Capacity Analysis. J. Electrochem. Soc. 2012, 159, A290. [Google Scholar] [CrossRef]
- Zheng, L.; Zhu, J.; Lu, D.D.C.; Wang, G.; He, T. Incremental capacity analysis and differential voltage analysis based state of charge and capacity estimation for lithium-ion batteries. Energy 2018, 150, 759–769. [Google Scholar] [CrossRef]
- Jehnichen, P.; Wedlich, K.; Korte, C. Degradation of high-voltage cathodes for advanced lithium-ion batteries—differential capacity study on differently balanced cells. Sci. Technol. Adv. Mater. 2019, 20, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Krupp, A.; Ferg, E.; Schuldt, F.; Derendorf, K.; Agert, C. Incremental capacity analysis as a state of health estimation method for lithium-ion battery modules with series-connected cells. Batteries 2021, 7, 2. [Google Scholar] [CrossRef]
- Zhang, S.; Guo, X.; Dou, X.; Zhang, X. A rapid online calculation method for state of health of lithium-ion battery based on coulomb counting method and differential voltage analysis. J. Power Sources 2020, 479, 228740. [Google Scholar] [CrossRef]
- Kurzweil, P.; Ober, J.; Wabner, D.W. Method for extracting kinetic parameters from measured impedance spectra. Electrochim. Acta 1989, 34, 1179–1185. [Google Scholar] [CrossRef]
- Guo, D.; Yang, G.; Zhao, G.; Yi, M.; Feng, X.; Han, X.; Lu, L.; Ouyang, M. Determination of the Differential Capacity of Lithium-Ion Batteries by the Deconvolution of Electrochemical Impedance Spectra. Energies 2020, 13, 915. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Pan, C.; Liu, L.; Cheng, Y.; Zhao, X. On-board state of health estimation of LiFePO4 battery pack through differential voltage analysis. Appl. Energy 2016, 168, 465–472. [Google Scholar] [CrossRef]
- Wang, L.; Zhao, X.; Liu, L.; Pan, C. State of health estimation of battery modules via differential voltage analysis with local data symmetry method. Electrochim. Acta 2017, 256, 81–89. [Google Scholar] [CrossRef]
- Sieg, J.; Storch, M.; Fath, J.; Nuhic, A.; Bandlow, J.; Spier, B.; Sauer, D.U. Local degradation and differential voltage analysis of aged lithium-ion pouch cells. J. Energy Storage 2020, 30, 101582. [Google Scholar] [CrossRef]
- Zhan, C.; Wu, T.; Lu, J.; Amine, K. Dissolution, migration, and deposition of transition metal ions in Li-ion batteries exemplified by Mn-based cathodes–a critical review. Energy Environ. Sci. 2018, 11, 243–257. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.F. The Art of Scientific Computing, 3rd ed.; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Christophersen, J.P.; Shaw, S.R. Using radial basis functions to approximate battery differential capacity and differential voltage. J. Power Sources 2010, 195, 1225–1234. [Google Scholar] [CrossRef]
- Kurzweil, P.; Scheuerpflug, W. State-of-charge monitoring and battery diagnosis of different lithium-ion chemistries using impedance spectroscopy. Batteries 2021, 7, 17. [Google Scholar] [CrossRef]
- Dubarry, M.; Beck, D. Analysis of Synthetic Voltage vs. Capacity Datasets for Big Data Li-ion Diagnosis and Prognosis. Energies 2021, 14, 2371. [Google Scholar] [CrossRef]
- Ouyang, D.; Chen, M.; Liu, J.; Wei, R.; Weng, J.; Wang, J. Investigation of a commercial lithium-ion battery under overcharge/over-discharge failure conditions. RSC Adv. 2018, 8, 33414. [Google Scholar] [CrossRef] [Green Version]

| Chemistry | Cell | Rated | Max./Min. | Capacity | Allowed Current (A) | ||
|---|---|---|---|---|---|---|---|
| Voltage | Voltage U (V) | Q (Ah) | Charge | Discharge | |||
| 1 | LFP | LithiumWerks ANR26650M1B (LiFePO4) | 3.3 | 3.6 … 2.0 | 2.6 | 10 (4 C) | 50 (20 C) |
| 2 | NMC | LG ICR18650HE2 | 3.65 | 4.2 … 2.0 | 2.5 | 4 | 20 |
| 3 | LCO | Sanyo/Panasonic UR18650FK, Li1-xCoO2 | 3.7 | 4.2 … 2.5 | 2.3 | 2.3 | 4.8 |
| 4 | NCA | SONY US18650VTC6 | 3.65 | 4.2 … 2.0 | 3.0 | 5 | 20 |
| Battery and Cell Chemistry | State-of-Health: Capacity Q0 and Electrolyte Resistance | Charge Window | Discharge Window | |||||
|---|---|---|---|---|---|---|---|---|
| V | SOC | mAh | V | SOC | mAh | |||
| LFP | LithiumWerks | New #0 2.5 Ah, 5.3 mΩ | 3.45 … 3.25 | 98 … 7.6 | 2493 … 192 | 3.29 … 3.10 | 98 … 7.6 | 2356 … 43 |
| See Figure 1 | Good #74 2.5 Ah, 5.0 mΩ | 3.46 … 3.24 | 98 … 7.5 | 2497 … 192 | 3.30 … 3.11 | 98 … 7.6 | 2365 … 40 | |
| Bad #32 2.5 Ah, 6.4 mΩ | 3.45 … 3.25 | 98 … 7.7 | 2463 … 192 | 3.30 … 3.10 | 98 … 7.7 | 2329 … 45 | ||
| Aged #3 2.0 Ah | 3.47 … 3.28 | 98 … 8.9 | 2088 … 189 | 3.25 … 3.06 | 98 … 9.2 | 1957 … 42 | ||
| NCM | LGSee Figure 2 | New 2.2 Ah | 4.2 … 3.46 | 100 … 7.5 | 2170 … 164 | 4.11 …3.35 | 99.6 … 14 | 1871 … 9 |
| DoD 20 1.9 Ah (0.3 A) | 4.2 … 3.49 | 100 … 7.6 | 1908 … 145 | 4.07 …3.36 | 99.4 … 12 | 1674 … 11 | ||
| DoD 100 1.6 Ah (0.3 A) | 4.2 … 3.55 | 100 … 11 | 1590 … 176 | 4.00 …3.35 | 98.5 … 15 | 1365 … 24 | ||
| NCA | Sony | New 3.1 Ah, 31 mΩ | – | – | – | 4.15 … 3.05 | 99.9 … 7.0 | 2850 … 0 |
| See Figure 3 | DoD 20 2.3 Ah, 74 mΩ | 4.21 … 3.43 | 100 … 6.5 | 2268 … 148 | 4.04 … 3.31 | 99.5 … 16 | 1921 … 10 | |
| See Figure 4 | DoD 100 1.7 Ah, 70 mΩ | 4.13 … 3.47 | 92 … 8.1 | 1607 … 142 | 3.97 … 3.36 | 98.7 … 19 | 1415 … 23 | |
| LCO | Panasonic | New #8 2.26 Ah | 4.09 … 3.73 | 86 … 5.3 | 1942 … 120 | 4.09 … 3.58 | 99.2 … 5.3 | 2128… 18 |
| DoD 20 #4 2.21 Ah | 4.21 … 3.70 | 100 … 4.8 | 2200 … 106 | 4.11 … 3.56 | 99.5 … 9.2 | 1702 … 9 | ||
| DoD 100 #6 2.26 Ah | 4.21 … 3.73 | 99 … 5.2 | 2237… 118 | 4.09 … 3.75 | 94.8 … 1.3 | 2152 … 29 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kurzweil, P.; Frenzel, B.; Scheuerpflug, W. A Novel Evaluation Criterion for the Rapid Estimation of the Overcharge and Deep Discharge of Lithium-Ion Batteries Using Differential Capacity. Batteries 2022, 8, 86. https://doi.org/10.3390/batteries8080086
Kurzweil P, Frenzel B, Scheuerpflug W. A Novel Evaluation Criterion for the Rapid Estimation of the Overcharge and Deep Discharge of Lithium-Ion Batteries Using Differential Capacity. Batteries. 2022; 8(8):86. https://doi.org/10.3390/batteries8080086
Chicago/Turabian StyleKurzweil, Peter, Bernhard Frenzel, and Wolfgang Scheuerpflug. 2022. "A Novel Evaluation Criterion for the Rapid Estimation of the Overcharge and Deep Discharge of Lithium-Ion Batteries Using Differential Capacity" Batteries 8, no. 8: 86. https://doi.org/10.3390/batteries8080086
APA StyleKurzweil, P., Frenzel, B., & Scheuerpflug, W. (2022). A Novel Evaluation Criterion for the Rapid Estimation of the Overcharge and Deep Discharge of Lithium-Ion Batteries Using Differential Capacity. Batteries, 8(8), 86. https://doi.org/10.3390/batteries8080086






