State of Health Trajectory Prediction Based on Multi-Output Gaussian Process Regression for Lithium-Ion Battery
Abstract
:1. Introduction
1.1. Literature Review
1.2. The Thought of This Paper
- (1)
- Two HIs, namely, cycle number and standard deviation of discharge capacity (stdQ) are combined to achieve a highly accurate SOH prediction for battery packs.
- (2)
- The proposed MOGPR model can maintain a high-precision SOH prediction of battery cells and battery packs under different working conditions.
- (3)
- Only 20% early aging data of battery packs are employed to achieve an accurate SOH trajectory prediction for the battery pack, which saves lots of time and energy in whole-life aging tests of battery packs.
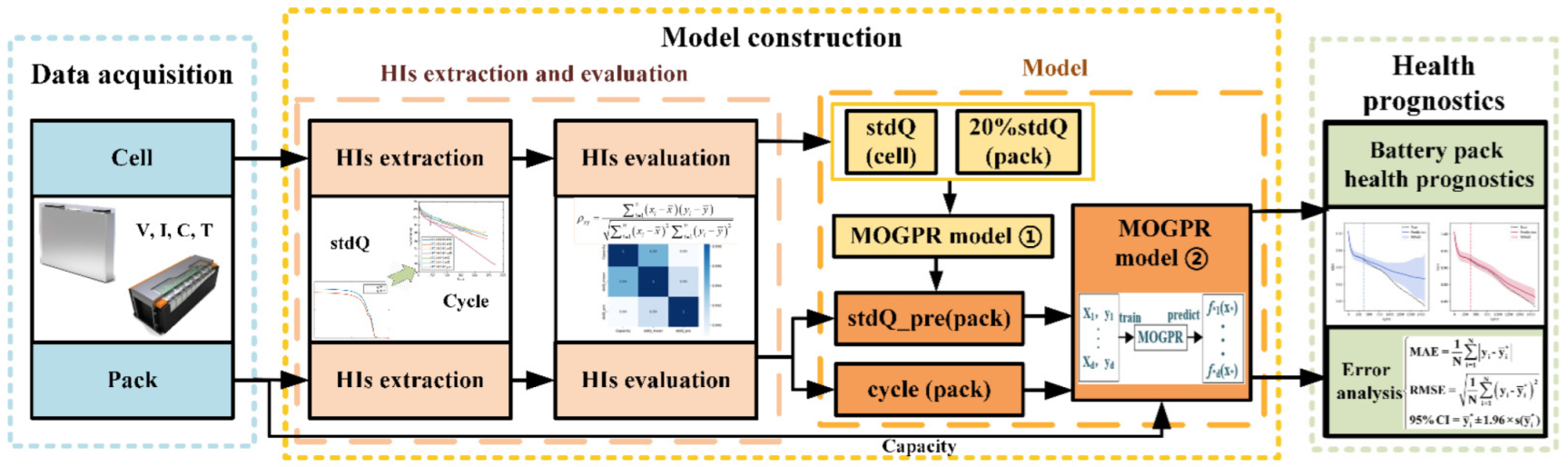
2. Results and Discussion
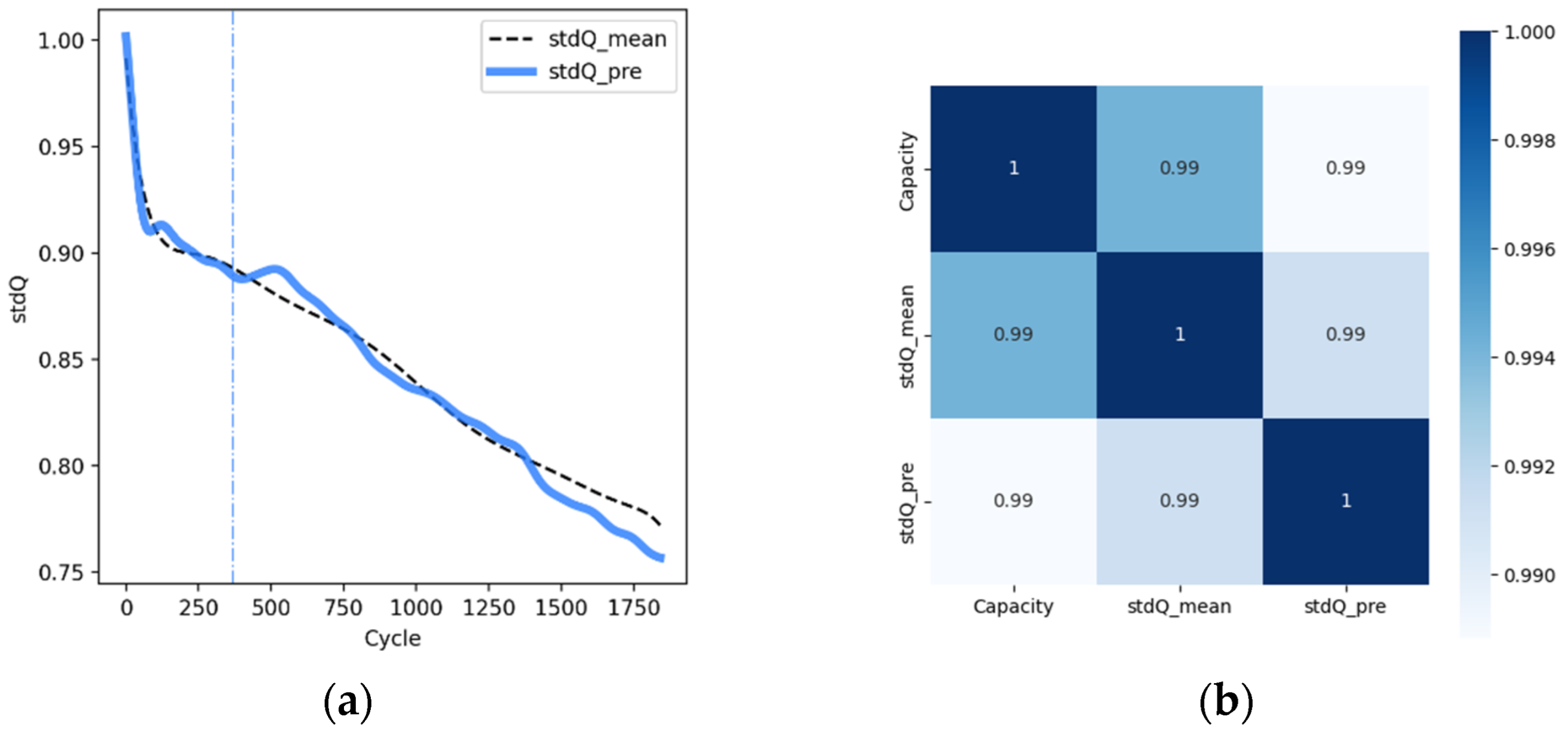
2.1. The HIs Prediction of Battery Pack
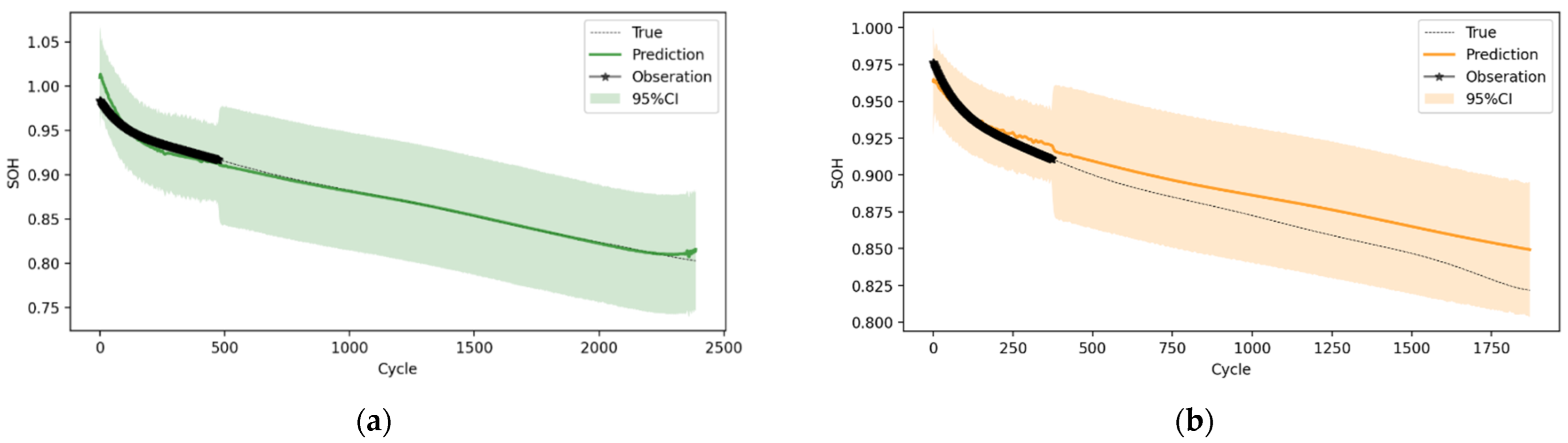
2.2. SOH Prediction of Battery Cells
2.2.1. Prediction Results of Two Different Models
2.2.2. Prediction Results for Two Different Conditions
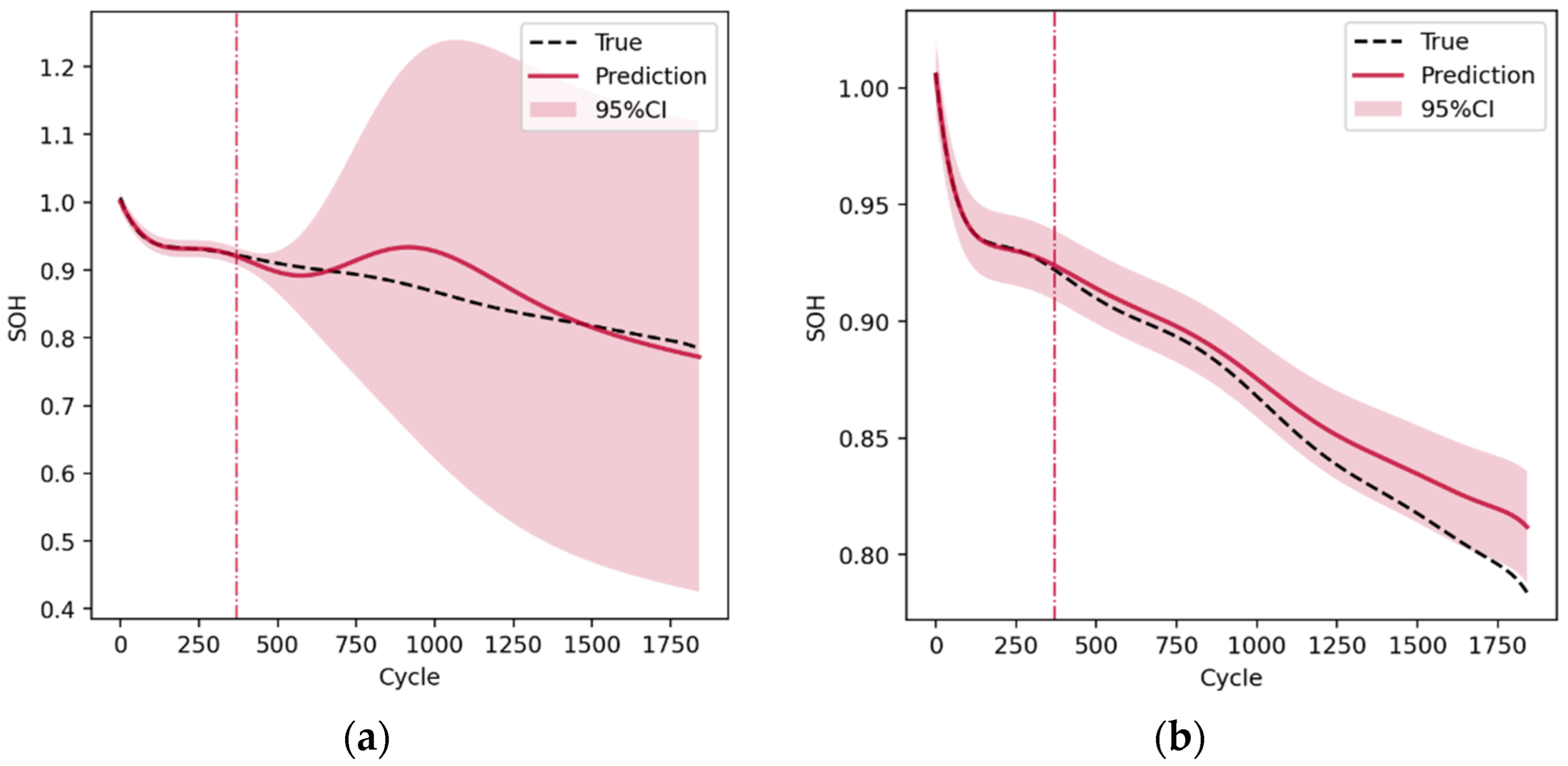
2.3. SOH Prediction of Battery Pack
2.3.1. Prediction Results Based on the SOGPR Model
2.3.2. Prediction Results Based on the MOGPR Model
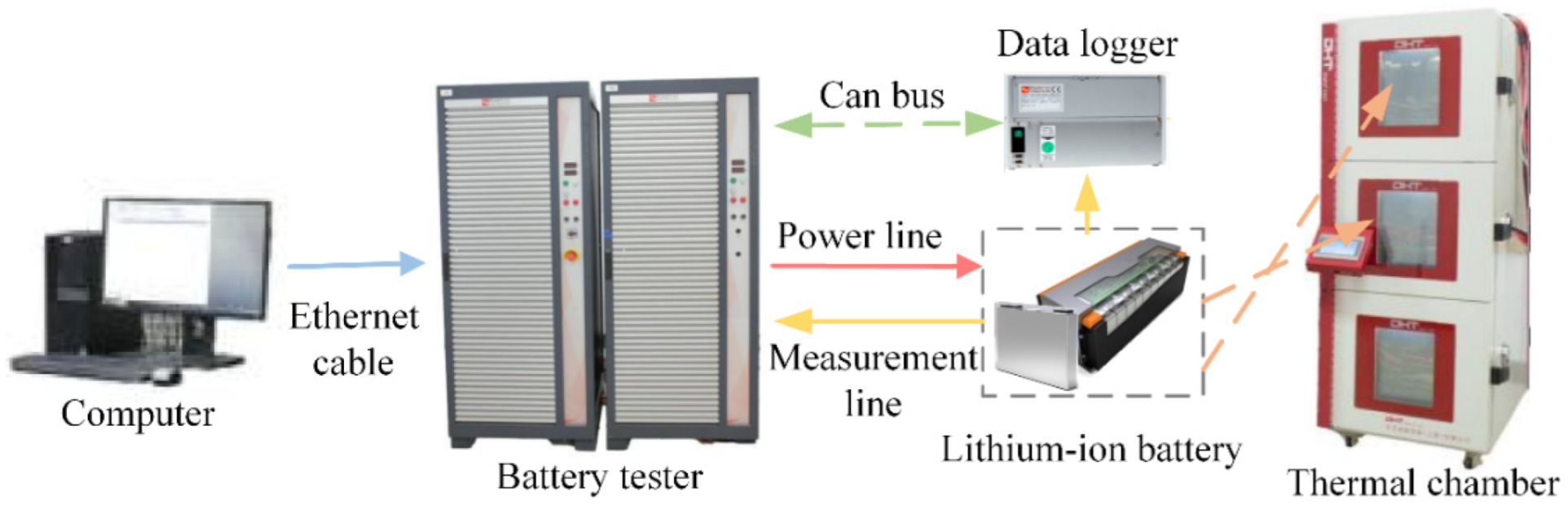
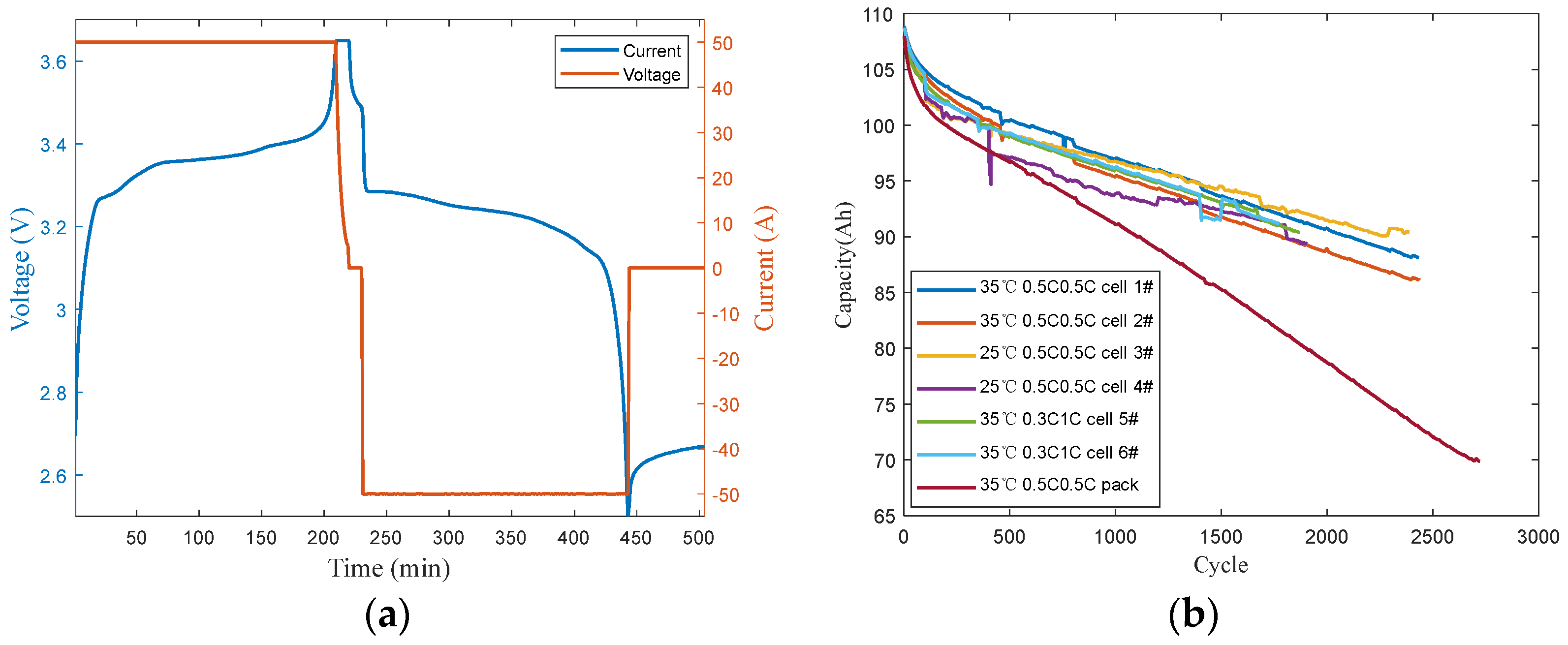
3. Experiment
4. Health Indicators Extraction and Evaluation
4.1. Health Indicators Extraction
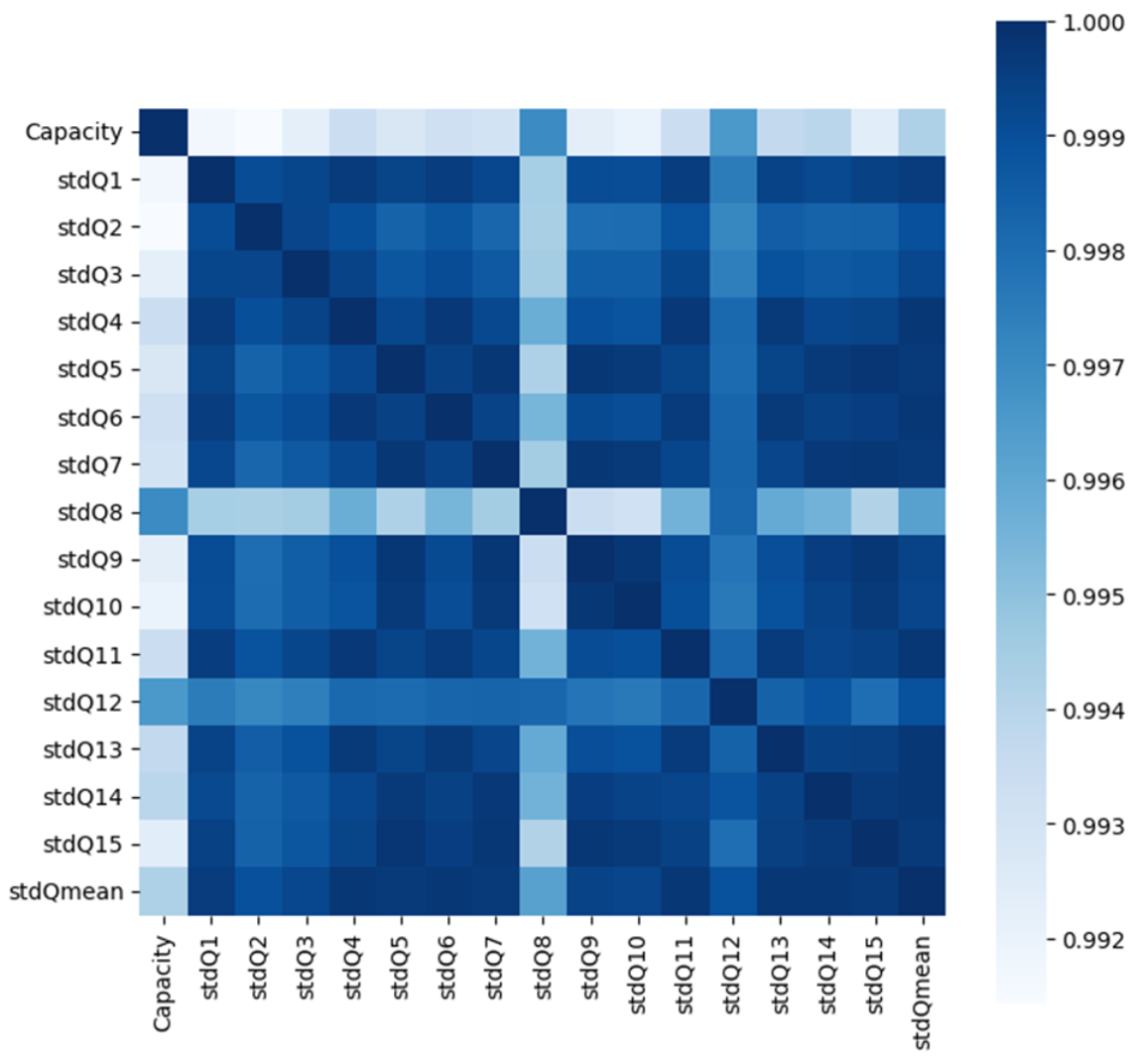
4.2. Health Indicators Evaluation
5. Methodology
5.1. Single-Output Gaussian Process Regression Model
5.2. Multi-Output Gaussian Process Regression Model
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Farmann, A.; Waag, W.; Marongiu, A.; Sauer, D.U. Critical review of on-board capacity estimation techniques for lithium-ion batteries in electric and hybrid electric vehicles. J. Power Sources 2015, 281, 114–130. [Google Scholar] [CrossRef]
- Liu, J.; Bao, Z.; Cui, Y.; Dufek, E.J.; Goodenough, J.B.; Khalifah, P.; Li, Q.; Liaw, B.Y.; Liu, P.; Manthiram, A. Pathways for practical high-energy long-cycling lithium metal batteries. Nat. Energy 2019, 4, 180–186. [Google Scholar] [CrossRef]
- Khumprom, P.; Yodo, N. A data-driven predictive prognostic model for lithium-ion batteries based on a deep learning algorithm. Energies 2019, 12, 660. [Google Scholar] [CrossRef]
- Zubi, G.; Dufo-López, R.; Carvalho, M.; Pasaoglu, G.; Reviews, S.E. The lithium-ion battery: State of the art and future perspectives. Renew. Sustain. Energy Rev. 2018, 89, 292–308. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, D.; Yang, B.; Cui, X.; Li, X. Electrochemical model of lithium-ion battery for wide frequency range applications. Electrochim. Acta 2020, 343, 136094. [Google Scholar] [CrossRef]
- Wang, Y.; Tian, J.; Sun, Z.; Wang, L.; Xu, R.; Li, M.; Chen, Z. A comprehensive review of battery modeling and state estimation approaches for advanced battery management systems. Renew. Sustain. Energy Rev. 2020, 131, 110015. [Google Scholar] [CrossRef]
- Xiong, R.; Li, L.; Li, Z.; Yu, Q.; Mu, H. An electrochemical model based degradation state identification method of Lithium-ion battery for all-climate electric vehicles application. Appl. Energy 2018, 219, 264–275. [Google Scholar] [CrossRef]
- Plett, G.L. Battery Management Systems, Volume II: Equivalent-Circuit Methods; Artech House: Norwood, MA, USA, 2015. [Google Scholar]
- Hu, X.; Li, S.; Peng, H. A comparative study of equivalent circuit models for Li-ion batteries. J. Power Sources 2012, 198, 359–367. [Google Scholar] [CrossRef]
- Hu, X.; Xu, L.; Lin, X.; Pecht, M. Battery lifetime prognostics. Joule 2020, 4, 310–346. [Google Scholar] [CrossRef]
- Ge, M.-F.; Liu, Y.; Jiang, X.; Liu, J. A review on state of health estimations and remaining useful life prognostics of lithium-ion batteries. Measurement 2021, 174, 109057. [Google Scholar] [CrossRef]
- Deng, Z.; Hu, X.; Lin, X.; Xu, L.; Li, J.; Guo, W. A reduced-order electrochemical model for all-solid-state batteries. IEEE Trans. Transp. Electrif. 2020, 7, 464–473. [Google Scholar] [CrossRef]
- Hu, X.; Jiang, J.; Cao, D.; Egardt, B. Battery health prognosis for electric vehicles using sample entropy and sparse Bayesian predictive modeling. IEEE Trans. Ind. Electron. 2015, 63, 2645–2656. [Google Scholar] [CrossRef]
- You, G.-w.; Park, S.; Oh, D. Real-time state-of-health estimation for electric vehicle batteries: A data-driven approach. Appl. Energy 2016, 176, 92–103. [Google Scholar] [CrossRef]
- Klass, V.; Behm, M.; Lindbergh, G. A support vector machine-based state-of-health estimation method for lithium-ion batteries under electric vehicle operation. J. Power Sources 2014, 270, 262–272. [Google Scholar] [CrossRef]
- Hu, C.; Jain, G.; Schmidt, C.; Strief, C.; Sullivan, M. Online estimation of lithium-ion battery capacity using sparse Bayesian learning. J. Power Sources 2015, 289, 105–113. [Google Scholar] [CrossRef]
- Deng, Z.; Hu, X.; Lin, X.; Xu, L.; Che, Y.; Hu, L. General discharge voltage information enabled health evaluation for lithium-ion batteries. IEEE/ASME Trans. Mechatron. 2020, 26, 1295–1306. [Google Scholar] [CrossRef]
- Wang, J.; Deng, Z.; Yu, T.; Yoshida, A.; Xu, L.; Guan, G.; Abudula, A. State of health estimation based on modified Gaussian process regression for lithium-ion batteries. J. Energy Storage 2022, 51, 104512. [Google Scholar] [CrossRef]
- Liu, K.; Hu, X.; Wei, Z.; Li, Y.; Jiang, Y. Modified Gaussian process regression models for cyclic capacity prediction of lithium-ion batteries. IEEE Trans. Transp. Electrif. 2019, 5, 1225–1236. [Google Scholar] [CrossRef]
- Li, X.; Wang, Z.; Yan, J. Prognostic health condition for lithium battery using the partial incremental capacity and Gaussian process regression. J. Power Sources 2019, 421, 56–67. [Google Scholar] [CrossRef]
- Zheng, X.; Deng, X. State-of-health prediction for lithium-ion batteries with multiple gaussian process regression model. IEEE Access 2019, 7, 150383–150394. [Google Scholar] [CrossRef]
- Boyle, P.; Frean, M. Dependent gaussian processes. Adv. Neural Inf. Process. Syst. 2004, 17, 17,217–224. [Google Scholar]
- Li, Y.; Sheng, H.; Cheng, Y.; Stroe, D.-I.; Teodorescu, R. State-of-health estimation of lithium-ion batteries based on semi-supervised transfer component analysis. Appl. Energy 2020, 277, 115504. [Google Scholar] [CrossRef]
- Li, J.; Deng, Z.; Liu, H.; Xie, Y.; Liu, C.; Lu, C. Battery capacity trajectory prediction by capturing the correlation between different vehicles. Energy 2022, 260, 125123. [Google Scholar] [CrossRef]
- Richardson, R.R.; Osborne, M.A.; Howey, D.A. Gaussian process regression for forecasting battery state of health. J. Power Sources 2017, 357, 209–219. [Google Scholar] [CrossRef]
- Deng, Z.; Hu, X.; Li, P.; Lin, X.; Bian, X. Data-driven battery state of health estimation based on random partial charging data. IEEE Trans. Power Electron 2021, 37, 5021–5031. [Google Scholar] [CrossRef]
- Lee Rodgers, J.; Nicewander, W.A. Thirteen ways to look at the correlation coefficient. Am. Stat. 1988, 42, 59–66. [Google Scholar] [CrossRef]
- Liu, H.; Cai, J.; Ong, Y.-S. Remarks on multi-output Gaussian process regression. Knowl. Based Syst. 2018, 144, 102–121. [Google Scholar] [CrossRef]



| Approach | Advantages | Disadvantages |
|---|---|---|
| ANN | support for multidimensional spaces; high prediction accuracy; ability to learn independently; | high computational complexity large-scale samples; poor uncertainty expression; complex structure; |
| SVM | support for multidimensional spaces; strong generalization ability; better performance in the nonlinear system; | kernel function satisfying the Mercer criterion; more computing resources are required; sensitive to missing data; |
| RVM | high sparsity; not subject to Mercer restrictions; | depends on kernel function selection; susceptibility to falling into a local optimum; |
| GPR | availability of uncertainty expressions; applicable to high-dimensional and small sample data; | poor long-term forecasting; high cost of computing large samples of data; |
| Conditions | Cell | Pack | ||
|---|---|---|---|---|
| Temperature (°C) | 35 | 25 | 35 | 35 |
| Charge rate (C) | 0.5 | 0.5 | 0.3 | 0.5 |
| Discharge rate (C) | 0.5 | 0.5 | 1 | 0.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Deng, Z.; Li, J.; Peng, K.; Xu, L.; Guan, G.; Abudula, A. State of Health Trajectory Prediction Based on Multi-Output Gaussian Process Regression for Lithium-Ion Battery. Batteries 2022, 8, 134. https://doi.org/10.3390/batteries8100134
Wang J, Deng Z, Li J, Peng K, Xu L, Guan G, Abudula A. State of Health Trajectory Prediction Based on Multi-Output Gaussian Process Regression for Lithium-Ion Battery. Batteries. 2022; 8(10):134. https://doi.org/10.3390/batteries8100134
Chicago/Turabian StyleWang, Jiwei, Zhongwei Deng, Jinwen Li, Kaile Peng, Lijun Xu, Guoqing Guan, and Abuliti Abudula. 2022. "State of Health Trajectory Prediction Based on Multi-Output Gaussian Process Regression for Lithium-Ion Battery" Batteries 8, no. 10: 134. https://doi.org/10.3390/batteries8100134
APA StyleWang, J., Deng, Z., Li, J., Peng, K., Xu, L., Guan, G., & Abudula, A. (2022). State of Health Trajectory Prediction Based on Multi-Output Gaussian Process Regression for Lithium-Ion Battery. Batteries, 8(10), 134. https://doi.org/10.3390/batteries8100134









