Advanced Electrochemical Impedance Spectroscopy of Industrial Ni-Cd Batteries
Abstract
:1. Introduction
2. Materials and Methods
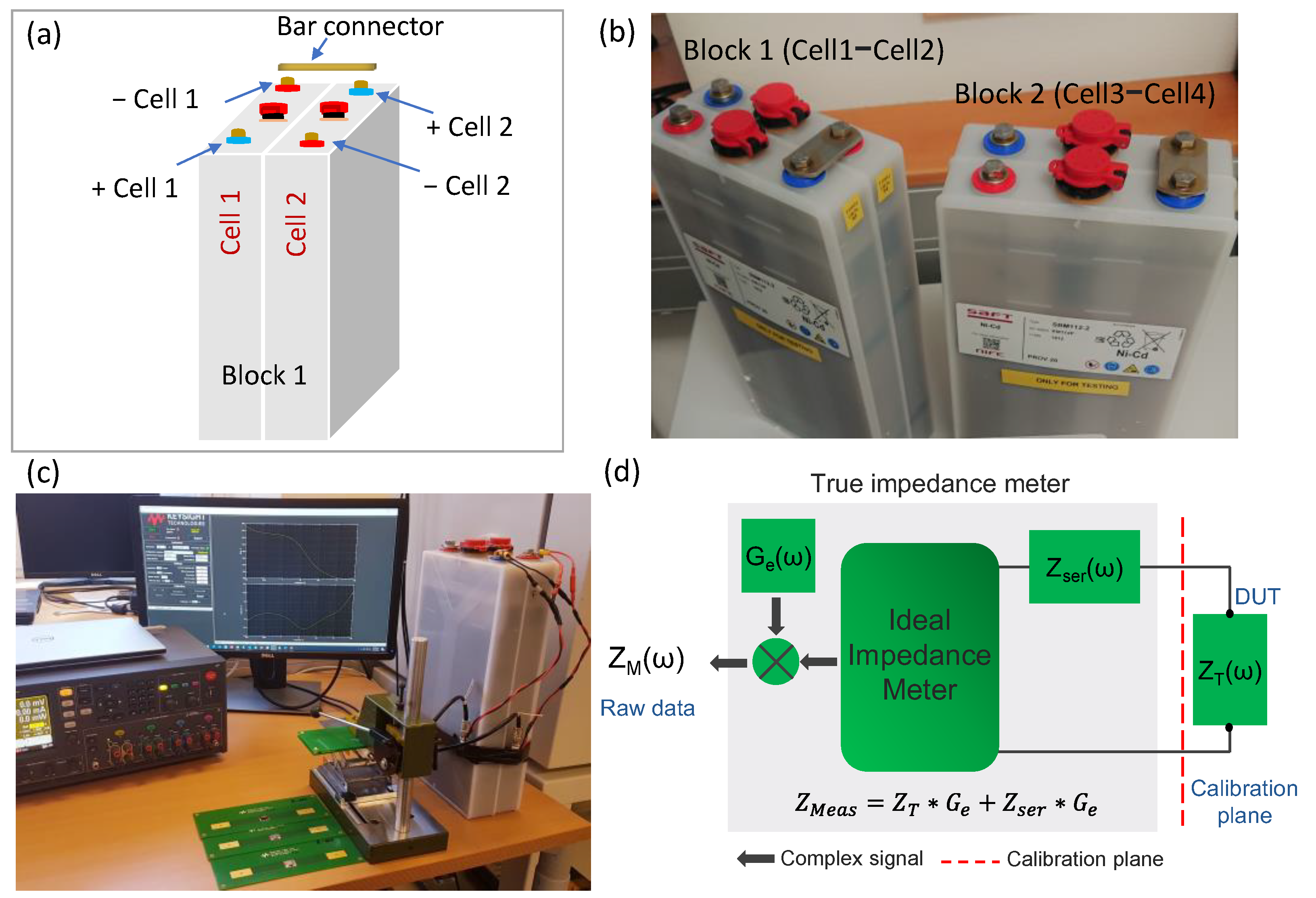
2.1. Ni-Cd Cells and Block Arrangements
2.2. Electrochemical Impedance Spectroscopy (EIS) and Calibration Method
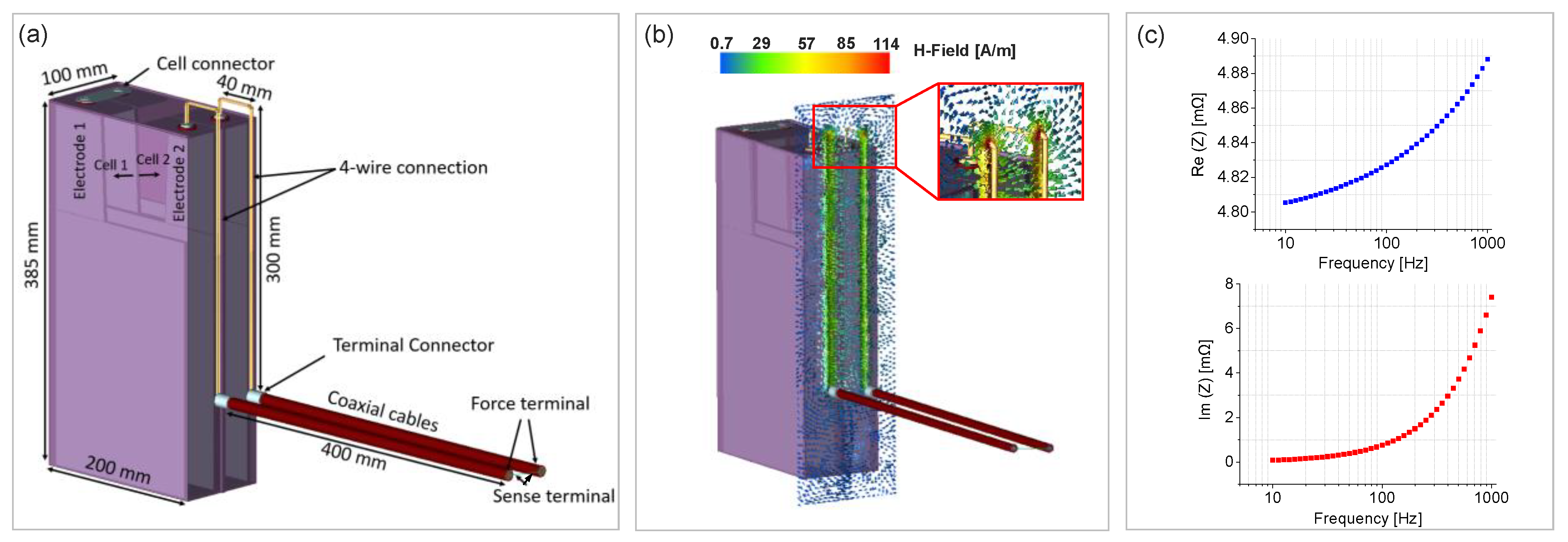
2.3. Electromagnetic Finite Element Method (FEM) Modeling
3. Results and Discussion
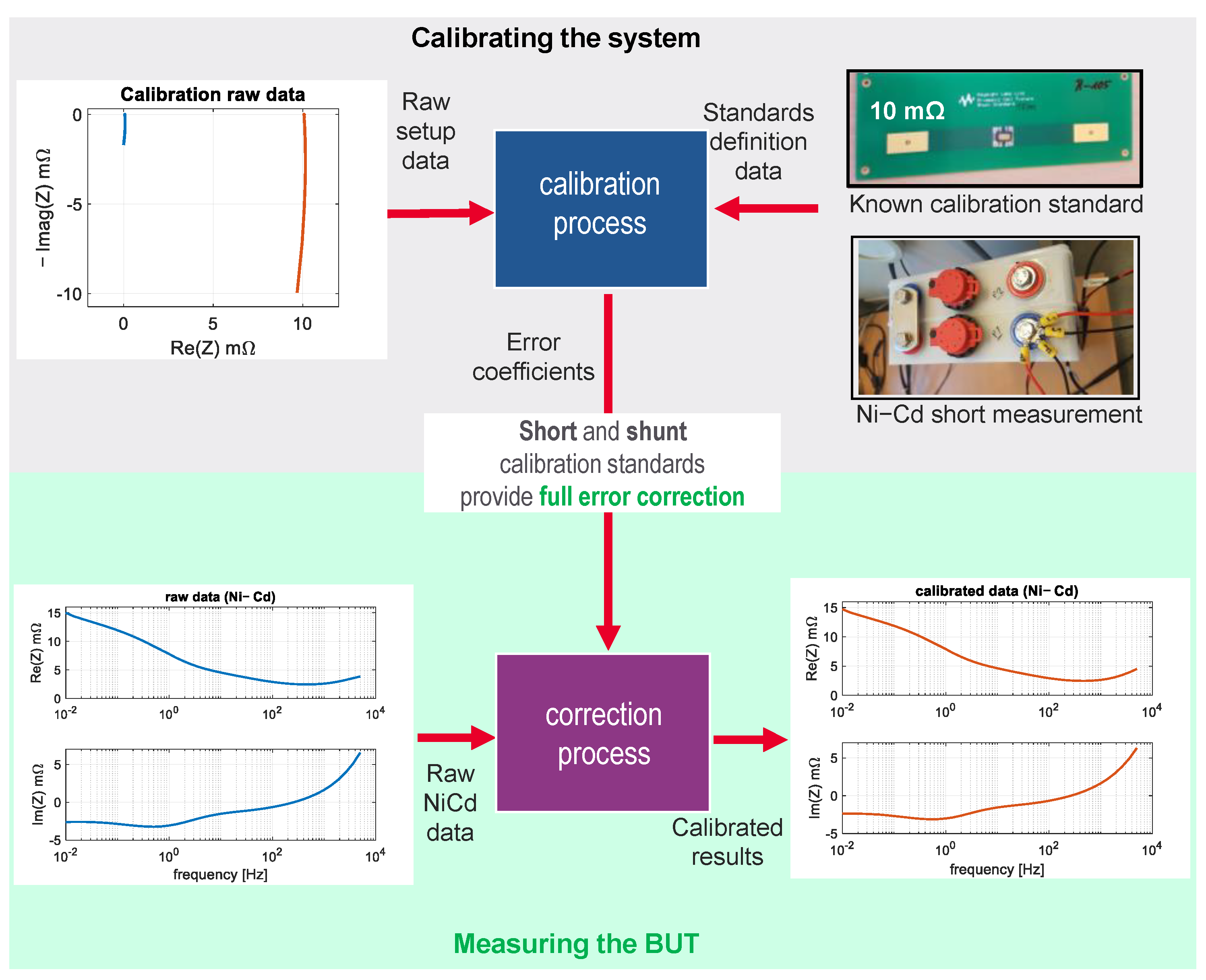
3.1. EIS Calibration Method
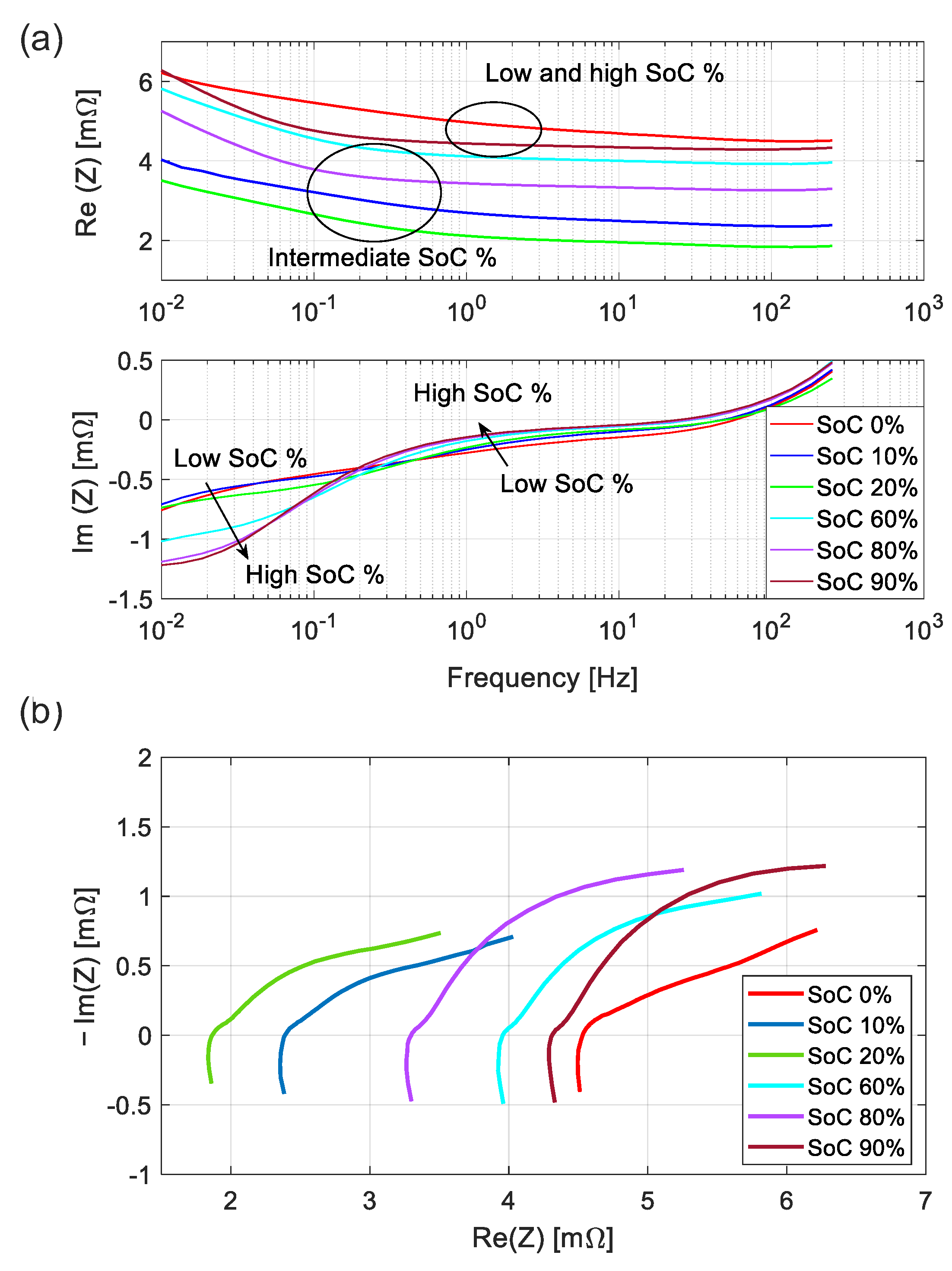
3.2. Calibrated EIS versus SoC
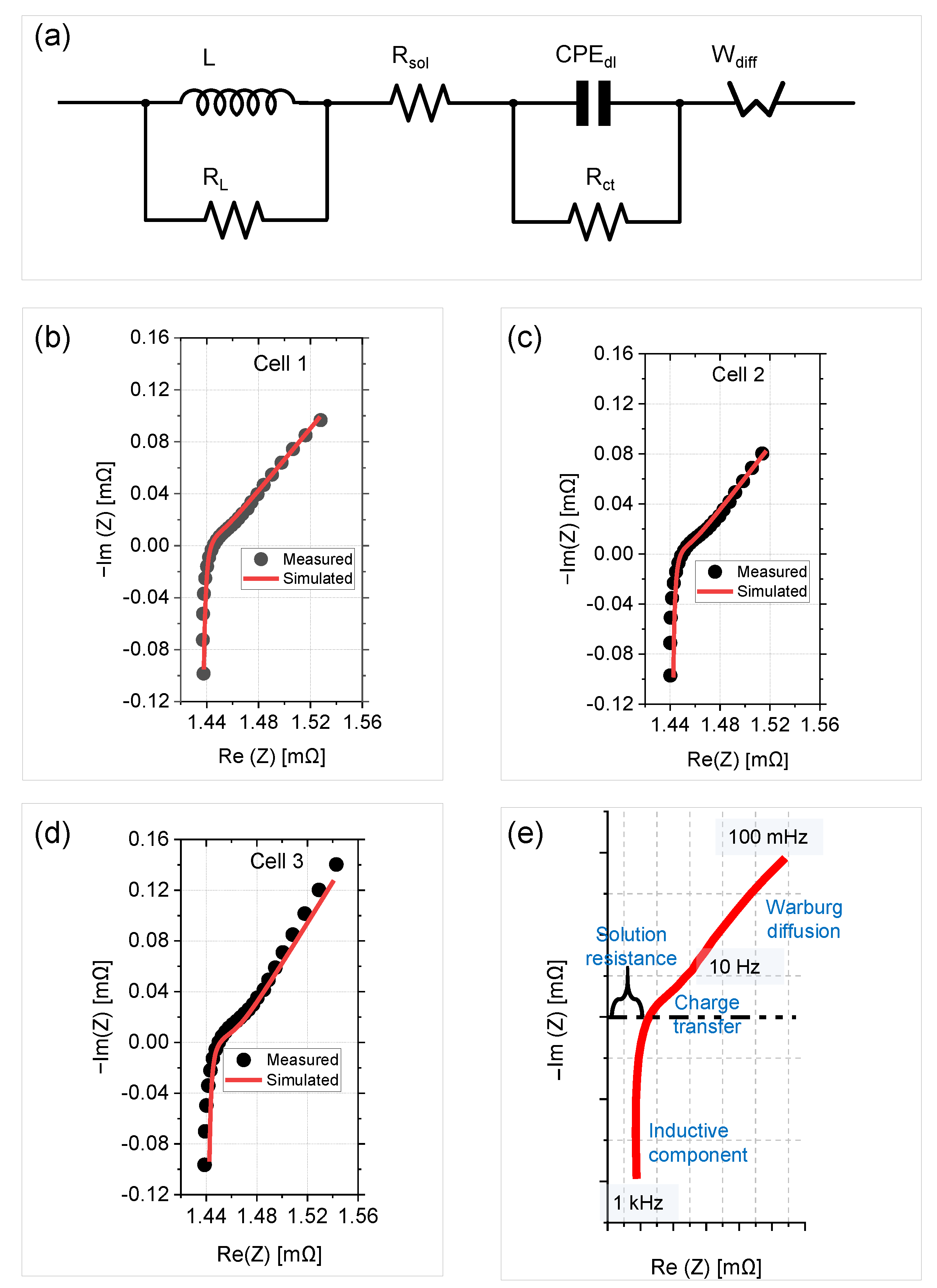
3.3. Equivalent Electric Circuit Model and Fit Parameters
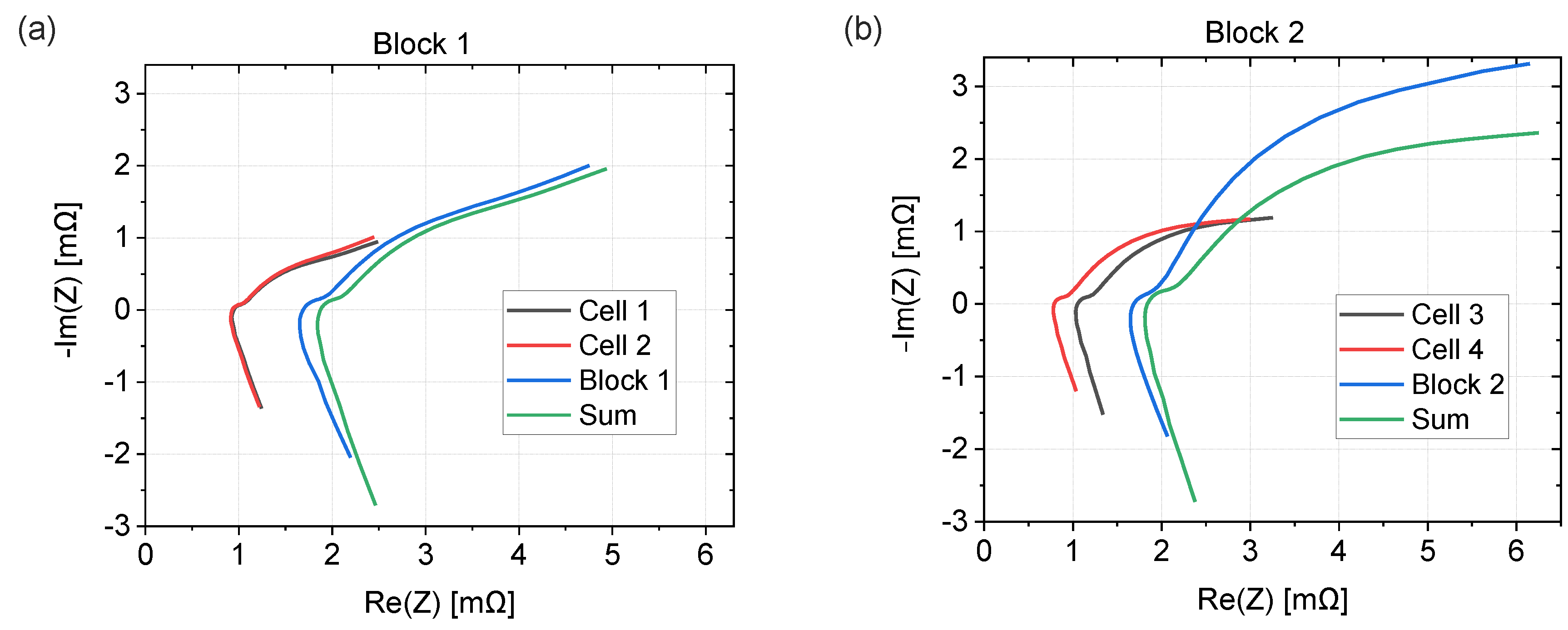
3.4. EIS Comparison of Cells and Blocks
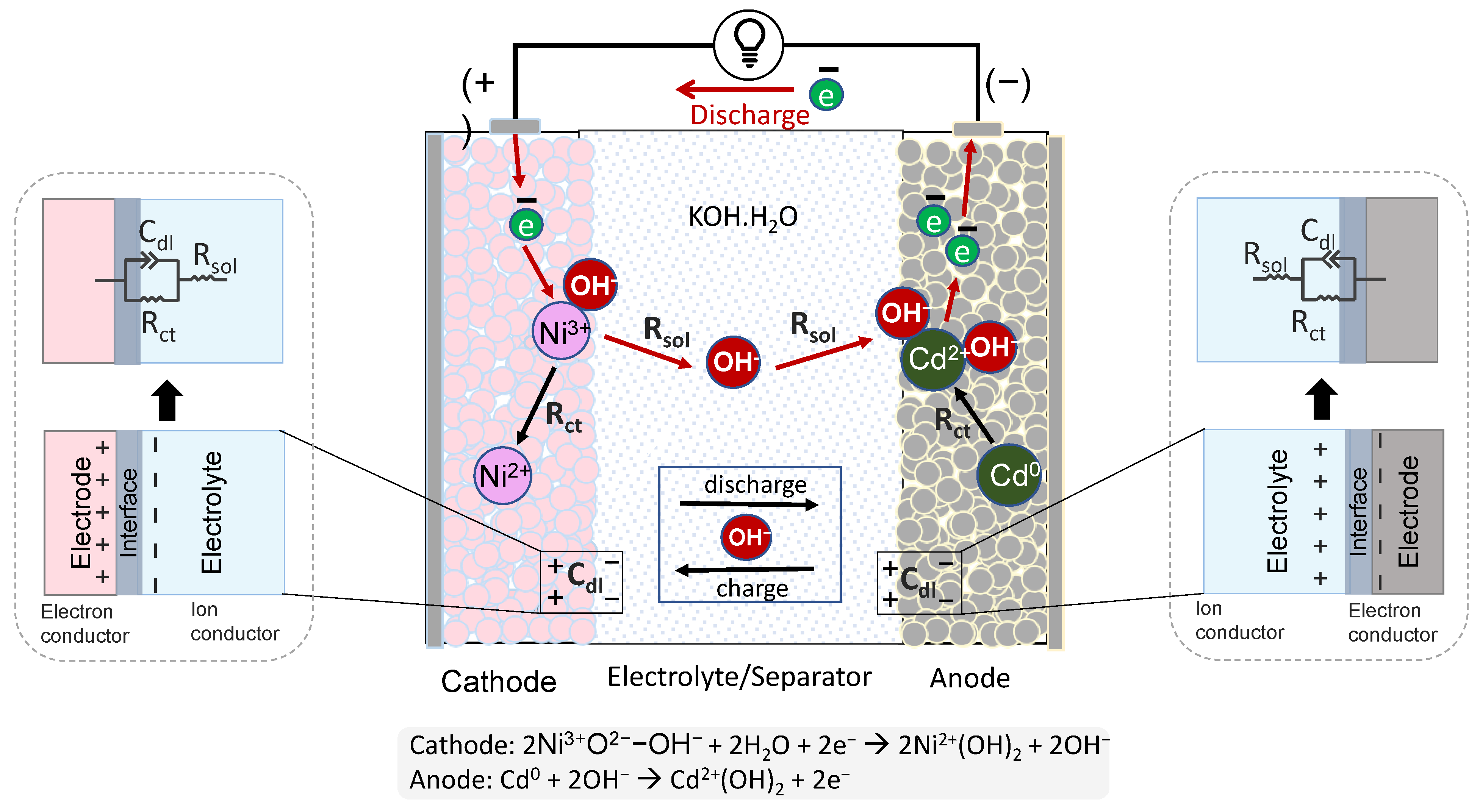
3.5. Electrochemical Interpretation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kasim, R.; Abdullah, A.R.; Selamat, N.A.; Basir, M.S.S.M.; Ramli, M.Z. Nickel-Cadmium battery analysis using spectrogram. ARPN J. Eng. Appl.Sci. 2016, 11, 3975–3979. [Google Scholar]
- Mcdermott, P.; Halpert, G.; Ekpanyaskun, S.; Nche, P. Secondary aerospace batteries and battery materials: A bibliography, 1969–1974. Bibliography 1976, 7044, 1923–1968. [Google Scholar]
- Nilsson, A.O. Nickel cadmium batteries in UPS design features. In Proceedings of the 10th International Telecommunications Energy Conference, San Diego, CA, USA, 30 October–2 November 1988; pp. 388–393. [Google Scholar] [CrossRef]
- Dirani, H.C.; Semaan, E.; Moubayed, N. Impact of the current and the temperature variation on the Ni-Cd battery functioning. In Proceedings of the 2013 The International Conference on Technological Advances in Electrical, Electronics and Computer Engineering (TAEECE), Konya, Turkey, 9–11 May 2013; pp. 339–343. [Google Scholar] [CrossRef]
- Jeyaseelan, C.; Jain, A.; Khurana, P.; Kumar, D.; Thatai, S. Ni-Cd Batteries. In Rechargeable Batteries; Boddula, R., Inamuddin, R.P., Asiri, A.M., Eds.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2020; pp. 177–194. [Google Scholar] [CrossRef]
- Mottard, J.-M.; Hannay, C.; Winandy, E.L. Experimental study of the thermal behavior of a water cooled Ni–Cd battery. J. Power Sources 2003, 117, 212–222. [Google Scholar] [CrossRef]
- Crescentini, M.; De Angelis, A.; Ramilli, R.; De Angelis, G.; Tartagni, M.; Moschitta, A.; Traverso, P.A.; Carbone, P. Online EIS and Diagnostics on Lithium-Ion Batteries by Means of Low-Power Integrated Sensing and Parametric Modeling. IEEE Trans. Instrum. Meas. 2020, 70, 1–11. [Google Scholar] [CrossRef]
- Babaeiyazdi, I.; Rezaei-Zare, A.; Shokrzadeh, S. State of charge prediction of EV Li-ion batteries using EIS: A machine learning approach. Energy 2021, 223, 120116. [Google Scholar] [CrossRef]
- Chevalier, S.; Auvity, B.; Olivier, J.C.; Josset, C.; Trichet, D.; Machmoum, M. Detection of Cells State-of-Health in PEM Fuel Cell Stack Using EIS Measurements Coupled with Multiphysics Modeling. Fuel Cells 2014, 14, 416–429. [Google Scholar] [CrossRef]
- Jungst, R.G.; Nagasubramanian, G.; Case, H.L.; Liaw, B.Y.; Urbina, A.; Paez, T.L.; Doughty, D.H. Accelerated calendar and pulse life analysis of lithium-ion cells. J. Power Sources 2003, 119, 870–873. [Google Scholar] [CrossRef]
- Stanciu, T.; Stroe, D.-I.; Teodorescu, R.; Swierczynski, M. Extensive EIS characterization of commercially available lithium polymer battery cell for performance modelling. In Proceedings of the 2015 17th European Conference on Power Electronics and Applications (EPE’15 ECCE-Europe), Geneva, Switzerland, 8–10 September 2015; pp. 1–10. [Google Scholar] [CrossRef]
- Windarko, N.A.; Choi, J.-H. SOC Estimation Based on OCV for NiMH Batteries Using an Improved Takacs Model. J. Power Electron. 2010, 10, 181–186. [Google Scholar] [CrossRef]
- Sathyanarayana, S.; Venugopalan, S.; Gopikanth, M.L. Impedance parameters and the state-of charge. I. Nickel-cadmium battery. J. Appl. Electrochem. 1979, 9, 125–139. [Google Scholar] [CrossRef]
- Bundy, K.; Karlsson, M.; Lindbergh, G.; Lundqvist, A. An electrochemical impedance spectroscopy method for prediction of the state of charge of a nickel-metal hydride battery at open circuit and during discharge. J. Power Sources 1998, 72, 118–125. [Google Scholar] [CrossRef]
- Karkuzhali, V.; Rangarajan, P.; Tamilselvi, V.; Kavitha, P. Analysis of battery management system issues in electric vehicles. IOP Conf. Ser. Mater. Sci. Eng. 2020, 994, 012013. [Google Scholar] [CrossRef]
- Hammouche, A.; Karden, E.; De Doncker, R.W. Monitoring state-of-charge of Ni–MH and Ni–Cd batteries using impedance spectroscopy. J. Power Sources 2004, 127, 105–111. [Google Scholar] [CrossRef]
- Olarte, J.; de Ilarduya, J.M.; Zulueta, E.; Ferret, R.; Kurt, E.; Lopez-Guede, J.M. Estimating State of Charge and State of Health of Vented NiCd Batteries with Evolution of Electrochemical Parameters. JOM 2021, 73, 4085–4090. [Google Scholar] [CrossRef]
- Reid, M.A. Impedance studies of nickel/cadmium and nickel/hydrogen cells using the cell case as a reference electrode. J. Power Sources 1990, 29, 467–476. [Google Scholar] [CrossRef]
- Blanchard, P. Electrochemical impedance spectroscopy of small Ni-Cd sealed batteries: Application to state of charge determinations. J. Appl. Electrochem. 1992, 22, 1121–1128. [Google Scholar] [CrossRef]
- Meddings, N.; Heinrich, M.; Overney, F.; Lee, J.-S.; Ruiz, V.; Napolitano, E.; Seitz, S.; Hinds, G.; Raccichini, R.; Gaberšček, M.; et al. Application of electrochemical impedance spectroscopy to commercial Li-ion cells: A review. J. Power Sources 2020, 480, 228742. [Google Scholar] [CrossRef]
- Mauracher, P.; Karden, E. Dynamic modelling of lead/acid batteries using impedance spectroscopy for parameter identification. J. Power Sources 1997, 67, 69–84. [Google Scholar] [CrossRef]
- Dai, H.; Jiang, B.; Wei, X. Impedance Characterization and Modeling of Lithium-Ion Batteries Considering the Internal Temperature Gradient. Energies 2018, 11, 220. [Google Scholar] [CrossRef] [Green Version]
- R-Smith, N.A.-Z.; Ragulskis, M.; Kasper, M.; Wagner, S.; Pumsleitner, J.; Zollo, B.; Groebmeyer, A.; Kienberger, F. Multiplexed 16 × 16 Li-Ion Cell Measurements Including Internal Resistance for Quality Inspection and Classification. IEEE Trans. Instrum. Meas. 2021, 70, 1–9. [Google Scholar] [CrossRef]
- Tuca, S.-S.; Badino, G.; Gramse, G.; Brinciotti, E.; Kasper, M.; Oh, Y.J.; Zhu, R.; Rankl, C.; Hinterdorfer, P.; Kienberger, F. Calibrated complex impedance of CHO cells andE.colibacteria at GHz frequencies using scanning microwave microscopy. Nanotechnology 2016, 27, 135702. [Google Scholar] [CrossRef]
- Piatek, Z.; Baron, B. Exact Closed Form Formula for Self Inductance of Conductor of Rectangular Cross Section. Prog. Electromagn. Res. M 2012, 26, 225–236. [Google Scholar] [CrossRef] [Green Version]
- Kasper, M.; Leike, A.; Thielmann, J.; Winkler, C.; R-Smith, N.A.-Z.; Kienberger, F. Electrochemical impedance spectroscopy error analysis and round robin on dummy cells and lithium-ion-batteries. J. Power Sources 2022, 536, 231407. [Google Scholar] [CrossRef]
- Qiao, S.; Hu, M.; Fu, C.; Qin, D.; Zhou, A.; Wang, P.; Lin, F. Experimental Study on Storage and Maintenance Method of Ni-MH Battery Modules for Hybrid Electric Vehicles. Appl. Sci. 2014, 9, 1742. [Google Scholar] [CrossRef] [Green Version]
- Cruz-Manzo, S.; Greenwood, P.; Chen, R. An Impedance Model for EIS Analysis of Nickel Metal Hydride Batteries. J. Electrochem. Soc. 2017, 164, A1446. [Google Scholar] [CrossRef] [Green Version]
- Cheng, S.; Zhang, J.; Zhao, M.; Cao, C. Electrochemical impedance spectroscopy study of Ni/MH batteries. J. Alloys Compd. 1999, 293–295, 814–820. [Google Scholar] [CrossRef]
- Wang, H.; Tahan, M.; Hu, T. Effects of rest time on equivalent circuit model for a li-ion battery. In Proceedings of the 2016 American Control Conference (ACC), Boston, MA, USA, 6–8 July 2016; pp. 3101–3106. [Google Scholar] [CrossRef]
- Łosiewicz, B.; Budniok, A.; Rówiński, E.; Łągiewka, E.; Lasia, A. The structure, morphology and electrochemical impedance study of the hydrogen evolution reaction on the modified nickel electrodes. Int. J. Hydrogen Energy 2004, 29, 145–157. [Google Scholar] [CrossRef]
- Agudelo, B.O.; Zamboni, W.; Monmasson, E. A Comparison of Time-Domain Implementation Methods for Fractional-Order Battery Impedance Models. Energies 2021, 14, 4415. [Google Scholar] [CrossRef]
- Chayambuka, K.; Mulder, G.; Danilov, D.L.; Notten, P.H. Determination of state-of-charge dependent diffusion coefficients and kinetic rate constants of phase changing electrode materials using physics-based models. J. Power Sources Adv. 2021, 9, 100056. [Google Scholar] [CrossRef]
- Krauskopf, T.; Mogwitz, B.; Hartmann, H.; Singh, D.K.; Zeier, W.G.; Janek, J. The Fast Charge Transfer Kinetics of the Lithium Metal Anode on the Garnet-Type Solid Electrolyte Li6.25Al0.25La3Zr2O12. Adv. Energy Mater. 2020, 10, 2000945. [Google Scholar] [CrossRef]
- Bard, A.J.; Faulkner, L.R. Electrochemical Methods; Wiley & Sons: New York, NY, USA, 1980. [Google Scholar]
- Amin, R.; Belharouak, I. Part-II: Exchange current density and ionic diffusivity studies on the ordered and disordered spinel LiNi0.5Mn1.5O4 cathode. J. Power Sources 2017, 348, 318–325. [Google Scholar] [CrossRef]
- KPL KPM KPH Ni-Cd Batteries. Saft Batteries|We Energize the World. 22 October 2020. Available online: https://www.saftbatteries.com/products-solutions/products/kpl-kpm-kph-ni-cd-batteries (accessed on 22 December 2021).
- Allebrod, F.; Chatzichristodoulou, C.; Mollerup, P.L.; Mogensen, M.B. Electrical conductivity measurements of aqueous and immobilized potassium hydroxide. Int. J. Hydrogen Energy 2012, 37, 16505–16514. [Google Scholar] [CrossRef]
- De Vidts, P.; White, R.E. Mathematical Modeling of a Nickel-Cadmium Cell: Proton Diffusion in the Nickel Electrode. J. Electrochem. Soc. 1995, 142, 1509. [Google Scholar] [CrossRef] [Green Version]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Zubaidi R-Smith, N.; Kasper, M.; Kumar, P.; Nilsson, D.; Mårlid, B.; Kienberger, F. Advanced Electrochemical Impedance Spectroscopy of Industrial Ni-Cd Batteries. Batteries 2022, 8, 50. https://doi.org/10.3390/batteries8060050
Al-Zubaidi R-Smith N, Kasper M, Kumar P, Nilsson D, Mårlid B, Kienberger F. Advanced Electrochemical Impedance Spectroscopy of Industrial Ni-Cd Batteries. Batteries. 2022; 8(6):50. https://doi.org/10.3390/batteries8060050
Chicago/Turabian StyleAl-Zubaidi R-Smith, Nawfal, Manuel Kasper, Peeyush Kumar, Daniel Nilsson, Björn Mårlid, and Ferry Kienberger. 2022. "Advanced Electrochemical Impedance Spectroscopy of Industrial Ni-Cd Batteries" Batteries 8, no. 6: 50. https://doi.org/10.3390/batteries8060050
APA StyleAl-Zubaidi R-Smith, N., Kasper, M., Kumar, P., Nilsson, D., Mårlid, B., & Kienberger, F. (2022). Advanced Electrochemical Impedance Spectroscopy of Industrial Ni-Cd Batteries. Batteries, 8(6), 50. https://doi.org/10.3390/batteries8060050






