SOC Estimation of a Rechargeable Li-Ion Battery Used in Fuel Cell Hybrid Electric Vehicles—Comparative Study of Accuracy and Robustness Performance Based on Statistical Criteria. Part II: SOC Estimators
Abstract
1. Introduction
2. State of the Art of Li-Ion Battery SOC Estimation Kalman Filter Techniques
3. Li-Ion Battery SOC—Adaptive and Particle Filter Estimators
3.1. Adaptive Extended Kalman Filter (AEKF) Overview Presentation
- Scenario R0—SOC estimator accuracy based on the SOC residual curve, for an SOC initial value SOCini = 70% (i.e., same as the advanced vehicle simulator (ADVISOR) SOC estimated value) and the statistical criteria values, i.e., RMSE, MSE, MAE, std, MAPE and R-squared, given in Table 1.
- Scenario R1—SOC estimator robustness to changes in initial SOC value, SOCini = 0.4. The MATLAB simulation results are shown in Appendix A.1, and the statistical criteria values are provided in Appendix A.2, Table A1.
- Scenario R2—SOC estimator robustness to simultaneous changes, i.e., SOCini = 1 and battery ageing effects (a decrease in battery capacity by 30%, i.e., Qnom decreases from 6 Ah to 4.2 Ah). The MATLAB simulation results are shown in the main part of the manuscript, and statistical criteria values are given in Appendix A.2, Table A2.
- Scenario R3—SOC estimator robustness to simultaneous changes, namely in SOCini (SOCini = 0.4) and to 10 times increase in measurement noise level (e.g., σ = 0.01). The MATLAB simulation results are shown in Appendix A.1, and the statistical criteria values are given in Appendix A.2, Table A3.
- Scenario R4—SOC estimator robustness to simultaneous changes, such as in SOCini (SOCini = 0.2), temperature effects on internal resistance Rin and polarization constant Kp (only for Simscape Li-ion battery model) to changes in ambient temperature ( °C), as is shown in Part 1 [20], p. 12 for thermal model.
3.1.1. MATLAB Simulation Results for 3RC ECM Battery Model—Accuracy and Robustness Scenarios
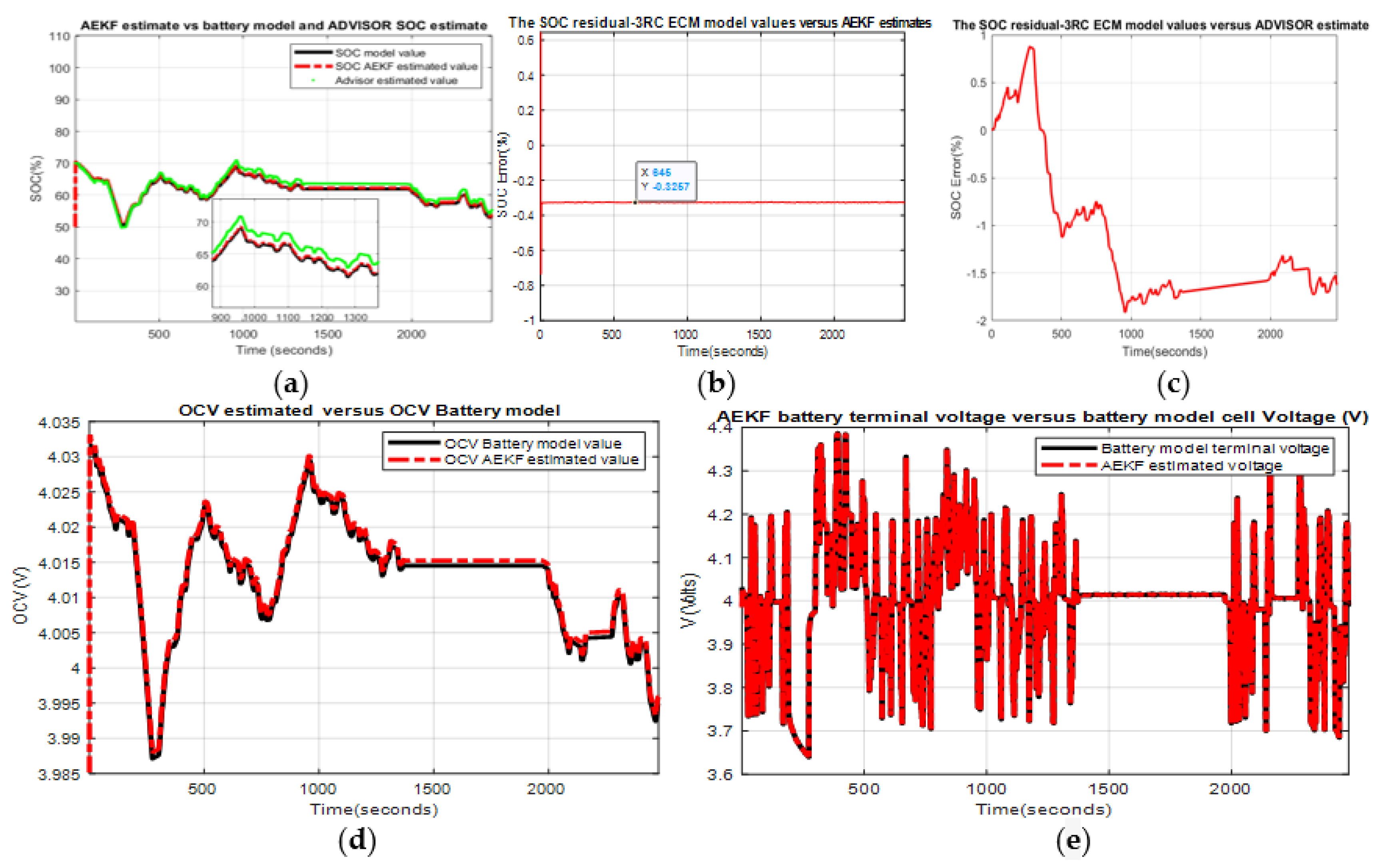
- Scenario R0. The MATLAB simulation results for this scenario are shown in Appendix A.1, Figure A12a–c, and the statistical criteria values are given in Table 1.Performance analysis:
- ○
- SOC of high accuracy and a great battery output voltage prediction.
- ○
- The residual error is quite close to 1.5%, which is comparable to the results reported in the literature.
- Scenario R1. The MATLAB simulation results for the first scenario are presented in Appendix A.1, Figure A13a–c, and the statistical criteria values are given in Appendix A.2, Table A1.Performance analysis:
- ○
- The simulation results reveal excellent SOC accuracy and a great robustness to changes in the initial SOC value.
- ○
- The steady-state residual error is quite close to zero, which is an excellent result.
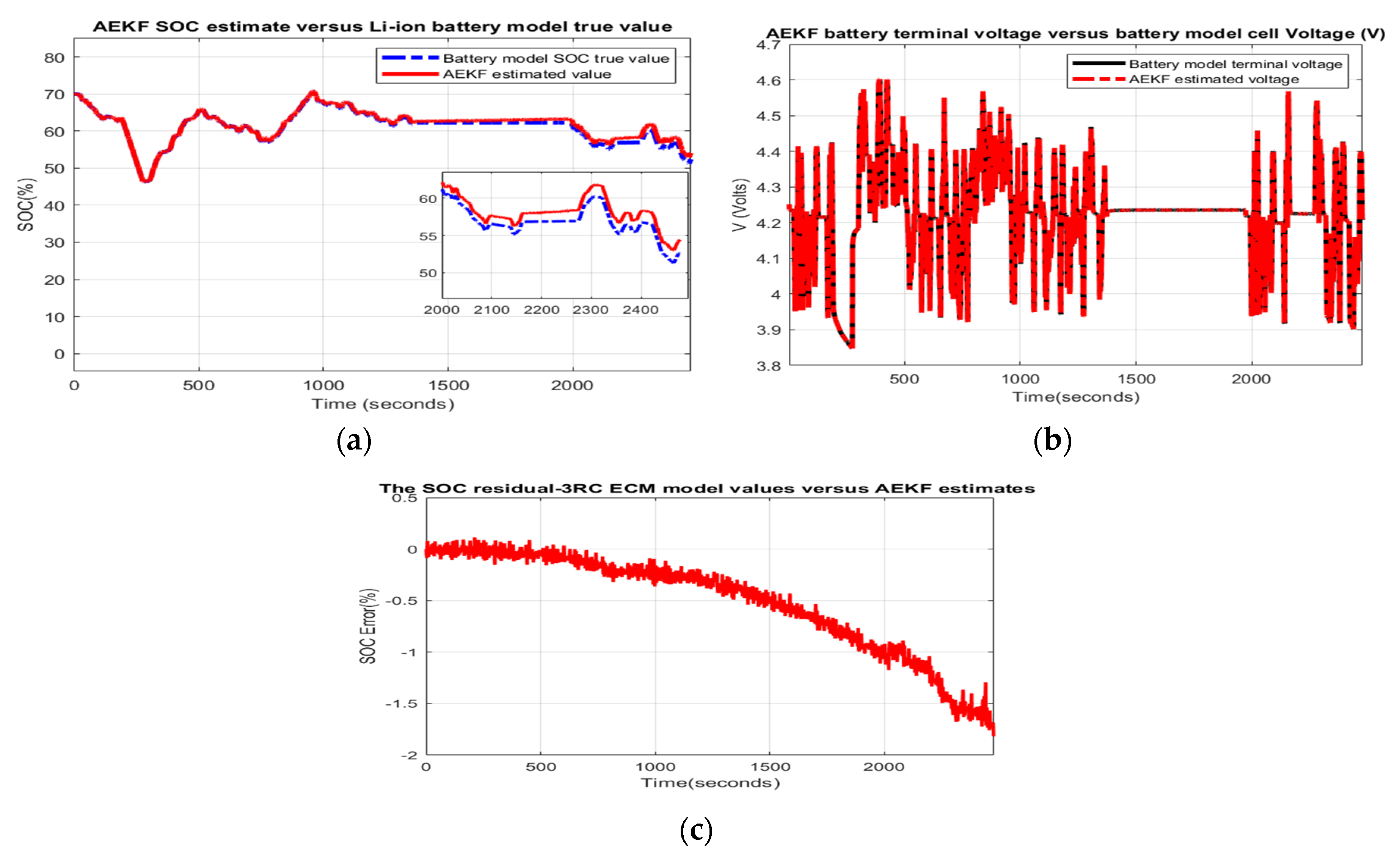
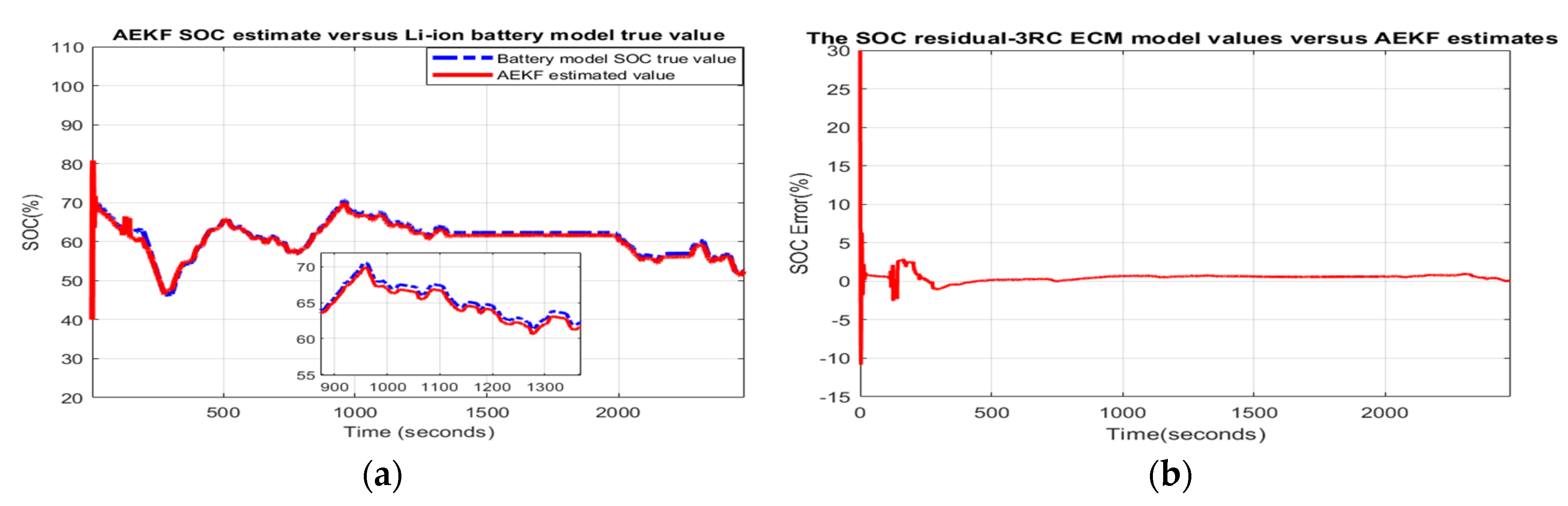
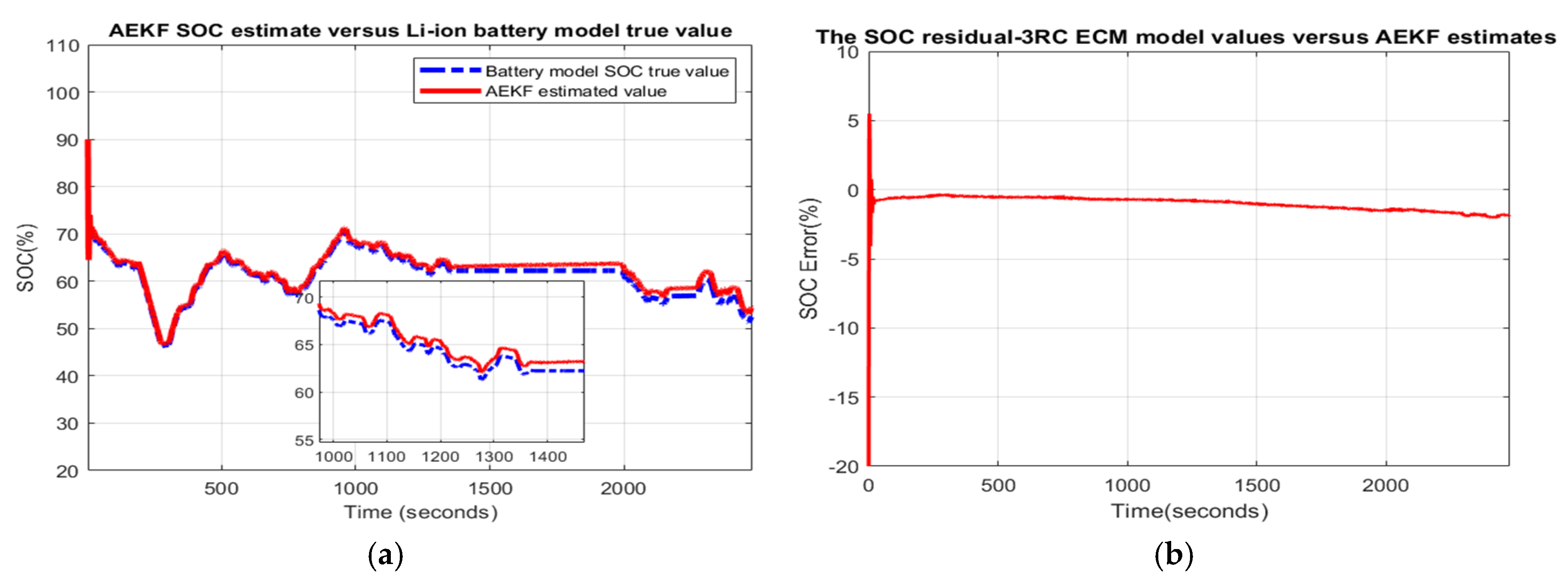
- Scenario R2. The MATLAB simulation results for the second scenario are depicted in Figure 2 and statistical criteria values are given in Appendix A.2, Table A2.Performance analysis:
- ○
- The SOC accuracy is good and the robustness to ageing effects is great.
- ○
- The steady-state residual error converges to −2%, which is a good result.
- Scenario R3. The MATLAB simulation results for the third scenario are shown in Appendix A.1, Figure A14a–c, and the statistical criteria values are given in Appendix A.2, Table A3.Performance analysis:
- ○
- The SOC accuracy is bad and the robustness to an increased noise level is bad.
- ○
- The steady-state residual error converges to −11%, which is a bad performance.
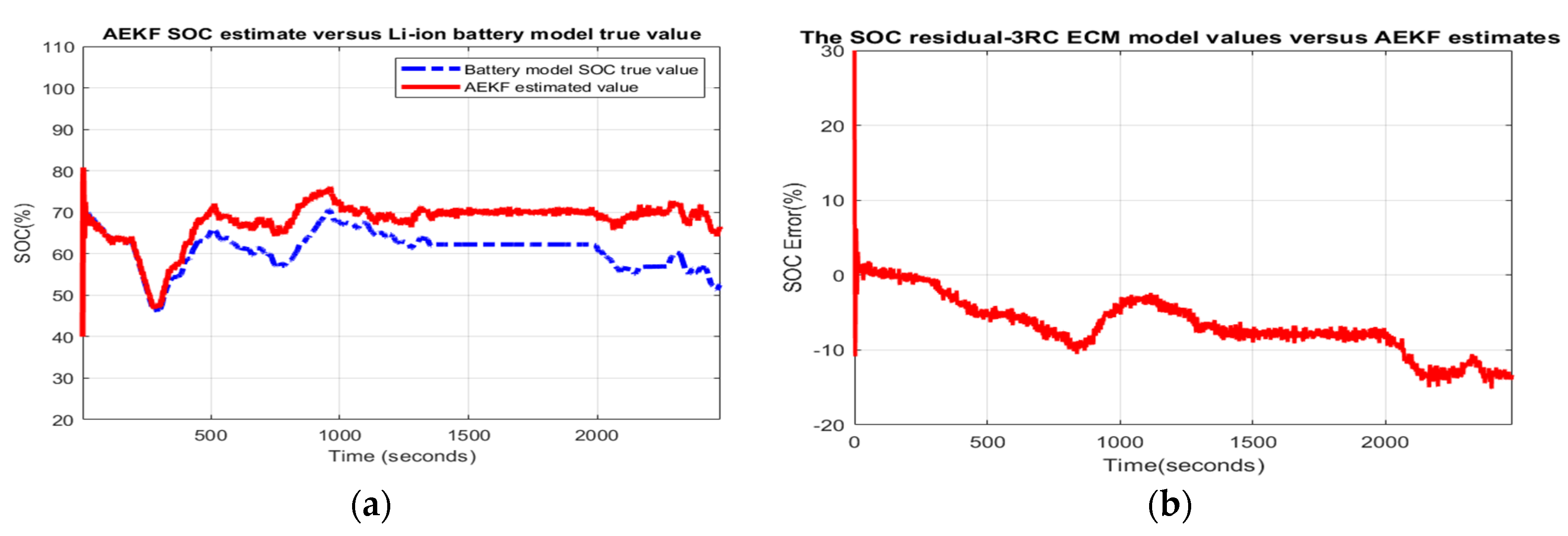
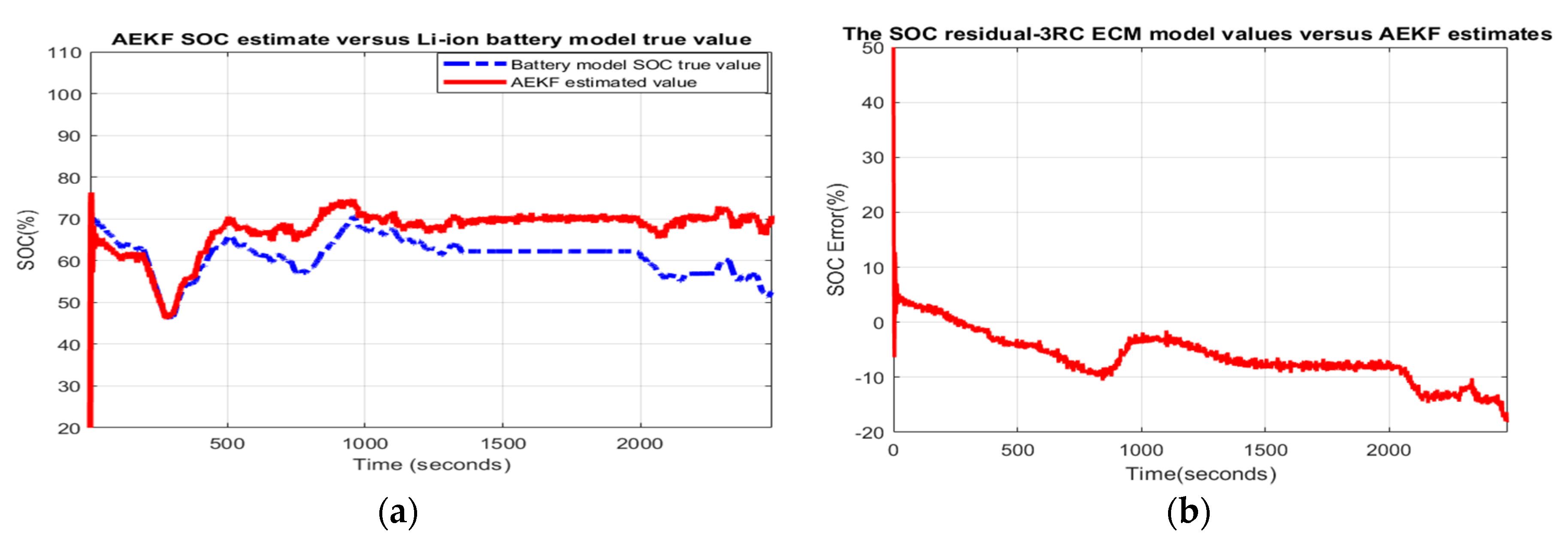
- Scenario R4: The MATLAB simulation results for the fourth scenario are shown in Figure 3 and the statistical criteria values are given in Appendix A.2, Table A4.Performance analysis:
- ○
- The SOC accuracy is bad and the robustness to temperature effects is bad.
- ○
- The steady-state residual error converges to −18%, which is a bad performance.
3.1.2. MATLAB Implementation and Simulation Results for Simulink Simscape Battery Model—Accuracy and Robustness Scenarios
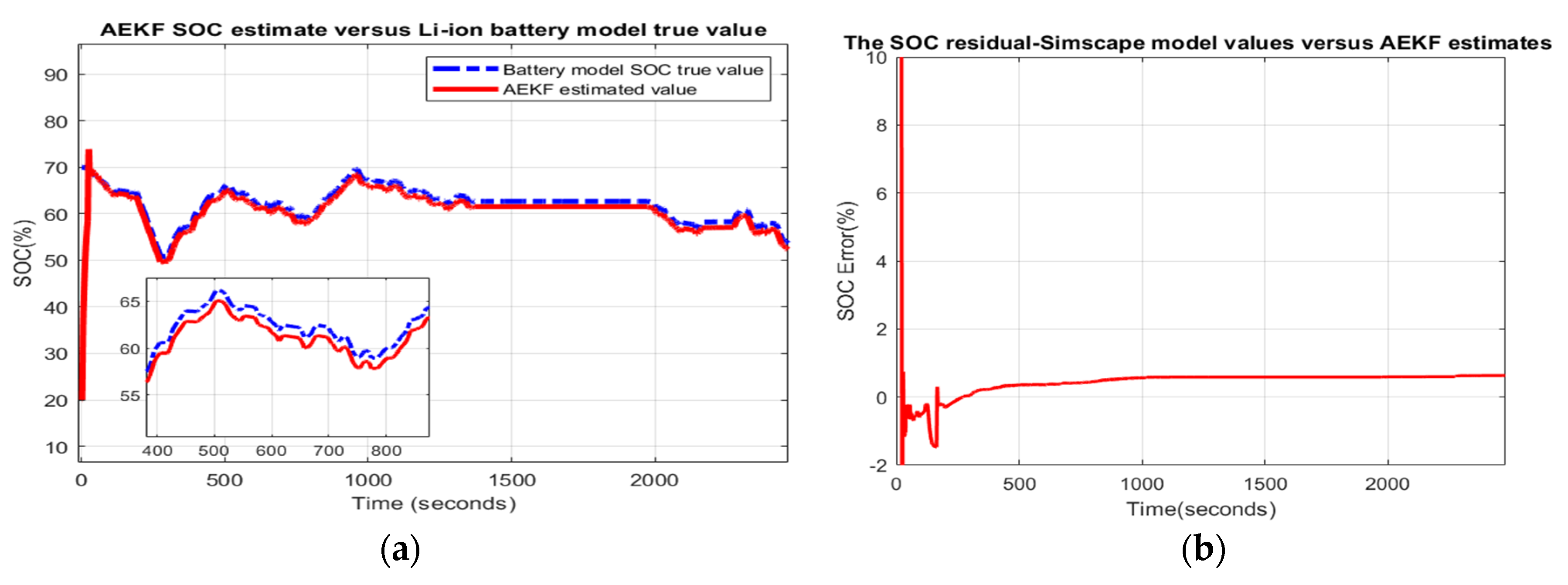
- Scenario R0. The MATLAB simulation results for this scenario are depicted in Appendix A.1, Figure A15a–c, and the statistical criteria values are given in Table 1.Performance analysis:
- ○
- SOC accuracy is excellent and battery output voltage prediction is great.
- ○
- The residual error is quite close to 0.4%, which is very good result.
- Scenario R1. The MATLAB simulation results for first scenario are exposed in Appendix A.1, Figure A16a–c, and the statistical criteria values are given in Appendix A.2, Table A1.Performance analysis:
- ○
- SOC accuracy is excellent and the robustness to changes in the SOCini is great.
- ○
- The residual error has some variations near the origin but is quite close to zero in steady state, which is very good result.
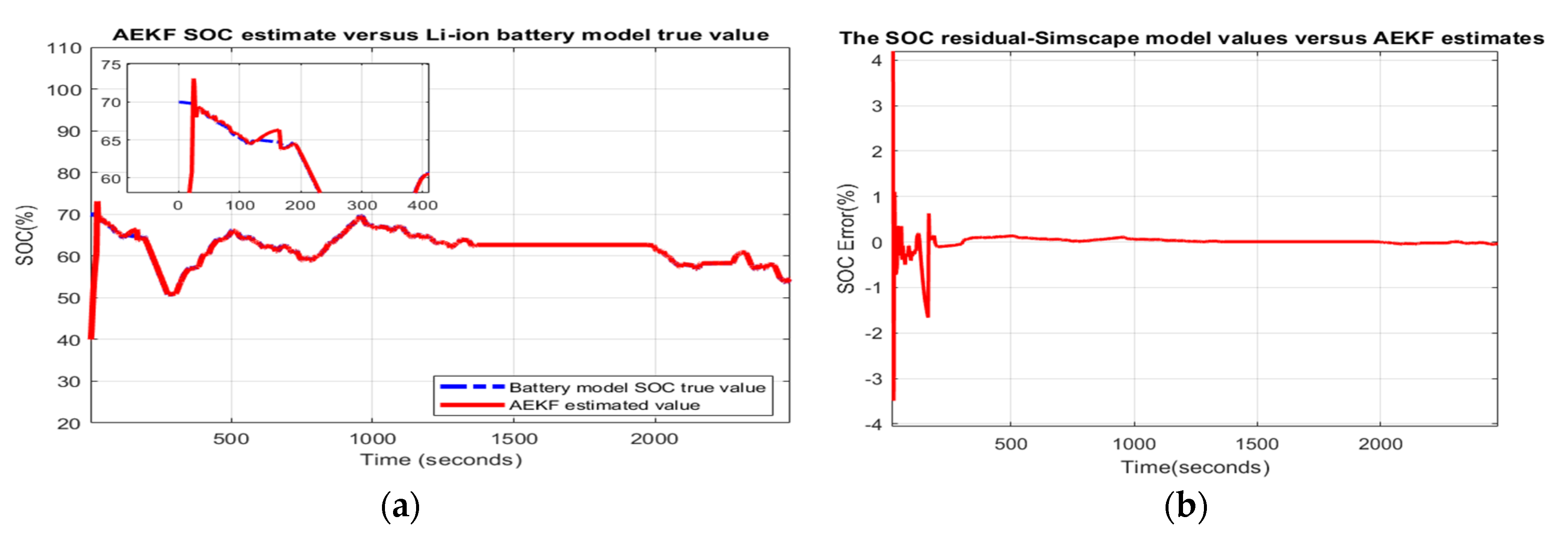
- Scenario R2. The MATLAB simulation results for the second scenario are visible in Figure 4 and statistical criteria values are given in Appendix A.2, Table A2.Performance analysis:
- ○
- SOC accuracy is good and robustness to ageing effects is great.
- ○
- The residual error is quite close to 2% in steady state, which is a good result
- Scenario R3. The MATLAB simulation results for the third scenario are shown in Appendix A.1, Figure A17a–c, and the statistical criteria values are given in Appendix A.2, Table A3.Performance analysis:
- ○
- SOC accuracy is good and robustness to noise level is great.
- ○
- The residual error has some variations near origin and in steady state it is quite close to 2%, which is a good result.
- Scenario R4. The MATLAB simulation results for the fourth scenario are depicted in Figure 5 and the statistical criteria values are given in Appendix A.2, Table A4.Performance analysis:
- ○
- SOC accuracy is good and robustness to temperature effects is great.
- ○
- The residual error is quite close to 0% in steady state, which is an excellent result.
3.2. Adaptive Unscented Kalman Filter (AUKF)
- 1.1
- The Simscape model is given by a set of two equations described in Part 1 [20], p. 20.
- 1.2
- The 3RC ECM is given by a compact set in a matrix representation, as is shown in Part 1 [20], p. 12.
- 1.3
- Model general formulation:
- 3.1
- Generate sigma points and weighting coefficients at time
- 4.1
- State estimate time update:
- 5.1
- Update the covariance output matrix and cross-covariance matrix.
- 5.2
- Compute the Kalman filter gain:
- 5.3
- State estimate update:
- 5.4
- State covariance matrix estimate update:
- 6.1
- Compute the output error:
- 6.2
- Compute the adjustment coefficient:
- 6.3
- Compute the covariance matrix of process noise:
- 6.4
- Compute the covariance matrix of the measurement noise:
- For the 3RC ECM Li-ion battery model: α = 0.05; β = 2 (optimal value); k = −1; L = 150; qw = I4×4(unity matrix); rv = 0.1; Px = 10−10 I4x4; SOCini = 70 (%); VarY = 0.001 (the variance of the noise level in the measurement output dataset used to test the robustness); η = 0.78 for charging cycle; and η = 0.9 for discharging cycle.
- For the Li-ion battery Simscape model: α = 1; β = 2 (optimal value); k = 0; L = 300; qw = 0.0001; rv = 0.00019; Px = 10−10; SOCini = 70 (%); VarY = 0.001; η = 0.765 for charging cycle; and η = 0.865 for discharging cycle.
3.2.1. MATLAB Implementation and Simulation Results for 3RC ECM Battery Model-AUKF SOC Estimator Accuracy and Robustness Scenarios
- Scenario R0. The MATLAB simulation results are shown in Appendix A.1, Figure A18a–c, and the statistical criteria values are given in Table 1.Performance analysis:
- ○
- SOC accuracy is great and battery output voltage prediction is excellent.
- ○
- The residual error is quite close to 0.6%, which is an excellent result.
- Scenario R1. The MATLAB simulations result are shown in Appendix A.1, Figure A19a,b, and the statistical criteria values are given in Appendix A.2, Table A1.Performance analysis:
- ○
- SOC of high accuracy.
- ○
- The residual error is quite close to 0.5%, which is an excellent result.
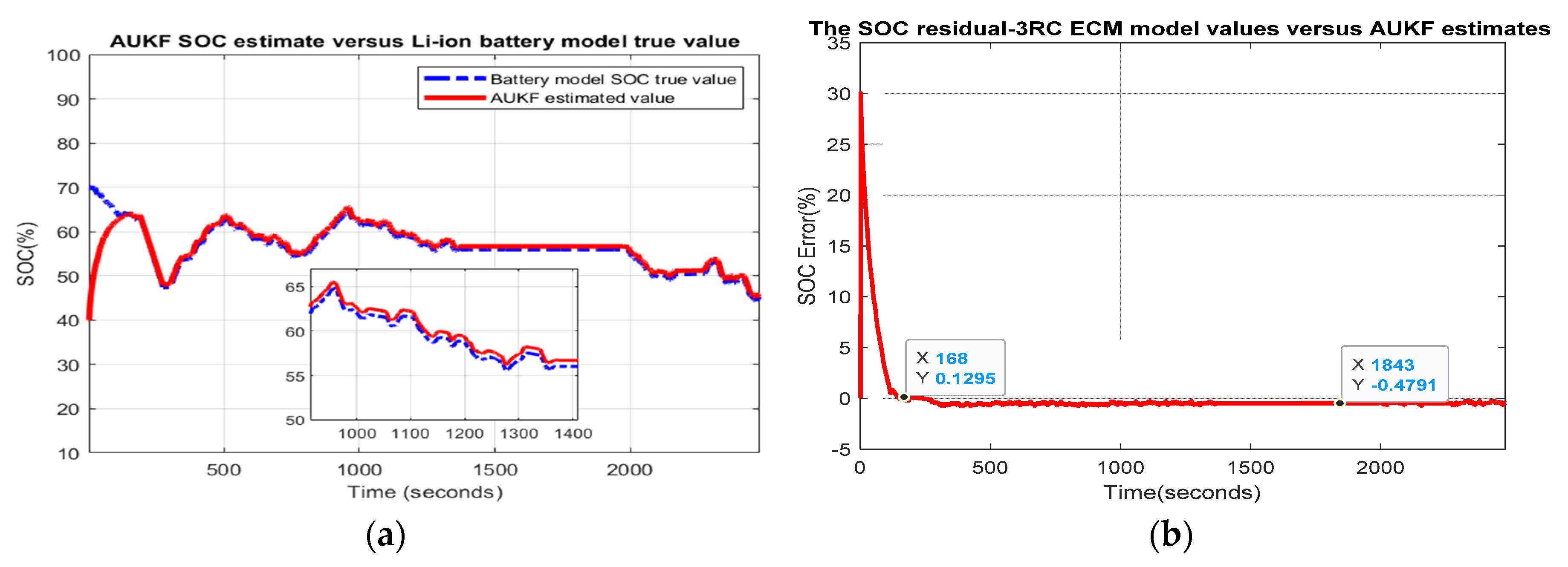
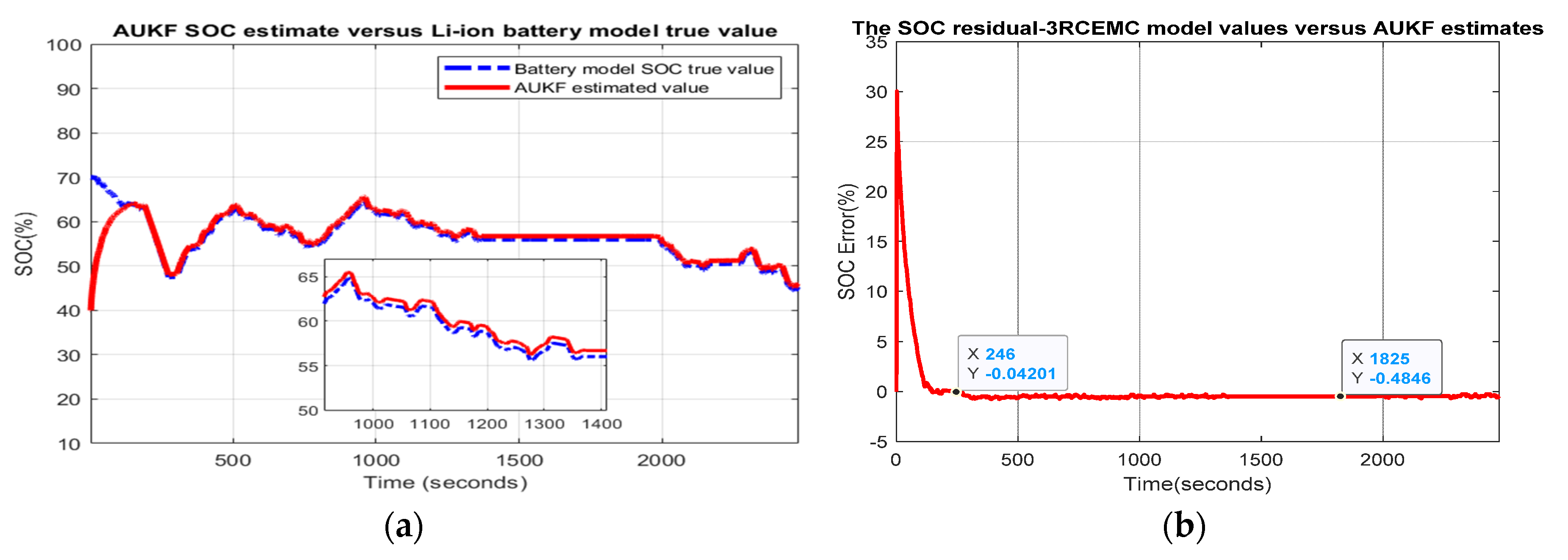
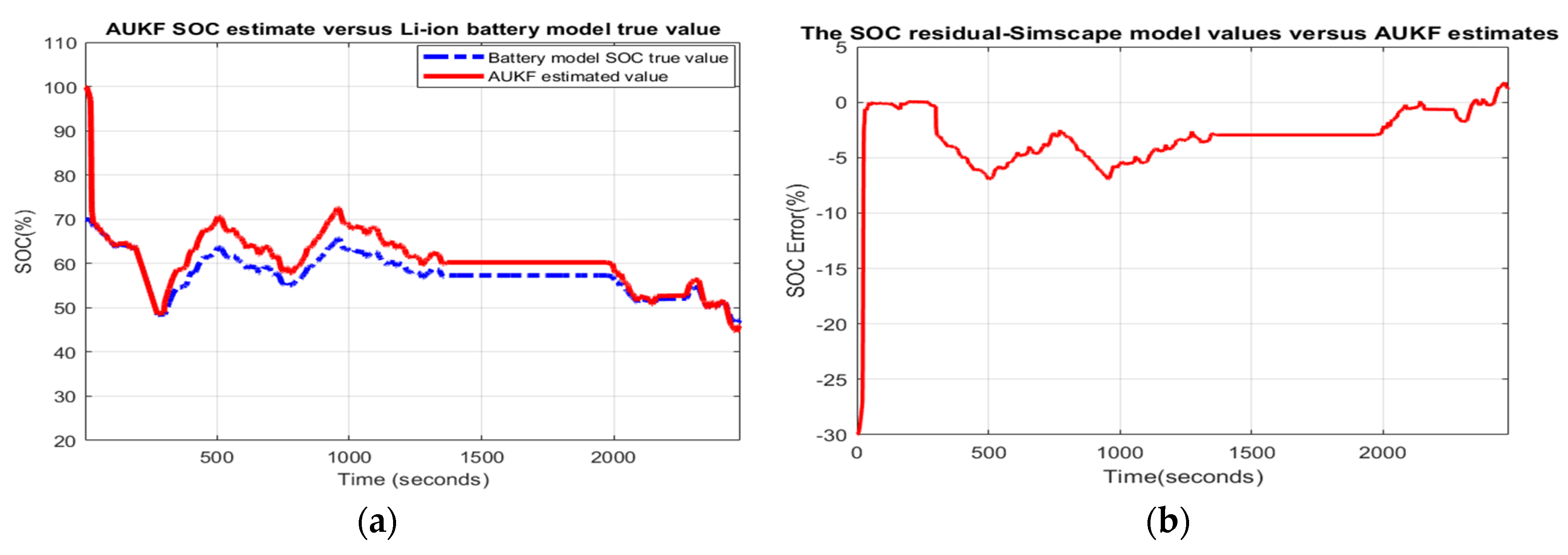
- Scenario R2. The MATLAB simulation results are shown in Figure 6, and statistical criteria values are given in Appendix A.2, Table A2.Performance analysis:
- ○
- SOC accuracy is good.
- ○
- The residual error is quite close to 5%, which is a weak performance.
- Scenario R3. The MATLAB simulation results are shown in Appendix A.1, Figure A20a–c, and the statistical criteria values are given in Appendix A.2, Table A3.Performance analysis:
- ○
- SOC accuracy is great.
- ○
- The residual error is quite close to 0.48%, which is excellent.
- Scenario R4. The MATLAB simulations result for fourth scenario is depicted in Figure 7a,b and the statistical criteria values are given in Appendix A.2, Table A4.Performance analysis:
- ○
- SOC accuracy is great.
- ○
- The residual error is quite close to zero in steady state, so an excellent result.
3.2.2. MATLAB Implementation and Simulation Results for Simulink Simscape Battery Model—AUKF SOC Estimator Accuracy and Robustness Scenarios
- Scenario R0. The MATLAB simulation results for this scenario are shown in Appendix A.1, Figure A21a–c, and the statistical criteria values are given in Table 1.Performance analysis:
- ○
- SOC accuracy is great and battery output voltage prediction is excellent.
- ○
- The residual error is quite close to 2%, which is a great result.
- Scenario R1. The MATLAB simulation results for the first scenario are depicted in Appendix A.1, Figure A22a–c, and the statistical criteria values are given in Appendix A.2, Table A1.Performance analysis:
- ○
- SOC accuracy is great.
- ○
- The residual error is quite close to 2%, which is an excellent result.
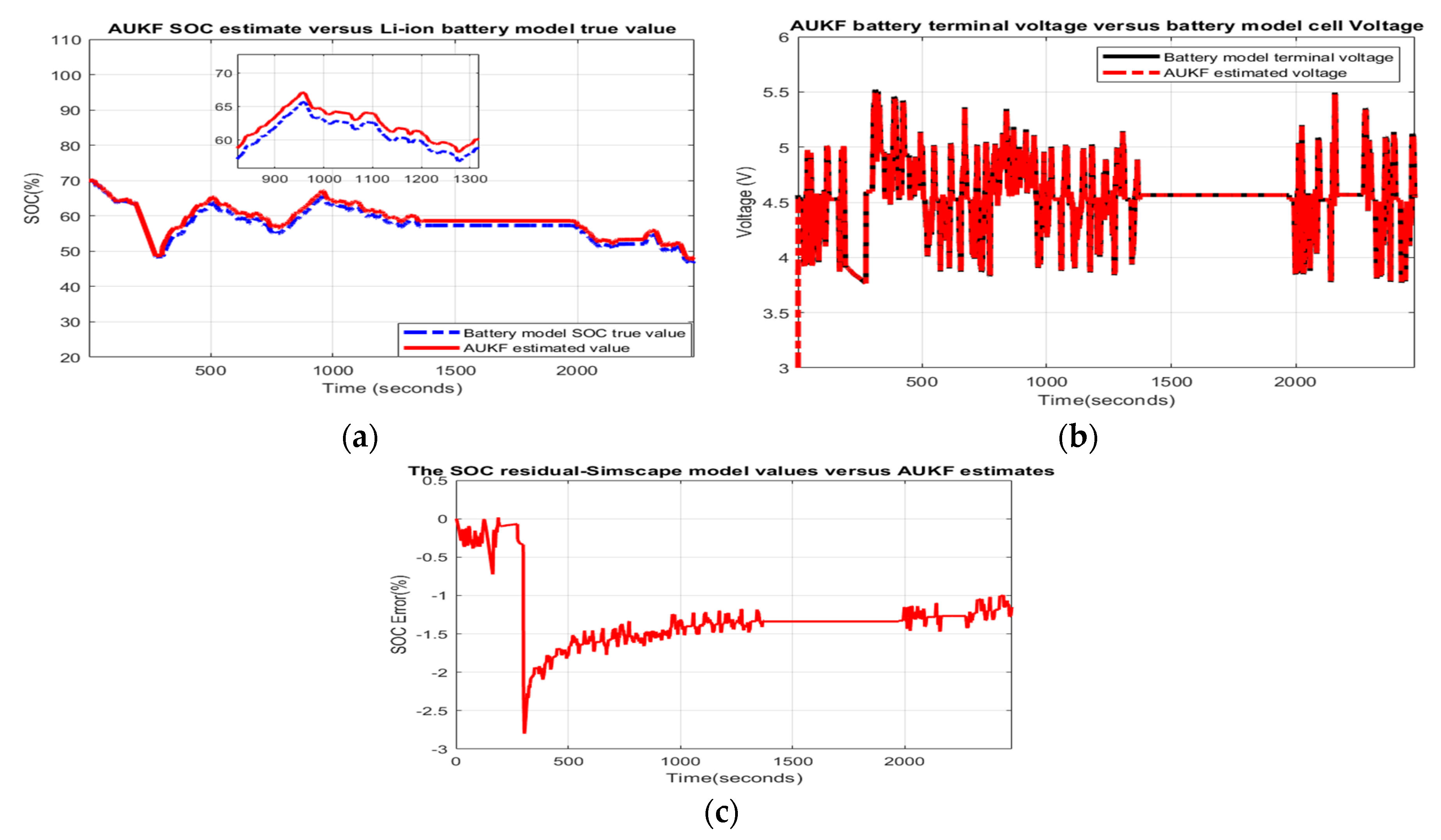
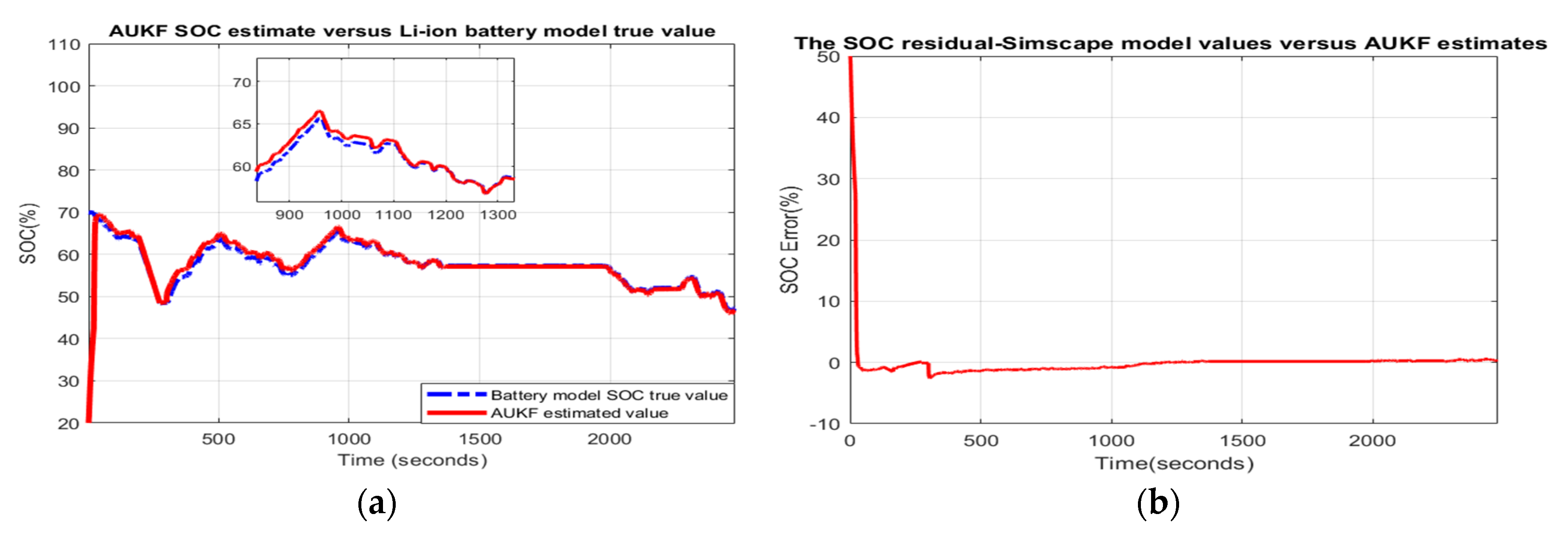
- Scenario R2. The MATLAB simulation results for the second scenario are visible in Figure 8 and statistical criteria values are given in Appendix A.2, Table A2.Performance analysis:
- ○
- SOC accuracy is good.
- ○
- The residual error is quite close to 7%, which is a bad result.
- Scenario R3. The MATLAB simulation results for third scenario are shown in Appendix A.1, Figure A23a–c, and the statistical criteria values are given in Appendix A.2, Table A3.Performance analysis:
- ○
- SOC accuracy is great.
- ○
- The residual error is quite close to 1%, which is excellent.
- Scenario R4. The MATLAB simulation results for the fourth scenario are depicted in Figure 9 and the statistical criteria values are given in Appendix A.2, Table A4.Performance analysis:
- ○
- SOC accuracy is great.
- ○
- The residual error is quite close to 1.2%, so is excellent.
3.3. Particle Filter SOC Estimator
3.4. PFE SOC Brief Presentation
3.5. PFE SOC Parameters’ Setup
- For the 3RC ECM Li-ion battery model: Np = 1000 (total number of particles); qw = 10−6I4×4 (I4×4 is a 4×4 identity matrix) in scientific notation (process state variables noise covariance matrix); rv = 0.0001 (measurement output noise); SOCini = 70 (%); VarY = 0.001 (variance of the noise level in the measurement output dataset used to test the robustness); VarX1 = VarX2 = VarX3 = VarX4 = 0.01 (variance in the initial values of the states variables); η = 0.8 for charging cycle; and η = 0.82 for discharging cycle.
- For the Li-ion battery Simscape model: Np = 1000 (total number of particles); qw =10−7 for SOC covariance noise; rv = 0.0001 (measurement output noise level); SOCini = 70 (%); VarY = 0.001 (the variance of the noise level in the measurement output dataset used to test the robustness); VarX1 = 0.004 (variance in SOCini); η = 0.76 for charging cycle; and η = 0.78 for discharging cycle.
3.6. MATLAB Simulation Results for 3RC ECM Battery Model—PFE SOC Estimator Accuracy and Robustness Scenarios
- Scenario R0. The MATLAB simulation results for this scenario are shown in Appendix A.1, Figure A24a–c, and the statistical criteria values are given in Table 1.Performance analysis:
- ○
- SOC accuracy is good and battery output voltage prediction is good.
- ○
- The residual error is quite close to 8%, which is weak.
- Scenario R1. The MATLAB simulation results for the first scenario are shown in Appendix A.1, Figure A25a–c, and the statistical criteria values are given in Appendix A.2, Table A1.Performance analysis:
- ○
- SOC accuracy is good.
- ○
- The residual error is quite close to 10%, which is weak.
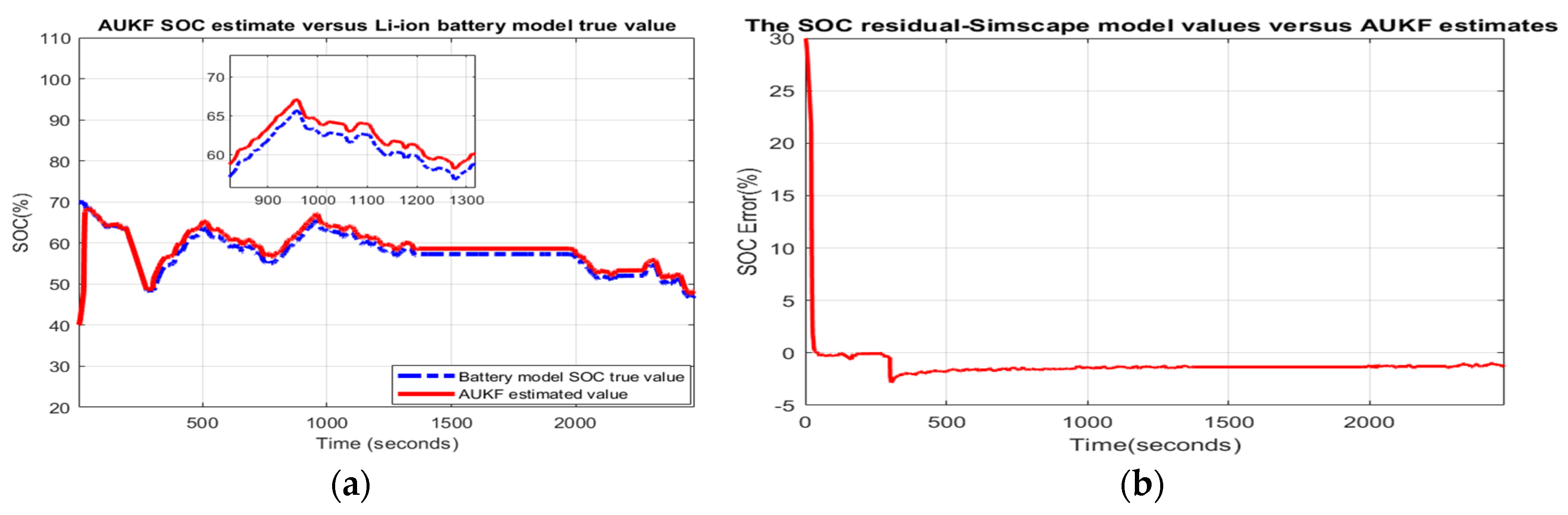
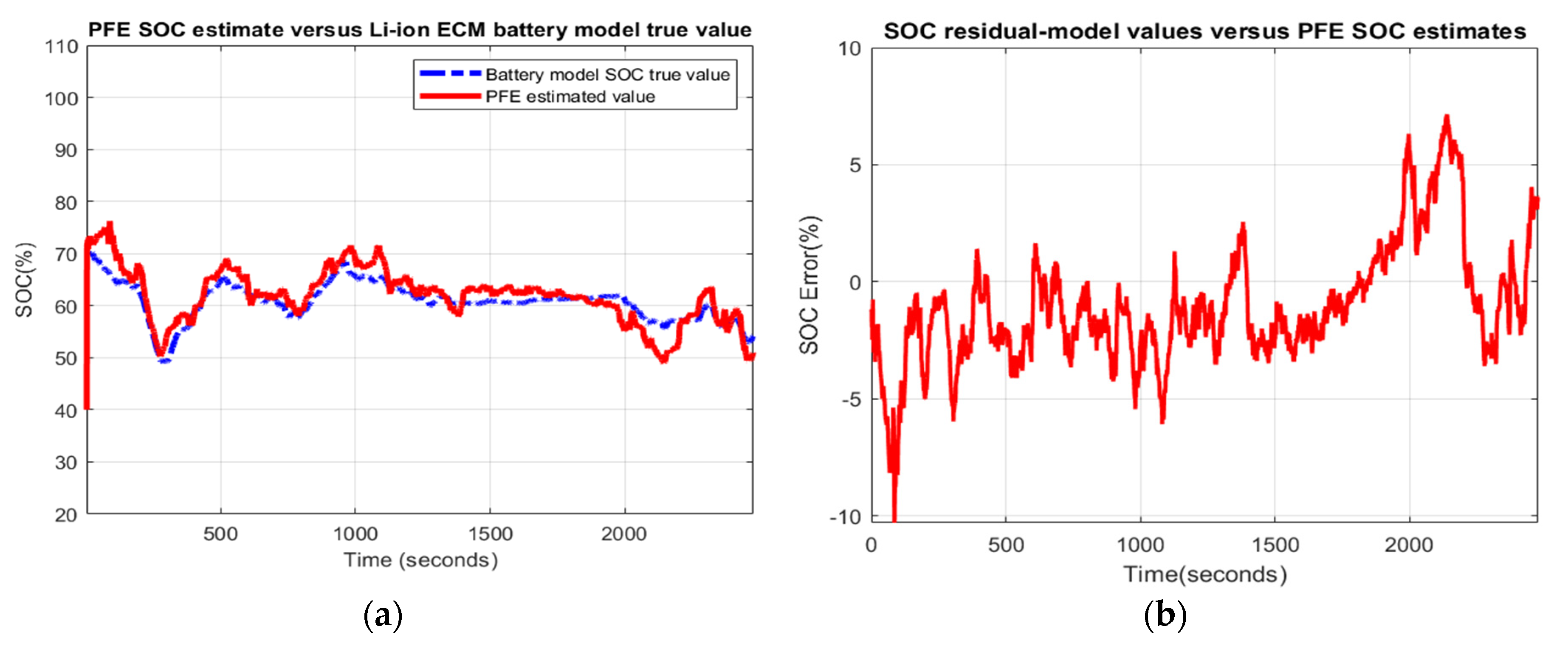
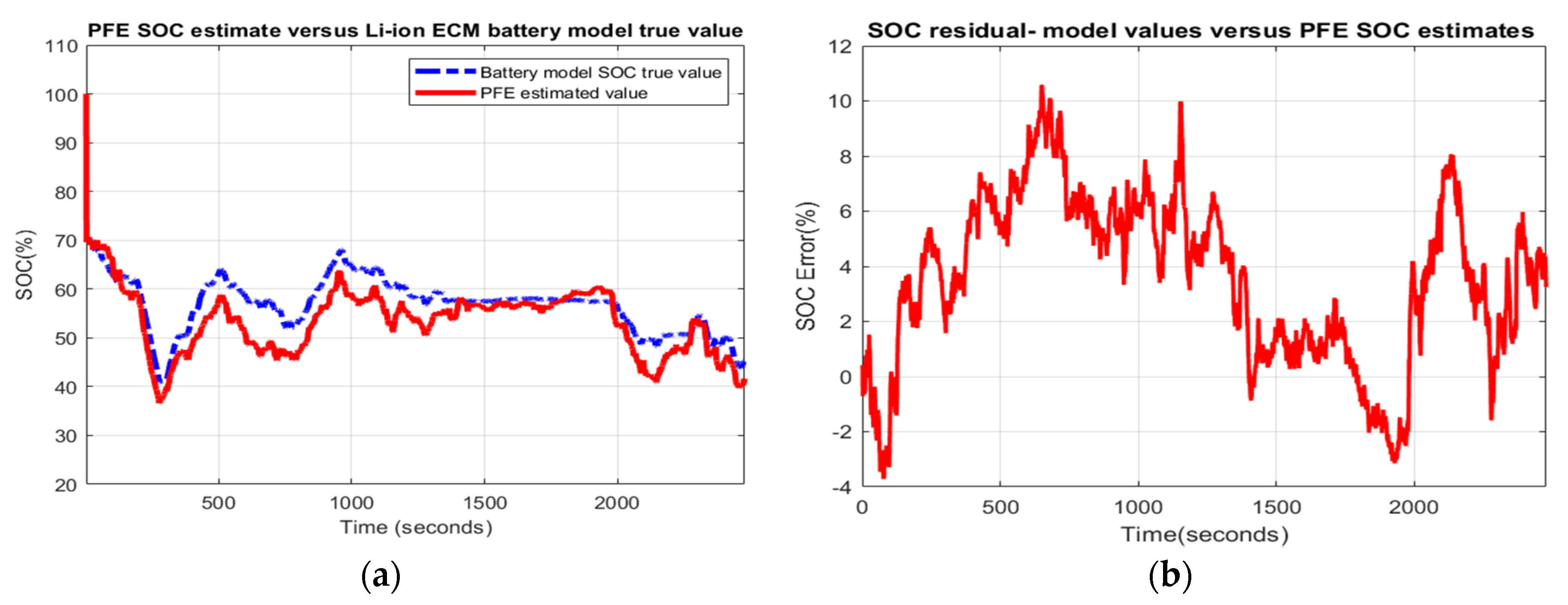
- Scenario R2. The MATLAB simulation results for the second scenario are visible in Figure 10 and statistical criteria values are given in Appendix A.2, Table A2.Performance analysis:
- ○
- SOC accuracy is weak.
- ○
- The residual error is quite close to 10%, which is bad.
- Scenario R3. The MATLAB simulation results for the third scenario are revealed in Appendix A.1, Figure A26a–c, and the statistical criteria values are given in Appendix A.2, Table A3.Performance analysis:
- ○
- SOC accuracy is good.
- ○
- The residual error is quite close to 4%, which is weak.
- Scenario R4. The MATLAB simulation results for fourth scenario are depicted in Figure 11 and the statistical criteria values are given in Appendix A.2, Table A4.Performance analysis:
- ○
- SOC accuracy is weak.
- ○
- The residual error is quite close to 20%, which is bad.
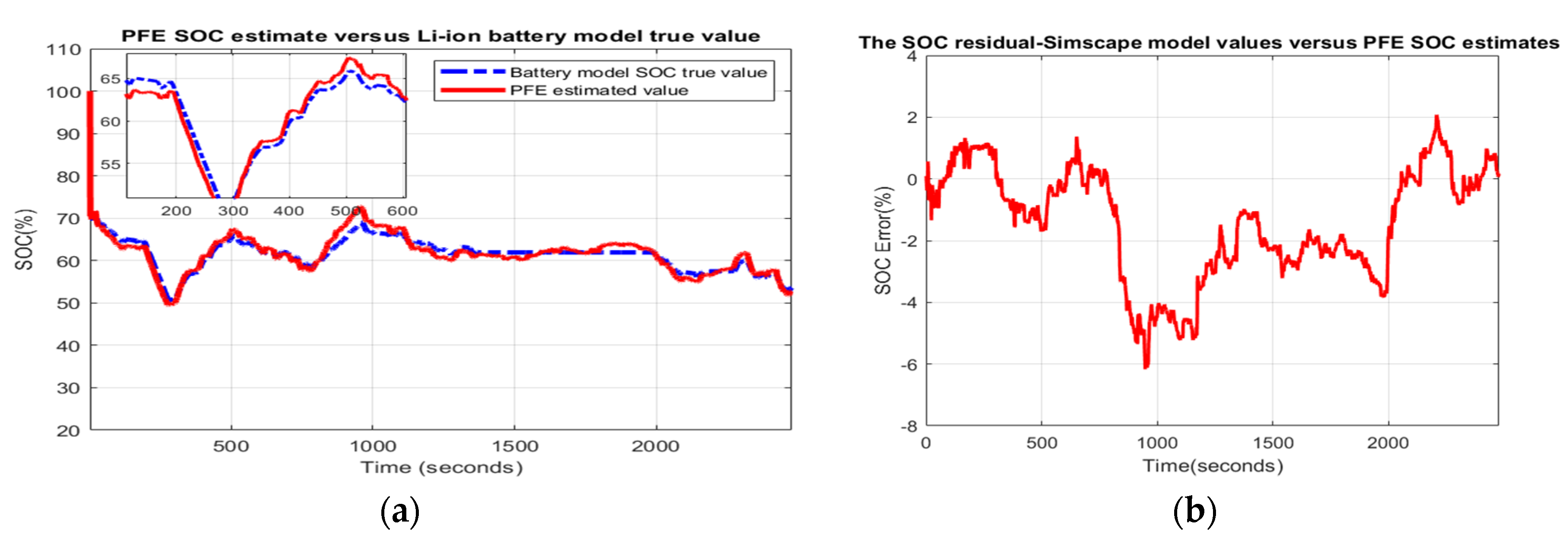
3.7. MATLAB Simulation Results for Simulink Simscape Battery Model—PFE SOC Estimator Accuracy and Robustness Scenarios
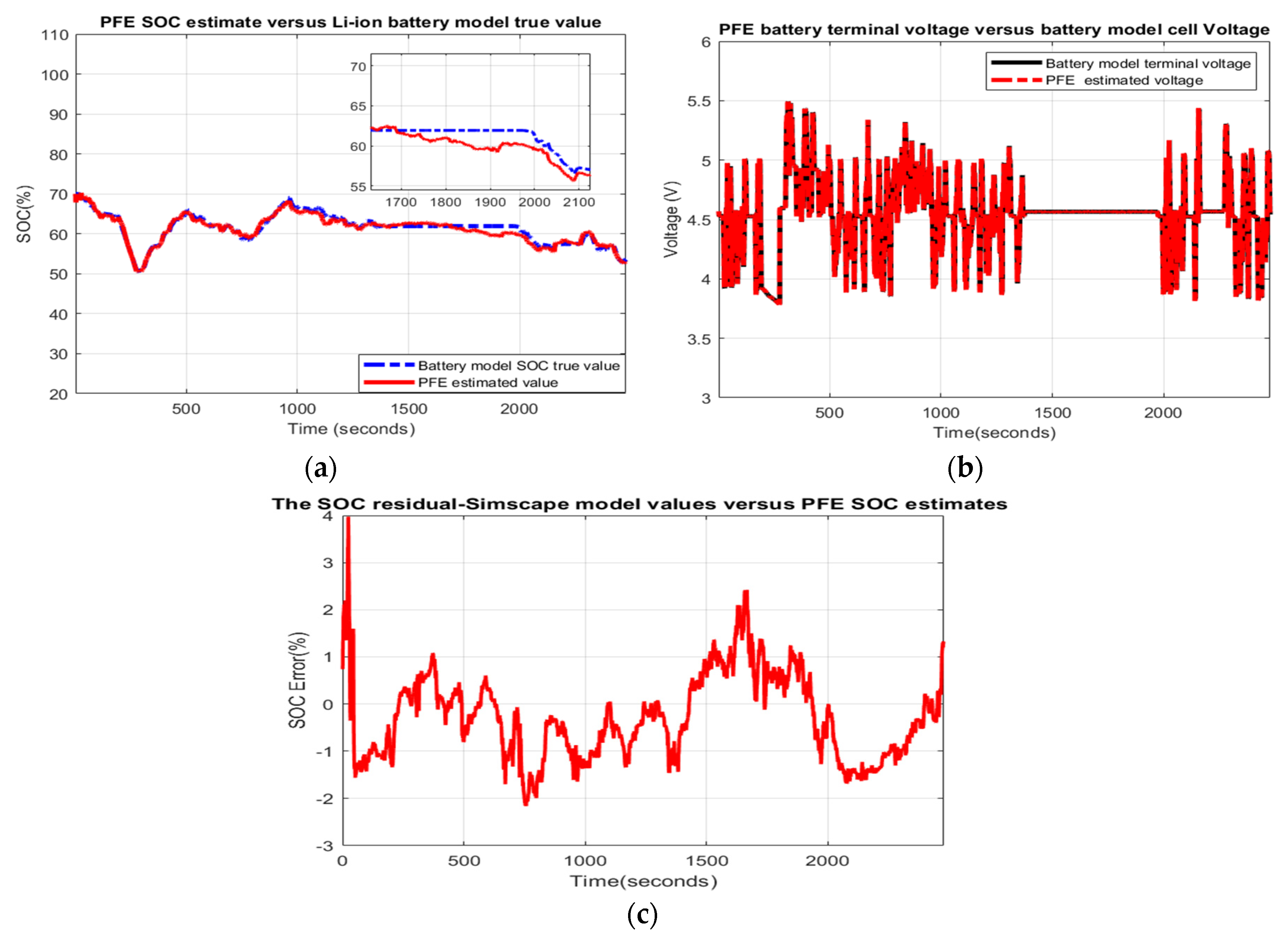
- Scenario R0. The MATLAB simulation results for this scenario are shown in Appendix A.1, Figure A27a–c, and the statistical criteria values are given in Table 1.Performance analysis:
- ○
- SOC accuracy is good.
- ○
- The residual error is quite close to 4%, which is weak.
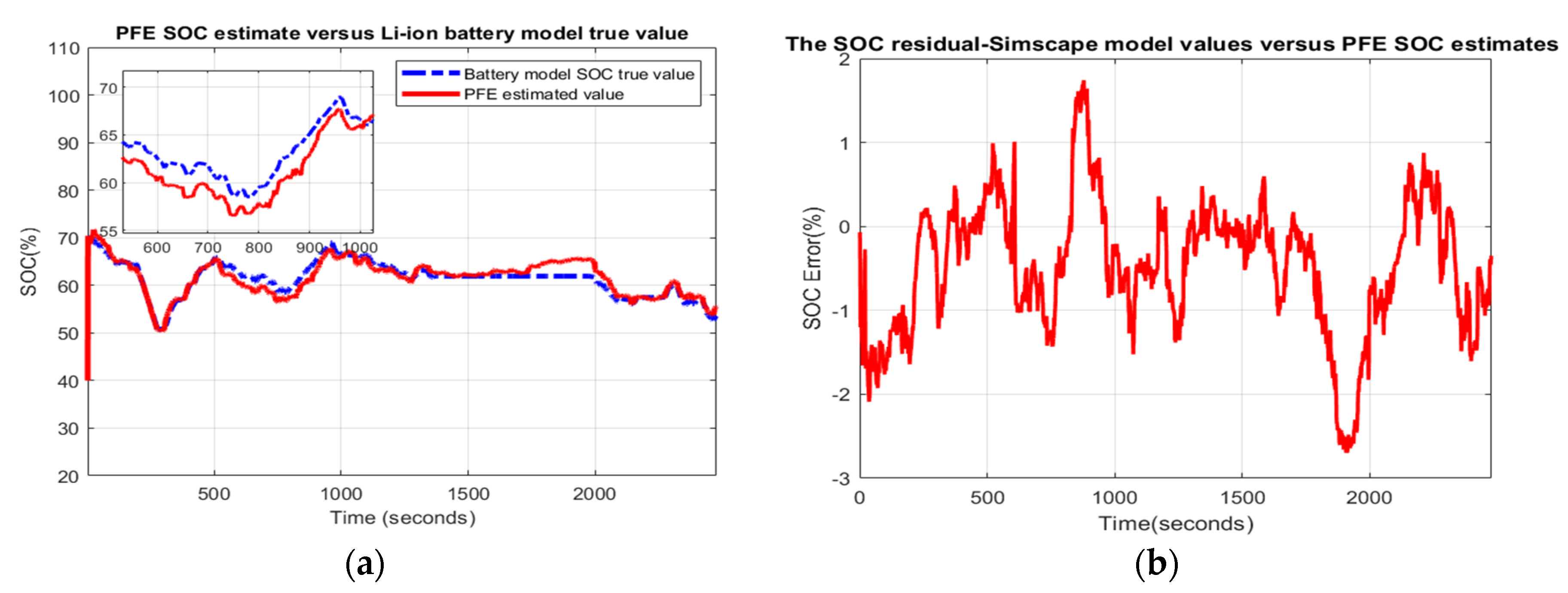
- Scenario R1. The MATLAB simulation results for the first scenario are revealed in Appendix A.1, Figure A28a–c, and the statistical criteria values are given in Appendix A.2, Table A1.Performance analysis:
- ○
- SOC accuracy is good.
- ○
- The residual error is quite close to 2%, which is good.
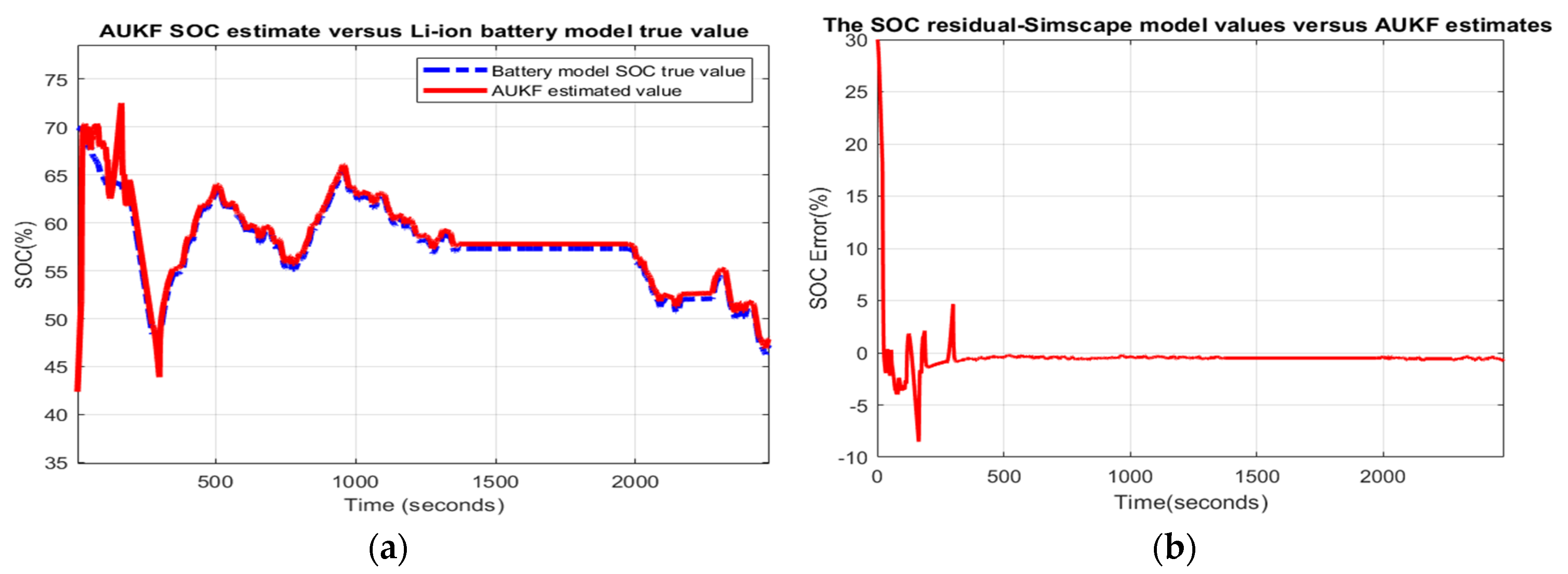
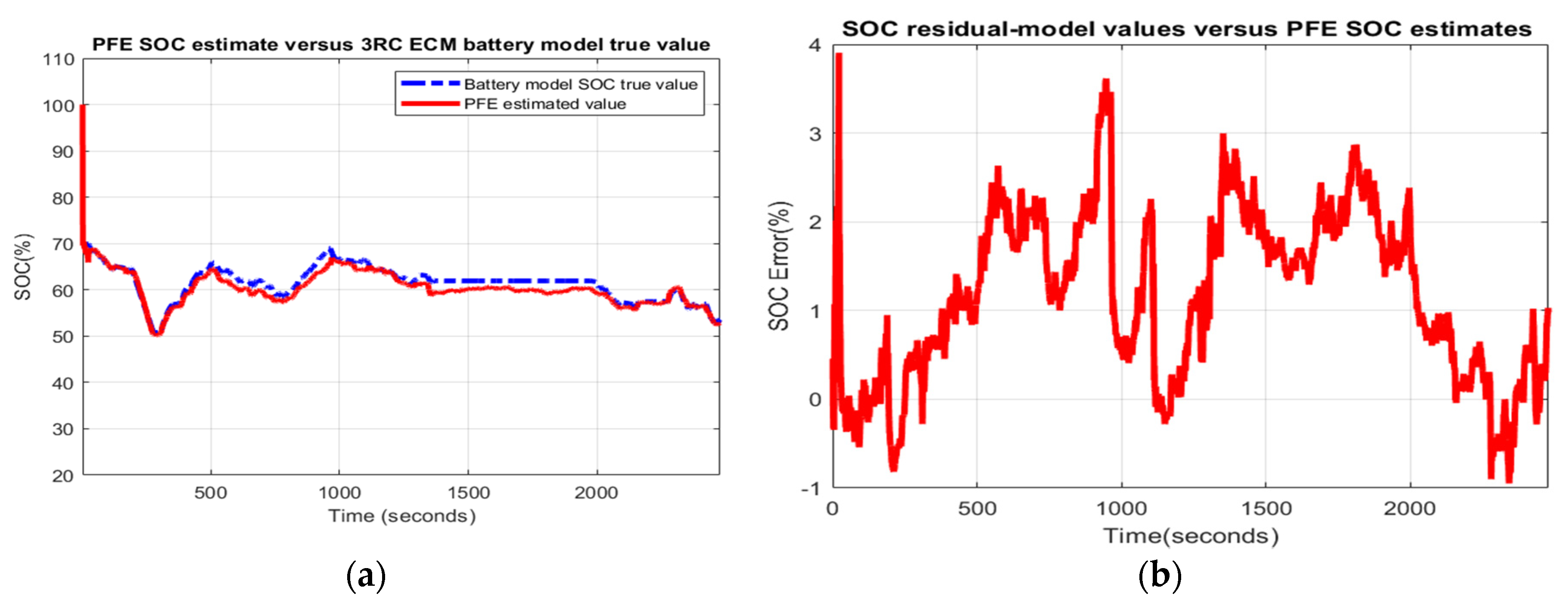
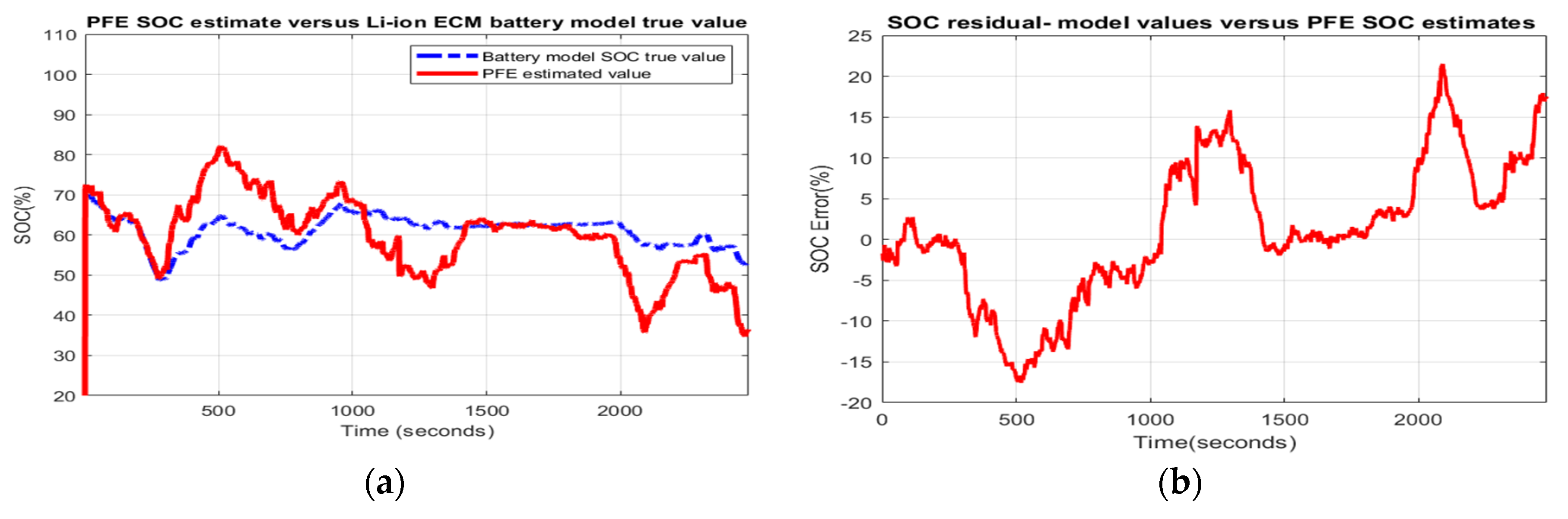
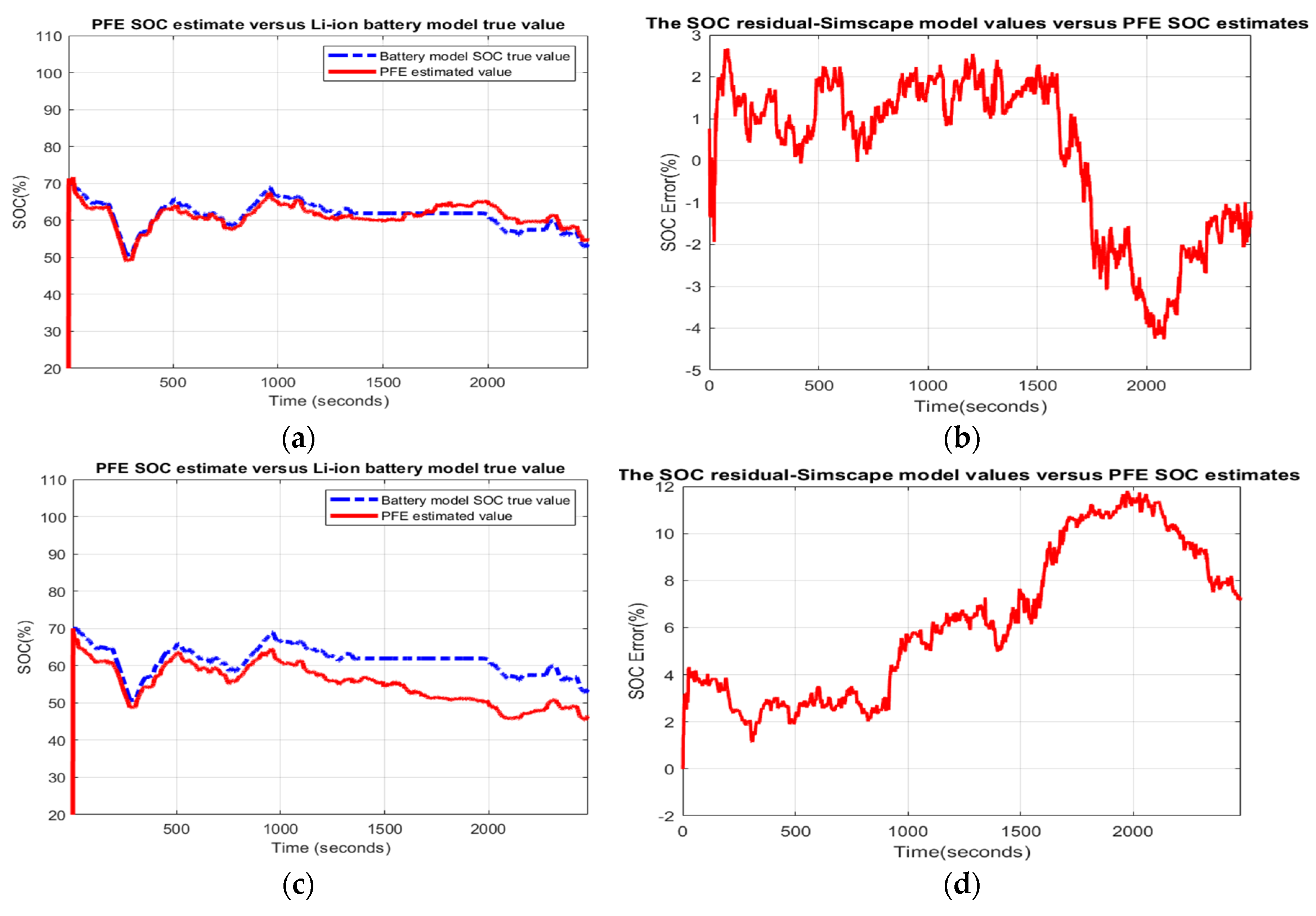
- Scenario R2. The MATLAB simulation results for the second scenario are depicted in Figure 12 and statistical criteria values are given in Appendix A.2, Table A2.Performance analysis:
- ○
- SOC accuracy is great.
- ○
- The residual error is quite close to 6%, which is weak.
- Scenario R3. The MATLAB simulation results for the third scenario are visible in Appendix A.1, Figure A29a–c, and the statistical criteria values are given in Appendix A.2, Table A3.Performance analysis:
- ○
- SOC accuracy is great.
- ○
- The residual error is quite close to 3%, which is good.
- Scenario R4. The MATLAB simulation results for the fourth scenario are shown in Figure 13a,b for changes in Kp, and Figure 13c,d for changes in Rin. The statistical criteria values are given in Appendix A.2, Table A4.Performance analysis:
- ○
- SOC accuracy is weak for changes in Rin and good for changes in Kp.
- ○
- The residual error is quite close to 12% for 10% changes in Rin, which is bad.
4. Discussion
4.1. SOC Estimators’ Convergence Speed
4.2. SOC Estimation Accuracy
4.3. SOC Estimator—Measurement Noise Filtration
4.4. SOC Estimators—Real Time Implementation
4.5. SOC Estimator Robustness Performance Analysis—Statistical Criteria
5. Conclusions
- Adaptive Extended Kalman Filter SOC estimator with fading feature and covariance matrices of noises correction—brief presentation and MATLAB application.
- Adaptive Unscented Kalman Filter SOC estimator with covariance matrices of process and measurement noise correction—design and MATLAB implementation.
- Adaptive Particle Filter SOC estimator—brief presentation and MATLAB application.
- MATLAB SOC simulations for all three SOC estimators.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Ni-Cad | nickel cadmium |
| Ni-MH | nickel metal hydride |
| Li-ion Co | lithium-ion cobalt |
| EV | electric vehicle |
| HEV | hybrid electric vehicle |
| BMS | battery management system |
| ADVISOR | advanced vehicle simulator |
| EPA | environmental protection agency |
| UDDS | urban dynamometer driving schedule |
| FTP-75 | Federal test procedure at 75 [degrees F] |
| SMO | sliding mode observer |
| LOE | linear observer estimator |
| RMSE | root mean squared error |
| MSE | mean squared error |
| MAE | mean absolute error |
| MAPE | mean absolute percentage error |
| R2/R-squared | coefficient of determination |
| std (σ) | standard deviation |
| OCV | open-circuit voltage |
| SOC | state of charge |
| SOE | state of energy |
| SOH | state of health |
| DOD | depth of discharge |
| NREL | National Renewable Energy Laboratory |
| EKF | extended Kalman filter |
| AEKF | adaptive extended Kalman filter |
| UKF | unscented Kalman filter |
| AUKF | adaptive unscented Kalman filter |
| PFE | particle filter estimator |
Appendix A
Appendix A.1. Figures
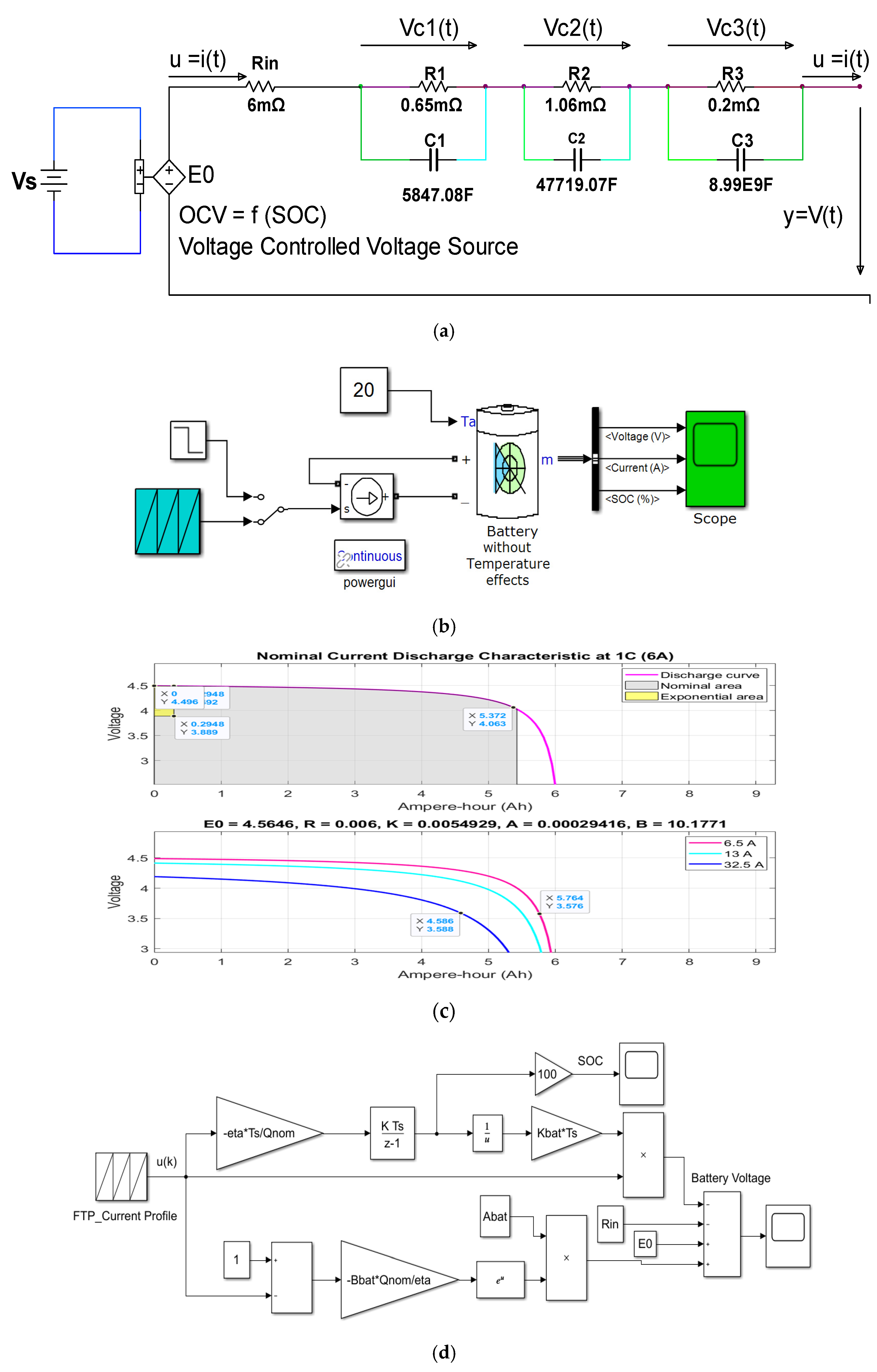



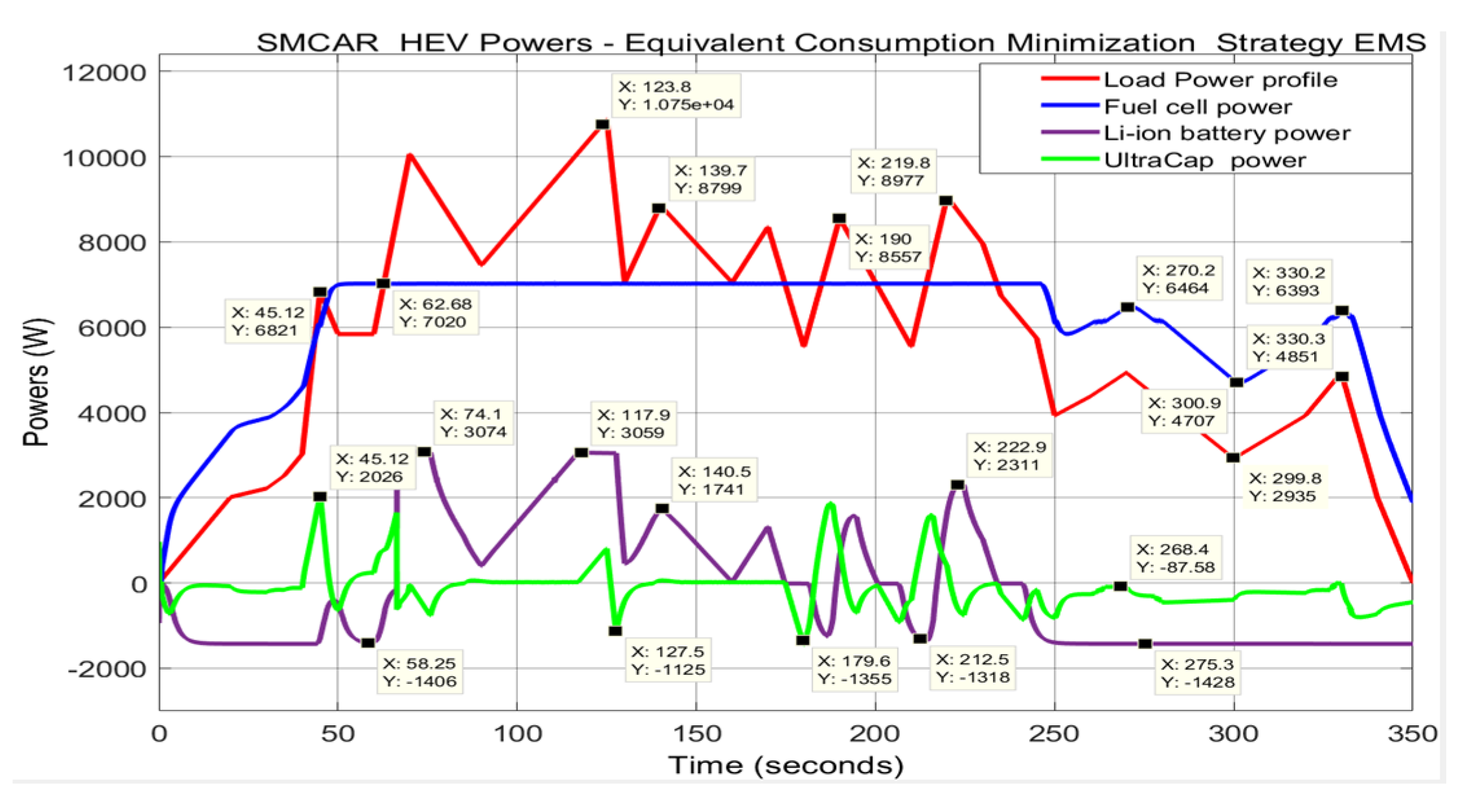

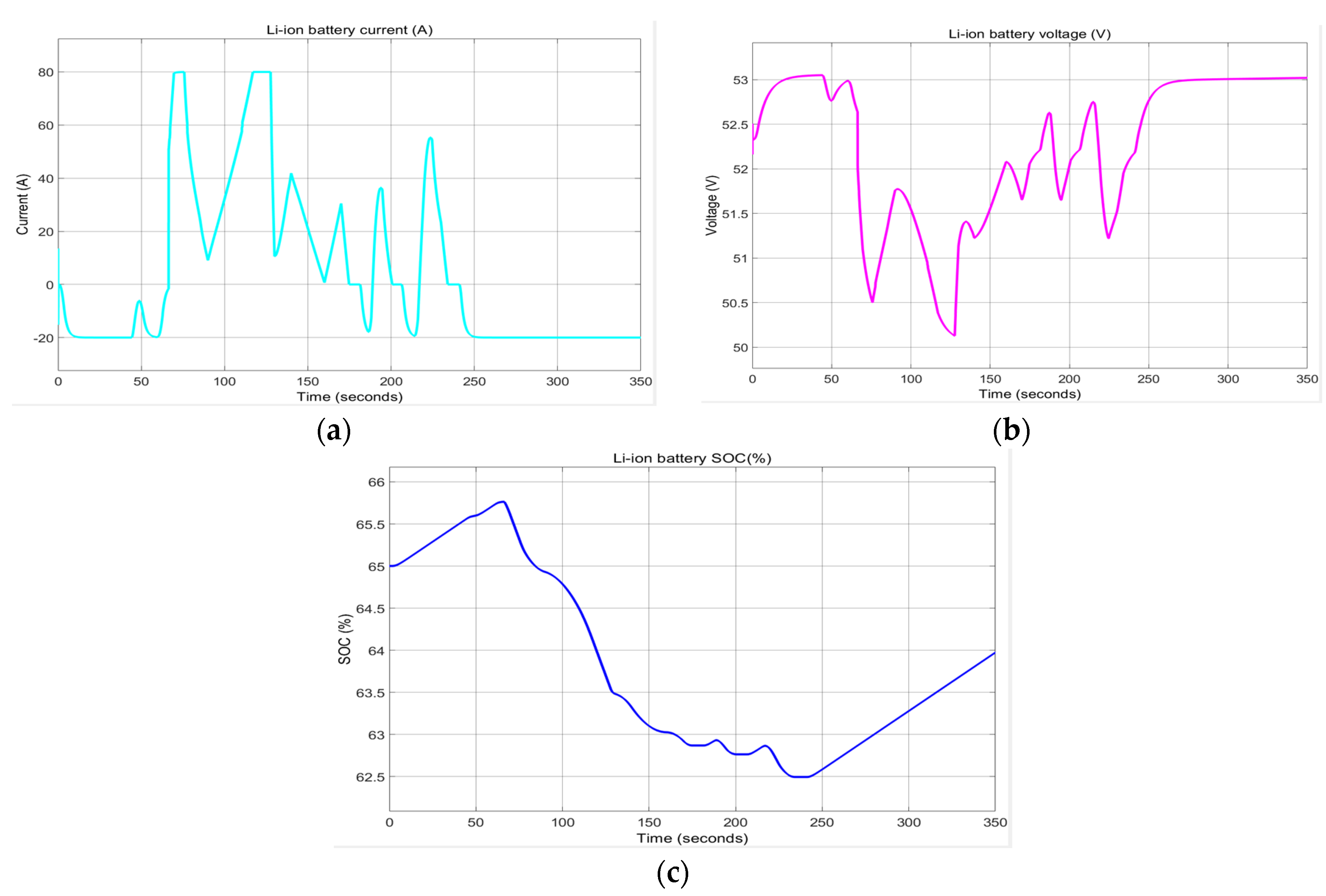
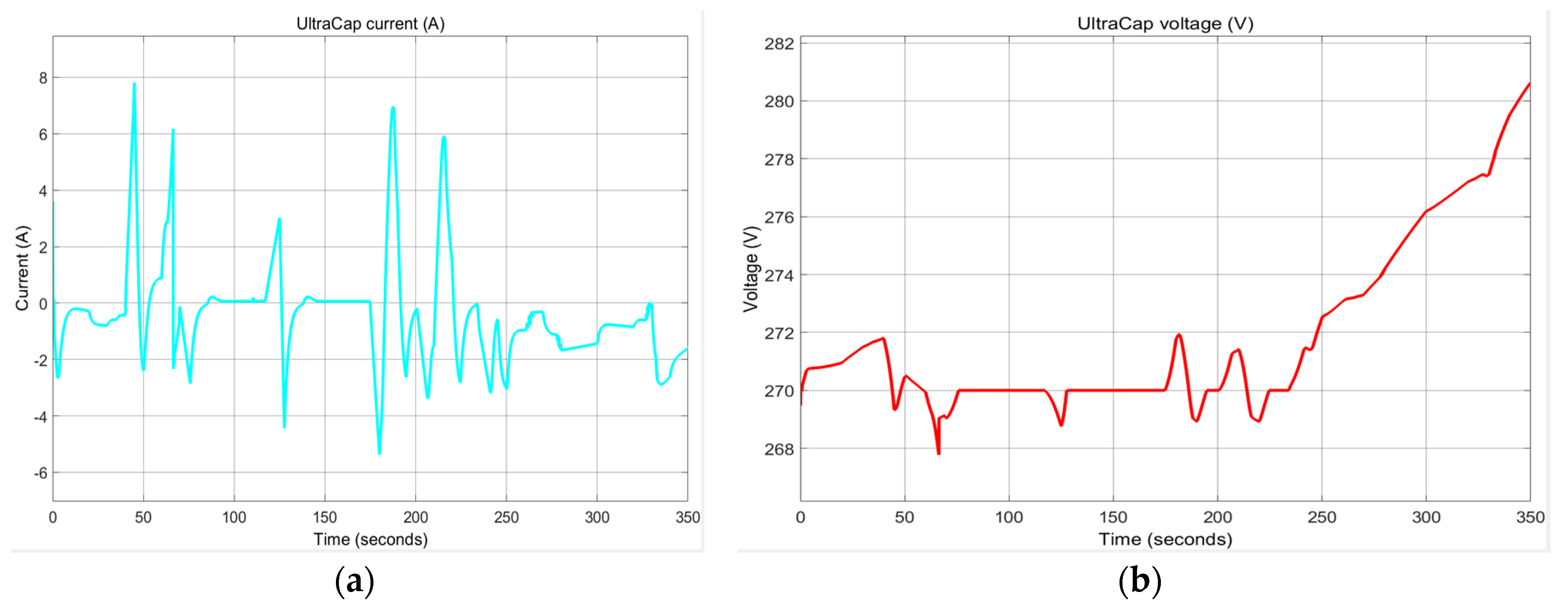
- 3RC EMC Li-Ion Battery Model—A EKF SOC Estimator.
- 3 RC AEKF Li-ion Battery Simscape Model.


- AUKF 3RC EMC Li-ion Battery Model

- AUKF Li-ion Battery Simscape Model
- PFE 3RC ECM Li-ion Battery Model

- Scenario R3: Robustness to simultaneous changes, namely in SOCini (SOCini = 0.4), and measurement noise level, e.g., an increase in noise level 10 times (σ noise = 0.01).

Appendix A.2. Tables
| Performance | Li-Ion Battery 3RC ECM σ = 0.03713 | Li-Ion Battery Simulink Simscape Model, σ= 0.036248 | ||||
|---|---|---|---|---|---|---|
| AEKF | AUKF | PF | AEKF | AUKF | PF | |
| RMSE | 0.0101 | 0.0289 | 0.0284 | 0.0185 | 0.0283 | 0.0163 |
| MSE | 1.0245 | 0.00008 | 0.0008 | 0.00034 | 0.0008 | 0.0002 |
| MAE | 0.0062 | 0.00111 | 0.0226 | 0.0666 | 0.0152 | 0.0119 |
| Standard deviation (σ) | 0.0431 | 0.0433 | 0.0524 | 0.0365 | 0.044 | 0.0379 |
| MAPE (%) | 1.034 | 2.01 | 1.4 | 1.156 | 2.71 | 1.89 |
| R2 | 0.948 | 0.636 | 0.404 | 0.737 | 0.598 | 0.8019 |
| Performance | Li-Ion Battery 3RC ECM σ = 0.03713 | Li-Ion Battery Simulink Simscape Model σ = 0.036248 | ||||
|---|---|---|---|---|---|---|
| AEKF | AUKF | PF | AEKF | AUKF | PF | |
| RMSE | 0.0117 | 0.0284 | 0.047 | 0.00248 | 0.0445 | 0.0146 |
| MSE | 0.000137 | 0.00008 | 0.00221 | 6.2e-6 | 0.00198 | 0.0002 |
| MAE | 0.0099 | 0.0203 | 0.03998 | 0.0101 | 0.0319 | 0.112 |
| Standard deviation (σ) | 0.0439 | 0.0728 | 0.0659 | 0.0552 | 0.067 | 0.0433 |
| MAPE (%) | 1.61 | 3.78 | 2.05 | 1.558 | 4.91 | 1.77 |
| R2 | 0.930 | 0.6483 | 0.286 | 0.3858 | 0.013 | 0.840 |
| Performance | Li-Ion Battery 3RC ECM σ = 0.03713 | Li-Ion Battery Simulink Simscape Model, σ= 0.036248 | ||||
|---|---|---|---|---|---|---|
| AEKF | AUKF | PF | AEKF | AUKF | PF | |
| RMSE | 0.0812 | 0.0289 | 0.016 | 0.0188 | 0.0252 | 0.012 |
| MSE | 0.0066 | 0.0008 | 0.00221 | 0.00035 | 0.00063 | 0.0001 |
| MAE | 0.0728 | 0.0109 | 0.3998 | 0.0029 | 0.00879 | 0.0083 |
| Standard deviation (σ) | 0.0457 | 0.0433 | 0.0659 | 0.0379 | 0.047 | 0.0366 |
| MAPE (%) | 10.55 | 1.9898 | 2.05 | 0.52 | 1.578 | 1.35 |
| R2 | −2.34 | 0.637 | 0.286 | 0.729 | 0.681 | 0.892 |
| Remark | Fail the Test | Pass the Test | ||||
| Performance | Li-Ion Battery 3RC ECM σ = 0.03713 | Li-Ion Battery Simulink Simscape Model, σ = 0.036248 | ||||
|---|---|---|---|---|---|---|
| AEKF | AUKF | PFE | AEKF | AUKF | PFE | |
| RMSE | 0.0789 | 0.042 | 0.0866 | 0.0267 | 0.036 | 0.0211 |
| MSE | 0.0062 | 0.0018 | 0.0075 | 0.000714 | 0.0012 | 0.0004 |
| MAE | 0.0687 | 0.0159 | 0.0668 | 0.0074 | 0.0092 | 0.0167 |
| Standard deviation (σ) | 0.0525 | 0.0464 | 0.0974 | 0.04 | 0.052 | 0.0337 |
| MAPE (%) | 10.5 | 3.19 | 3.87 | 1.44 | 2.08 | 1.01 |
| R2 | −2.155 | 0.233 | −4.2 | 0.456 | 0.352 | 0.666 |
References
- Farag, M. Lithium-Ion Batteries, Modeling and State of Charge Estimation. Master’s Thesis, McMaster University of Hamilton, Hamilton, ON, Canada, 2013. [Google Scholar]
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 3. State and parameter estimation. J. Power Sources 2004, 134, 277–292. [Google Scholar] [CrossRef]
- Tudoroiu, R.-E.; Zaheeruddin, M.; Radu, S.-M.; Tudoroiu, N. Real-Time Implementation of an Extended Kalman Filter and a PI Observer for State Estimation of Rechargeable Li-Ion Batteries in Hybrid Electric Vehicle Applications—A Case Study. Batteries 2018, 4, 19. [Google Scholar] [CrossRef]
- Tudoroiu, R.-E.; Zaheeruddin, M.; Radu, S.M.; Tudoroiu, N. New Trends in Electrical Vehicle Powertrains-Chapter 4. In New Trends in Electrical Vehicle Powertrains, 4th ed.; Martinez, L.R., Prieto, M.D., Eds.; IntechOpen: London, UK, 2019. [Google Scholar] [CrossRef]
- Tudoroiu, N.; Zaheeruddin, M.; Tudoroiu, R.-E. Real Time Design and Implementation of State of Charge Estimators for a Rechargeable Li-ion Cobalt Battery with Applicability in HEVs/EVs-A comparative Study. Energies 2020, 13, 2749. [Google Scholar] [CrossRef]
- Zhang, R.; Xia, B.; Li, B.; Cao, L.; Lai, Y.; Zheng, W.; Wang, H.; Wang, W. State of the Art of Li-ion Battery SOC Estimation for Electrical Vehicles. Energies 2018, 11, 1820. [Google Scholar] [CrossRef]
- Simon, J.J.; Uhlmann, J.K. A New Extension of the Kalman Filter to Nonlinear Systems. In Proceedings of the SPIE 3068, Signal Processing, Sensor Fusion, and Target Recognition VI, Orlando, FL, USA, 28 July 1997; p. 3068. Available online: https://people.eecs.berkeley.edu/~pabbeel/cs287-fa09/readings/JulierUhlmann-UKF.pdf (accessed on 21 January 2018).
- Ge, B.; Zhang, H.; Jiang, L.; Li, Z.; Butt, M.M. Adaptive Unscented Kalman Filter for Target Tracking with Unknown Time-Varying Noise Covariance. Sensors 2019, 19, 1371. [Google Scholar] [CrossRef] [PubMed]
- Han, J.; Song, Q.; He, Y. Adaptive Unscented Kalman Filter and its Applications in Nonlinear Control. In Kalman Filter: Recent Advances and Applications; Moreno, V.M., Pigazo, A., Eds.; I-Tech: Vienna, Austria, 2009; pp. 1–24. [Google Scholar]
- Tudoroiu, N.; Radu, S.M.; Tudoroiu, R.-E. Improving Nonlinear State Estimation Techniques by Hybrid. Structures, 1st ed.; LAMBERT Academic Publishing: Saarbrucken, Germany, 2017; p. 56. ISBN 978-3-330-04418-0. [Google Scholar]
- Arulampalam, M.S.; Maskell, S.; Gordon, N.; Clapp, T. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking. IEEE Trans. Signal Process. 2002, 50, 174–188. [Google Scholar] [CrossRef]
- Alvarez, J.M.; Sachenbacher, M.; Ostermeier, D.; Stadlbauer, H.J.; Hummitzsch, U.; Alexeev, A. Analysis of the State of the Art on BMS; Everlasting D6.1 Report; Lion Smart GmbH: Munchen, Germany, 2017. [Google Scholar]
- Chang, W.-Y. The State of Charge Estimating Methods for Battery: A Review. ISRN Appl. Math. 2013, 2013, 953792. [Google Scholar] [CrossRef]
- Lee, S.J.; Kim, J.H.; Lee, J.M.; Cho, B.H. The state and parameter estimation of an Li-Ion battery using a new OCV-SOC concept. In Proceedings of the 2007 Power Electronics Specialists conference, Orlando, FL, USA, 17–21 June 2007; pp. 2799–2803. [Google Scholar]
- He, H.; Liu, Z.; Hua, Y. Adaptive Extended Kalman Filter Based Fault Detection, and Isolation for a Lithium-Ion Battery Pack. Energy Procedia 2015, 75, 1950–1955. [Google Scholar] [CrossRef]
- Zhao, Y.; Xu, J.; Wang, X.; Mei, X. The Adaptive Fading Extended Kalman Filter SOC Estimation Method for Lithium-ion Batteries. Energy Procedia 2018, 145, 357–362. [Google Scholar] [CrossRef]
- Feng, K.; Huang, B.; Li, Q.; Yan, H. Online Estimation of battery SOC for Electric Vehicles Based on An Improved AEKF. E3S Web Conf. 2019, 118, 02025. [Google Scholar] [CrossRef]
- Ma, M.; Qiu, D.; Tao, Q.; Zhu, D. Sate of Charge Estimation of a Lithium Ion Battery Based on Adaptive Kalman Filter Method for Equivalent Circuit Model. Appl. Sci. 2019, 9, 2765. [Google Scholar] [CrossRef]
- Cui, X.; Shen, W.; Zhang, Y.; Cungang, H. A Novel Active Online State of Charge Based Balancing Approach for Lithium-Ion Battery Packs during Fast Charging Process in Electric Vehicles. Energies 2017, 10, 1766. [Google Scholar] [CrossRef]
- Tudoroiu, R.-E.; Zaheeruddin, M.; Tudoroiu, N.; Radu, S.M. SOC Estimation of a Rechargeable Li-Ion Battery in fuel-Cell Hybrid Electric Vehicles-Comparative Study of Accuracy and Robustness performance Based on Statistical Criteria. Part I: Equivalent Models. Batteries 2020, 6, 40. [Google Scholar]



| Performance | Li-Ion Battery 3RC ECM, σ = 0.03713 | Li-Ion Battery Simulink Simscape Model, σ = 0.036248 | ||||||
|---|---|---|---|---|---|---|---|---|
| ADV | AEKF | AUKF | PFE | ADV | AEKF | AUKF | PFE | |
| RMSE | 0.0075 | 0.007 | 0.0052 | 0.02398 | 0.0079 | 0.0037 | 0.0135 | 0.0084 |
| MSE | 0.00005 | 0.000049 | 2.6 × 10−5 | 0.0005 | 6 × 10−5 | 1.4 × 10−7 | 0.00018 | 7 × 10−5 |
| MAE | 0.0070 | 0.0051 | 0.0059 | 0.0179 | 0.0075 | 0.000214 | 0.0127 | 0.0065 |
| Standard deviation (σ) | 0.0384 | 0.043 | 0.0369 | 0.0554 | 0.0384 | 0.036242 | 0.044 | 0.0358 |
| MAPE (%) | 1.1249 | 0.849 | 0.7972 | 1.08 | 1.1965 | 0.50 | 2.178 | 1.06 |
| R2 | 0.9591 | 0.864 | 0.9805 | 0.679 | 0.9515 | 0.999 | 0.908 | 0.946 |
| Result Hierarchy | 2 | 1 | 3 | 1 | 3 | 2 | ||
| Li-Ion Battery Model | 3RC ECM | Simscape | ||||
|---|---|---|---|---|---|---|
| SOC Estimator | SOCini = 0.2 | SOCini = 0.4 | SOCini = 0.9 | SOCini = 0.2 | SOCini = 0.4 | SOCini = 0.9 |
| AEKF | 188 | 10 | 21 | 25 | 23 | 25 |
| AUKF | 194 | 140 | 170 | 36 | 34 | 30 |
| PFE | 23 | 22 | 35 | 32 | 26 | 28 |
| Li-Ion Battery Model | 3RC ECM | Simscape | ||||
|---|---|---|---|---|---|---|
| SOC Estimator | AEKF | AUKF | PFE | AEKF | AUKF | PFE |
| Figure A11 | <1.6 | |||||
| Figure A14 | <0.4 | |||||
| Figure A17 | <0.8 | |||||
| Figure A20 | <2 | |||||
| Figure A23 | < 8 | |||||
| Figure A26 | <2 | |||||
| Result | Good | High | Low | High | Good | Good |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tudoroiu, R.-E.; Zaheeruddin, M.; Tudoroiu, N.; Radu, S.-M. SOC Estimation of a Rechargeable Li-Ion Battery Used in Fuel Cell Hybrid Electric Vehicles—Comparative Study of Accuracy and Robustness Performance Based on Statistical Criteria. Part II: SOC Estimators. Batteries 2020, 6, 41. https://doi.org/10.3390/batteries6030041
Tudoroiu R-E, Zaheeruddin M, Tudoroiu N, Radu S-M. SOC Estimation of a Rechargeable Li-Ion Battery Used in Fuel Cell Hybrid Electric Vehicles—Comparative Study of Accuracy and Robustness Performance Based on Statistical Criteria. Part II: SOC Estimators. Batteries. 2020; 6(3):41. https://doi.org/10.3390/batteries6030041
Chicago/Turabian StyleTudoroiu, Roxana-Elena, Mohammed Zaheeruddin, Nicolae Tudoroiu, and Sorin-Mihai Radu. 2020. "SOC Estimation of a Rechargeable Li-Ion Battery Used in Fuel Cell Hybrid Electric Vehicles—Comparative Study of Accuracy and Robustness Performance Based on Statistical Criteria. Part II: SOC Estimators" Batteries 6, no. 3: 41. https://doi.org/10.3390/batteries6030041
APA StyleTudoroiu, R.-E., Zaheeruddin, M., Tudoroiu, N., & Radu, S.-M. (2020). SOC Estimation of a Rechargeable Li-Ion Battery Used in Fuel Cell Hybrid Electric Vehicles—Comparative Study of Accuracy and Robustness Performance Based on Statistical Criteria. Part II: SOC Estimators. Batteries, 6(3), 41. https://doi.org/10.3390/batteries6030041






