Abstract
Thermal management is pivotal for ensuring the safe and efficient operation of LIBs under dynamic conditions. Accurate core temperature monitoring remains a key BTMS challenge for predicting thermal distributions and mitigating TR risks. This study proposes a real-time core temperature estimation framework integrating joint EKF with an electro-thermal-aging model (ECM-1D). Using only surface temperature and voltage measurements, it simultaneously estimates core temperature, SOC, and capacity with bidirectional electro-thermal coupling. The hybrid approach pre-calibrates temperature/SOC/SOH-dependent parameters offline while updating capacity online. Validation under extreme conditions (high-rate cycling, aging, and ISCs) demonstrates 60% lower core temperature RMSE during high-rate cycling, a maximum estimation error below 0.9 K, and 58.9% reduction in SOC estimation error under aging conditions versus existing methods. The framework reliably tracks core temperature trends despite parasitic heat and signal noise, enabling earlier critical temperature warnings. This provides a foundation for TR prevention, advancing battery safety for EV and grid storage applications. Future extensions could integrate physical aging mechanisms and enhance fault detection capabilities.
1. Introduction
The accelerating depletion of fossil fuels and the relentless rise in emissions have intensified global efforts to transition toward sustainable energy systems in recent decades [1]. Among emerging energy storage technologies, LIBs have emerged as a cornerstone due to their high energy density, decreasing costs, and long life cycle [2]. These attributes have enabled transformative applications across portable electronics, EVs, and grid-scale renewable energy storage systems [3]. However, the growing demand for high-performance LIBs—particularly in EVs requiring rapid charging (high C-rate operation), extended environmental tolerance, and enhanced energy density—can promote higher temperature variations which create thermal management complexities and have exposed critical limitations in conventional thermal management systems [4,5].
Central to these limitations is the strong temperature dependence of LIBs. Extensive studies have demonstrated that their electrochemical performance is optimal only within a narrow thermal window (288.15–308.15 K) [6,7,8]. Deviation from this range initiates multiscale degradation processes, such as SEI decomposition, lithium plating, and capacity fade, which collectively escalate the risk of TR [9,10]. More critically, spatial temperature gradients within cells—driven by heterogeneous heat generation under extreme operating conditions—exacerbate these degradation mechanisms [11,12]. For example, mild thermal gradients (3 K) within the battery’s active region can accelerate battery degradation by 300% [13]. Also, it has been reported that the radial temperature differentials exceed 10 K in cylindrical cells during high-rate discharging [14,15,16], while similar gradients in large-format cells exacerbate three-dimensional heat accumulation and local hotspots [12]. Such localized thermal variations promote uneven aging patterns that critically compromise both performance metrics and safety parameters [17,18].
The development of BTMS and BMS capable of monitoring the battery SOT is critical for ensuring LIB’s operational reliability and thermal stability, while effective thermal regulation safeguards against electrochemical degradation driven by thermal variations, conventional surface-mounted sensors cannot directly measure internal thermal dynamics due to structural encapsulation [19]. This limitation is particularly significant because core temperature—a more direct indicator of SOT than surface temperature—is essential for optimizing BMS/BTMS control strategies [20].
To address this challenge, accurate multiphysics analysis of internal thermal gradients and electrothermal coupling mechanisms is imperative. Such analysis enables online estimation of core temperatures, which has emerged as a crucial research priority [20,21]. Enhanced SOT estimation facilitates intelligent thermal management through adaptive control strategies, improving operational efficiency and mitigating degradation induced by thermal gradients. Furthermore, integrating multiphysics electrothermal coupling characteristics supports battery health prognostics and early failure detection, while precise remaining useful life predictions enhance both safety and economic viability—key to sustainable battery lifecycle management.
Current methodologies for estimating or predicting battery core temperature are broadly categorized into data-driven and model-based approaches. Data-driven methods leverage machine learning algorithms trained on historical datasets to infer thermal and electrical states. Representative examples include the 2D-CNN developed by Li et al. for simultaneous core temperature and SOC estimation [22], and the spatiotemporal neural network by Liu et al., which integrates RGB neural networks with EKF [23]. EIS-based methods also have been extensively researched and combined with data-driven approaches in recent years for battery temperature prediction [24]. For example, Yuan et al. developed an advanced hybrid framework that integrates EIS-based volume-averaged temperature estimation with LSTM networks for thermodynamic parameter analysis, significantly improving core temperature prediction accuracy [25]. Additionally, comparative studies have systematically evaluated the performance of various data-driven models for this application [26]. Despite the high predictive accuracy, data-driven approaches face inherent limitations: their reliance on battery-specific historical datasets hinders generalization across diverse configurations and operating conditions, while their black-box nature complicates integration with functional safety-critical BMS requirements.
The evolution of model-based approaches for battery thermal management reflects a progressive integration of thermal and electrical dynamics to enhance estimation accuracy and computational efficiency. Initially, Sun et al. pioneered a KF-based framework that integrated Forgez’s reduced-order thermal model [15], achieving internal temperature estimation with a maximum error of 1 K [27]. This work laid the foundation for thermal-centric state estimation but did not account for temperature-dependent electrical behaviors. Subsequently, Ma et al. advanced this paradigm by incorporating temperature-dependent electrical resistance into a ROM, enabling more accurate heat generation calculations and improving temperature estimation precision [28]. Building on these insights, researchers recognized the necessity of capturing bidirectional electrothermal coupling—where electrical parameters influence heat generation, and temperature variations conversely alter electrical dynamics [29]. For instance, Zhang et al. developed a simplified thermoelectric model that combined a 1RC ECM with a lumped 1D thermal model, explicitly deriving heat generation from ohmic losses and achieving real-time temperature estimation with an RMSE of 1 K [30]. These iterative advancements underscore the transition from standalone thermal models to tightly coupled electrothermal frameworks, balancing accuracy with computational tractability for real-time BMS applications.
Despite advancements in online core temperature estimation, existing approaches rarely address aging-induced variations in electrical–thermal parameters under dynamic operational conditions. Chen et al. [31] proposed an AFFRLS-dual EKF algorithm to concurrently update all ECM and thermal model parameters alongside SOC, SOH, and SOT across the battery’s lifecycle. Although their method demonstrated robust temperature estimation under varying SOH levels and ambient temperatures, several limitations persist: simultaneous estimation of multiple parameters complicates filter-parameter adjustments and introduces computational complexity for real-time implementation; validation is restricted to constant current discharging profiles rather than real-world dynamic profiles; and critical scenarios such as high-rate charge–discharge cycles or fault-induced thermal transients—significantly impacting temperature distribution and model stability—remain unexamined. Additionally, parameter dependencies were indirectly derived from SOH-dependent OCV relationships instead of direct correlations.
To address these challenges, this study develops a model-based framework for online battery core temperature estimation by integrating SOC and capacity tracking through a coupled electrothermal model. To ensure computational efficiency without sacrificing accuracy, a hybrid parameterization strategy is implemented: temperature- and SOC-dependent parameters (e.g., entropy coefficient) are pre-calibrated offline through designed experiments, while temperature-, SOC-, and SOH-dependent ECM parameters are pre-calibrated offline via high-fidelity simulations. Both sets of parameters are stored as lookup tables. Only battery capacity—a key parameter linking SOC, SOH, and heat generation—is dynamically updated online. Simultaneously, the core temperature and SOC, and capacity are estimated online through a joint EKF algorithm. This proposed method is tested under extreme scenarios—including high rate charge–discharge cycles, ISCs, and accelerated aging protocols—the framework achieves RMSE < 0.9 K for core temperature estimation. Notably, it enables real-time capacity fade tracking under continuous aging stress and offers relatively good performance even under battery ISC faults. Compared to prior work, this approach advances the field as follows: (i) Enhancing core temperature estimation accuracy through a coupled thermal-electrical–aging model that dynamically captures parameter interactions. (ii) Achieving online multi-state joint estimation within a lean computational framework. (iii) Demonstrating robustness across diverse extreme dynamic profiles built by a high-fidelity battery model. By explicitly embedding aging effects into the estimation architecture, this method provides a physically interpretable and computationally efficient solution for adaptive thermal management in real-world applications.
The remainder of this paper is structured as follows: Section 2 first presents the proposed methodology, detailing the coupled electro-thermal model formulation, parameter estimation framework, and algorithm implementation. Building upon this foundation, Section 3 systematically analyzes the core temperature estimation accuracy under diverse operating conditions through comprehensive simulation studies. Finally, Section 4 concludes with key findings and discusses future work.
2. Methodology
The proposed methodology establishes a closed-loop framework for online core temperature estimation, integrating offline parameter characterization with real-time state observation. As illustrated in Figure 1, the framework operates through two sequential phases: offline parameter identification and online joint state estimation.
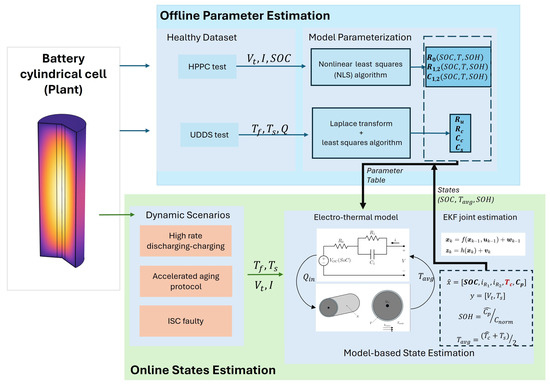
Figure 1.
Overall online core temperature estimation framework.
In the offline phase, critical model parameters are systematically determined through simulated characterization studies under controlled variations of thermal conditions, SOC levels, and aging states. These parameters form the foundation for a reduced-order coupled electro-thermal model that explicitly incorporates multi-domain dynamics, including temperature-dependent electrical responses and aging-induced capacity fade.
The online phase employs an EKF algorithm to simultaneously track three interdependent states: (i) SOC through voltage-current dynamics, (ii) core temperature via thermal state propagation, and (iii) capacity degradation through incremental parameter adaptation. The algorithm embeds the reduced-order ECM-1D thermal battery model to maintain computational efficiency while preserving essential electro-thermal couplings. Subsequent sections provide detailed technical implementation of three core components: reduced-order model development; offline parameter estimation process; and joint EKF algorithm implementation.
2.1. Model Development
The proposed electro-thermal model architecture extends the framework by Lin et al. [32] through enhanced parameter coupling mechanisms, as illustrated in Figure 2.
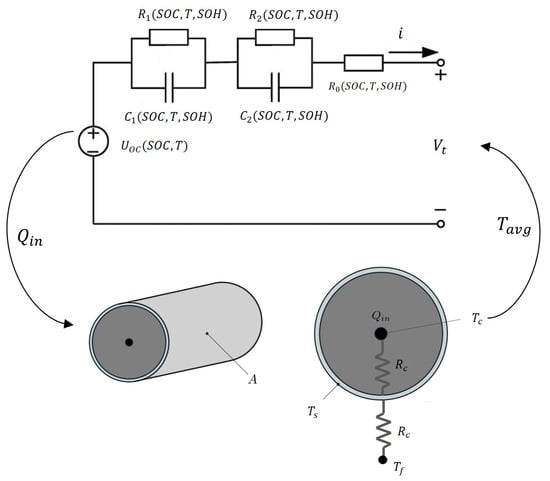
Figure 2.
Reduced-order battery model.
This control-oriented formulation synergistically integrates electrical and thermal dynamics via two coupled subsystems.
The electrical subsystem employs a second-order ECM with temperature- and state-dependent parameters, as defined by Equation (1).
where
- is the OCV, which incorporates temperature and SOC compensation as reported in Equation (2);
- and (for ) denote the ohmic and polarization resistances, respectively, each dependent on temperature (T), , and ;
- In this coupled model, the electrical subsystem’s temperature T is represented by the average temperature , which is derived from the thermal model.
The OCV with temperature compensation is defined by Equation (2).
with the reference temperature defined as 293.15 K.
Here, is the reference OCV at , and is the entropic (temperature sensitivity) coefficient, typically provided as a function of SOC.
The state-of-charge evolution is described via coulomb counting, as defined by Equation (3).
where
- is the initial SOC;
- is the battery capacity, which may degrade over time;
- The integration is performed with a 1 s time step.
The polarization currents are modeled by first-order dynamics, as defined by Equation (4).
with the time constants defined as . All parameters in the electrical model are summarized in Table 1.

Table 1.
Model nomenclature.
The thermal behavior of the battery is captured using a two-state lumped parameter model, which divides the battery into the core and the surface regions through the radial direction of the cell. This model provides a balance between model accuracy and computational efficiency by capturing essential temperature gradients without resorting to a full spatial model. It is built based on the following considerations:
- Longitudinal simplification: The high thermal conductivity along the longitudinal axis ensures a uniform temperature distribution, allowing the neglect of temperature variations along the axial direction of the cell.
- Radial resolution: Significant temperature gradients in the radial direction of the cell motivate a core-surface discretization.
The governing equations for radial heat transfer are as follows:
where and denote the core and surface temperatures, respectively.
The heat generation combines irreversible and reversible (entropic) components, as defined in Equation (7).
Here, is defined later as the average battery temperature. Natural air convection between the cell surface and air is considered as the cooling type in this research, as defined in Equation (6), which can be extended to other cooling types via the tunable thermal parameter . Other parameters in the thermal model are summarized in Table 1.
The proposed model incorporates three essential coupling mechanisms:
- Thermal feedback: The average battery temperature is dynamically updated as Equation (8).which in turn updates the temperature-dependent ECM parameters.
- Entropic heating: Reversible thermodynamic effects are captured via the entropic heating term in Equation (7).
- Aging mechanisms: Battery degradation is characterized at each time step and dynamically updates the SOH-dependent ECM parameters. The state-of-health is defined as follows:where denotes the nominal battery capacity and SOH modifies ECM parameters through pre-calibrated aging maps.
The SOC-OCV curve and the entropy coefficient curve, both as functions of SOC, are typically provided in battery data sheets or determined experimentally.
2.2. Offline Parameter Estimation
The parameter identification framework employs a hybrid approach combining physical characterization and data-driven optimization. The study focuses on a commercial 18650 LIB (1.258 Ah nominal capacity), with simulated datasets generated through a validated COMSOL 6.3 Multiphysics® air-cooled battery model. This model couples a lumped-parameter simplification of the SPM with a 2D axisymmetric thermal model, where the thermal-electrical coupling is achieved through joule heating terms calculated from ECM parameters, referred as ’plant model’. Detailed specifications can be found in [33].
The overall framework for electrical and thermal parameter identification is summarized in Table 2. Both approaches utilize hybrid methodologies combining physical insights with gray-box parameter optimization, enabling systematic analysis of battery behaviors through distinct identification procedures. This offline parameter calibration process can be extended to other LIB types by leveraging either existing model parameters from the literature or experimental characterization data, ensuring broader applicability of the proposed approach. For the battery states or working conditions beyond the range mentioned in Table 2, a re-calibration will be required.

Table 2.
Comparative framework for parameter identification.
The parameter estimation results revealed distinct characteristics among the ECM components. It can be observed that the resistance parameters exhibited marked variations across different SOH, which evidenced the importance of integrating the SOH-dependency into the model. The complete parameterization results are presented in Figure 3, with complementary thermal characteristics detailed in Table 1.
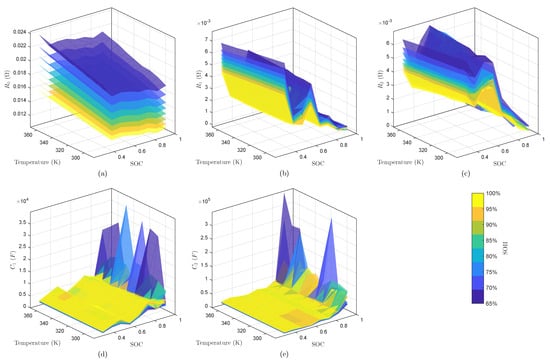
Figure 3.
ECM parameters: (a) , (b) , (c) , (d) , (e) .
2.3. Joint EKF Algorithm Implementation
Joint EKF enables simultaneous tracking of the battery cell’s dynamic states and unknown parameters by augmenting them into a unified state vector, which is recursively updated using the EKF framework [34]. In this study, the algorithm is adapted to enhance the estimation accuracy of the SOT while accounting for battery aging effects through capacity estimation integration. The joint estimation process addresses the coupled dynamics between the thermal behavior and battery health, where aging-induced capacity loss alters both the heat generation rates and the thermal response. The algorithm implementation follows the phased structure detailed in Table 3. In the kth step, the augmented state vector is denoted as follows:
where represents the battery’s state-of-charge, and denote the polarization currents of the first and second RC branches (capturing fast and slow dynamic effects, respectively), is the core temperature, and corresponds to the battery capacity that reflects aging effects. The input vector is given as follows:
where is the battery current input, is the terminal voltage, and represents the coolant or ambient temperature for thermal management. The measurement vector is defined as follows:
with being the measured terminal voltage and the measured surface temperature of the battery.

Table 3.
Joint extended Kalman filter algorithm steps.
According to the coupled model introduced in Section 2.1, the discrete-time electro-thermal dynamics are described and observed by the following process and measurement equations:
Process equations:
where is the sampling time interval. The denote the process noise terms associated with , polarization currents, core temperature, and battery capacity, respectively. Other parameters has been explained in previous Section 2.1.
Measurement equations:
where and represent the measurement noise associated with the terminal voltage and the surface temperature, respectively.
As demonstrated above in Section 2.2, key model parameters exhibit coupled dependencies on SOC, SOH, and thermal conditions. These relationships are characterized by the following: (i) temperature/SOC-dependent polarization components: ; (ii) aging-sensitive ohmic resistance: ; (iii) capacity degradation metric: .
This proposed online battery core temperature estimation method is tested through diverse dynamic battery operating conditions, with the corresponding results presented and discussed in the subsequent chapter.
3. Results and Discussion
This chapter evaluates the performances of the proposed algorithm under three dynamic operational scenarios characterized by significant temperature variations: high-rate current charge–discharge cycles, accelerated aging simulations, and ISC fault conditions. The ambient temperature under simulations is set as 298.15 K. Validation is performed via coupled SPM-2D thermal simulations (adapted from [33]), addressing the technical constraints associated with non-disruptive experimental validation [35], while the model has certain limitations, including the absence of explicating aging mechanisms and the assumption of homogeneous material distribution, it effectively overcomes experimental challenges associated with core temperature measurement while simulating various dynamical operation conditions. The simulations employ a standard (’Normal’) mesh element size in ’plant model’, which has been verified through grid independence studies to provide sufficient accuracy while maintaining computational efficiency.
High-rate charge–discharge cycles are first examined to assess the algorithm’s capability in capturing thermal dynamics through comparative analysis with the conventional standalone thermal model applied by Sun et al. [27], as well as to evaluate the stability of the aging-related parameter estimates. In accelerated aging simulations, the method adapts to capacity fade and parameter drift, leading to enhanced core temperature and SOC tracking compared with the prior work proposed by [36], while enabling real-time SOH monitoring. Finally, under ISC fault conditions, the algorithm maintains reliable core temperature estimation despite electrical–thermal disturbances, thereby facilitating early detection of TR. These comparative analyses underscore the algorithm’s advantages in dynamic performance, aging adaptability, and fault robustness. Notably, on a laptop equipped with an AMD Ryzen 7 5800H processor (AMD, Santa Clara, CA, USA), each estimation step was completed within 0.06 s, outperforming most existing approaches reported in the literature [37] and demonstrating compatibility with real-time BMS implementation.
3.1. Dynamic Performance Evaluation
This subsection evaluates the algorithm’s capability to capture rapid thermal dynamics under extreme power conditions through high-rate charge–discharge cycle testing. A custom high-rate current profile (Figure 4) is designed to rigorously assess dynamic response performance. Under peak current rates exceeding 20 C, substantial heat accumulation induces pronounced core-to-surface temperature differentials (up to 6 K) and elevates the overall battery temperature to approximately 365 K within minutes.
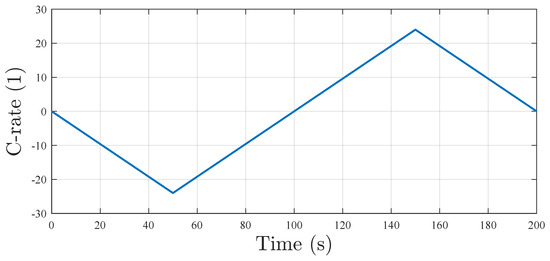
Figure 4.
High rate discharging/charging current profile.
A comparative analysis with a standalone thermal model (referred to as ‘thermal model’ in subsequent sections) highlights the critical role of electrothermal coupling in the proposed framework. Specifically, the compared method proposed by Lin et al. [38] integrates a two-state thermal model into an EKF but excludes electrical measurements and neglects electrothermal interactions. This conventional approach assumes simplified Joule heating with a fixed internal resistance (), derived from average parameter estimates (typically sourced from datasheet in practical applications).
As demonstrated in Figure 5, the proposed methodology achieves superior estimation accuracy throughout the operational cycles. A 62.5% reduction in RMSE quantifies the model’s enhanced performance. Crucially, under healthy battery conditions (SOH = 1), the estimated capacity exhibits minimal variations (relative error < 0.16%), as shown in Figure 5c, confirming immunity to false degradation indications in non-aging scenarios.
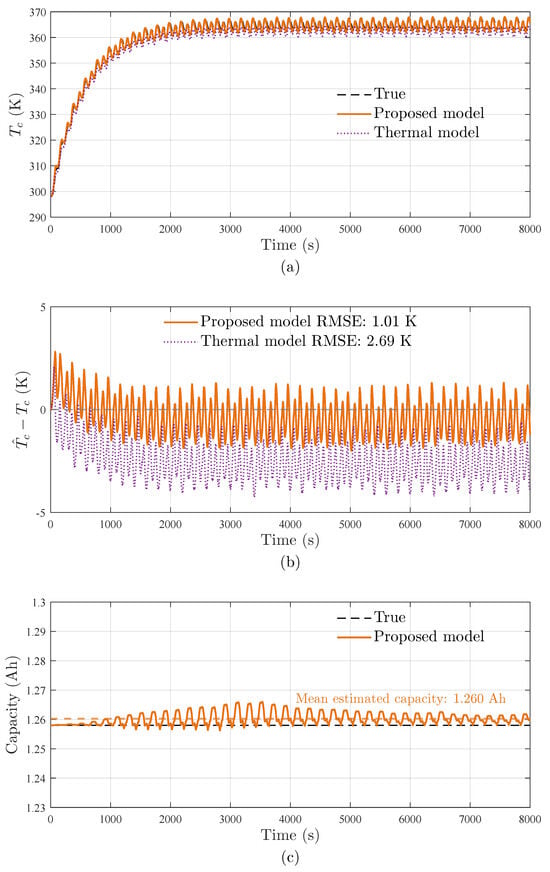
Figure 5.
Core temperature and capacity estimation results under high-rate discharging/charging profiles: (a) the estimated core temperature (), (b) temperature estimation error of core temperature with RMSE comparison, (c) the estimated battery capacity ().
The performance enhancement primarily stems from a bidirectional electro-thermal coupling mechanism that operates through two critical pathways: (1) dynamic quantification of reversible heat generation during phase transitions via SOC-dependent entropy coefficients, and (2) continuous compensation of RC network parameters through real-time thermal adaptation. This dual-path architecture enables simultaneous thermal–electrical state co-estimation while maintaining parameter consistency across operational temperature gradients.
3.2. Health-Adaptive Capability Analysis
This subsection evaluates the algorithm’s ability to adapt to battery aging by simultaneously tracking SOH, SOC, and core temperature under dynamic operational conditions. An accelerated aging protocol is designed using UDDS cycles combined with a controlled capacity fade profile (Figure 6d). The capacity loss () is governed by calendar aging dynamics, where the degradation rate () depends on the nominal capacity () and aging time constant () through the linear relationship defined in Equations (20)–(22).
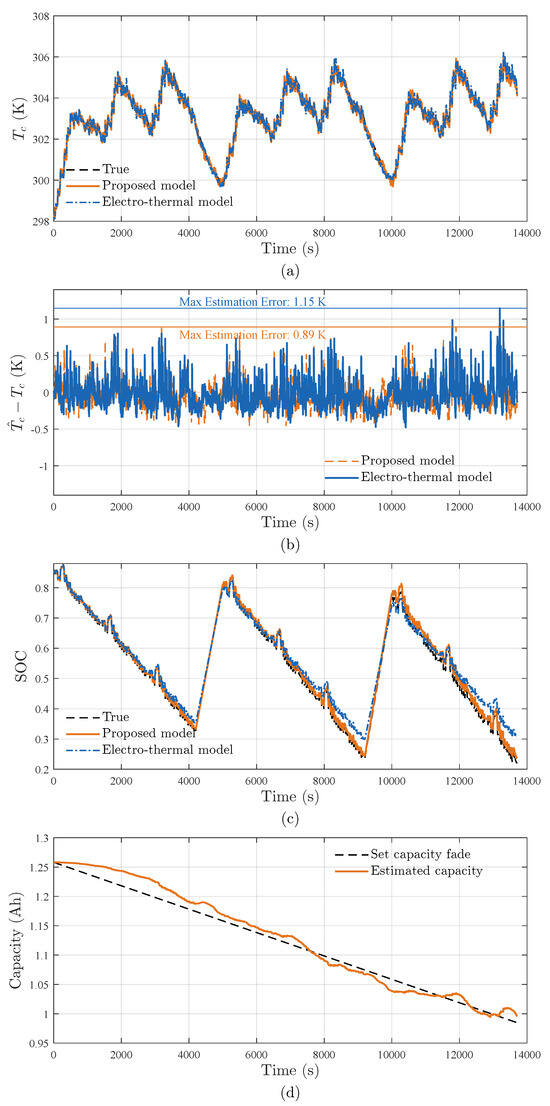
Figure 6.
Online state estimation performance during accelerated aging tests demonstrating: (a) core temperature () estimation, (b) core temperature estimation error, (c) SOC estimation, and (d) capacity () estimation.
Unlike constant current profiles, the UDDS cycles impose dynamic and variable loads, adding significant electro-thermal complexity that closely mimics real driving conditions. This protocol utilized to test two interconnected functionalities of the proposed method: (1) core temperature estimation accuracy under aging, and (2) joint SOH-SOC tracking performance.
The proposed method is compared with Pang et al.’s electrothermal framework [36] (referred as ‘electro-thermal model’), which integrates a simplified thermal model with temperature-dependent ECM parameters and irreversible heating assumptions (Equation (7)). Unlike the proposed aging-adaptive architecture, Pang’s approach lacks explicit capacity loss. Which means, it assumes a fixed battery capacity and does not update parameters as the cell ages. This comparison highlights the improvements gained through our SOH-adaptive framework.
Figure 6 shows the estimation results of battery states of the proposed method and the compared method. Key results are summarized as follows: First, with the SOH-adaptive framework, our proposed method reduces maximum core temperature error from 1.15 K to 0.89 K (RMSE decreased by 11%). Second, real-time capacity estimation enables significant SOC tracking enhancement, yielding a 58.9% reduction in RMSE. In contrast, Pang’s model exhibits accumulated SOC errors (Figure 6c) due to unaccounted capacity loss, which further degrade temperature estimation accuracy (since incorrect SOC affects predicted voltage and heat generation). Third, The proposed framework reliably tracks the battery’s capacity fade over time (Figure 6d), confirming its ability to estimate SOH in real time alongside SOC and temperature. This joint estimation capability not only enhances the model’s accuracy in reflecting aging but also provides a foundation for advanced health monitoring strategies for the battery management.
Comparative analysis confirms the framework’s superiority in sustaining temperature estimation accuracy below 1 K throughout the battery lifespan—a critical advancement over conventional electrothermal models without capacity adaptation. This performance gap highlights the necessity of online co-estimating electrical, thermal, and degradation states of the battery, a capability absent in prior approaches.
3.3. Fault Scenario Robustness Analysis
The accurate estimation of battery SOT becomes increasingly critical under ISC faults, as elevated internal temperature gradients exacerbate TR risks [39]. Simultaneously, ISC-induced electrical–thermal disturbances—including abrupt voltage collapse, abnormal heat generation, and accelerated SOC depletion—severely distort observable signals [10], thereby degrading temperature estimation reliability. To evaluate the robustness of the proposed algorithm, three ISC severity levels (soft: , moderate: , severe: ) as classified in related studies and a progressive ISC scenario ( to over 70 min) are simulated within UDDS cycles [40,41]. The ISC heat source is modeled as uniformly distributed across electrode layers, while equivalent resistances () emulate fault dynamics, consistent with our prior ISC detection framework [42].
Figure 7a demonstrates core temperature estimation performance under abrupt ISC levels. Despite increased RMSE (>1 K) compared to healthy conditions introduced in the previous subchapter, the algorithm relatively reliably tracks core temperature trends across all fault levels. This resilience stems from real-time reconciliation of SOC and thermal feedback, which mitigates error propagation caused by abnormal charge depletion. Additionally, the capacity estimation exhibits a gradual decline during ISC operation—a misinterpretation of actual capacity loss but a potential indicator of SOH degradation induced by ISC-induced damage. This phenomenon and its implications for SOT accuracy will be further investigated in future work.
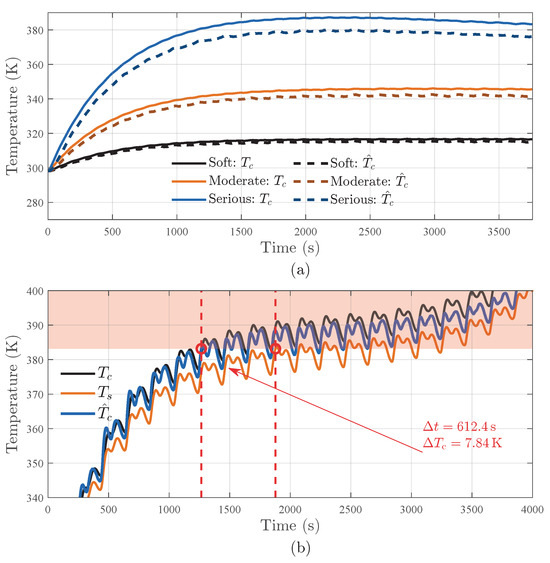
Figure 7.
Core temperature estimation results under ISC conditions: (a) abrupt ISCs, and (b) SOT under evolving ISC event.
Figure 7b illustrates the evolution of estimated core temperature (), true core temperature (), and surface temperature () under the progressive ISC event. A significant thermal gradient (up to 9 K) between the core and surface is observed during fault progression, highlighting the inadequacy of surface temperature monitoring for internal risk detection.
To quantify the safety improvements, a critical temperature threshold (383.15 K, corresponding to separator melting [39]) is established. Beyond this threshold, separator melting initiates more micro ISCs within the battery cell, which rapidly progress to macroscopic ISCs as the separator structural integrity fails. This cascade effect leads to accelerated temperature rise rates, ultimately culminating in thermal runaway and fire incidents. In Figure 7b, the red zone marks the hazardous temperature range (≥383.15 K) where TR becomes imminent. The proposed framework detects when the core hotspot enters this critical zone, enabling earlier alarm triggering and higher TR prevention likelihood compared with relying solely on as the direct input signal. The proposed method triggers the critical temperature alarm 612.4 s earlier via real-time core temperature estimation () compared to surface temperature-based alerts (). During this critical interval, the core temperature rises by 7.84 K, while surface measurements lag significantly, failing to reflect internal hotspot development. This delayed surface response risks catastrophic failure, as localized core temperatures may exceed safety limits long before surface sensors react. Overall, relying solely on surface temperature (Figure 7b) critically underestimates internal risks during fault evolution. Bridging this gap, the proposed framework can potentially help BTMS to deploy preventive measures earlier, decisively enhancing safety in real-world fault scenarios.
4. Conclusions
This study presents an online framework for estimating the core temperature of LIBs by integrating the EKF algorithm with an electro-thermal–aging coupled model (ECM-1D). The framework enables real-time joint estimation of core temperature, SOC, and capacity (indicative of SOH) through dynamic updates of temperature-dependent electrical parameters and aging-induced capacity degradation. By explicitly capturing bidirectional electro-thermal interactions, the method achieves enhanced accuracy in battery state estimation compared to prior approaches under extreme conditions, including a 62.5% reduction in RMSE during high-rate cycling, a maximum core temperature estimation error of <0.9 K, and a 58.9% RMSE reduction in SOC estimation under accelerated aging. Furthermore, the proposed approach demonstrates robust performance under challenging operating conditions, such as ISC scenarios.
The framework offers practical value for BTMS and BMS by improving battery core temperature estimation and enabling simultaneous monitoring of SOC, SOH. Its computational efficiency, achieved through hybrid offline calibration and online parameter adaptation, ensures compatibility with embedded BMS implementations. Future work will focus on integrating the physical correlations between complex aging mechanisms and electro-thermal measurements to further enhance multi-state estimation accuracy of the algorithm. Also, to enhance the framework’s generality, future work may integrate physics-based aging mechanisms (e.g., lithium plating, SEI growth) into the ‘plant model’, enabling systematic robustness analysis. Further validation through experimental tests or high-fidelity simulations under real-world operational scenarios would strengthen its practical relevance. Additionally, combining the framework with advanced fault detection modules will establish a comprehensive health monitoring system. These advancements contribute to safer and more reliable LIB operation in EVs and grid-scale energy storage applications.
Author Contributions
Conceptualization, Y.J. and F.C.; methodology, Y.J., L.B. and F.C.; software, Y.J. and L.B.; validation, Y.J.; formal analysis, Y.J.; investigation, Y.J. and F.C.; resources, M.G. and F.C.; data curation, Y.J.; writing—original draft preparation, Y.J.; writing—review and editing, Y.J., L.B. and F.C.; visualization, Y.J.; supervision, F.C.; project administration, M.G. and F.C.; funding acquisition, Y.J. and M.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by China Scholarship Council grant number No.202108320086.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
The author Yiqi Jia would like to thank the China Scholarship Council for the financial support (CSC, No.202108320086).
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| LIB | Lithium-Ion Battery |
| TR | Thermal Runaway |
| BTMS | Battery Thermal Management System |
| EKF | Extended Kalman Filter |
| ECM | Equivalent Circuit Model |
| SOC | State of Charge |
| SOH | State of Health |
| ISC | Internal Short Circuit |
| RMSE | Root Mean Square Error |
| EV | Electric Vehicle |
| SEI | solid-electrolyte interphase |
| BMS | Battery Management System |
| SOT | State of Temperature |
| 2D-CNN | Two-Dimensional Convolutional Neural Network |
| EIS | Electrochemical Impedance Spectroscopy |
| LSTM | Long Short-Term Memory |
| KF | Kalman Filter |
| ROM | Reduced-Order Model |
| RC | Resistor-Capacitor |
| AFFRLS | Adaptive Forgetting Factor Recursive Least Squares |
| OCV | Open-Circuit Voltage |
| SPM | Single Particle Model |
| HPPC | Hybrid Pulse Power Characterization |
| UDDS | Urban Dynamometer Driving Schedule |
| NLS | Nonlinear Least Squares |
References
- Abas, N.; Kalair, A.; Khan, N. Review of fossil fuels and future energy technologies. Futures 2015, 69, 31–49. [Google Scholar] [CrossRef]
- Ren, D.; Feng, X.; Lu, L.; Ouyang, M.; Zheng, S.; Li, J.; He, X. An electrochemical-thermal coupled overcharge-to-thermal-runaway model for lithium ion battery. J. Power Sources 2017, 364, 328–340. [Google Scholar] [CrossRef]
- Goodenough, J.; Kim, Y. Challenges for rechargeable batteries. J. Power Sources 2011, 196, 6688–6694. [Google Scholar] [CrossRef]
- Xiao, H.; Zhao, J.; Gao, Q.; Zhang, W.; Cheng, X.; Song, C.; Li, G. Recent Advances in Fast-Charging Lithium-Ion Batteries: Mechanism, Materials, and Future Opportunities. Chem. Eng. J. 2025, 506, 159927. [Google Scholar] [CrossRef]
- Gerssen-Gondelach, S.J.; Faaij, A.P. Performance of Batteries for Electric Vehicles on Short and Longer Term. J. Power Sources 2012, 212, 111–129. [Google Scholar] [CrossRef]
- Ma, S.; Jiang, M.; Tao, P.; Song, C.; Wu, J.; Wang, J.; Deng, T.; Shang, W. Temperature Effect and Thermal Impact in Lithium-Ion Batteries: A Review. Prog. Nat. Sci. Mater. Int. 2018, 28, 653–666. [Google Scholar] [CrossRef]
- Ouyang, D.; Weng, J.; Chen, M.; Wang, J. Impact of High-Temperature Environment on the Optimal Cycle Rate of Lithium-Ion Battery. J. Energy Storage 2020, 28, 101242. [Google Scholar] [CrossRef]
- Zhu, G.; Wen, K.; Lv, W.; Zhou, X.; Liang, Y.; Yang, F.; Chen, Z.; Zou, M.; Li, J.; Zhang, Y.; et al. Materials Insights into Low-Temperature Performances of Lithium-Ion Batteries. J. Power Sources 2015, 300, 29–40. [Google Scholar] [CrossRef]
- Yang, S.; Hua, Y.; Qiao, D.; Lian, Y.; Pan, Y.; He, Y. A Coupled Electrochemical-Thermal-Mechanical Degradation Modelling Approach for Lifetime Assessment of Lithium-Ion Batteries. Electrochim. Acta 2019, 326, 134928. [Google Scholar] [CrossRef]
- Feng, X.; Ouyang, M.; Liu, X.; Lu, L.; Xia, Y.; He, X. Thermal Runaway Mechanism of Lithium Ion Battery for Electric Vehicles: A Review. Energy Stor. Mater. 2018, 10, 246–267. [Google Scholar] [CrossRef]
- Troxler, Y.; Wu, B.; Marinescu, M.; Yufit, V.; Patel, Y.; Marquis, A.J.; Brandon, N.P.; Offer, G.J. The effect of thermal gradients on the performance of lithium-ion batteries. J. Power Sources 2014, 247, 1018–1025. [Google Scholar] [CrossRef]
- Xia, G.; Cao, L.; Bi, G. A Review on Battery Thermal Management in Electric Vehicle Application. J. Power Sources 2017, 367, 90–105. [Google Scholar] [CrossRef]
- Li, S.; Zhang, C.; Zhao, Y.; Offer, G.J.; Marinescu, M. Effect of thermal gradients on inhomogeneous degradation in lithium-ion batteries. Commun. Eng. 2023, 2, 74. [Google Scholar] [CrossRef]
- Zhang, G.; Cao, L.; Ge, S.; Wang, C.Y.; Shaffer, C.E.; Rahn, C.D. In Situ Measurement of Radial Temperature Distributions in Cylindrical Li-Ion Cells. J. Electrochem. Soc. 2014, 161, A1499. [Google Scholar] [CrossRef]
- Forgez, C.; Do, D.V.; Friedrich, G.; Morcrette, M.; Delacourt, C. Thermal Modeling of a Cylindrical LiFePO4/Graphite Lithium-Ion Battery. J. Power Sources 2010, 195, 2961–2968. [Google Scholar] [CrossRef]
- Yu, Y.; Vergori, E.; Worwood, D.; Tripathy, Y.; Guo, Y.; Somá, A.; Greenwood, D.; Marco, J. Distributed Thermal Monitoring of Lithium Ion Batteries with Optical Fibre Sensors. J. Energy Storage 2021, 39, 102560. [Google Scholar] [CrossRef]
- Carter, R.; Kingston, T.A.; Atkinson, R.W.; Parmananda, M.; Dubarry, M.; Fear, C.; Mukherjee, P.P.; Love, C.T. Directionality of thermal gradients in lithium-ion batteries dictates diverging degradation modes. Cell Rep. Phys. Sci. 2021, 2, 100351. [Google Scholar] [CrossRef]
- Olabi, A.; Maghrabie, H.M.; Adhari, O.H.K.; Sayed, E.T.; Yousef, B.A.; Salameh, T.; Kamil, M.; Abdelkareem, M.A. Battery Thermal Management Systems: Recent Progress and Challenges. Int. J. Thermofluids 2022, 15, 100171. [Google Scholar] [CrossRef]
- Bandhauer, T.M.; Garimella, S.; Fuller, T.F. A Critical Review of Thermal Issues in Lithium-Ion Batteries. J. Electrochem. Soc. 2011, 158, R1. [Google Scholar] [CrossRef]
- Zheng, Y.; Che, Y.; Hu, X.; Sui, X.; Stroe, D.I.; Teodorescu, R. Thermal state monitoring of lithium-ion batteries: Progress, challenges, and opportunities. Prog. Energy Combust. Sci. 2024, 100, 101120. [Google Scholar] [CrossRef]
- Li, S.; Patel, A.N.; Zhang, C.; Amietszajew, T.; Kirkaldy, N.; Offer, G.J.; Marinescu, M. Internal temperature estimation for lithium-ion batteries through distributed equivalent circuit network model. J. Power Sources 2024, 611, 234701. [Google Scholar] [CrossRef]
- Li, Y.; Ma, C.; Liu, K.; Chang, L.; Zhang, C.; Duan, B. A Novel Joint Estimation for Core Temperature and State of Charge of Lithium-Ion Battery Based on Classification Approach and Convolutional Neural Network. Energy 2024, 308, 132721. [Google Scholar] [CrossRef]
- Liu, K.; Li, K.; Peng, Q.; Guo, Y.; Zhang, L. Data-Driven Hybrid Internal Temperature Estimation Approach for Battery Thermal Management. Complexity 2018, 2018, 9642892. [Google Scholar] [CrossRef]
- Li, D.; Wang, L.; Duan, C.; Li, Q.; Wang, K. Temperature prediction of lithium-ion batteries based on electrochemical impedance spectrum: A review. Int. J. Energy Res. 2022, 46, 10372–10388. [Google Scholar] [CrossRef]
- Yuan, A.; Cai, T.; Luo, H.; Song, Z.; Wei, B. Core Temperature Estimation of Lithium-Ion Battery Based on Numerical Model Fusion Deep Learning. J. Energy Storage 2024, 102, 114148. [Google Scholar] [CrossRef]
- Arafat, K.A.A.; Yousuf Bhuiyan, S.M.; Mahamud, R.; Parvez, I. Investigating the Performance of Different Machine Learning Models for Forecasting Li-ion Battery Core Temperature Under Dynamic Loading Conditions. In Proceedings of the eIT, Eau Claire, WI, USA, 30 May–1 June 2024; pp. 1–7. [Google Scholar] [CrossRef]
- Sun, J.; Wei, G.; Pei, L.; Lu, R.; Song, K.; Wu, C.; Zhu, C. Online Internal Temperature Estimation for Lithium-Ion Batteries Based on Kalman Filter. Energies 2015, 8, 4400–4415. [Google Scholar] [CrossRef]
- Ma, Y.; Cui, Y.; Mou, H.; Gao, J.; Chen, H. Core Temperature Estimation of Lithium-Ion Battery for EVs Using Kalman Filter. Appl. Therm. Eng. 2020, 168, 114816. [Google Scholar] [CrossRef]
- Li, J.; Cheng, Y.; Jia, M.; Tang, Y.; Lin, Y.; Zhang, Z.; Liu, Y. An Electrochemical-Thermal Model Based on Dynamic Responses for Lithium Iron Phosphate Battery. J. Power Sources 2014, 255, 130–143. [Google Scholar] [CrossRef]
- Zhang, C.; Li, K.; Deng, J. Real-Time Estimation of Battery Internal Temperature Based on a Simplified Thermoelectric Model. J. Power Sources 2016, 302, 146–154. [Google Scholar] [CrossRef]
- Chen, S.; Wang, Z.; Zhang, P.; Yu, Y.; Liu, X.; Li, L.; Sun, J. Online core temperature estimation method for lithium-ion batteries over the entire lifecycle. J. Energy Storage 2025, 107, 115033. [Google Scholar] [CrossRef]
- Lin, X.; Perez, H.E.; Mohan, S.; Siegel, J.B.; Stefanopoulou, A.G.; Ding, Y.; Castanier, M.P. A lumped-parameter electro-thermal model for cylindrical batteries. J. Power Sources 2014, 257, 1–11. [Google Scholar] [CrossRef]
- Multiphysics, C. Thermal Modeling of a Cylindrical Lithium-Ion Battery in 2D. COMSOL Application Library: Battery_Design_Module/Thermal_Management/li_battery_thermal_2d_axi. 2023. Available online: https://www.comsol.com/model/thermal-modeling-of-a-cylindrical-lithium-ion-battery-in-2d-10221 (accessed on 10 March 2025).
- Plett, G.L. Dual and Joint EKF for Simultaneous SOC and SOH Estimation. In Proceedings of the 21st International Battery, Hybrid and Fuel Cell Electric Vehicle Symposium & Exhibition (EVS21), Monte Carlo, Monaco, 2–6 April 2005; pp. 1–12. [Google Scholar]
- Sun, L.; Sun, W.; You, F. Core temperature modelling and monitoring of lithium-ion battery in the presence of sensor bias. Appl. Energy 2020, 271, 115243. [Google Scholar] [CrossRef]
- Pang, H.; Guo, L.; Wu, L.; Jin, J.; Zhang, F.; Liu, K. A novel extended Kalman filter-based battery internal and surface temperature estimation based on an improved electro-thermal model. J. Energy Storage 2021, 41, 102854. [Google Scholar] [CrossRef]
- Hossain Lipu, M.; Abd Rahman, M.; Mansor, M.; Ansari, S.; Meraj, S.T.; Hannan, M. Hybrid and combined states estimation approaches for lithium-ion battery management system: Advancement, challenges and future directions. J. Energy Storage 2024, 92, 112107. [Google Scholar] [CrossRef]
- Lin, X.; Perez, H.E.; Siegel, J.B.; Stefanopoulou, A.G.; Li, Y.; Anderson, R.D.; Ding, Y.; Castanier, M.P. Online Parameterization of Lumped Thermal Dynamics in Cylindrical Lithium Ion Batteries for Core Temperature Estimation and Health Monitoring. IEEE Trans. Control Syst. Technol. 2013, 21, 1745–1755. [Google Scholar] [CrossRef]
- Feng, X.; Fang, M.; He, X.; Ouyang, M.; Lu, L.; Wang, H.; Zhang, M. Thermal runaway features of large format prismatic lithium-ion battery using extended volume accelerating rate calorimetry. J. Power Sources 2014, 255, 294–301. [Google Scholar] [CrossRef]
- Lai, X.; Jin, C.; Yi, W.; Han, X.; Feng, X.; Zheng, Y.; Ouyang, M. Mechanism, modeling, detection, and prevention of the internal short circuit in lithium-ion batteries: Recent advances and perspectives. Energy Stor. Mater. 2021, 35, 470–499. [Google Scholar] [CrossRef]
- Zhang, G.; Wei, X.; Tang, X.; Zhu, J.; Chen, S.; Dai, H. Internal short circuit mechanisms, experimental approaches and detection methods of lithium-ion batteries for electric vehicles: A review. Renew. Sustain. Energy Rev. 2021, 141. [Google Scholar] [CrossRef]
- Jia, Y.; Brancato, L.; Giglio, M.; Cadini, F. Temperature enhanced early detection of internal short circuits in lithium-ion batteries using an extended Kalman filter. J. Power Sources 2024, 591, 233874. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).