Comparison of Kalman Filter and H-Infinity Filter for Battery State of Charge Estimation with a Detailed Validation Method

Abstract

Accurate and reliable estimation of the state of charge (SOC) of lithium-ion batteries is essential for the performance and safety of battery management systems (BMS) in applications such as electric vehicles and energy storage systems. However, there is a lack of comprehensive comparative studies evaluating different SOC estimation methods under standardized conditions. In this paper, we address this gap by providing a comprehensive, objective comparison of various Kalman and H-Infinity filter variants for battery SOC estimation, utilizing a detailed validation method based on well-defined criteria. The main contributions of this work are: (1) Implementation of multiple filter variants using a consistent equivalent circuit battery model; (2) Development of a standardized validation method for objective performance evaluation; (3) Detailed mathematical formulations enhancing reproducibility; (4) Evaluation of computational efficiency on a digital signal processor (DSP) to provide practical insights for real-time applications. Our findings reveal that while neither filter type is universally superior, the Extended Kalman Filter (EKF) and H-Infinity Filter (HIF) offer a solid balance between estimation accuracy and computational load, making them reliable choices for general applications. This work advances the understanding of SOC estimation methods and aids practitioners in balancing accuracy and computational efficiency for real-world applications.

1. Introduction

Accurate estimation of a battery’s state of charge is crucial. Beyond accuracy, the speed of convergence, temperature dependence, and behavior during long-term measurements are also significantly important. In the field of home storage and in the automotive sector, the reliability of the estimate plays a major role. In the automotive sector, the possible range of the vehicle can be calculated directly from the state of charge [1,2,3,4]. Recent studies, such as [4], have investigated various filtering methods for SOC estimation of lithium-ion batteries, observing that filter performance tends to decrease at lower temperatures.

For lithium-ion batteries, various methods and algorithms for state of charge determination exist. The simplest method is to integrate the current flowing in and out of the battery over time. This method is called Coulomb Counting. The advantage of Coulomb Counting is its short computation time, since here only a simple addition and multiplication takes place. The method is therefore also fully capable in real-time and is the basis for other techniques. Coulomb Counting has two significant drawbacks: it cannot detect and correct an incorrect state of charge, and it integrates measurement errors. An incorrect state means that the procedure does not know the initial state, which is however necessary to calculate the new state. This can happen if the battery management system loads the initial state incorrectly or if the initial state is unknown, for example with new batteries.

Mathematical filters can be used to counteract this problem. Probably the best-known filter is the Kalman filter [5]. The Kalman filter integrates measured values with model values. These measured values originate from Coulomb Counting and are subject to the advantages and disadvantages previously mentioned. Model values are added to the filter to compensate for the disadvantages mentioned above. The battery model can be an equivalent circuit model describing the behavior of the battery at different temperatures, states of charge and currents. The filter weighs the measured values and model values at each time step to determine the best possible state of the system, in this case, the state of charge of the battery.

Another comparable and well-known filter from control theory is the H-Infinity filter [6,7,8,9]. The H-Infinity filter is an estimation technique that aims to minimize the influence of noise and interference in a system. The filter also uses measured values and model values to estimate the states of a system, minimizing the variance of the disturbances. The filter provides the best possible estimate in terms of disturbance reduction, while the Kalman filter uses the mean square deviation between the estimate and the true state. On the one hand, the H-Infinity filter is more robust to uncertainties and model errors than the Kalman filter, which can be more sensitive to such errors. On the other hand, the H-Infinity filter is more complex to model and implement for any system.

Recent studies, such as that by [4], have explored alternative filtering methods like the ensemble Kalman-Bucy filter (EnKBF) and deterministic ensemble Kalman-Bucy filter (DEnKBF) for SOC estimation. They observed that filter performance decreases at lower temperatures, which is consistent with observations in other filtering techniques. Furthermore, they emphasized the computational efficiency of these methods, noting that execution times were comparable to traditional filters.

Although our primary focus is on the comparative analysis of Kalman and H-Infinity filters due to their similarity and widespread adoption, we briefly mention alternative approaches such as particle filters, machine learning and neural networks to acknowledge the breadth of research in SOC estimation and to provide a comprehensive overview of the evolving landscape of battery management techniques [2,10]. Recent studies have explored integrating aging mechanisms with machine learning techniques to improve capacity estimation accuracy under abnormal operating conditions. For instance, ref. [11] proposed an integrated framework combining aging mechanism analysis and machine learning methods for capacity estimation of LiFePO₄ batteries under slight overcharge cycling. The particle filter uses a probabilistic approach and works with a set of samples or “particles”. Each particle represents a possible state of the system. Particles are weighted according to the probability that a particle corresponds to the actual state of the system, based on measurements. The particle filter can be computationally intensive due to the use of a particle set, especially if the number of particles is high. This can affect the efficiency of the filter in real-time applications, as it requires a larger number of calculations compared to other filtering methods.

The neural network method involves collection of large data sets on the battery state and input parameters, preparation and partitioning of the data into training, validation, and test sets, training with the data, validation, and finally application of the trained network. The disadvantages of neural networks compared to the filtering methods described above are the high demand for training data, the black-box approach without interpretable rules, the susceptibility to outliers, and the limited extrapolation capability when, for example, the battery ages [10,12].

To find the appropriate method for a specific application, a comparison of the methods is necessary. On the one hand the accuracy of the result is relevant, on the other hand the computation time is important. In this paper, we focus on the two filtering methods Kalman filter and H-Infinity filter. These are based on the same battery model and are similar in their implementation at the software level. The particle filter and neural networks are not discussed in this paper because they are not comparable to the other filters in terms of structure and complexity.

For the objective comparison of the filters for a given battery we implemented the Kalman filter and the H-Infinity filter and their most common extensions. The Extended Kalman Filter (EKF) for non-linear systems, which extends the models by linearizing system and measurement models. The Adaptive Extended Kalman Filter (AEKF) improves the EKF by additionally adjusting the process and noise covariance matrices during the filtering process. The Dual Extended Kalman Filter (DEKF) splits the state vector into multiple parts and filters them separately to reduce filter complexity and increase estimation accuracy. As an alternative for nonlinear systems, the Unscented Kalman Filter (UKF) is available, which uses the Unscented Transform to achieve a better approximation of the probability distribution. For the H-Infinity Filter, the two variants Adaptive H-Infinity Filter and Dual H-Infinity Filter have been implemented. The mode of operation is the same as for the Kalman filter extensions.

Campestrini et al. have developed a method in [13] to compare the Kalman-Filter against the extended Kalman-Filter. Six criteria were defined, each of which is given a score. The higher the score, the better the result. However, the running time of the algorithms is not evaluated in [13], so in this paper the two filters, Kalman and H-Infinity filters, were implemented on a digital signal processor (DSP). Due to the constant running time of both filters and the deterministic behavior of a DSP, implementing them on the DSP makes sense and provides an objective comparison.

Various methods exist for modeling a battery. There are mainly two different approaches: electrochemical models (white box model) and equivalent circuit models (grey box model) [14]. In this paper, the battery model (ECM) was generated using the newly developed method from [15]. This model relies on an equivalent circuit. It consists of an open-circuit voltage source in series with a resistor and one to four RC elements connected in series (R and C are each connected in parallel). The model can be extended with more RC elements, but we could not see any improvement in the results and therefore the model was limited to a maximum of four RC elements. More RC elements would only increase the computation time in our case. All mentioned electrical components must be parameterized. Bruch et al use a current pulse method with subsequent fitting in [15]. Short current pulses are applied to the battery and the voltage response is recorded. This is done for different states of charge, temperatures and currents. Subsequently, the measured data is fitted to the present equivalent circuit using an optimizer. The results of the fitting are a battery model, which is the basis for both filters.

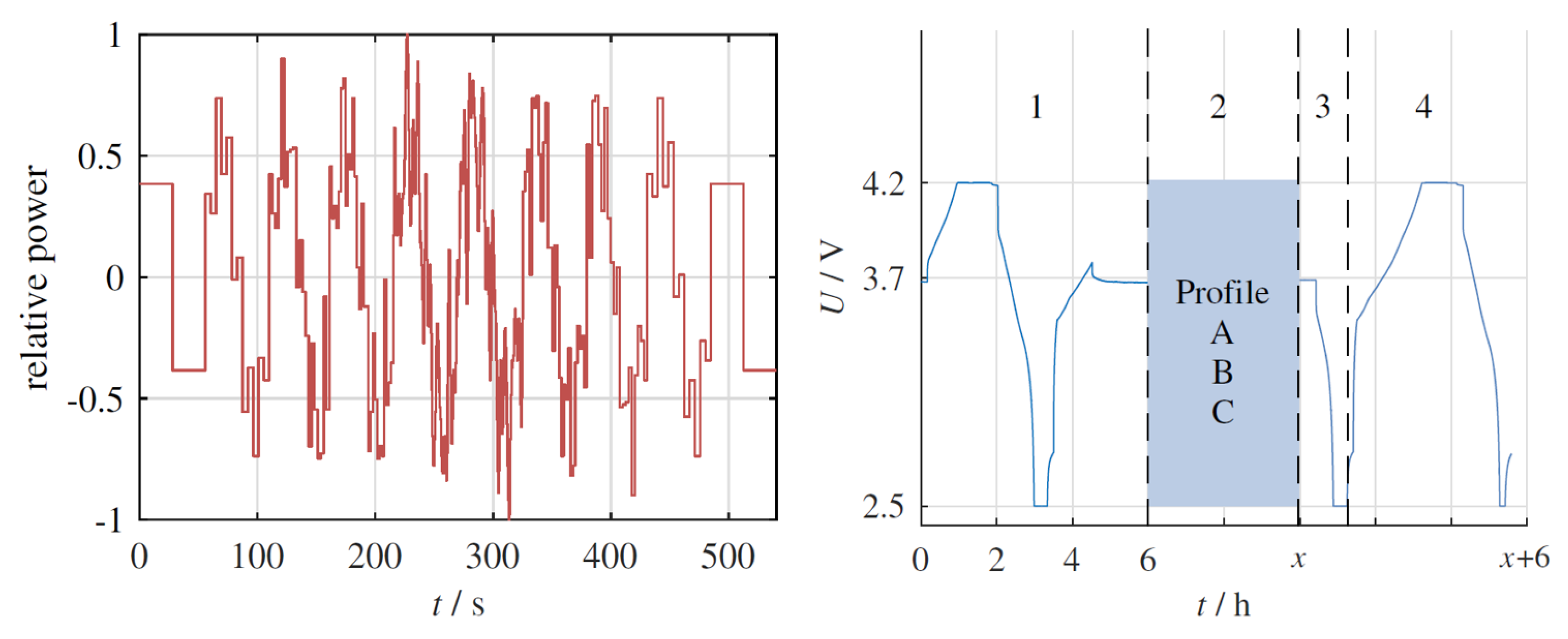
This paper is organized as follows. First, we introduce the methods and describe briefly basic principles of a digital signal processor in Section 2. In Section 3, the experimental setup is described. The testing profiles and the test procedure are presented in Section 4. After the definition of the evaluation criteria in Section 5, we show the results in Section 6, and finally, in Section 7, we conclude the paper.

1.1. Contributions

To address these gaps, this paper provides a comprehensive, objective comparison of various Kalman and H-Infinity filter variants for battery SOC estimation, utilizing a detailed validation method. The main contributions are as follows:

• Implementation of Multiple Filter Variants: Several Kalman filter variants—including Extended Kalman Filter (EKF), Adaptive Extended Kalman Filter (AEKF), Dual Extended Kalman Filter (DEKF), and Unscented Kalman Filter (UKF)—as well as corresponding H-Infinity filter variants are implemented. All filters are applied using a consistent equivalent circuit battery model, ensuring that performance differences are due to the filters themselves rather than different models.
• Development of a Standardized Validation Method: A detailed validation method based on well-defined criteria is developed to objectively evaluate the performance of each filter variant. This includes criteria such as estimation accuracy, temperature stability, transient behavior, residual charge determination, and drift behavior.
• Mathematical Formulation and Reproducibility: Detailed mathematical descriptions of each filter algorithm and the evaluation criteria are provided, enhancing the reproducibility of the study and facilitating further research in this area.
• Evaluation of Computational Efficiency on DSP Hardware: The computational demands of each filter implementation are evaluated on a digital signal processor (DSP), providing practical insights into their suitability for real-time applications with limited processing capabilities. Comprehensive Analysis and Guidance: By providing this comprehensive analysis, valuable guidance is offered for selecting appropriate SOC estimation methods for specific applications, balancing estimation accuracy and computational efficiency.

1.2. Research Gap

Accurate estimation of the state of charge (SOC) of lithium-ion batteries is critical for the performance and safety of battery management systems (BMS) in applications such as electric vehicles and energy storage systems [16,17]. Over the years, various methods have been developed for SOC estimation, broadly categorized into model-based methods, data-driven methods, and hybrid approaches [18].

Recent work by [4] investigated the use of the ensemble Kalman-Bucy filter (EnKBF) and deterministic ensemble Kalman-Bucy filter (DEnKBF) for high-capacity Nickel Manganese Cobalt Oxide (NMC) lithium-ion batteries. Their study focused on improving SOC estimation accuracy while also enhancing computational efficiency. They found that both EnKBF and DEnKBF exhibited reduced accuracy at lower temperatures, highlighting the challenges of SOC estimation in cold environments. Additionally, the execution times of EnKBF and DEnKBF were efficient, with values comparable to other methods.

Model-based methods rely on mathematical representations of the battery’s physical and chemical processes. These include equivalent circuit models (ECMs) and electrochemical models (EMs). ECMs, such as Thevenin and Randles models, simplify the battery behavior using electrical components but may lack accuracy under varied operating conditions [19]. EMs provide detailed insights into the electrochemical processes but are computationally intensive and challenging to implement in real-time applications [20,21].

Data-driven methods utilize historical data to model the complex nonlinear behavior of batteries without requiring detailed physical models. Techniques such as neural networks, support vector machines, and Gaussian process regression have been applied for SOC estimation [10,12,22]. While these methods can achieve high estimation accuracy, they often require extensive training data and may lack robustness when the battery operates outside the conditions represented in the training set.

Hybrid models aim to combine the strengths of model-based and data-driven approaches to improve estimation accuracy and adaptability [23,24]. These models can mitigate the limitations of individual methods but may introduce additional complexity and computational demands.

Despite these advancements, several challenges remain:

• Limited Comparative Analysis: There is a lack of comprehensive comparative studies that objectively evaluate different SOC estimation methods under standardized conditions. Existing research often focuses on individual methods without providing insights into their relative performance [13].
• Reproducibility Issues: The absence of detailed mathematical formulations and standardized evaluation criteria hinders the reproducibility of results and the ability to generalize findings across different applications [18].
• Computational Efficiency: Real-time implementation of SOC estimation algorithms on hardware with limited processing capabilities, such as digital signal processors (DSPs), requires methods that are both accurate and computationally efficient [4,17,25].
• Robustness to Battery Aging and Operating Conditions: SOC estimation methods need to maintain accuracy over the battery’s lifespan and under varying temperatures, loads, and aging conditions [11,24,26].

Therefore, the research gap lies in the need for a comprehensive, objective comparison of various SOC estimation methods, particularly focusing on different variants of Kalman filters and H-infinity filters. Such a comparison should:

• Implement multiple filter variants using a consistent battery model and standardized testing procedures.
• Provide detailed mathematical descriptions of the filters and evaluation criteria to ensure reproducibility.
• Evaluate the filters using a set of well-defined criteria that reflect real-world performance requirements, including estimation accuracy, computational efficiency, and robustness.
• Analyze the computational demands of each filter implementation on practical hardware platforms, such as DSPs.

Addressing this gap is essential for advancing SOC estimation techniques and guiding the selection of appropriate filters for specific applications. By providing a detailed comparative analysis, this work aims to contribute to the development of more reliable and efficient BMS.

2. Filter Methods and Digital Signal Processing

2.1. Battery Modeling Techniques and Focus on Equivalent Circuit Models

Accurate SOC estimation relies heavily on the underlying battery model used. Various methods exist for modeling a battery, which can be mainly categorized into electrochemical models (white-box models) and equivalent circuit models (gray-box models) [14].

Electrochemical models provide a detailed representation of the internal chemical processes of the battery by solving complex partial differential equations [20,21]. While they offer high accuracy and deep insight into battery behavior, their computational complexity makes them impractical for real-time applications, especially on hardware with limited processing capabilities.

Data-driven models, including those based on machine learning and neural networks, capture battery behavior by learning from historical data [10,12]. Although they can model complex nonlinearities and may adapt to different battery types, they require large training datasets and may suffer from reduced accuracy when operating conditions deviate from the training data. Additionally, their high computational demands and lack of transparency (black-box nature) can be drawbacks in practical implementations.

In this paper, equivalent circuit models (ECMs) are focused on due to their balance between modeling accuracy and computational simplicity, which is crucial for real-time SOC estimation in battery management systems (BMS). ECMs simplify the complex electrochemical reactions within a battery into electrical components such as resistors, capacitors, and voltage sources, representing phenomena like internal resistance, capacitance, and open-circuit voltage. This simplification allows for efficient computation while capturing the essential dynamics of the battery.

By using ECMs, SOC estimation methods become applicable to practical BMS implementations where computational resources are limited, and real-time operation is required. The ECM approach is widely adopted in industry for its ease of implementation and sufficient accuracy for many applications.

To ensure an objective comparison, each filter variant is implemented using the same battery model parameters and testing conditions. Unlike previous studies that may use different models or parameters for each method, this approach ensures that differences in performance are attributable to the filter algorithms themselves. Additionally, by implementing the filters on a DSP, practical considerations of computational efficiency and real-time applicability are addressed, which are often overlooked in theoretical analyses.

2.2. Kalman Filter

The Kalman filter (KF) was first introduced by R.E. Kalman in 1960 as a new approach to linear filtering [5]. Based on a model consisting of differential equations, the filter predicts the state of a physical process. By adapting the state variables, the algorithm minimizes the error between the measured and predicted outputs [5]. The model represents the knowledge of the physical process and the changes due to the input. Conversely, the measurements show the current state of the physical system as another input for the filter. The task of the filter is to determine the best estimation of the real value of the system using both the model and the measurements. A predetermined weighting factor for measurement and model noise shows the level of trust for each of the sources. These factors, as well as the initial state and covariance, must be provided to the filter. Finding values which lead to good estimation behavior is called filter tuning. Often this procedure is done offline before the operation with a parameter variation [27]. The Kalman filter operates through a distinct initialization phase that occurs only once at the beginning. Subsequently, at each step of the system, it goes through a cyclical process consisting of prediction, computation of the correction gain, and application of the correction.

For linear dynamic systems modeled in state-space form, the standard KF equations are:

$$\begin{array}{cc}\hfill x_k& =A_{k-1}{x}_{k-1}+B_{k-1}{u}_{k-1}+w_{k-1},\hfill \\ \hfill y_k& =C_k{x}_k+v_k,\hfill \end{array}$$

(1)

where:

• $x_k$ is the state vector at time k,
• $A_{k-1}$ is the state transition matrix,
• $B_{k-1}$ is the control input matrix,
• $u_{k-1}$ is the control input,
• $w_{k-1}$ is the process noise, assumed to be zero-mean Gaussian with covariance $Q_{k-1}$,
• $y_k$ is the measurement vector,
• $C_k$ is the measurement matrix,
• $v_k$ is the measurement noise, assumed to be zero-mean Gaussian with covariance $R_k$.

The Kalman filter algorithm consists of two main steps for each time step k:

Prediction step:

$$\begin{array}{cc}\hfill {\widehat{x}}_{k|k-1}& =A_{k-1}{\widehat{x}}_{k-1|k-1}+B_{k-1}{u}_{k-1},\hfill \\ \hfill P_{k|k-1}& =A_{k-1}{P}_{k-1|k-1}{A}_{k-1}^{\top }+Q_{k-1},\hfill \end{array}$$

(2)

where ${\widehat{x}}_{k|k-1}$ is the predicted state estimate, and $P_{k|k-1}$ is the predicted error covariance.

Update step:

$$\begin{array}{cc}\hfill K_k& =P_{k|k-1}{C}_k^{\top }{\left(C_k{P}_{k|k-1}{C}_k^{\top }+R_k\right)}^{-1},\hfill \\ \hfill {\widehat{x}}_{k|k}& ={\widehat{x}}_{k|k-1}+K_k\left(y_k-C_k{\widehat{x}}_{k|k-1}\right),\hfill \\ \hfill P_{k|k}& =\left(I-K_k{C}_k\right)P_{k|k-1},\hfill \end{array}$$

(3)

where $K_k$ is the Kalman gain, ${\widehat{x}}_{k|k}$ is the updated state estimate, and $P_{k|k}$ is the updated error covariance.

Since a battery model is not a linear system, the concept of the extended Kalman filter (EKF) was introduced. The EKF linearizes the non-linear system by a first-order Taylor approximation. This, of course, can add inaccuracies to the calculations and can cause the filter to diverge [19]. Despite the potential for inaccuracies and divergence due to the linearization process in the extended Kalman filter, its utilization remains prevalent because it provides a practical balance between computational complexity and the ability to handle non-linear system dynamics effectively.

In the EKF, the non-linear system is represented as:

$$\begin{array}{cc}\hfill x_k& =f\left(x_{k-1},u_{k-1}\right)+w_{k-1},\hfill \\ \hfill y_k& =h\left(x_k\right)+v_k,\hfill \end{array}$$

(4)

where $f(·)$ and $h(·)$ are non-linear state transition and measurement functions, respectively.

At each time step, the system is linearized by computing the Jacobian matrices:

$$\begin{array}{cc}\hfill F_{k-1}& ={\left.{\displaystyle \frac{\partial f}{\partial x}}\right|}_{x={\widehat{x}}_{k-1|k-1},u=u_{k-1}},\hfill \\ \hfill H_k& ={\left.{\displaystyle \frac{\partial h}{\partial x}}\right|}_{x={\widehat{x}}_{k|k-1}}.\hfill \end{array}$$

(5)

The EKF algorithm then proceeds with the following steps:

Prediction step:

$$\begin{array}{cc}\hfill {\widehat{x}}_{k|k-1}& =f\left({\widehat{x}}_{k-1|k-1},u_{k-1}\right),\hfill \\ \hfill P_{k|k-1}& =F_{k-1}{P}_{k-1|k-1}{F}_{k-1}^{\top }+Q_{k-1}.\hfill \end{array}$$

(6)

Update step:

$$\begin{array}{cc}\hfill K_k& =P_{k|k-1}{H}_k^{\top }{\left(H_k{P}_{k|k-1}{H}_k^{\top }+R_k\right)}^{-1},\hfill \\ \hfill {\widehat{x}}_{k|k}& ={\widehat{x}}_{k|k-1}+K_k\left(y_k-h\left({\widehat{x}}_{k|k-1}\right)\right),\hfill \\ \hfill P_{k|k}& =\left(I-K_k{H}_k\right)P_{k|k-1}.\hfill \end{array}$$

(7)

Another filter variation is the Adaptive Extended Kalman Filter (AEKF). This filter skips the offline filter tuning by performing online calculations of the measurement and process noises. Moreover, the filter can adjust itself to changing environmental influences. At every time step, the noise values are adapted based on the error between measured and predicted output voltage [13,14,28].

In the AEKF, the measurement noise covariance $R_k$ and process noise covariance $Q_k$ are updated online using methods such as covariance matching. The innovation (or residual) is computed as:

$$e_k=y_k-h\left({\widehat{x}}_{k|k-1}\right).$$

(8)

Then, over a sliding window of size M, the innovation covariance is estimated as:

$$S_k={\displaystyle \frac{1}{M}}\sum _{i=k-M+1}^k{e}_i{e}_i^{\top }.$$

(9)

The measurement noise covariance is then updated:

$$R_k=S_k-H_k{P}_{k|k-1}{H}_k^{\top }.$$

(10)

Similarly, the process noise covariance can be updated based on the discrepancies between the predicted and corrected state estimates.

The Dual Extended Kalman Filter (DEKF) estimates not only the SOC of the battery but also keeps track of the model parameters of the Equivalent Circuit Model (ECM), especially the actual battery capacity which is necessary to calculate the State-of-Health (SOH). All parameters of the ECM undergo measurement errors and change over time due to aging effects. The DEKF consists of two extended Kalman filters which run in parallel. For the SOC estimation, the EKF stays the same as described earlier [29,30]. Since the ECM parameters cannot be predicted, only the covariance values are updated. For the ECM parameter correction, the state vector of the SOC estimation is used. The updated ECM parameter vector is then the input for the next time step of the SOC estimation [30,31].

Let the state vector for SOC estimation be $x_k^{\left(1\right)}$ and for parameter estimation be $x_k^{\left(2\right)}$. The DEKF performs the following steps:

State Estimation EKF:

$${\widehat{x}}_{k|k-1}^{\left(1\right)}=f\left({\widehat{x}}_{k-1|k-1}^{\left(1\right)},u_{k-1},{\widehat{x}}_{k-1|k-1}^{\left(2\right)}\right),$$

(11)

with corresponding updates for $P_{k|k-1}^{\left(1\right)}$.

Parameter Estimation EKF:

$${\widehat{x}}_{k|k-1}^{\left(2\right)}={\widehat{x}}_{k-1|k-1}^{\left(2\right)},$$

(12)

since parameters are usually assumed to be constant over one time step, but their covariance is updated to reflect uncertainty.

The Unscented Kalman Filter (UKF) has a different structure than the other filters, since it does not use the first-order Taylor approximation. Instead, it is based on the Unscented Transformation for the linearization and uses sigma points. Instead of calculating the Jacobian for the linearization of the function, the filter uses deterministic samples of the state distribution [32]. The model can approximate the expected value and the covariance of a random variable which is propagated through a non-linear function. This is achieved by omitting the derivation of system and measurement matrices [33,34].

In the UKF, sigma points are generated around the mean and are propagated through the non-linear functions:

$${\chi }_0={\widehat{x}}_{k-1|k-1},$$

(13)

$${\chi }_i={\widehat{x}}_{k-1|k-1}+{\left(\sqrt{(L+\lambda )P_{k-1|k-1}}\right)}_i,i=1,\dots ,L,$$

(14)

$${\chi }_{i+L}={\widehat{x}}_{k-1|k-1}-{\left(\sqrt{(L+\lambda )P_{k-1|k-1}}\right)}_i,i=1,\dots ,L,$$

(15)

where L is the dimension of the state vector, and $\lambda$ is a scaling parameter.

These sigma points are propagated through the state and measurement equations, and the mean and covariance are recalculated based on the transformed sigma points.

2.3. H-Infinity Filter

The H-Infinity filter, also known as the $H_{\infty }$ filter, is an estimation algorithm based on control theory and signal processing [6]. It is designed to deal with uncertainties, disturbances, and noise in dynamic systems, making it suitable for battery state estimation tasks. The main objective of the H-Infinity filter is to minimize the effects of disturbances and measurement errors on estimation accuracy and to provide robust and reliable state estimates [6].

In contrast to the Kalman filter, which minimizes the expected value of the estimation error covariance, the $H_{\infty }$ filter seeks to minimize the worst-case estimation error under all possible disturbances with bounded energy [7].

The system dynamics are modeled as:

$$\begin{array}{cc}\hfill x_k& =A_{k-1}{x}_{k-1}+B_{k-1}{u}_{k-1}+w_{k-1},\hfill \\ \hfill y_k& =C_k{x}_k+v_k,\hfill \end{array}$$

(16)

where $w_{k-1}$ and $v_k$ represent disturbances and noises.

The $H_{\infty }$ filter aims to find an estimator gain $K_k$ that minimizes the worst-case amplification from the disturbances $[w_{k-1},v_k]$ to the estimation error $e_k=x_k-{\widehat{x}}_{k|k}$, such that:

$$\underset{\begin{array}{c}{w}_{k-1},v_k\\ w_{k-1}^{\top }{w}_{k-1}+v_k^{\top }{v}_k\le 1\end{array}}{sup}{e}_k^{\top }{e}_k<{\gamma }^2,$$

(17)

where $\gamma$ is a prescribed attenuation level.

The $H_{\infty }$ filter algorithm involves solving a Riccati difference equation at each time step. The filter equations are similar in structure to the Kalman filter but differ in the gain calculation.

The filter equations are:

Prediction Step:

$${\widehat{x}}_{k|k-1}=A_{k-1}{\widehat{x}}_{k-1|k-1}+B_{k-1}{u}_{k-1},$$

(18)

$$P_{k|k-1}=A_{k-1}{P}_{k-1|k-1}{A}_{k-1}^{\top }+Q_{k-1}.$$

(19)

Update Step:

$$K_k=P_{k|k-1}{C}_k^{\top }{\left(C_k{P}_{k|k-1}{C}_k^{\top }-{\gamma }^{-2}I\right)}^{-1},$$

(20)

$${\widehat{x}}_{k|k}={\widehat{x}}_{k|k-1}+K_k\left(y_k-C_k{\widehat{x}}_{k|k-1}\right),$$

(21)

$$P_{k|k}=P_{k|k-1}-K_k\left(C_k{P}_{k|k-1}-{\gamma }^{-2}{K}_k^{\top }\right).$$

(22)

The adaptive and dual variations of the $H_{\infty }$ filter (AHIF and DHIF) work in the same way as their Kalman filter counterparts. The adaptive $H_{\infty }$ filter adjusts the disturbance attenuation level $\gamma$ or the weighting matrices online based on observed performance, enhancing robustness under varying conditions [35].

2.4. Application to Battery State of Charge Estimation

In the context of battery state estimation, these filters utilize an equivalent circuit model (ECM) of the battery, incorporating elements like the open-circuit voltage ($U_{\mathrm{OCV}}$), internal resistances, and RC networks representing dynamic behaviors.

The state vector typically includes the State of Charge (SOC) and voltages across the RC network capacitors:

$$x_k=\left[\begin{array}{c}{\mathrm{SOC}}_k\\ V_{1,k}\\ ⋮\\ V_{n,k}\end{array}\right].$$

(23)

The SOC can be modeled using the coulomb counting method:

$${\mathrm{SOC}}_k={\mathrm{SOC}}_{k-1}-{\displaystyle \frac{\mathsf{\Delta }t}{C_{\mathrm{nom}}}}{I}_{k-1},$$

(24)

where $I_{k-1}$ is the battery current, $\mathsf{\Delta }t$ is the sampling interval, and $C_{\mathrm{nom}}$ is the nominal capacity.

The voltage across each RC network can be modeled as:

$$V_{j,k}=e^{-{\displaystyle \frac{\mathsf{\Delta }t}{R_j{C}_j}}}{V}_{j,k-1}+R_j\left(1-e^{-{\displaystyle \frac{\mathsf{\Delta }t}{R_j{C}_j}}}\right)I_{k-1},$$

(25)

where $R_j$ and $C_j$ are the resistance and capacitance of the j-th RC element.

The output equation relates the terminal voltage $U_k$ to the state variables:

$$U_k=U_{\mathrm{OCV}}\left({\mathrm{SOC}}_k\right)-\sum _{j=1}^n{V}_{j,k}-R_0{I}_k,$$

(26)

where $U_{\mathrm{OCV}}$ is the open-circuit voltage as a function of SOC, and $R_0$ is the ohmic resistance.

By implementing the filters described above with the appropriate battery model, SOC estimation can be performed accurately and robustly, accounting for model nonlinearities and uncertainties.

In conclusion, both Kalman filters and H-Infinity filters, along with their various adaptations, play significant roles in battery SOC estimation. The choice between them depends on the specific requirements of the application, such as computational complexity, required accuracy, and robustness against disturbances and model uncertainties.

2.5. Digital Signal Processors (DSP)

Digital signal processors (DSPs) are specialized hardware for the computation of digital signals. Computation speed and reliability are key parameters for handling continuous input data streams. Critical control applications like medical diagnostics or other real-time dependent tasks often use DSPs [36,37].

The processors are optimized for the calculation rather than manipulation of digital data or testing of values. DSPs usually go back to the Harvard processor architecture than to the Von Neumann architecture. This massively improves data processing since the architecture uses separate memory to store data and program. The Super Harvard architecture even allows data to be stored in the program memory which can be used to load two data values into the core at the same time.

In this work a DSP is used for state estimation, the CPU cycles needed for the filters applied are measured and compared. Complex pipeline structures as in general-purpose CPUs can be skipped because DSP tasks usually are pure mathematics which do not have cyclic conditions that must be proved. For more advanced and calculation intensive processes for which loops are crucial, the DSP provides additional hardware, called zero-overhead-loop, which makes the loop executable without the overhead of checking the loop conditions. This makes DSP programs predictable, fast and even cycle precise and a DSP is best suited for real-time applications [38].

3. Experimental Setup

The batteries used were Samsung INR18650-29E lithium-ion cells (Samsung Electronics, Seoul, Republic of Korea). The specifications of the batteries were adapted for the stationary energy storage application found in [39], which were implemented in the BMS software. In

Table 1. Specifications of the Samsung INR18650-29E lithium-ion cell [39].

Property	Value
Charge cut-off voltage	4.05 V
Discharge cut-off voltage	2.5 V
Charging current rate	0.5 C
Discharging current rate	1.0 C
Capacity	2200 mAh
Temperature range charging	0–45 °C
Temperature range discharging	−20–60 °C

the specifications used can be found. The batteries were placed in a Weiss KWP 120/70 climate chamber (Weiss Technik GmbH, Reiskirchen, Germany) and tested by a BaSyTec CTS-Lab tester (BaSyTec GmbH, Asselfingen, Germany).

All filters were implemented on the ADSP-21489 EZ-Board (Analog Devices, Inc., Wilmington, NC, USA) in C. The DSP had a processor frequency of 400 MHz and 5 Mbit internal memory. It related to a JTAG ICE and a USB connection to the computer. The software was written with the IDE VisualDSP++ 5.1.2 and used the standard matrix.h library.

The software implementation on the PC was written with Python 3.7.0 using Anaconda Spyder 3.3.1 and the numpy package 1.18.5.

Prior to testing, filter tuning was conducted. The ratio between the covariance values of the system and measurement noise matrices is crucial. Otherwise, the filters suffer from bad selected starting values. The simulation was a parameter sweep (over the initial values of the Kalman filter) done with Python. In contrast to [40] different initial values for every filter were selected, because the filters scale differently with their parameters and the Kalman-filter and H-infinity-filter share just a subset of parameters.

The influence of the number of RC-terms was investigated on the DSP, due to the predictability and cycle-precise execution.

4. Testing Profiles and Procedure

4.1. Profiles

Comparing the effect and accuracy of various SOC estimation methods can be difficult. A first step to a scientific basis is the use of generalized reproducible current profiles. Common profiles as the vehicle driving cycles like in [41,42] do not necessarily include all characteristics to compare different methods, especially if the application changes.

In [13] three profiles were presented for application independent tests. The three profiles were called A, B and C, respectively:

• Profile A described the short term low dynamic behavior
• Profile B the short term high dynamic behavior
• Profile C the long-term behavior with temperature variations.

The basis of all profiles was the synthetic load cycle (SLC) which was a normalized power profile, meaning that the sum of incoming and outgoing charge is zero. Each profile started with a CCCV charge and discharge cycle, following with a CCCV charge to the desired SOC value. After the test the residual charge was determined. For profile C the capacity of the battery must be measured after the test to see whether the capacity has changed during the test. Figure 1 summarizes the general test setup.

4.2. Procedure

Test profile A was run at three different starting SOC values. The most distinct values for lithium-ion batteries are 10%, 50% and 90% [13]. The profile started at 50% was then charged with a C-rate of 0.5 up to 90%. After a relaxation time of 30 min the SLC was performed followed by another 30 min of relaxation. The discharge to 10% SOC was done with 1 C. Test profile A was set up for three different temperatures: 5 °C, 25 °C and 40 °C.

Test profile B was chained by SLC profiles shifted towards the discharge direction to artificially achieve a discharge behavior for the high dynamic test [13]. The profile started at 90% SOC and goes down to 10% SOC. Profile B ran at the same temperatures as profile A.

To assess the long-term stability of the system, Profile C is employed, with a particular emphasis on analyzing the predictive accuracy in response to temperature fluctuations. This profile is constructed upon the repeated execution of the coulomb-neutral SLC profile, maintaining the SOC consistently at 50%. Over a span of 24 h, the temperature undergoes adjustments to three distinct test temperatures. Both the temperature transition and the stabilization period at the target temperature are allotted a duration of 3 h each. Initially, the temperature in the chamber is raised from the starting point of 25 °C to 40 °C, followed by a rest phase. Subsequently, after the second interval, the temperature is brought back down to 25 °C, succeeded by another period of rest. The subsequent step involves cooling the chamber to 5 °C. After the final 3-hour rest phase, the temperature is once again elevated to 25 °C. This entire cycle is reiterated seven times, culminating in a total profile period of seven days.

5. Evaluation Criteria

For a better comparison of different filter techniques, a standardized scoring system was used. Here we only describe the criteria. A detailed mathematical derivation can be found in [13]. Ref. [13] proposed a system of six criteria with a scoring system from 0 (worst) to 5 (best). The criteria were estimation accuracy K_est, drift K_drift, residual charge determination K_res, transient behavior K_trans, failure stability K_fail and temperature stability K_temp.

Table 2. Scoring System for the different error boundaries.

Score P($\mathit{ϵ}$)	Error Boundary $\mathit{ϵ}$
5	0–0.5%
4	0.5–1%
3	1–2%
2	2–4%
1	4–8%
0	>8%

shows the scoring system for different error boundaries $ϵ$ [13].

5.1. Estimation Accuracy ($K_{\mathit{est}}$)

The estimation accuracy criterion $K_{\mathrm{est}}$ quantifies how well the SOC estimation method maintains the estimation error within predefined error boundaries over the test duration.

First, the estimation error $e\left(t\right)$ at time t is calculated as:

$$e\left(t\right)={\mathrm{SOC}}_{\mathrm{ref}}\left(t\right)-{\mathrm{SOC}}_{\mathrm{est}}\left(t\right)$$

(27)

The total time $\mathsf{\Delta }{t}_i$ during which the estimation error remains within each error boundary ${ϵ}_i$ is determined:

$$\mathsf{\Delta }{t}_i=\sum _{\begin{array}{c}t\in [0,T_{\mathrm{total}}]\\ \left|e\left(t\right)\right|\in {ϵ}_i\end{array}}\mathsf{\Delta }t$$

(28)

where $\mathsf{\Delta }t$ is the sampling interval, and $T_{\mathrm{total}}$ is the total test duration.

The proportion ${\alpha }_i$ of the total test duration spent within each error boundary is calculated as:

$${\alpha }_i={\displaystyle \frac{\mathsf{\Delta }{t}_i}{T_{\mathrm{total}}}}$$

(29)

The estimation accuracy score $K_{\mathrm{est}}$ is then computed by:

$$K_{\mathrm{est}}=\sum _i\left(P\left({ϵ}_i\right)·{\alpha }_i\right)$$

(30)

This calculation weighs the time spent within each error boundary by the corresponding point score and sums these values across all boundaries.

5.2. Drift ($K_{\mathit{drift}}$)

The drift criterion $K_{\mathrm{drift}}$ evaluates the tendency of the SOC estimation to accumulate errors over time due to systematic inaccuracies.

A linear regression is performed on the estimation error $e\left(t\right)$ over the test duration to obtain the drift rate a:

$$e\left(t\right)=at+b$$

(31)

where t is time, a is the drift rate (error per unit time), and b is the intercept.

The drift error over a standard time period $t_{\mathrm{std}}$ (e.g., one hour or one week) is calculated:

$$e_{\mathrm{drift}}=a·t_{\mathrm{std}}$$

(32)

The drift score $K_{\mathrm{drift}}$ is determined by the point score corresponding to $|e_{\mathrm{drift}}|$:

$$K_{\mathrm{drift}}=P\left(|e_{\mathrm{drift}}|\right)$$

(33)

This criterion ensures that estimators with minimal long-term error accumulation receive higher scores.

5.3. Residual Charge Determination ($K_{\mathit{res}}$)

The residual charge determination criterion $K_{\mathrm{res}}$ assesses the accuracy of the SOC estimation at the end of the test profile by comparing it with the actual residual capacity measured after the test.

The residual estimation error is calculated as:

$$e_{\mathrm{res}}={\mathrm{SOC}}_{\mathrm{est}}\left(t_{\mathrm{end}}\right)-{\mathrm{SOC}}_{\mathrm{res}}$$

(34)

where:

$${\mathrm{SOC}}_{\mathrm{res}}={\displaystyle \frac{C_{\mathrm{res}}}{C_{\mathrm{act}}}}$$

(35)

In this equation, ${\mathrm{SOC}}_{\mathrm{est}}\left(t_{\mathrm{end}}\right)$ is the estimated SOC at the end of the test, $C_{\mathrm{res}}$ is the residual capacity determined by discharging the battery at the end of the test, and $C_{\mathrm{act}}$ is the actual capacity measured after the test.

The score $K_{\mathrm{res}}$ is then:

$$K_{\mathrm{res}}=P\left(|e_{\mathrm{res}}|\right)$$

(36)

This criterion emphasizes the importance of accurate SOC estimation at the end of the test, which is critical for applications requiring precise knowledge of the remaining capacity.

5.4. Transient Behavior ($K_{\mathit{trans}}$)

The transient behavior criterion $K_{\mathrm{trans}}$ evaluates how quickly the SOC estimation converges to the true SOC when starting from an incorrect initial value.

First, the initial estimation error $e_{\mathrm{init}}$ is defined:

$$e_{\mathrm{init}}={\mathrm{SOC}}_{\mathrm{ref}}\left(t_0\right)-{\mathrm{SOC}}_{\mathrm{est}}\left(t_0\right)$$

(37)

The estimation error after a specified transient period $t_{\mathrm{trans}}$, typically 10% of the total test duration $T_{\mathrm{total}}$, is determined:

$$e_{\mathrm{trans}}={\mathrm{SOC}}_{\mathrm{ref}}(t_0+t_{\mathrm{trans}})-{\mathrm{SOC}}_{\mathrm{est}}(t_0+t_{\mathrm{trans}})$$

(38)

The transient score $K_{\mathrm{trans}}$ is calculated as:

$$K_{\mathrm{trans}}=P\left(|e_{\mathrm{trans}}|\right)·{\displaystyle \frac{|e_{\mathrm{init}}|}{{\mathrm{SOC}}_{\mathrm{ref}}\left(t_0\right)}}$$

(39)

This scaling ensures that estimators are rewarded for rapid convergence from larger initial errors.

5.5. Temperature Stability ($K_{\mathit{temp}}$)

The temperature stability criterion $K_{\mathrm{temp}}$ evaluates the consistency of the SOC estimation performance across different temperatures.

For each criterion x, the standard deviation ${\sigma }_x$ of the scores obtained at different temperatures is calculated:

$${\sigma }_x=\sqrt{{\displaystyle \frac{1}{m}}\sum _{i=1}^m{\left(K_{x,i}-{\overline{K}}_x\right)}^2}$$

(40)

where:

• $K_{x,i}$ is the score for criterion x at temperature $T_i$.
• ${\overline{K}}_x$ is the mean score for criterion x across all temperatures.
• m is the number of temperature points.

The temperature stability score $K_{\mathrm{temp},x}$ is then:

$$K_{\mathrm{temp},x}=P(e=0)-2{\sigma }_x$$

(41)

The overall temperature stability score is the average of the individual scores:

$$K_{\mathrm{temp}}={\displaystyle \frac{1}{n}}\sum _x{K}_{\mathrm{temp},x}$$

(42)

where n is the number of criteria considered (e.g., estimation accuracy, drift, transient behavior, residual charge determination).

The failure stability criterion was skipped in this work because of the additional complexity and timing demand to rerun all tests with incorrect voltage and current values and due to the extra requirements of changing the model parameters.

6. Results

The effectiveness of filter-based methods for state of charge estimation heavily relies on the accuracy of the battery model used. Like the findings of [4], it was observed that all filters exhibit decreased performance at lower temperatures. This decline in performance is likely due to unmodeled heating effects and increased internal resistance at low temperatures. Zaki et al. [4] (2025) reported higher estimation errors for the EnKBF and DEnKBF filters at lower temperatures, highlighting the challenges of SOC estimation in such conditions. In this work, we utilized the model developed by [15] and compared it with the one from [40] to examine the effects of different modeling approaches and validation techniques. Our validation method and criteria are designed to be applicable to a wide range of lithium-ion battery models, reflecting a general approach suitable for various chemistries.

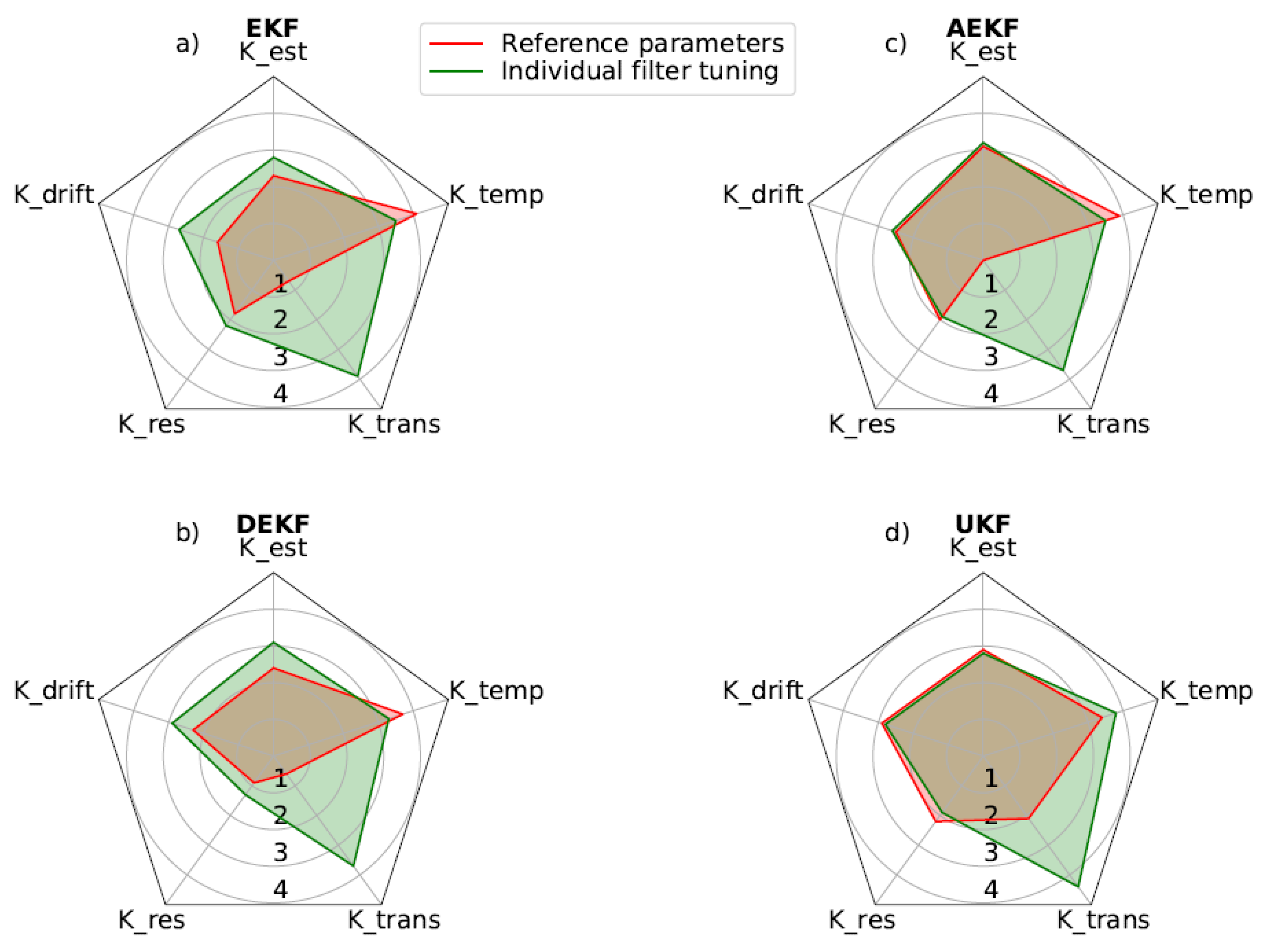
As shown in Figure 2, the comparison between the reference from [40] and our evaluation highlights the influence of using own battery models. Except for the temperature coefficient K_temp, the performance of all criteria is significantly affected using a different model. The smaller temperature range in our work, especially the lower scores at reduced temperatures, results in a reduced value for K_temp.

The dependency on the battery model is evident in all other parameters, but the unscented Kalman filter stands out as it shows more consistent results, suggesting it is less sensitive to model variations. This is also due to a different approach to noise approximation and the consequences of using a mismatched battery cell, which introduces more noise.

Fine-tuning filter parameters is essential for each method. This work opted for a measurement noise matrix value that was significantly higher, by a factor of about 10,000, compared to [40]. The covariance values for overpotentials had a minor impact across a wide range of parameters. A higher initial uncertainty in SOC estimation led to better transient behavior for all filters, as they could compensate for the expected initial inaccuracy. Initially, the convergence shown in Figure 2 was not ideal because the filter parameters were not well-matched with the battery model. After adjusting the covariance matrix, the K_trans score improved by 3.2 for the EKF, 3.7 for the AEKF, 3.1 for the DEKF, and 2.3 for the UKF.

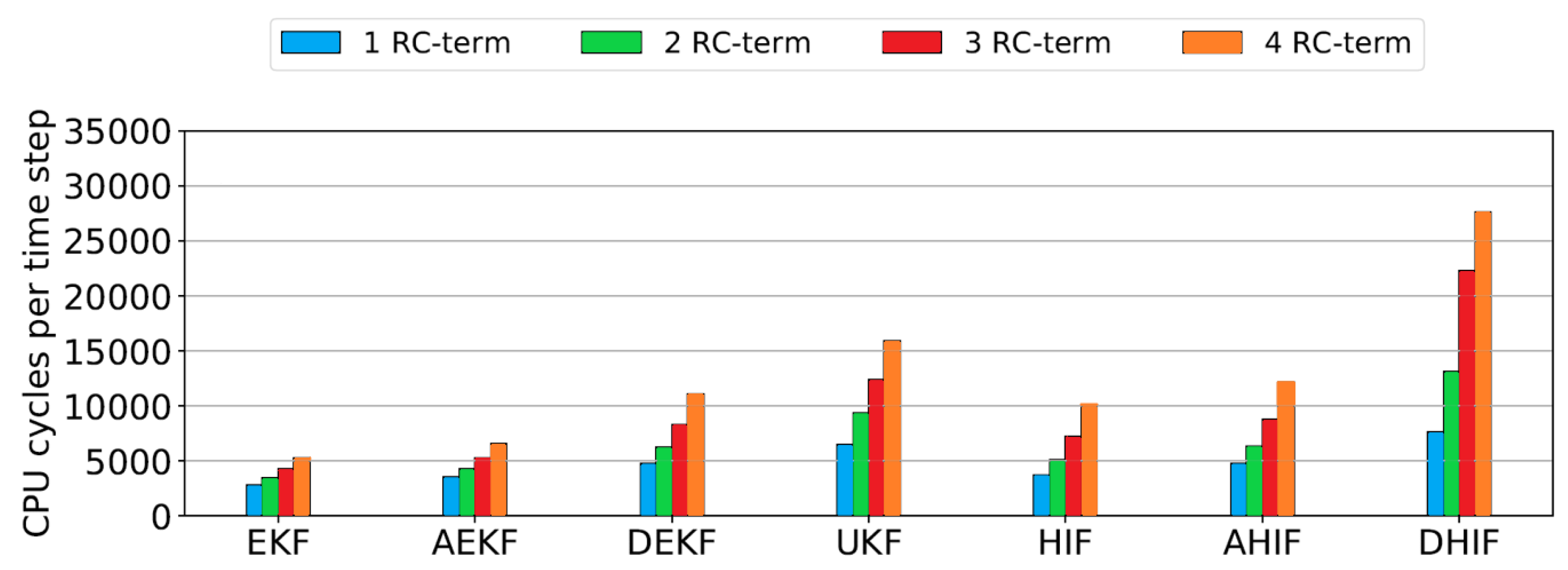
To investigate the relationship between the number of RC-terms in the model and the computation time, all filters were executed on a digital signal processor. The consistent CPU cycle count offered by a DSP allows for precise measurement of computation steps. As computation time in seconds varies across different processor platforms, we measured computation steps instead. These values can be converted to time by dividing by the processor’s frequency if needed.

The DSP compiler was set up to produce optimized code, using the internal compiler in VisualDSP++ without additional adjustments. Among the filters, the extended Kalman filter required the fewest computation cycles, ranging from 2825 cycles with one RC-term to 5278 cycles with four RC-terms. On the DSP, only the size of the matrices matters because the system and the filter’s mathematical structure are fixed. The correlation between the number of RC-terms and computation cycles is nearly linear, as anticipated, due to the matrix dimensions for the filters increasing linearly with more RC-terms. The increase in cycles per RC-term varied from about 700 for the EKF to 6000 for the dual H-infinity filter. In general, H-infinity filters had a steeper increase in cycles than Kalman filters. The adaptive extended Kalman filter recalculates the covariance matrices of measurement and process noise at each time step, unlike the EKF, which has predetermined parameters. Both dual filters run their algorithms twice per time step. H-infinity filters typically require more computation steps due to additional multiplications and inversions. Figure 3 presents a summary of the CPU cycle counts for the seven filters we tested.

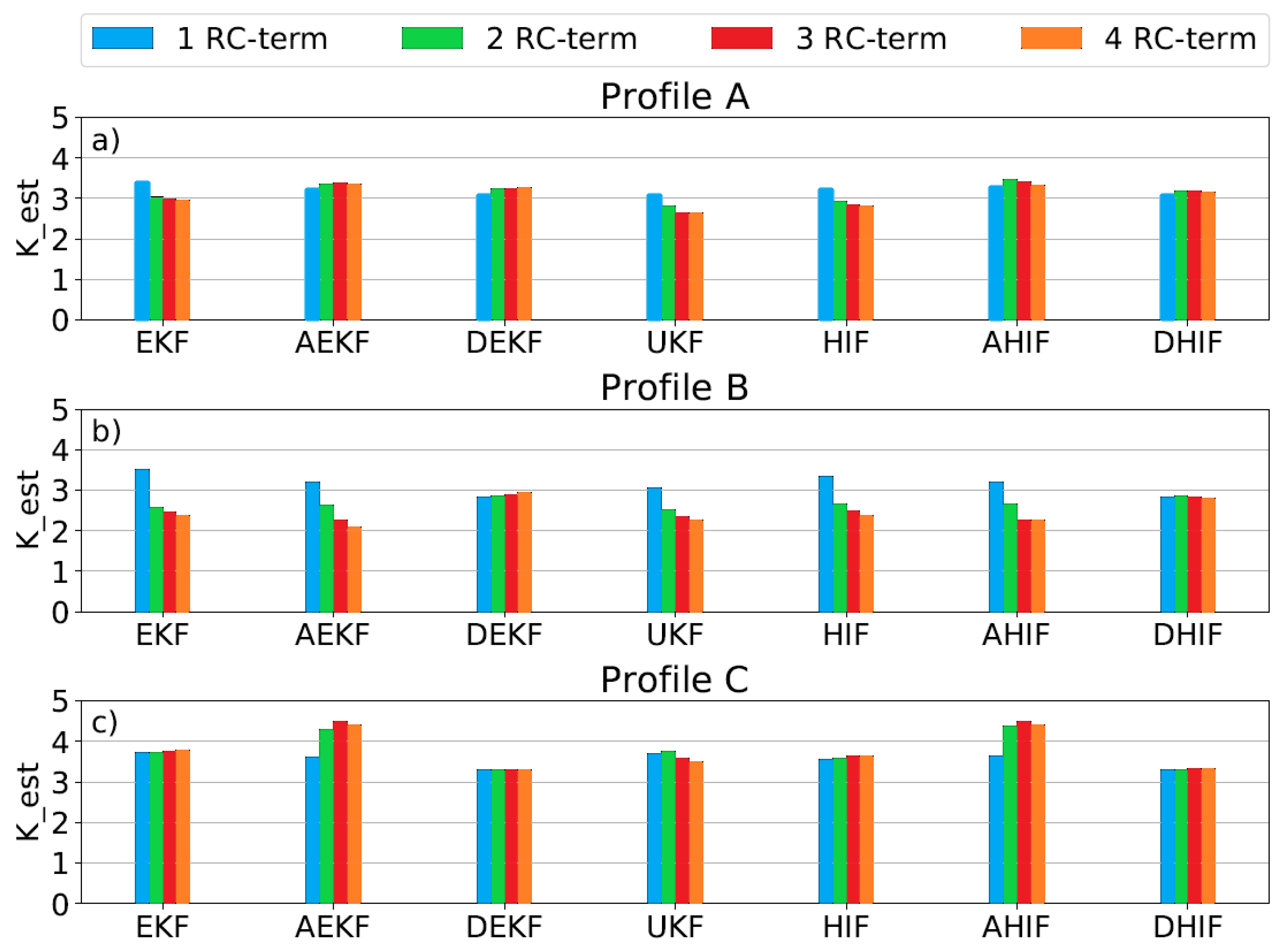
Exploring the link between the number of RC-terms in a battery model and the precision of SOC estimation is also crucial. The model by [15] features four RC-terms. For each filter, across all test profiles, and for each model variant, we computed the parameter K_est from the validation criteria.

The findings, illustrated in Figure 4, reveal that the extended Kalman filter and the H-infinity filter experience a drop in estimation accuracy for profiles A and B when utilizing more than one RC-term. In contrast, the adaptive filters achieved their best results for profiles A and C with two and three RC-terms, respectively. The adaptive filters with three RC-terms performed notably well in profile C. The unscented Kalman filter displayed a similar pattern to the EKF and HIF in profiles A and B, with a significant decrease in performance when moving from one to two RC-terms. Profile B shows the most considerable variation in scores, with values decreasing for all filters except the dual versions. This contrasts with the findings of [40], which indicated that additional RC-terms could enhance accuracy under dynamic loads. As batteries heat up during dynamic loads, models failing to emulate this behavior can lead to errors. However, dual filters seem to counteract this issue, thereby maintaining consistent performance in profile B.

Adaptive filters excel under low dynamic loads and can even improve their scores with an increased number of RC-terms. Yet, under dynamic conditions, they struggle as they take time to search for the correct filter parameters, leading to a slow convergence towards the accurate SOC value, and ultimately scoring similarly to their non-adaptive counterparts.

In conclusion, no single filter consistently outperforms the others across all conditions. Compromises must be tailored to each specific situation. The results depicted in Figure 4 do not support the notion that more RC-terms invariably result in enhanced estimation accuracy. On average, models with two RC-terms tend to yield the best performance.

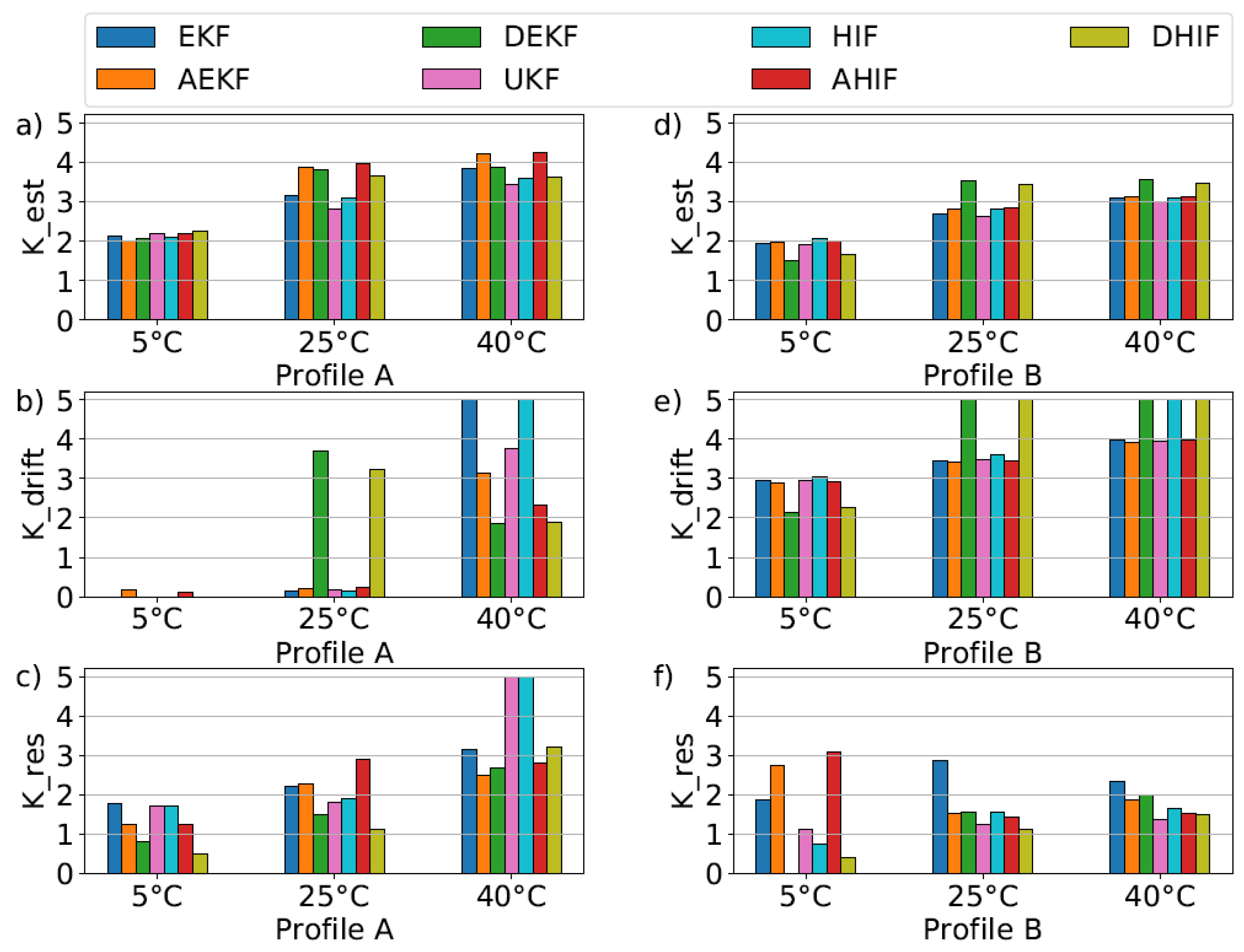
For our analysis, we compared the Kalman and H-infinity filters using a model with two RC-elements. We evaluated the filters across all five validation criteria, starting with transient behavior and the K_trans score. The greatest discrepancies occurred at 5 °C, with scores ranging from 2.64 for AEKF to 4.31 for UKF. The UKF’s performance is less affected by the model, which is advantageous at lower temperatures where model inaccuracies are more pronounced, making it the top performer in cold conditions. At room temperature (25 °C), the scores were close, between 4.16 and 4.44, indicating similar transient behaviors among the filters. At a temperature of 40 °C, the UKF led again with a score of 4.42. Overall, the UKF consistently scored highest on average for transient behavior, with H-infinity variations outperforming their Kalman counterparts for this metric.

The temperature analysis for profiles A and B is encapsulated by the K_temp criterion. For the low-dynamic profile A, all filters scored similarly, around 3.0. However, for profile B, both dual filters scored over 1 point lower than the highest score for K_temp, despite nearly topping the chart for profile A.

In the long-term, temperature-dependent profile C, all filters achieved a K_est score above 3.0. Adaptive filters led with scores of 4.3 (Kalman) and 4.37 (H-infinity). They also maxed out at 5.0 for K_drift and K_res. In contrast, both dual filters scored the lowest across all criteria, with DEKF scoring 3.31 for K_est, 2.71 for K_drift, and 2.28 for K_res. DHIF was slightly better with scores of 3.31, 2.74, and 3.3, respectively.

Figure 5 summarizes the other criteria. It shows that filters generally score higher in profile A than in profile B and perform better at higher temperatures. The score differences for various temperatures in profile A range from 0.6 to 1.8, and in profile B from 0.7 to 2.0. At the same temperature, corresponding Kalman and H-infinity filters yield similar results, with differences below 0.27 for profile A and 0.14 for profile B. Notably, the specific type of filter within the Kalman or H-infinity family has a more significant impact on the estimation score than the choice between Kalman or H-infinity filters. The maximum deviation for K_est at 5 °C for profile A is only 0.25, indicating that all filters can estimate SOC with comparable quality for low-dynamic profiles.

However, the drift score K_drift presents a different picture, as shown in Figure 5b,e. The filters struggle to match the reference SOC precisely at low temperatures. Model inaccuracies and higher internal resistance values at lower temperatures hinder the filters’ ability to converge swiftly to the correct SOC. For profile A, the type of filter variation again plays a more decisive role than the filter family itself. At 5 °C, adaptive filters score above 0, while dual filters excel at 25 °C. At 40 °C, the standard filter versions perform best. Profile B results are more uniform, with scores increasing alongside temperature. Both dual filters hit the top score of 5.0 at 25 °C and 40 °C. The difference between filters in profile B is minimal, except for EKF and HIF at 40 °C, which have a notable gap of 1.03. H-infinity filters generally score higher in profile B.

Figure 5c,f display the residual charge scores. The results vary significantly across different profiles and temperatures. For profile B, most filters score lower than in profile A. While scores for profile A rise with temperature, this trend does not hold for profile B. The range of scores for profile A spans from 0.49 to 5.0, and for profile B from 0.0 to 3.09. EKF outperforms HIF at every temperature for profile B.

Despite lower scores for EKF in K_est and K_drift compared to HIF in profile B across all temperatures, this does not necessarily correlate with residual charge estimation, suggesting that drift behavior and residual charge estimation are independent.

Industrial Applicability

Insights gained from this study are directly relevant to the industrial deployment of battery management systems (BMS), especially in sectors such as electric vehicles and stationary energy storage systems. Implementing state-of-charge estimation algorithms on hardware platforms with constrained computational resources, such as digital signal processors (DSPs), poses significant real-world challenges.

By evaluating the computational demands of Kalman and H-Infinity filters on a DSP, practical guidance is provided for industry practitioners. The successful implementation of these filters on a DSP demonstrates their feasibility for real-time applications, which is a critical requirement for industrial systems.

Moreover, the detailed assessment of estimation accuracy versus computational load helps in selecting SOC estimation methods that are both reliable and efficient, aligning with the performance and cost considerations inherent in industrial settings. The methodologies and results presented can aid engineers in optimizing BMS designs for commercial products, ensuring robust SOC estimation under the practical constraints of hardware capabilities and operational environments.

7. Conclusions and Outlook

This paper conducted a comprehensive comparative analysis of seven filters for battery state of charge (SOC) estimation, including the Extended Kalman Filter (EKF), Adaptive Extended Kalman Filter (AEKF), Dual Extended Kalman Filter (DEKF), Unscented Kalman Filter (UKF), H-Infinity Filter (HIF), Adaptive H-Infinity Filter (AHIF), and Dual H-Infinity Filter (DHIF). The observations indicate that the performance of these filters tends to decrease at lower temperatures, corroborating the results reported by [4] for the ensemble Kalman-Bucy filters. This consistent observation across different filtering methods emphasizes the need for improved models and estimation techniques that account for temperature effects in lithium-ion batteries. Integrating aging mechanisms with machine learning approaches, as demonstrated by [11], may offer a pathway to address these challenges. By incorporating detailed insights into battery degradation processes, higher estimation accuracy under varying operating conditions can be achieved.

The impact of the battery model on estimation accuracy and the computational demand on a digital signal processor (DSP) were examined. Three test profiles and a standardized validation method were applied to evaluate all filters. Through comparison with a reference implementation and subsequent individual filter tuning, the filters’ performance for the specific battery cell used was enhanced.

By implementing multiple filter variants using a consistent equivalent circuit battery model and standardized testing procedures, this work addresses the lack of comprehensive comparative studies identified in the literature. The detailed mathematical formulations and evaluation criteria provided enhance the reproducibility of the study and facilitate further research in this area. The evaluation of computational demands on DSP hardware offers practical insights into the suitability of each filter for real-time applications with limited processing capabilities.

The validation method proved robust as it yielded consistent results across tests. A notable issue, transient behavior, was addressed through parameter adjustments. All filters exhibited low drift scores at temperatures below 40 °C, which aligns with the thermal effects observed during charge and discharge cycles. This phenomenon warrants further investigation and should be incorporated into future modeling efforts. Future research could explore the integration of aging mechanism analyses with machine learning techniques, as proposed by [11], to develop more accurate and robust SOC estimation methods that can handle abnormal operating conditions like slight overcharging.

In conclusion, no single filter stood out as the definitive choice across all scenarios; performance was generally consistent overall. Kalman and H-Infinity filters performed similarly, although H-Infinity filters showed quicker convergence from incorrect SOC initialization. Considering both estimation accuracy and computational load, the EKF and HIF demonstrated solid performance, making them reliable choices for general applications. These findings provide valuable guidance for selecting appropriate SOC estimation methods for specific applications, balancing estimation accuracy and computational efficiency.

The analysis of the computational demands on a DSP adds practical relevance, especially for real-time applications in industrial settings such as electric vehicles and stationary energy storage systems. Implementing SOC estimation algorithms on resource-constrained hardware requires a balance between accuracy and efficiency. The insights gained from this study guide practitioners in selecting SOC estimation methods that meet computational limitations while providing reliable performance in real-world deployment.

A common trend observed was the reduced performance of all filters at lower temperatures, likely due to unmodeled heating effects, suggesting a need for improved model parameter extraction methods. Establishing a standardized measurement setup is essential to ensure not only filter comparison but also measurement reliability. While the validation method is broadly applicable, it can be further tailored with additional criteria for specific applications. Moreover, exploring methods that integrate aging mechanisms with data-driven models, such as the approach by [11], could enhance model accuracy and adaptability.

Experiments with different battery cells, particularly for automotive use, should extend to temperatures as low as −40 °C, given that sub-zero operations were not covered in this work. Future research should also explore the adaptation of the methodology for other battery chemistries, including solid-state batteries, and consider integrating advanced estimation techniques that combine physical models with machine learning, to enhance the generalizability and industrial applicability of the findings. By providing a robust foundation for such studies, this work facilitates advancements in reliable and efficient battery management systems.