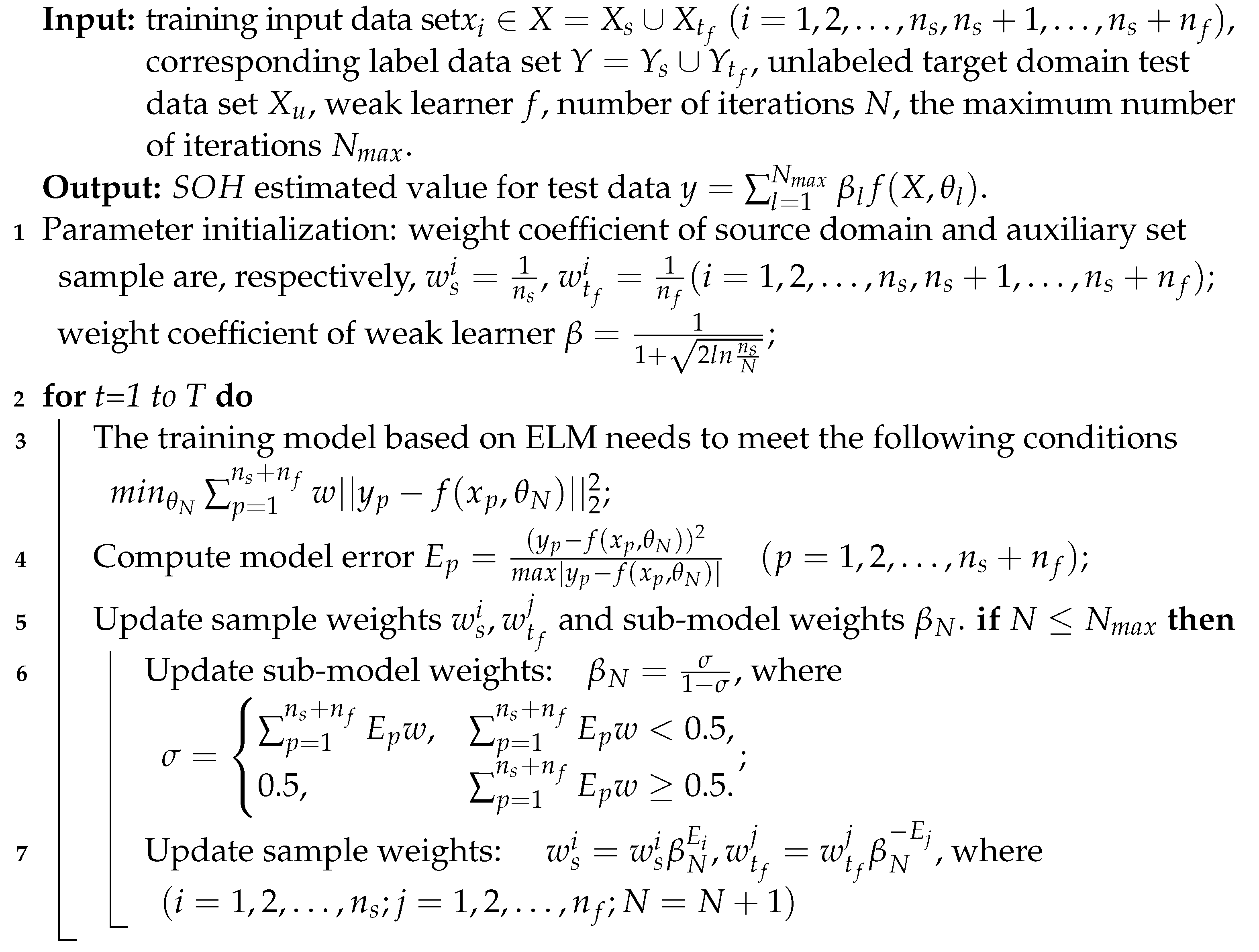State of Health Estimation for Lithium-Ion Battery Based on Sample Transfer Learning under Current Pulse Test

Abstract

Considering the diversity of battery data under dynamic test conditions, the stability of battery working data is affected due to the diversity of charge and discharge rates, variability of operating temperature, and randomness of the current state of charge, and the data types are multi-sourced, which increases the difficulty of estimating battery SOH based on data-driven methods. In this paper, a lithium-ion battery state of health estimation method with sample transfer learning under dynamic test conditions is proposed. Through the Tradaboost.R2 method, the weight of the source domain sample data is adjusted to complete the update of the sample data distribution. At the same time, considering the division methods of the six auxiliary and the source domain data set, aging features from different state of charge ranges are selected. It is verified that while the aging feature dimension and the demand for target domain label data are reduced, the estimation accuracy of the lithium-ion battery state of health is not affected by the initial value of the state of charge. By considering the mean absolute error, mean square error and root mean square error, the estimated error results do not exceed 1.2% on the experiment battery data, which highlights the advantages of the proposed methods.

1. Introduction

Lithium-ion batteries have the advantages of high operating voltage, high energy density, long cycle life, no memory effect, and environmental friendliness. They have been widely used in portable electronic devices such as mobile phones and notebook computers, and are gradually expanding into the fields of electric vehicles and large battery energy storage. As one of the important energy storage technologies, lithium-ion batteries play an important role in changing the energy consumption structure and electrifying traditional energy sources [1,2,3,4]. However, the storage capacity of lithium-ion batteries will continue to decline as they age, which shows a decrease in power, causing the battery capacity to decay and the internal resistance to increase. In existing research, battery state of health (SOH) is usually used as a quantitative indicator to evaluate battery aging. Nevertheless, the battery SOH will be affected by many factors, such as temperature, discharge depth and state of charge (SOC), etc., which further increases the difficulty of estimating the battery SOH. Therefore, in order to avoid safety hazards caused by battery capacity fading and maximum available power reduction, it is crucial to select an appropriate estimation method to complete battery SOH identification.

Generally speaking, these methods are mainly divided into two categories: traditional estimation methods and data-driven estimation methods.

Traditional methods focus on identifying and analyzing important external characteristic parameters in lithium-ion batteries. They usually analyze the collected experimental data such as battery current, voltage, temperature, etc., and relatively directly obtain the characteristic parameters that can reflect battery degradation and estimate battery SOH. The method includes experimental analysis method [5], electrochemical model method [6] and equivalent circuit model method [7].

The experimental analysis method evaluates the battery SOH by directly measuring certain characteristic parameters of the battery, mainly including capacity measurement, ohmic internal resistance measurement and impedance measurement. Although the experimental analysis method can accurately calibrate the battery SOH, the limitations of battery experimental equipment, experimental sites, and experimental test plans will increase the difficulty of implementing this method [8]. The electrochemical model is a first-principle model that can not only accurately simulate the external characteristics of the battery, but also simulate the distribution and changes in the internal characteristics [9]. The electrochemical model can deeply describe the microscopic reactions inside the battery and has very clear physical meanings. However, the electrochemical model contains complex partial differential equations and numerous electrochemical parameters, which not only brings accuracy advantages but also greatly increases the complexity and computational load of the model. A large number of unmeasured parameters in the model affect the application of the model in battery management systems, and its ability to dynamically track changes in environmental conditions is limited. The equivalent circuit model method usually uses traditional circuit components (such as capacitors, internal resistances, voltage sources, etc.) to form a circuit network to describe the external characteristics of the battery. The equivalent circuit model has good applicability to various working states of the battery. The state equation of the model can be easily derived, and the dynamic response and attenuation behavior of the battery can be constructed by identifying the model parameters [10]. However, the estimation results under this method usually depend on the structure of the equivalent circuit, resulting in increasing model errors.

Since the aging process of a lithium-ion battery is a dynamic coupling process and its internal electrochemical mechanism is very complex, traditional battery SOH estimation methods have problems such as model complexity and limited robustness, dynamic adaptability and accuracy. They also have limited ability to describe the dynamic and static comprehensive characteristics of lithium-ion batteries, which is not conducive to practical application. The data-driven method provides another solution for estimating battery SOH. By collecting a large amount of historical data and analyzing the original data, we can only establish the relationship between battery capacity and external features from the perspective of data information, without deeply exploring the complex internal mechanism changes in lithium-ion batteries. Relying on the data-driven method’s ability to autonomously learn data information, this method has received widespread attention in battery SOH estimation [11,12,13,14].

Data-driven methods include the optimization algorithm method, sample entropy method, performance characteristics method, and machine learning method [15,16,17,18,19,20]. The optimization algorithm method used is to identify the battery model parameters through a suitable algorithm and then use the model parameters to estimate the battery SOH. A multi-time joint framework for predicting the battery SOC, SOH and SOP (state of power) has been established in [18]. The sample entropy method is a useful tool for assessing the predictability of time series, while also quantifying the regularity of the data series. For example, in [21], Sun et al. have established a battery capacity model through the sample entropy of voltage and temperature sequences, and then have estimated the battery SOH. In addition, the data-driven method can also complete the battery SOH estimation by analyzing the aging characteristics related to the degradation process of lithium-ion batteries, that is, the performance characteristics method. This method is to establish a mapping relationship between these parameters and the lithium-ion battery capacity through the evolution of dominant characteristics during the degradation process [22,23]. These dominant parameters are usually named aging features. Most of the current research focuses on the aging features that are obtained in a relatively stable working environment with a single working mode. The aging features obtained in this way are time-consuming and unfavorable for practical development. Machine learning only relies on battery historical data and uses advanced algorithms to train complex non-linear degradation behaviors of battery to achieve accurate estimation of the battery SOH [24,25,26,27,28]. Commonly used methods include neural networks (NN), support vector machines (SVM), Monte Carlo, Gaussian process regression (GPR) and long short-term memory networks (LSTM), etc. Although the data-driven method is easy to implement, the implementability of this method is based on sufficient aging data, and it usually takes several months or even longer to obtain aging data. That is to say, there are several issues with these methods, which have to be overcome: (1) Most references that extract the battery feature need to consider the battery’s entire working condition, which increases the computing burden and lab force. (2) Different working conditions will affect the performance of the lithium-ion battery in reality, but most research has extracted features from one single stable working condition (e.g., 1 C charging/discharging rate), and the performance of these features under dynamic working conditions is doubtful.

In summary, considering that in actual scenarios, batteries usually work in complex and changeable environments, it is often necessary to obtain useful battery aging features in a very short time to perform battery SOH calibration. At the same time, considering the practical factors of the high cost of obtaining label data in the battery field, the insufficient amount of data is directly related to the effect of data information analysis and mining and affects the accuracy of the battery SOH estimation. Therefore, this paper considers how to obtain effective battery data information from the current pulse test stage, extract battery aging features in a short time, and complete accurate battery SOH estimation under small sample data.

Based on the above analysis, this paper addresses the issues discussed above from three aspects. First, the response voltage curve characteristics of the pulse test current at four rates are analyzed, and the aging features in a very short time that can reflect the battery capacity decay are extracted. Then, the proposed method in this paper is verified in two cases. The first case is based on the complete current pulse test data and considers using the aging features under all SOC intervals as the battery SOH estimation model input while verifying the universality of the proposed method in this paper. The second case is to assume that the current pulse test process is incomplete while ensuring that the auxiliary data and the source domain data set come from aging feature data in different SOC intervals. Six ways of dividing the auxiliary and the source domain data set are considered to verify the mapping relationship for battery SOH estimation model of the proposed method under different SOC intervals is not affected. Finally, it is also verified that the proposed method can still ensure the accuracy of lithium-ion battery SOH estimation in the above two application modes, whether in a single-temperature operating mode or in different temperature operating modes.

In detail, the main contributions of this paper are summarized as follows:

(1)

This paper analyzes the voltage response curve characteristics under pulse current, and aging features are extracted over a very short time, which provides a basis for establishing the nonlinear relationship between the battery SOH and the aging feature.

(2)

In the case of inconsistent initial SOC values, the proposed method can still ensure that the estimation accuracy of the battery SOH under different SOC interval is not affected.

(3)

The proposed method in this paper can still ensure the battery SOH estimation accuracy while reducing the model feature dimension and the demand for target domain label data.

This paper is organized as follows: Section 2 introduces the method of extracting the aging feature. The related algorithms Tradaboost.R2 are introduced in Section 3. It also still introduces the battery SOH estimation under the complete SOC range. Battery SOH estimations under different SOC ranges are presented in Section 4. The conclusions and future work are given in Section 5. The specific framework for the proposed method is shown in Figure 1.

2. Aging Feature under Pulse Current

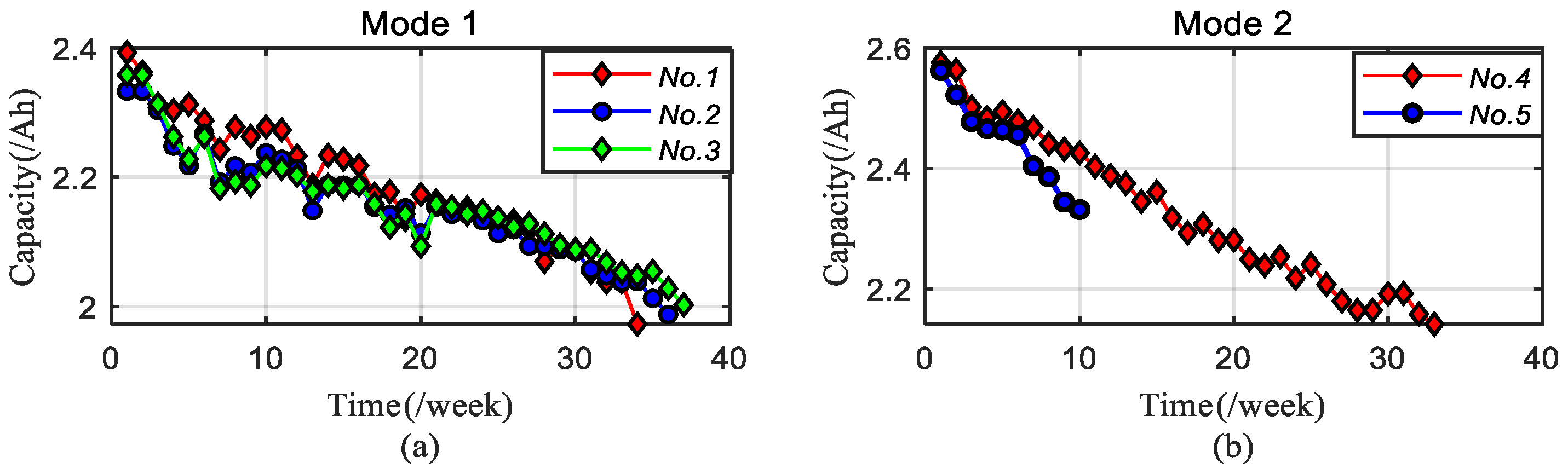
In this work, lithium iron phosphate battery cells (LFP/C) are considered, while

Table 1. The working mode condition for battery data.

Test Mode	LFP/C Battery	Temperature	Average SOC
B1	No.1, No.2, No.3	35 °C	50%
B2	No.4, No.5	25 °C	50% (arbitrary)

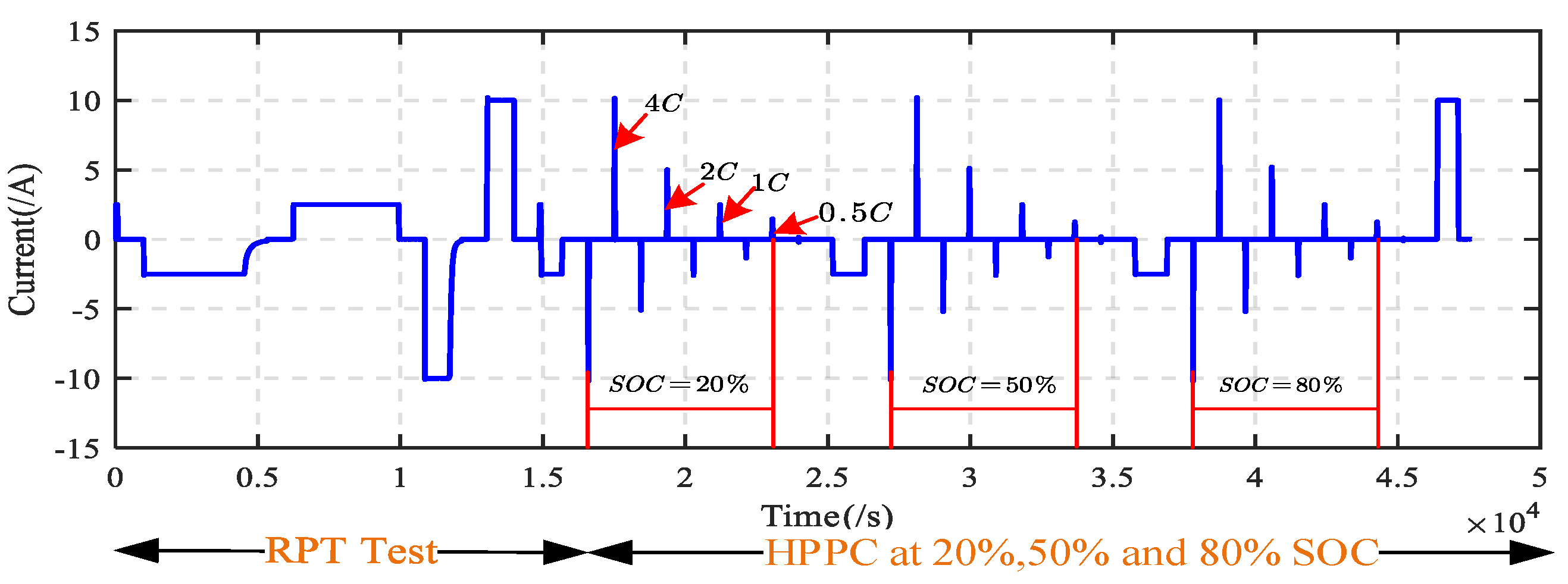
describing the cell’s basic electric parameters. Five LFP/C cells are aged at two different temperatures, i.e., $35$ °C and $25$ °C, which is divided into two modes and summarised in Table 1. The capacity variations in the five LFP/C cells are presented in Figure 2. During the non-constant charging and discharging stage, three SOC and pulse currents at four rates are considered. 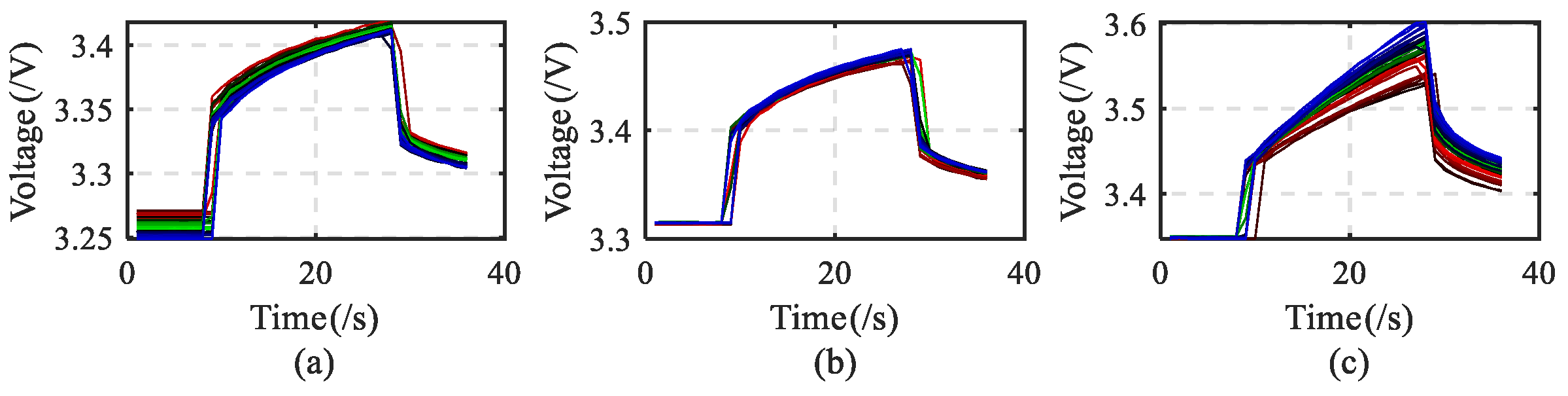The whole battery testing process are shown in Figure 3. First, the battery is charged to SOC = 20%, SOC = 50% and SOC = 80% with a constant current of 1 C rate. And in each SOC stage, pulse charge and discharge currents of 4 C, 2 C, 1 C and 0.5 C are applied to the battery. A negative current indicates a charging process and a positive current indicates a discharging process. Figure 4 shows the current changes in the battery under the pulse test.

The test process is divided into three parts, namely reference performance test (RPT), which is also called capacity test, pulse test and aging test. RPT test is used for capacity calibration. The aging features extracted in this paper come from the battery data in the pulse test stage, while the aging test is used to accelerate the aging of the battery. This paper considers two temperature modes, that is, accelerated aging modes with different temperatures selected during the aging test stage.

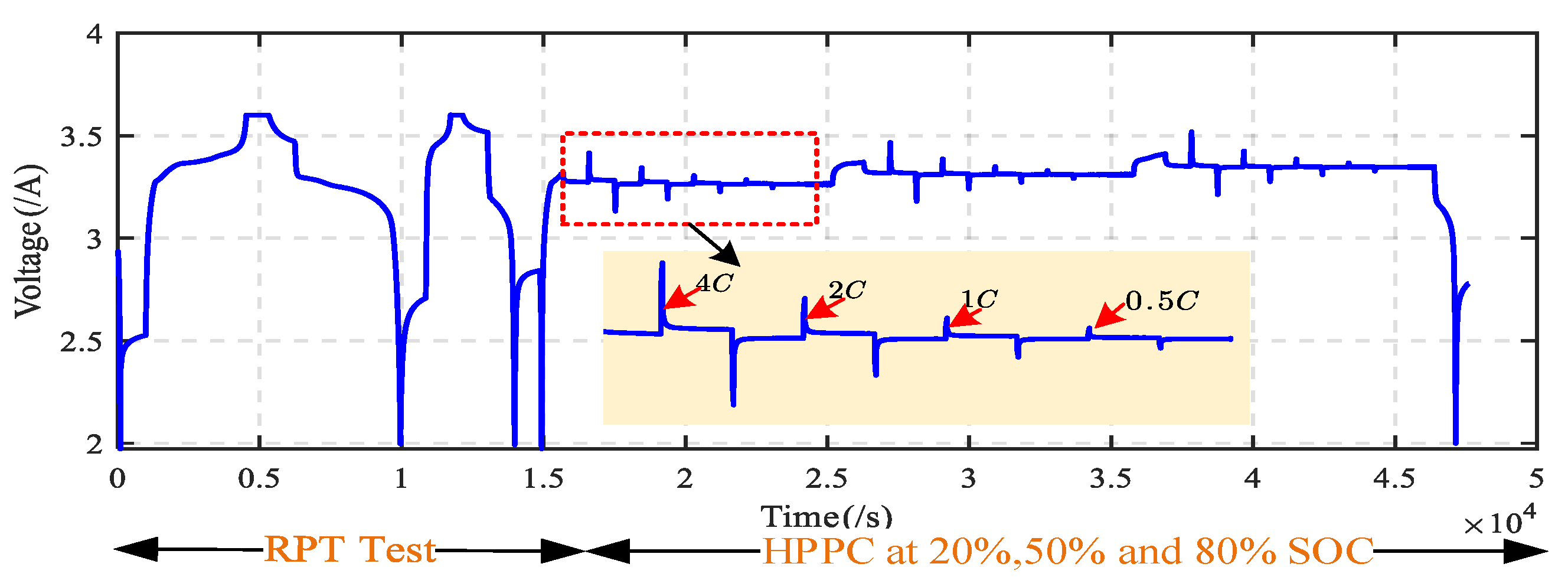
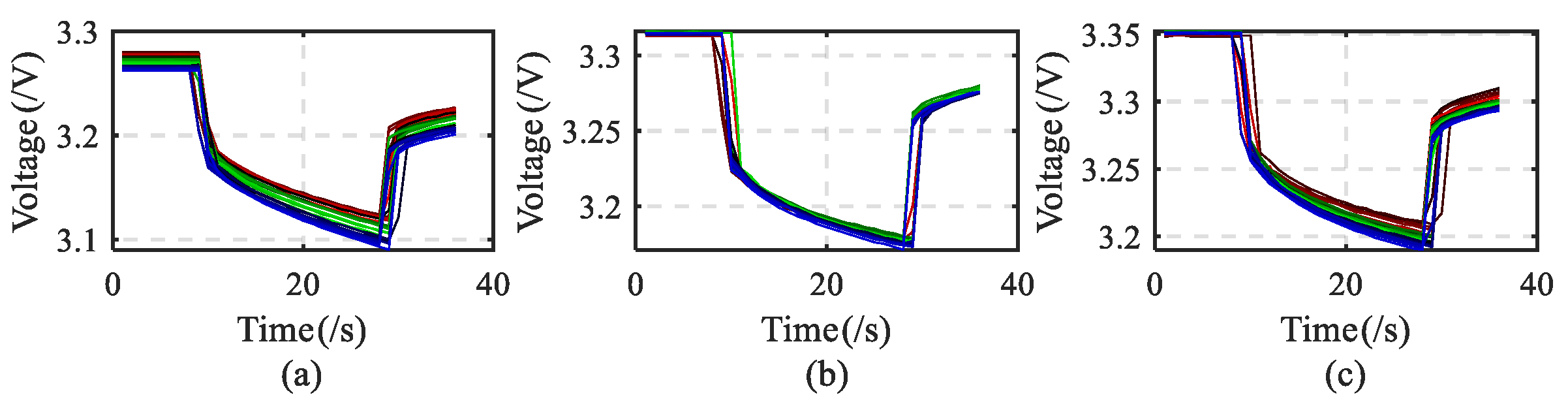
Figure 4 and Figure 5 show the current/voltage changes in the lithium-ion battery under three SOC during the pulse current test. It can be seen that the response voltage value changes significantly in different SOC stages, for example, in the charging stage where the SOC changes in the range of $20\%$ to $80\%$, compared with the two stages of SOC = 20% and SOC = 50%, the response voltage value of the corresponding point is the largest at the stage of SOC = 80%, and the response voltage value of SOC = 50% is larger than that of SOC = 20%. It can be said that when the SOC is in the charging stage belonging to this area, the response voltage value of the corresponding point increases with the increase in the initial SOC value. Under the same conditions, the same results can be obtained in the discharging stage as in the charging stage.

Since the pulse current value is always at a stable value, this paper only considers the changing characteristics of the response voltage under the current pulse test. Now, we analyze the specific changing trend of the current pulse test response voltage curve in detail, taking the response voltage curve at the SOC = 20% stage as an example. During the charging stage, Figure 6 shows the lithium-ion battery at SOC = 20% at different rates. From the response voltage change curve, it can be seen that the overall trend of the response voltage curve is downward (showing a “red–green–blue” color change); similarly, the discharge stage under this condition also shows the same trend, as shown in Figure 7.

Let us analyze the specific changing trends of the response voltage curves under different initial SOC stages. Taking the charging response voltage curve at a rate of 4 C as an example, Figure 8 shows the response voltage change curve of lithium-ion battery under different initial SOC stages. It can be seen that as the initial value of SOC changes, the voltage response curve changes. When SOC = 20%, the overall trend is downward, but when SOC = 50% and SOC = 80%, the overall trend of the response voltage curve is upward. In the discharging stage under the same conditions, no matter which SOC stage it is in, the overall trend of the response voltage curve is downward, as shown in Figure 9.

The aging features selected in this paper come from the data in the pulse test stage. The purpose of extracting the aging features is to find features that are highly correlated with battery SOH as model input. According to Figure 6, Figure 7, Figure 8 and Figure 9, the battery voltage shows an obvious downward or upward trend, and it is feasible to perform feature extraction based on this phenomenon.

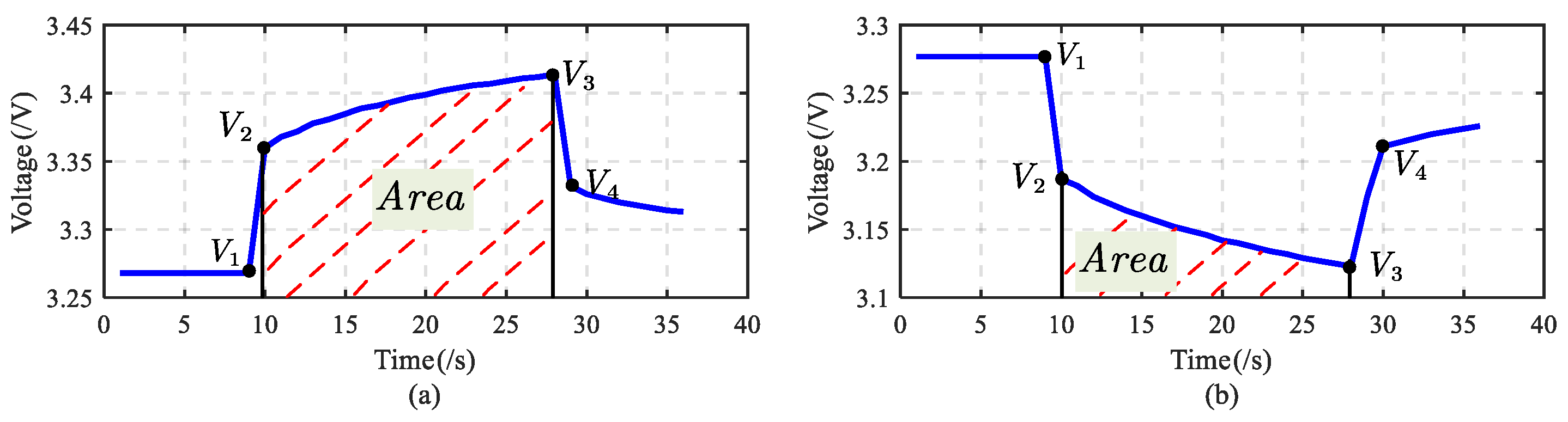
According to Figure 10, the four voltage values $V_1$, $V_2$, $V_3$, $V_4$ on the response voltage curve and the integrated area S between the response voltage values $V_2$ and $V_3$ are selected as the battery aging features. Based on the above analysis, ten aging features can be obtained at each charging/discharging rate of each SOC stage. For example, during the charging period at a rate of 4 C, there are four response voltage values and one integration area, and there are a total of five aging features. Similarly, there are five aging features during the discharge stage, so there are a total of ten aging features at a rate of 4 C. Therefore, in each SOC stage, there are a total of forty aging features, and by analogy, in the three SOC stages, a total of one hundred and twenty aging features can be obtained.

3. Lithium-Ion Battery SOH Estimation under Complete SOC Range

Due to the diversity of dynamic working conditions in the battery aging experiment test process, such as differences in charge and discharge rates, variability in operating temperature, and randomness of the current SOC, which increases the types of source domain data and affects the effectiveness of the lithium-ion battery SOH estimation model. On the other hand, the dynamic working conditions of the battery are changing, and the previous battery aging data information is not necessarily applicable to the current new application scenarios. Considering how to select data relevant to the current scenario from diverse source domain data is a prerequisite to ensure accurate estimation of the battery SOH under multiple working conditions.

This paper selects five lithium-ion batteries in two temperature modes as shown in Table 1. First, the battery aging features are extracted from the current pulse test data. Secondly, considering the impact of differences in different battery data on model estimation accuracy, a battery SOH estimation framework based on the sample transfer learning method is established. Then, by constructing an auxiliary data set to enhance the learning ability of the battery SOH model, it can obtain an accurate estimation of the battery SOH under dynamic testing conditions. Finally, comparative experiments are designed and combined with multiple error index methods to verify the effectiveness of the method.

3.1. Lithium-Ion Battery SOH Estimation Framework Based on the Tradaboost.R2 Algorithm

The Tradaboost.R2 algorithm is evolved from the Adaboost.R2 algorithm, which is essentially a machine learning method based on the concept of ensemble learning. The purpose of the Adaboost.R2 algorithm is to update and iterate two weight parameters; one is the weight parameter for the sample data, and the other is the weight parameter for the weak learner. The significance of updating the sample data weight parameters is to adjust the distribution of the training data set for the next iteration based on the previous round for the source domain. In other words, in each iteration process, the weight coefficient for the source domain sample data that makes the estimation result error of the target domain smaller is reduced in the next iteration. And for the source domain sample data that makes the prediction result of the target domain have a larger error, its weight coefficient will be increased in the next iteration, because in the next iteration, these sample data that make the error result larger may make the error result smaller in this iteration, but if the error result does not decrease in this iteration, then it continues to increase the weight of the sample data and proceeds to the next round of iteration. On the other hand, the purpose of updating the weight parameters for the weak learner is to increase the weight coefficient for the weak learner with a smaller overall error result.

Tradaboost.R2 is based on the Adaboost.R2 algorithm, adding the original source domain data and target domain data to the source domain, target domain and auxiliary data set. The auxiliary data set comes from a small amount of labeled data in the target domain. At this time, the training set consists of the source domain data and the auxiliary data. The goal of the Tradaboost.R2 algorithm is to reduce the sample data in the auxiliary data set that makes the prediction result error larger, so that after several iterations, the sample data in the auxiliary set related to the source domain data will have a larger weight coefficient, and the weight coefficient of sample data in the auxiliary data set that is not related to the source domain will be reduced.

This paper chooses extreme learning machines (ELMs) as the weak learner; an ELM is actually a single hidden layer feedforward neural network method. Compared with the traditional feedforward neural network, the structure still includes an input layer, a hidden layer and an output layer. However, in terms of training effect, since the ELM does not require the backpropagation method based on gradient descent to adjust the weight coefficients, its network training speed is fast and it has good generalization ability, while it does not easily fall into local minimum points. Therefore, this paper will use an ELM as the weak learner to establish a lithium-ion battery SOH estimation framework based on the Tradaboost.R2 method.

Consider a large amount of labeled source domain data $D_s=\{(x_{s1},y_{s1}),\cdots ,(x_{sn},y_{sn})\}$, where $x_{si}\in X_s$ is input data and $y_{si}\in Y_s$ is output data. Dividing the target domain data into two parts, the auxiliary data set $X_{t_f}$ and the testing set $X_{t_t}$, where the auxiliary data set $X_{t_f}$ is a small amount of labeled data in the target domain, and the corresponding sample label is $Y_{t_f}$, while the test data set $X_{t_t}$ is a large amount of unlabeled data in the target domain. Now the entire training data consist of the source domain data set and auxiliary data set, that is $X=X_s\cup X_{t_f}$, and the corresponding sample label is $Y=Y_s\cup Y_{t_f}$. Assume that the amount of sample data in the source domain is $n_s$ and the number of samples in the auxiliary data set is $n_f$. For simplicity of writing, the test data in the target domain are written as $X_u$. Therefore, the current goal is to predict the output of the corresponding sample through the trained model when the model has a new test sample input $x_i^{*}\in X_u$. The specific process of the Tradaboost.R2 method is shown in Algorithm 1.

3.2. Battery SOH Estimation Based on Complete SOC Range

Based on the research and analysis of battery aging features in Section 2, it can be seen that 40 battery aging features can be extracted from each SOC interval, and a total of 120 aging features are obtained. In order to establish a battery SOH estimation model under different temperature modes, all the aging features of the three SOC intervals are used as the input of the model, and the application scenarios in single-temperature mode and multi-temperature mode are considered, respectively. Next, considering that the source domain and the target domain come from two different battery data sets, the entire data set is divided into source domain, auxiliary and target domain data sets. By using a small amount of target domain label sample data to establish an auxiliary data set, the impact of insufficient source domain information on the model estimation accuracy is reduced.

Table 2. Division of source domain, auxiliary and target domain data sets under complete SOC intervals.

Data	Single Temperature			Multiple Temperature
	$\mathit{S}\mathbf{1}$	$\mathit{S}\mathbf{2}$	$\mathit{S}\mathbf{3}$	$\mathit{S}\mathbf{4}$	$\mathit{S}\mathbf{5}$	$\mathit{S}\mathbf{6}$
$T_s$	No.1	No.2	No.5	No.1	No.2	No.3
$T_f$	No.3 (15%)	No.3 (15%)	No.4 (30%)	No.4 (15%)	No.4 (15%)	No.4 (15%)
$T_t$	No.3 (85%)	No.3 (85%)	No.4 (70%)	No.4 (85%)	No.4 (85%)	No.4 (85%)

shows the division of source domain, auxiliary and target domain data sets under the complete SOC interval, where $T_s$ represents source domain data, $T_f$ represents auxiliary data and $T_t$ represents target domain data. At the same time, in order to verify the effectiveness of the battery SOH estimation model under different temperature modes, six scenarios are considered and represented by the symbol $Si$, where $S1$–$S3$ are single-temperature scenarios, that is, the source domain and the target domain have the same temperatures, and $S4$–$S6$ are multi-temperature scenarios, that is, battery data from the source domain and target domain at different temperatures.

Algorithm 1: Tradaboost.R2 algorithm.

Furthermore, in order to verify the effectiveness of the battery SOH estimated model, the mean absolute error (MAE), mean square error (MSE) and root mean square error (RMSE) analysis methods are used, which are expressed in Equation (1)–(3). Finally, the coefficient of determination $R^2$ is used to verify the performance of the estimated model, where the larger the $R^2$ value, the better the model fitting effect.

$$E_{MAE}=\frac{1}{N}\sum _{i=1}^N|Y_{i,true}-{\overline{Y}}_i|$$

(1)

$$E_{MSE}=\frac{1}{N}\sum _{i=1}^N{(Y_{i,true}-{\overline{Y}}_i)}^2$$

(2)

$$E_{RMSE}=\sqrt{\frac{1}{N}\sum _{i=1}^N|Y_{i,true}-{\overline{Y}}_i|}$$

(3)

$$R^2=1-\frac{{\sum }_{i=1}^N{(Y_{i,true}-{\overline{Y}}_i)}^2}{{\sum }_{i=1}^N{(Y_{i,true}-Y_{mean})}^2}$$

(4)

where N is the number of samples, and $Y_{i,true}$ is the true value for battery SOH, ${\overline{Y}}_i$ is the estimated value for battery SOH, and the $Y_{mean}$ is the mean value for battery SOH.

This paper selects the Adaboost method, GPR, SVM and CNN-LSTM, as well as the case where the auxiliary set is not considered in the proposed method as the comparison methods. The symbol $Adaboost$ represents the estimated results based on the Adaboost.R2 method, the symbol $GPR$ represents the estimated results based on the GPR method, the symbol $SVM$ represents the estimated results based on the SVM method, the symbol $CNN$-$LSTM$ represents the estimated results based on the CNN-LSTM method, the symbol $No$-$Transfer$ represents the estimated results without the transfer learning step (that is, the proposed method does not include the auxiliary data), and the symbol $Transfer$ represent the estimated results of the method which proposed in this paper.

Due to the different temperatures of lithium-ion batteries, the entire battery data can be divided into two modes, namely mode 1 and mode 2. Regarding the division of data sets in single-temperature mode, take the three battery data sets in mode 1 as an example. There are three battery data sets in mode 1, namely No.1, No.2 and No.3. Choose one of these three data sets as the target domain, and the other two data sets as the source domain, such as scenario 1 ($S1$) and scenario 2 ($S2$). In the multi-temperature mode, select the data set in one mode as the source domain, such as No.1 in mode 1, and the data set in another temperature mode as the target domain, such as No.4 in mode 2, and divide it into scenarios 4, 5 and 6 ($S4$, $S5$, $S6$). In these two modes, in order to improve the estimation accuracy of the model and verify the necessity of transfer learning, the construction of auxiliary data sets is considered, as shown in Table 2.

3.3. Analysis and Discussion of Experimental Results

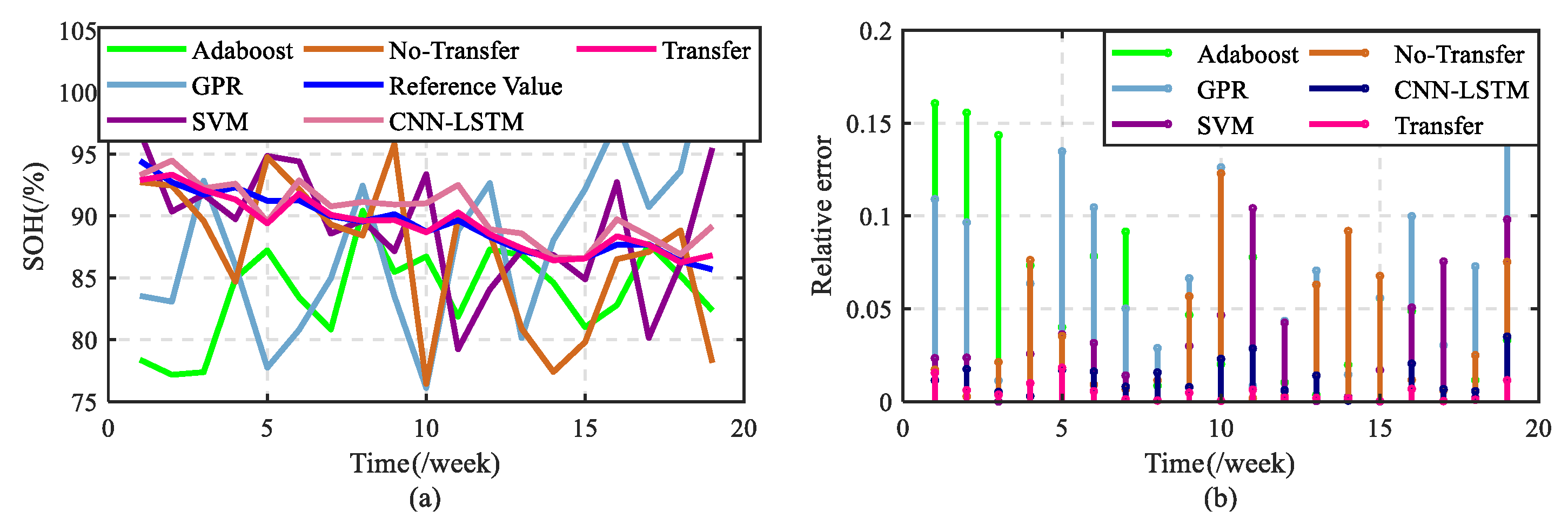
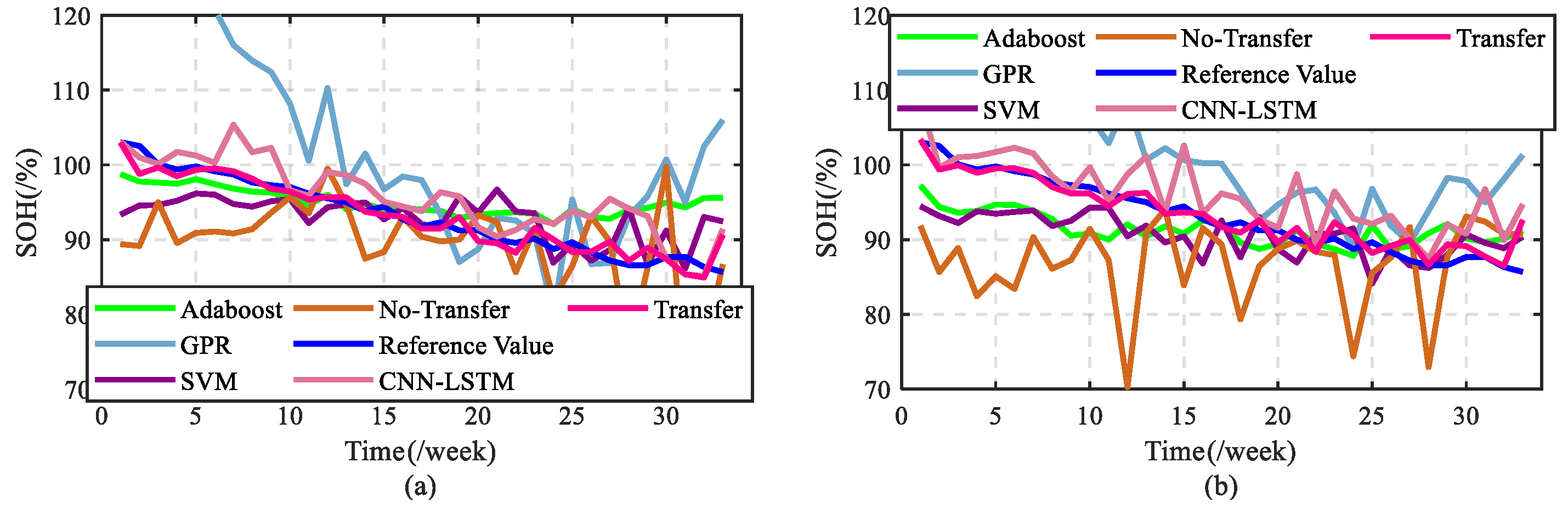
In this part, based on the previous aging feature extraction and model optimization, the battery SOH estimation under single-temperature and multi-temperature modes are analyzed. First, the estimation results under single-temperature mode are analyzed, and the experimental results based on different models are considered to verify the necessity of transfer learning.

Figure 11 and Figure 12 show the battery SOH estimation results for scenario 1 ($S1$)–scenario 3 ($S3$) under the single-temperature mode. It can be found that in the three scenarios, the battery SOH estimation based on the $Transfer$ method are closer to the reference value, and its effect of tracking the reference value is more obvious, while the battery SOH estimation based on the $No$-$Transfer$ method obviously does not accurately track the true value. In addition, considering that the Tradaboost.R2 algorithm is improved from the Adaboost.R2 algorithm, the battery SOH estimation based on the basic algorithm Adaboost is also unsatisfactory. At the same time, regardless of the scenario, the trend of estimation results based on CNN-LSTM, GPR and SVM is not ideal.

Table 3. Three error values and coefficients of determination for scenario 1 and scenario 2.

Model	S1				S2
	MAE	MSE	RMSE	${\mathit{R}}^{\mathbf{2}}$	MAE	MSE	RMSE	${\mathit{R}}^{\mathbf{2}}$
$Adaboost$	0.0211	7.48 × ${10}^{-4}$	0.0273	0.2178	0.0223	6.59 × ${10}^{-4}$	0.0257	0.7780
$GPR$	0.0229	9 × ${10}^{-4}$	0.03	0.1063	0.0222	8.83 × ${10}^{-4}$	0.0297	0.0268
$SVM$	0.0186	5.19 × ${10}^{-4}$	0.0228	0.7209	0.0212	7.02 × ${10}^{-4}$	0.0265	0.6753
$No$-$Transfer$	0.0503	0.0051	0.0716	0.522	0.0199	6.89 × ${10}^{-4}$	0.0262	0.6497
$CNN$-$LSTM$	0.0158	2.36 × ${10}^{-4}$	0.0154	0.8178	0.0118	3.41 × ${10}^{-4}$	0.0185	0.7523
$Transfer$	0.0103	1.5 × ${10}^{-4}$	0.0123	0.8965	0.0079	1.12 × ${10}^{-4}$	0.0106	0.8896

and

Table 4. Three error values and coefficients of determination for scenario 3 and scenario 4.

Model	S3				S4
	MAE	MSE	RMSE	${\mathit{R}}^{\mathbf{2}}$	MAE	MSE	RMSE	${\mathit{R}}^{\mathbf{2}}$
$Adaboost$	0.0568	0.0057	0.0754	0.4371	0.0342	0.0018	0.0428	0.2637
$GPR$	0.0722	0.0073	0.0855	0.4084	0.1045	0.0173	0.1314	0.5953
$SVM$	0.0329	0.0020	0.0448	0.5383	0.0327	0.0017	0.0410	0.3319
$No$-$Transfer$	0.0371	0.0026	0.0512	0.5959	0.0553	0.0050	0.0706	0.5073
$CNN$-$LSTM$	0.01	1.52 × ${10}^{-4}$	0.0123	0.7887	0.0257	0.0011	0.0325	0.7310
$Transfer$	0.0051	5.30 × ${10}^{-5}$	0.0073	0.8981	0.0108	2.32 × ${10}^{-4}$	0.0152	0.9045

give three error values and coefficients of determination for $S1$–$S3$. It can be seen from these two tables that the MAE of the estimated value based on the $Transfer$ method does not exceed 1.5%, which is significantly smaller than the MAE of other comparison methods; in terms of MSE, the MSE based on the $Transfer$ method is lower than 0.015% and the corresponding RMSE is less than 1.5%, which also shows that the estimation accuracy based on the $Transfer$ method is higher than the other methods. On the other hand, in terms of verifying the model fitting effect, the coefficient of determination $R^2$ based on the $Transfer$ method is not less than 88% in the three scenarios. Compared with the corresponding coefficient of determination values of other methods, the model fitting effect based on the $Transfer$ method is better. Therefore, it can be seen that the method after the transfer learning step can improve the accuracy of the estimation results, but the estimation results without the transfer learning step cannot guarantee the estimation accuracy, which further illustrates the necessity of transfer learning.

On the other hand, according to Table 2, it can be seen that when no auxiliary set is constructed, taking $S1$ as an example, the MAE is 0.0503, which shows that the estimation model obtained only with the help of source domain data information is not well adapted to the test environment of the target domain. When constructing the auxiliary data set, only the first 15% of the label data information in the target domain can obtain better estimation results to verify the necessity of transfer learning. It can be seen that lithium-ion battery SOH estimation can be completed with a small amount of label sample data. Therefore, this method verifies that the accuracy of battery SOH estimation based on a small number of label sample data is not affected.

Besides that, Table 3 and Table 4 present the error estimation results of the battery SOH under different models. These tables also depict the error estimation results of the battery SOH under different types. In order to analyze the estimated result clearly, we use the estimated results based on GPR, SVM, CNN-LSTM, Adaboost.R2 and without using the transfer method under the same conditions to compare with the Tradaboost.R2 algorithm estimated results.

After analyzing the battery SOH estimation results in single-temperature mode, this part starts to analyze the multi-temperature mode. Battery No.5 in mode 2 only has ten sample points that select battery No.4 in mode 2 as the target domain, and the three batteries No.1, No.2 and No.3 in mode 1 are used as the source domain to verify the battery SOH estimation under multi-temperature mode.

Figure 13 and Figure 14 show the battery SOH estimation results for scenario 4 ($S4$)–scenario 6 ($S6$) under multiple-temperature mode. It can be found that in the three scenarios, the battery SOH estimation based on the $Transfer$ method is closer to the reference value, and its effect of tracking the reference value is more obvious, while the battery SOH estimation based on the $No$-$Transfer$ method obviously does not accurately track the true value. In addition, considering that the Tradaboost.R2 algorithm is improved from the Adaboost.R2 algorithm, the battery SOH estimation based on the basic algorithm Adaboost is also unsatisfactory. At the same time, regardless of the scenario, the trend of estimation results based on CNN-LSTM, GPR and SVM is not ideal.

Table 4 and

Table 5. Three error values and coefficients of determination for scenario 5 and scenario 6.

Model	S5				S6
	MAE	MSE	RMSE	${\mathit{R}}^{\mathbf{2}}$	MAE	MSE	RMSE	${\mathit{R}}^{\mathbf{2}}$
$Adaboost$	0.0356	0.0017	0.0417	0.3034	0.0240	8.11 × ${10}^{-4}$	0.0285	0.6668
$GPR$	0.0908	0.0106	0.1028	0.5998	0.0992	0.0156	0.1249	0.6019
$SVM$	0.0327	0.0017	0.0410	0.3319	0.0313	0.0016	0.0397	0.4618
$No$-$Transfer$	0.0553	0.0050	0.0706	0.5073	0.0666	0.0068	0.0822	0.4413
$CNN$-$LSTM$	0.0287	0.0013	0.0364	0.6725	0.0267	0.0015	0.0381	0.6589
$Transfer$	0.0123	3.21 × ${10}^{-4}$	0.0179	0.8583	0.0125	2.66 × ${10}^{-4}$	0.0163	0.8872

give three error values and coefficients of determination for scenario $S4$–$S6$. It can be seen from these two tables that the MAE of the battery SOH estimated value based on the $Transfer$ method does not exceed 1.3%, which is significantly smaller than the MAE of other comparison methods; in terms of MSE, the MSE based on the $Transfer$ method is lower than 0.033% and the corresponding RMSE is less than 1.8%, which also shows that the estimation accuracy based on the $Transfer$ method is higher than that of other methods. On the other hand, in terms of verifying the model fitting effect, the coefficient of determination $R^2$ based on the $Transfer$ method is not less than 85% in the three scenarios. Compared with the corresponding coefficient of determination values of other methods, the model fitting effect based on the $Transfer$ method is better than other methods.

In the three scenarios under multi-temperature mode, taking scenario $S4$ as an example, when the auxiliary data set is not constructed, the MAE is 0.0553, compared with the MAE value (0.0108) under the method proposed in this paper, which shows that the estimation model obtained only with the help of source domain information has no way to learn the data information for the target domain, and when the top 15% of the label data in the target domain is used to build an auxiliary data set, the error value of the prediction results has dropped significantly. This shows that 15% of labeled data information plays an important role in model training and verifies the necessity of transferring data information. The same results are also reflected in scenarios $S5$ and $S6$, which means that when the auxiliary data set only accounts for 15% of the target domain, the accuracy of battery SOH estimation under multi-temperature mode still can be guaranteed.

4. Lithium-Ion Battery SOH Estimation under Different SOC Ranges

In the previous section, we discuss the battery SOH estimation problem under the complete SOC interval, which means that when establishing the estimation model framework, all aging features are used as input of the model. However, if there is a lack of aging features in a certain range, will it make it difficult to estimate the batter SOH? Under laboratory conditions, pulse test data for three complete SOC intervals can be easily obtained. However, in actual applications, depending on the needs of different application scenarios, it may not be possible to complete the pulse test under three complete SOC intervals. At this time, it is necessary to consider whether the battery SOH estimation under different SOC intervals can be achieved. In other words, comparing with the battery SOH estimation under the complete SOC interval, can it be ensured that the mapping relationship under different SOC intervals will not be affected.

4.1. Data Set Division under Different SOC Intervals

In order to illustrate the aging features under different SOC intervals, the symbol $I_1$ is used to represent the forty aging features at SOC = 20%, the symbol $I_2$ is used to represent the forty aging features at SOC = 50% and the symbol $I_3$ is used to represent the forty aging features at SOC = 80%.

In order to verify that the mapping relationship of the battery SOH estimation model under different SOC intervals is not affected, aging feature data from different initial SOC is selected when constructing the auxiliary and the source domain data set. For example, it is now necessary to use the label data information of battery No.1 to estimate SOH of battery No.3. If battery No.3 only contains pulse test data with SOC = 20%, and battery No.1 contains pulse test data with a complete SOC range, then the target domain data set of the model is the aging features $I_1$ of battery No.3, and source domain data set contains the aging characteristics $I_1\cup I_2\cup I_3$ of battery No.1. Under the assumption of this scenario condition, the dimensions of the source domain and target domain data of the model are different. Therefore, the aging feature $I_1$ of battery No.1 can be selected as the auxiliary data set of the model to learn the data information of $I_1$, and the aging feature $I_2$ or $I_3$ can be used as the source domain data set of the model, thus ensuring the dimensions of the three data sets are the same, and the selection of the auxiliary data set only requires aging features from the same SOC interval as the target domain data set. At the same time, there is no restriction that the auxiliary data must come from the same dataset as the target domain. Therefore, based on the battery pulse test data in different SOC intervals, in each scenario, the source domain, auxiliary data and target domain data can be divided as shown in

Table 6. Division of source domain, auxiliary and target domain data sets under different SOC intervals.

	$\mathit{M}1$	$\mathit{M}2$	$\mathit{M}3$	$\mathit{M}4$	$\mathit{M}5$	$\mathit{M}6$
$T_s$	$I_2$	$I_3$	$I_1$	$I_3$	$I_2$	$I_1$
$T_f$	$I_1$	$I_1$	$I_2$	$I_2$	$I_3$	$I_3$
$T_t$	$I_1$	$I_1$	$I_2$	$I_2$	$I_3$	$I_3$

.

4.2. Battery SOH Estimation Based on Different SOC Ranges

When considering the battery SOH estimation based on sample transfer learning under different SOC intervals, six scenarios are considered and are divided as shown in

Table 7. Division of source domain and target domain data sets under different SOC intervals.

Data	Single Temperature			Multiple Temperature
	$\mathit{S}\mathbf{1}$	$\mathit{S}\mathbf{2}$	$\mathit{S}\mathbf{3}$	$\mathit{S}\mathbf{4}$	$\mathit{S}\mathbf{5}$	$\mathit{S}\mathbf{6}$
$T_s$	No.1	No.2	No.5	No.1	No.2	No.3
$T_t$	No.3	No.3	No.4	No.4	No.4	No.4

. Scenario 1 ($S1$)–Scenario 3 ($S3$) verify the battery SOH estimation based on a single-temperature mode, that is, although the source domain and the target domain data set come from different battery data, they remain in the same temperature mode. The battery SOH estimation under multi-temperature mode is reflected by Scenario 4 ($S4$)–Scenario 6 ($S6$), that is, the source domain and the target domain data set are derived from different temperature modes. The purpose is to verify the performance based on the idea that when using data in different temperature modes, the battery SOH estimation can still be achieved. In each scenario of this part, the source domain, auxiliary data and target domain data set are divided in six ways. Different from the construction method of the auxiliary data set under the complete SOC interval, here, there is no requirement that the auxiliary data must come from the same target domain data set. It is only required that the auxiliary data set and the target domain data set come from the aging features under the same SOC interval. This greatly reduces the demand for target domain label data and has more practical research significance.

4.3. Analysis and Discussion of Experimental Results

In this section, the battery SOH estimation under single-temperature and multi-temperature modes are analyzed, respectively. First, the experimental results under the single-temperature mode are analyzed. Based on Section 3.2, the battery SOH estimation under the six division methods is verified in each scenario; secondly, compared with the battery SOH estimation framework under the complete SOC interval, the feature dimension of the model is not only reduced but also the demand for target domain label data is reduced. Therefore, in this section, the estimation results under the six partitioning methods will be compared with the estimation results based on the $Transfer$ method in the complete SOC interval of Section 3.2. In addition, since the Tradaboost.R2 algorithm is an ensemble method, considering the final estimation result is synthesized based on other sub-models, the relative error between each sub-model and the final result is analyzed. Similarly, the battery SOH estimation under multi-temperature mode is also analyzed in the same way.

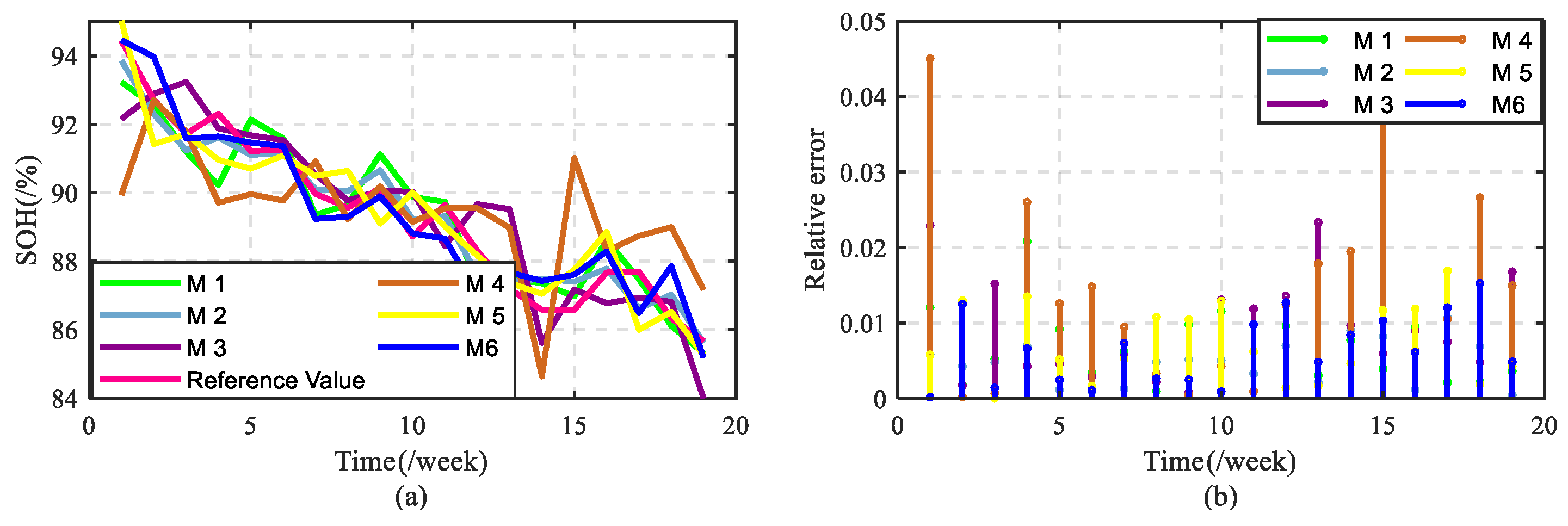
Figure 15 and Figure 16 show the battery SOH estimation results for scenario 1 ($S1$)–scenario 3 ($S3$). It can be seen from Figure 15 that in $S1$ and $S2$, compared with the estimation results for the other five methods, the estimation results based on method 6 ($M6$) are closer to the reference value, and its effect of tracking the reference value is more obvious. The absolute error also can reflect the better estimation effect is shown in Figure 16b.

Table 8. Three error values and coefficients of determination for scenario 1 and scenario 2.

Model	S1				S2
	MAE	MSE	RMSE	${\mathit{R}}^{\mathbf{2}}$	MAE	MSE	RMSE	${\mathit{R}}^{\mathbf{2}}$
$M1$	0.0123	2.96 × ${10}^{-4}$	0.0172	0.7576	0.0113	2.74 × ${10}^{-4}$	0.0166	0.7524
$M2$	0.0130	3.32 × ${10}^{-4}$	0.0182	0.6934	0.0119	3.04 × ${10}^{-4}$	0.0174	0.7089
$M3$	0.0198	4.92 × ${10}^{-4}$	0.0222	0.4473	0.0198	4.97 × ${10}^{-4}$	0.0223	0.4396
$M4$	0.0238	7.78 × ${10}^{-4}$	0.0279	0.2215	0.0226	6.98 × ${10}^{-4}$	0.0264	0.2618
$M5$	0.0107	1.77 × ${10}^{-4}$	0.0133	0.8269	0.0096	1.51 × ${10}^{-4}$	0.0123	0.8475
$M6$	0.0075	9.48 × ${10}^{-5}$	0.0097	0.9143	0.0072	8.78 × ${10}^{-5}$	0.0094	0.9183
$Transfer$	0.0103	1.5 × ${10}^{-4}$	0.0123	0.8965	0.0079	1.12 × ${10}^{-4}$	0.0106	0.8896

and

Table 9. Three error values and coefficients of determination for scenario 3 and scenario 4.

Model	S3				S4
	MAE	MSE	RMSE	${\mathit{R}}^{\mathbf{2}}$	MAE	MSE	RMSE	${\mathit{R}}^{\mathbf{2}}$
$M1$	0.0065	6.66 × ${10}^{-5}$	0.0082	0.8811	0.0174	4.73 × ${10}^{-4}$	0.0217	0.7290
$M2$	0.0047	3.04 × ${10}^{-5}$	0.0055	0.9397	0.0188	5.59 × ${10}^{-4}$	0.0237	0.7009
$M3$	0.0092	1.29 × ${10}^{-4}$	0.0114	0.8324	0.0277	0.0013	0.0364	0.4869
$M4$	0.0142	3.74 × ${10}^{-4}$	0.0193	0.4273	0.0326	0.0016	0.0406	0.2945
$M5$	0.0073	7.81 × ${10}^{-5}$	0.0088	0.8737	0.0094	2.00 × ${10}^{-4}$	0.0142	0.9094
$M6$	0.0064	6.18 × ${10}^{-5}$	0.0079	0.9043	0.0102	1.52 × ${10}^{-4}$	0.0124	0.9406
$Transfer$	0.0051	5.30 × ${10}^{-5}$	0.0073	0.8981	0.0108	2.32 × ${10}^{-4}$	0.0152	0.9045

give three error values and coefficients of determination for $S1$–$S3$. It can be seen from these two tables that the optimal estimation results can be obtained based on $M6$ in $S1$ and $S2$, while the optimal results in $S3$ are obtained by $M2$. In the optimal estimation results of these three scenarios, the MAE does not exceed 0.75%, which is significantly smaller than the MAE under the other methods; at the same time, the MSE is lower than 0.0095% and the corresponding RMSE does not exceed 0.98%; compared with the complete SOC interval based on $Transfer$ method, the optimal estimation errors of the three scenarios are smaller than the estimation errors based on the $Transfer$ method. On the other hand, in terms of verifying the model fitting effect, the coefficient of determination $R^2$ of the optimal result reaches 90% in all three scenarios. Compared with the coefficient of determination value based on the $Transfer$ method, it can be seen that the model fitting effect based on different SOC intervals is better than the model effect based on the complete SOC interval. This can also show that while the feature dimension and the demand for label data in the target domain are reduced, the battery SOH estimation accuracy has not been reduced.

Table 8 and Table 9 present the error estimation results of the battery SOH under different SOC ranges. In order to ensure that the mapping relationship of the lithium-ion battery SOH estimation model in different SOC intervals is not affected, it adopts the way of dividing the data set in Table 6 and Table 7.

After analyzing the battery SOH estimation results in single-temperature mode, this part starts to analyze the multi-temperature mode. We select battery No.4 in mode 2 as the target domain and use the three batteries No.1, No.2 and No.3 in mode 1 as the source domain to verify the battery SOH estimation under multi-temperature mode.

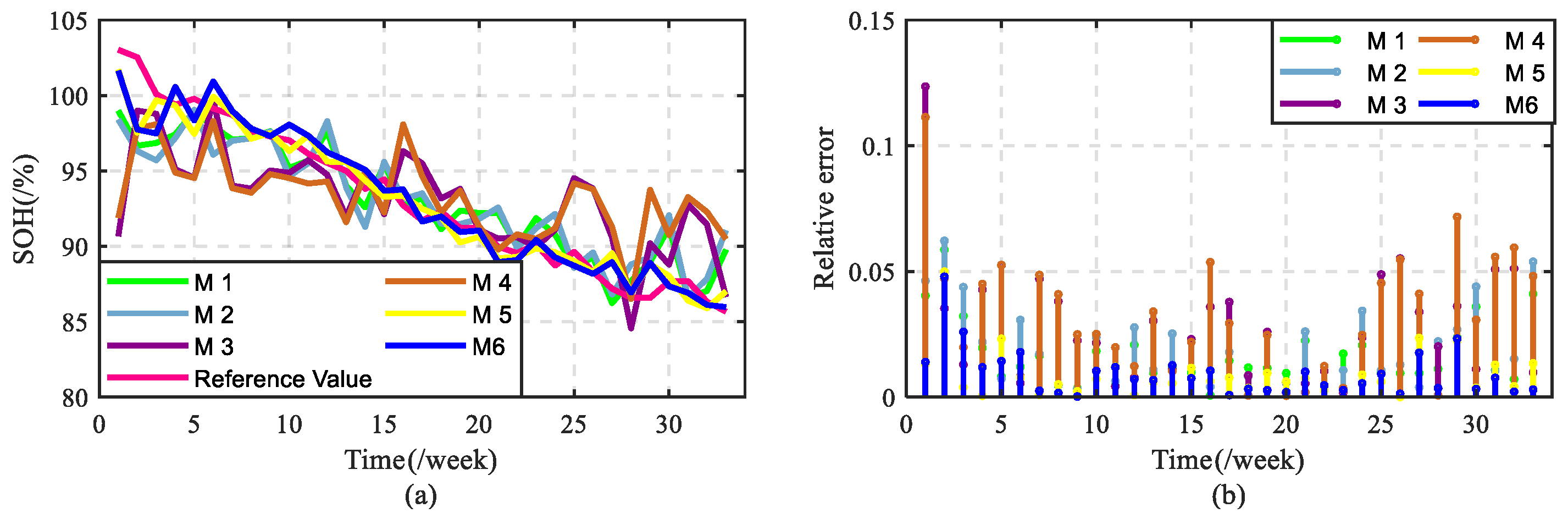
Figure 17 and Figure 18 show the battery SOH estimation results for scenario 4 ($S4$)–scenario 6 ($S6$). It can be seen from Figure 17 that in $S4$ and $S5$, comparing with the estimation results of the other five methods, the estimation results based on method 5 ($M5$) are closer to the reference value, and its effect of tracking the reference value is more obvious, which the absolute error also can reflect the better estimation effect that shown in Figure 18b. Completing the verification of the estimation results of three scenarios under the multi-temperature mode, which demonstrates that the method proposed in this paper has stronger generalization ability in estimating battery SOH under different temperature modes.

Table 9 and

Table 10. Three error values and coefficients of determination for scenario 5 and scenario 6.

Model	S5				S6
	MAE	MSE	RMSE	${\mathit{R}}^{\mathbf{2}}$	MAE	MSE	RMSE	${\mathit{R}}^{\mathbf{2}}$
$M1$	0.0195	5.66 × ${10}^{-4}$	0.0238	0.6905	0.0165	4.27 × ${10}^{-4}$	0.0207	0.7704
$M2$	0.0171	4.89 × ${10}^{-4}$	0.0221	0.7365	0.0199	6.40 × ${10}^{-4}$	0.0253	0.6576
$M3$	0.0285	0.0014	0.0374	0.4889	0.0287	0.0014	0.0371	0.4326
$M4$	0.0327	0.0016	0.0403	0.3162	0.0328	0.0016	0.0406	0.2835
$M5$	0.0157	4.38 × ${10}^{-4}$	0.0209	0.8155	0.0090	1.69 × ${10}^{-4}$	0.0130	0.9249
$M6$	0.0114	1.90 × ${10}^{-4}$	0.0138	0.9294	0.0093	1.73 × ${10}^{-4}$	0.0132	0.9290
$Transfer$	0.0123	3.21 × ${10}^{-4}$	0.0179	0.8583	0.0125	2.66 × ${10}^{-4}$	0.0163	0.8872

give three error values and coefficients of determination for $S4$–$S6$. It can be seen from these two tables that the optimal estimation results can be obtained based on $M6$ in $S4$ and $S5$, while the optimal results in $S6$ are obtained by $M5$. In the optimal estimation results of these three scenarios, the MAE does not exceed 1.2%, which is significantly smaller than the MAE under other methods; at the same time, the MSE is lower than 0.02% and the corresponding RMSE does not exceed 1.4%. Compared with the complete SOC interval based on the $Transfer$ method, the optimal estimation errors of the three scenarios are smaller than the estimation errors based on the $Transfer$ method. On the other hand, in terms of verifying the model fitting effect, the coefficient of determination $R^2$ of the optimal result reaches 92% in all three scenarios. Therefore, no matter in terms of battery SOH estimation accuracy or model fitting effect, the optimal results based on different SOC intervals are better than complete SOC intervals.

Based on the above discussion, it can be proved from three aspects that the method proposed in this paper can achieve higher accuracy in battery SOH estimation:

(1)

In the comparison model that combines various errors to depict the performance of the method, we use the estimated results based on GPR, SVM, CNN-LSTM, Adaboost and without using the transfer method under the same conditions to compare with the Tradaboost.R2 algorithm estimated results. The various error results show that the estimated results based on the Tradaboost.R2 algorithm are better than other algorithms.

(2)

The performance of model fitting is measured by the coefficient of determination $R^2$. The better the model fitting performance, the closer its value is to 1. The values of the coefficient of determination $R^2$ prove that the estimated results based on the Tradaboost.R2 algorithm are better than other algorithms.

(3)

This paper proposes a lithium-ion battery SOH estimation framework based on the Tradaboost.R2 method under pulse testing. The proposed method can ensure that the mapping relationship of the lithium-ion battery SOH estimation model in different SOC intervals is not affected.

(4)

By verifying the estimation results based on the complete SOC interval and different SOC intervals, it can be seen that while the model feature dimension and the demand for target domain label data is reduced, the estimation accuracy of the model can still be guaranteed.

5. Conclusions and Future work

In order to estimate the lithium-ion battery SOH under different dynamic working conditions, this paper establishes a battery SOH estimation model based on the Tradaboost.R2 algorithm. Considering the shortened time to obtain aging features under dynamic test conditions, the aging features that can reflect the attenuation of battery capacity are extracted from the 18s pulse current. At the same time, five lithium-ion batteries are tested in two temperature modes. For the cyclic aging test, the weight of the source domain data samples is adjusted through the Tradaboost.R2 algorithm. Under laboratory conditions, two verification scenarios for lithium-ion battery SOH estimation are designed, which verified that while the age feature dimension is reduced and the demand for target domain label data is reduced, the mapping relationship of the lithium-ion battery SOH estimation model is not affected by the initial value of the SOC.

Considering the impact of aging features on model estimation results, in future work, a framework for automatically extracting battery aging features under dynamic conditions will be established while ensuring that the extracted aging features have a strong correlation with battery SOH. In addition, adaptive online learning should be considered in the future such that the battery model can be adjusted adaptively to achieve the best state whenever new data are available.