Abstract
Effectively extracting a lithium-ion battery’s impedance is of great importance for various onboard applications, which requires consideration of both the time consumption and accuracy of the measurement process. Although the pseudorandom binary sequence (PRBS) excitation signal can inject the superposition frequencies with high time efficiency and an easily implementable device, processing the data of the battery’s impedance measurement is still a challenge at present. This study proposes a fast impedance spectrum construction method for lithium-ion batteries, where a multi-density clustering algorithm was designed to effectively extract the useful impedance after PRBS injection. According to the distribution properties of the measurement points by PRBS, a density-based spatial clustering of applications with noise (DBSCAN) was used for processing the data of the lithium-ion battery’s impedance. The two key parameters of the DBSCAN were adjusted by a delicate workflow according to the frequency range. The validation of the proposed method was proved on a 3 Ah lithium-ion battery under nine different test conditions, considering both the SOC and temperature variations.
1. Introduction
In recent years, green low-carbon development has gradually become the consensus and development goal of our future society. Under the demand of the low-carbon concept, a high proportion of intermittent and stochastic renewable energy sources merging into the grid will bring new challenges to the stability of the grid’s operation. The energy storage technology represented by lithium-ion batteries can cope with the challenges and provide technologies and solutions for power regulation and supporting the stability of the grid [1,2,3]. A lithium-ion battery has high energy density and a fast response speed, which can meet the scheduling needs of the grid. However, a lithium-ion battery based on an energy storage system needs to be combined with the states to control the charging and discharging process to avoid overcharging, over-discharging, and other safety issues. Thus, an efficient battery energy management system (BMS) is the key to the reliable operation of a battery energy storage system [4,5,6].
A BMS contains several functions, such as signal measurement, cell equalization, state estimation, and protective fault warnings. The signal measurement module aims to measure the voltage and temperature in real time through the analog front-end (AFE) and monitors the batteries’ external performance [7,8]. The equalization circuit enables a consistent control of individual cells by transferring energy. The function of the state estimation is to capture the internal states of the battery, including state of charge (SOC) and state of health (SOH), thus, providing data support for controlling, operating, and maintaining the battery energy storage system [9,10]. The protection and warning function combines external measurement and the internal state to realize the regulation of and protection against abnormal working conditions during the battery’s operation, as well as warnings of safety-related failures [11,12,13]. Current BMS systems rely on the detection of basic electrothermal information such as voltage, current, and temperature; however, it is difficult to effectively obtain the changes in the internal electrochemical states of the battery. To realize the accurate estimation of SOC and SOH, there is an urgent need to carry out research on methodologies of detecting the battery’s electrochemical state for onboard applications [14,15].
Electrochemical impedance spectroscopy (EIS) is a technique for obtaining changes in the impedance of a battery in the broadband frequency range and realizing the observation of electrochemical reactions such as lithium ions’ kinetics, charge transfer, and diffusion process, and thus can reflect the battery’s state. The impedance spectrum provides a new characterization method for sensing the internal states of a battery, which has gained extensive attention and been the focus of much research in recent years [16,17]. The authors of [18] connected the trend of the impedance spectral curve to the degradation process of 18650 lithium-ion batteries and explored the impedance characteristics corresponding to the batteries’ SOC and SOH. It was concluded that the ohmic resistance could reflect the batteries’ SOH and the transfer resistance was closely related to the variation in SOC. The authors of [19] used EIS to establish a frequency domain model and then chose the parameters of the model as the features to achieve SOC estimation using light computing machine learning algorithms. The authors of [20] used the imaginary parts of the mid-frequency band in the EIS, which were believed to have no obvious dependence on the temperature, as a feature for predicting the battery’s remaining useful life (RUL) with a one-dimensional convolutional neural network-self-attention mechanism, and achieved an accurate RUL of lithium-ion batteries.
As a non-invasive technology for estimating a battery’s, EIS has received increasing attention. However, a battery’s EIS measurement uses electrochemical workstations applying the sine sweeping method. It has been realized that the sine sweeping method is time-consuming and needs expensive test equipment, and is mostly used for laboratory measurements. The realization of fast online measurement of impedance is a current research hotspot for battery system applications.
The authors of [21] proposed a multi-sine wave aggregation detection method, where multi-frequency sinusoidal superposition was performed at the same time to realize the detection of impedance over the entire frequency range. Fast detection of the impedance spectrum within the 0.1 Hz–1 kHz frequency interval was achieved using a 20 s step excitation [22]. The pseudorandom binary sequence (PRBS), as an easily generated excitation signal with good power consistency, has received increasing attention in the rapid detection of batteries’ impedance. The authors of [23,24] investigated the spectral characterization of the PRBS signal and the extraction method of the cell’s impedance. The authors of [25,26] proposed an optimized three-level sequence to improve the power spectral density of conventional PRBS excitation, which was suitable for measuring batteries’ impedance. The authors of [27] proposed a novel hybrid pseudorandom sequence (HPRS) to boost the signal power in the low-frequency region.
The impedance measurement method based on PRBS excitation is characterized by a fast measurement speed and high-power consistency. Due to the limitation in the amplitude of the signal, the power density at each frequency of the measurement interval is generally low and susceptible to interference from the measurement noise, which leads to large impedance errors. Therefore, filtering and processing the original data from the impedance calculation is an important challenge for the fast measurement of batteries’ impedance. The authors of [28] proposed a new measurement evaluation procedure (MEP) and a two-dimensional Gaussian filter (2-DGF) to improve the performance of PRS. In [29,30], the moving average filter (MAF) was used to smooth the impedance curve and reduce the measurement error, which was suitable for suppressing the noise in the middle and low-frequency ranges. The authors of [31,32] proposed an impedance denoising and filtering method using the power spectral density and frequency characteristics of PRBS to accurately extract the impedance in the full frequency interval [0.21 Hz, 3.5 kHz]. It was noticed that the impedance extraction method based on MAF had a large calculation error because it failed to effectively eliminate the measurement noise. In addition, the processing based on features of fusion such as frequency and power spectra increased the dimensionality and computational effort of data processing in extraction of the impedance.
This study proposes a filtering and denoising method using impedance data’s sparsity according to the inherent properties of PRBS excitation. By characterizing the distribution of the original impedance data, the noise, and useful impedance were identified to effective extraction of the impedance spectrum. The main contributions of this study are as follows:
- (1)
- A density-based spatial clustering of applications with a noise-based (DBSCAN-based) impedance data processing method is proposed to utilize the distribution properties of the measurement points by PRBS excitation.
- (2)
- A parameter setting workflow was designed to properly cluster the data points of the impedance measured by DBSCAN, where the key parameters, that is, the neighborhood radius and the minimum number of points within the specific neighborhood, can be adjusted according to the frequency ranges.
- (3)
- The fast measurement of a battery’s impedance by integrating the PRBS and the data processing method was verified at various temperatures and SOCs on a 3 Ah lithium-ion battery.
This article is divided into five parts. Section 2 introduces the principle of fast measurement of the impedance spectrum. Section 3 describes the extraction method for the multi-density distribution EIS data of lithium batteries. Section 4 introduces the experimental validation. Section 5 summarizes the above work.
2. The Principle of Rapid Measurement of a Battery’s Impedance Spectrum
A highly aggregated carrier, PRBS, was chosen as the excitation signal to realize the extraction of the full frequency band impedance spectrum of a lithium-ion battery in a short period. In this section, the principle of PRBS generation and the method for calculating the battery’s impedance spectrum are introduced.
2.1. PRBS Generation
In this study, the maximum length sequence (MLS) (a typical PRBS) was used as the excitation signal for measuring the battery’s impedance. The MLS can be generated offline by shifts and different or simultaneous operations, and its algorithmic structure is shown in Figure 1.
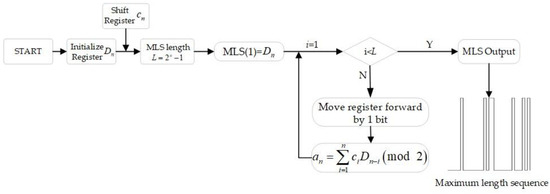
Figure 1.
The generation of MLS.
In Figure 1, represents the states of the n shift registers at a given moment, denotes the feedback coefficients of the shift register, and L is the total length of the sequence. The first bit of the MLS is the n-th bit of the initialization register; next, the adder uses the addition of Module 2.
The general form of the linear feedback logic expression is shown in Equation (1):
According to the MLS generation flowchart above, the data bits in the shift register cn are shifted one bit to the right register from Dn−1 to Dn−2 in each clock cycle fgen to produce a new bit an. The complete MLS sequence is obtained after L × fgen cycles, where fgen is the clock period of the algorithm and L is the total length of the sequence. Moreover, fgen limits the upper range of the measurable frequency for the MLS to fmax = 0.45 fgen. The register order l determines the length of the MLS as L = 2l− 1 and L limits the resolution of the measured frequency to fmin = fgen/L.
2.2. Calculation of the Battery’s Impedance
During testing a battery’s impedance, it is necessary to set the parameters fgen and generate the MLS sequence offline according to the measurement bandwidth [fmin, fmax] for the battery to be tested. Afterward, the MLS sequence is injected into the lithium-ion battery as an excitation, and the battery’s impedance in the whole frequency domain is calculated by collecting the voltage and current measurements. Thus, a spectral curve of the impedance is obtained. The whole process is shown in Figure 2.
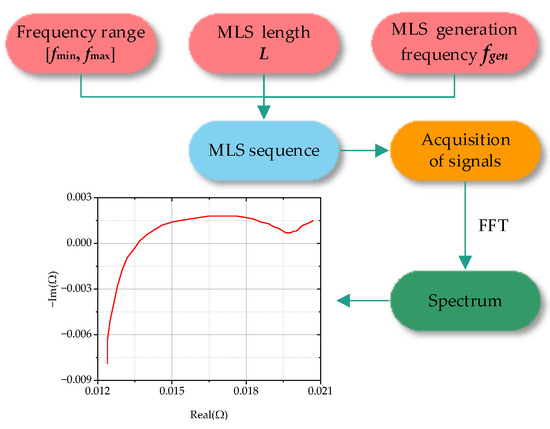
Figure 2.
Impedance spectrum using the FFT transform.
The exact calculation process is as follows. The MLS is injected as an excitation signal into the lithium-ion battery, and the terminal voltage u[n] and current i[n] are collected. The frequency domain distribution of voltage and current U() and I() using FFT are calculated as shown in Equations (2) and (3).
The lithium-ion battery’s impedance Z() can be calculated in the frequency domain as shown in Equation (4).
Through the above steps, the impedance of the lithium-ion battery at different frequencies is sequentially obtained. The real part ZRe() and the imaginary part ZIm() of the impedance can be obtained as follows:
3. Extraction of the Lithium-Ion Battery’s EIS Using Multi-Density Data Clustering
3.1. Characterization of the Distribution of Batteries’ Impedance Based on PRBS Excitation
The EIS measurement relies on a small perturbation signal. In [28], it was found that the amplitude of the excitation signal should be less than 1 C without destroying the equilibrium state of the cell, and greater than 0.4 C to ensure a sufficient signal-to-noise ratio. In this study, the amplitude was chosen to be 0.8 C. To enable a convenient battery EIS measurement in a real application, this work used the PRBS excitation signal instead of the traditional single sine sweeping injection. Since the amplitude of the PRBS was limited, the decomposition of the PRBS’s amplitude at each frequency point was even smaller compared with the sine sweeping method. In addition, the aggregated carrier class excitation method has a disadvantage in power density. The original impedance spectra of the battery calculated directly from the voltage and current responses under PRBS is shown in Figure 3. The direction of the arrow in the legend of Figure 3 is where the data density is concentrated. The measurable impedance data are chaotically dispersed at each frequency point, which increased the difficulties in extracting the useful impedance accurately and made it difficult to form an effective EIS for the battery.
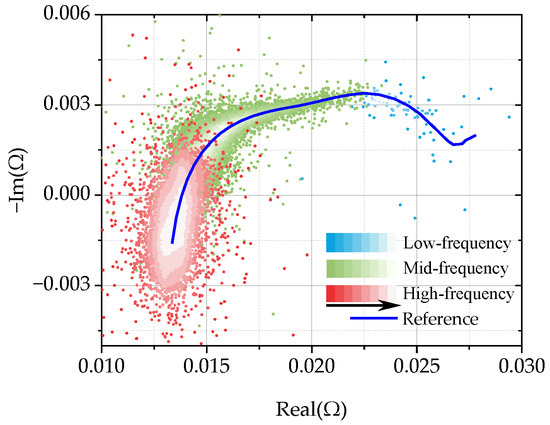
Figure 3.
The original impedance spectrum obtained from the injection of the PRBS.
The low power density characteristic of PRBS excitation leads to a poor signal-to-noise ratio in the original impedance measurement results and the presence of noise interference. However, it can still be found from Figure 3 that the useful impedance and the noise had some differences in their density distribution. The effective impedance points had a relationship with the frequency variation and were arranged with high density relative to the reference (the blue line in Figure 3). Meanwhile, the noise was in a disordered and dispersed distribution. According to the basic regularity in Figure 3, we propose a new method in this work to extract the useful impedance of the battery and synchronously remove the noise with a density clustering algorithm.
3.2. Impedance Extraction Algorithm with DBSCAN
Although the battery’s impedance measured by PRBS is fast and convenient, it suffers from a low signal-to-noise ratio and high difficulty in extraction. In this study, the sparse density of the original impedance measurement was characterized by DBSCAN for effective discrimination of data and noise.
3.2.1. Parameters Setting for DBSCAN
DBSCAN contains two parameters to be properly set before performing the discrimination of the impedance data’s sparsity in a clustering manner, i.e., the minimum number of points in the neighborhood MinPts, and the neighborhood radius Eps.
- (1)
- Minpts
When processing a large-scale dataset, MinPts = 2·D (D is the dimension of the sample data) is usually set for DBSCAN. When the measurement data contain high noise, Minpts should be appropriately increased on the basis of 2·D. In this study, the MinPts was selected as 5 for clustering the battery’s impedance data. This was because the battery’s impedance contained two dimensions of real and imaginary parts with extensive noise.
- (2)
- Eps
The selection of the neighborhood radius Eps in DBSCAN is rather complicated, especially when dealing with large-scale and noisy battery impedance data. The parameter Eps can be selected with the aid of constructing a k-distance curve characterizing the sparsity of the data. This curve is made up of the distances between the data points, where the distance d1i between a sample point (x1,y1) and all other points (xi,yi|i ≠ 1) in the dataset is calculated. The distance metric is based on Euclidean distance, which is calculated using Equation (8):
After calculating the distance between any two data points in the dataset, those distances are sorted in descending order. Then, after selecting the k points that are closest to a sample point, the distances between these k points and this sample point are plotted as a k-distance curve. A mutation point is found at the location of the curve’s inflection point. According to the elbow method, the value at the point of inflection can be set as Eps.
3.2.2. Clustering Impedance Data
For the impedance data sparsity discrimination, the DBSACN needs to set the neighborhood radius Eps and the minimum number of points within the specific neighborhood MinPts to distinguish the sparsity of the data. The structure of the algorithm is shown in Figure 4.
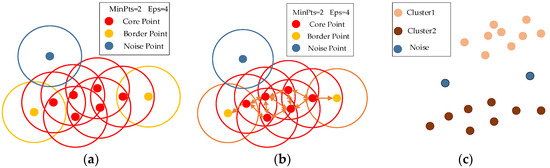
Figure 4.
Schematic diagram of the clustering algorithm. The process is as follows: (a) selection of all core points; (b) constructing the neighborhood chains; (c) completing the classification of the clusters.
As shown in Figure 4, the formation of clusters requires three steps:
- (a)
- Determination of the cluster cores based on clustering parameters: if a data point has more than MinPts points in its neighborhood with a radius of Eps, this data point is marked as a core point. We can then find all core points in the dataset. The circles of different colors in subfigures (a) and (b) represent the neighborhood of the point with radius Eps.
- (b)
- Formation of a neighborhood chain: for each core point, find all points that are densely accessible from that core point, forming a chain of neighborhoods.
- (c)
- Labeling the cluster classes and noise points: All points contained in a neighborhood chain are labeled as a cluster class, boundary points are assigned to the core point cluster class to which they are connected, and points that are not assigned to any cluster class are labeled as noise. The entire impedance test dataset is scanned and then labeled with noise points and several data clusters consisting of core and boundary points.
3.2.3. The Proposed Multi-Density Clustering Algorithm
After obtaining the two clustering parameters, the clustering calculation can be performed on the battery’s test data. DBSCAN clusters the data according to the Eps and MinPts obtained from the calculation and divides the whole test sample set into multiple clusters. DBSCAN searches for clusters by examining the Eps neighborhood of each point in the dataset, and if the Eps neighborhood of a point p contains more points than MinPts points, a cluster is created with p as the core object. DBSCAN then iteratively aggregates the objects directly density-reachable from these core objects, a process that may involve some merging of the density-reachable clusters. The process ends when no new points are added to any cluster and a cluster class is formed, followed by repeating the process until all the data have been labeled. The steps of the algorithm are shown in Algorithm 1, where the set of core points is defined as Ω, the neighborhood of a sample point xj is defined as the number of clustering clusters defined as k, the set of unvisited sample points is defined as , the current set of unvisited sample points is defined as , a queue is defined as Q, any of the core objects in Ω are defined as o, the first sample point in queue Q is defined as q, and a clustering cluster is defined as Ck.
| Algorithm 1 The proposed multi-density clustering algorithm. |
| Input: Dataset: D = {x1,x2, …,xm}, Eps:, MinPts |
| 1. Ω |
| 2. for j = 1,2,…, m do |
| 3. if then |
| 4. Ω = Ω ∪ {xj} |
| 5. end if |
| 6. end for |
| 7. k = 0 |
| 8. = D |
| 9. while do |
| 10. |
| 11. Q = <o> |
| 12. |
| 13. while do |
| 14. if then |
| 15. |
| 16. |
| 17. end if |
| 18. end while |
| 19.k = k+1, |
| 20. Ω = Ω\Ck |
| 21. end while |
| Output: Clustering result: C = {C1,C2, …,Ck} |
The clusters of data completed by clustering need to be type-discriminated to determine whether they are valid points or noisy points. In this study, a contour coefficient method was used to calculate the density of the data in the clusters after clustering. Data clusters with high density were judged as valid points, and data clusters with low density were treated as noisy points. The method of judging the data cluster’s type is as follows
where S(i) represents the contour coefficient, a(i) denotes the average distance from a sample point to other sample points in its cluster class, and b(i) denotes the average distance of a sample point to all sample points of its nearest cluster class.
The mean value of the contour coefficients within the data clusters close to 1 () can be recognized as valid signals, and the rest of the clusters are the noise clusters to be eliminated from the dataset.
4. Experimental Verification
4.1. Experimental Platform
In this section, an experimental test platform for the battery’s impedance spectrum was built, as shown in Figure 5. The experimental platform included a controller, an acquisition module, and a power module. First, an MLS was generated with a length of 32,767 bits using a 15-bit shift register. Second, this signal was injected into the battery via an external bipolar power supply, that is, the PBZ20-20, which was made by KIKUSUI, Yamanashi, Japan. Next, an instrumentation amplifier performed a differential operation on the signals from the two terminals of the cell to obtain the battery’s response. Next, the dual-channel high-speed digital-to-analog converter used the same clock to sample the response signal and the excitation signal, and the sampling results were cached by SRAM in real time and then uploaded to the host computer. Finally, the host computer uses MatlabR2022b to perform FFT analysis on the data and calculated the spectra of the excitation and response signals to obtain the amplitude and phase characteristics of the measured impedance.
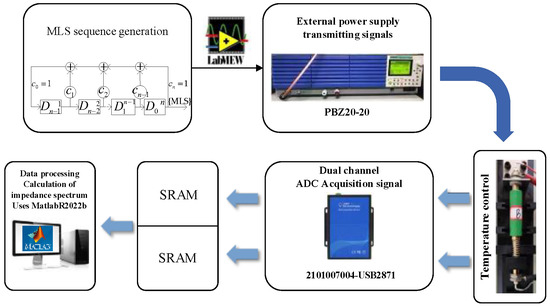
Figure 5.
Construction of the experimental platform.
In this experiment, a SONY VT5C 18650 lithium-ion battery which is manufactured by SONY of Tokyo, Japan was selected as the test sample, and the battery’s specifications are shown in Table 1.

Table 1.
The specifications of the SONY VT5C 18650 lithium-ion battery.
4.2. Validation of the Impedance Measurement
The proposed impedance extraction algorithm utilizes the difference in the sparse density between the impedance data to remove the disordered and dispersive noise points and realize the extraction of reliable impedance measurements. In this study, the results of the battery’s impedance under PRBS excitation showed some characteristics. The higher the injection frequency, the more scattered the results of the impedance calculation were. Therefore, the whole test interval was divided into three frequency bands, namely, the low-frequency interval, the middle-frequency interval, and the high-frequency interval. There were differences in data’s density at different frequency intervals, and the parameters of the corresponding impedance extraction algorithms were changed. The process of extracting the impedance is shown in Figure 6.

Figure 6.
The process of extracting the impedance in the proposed method.
The impedance calculations in the high-frequency interval were taken as an example to verify the process of parameter selection and data processing in Section 3. As shown in Figure 7a, Minpts1 was set to 5 to construct the k-distance (k = 5) curve for data in the high-frequency interval, and the curve’s inflection point was selected as Eps1. The first clustering was carried out using the parameters above, and the results of the data discrimination are shown in Figure 7b.
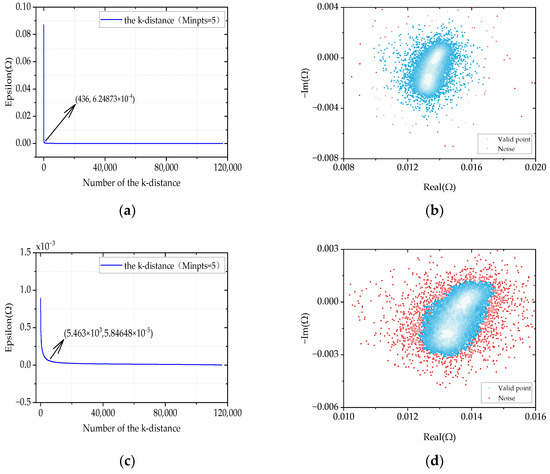
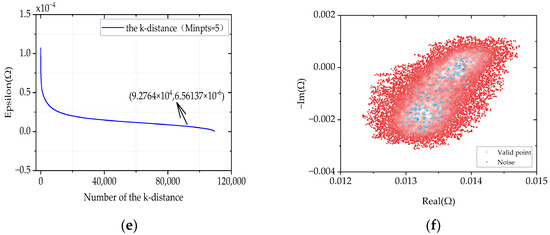
Figure 7.
Process of clustering data from the high-frequency region. (a) The parameters selected in the first round. (b) The first clustering results. (c) The parameters selected in the second round. (d) The second set of clustering results. (e) The parameters selected for the third round. (f) The third set of clustering results.
From Figure 7b, it can be seen that the impedance data were classified into a peripheral data cluster with high dispersion and an inner data cluster with high aggregation after the first clustering procedure. A large amount of noise was effectively excluded by clustering even in the first round. Due to the dispersion and the large amount of data in the high-frequency interval, the ideal extraction results could not be obtained by using the clustering method only once. The useful impedance of the battery was retained for the density clustering after enough clustering had been completed. The EIS points retained after three rounds of clustering are shown in Figure 7f. The algorithm effectively filtered out a large amount of noise, and the retained data can be judged as effective test points, that is, the battery’s EIS.
After processing the data in the high-frequency interval, the process above was used again to extract the effective impedance from the mid-frequency and low-frequency intervals. Due to the differences in the density characteristics of the data in the mid-frequency and low-frequency regions, it was necessary to select appropriate clustering parameters based on the distribution characteristics of the test data in different frequency intervals. For example, as the data’s density decreased during the clustering process, a large value of MinPts caused two neighboring clusters to merge into a single one, causing the extraction algorithm to fail. Therefore, in the mid- and the low-frequency ranges, MinPts was reduced appropriately. Table 2 shows the parameters of clustering in the three frequency ranges.

Table 2.
The parameters for clustering in the three frequency intervals.
By using the proposed method, the impedance measurements in the high-, medium-, and low-frequency intervals kept a similar number of the data points (Figure 8). It also indicated that the proposed method could effectively extract the battery’s impedance after denoising.
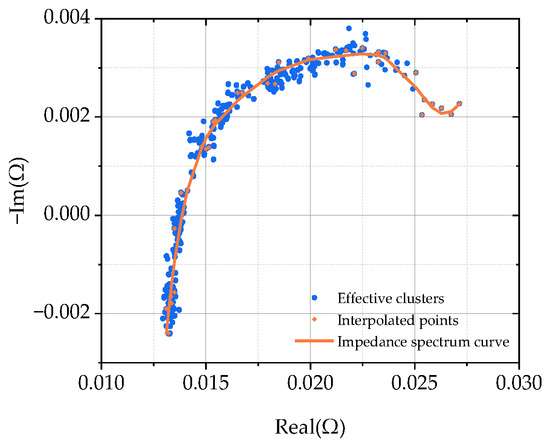
Figure 8.
The impedance obtained by the proposed method.
After the effective clusters had been formed, interpolation was used to extend the relationships between the impedance data points of known frequencies to those of unknown frequencies. This resulted in a smooth impedance spectrum curve, as shown in Figure 8. The interpolated impedance spectrum offered more detailed and smoother information on the frequency response.
4.3. Validation at Different SOCs and Temperatures
In this section, the impedance curves were extracted from the sample lithium-ion battery at different SOCs and temperatures, as shown in Figure 9.
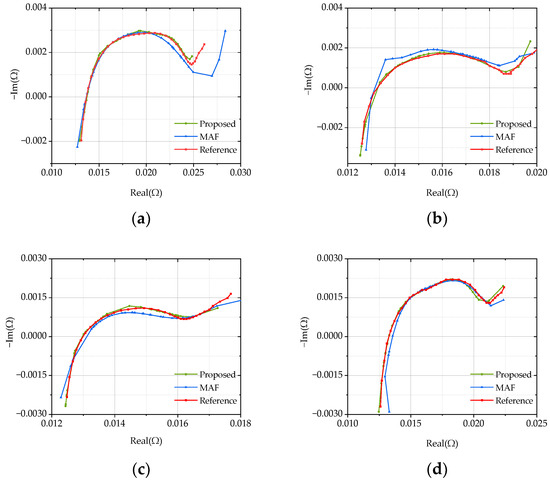
Figure 9.
Lithium-ion battery’s impedance under different test conditions: (a) T = 15 °C, SOC = 50%; (b) T = 25 °C, SOC = 50%; (c) T = 35 °C, SOC = 50%; (d) T = 25 °C, SOC = 80%.
The root mean square error (RMSE) and the mean absolute percentage error (MAPE) were used to evaluate the overall error for the impedance curves after data processing. The impedance results of the lithium-ion battery in four cases are shown in Figure 9. The superiority of the proposed method was highlighted by calculating the RMSE and MAPE for the high-, medium-, and low-frequency intervals. The MAPE of the impedance in the low-frequency range obtained by the proposed method was 0.0668 when the lithium-ion battery was at 15 °C and the SOC was 50%, while the MAPE obtained by the MAF was 0.3127, which is 4.6 times higher than that of our method. As shown in Figure 9a, it can be noticed that the impedance data obtained by the MAF in the low-frequency range were far from the reference. An increase in temperature affected the impedance spectrum of the lithium-ion battery in the mid-frequency range. At 25 °C, the MAPE of the mid-frequency range measured by the MAF was twice that of the proposed method, as seen in Figure 9b. When the temperature was 35 °C, the gap between the two methods increased further, as shown in Figure 9c. The MAPE of the impedance spectrum in the mid-frequency interval measured by the MAF (0.0704) was five times higher than that of the proposed method (0.0141). Figure 9d shows the case where the Li-ion battery had SOC = 80% and T = 25 °C. It is clear that the proposed method still had significantly high accuracy, while the impedance spectrum measured by the MAF showed a large deviation in the high-frequency range. Thus, the proposed multi-density clustering method has good computational accuracy in different cases.
In contrast, traditional MAF filtering could not carefully screen the measured data points. That is because the MAF filtering process treats the useful impedance and noise data homogeneously for suppressing the noise. In the high-frequency interval, the number of noise points was much larger than the number of valid test points, so the error of MAF filtering was larger in the high-frequency interval. Due to the small number of data points in the low-frequency range, the noise had a large impact on the results from the MAF. The key for the MAF is to choose an appropriate window size and window function; however, the lithium-ion battery’s impedance spectrum processed in this study had the characteristics of a non-uniform distribution of density. Thus, the MAF for processing the sparse data in the low-frequency interval was not as good as expected.
The RMSE and MAPE of the two methods in different cases were compared, as shown in Figure 10. When the lithium-ion battery was at an ambient temperature of 15 °C and 50% SOC, the difference in RMSE and MAPE between the two methods was the largest. The RMSE and MAPE of the proposed method were reduced by 85.6% and 82.3% compared with those of the MAF.
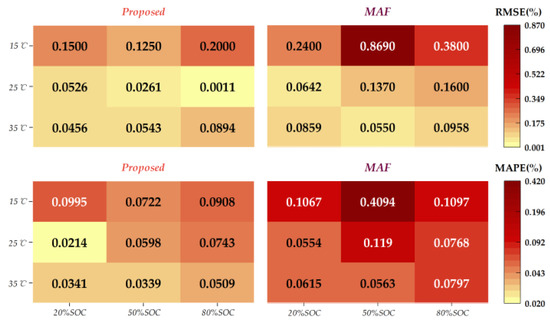
Figure 10.
A comparison of the RMSE and MAPE of the two methods in nine test cases.
5. Conclusions
In this article, a denoising method for processing multi-density impedance data is proposed. The algorithm analyzes the density characteristics of the measurement data of impedance and determines two core parameters to discriminate the noisy points and valid data points by DBSCAN, realizing the cleaning of the dataset and the effective extraction of the impedance spectrum. The effectiveness and superiority of the method were verified experimentally, and the results showed that the RMSE and MAPE calculated by the method proposed were smaller than those of the MAF filtering method at different SOCs and temperatures of the lithium-ion battery. The average RMSE of the proposed method was 0.082, which was smaller than that of the MAF (0.15). The average MAPE of the method in this study was 0.06, which was smaller than that of the MAF (0.12). In addition, the curves obtained by the proposed impedance extraction algorithm were closer to the reference curve for all the validation cases. Thus, the data processing method based on multi-density clustering DBSCAN solves the problem of the low signal-to-noise ratio of PRBS in rapid measurements of EIS and improves the accuracy of the impedance measurements. The proposed method is effective and can provide accurate impedance information for the estimating the battery’s status in BMS.
Author Contributions
Conceptualization, J.P. and J.M.; methodology, J.P. and L.Z.; software, J.P., L.Z. and J.M.; validation, C.S., L.C. and Z.Q.; formal analysis, J.P. and L.Z.; investigation, J.M.; writing—original draft preparation, J.P. and L.Z.; writing—review and editing, J.P. and J.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Natural Science Foundation of China under Grant 52107229), the Key Research and Development Program of Shaanxi Province (2024GX-YBXM-442), and the Fundamental Research Funds for the Central Universities under Grant xxj032023002.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Lawder, M.T.; Suthar, B.; Northrop, P.W.C.; De, S.; Hoff, C.M.; Leitermann, O.; Crow, M.L.; Santhanagopalan, S.; Subramanian, V.R. Battery Energy Storage System (BESS) and Battery Management System (BMS) for Grid-Scale Applications. Proc. IEEE 2014, 102, 1014–1030. [Google Scholar] [CrossRef]
- Xiong, R.; Pan, Y.; Shen, W.; Li, H.; Sun, F. Lithium-Ion Battery Aging Mechanisms and Diagnosis Method for Automotive Applications: Recent Advances and Perspectives. Renew. Sustain. Energy Rev. 2020, 131, 110048. [Google Scholar] [CrossRef]
- Han, X.; Ouyang, M.; Lu, L.; Li, J. Cycle Life of Commercial Lithium-Ion Batteries with Lithium Titanium Oxide Anodes in Electric Vehicles. Energies 2014, 7, 4895–4909. [Google Scholar] [CrossRef]
- Qays, M.O.; Buswig, Y.; Hossain, M.L.; Abu-Siada, A. Recent Progress and Future Trends on State of Charge Estimation Methods to Improve Battery-Storage Efficiency: A Review. CSEE J. Power Energy Syst. 2019, 8, 105–114. [Google Scholar] [CrossRef]
- Hao, X.; Wu, J. Online State Estimation Using Particles Filters of Lithium-Ion Polymer Battery Packs for Electric Vehicle. In Proceedings of the 2015 IEEE International Conference on Systems, Man, and Cybernetics, Hong Kong, China, 9–12 October 2015; pp. 783–788. [Google Scholar] [CrossRef]
- Meng, J.; Cai, L.; Stroe, D.-I.; Luo, G.; Sui, X.; Teodorescu, R. Lithium-Ion Battery State-of-Health Estimation in Electric Vehicle Using Optimized Partial Charging Voltage Profiles. Energy 2019, 185, 1054–1062. [Google Scholar] [CrossRef]
- Hannan, M.A.; Lipu, M.S.H.; Hussain, A.; Mohamed, A. A Review of Lithium-Ion Battery State of Charge Estimation and Management System in Electric Vehicle Applications: Challenges and Recommendations. Renew. Sustain. Energy Rev. 2017, 78, 834–854. [Google Scholar] [CrossRef]
- Peng, J.; Meng, J.; Chen, D.; Liu, H.; Hao, S.; Sui, X.; Du, X. A Review of Lithium-Ion Battery Capacity Estimation Methods for Onboard Battery Management Systems: Recent Pro-Gress and Perspectives. Batteries 2022, 8, 229. [Google Scholar] [CrossRef]
- Meng, J.; Luo, G.; Ricco, M.; Swierczynski, M.; Stroe, D.-I.; Teodorescu, R. Overview of Lithium-Ion Battery Modeling Methods for State-of-Charge Estimation in Electrical Vehicles. Appl. Sci. 2018, 8, 659. [Google Scholar] [CrossRef]
- Li, L.; Li, Y.; Cui, W.; Chen, Z.; Wang, D.; Zhou, B.; Hong, D. A Novel Health Indicator for Online Health Estimation of Lithium-Ion Batteries Using Partial Incremental Capacity and Dynamic Voltage Warping. J. Power Sources 2022, 545, 231961. [Google Scholar] [CrossRef]
- Feng, X.; Ouyang, M.; Liu, X.; Lu, L.; Xia, Y.; He, X. Thermal Runaway Mechanism of Lithium Ion Battery for Electric Vehicles: A Review. Energy Storage Mater. 2018, 10, 246–267. [Google Scholar] [CrossRef]
- Han, X.; Lu, L.; Zheng, Y.; Feng, X.; Li, Z.; Li, J.; Ouyang, M. A Review on the Key Issues of the Lithium Ion Battery Degradation among the Whole Life Cycle. eTransportation 2019, 1, 100005. [Google Scholar] [CrossRef]
- Gao, Y.; Jiang, J.; Zhang, C.; Zhang, W.; Jiang, Y. Aging Mechanisms under Different State-of-Charge Ranges and the Multi-Indicators System of State-of-Health for Lith-Ium-Ion Battery with Li(NiMnCo)O2 Cathode. J. Power Sources 2018, 400, 641–651. [Google Scholar] [CrossRef]
- Huang, Q.; Shen, Y.; Huang, Y.; Zhang, L.; Zhang, J. Electrochimica Acta Impedance Characteristics and Diagnoses of Automotive Lithium-Ion. Electrochim. Acta 2016, 219, 751–765. [Google Scholar] [CrossRef]
- Wang, X.; Wei, X.; Chen, Q.; Dai, H. A Novel System for Measuring Alternating Current Impedance Spectra of Series-Connected Lithium-Ion Batteries with a High-Power Dual Active Bridge Converter and Distributed Sampling Units. IEEE Trans. Ind. Electron. 2021, 68, 7380–7390. [Google Scholar] [CrossRef]
- Du, X.; Meng, J.; Peng, J.; Zhang, Y.; Liu, T.; Teodorescu, R. Sensorless Temperature Estimation of Lithium-Ion Battery Based on Broadband Impedance Measurements. IEEE Trans. Power Electron. 2022, 37, 10101–10105. [Google Scholar] [CrossRef]
- Cai, J.; Zhang, L.; Wang, X.; Zhu, J.; Yuan, Y.; Wang, Y.; Wei, X.; Dai, H. Investigation of an M-Sequence Based Impedance Spectrum Acquisition Method for Lithium-Ion Batteries from the Engineering Application Perspective. J. Energy Storage 2023, 59, 106428. [Google Scholar] [CrossRef]
- Shu, X.; Yang, W.; Yang, B.; Wei, K.; Punyawudho, K.; Liu, C. Research on EIS Characterization and Internal Morphological Changes of LIBs during Degradation Process. Eng. Fail. Anal 2024, 155, 107764. [Google Scholar] [CrossRef]
- Buchicchio, E.; De Angelis, A.; Santoni, F.; Carbone, P.; Bianconi, F.; Smeraldi, F. Battery SOC Estimation from EIS Data Based on Machine Learning and Equivalent Circuit Model. Energy 2023, 283, 128461. [Google Scholar] [CrossRef]
- Li, J.; Zhao, S.; Miah, M.S.; Niu, M. Remaining Useful Life Prediction of Lithium-Ion Batteries via an EIS Based Deep Learning Approach. Energy Rep. 2023, 10, 3629–3638. [Google Scholar] [CrossRef]
- De Angelis, A.; Buchicchio, E.; Santoni, F.; Moschitta, A.; Carbone, P. Practical Broadband Measurement of Battery EIS. In Proceedings of the 2021 IEEE International Workshop on Metrology for Automotive, MetroAutomotive, Bologna, Italy, 1–2 July 2021; pp. 25–29. [Google Scholar] [CrossRef]
- Wang, X.; Kou, Y.; Wang, B.; Jiang, Z.; Wei, X.; Dai, H. Fast Calculation of Broadband Battery Impedance Spectra Based on S Transform of Step Disturbance and Response. IEEE Trans. Transp. Electrif. 2022, 7782, 3659–3672. [Google Scholar] [CrossRef]
- Roinila, T.; Abdollahi, H.; Santi, E. Frequency-Domain Identification Based on Pseudorandom Sequences in Analysis and Control of Dc Power Distribution Systems: A Review. IEEE Trans. Power Electron 2021, 36, 3744–3756. [Google Scholar] [CrossRef]
- Sihvo, J.; Messo, T.; Roinila, T.; Luhtala, R. Online Internal Impedance Measurements of Li-Ion Battery Using PRBS Broadband Excitation and Fourier Techniques: Methods and Injection Design. In Proceedings of the 2018 International Power Electronics Conference, IPEC-Niigata—ECCE Asia 2018, Niigata, Japan, 20–24 May 2018; pp. 2470–2475. [Google Scholar]
- Sihvo, J.; Messo, T.; Roinila, T.; Luhtala, R.; Stroe, D.I. Online Identification of Internal Impedance of Li-Ion Battery Cell Using Ternary-Sequence Injection. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition, ECCE 2018, Portland, OR, USA, 23–27 September 2018; pp. 2705–2711. [Google Scholar]
- Sihvo, J.; Stroe, D.I.; Messo, T.; Roinila, T. Fast Approach for Battery Impedance Identification Using Pseudo-Random Sequence Signals. IEEE Trans. Power Electron. 2020, 35, 2548–2557. [Google Scholar] [CrossRef]
- Du, X.; Du, X.; Meng, J.; Meng, J.; Peng, J.; Peng, J. Hybrid Pseudorandom Sequence for Broadband Impedance Measurements of Lithium-Ion Batteries. IEEE Trans. Ind. Electron. 2022, 70, 6856–6864. [Google Scholar] [CrossRef]
- Zhang, Y.; Du, X.; Meng, J.; Jiang, Q.; Peng, J.; Liu, T. Rapid Broadband Impedance Acquisition of Lithium-Ion Batteries Based on Measurement Evaluating and Impedance Filtering. IEEE Trans. Transp. Electrif. 2023, 9, 4888–4897. [Google Scholar] [CrossRef]
- Sihvo, J.; Roinila, T.; Stroe, D.I. Novel Fitting Algorithm for Parametrization of Equivalent Circuit Model of Li-Ion Battery from Broadband Impedance Measurements. IEEE Trans. Ind. Electron. 2021, 68, 4916–4926. [Google Scholar] [CrossRef]
- Gücin, T.N.; Ovacik, L. Online Impedance Measurement of Batteries Using the Cross-Correlation Technique. IEEE Trans. Power Electron. 2020, 35, 4365–4375. [Google Scholar] [CrossRef]
- Peng, J.; Meng, J.; Du, X.; Cai, L.; Stroe, D.I. A Fast Impedance Measurement Method for Lithium-Ion Battery Using Power Spectrum Property. IEEE Trans. Ind. Inform. 2023, 19, 8253–8261. [Google Scholar] [CrossRef]
- Meng, J.; Peng, J.; Cai, L.; Song, Z. Rapid Impedance Extraction for Lithium-Ion Battery by Integrating Power Spectrum and Frequency Property. IEEE Trans. Ind. Electron. 2023, 1–10. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).