Nuclear Dipole Moments and Shielding Constants of Light Nuclei Measured in Magnetic Fields
Abstract
1. Introduction
2. Methodology for Determination of Nuclear Magnetic Moments
2.1. Nuclear Magnetic Resonance Spectroscopy (NMR)
2.2. Atomic Beam Magnetic Resonance (ABMR)
2.3. Penning Trap Experiments
2.4. Theoretical Approach
3. Magnetic Moments of Selected Nuclei
3.1. Magnetic Moments of Hydrogen Isotopes
3.2. Proton ( Nucleus)
3.3. Deuteron ( Nucleus)
3.4. Triton ( Nucleus)
3.5. Magnetic Moment of Helium-3
3.6. Magnetic Moments of 6,7-Lithium Isotopes
3.7. Magnetic Moment of the Beryllium-9 Isotope
| Solution | Atom | ν0/MHz | δ/ppm | σ(rel.)/ppm | σ(abs.)/ppm | µ(nX)/µN |
|---|---|---|---|---|---|---|
| BeSO4 | 3He | 381.3564692 | 2.858 | −0.267 | 59.700 | −2.127625309 |
| 1H | 500.6081735 | 4.104 | −7.11 | 25.705 | 2.792847345 | |
| 9Be | 70.344232 | 0.104 | 112.18 | −1.177432(5) a | ||
| −1.175 b | ||||||
| −1.1778(9) c | ||||||
| −1.177432(3) d | ||||||
| −1.17747(27) e | ||||||
| −1.17743159(3) f | ||||||
| −1.177430(5) g |
3.8. Magnetic Moments of 10,11-Boron Isotopes
4. Conclusions
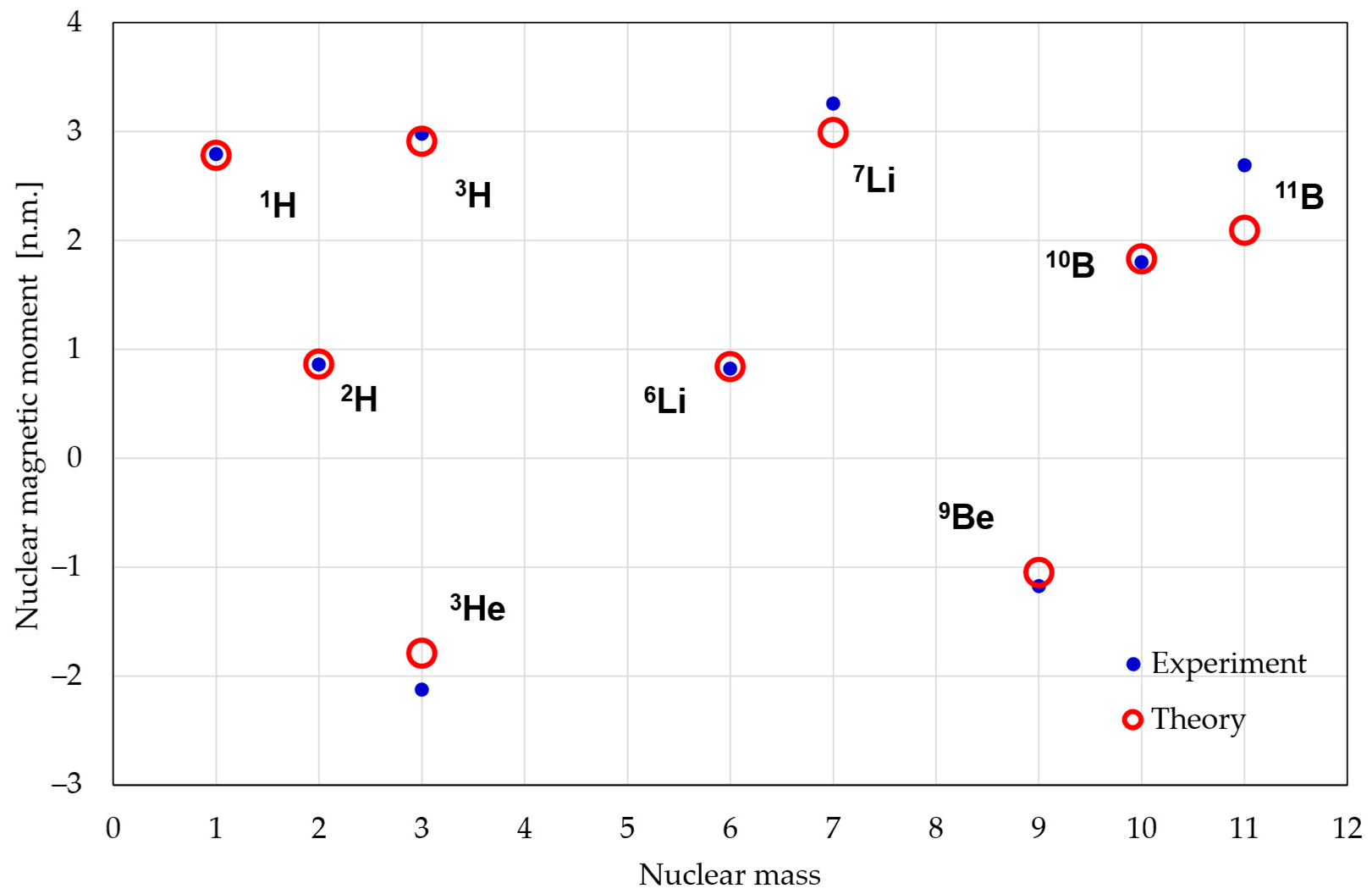
| Nuclide | Iπ | Q (Barn) | Abundance % | μexp. | Ref. | μtheor. | Ref. |
|---|---|---|---|---|---|---|---|
| 1H | 1/2+ | 99.9885 | 2.79284734462(82) | [2,4] | 2.792(37) | [25] | |
| 2H(D) | 1+ | 0.00286(2) | 0.0115 | 0.857438228(9) | [35] | 0.8615978 | [71] |
| 0.8748046 | [71] | ||||||
| 3H(T) | 1/2+ | 10−18 | 2.978962471(10) | [29,33,39] | 2.79284734(3) | [67] | |
| 2.91(20) 3.56(18) | [67] [25] | ||||||
| 3He | 1/2+ | 0.000134 | −2.127625308(25) | [68] | −2.004914 | [69] | |
| −1.913042 −2.2905 | [69] [25] | ||||||
| 6Li | 1+ | 0.000806(6) | 7.59(4) | 0.8220454(25) | [54] | 0.8339 | [72] |
| 0.843 | [73] | ||||||
| 7Li | 3/2 | 0.0400(3) | 92.41(4) | 3.2564171(98) | [54] | 3.168(13) | [74] |
| 2.954(5) 3.01(2) | [72] [73] | ||||||
| 9Be | 3/2 | −0.0529(4) | 100 | −1.177743185(15) | [59] | −1.06(6) 1.22(9) | [75] [75] |
| 10B | 3+ | 0.0845(2) | 19.9 | 1.86004636(8) | [52] | 1.83 | [76] |
| 11B | 3/2− | 0.04059(10) | 80.1 | 2.6883781(11) | [52] | 2.09 | [76] |
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Odom, B.; Hanneke, D.; D’Urso, B.; Gabrielse, G. New Measurement of the Electron Magnetic Moment Using a One-Electron Quantum Cyclotron. Phys. Rev. Lett. 2006, 97, 030801. [Google Scholar] [CrossRef] [PubMed]
- Tiesinga, E.; Mohr, P.J.; Newell, D.B.; Taylor, B.N. CODATA Recommended Values of the Fundamental Physical Constants: 2018. J. Phys. Chem. Ref. Data 2021, 50, 033105. [Google Scholar] [CrossRef] [PubMed]
- Gabrielse, G.; Fayer, S.E.; Myers, T.G.; Fan, X. Towards an Improved Test of the Standard Model’s Most Precise Prediction. Atoms 2019, 7, 45. [Google Scholar] [CrossRef]
- Schneider, G.; Mooser, A.; Bohman, M.; Schön, N.; Harrington, J.; Higuchi, T.; Nagahama, H.; Sellner, S.; Smorra, C.; Blaum, K.; et al. Double-Trap Measurement of the Proton Magnetic Moment at 0.3 Parts per Billion Precision. Science 2017, 358, 1081–1084. [Google Scholar] [CrossRef]
- Oerter, R. The Theory of Almost Everything: The Standard Model. In The Unsung Triumph of Modern Physics, Kindle ed.; Penguin Group: London, UK, 2006. [Google Scholar]
- Aoyama, T.; Asmussen, N.; Benayoun, M.; Bijnens, J.; Blum, T.; Bruno, M.; Caprini, I.; Carloni Calame, C.M.; Cè, M.; Colangelo, G.; et al. The Anomalous Magnetic Moment of the Muon in the Standard Model. Phys. Rep. 2020, 887, 1–166. [Google Scholar] [CrossRef]
- Blum, T.; Christ, N.; Hayakawa, M.; Izubuchi, T.; Jin, L.; Jung, C.; Lehner, C. Hadronic Light-by-Light Scattering Contribution to the Muon Anomalous Magnetic Moment from Lattice QCD. Phys. Rev. Lett. 2020, 124, 132002. [Google Scholar] [CrossRef]
- Billard, J.; Johnston, J.; Kavanagh, B.J.; Heger, A.; Friedland, A.; Studenikin, A. Status and Perspectives of Neutrino Magnetic Moments. J. Phys. Conf. Ser. 2016, 718, 062076. [Google Scholar] [CrossRef]
- Aker, M.; Beglarian, A.; Behrens, J.; Berlev, A.; Besserer, U.; Bieringer, B.; Block, F.; Bobien, S.; Böttcher, M.; Bornschein, B.; et al. Direct Neutrino-Mass Measurement with Sub-Electronvolt Sensitivity. Nat. Phys. 2022, 18, 160–166. [Google Scholar] [CrossRef]
- Cook, N.D. Models of the Atomic Nucleus, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2010; ISBN 978-3-642-14736-4. [Google Scholar]
- Holt, R.J.; Gilman, R. Transition between Nuclear and Quark–Gluon Descriptions of Hadrons and Light Nuclei. Rep. Prog. Phys. 2012, 75, 086301. [Google Scholar] [CrossRef]
- Abov, Y.G.; Gulko, A.D.; Dzheparov, F.S. Beta-NMR Spectroscopy: Modern State and Prospects. Phys. At. Nucl. 2006, 69, 1701–1710. [Google Scholar] [CrossRef]
- Harding, R.D.; Pallada, S.; Croese, J.; Antušek, A.; Baranowski, M.; Bissell, M.L.; Cerato, L.; Dziubinska-Kühn, K.M.; Gins, W.; Gustafsson, F.P.; et al. Magnetic Moments of Short-Lived Nuclei with Part-per-Million Accuracy: Toward Novel Applications of β-Detected NMR in Physics, Chemistry, and Biology. Phys. Rev. X 2020, 10, 041061. [Google Scholar] [CrossRef]
- Forman, P. Molecular Beam Measurements of Nuclear Moments before Magnetic Resonance. Part I: I. I. Rabi and Deflecting Magnets to 1938. Ann. Sci. 1998, 55, 111–160. [Google Scholar] [CrossRef]
- Bloch, F.; Hansen, W.W.; Packard, M. The Nuclear Induction Experiment. Phys. Rev. 1946, 70, 474–485. [Google Scholar] [CrossRef]
- Purcell, E.M.; Pound, R.V.; Bloembergen, N. Nuclear Magnetic Resonance Absorption in Hydrogen Gas. Phys. Rev. 1946, 70, 986–987. [Google Scholar] [CrossRef]
- Zimmerman, J.R.; Williams, D. Determination of Nuclear Gyromagnetic Ratios I. Phys. Rev. 1949, 76, 350. [Google Scholar] [CrossRef]
- Antušek, A.; Jackowski, K.; Jaszuński, M.; Makulski, W.; Wilczek, M. Nuclear Magnetic Dipole Moments from NMR Spectra. Chem. Phys. Lett. 2005, 411, 111–116. [Google Scholar] [CrossRef]
- Jaszuński, M.; Antušek, A.; Garbacz, P.; Jackowski, K.; Makulski, W.; Wilczek, M. The Determination of Accurate Nuclear Magnetic Dipole Moments and Direct Measurement of NMR Shielding Constants. Prog. Nucl. Magn. Reson. Spectrosc. 2012, 67, 49–63. [Google Scholar] [CrossRef]
- Winkler, P.F.; Kleppner, D.; Myint, T.; Walther, F.G. Magnetic Moment of the Proton in Bohr Magnetons. Phys. Rev. A 1972, 5, 83–114. [Google Scholar] [CrossRef]
- Rabi, I.I.; Zacharias, J.R.; Millman, S.; Kusch, P. A New Method of Measuring Nuclear Magnetic Moment. Phys. Rev. 1938, 53, 318. [Google Scholar] [CrossRef]
- Dehmelt, H.G. Radiofrequency Spectroscopy of Stored Ions I: Storage. Adv. At. Mol. Opt. Phys. 1968, 3, 53–72. [Google Scholar] [CrossRef]
- Dehmelt, H.G. Radiofrequency Spectroscopy of Stored Ions II: Spectroscopy. Adv. At. Mol. Opt. Phys. 1969, 5, 109–154. [Google Scholar] [CrossRef]
- Dehmelt, H.G.; Ekstrom, P. Proposed G-2 Experiment on Stored Single Electron or Positron. Am. Phys. Soc. 1973, 727–731. [Google Scholar]
- Beane, S.R.; Chang, E.; Cohen, S.; Detmold, W.; Lin, H.W.; Orginos, K.; Parreño, A.; Savage, M.J.; Tiburzi, B.C. Magnetic Moments of Light Nuclei from Lattice Quantum Chromodynamics. Phys. Rev. Lett. 2014, 113, 252001. [Google Scholar] [CrossRef] [PubMed]
- Zhao, E.G. Recent Progress in Theoretical Studies of Nuclear Magnetic Moments. Chin. Sci. Bull. 2012, 57, 4394–4399. [Google Scholar] [CrossRef]
- Nagahama, H.; Smorra, C.; Sellner, S.; Harrington, J.; Higuchi, T.; Borchert, M.J.; Tanaka, T.; Besirli, M.; Mooser, A.; Schneider, G.; et al. Sixfold Improved Single Particle Measurement of the Magnetic Moment of the Antiproton. Nat. Commun. 2017, 8, 14084. [Google Scholar] [CrossRef]
- Stone, N.J. New Table of Recommended Nuclear Electric Quadrupole Moments. Hyperfine Interact. 2015, 230, 7–16. [Google Scholar] [CrossRef]
- Garbacz, P.; Łach, G. Isotope Effects on Nuclear Magnetic Shielding in Molecular Hydrogen. J. Phys. Chem. A 2018, 122, 590–593. [Google Scholar] [CrossRef]
- Jaszuński, M.; Łach, G.; Strasburger, K. NMR Shielding Constants in Hydrogen Molecule Isotopomers. Theor. Chem. Acc. 2011, 129, 325–330. [Google Scholar] [CrossRef]
- Sundholm, D.; Gauss, J. Isotope and Temperature Effects on Nuclear Magnetic Shieldings and Spin-Rotation Constants Calculated at the Coupled-Cluster Level. Mol. Phys. 1997, 92, 1007–1014. [Google Scholar] [CrossRef]
- Karshenboim, S.G.; Ivanov, V.G.; Neronov, Y.I.; Nikolaev, B.P.; Tolparov, Y.N. A New Determination of the Proton-to-Deuteron Ratio of Magnetic Moments. Can. J. Phys. 2005, 83, 405–412. [Google Scholar] [CrossRef]
- Puchalski, M.; Komasa, J.; Pachucki, K. Deuteron and Triton Magnetic Moments from NMR Spectra of the Hydrogen Molecule. Phys. Rev. A 2015, 92, 020501. [Google Scholar] [CrossRef]
- Puchalski, M.; Komasa, J.; Spyszkiewicz, A.; Pachucki, K. Nuclear Magnetic Shielding in HD and HT. Phys. Rev. A 2022, 105, 042802. [Google Scholar] [CrossRef]
- Stone, N.J. Table of Nuclear Magnetic Dipole and Electric Quadrupole Moments (INDC(NDS)—0658); International Atomic Energy Agency (IAEA): Vienna, Austria, 2014. [Google Scholar]
- Duffy, W. Magnetic Moment of the Triton in Units of the Magnetic Moment of the Proton. Phys. Rev. 1959, 115, 1012. [Google Scholar] [CrossRef]
- Neronov, Y.I.; Barzakh, A.E. NMR Determination of the Triton-Proton Magnetic Moment Ratio to within 10−6%. Sov. Phys. JETP 1977, 45, 871–876. [Google Scholar]
- Neronov, Y.I.; Karshenboim, S.G. NMR Spectroscopy of Hydrogen Deuteride and Magnetic Moments of Deuteron and Triton. Phys. Lett. A 2003, 318, 126–132. [Google Scholar] [CrossRef]
- Aleksandrov, V.S.; Neronov, Y.I. Study of the NMR Spectra of Hydrogen Isotopic Analogs and Estimation of the Magnetic Moment of the Triton. JETP Lett. 2011, 93, 305–307. [Google Scholar] [CrossRef]
- Tanabe, T. Characteristics of Tritium. In Tritium: Fuel of Fusion Reactors; Springer: Tokyo, Japan, 2017; pp. 27–48. [Google Scholar]
- Rudziński, A.; Puchalski, M.; Pachucki, K. Relativistic, QED, and Nuclear Mass Effects in the Magnetic Shielding of 3He. J. Chem. Phys. 2009, 130, 244102. [Google Scholar] [CrossRef]
- Jackowski, K.; Jaszuński, M.; Kamieński, B.; Wilczek, M. NMR Frequency and Magnetic Dipole Moment of 3He Nucleus. J. Magn. Reson. 2008, 193, 147–149. [Google Scholar] [CrossRef]
- Makulski, W. Explorations of Magnetic Properties of Noble Gases: The Past, Present, and Future. Magnetochemistry 2020, 6, 65. [Google Scholar] [CrossRef]
- Aruev, N.N.; Neronov, Y.I. Gas Samples with a Mixture of Hydrogen Isotopes and 3He for NMR Spectroscopy and Estimation of the Magnetic Moment of the 3He Nucleus. Technol. Phys. 2012, 57, 1579–1584. [Google Scholar] [CrossRef]
- Neronov, Y.I.; Seregin, N.N. High-Precision Evaluation of the Magnetic Moment of the Helion. J. Exp. Theor. Phys. 2012, 115, 777–781. [Google Scholar] [CrossRef]
- Nörtershäuser, W.; Sánchez, R.; Ewald, G.; Dax, A.; Behr, J.; Bricault, P.; Bushaw, B.A.; Dilling, J.; Dombsky, M.; Drake, G.W.F.; et al. Isotope-Shift Measurements of Stable and Short-Lived Lithium Isotopes for Nuclear-Charge-Radii Determination. Phys. Rev. A 2011, 83, 012516. [Google Scholar] [CrossRef]
- Rabi, I.I.; Millman, S.; Kusch, P.; Zacharias, J.R. The Molecular Beam Resonance Method for Measuring Nuclear Magnetic Moments the Magnetic Moments of 3Li6, 3Li7 and 9F19. Phys. Rev. 1939, 55, 526–535. [Google Scholar] [CrossRef]
- Beckmann, A.; Böklen, K.D.; Elke, D. Precision Measurements of the Nuclear Magnetic Dipole Moments of 6Li, 7Li, 23Na, 39K and 41K. Z. Für. Phys. 1974, 270, 173–186. [Google Scholar] [CrossRef]
- Lutz, O. The GI-Factors and the Magnetic Moments of Alkali Nuclei and the Shielding of Rb+ by Water. Phys. Lett. A 1967, 25, 440–441. [Google Scholar] [CrossRef]
- Makulski, W. The Radiofrequency NMR Spectra of Lithium Salts in Water; Reevaluation of Nuclear Magnetic Moments for 6Li and 7Li Nuclei. Magnetochemistry 2018, 4, 9. [Google Scholar] [CrossRef]
- Antušek, A.; Kędziera, D.; Kaczmarek-Kędziera, A.; Jaszuński, M. Coupled Cluster Study of NMR Shielding of Alkali Metal Ions in Water Complexes and Magnetic Moments of Alkali Metal Nuclei. Chem. Phys. Lett. 2012, 532, 1–8. [Google Scholar] [CrossRef]
- Jackowski, K.; Makulski, W.; Szyprowska, A.; Antušek, A.; Jaszuński, M.; Jusélius, J. NMR Shielding Constants in BF3 and Magnetic Dipole Moments of 11B and 10B Nuclei. J. Chem. Phys. 2009, 130, 044309. [Google Scholar] [CrossRef]
- Makulski, W.; Szyprowska, A.; Jackowski, K. Precise Determination of the 13C Nuclear Magnetic Moment from 13C, 3He and 1H NMR Measurements in the Gas Phase. Chem. Phys. Lett. 2011, 511, 224–228. [Google Scholar] [CrossRef]
- Neronov, Y.I. Simultaneous Determination of the Magnetic Moments of 6Li and 7Li Nuclei Using an NMR Spectrometer. Meas. Technol. 2020, 63, 667–673. [Google Scholar] [CrossRef]
- Raghavan, P. Table of Nuclear Moments. At. Data Nucl. Data Tables 1989, 42, 189–291. [Google Scholar] [CrossRef]
- Kusch, P.; Millman, S.; Rabi, I.I. On the Nuclear Magnetic Moment of Beryllium. Phys. Rev. 1939, 55, 666. [Google Scholar] [CrossRef]
- Alder, F.; Yu, F.C. On the Magnetic Moments of Mg25, Re185, Re187, and Be9. Phys. Rev. 1951, 82, 105. [Google Scholar] [CrossRef]
- Hatton, J.; Rollin, B.V.; Seymour, E.F.W. Nuclear Magnetic Resonance Measurements on Be9, Al27, and Si29 in Beryl. Phys. Rev. 1951, 83, 672. [Google Scholar] [CrossRef]
- Pachucki, K.; Puchalski, M. Accurate Determination of Be Magnetic Moment. Opt. Commun. 2010, 283, 641–643. [Google Scholar] [CrossRef]
- Wineland, D.J.; Wells, J.S.; Weber, H.P.; Luthy, W.; Verlag, S. Precision Measurements of Laser Cooled 9Be+ Ions. In Proceedings of the Laser Spectroscopy VI: Proceedings of the Sixth International Conference, Interlaken, Switzerland, 27 June–1 July 1983; Volume 40, p. 168. [Google Scholar]
- Tossell, J.A. The Effects of Hydrolysis and Oligomerization upon the NMR Shieldings of Be2+ and Al3+ Species in Aqueous Solution. J. Magn. Reson. 1998, 135, 203–207. [Google Scholar] [CrossRef]
- Dickinson, W.C.; Wimett, T.F. The Magnetic Moment of Be9. Phys. Rev. 1949, 75, 1769. [Google Scholar] [CrossRef]
- Plieger, P.G.; John, K.D.; Keizer, T.S.; McCleskey, T.M.; Burrell, A.K.; Martin, R.L. Predicting 9Be Nuclear Magnetic Resonance Chemical Shielding Tensors Utilizing Density Functional Theory. J. Am. Chem. Soc. 2004, 126, 14651–14658. [Google Scholar] [CrossRef]
- Stone, N.J. Table of Nuclear Magnetic Dipole and Electric Quadrupole Moments. At. Data Nucl. Data Tables 2005, 90, 75–176. [Google Scholar] [CrossRef]
- Antušek, A.; Rodziewicz, P.; Kȩdziera, D.; Kaczmarek-Kȩdziera, A.; Jaszuński, M. Ab Initio Study of NMR Shielding of Alkali Earth Metal Ions in Water Complexes and Magnetic Moments of Alkali Earth Metal Nuclei. Chem. Phys. Lett. 2013, 588, 57–62. [Google Scholar] [CrossRef]
- Rudolph, W.W.; Fischer, D.; Irmer, G.; Pye, C.C. Hydration of Beryllium(II) in Aqueous Solutions of Common Inorganic Salts. A Combined Vibrational Spectroscopic and Ab Initio Molecular Orbital Study. Dalton Trans. 2009, 6513. [Google Scholar] [CrossRef] [PubMed]
- Pirahmadian, M.H.; Ghahramany, N. Non-Dynamical Calculation of Triton Magnetic Moment via Quark Constituents. Iran. J. Sci. Technol. Trans. A Sci. 2019, 43, 1345–1350. [Google Scholar] [CrossRef]
- Makulski, W. Probing Nuclear Dipole Moments and Magnetic Shielding Constants through 3-Helium NMR Spectroscopy. Physchem 2022, 2, 116–130. [Google Scholar] [CrossRef]
- Pirahmadian, M.H.; Ghahramany, N. Helium-3 Magnetic Dipole Moment Determination by Using Quark Constituents for All Possible Baryon Formations. Results Phys. 2017, 7, 2771–2774. [Google Scholar] [CrossRef]
- Jackowski, K.; Garbacz, P. Nuclear Magnetic Moments and NMR Measurements of Shielding. In Gas Phase NMR; The Royal Society of Chemistry: London, UK, 2016; p. 108. [Google Scholar]
- Ghahramany, N.; Yazdankish, E. Determination of Deuteron Dipole Moment in Nuclear Quark-Like Model. Commun. Theor. Phys. 2013, 59, 579. [Google Scholar] [CrossRef]
- Cockrell, C.; Vary, J.P.; Maris, P. Lithium Isotopes within the Ab Initio No-Core Full Configuration Approach. Phys. Rev. C Nucl. Phys. 2012, 86, 034325. [Google Scholar] [CrossRef]
- Forssén, C.; Caurier, E.; Navrátil, P. Charge Radii and Electromagnetic Moments of Li and Be Isotopes from the Ab Initio No-Core Shell Model. Phys. Rev. C Nucl. Phys. 2009, 79, 021303. [Google Scholar] [CrossRef]
- Marcucci, L.E.; Pervin, M.; Pieper, S.C.; Schiavilla, R.; Wiringa, R.B. Quantum Monte Carlo Calculations of Magnetic Moments and M1 Transitions in A ≤ 7 Nuclei Including Meson-Exchange Currents. Phys. Rev. C Nucl. Phys. 2008, 78, 065501. [Google Scholar] [CrossRef]
- Forssén, C.; Navrátil, P.; Ormand, W.E.; Caurier, E. Large Basis Ab Initio Shell Model Investigation of 9Be and 11Be. Phys. Rev. C Nucl. Phys. 2005, 71, 044312. [Google Scholar] [CrossRef]
- Froese, P.; Navrátil, P. Ab Initio Calculations of Electric Dipole Moments of Light Nuclei. Phys. Rev. C 2021, 104, 025502. [Google Scholar] [CrossRef]
- Borremans, D.; Yordanov, D.; Balabanski, D.L.; Neyens, G.; Lassen, J.; Blaum, K.; Kowalska, M.; Vermeulen, N.; Himpe, P.; Lievens, P.; et al. New Measurement and Reevaluation of the Nuclear Magnetic Andquadrupole Moments of 8Li and 9Li. Phys. Rev. C Nucl. Phys. 2005, 72, 044309. [Google Scholar] [CrossRef]
- Geithner, W.; Kappertz, S.; Keim, M.; Lievens, P.; Neugart, R.; Vermeeren, L.; Wilbert, S.; Fedoseyev, V.N.; Köster, U.; Mishin, V.I.; et al. Measurement of the Magnetic Moment of the One-Neutron Halo Nucleus 11Be. Phys. Rev. Lett. 1999, 83, 3792. [Google Scholar] [CrossRef]
- Mack, J.E. A Table of Nuclear Moments, January 1950. Rev. Mod. Phys. 1950, 22, 64–76. [Google Scholar] [CrossRef]
- Walchli, H.E. Some Improved Measurements of Nuclear Magnetic Dipole Moments by Means of Nuclear Magnetic Resonance; Oak Ridge National Lab: Oak Ridge, TN, USA, 1954. [Google Scholar]
- Schintlmeister, J.; Kunz, W. Tabellen Der Atomkerne; Akademie-Verlag: Berlin, Germany, 1958; Volume Teil I. [Google Scholar]
- Fuller, G.H. Nuclear Spins and Moments. J. Phys. Chem. Ref. Data 1976, 5, 835–1092. [Google Scholar] [CrossRef]
- Mertzimekis, T.J. Development of a Dedicated Online Database for Nuclear Moments Data; International Atomic Energy Agency (IAEA): Vienna, Austria, 2016. [Google Scholar]
- MacDonald, A.; Karamy, B.; Setoodehnia, K.; Singh, B. Compilation of Directly Measured Nuclear Spins of Ground States and Long-Lived Isomers. Nucl. Data Sheets 2013, 114, 397–433. [Google Scholar] [CrossRef]
- Gustavsson, M.G.H.; Mårtensson-Pendrill, A.-M. Need for Remeasurements of Nuclear Magnetic Dipole Moments. Phys. Rev. A 1998, 58, 3611–3618. [Google Scholar] [CrossRef]
| Particle | Spin Number | Magnetic Dipole Moment, 10−27 JT−1 | Lifetime | g-Factor | Electric Quadrupole Moment, Barn |
|---|---|---|---|---|---|
| electron (e−) | 1/2 | −9284.7647043(28) | >6.6 × 1028 y | −2.00231930436146(056) | |
| positron (e+) | 1/2 | 9284.764704(430) | stable (as for e−) | 2.00231930437580(860) | |
| proton (p, 1H+) | 1/2 | 14.1060679736(66) | >1.67 × 1034 y | 5.5856946893(16) | |
| neutron (n) | 1/2 | −9.6623651(23) | 14.6 min | −3.82608545(90) | |
| deuteron (2H+) | 1 | 4.330735094(11) | stable | 0.8574382338(22) | 0.00286(2) |
| muon (μ−) | 1/2 | −44.9044830(10) | 2.19703(4) μs | −2.00233184121(82) |
| Gaseous Mixtures | ν0(HD) MHz | ν0(HD) MHz | Correction Factor 1H/2H | References | μ(D)/μN |
|---|---|---|---|---|---|
| pure HD | 500.60906811(37) | 76.84654599(52) | 1.000026339(3)/ | 0.8574382214(133) | |
| 1.000026327(5) | [19] | ||||
| 1.00002634242/ | 0.8574382190(64) | ||||
| 1.00002633323 | [30] | ||||
| 1.0000263436(48)/ | 0.8574382203(64) | ||||
| 1.0000263329(12) | [31] | ||||
| ν0(H2)MHz | ν0(D2)MHz | ||||
| H2/D2/CO2 | 500.609339 | 76.846713 | 1.000026388(3)/ | 0.857439692 | |
| 1.000026293(5) | [29] | ||||
| [33] | 0.8574382346(53) | ||||
| [34] | 0.8574382338(26) | ||||
| [2] | 0.8574382308(72) | ||||
| [35] | 0.857438228(91) |
| Experimental Details | ν(3T)/ν(1H) * | Correction Factor | References | µ(3T)/µN |
|---|---|---|---|---|
| H2O/HOT/T2O liquid | 1.06663975(2) | 1.000000 | [36] | 2.978961993 |
| HT gaseous | 1.066693887(33) | 1.000000221877 | [37] | 2.979113851(1) |
| HT gaseous | 1.066639908(10) | 1.000000221877 | [38] | 2.978963095(28) |
| HT gaseous | 1.066693898(2) | 1.000000221877 | [39] | 2.979113881(1) |
| HT extrapolated | 1.066639898(2) | 1.000000221877 | [29] | 2.978963044(10) |
| T2/H2 | 1.066639768 | 1.0000001900 | [29] | 2.978962609 |
| T2/D2 | 6.948505774 | 1.000000086 | [29] | 2.978962582 |
| Gaseous Mixtures | ν0(H2) MHz | ν0(3He) MHz | Correction Factor | References | μ(3He)/μN |
|---|---|---|---|---|---|
| H2/3He/CO2 | 500.6089846(8) | 381.3572152(2) | 1.000026293(5) | [19] | 2.127625319(16) |
| 1.000026298 | [30] | 2.127625304(16) | |||
| 1.0000262886(15) | [31] | 2.127625328(16) | |||
| H2/3He/N2O | 500.6089867(7) | 381.3572161(2) | 1.000026293(5) | [19] | 2.127625315(16) |
| 1.000026298 | [30] | 2.127625304(16) | |||
| 1.0000262886(15) | [31] | 2.127625324(16) | |||
| H2/3He/CF4 | 500.6089905(7) | 381.3572162(2) | 1.000026293(5) | [19] | 2.127625300(16) |
| 1.000026298 | [30] | 2.127625289(16) | |||
| 1.0000262886(15) | [31] | 2.127625309(16) |
| Solution | Nuclide | ν0 (Radiofrequency) (MHz) | δ0/ppm | σ0/ppm (Relative) | σ0/ppm (Absolute) |
|---|---|---|---|---|---|
| CH3COOLi | 1H(H2O) | 500.6081739(2) | 4.096(2) | −7.101 | 25.714 |
| 1H(CH3) | 500.6067408(37) | 1.23 1(1) | −4.236 | 28.579 | |
| 13C(CH3) | 125.8803604(2) | 23.383(1) | −26.388 | 159.982 | |
| 13C(COOLi) | 125.9002810(10) | 181.642(2) | −184.64 | 1.723 | |
| 6Li | 73.6695828(4) | 0.110(2) | −3.116 | ||
| 7Li | 194.5544566(1) | 0.111(2) | −3.117 | ||
| LiBF4 | 11B | 160.6140109(1) | −1.711(1) | −1.294 | 109.60 |
| 19F(10BF4) | 470.9694439(38) | −150.125(1) | 147.119 | 339.82 | |
| 19F(11BF4) | 470.9694194(39) | −150.177(1) | 147.171 | 339.87 | |
| 7Li | 194.5544570(11) | 0.110(1) |
| Solution | μ(7Li) a | μ(13C) | Correction Factor g | σ (7Li) (ppm) | μ(6Li) a | σ (6Li) (ppm) |
|---|---|---|---|---|---|---|
| CH3COOLi | 3.2564169(98) | 0.70236944(68) b | 1.000159982 | 90.76 | 0.8220453(25) | 90.71 |
| 1.000001723 | 90.72 | 90.68 | ||||
| 3.2564195(98) | 1.000159982 | 91.55 | 0.8220459(25) | 91.44 | ||
| 1.000001723 | 91.52 | 91.41 | ||||
| 3.2564169(98) | 0.7024118(14) c,d | 1.000159982 | 30.45 | 0.8220453(25) | 30.41 | |
| 1.000001723 | 30.42 | 30.38 | ||||
| 3.2564195(98) | 1.000159982 | 31.25 | 0.8220459(25) | 30.41 | ||
| 1.000001723 | 31.22 | 30.38 | ||||
| μ(1H) | ||||||
| 3.2564169(98) | 2.7928477350(9) e | 1.000028579 | 90.74 | 0.8220453(25) | 90.66 | |
| 91.53 | 91.43 | |||||
| 3.2564195(98) | 1.000025714 | 90.73 | 0.8220459(25) | 90.69 | ||
| 91.53 | 91.42 | |||||
| μ(7Li) | μ(11B) | |||||
| LiBF4 | 3.2564169(98) | 2.6883781(11) f | 1.0001096 | 90.93 | ||
| 3.2564195(98) | 91.73 | |||||
| 3.2564169(98) | 2.6886489(10) c,d | 1.0001096 | −9.79 | |||
| 3.2564195(98) | −8.98 | |||||
| μ(19F) | ||||||
| 3.2564169(98) | 2.6283214(132) c,d | 1.00033987 | 90.78 | |||
| 1.00033982 | 90.79 | |||||
| 3.2564195(98) | 1.00033987 | 91.16 | ||||
| 1.00033982 | 91.16 | |||||
| 3.2564169(98) | 2.628868(8) c,d | 1.00033987 | −117.2 | |||
| 3.2564195(98) | 2.628868(8) d | 1.00033982 1.00033987 1.00033982 | −117.2 −117.1 −117.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Makulski, W.; Słowiński, M.A.; Garbacz, P. Nuclear Dipole Moments and Shielding Constants of Light Nuclei Measured in Magnetic Fields. Magnetochemistry 2023, 9, 148. https://doi.org/10.3390/magnetochemistry9060148
Makulski W, Słowiński MA, Garbacz P. Nuclear Dipole Moments and Shielding Constants of Light Nuclei Measured in Magnetic Fields. Magnetochemistry. 2023; 9(6):148. https://doi.org/10.3390/magnetochemistry9060148
Chicago/Turabian StyleMakulski, Włodzimierz, Mateusz A. Słowiński, and Piotr Garbacz. 2023. "Nuclear Dipole Moments and Shielding Constants of Light Nuclei Measured in Magnetic Fields" Magnetochemistry 9, no. 6: 148. https://doi.org/10.3390/magnetochemistry9060148
APA StyleMakulski, W., Słowiński, M. A., & Garbacz, P. (2023). Nuclear Dipole Moments and Shielding Constants of Light Nuclei Measured in Magnetic Fields. Magnetochemistry, 9(6), 148. https://doi.org/10.3390/magnetochemistry9060148





