Next Article in Journal
Dissolution of Lysozyme Amyloid Fibrils Using Magnetic Nanoparticles in an Alternating Magnetic Field: Design of an Effective Treatment for Cutaneous Amyloidosis
Next Article in Special Issue
Improving the Path to Obtain Spectroscopic Parameters for the PI3K—(Platinum Complex) System: Theoretical Evidences for Using 195Pt NMR as a Probe
Previous Article in Journal
Magnetic Inversion and Regional Tectonics of the Dabie Orogen
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Magnetochemistry
Volume 9
Issue 3
10.3390/magnetochemistry9030083
magnetochemistry-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Four-Component Relativistic Calculations of NMR Shielding Constants of the Transition Metal Complexes—Part 3: Fe, Co, Ni, Pd, and Pt Glycinates

by
Dmitry O. Samultsev
,
Valentin A. Semenov
and
Leonid B. Krivdin
*
A. E. Favorsky Irkutsk Institute of Chemistry, Siberian Branch of the Russian Academy of Sciences, Favorsky St. 1, 664033 Irkutsk, Russia
*
Author to whom correspondence should be addressed.
Magnetochemistry 2023, 9(3), 83; https://doi.org/10.3390/magnetochemistry9030083
Submission received: 28 February 2023 / Revised: 10 March 2023 / Accepted: 14 March 2023 / Published: 16 March 2023
(This article belongs to the Special Issue Nuclear Magnetic Resonance Spectroscopy in Coordination Compounds)
Browse Figures
Versions Notes

Abstract

:
The relativistic effects of the values of the shielding constants of 1H, 13C, 15N, 57Fe, 59Co, 61Ni, 105Pd, and 195Pt nuclei were studied at the four-component relativistic level and were compared to the results of non-relativistic calculations perfomed on a series of biologically important Fe(II), Co(III), Ni, Pd, and Pt glycinates. The accuracy factors affecting the calculation of the chemical shifts of the title heavy nuclei were analyzed. First of all, the advantages and limitations of the different levels of theory used to take into account the electron correlation effects (namely HF, DFT, MP2, and CCSD) at the geometry optimization stage were thoroughly scrutinized. Among the employed DFT functionals, the behavior of 11 dedicated functionals of different types and hierarchies were analyzed. The contribution of the exact-exchange admixture was established both in the geometrical search and during the calculation of the shielding constants, which was exemplified with the PBE family of functionals. The main result of the performed study was that relativistic effects were of major importance to the theoretical calculations of the shielding constants and chemical shifts of the chelate complexes of the transition metals of the 8–10 groups. Thus, the relativistic effects of the values of the shielding constants of those metals, as well as those of the light nuclei located in the α-position to the latter, were found to reach as much as 35 ppm for nitrogen and up to an enormous 4300 ppm for platinum.

1. Introduction

The term “heavy-atom effect”, which initially referred to the nuclear shielding of the heavy atom itself, was later renamed the “Heavy-Atom effect on the Heavy-Atom shielding” (HAHA effect) [1]. The effect of a heavy atom on a neighboring light atom was subsequently termed the “Heavy-Atom effect on the Light-Atom shielding” (HALA effect), even though this effect also occurs when the NMR nucleus is itself a heavy atom. It is well known that the HALA and HAHA effects originate in the nuclear shielding of light and heavy atoms, accordingly, mainly from the third-order perturbation energy corrections, which contain many different combinations of hyperfine interaction operators. Because of this, a many different types of HALA- and HAHA-effect mechanisms may occur.
In this representation, one can distinguish two qualitatively different types of HALA effects, namely the so-called spin–orbit HALA effect (SO-HALA) and the scalar or spin-free relativistic HALA effect (SFR-HALA). The SO-HALA and SFR-HALA effects in NMR chemical shifts of magnetic isotopes of light atoms are of prime importance for many transition metals. Many HALA effects are due to spin–orbit (SO) coupling, but there are also scalar relativistic or spin-free relativistic HALA effects. Because it is far more difficult to derive useful qualitative chemical concepts of the relativistic effects of a heavy atom on its own shielding, HAHA effects are less studied and less exploited as compared to HALA effects. In addition, HAHA effects mostly cancel each other out in the relative shifts that NMR spectroscopy is based on. A state-of-the-art theoretical description of this matter was presented in the recent reviews by Vícha and coauthors [2] and by Rusakova and Rusakov [3,4]. In line with those reviews, the elements of three small periods are regarded as “light” while those of large periods are regarded as “heavy” ones.
In continuation of our serial studies on the NMR shielding constants of the transition metal complexes at the four-component relativistic level [5,6], in this paper, we turn to the glycinates of iron(II), cobalt(III) (fac- and mer-isomers), nickel, palladium, and platinum, which are presented in Figure 1. In this series of complexes, strong relativistic effects were expected in the values of the shielding constants of these metals, especially in the platinum complexes.
It is well known that to increase the accuracy of NMR calculations, including calculations on the complexes of heavy metals, ab initio molecular dynamics (AIMD) simulations can be applied. Indeed, taking the vibrationic motions into account can drastically change the calculated isotropic shielding values, which will probably be the subject of our next NMR investigation on transition metal complexes.

2. Materials and Methods

The geometry optimization of the glycinates of iron(II), cobalt(III), nickel, palladium, and platinum was performed at the non-relativistic HF, DFT, MP2, and CCSD levels in combination with the Jorge-TZP basis set [7] using the Gaussian 09 code [8]. The corresponding Cartesian coordinates of all the studied compounds are provided in the Supplementary Materials. Geometry optimization at the two-component relativistic level was carried out in the framework of Douglas–Kroll–Hess formalism [9] by using the 2cPBE0-DKH/ATZP calculation scheme within the GAMESS 2019 R2 software package [10].
All one- and four-component calculations of the 1H, 13C, 15N, 57Fe, 59Co, 61Ni, 105Pd, and 195Pt NMR shielding constants were performed at the DFT level within the GIAO framework using the GIAO-4cPBE0/pc-1//aug-pcS-2//dyall.ae3z scheme with the Dirac 2016 [11] and Gaussian 09 [8] programs. It is well known that the PBE0 exchange–correlation functional provides very accurate results for NMR chemical shifts, as was demonstrated by Adamo and Barone [12], who performed a computational study on the performances of PBE and PBE0 functionals when applying the shielding constants of the light NMR nuclei of the first and second periods.
In the present study, a relativistic Dyall’s core-valence basis set of triple zeta quality, dyall.cv3z [13,14], was placed on “heavy” iron, cobalt, nickel, palladium, and platinum atoms, while the “light” atoms (hydrogen, carbon, and nitrogen) were specified with Jensen’s triple zeta basis set with diffuse functions, aug-pcS-2 [15] (the diffuse functions were selectively used for the nitrogen atom possessing one lone pair).

3. Results and Discussion

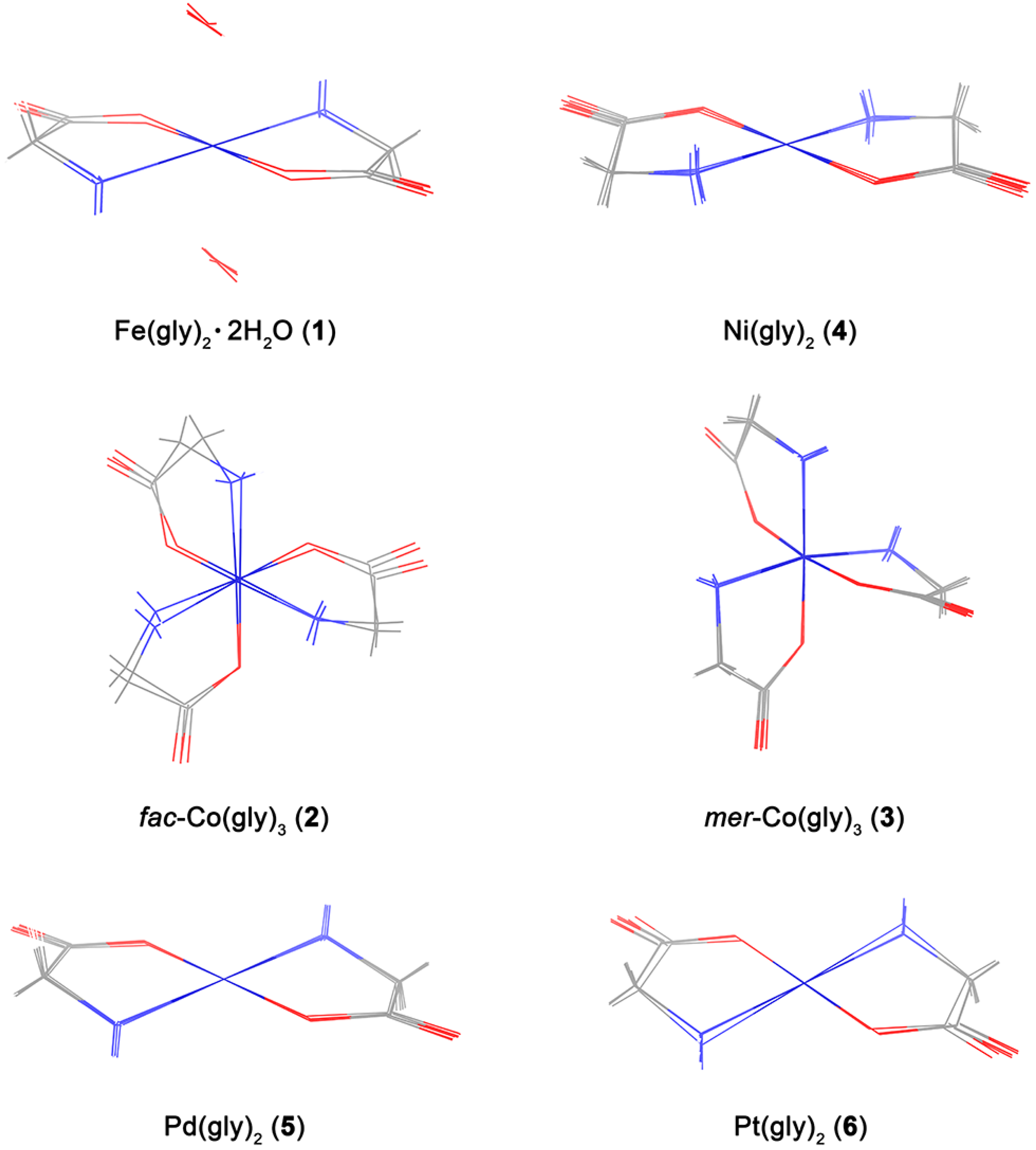
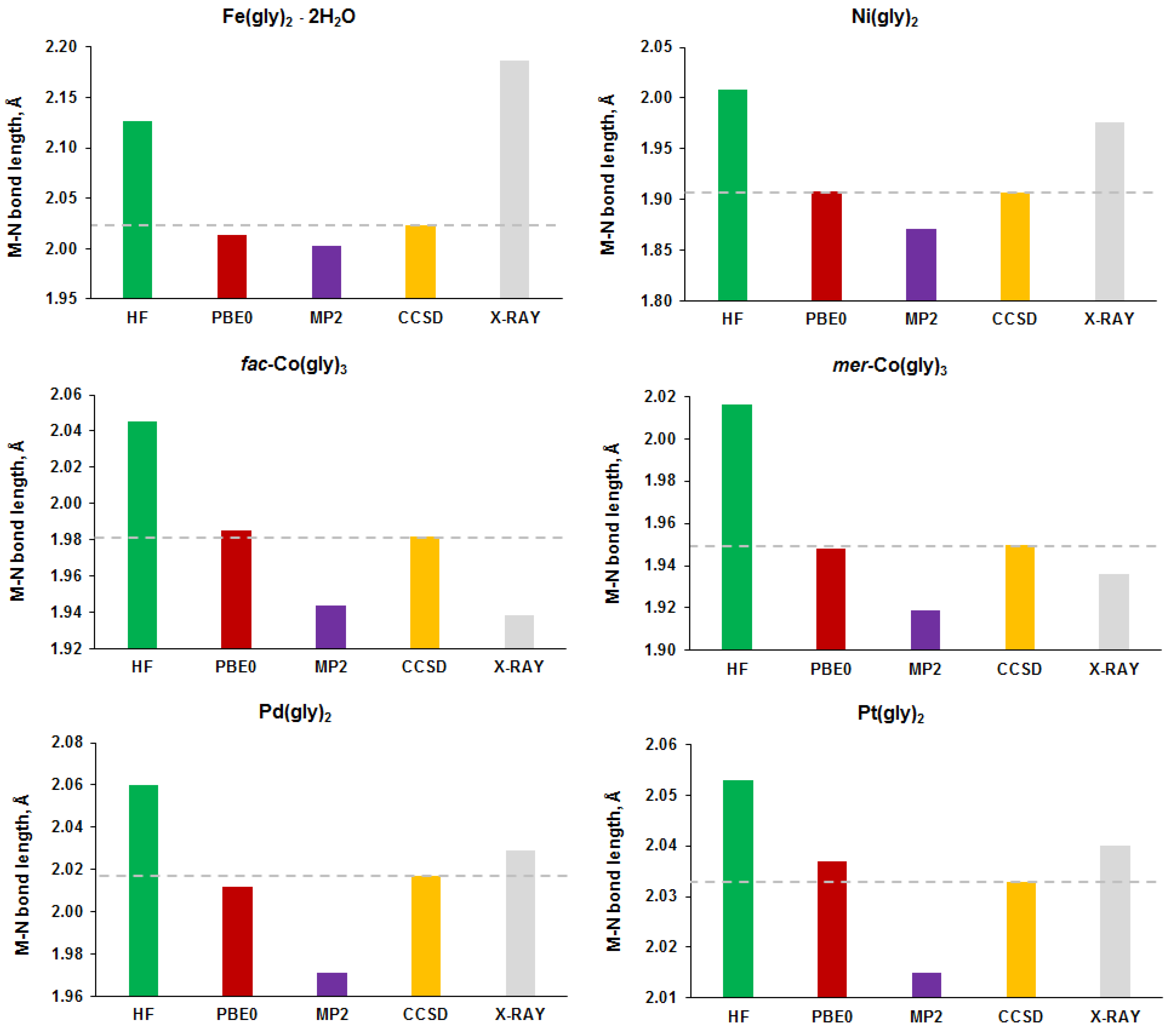
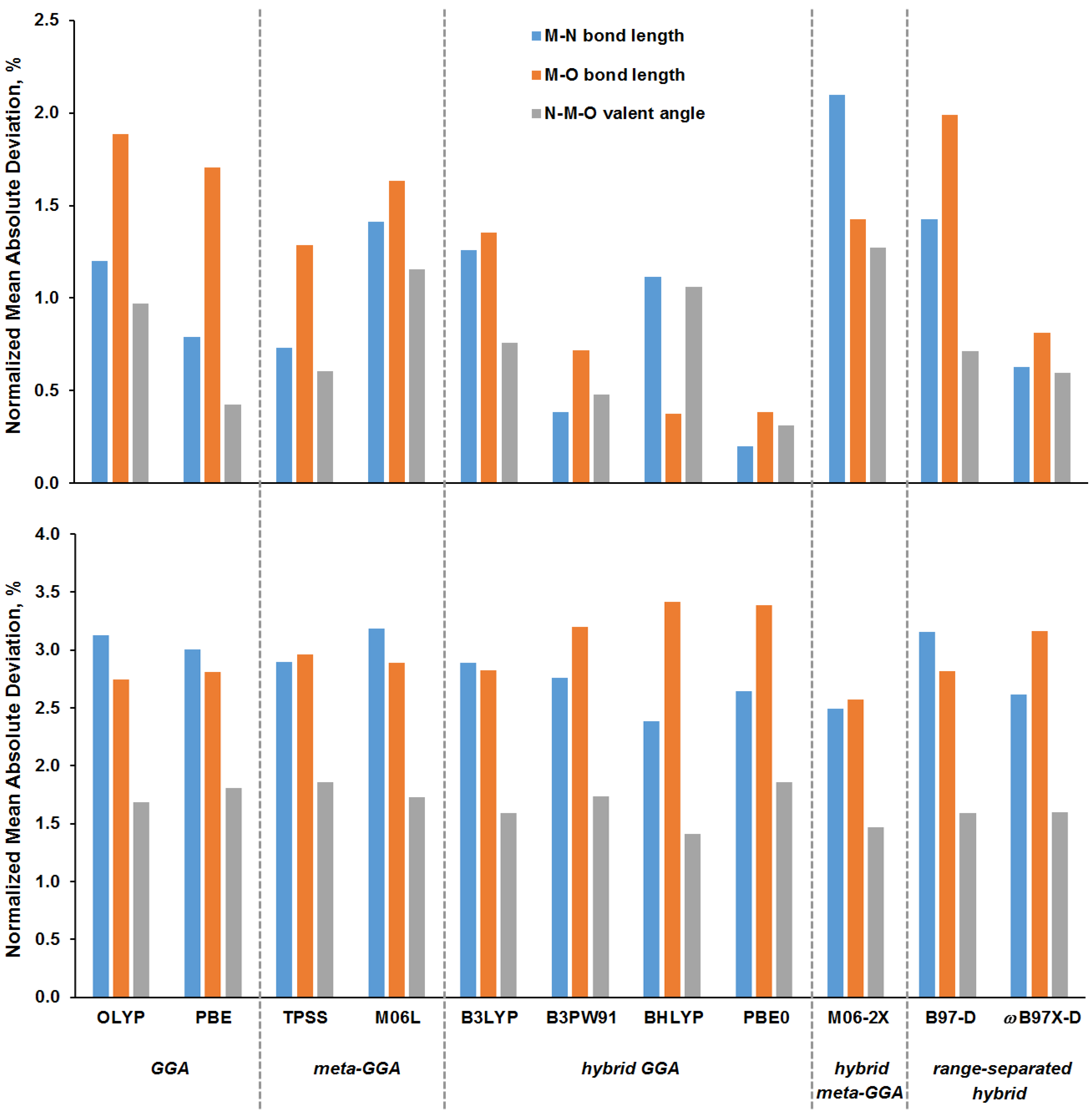
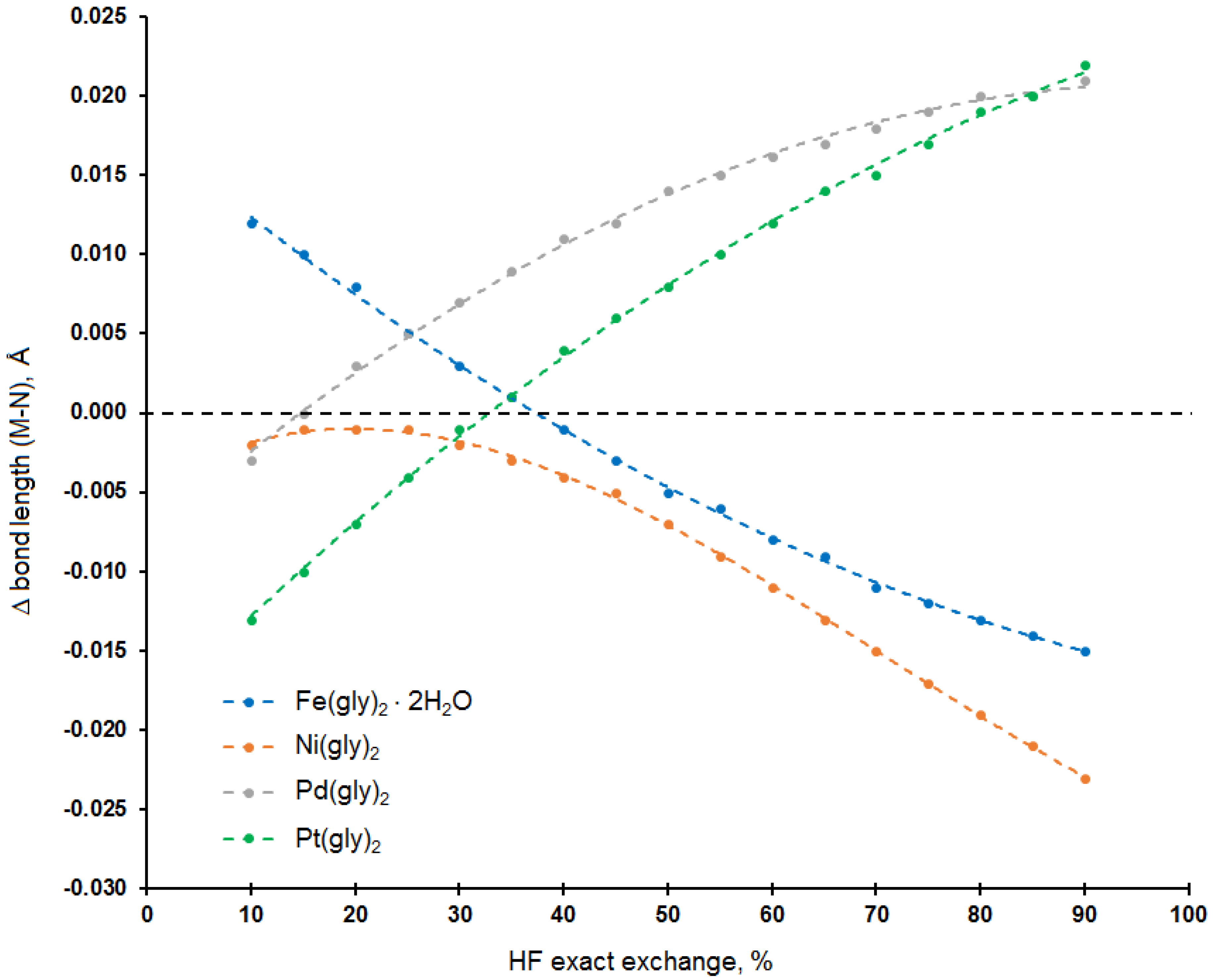
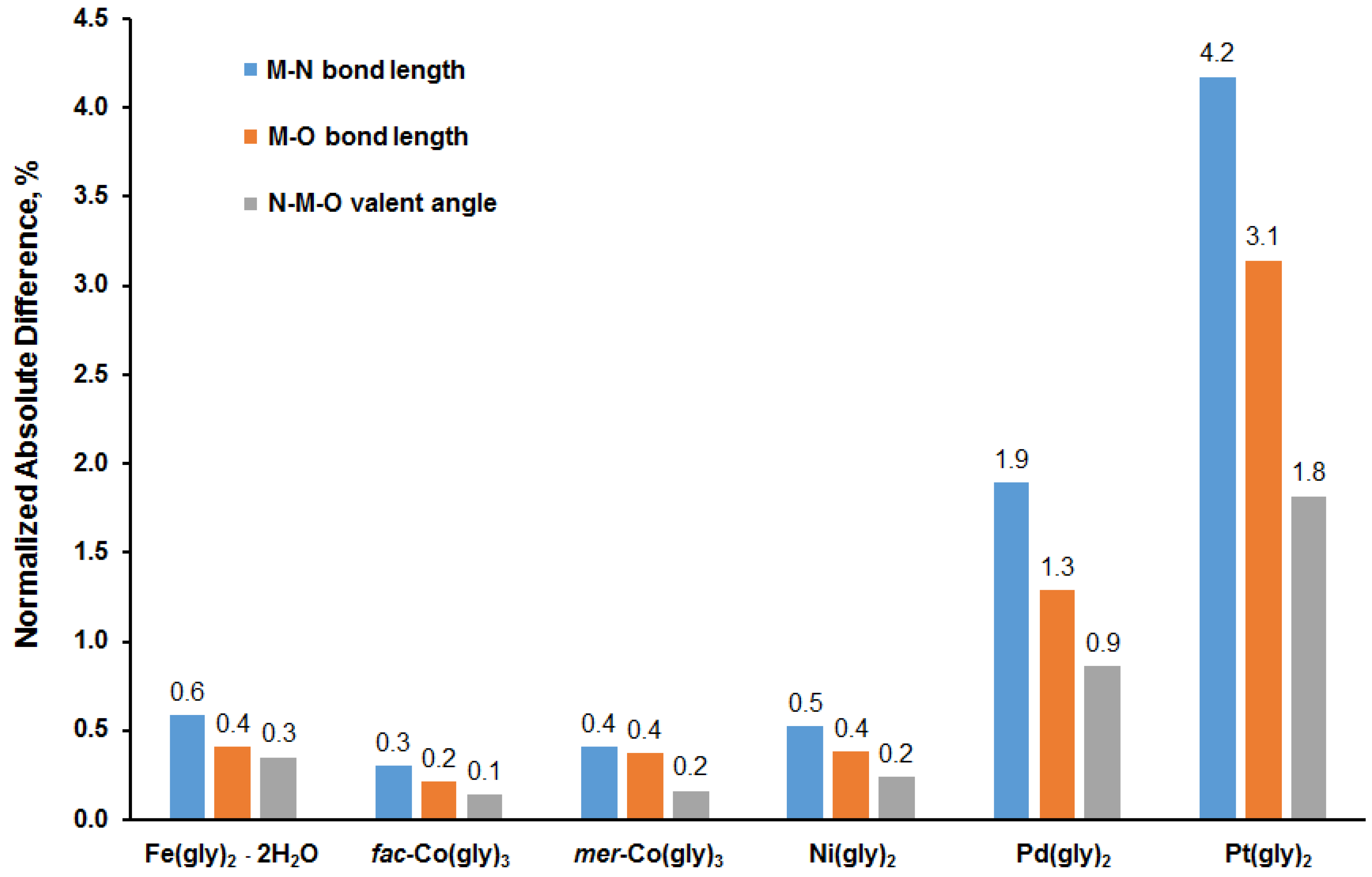
3.1. Calculation of Molecular Geometry

It is well known that a particular set of geometrical parameters evaluated for a particular molecular conformation drastically affects the results of the calculated NMR shielding constants compared to the results obtained experimentally. Therefore, the problem of choosing the proper method that can most adequately estimate the equilibrium geometry of the molecule at the initial stage of the study is of crucial importance.
To solve this problem, a reasonable approach seems to be one which evaluates a number of basic geometric parameters (mainly the lengths of the metal–ligand bonds and corresponding bond angles) that are calculated at different levels of theory as compared to the X-ray data or calculated at a higher level of theory, such as CCSD or CCSD(T). Since it is not correct to compare the geometric parameters calculated in the liquid phase with those obtained in the crystalline form for a number of reasons, in this study, they were compared with the parameters calculated at the CCSD level.
Presented in Figure 2 are the superimposed structures of the studied glycinates 1–6 optimized at the HF, DFT(PBE0), MP2, and CCSD levels, as compared to their experimental X-ray geometries [16,17,18,19,20,21]. For clarity, all structures are centered with respect to the complexing metal. As can be seen at first glance, most of the structures are just similar. However, even slight differences in bond lengths and molecular angles can lead to significant changes in the calculated shielding constants.
The metal–nitrogen bond lengths of compounds 1–6 are presented in Figure 3. These results clearly demonstrate the difference in bond lengths when performing calculations at different levels of the electron correlation theory. It can be seen that in most cases, the M-N bond lengths calculated at the CCSD level differed significantly from those derived from the X-ray experiment. The results of the geometry optimization at the HF level also differed significantly from those performed at the CCSD level. However, the optimization at the DFT-PBE0 level produced results that were the same as the CCSD results, with the former being less computationally demanding by 1–2 orders of magnitude.
Taking into account the high degree of correlation between the results of the geometry optimization at the DFT and CCSD levels, it was further decided to test a number of DFT functionals in the series of complexes 1–6 to determine their suitability for geometry optimization.
For this purpose, non-relativistic calculations were carried out by using a wide range of popular DFT functionals considered in accordance with their hierarchy of the so-called “Jacob’s ladder” [22]. Figure 4 shows the results of these calculations as compared to experimental X-ray geometry and CCSD values.
In this study, we used five different types of functionals that we deemed to be the most reliable from our many years of experience. Namely, we used OLYP and PBE from the Generalized Gradient Approximation (GGA) family; TPSS and M06L (meta-GGA); B3LYP, B3PW91, BHLYP, and PBE0 (hybrid GGA); M06–2X (hybrid meta-GGA); and B97-D and ωB97X-D (range-separated hybrid). The PBE0 functional resulted in the smallest values of the Normalized Mean Absolute Deviations (NMAD) for all three parameters as compared to the other DFT functionals.
The influence of the fraction of the exact-exchange admixture on the geometric parameters of the studied complexes was determined at the DFT level based on the PBE functional. At that, the initial zero values of the M-N bond lengths were adopted from the calculation at the CCSD level. For the square planar complexes 1, 4–6, the proportions of the HF admixture in the DFT functional were varied from 10 to 90%, and the resulting hybrid functionals were used further for the geometry optimizations.
Based on these calculations, Figure 5 presents correlations of the deviations of the M-N bond lengths from the CCSD results versus the exact-exchange admixture. It follows that in all four cases, the contributions of HF were essentially providing an effect of about 0.001 Å per every 1% of exact exchange.
At that, the intersection with zero deviations (with respect to the CCSD geometry) in the M-N bond lengths was observed in the region with about 33–38% exact exchanges for the complexes of iron (1) and platinum (6), while for the chelates of nickel (4) and palladium (5), this value was approximately 15–20%. Thus, here we can make a preliminary conclusion that when optimizing the geometric parameters for the complexes of each transition metal, it is necessary to select the amount of exact-exchange admixtures in a particular DFT functional.
It is well known that the relativistic contribution to the total energy of the system is one more important factor that must be taken into account when searching for the equilibrium geometry of molecules containing heavy atoms. Relativistic effects could result in noticeable changes in the values of bond lengths and bond angles which, in turn, could affect the values of the magnetic shielding constants of all the atoms in a molecule.
The salient geometric parameters of glycinates 1–6 optimized at the non-relativistic and two-component relativistic levels are presented in Figure 6. Expectedly, the difference in the geometric parameters calculated at the non-relativistic (PBE0/ATZP) and relativistic (2cPBE0-DKH/ATZP) levels increased with the atomic number of the element. For the relatively light atoms Fe, Co, and Ni, it ranged from 0.1 to 0.6%; for the heavier Pd, it ranged from 0.9 to 1.9%; and for the heaviest in this series, Pt, it was as much as 1.8 to 4.2%. At the same time, it is interesting to note that the equilibrium geometry of the studied complexes evaluated at the 2cPBE0-DKH level had, in general, a better correlation with the geometry calculated at the CCSD level (see Supplementary Materials, Figure S1). It is essential that deviations from the reference CCSD geometry of the M-N and M-O bond lengths in the palladium and platinum complexes evaluated within the Douglas–Kroll–Hess formalism are an order of magnitude lower than those of the non-relativistic level. Thus, it is essential to optimize the geometric parameters of the transition metal complexes of the 5th and 6th periods when taking into account the relativistic effect, mainly the spin–orbit interaction, at the two- or four-component levels.

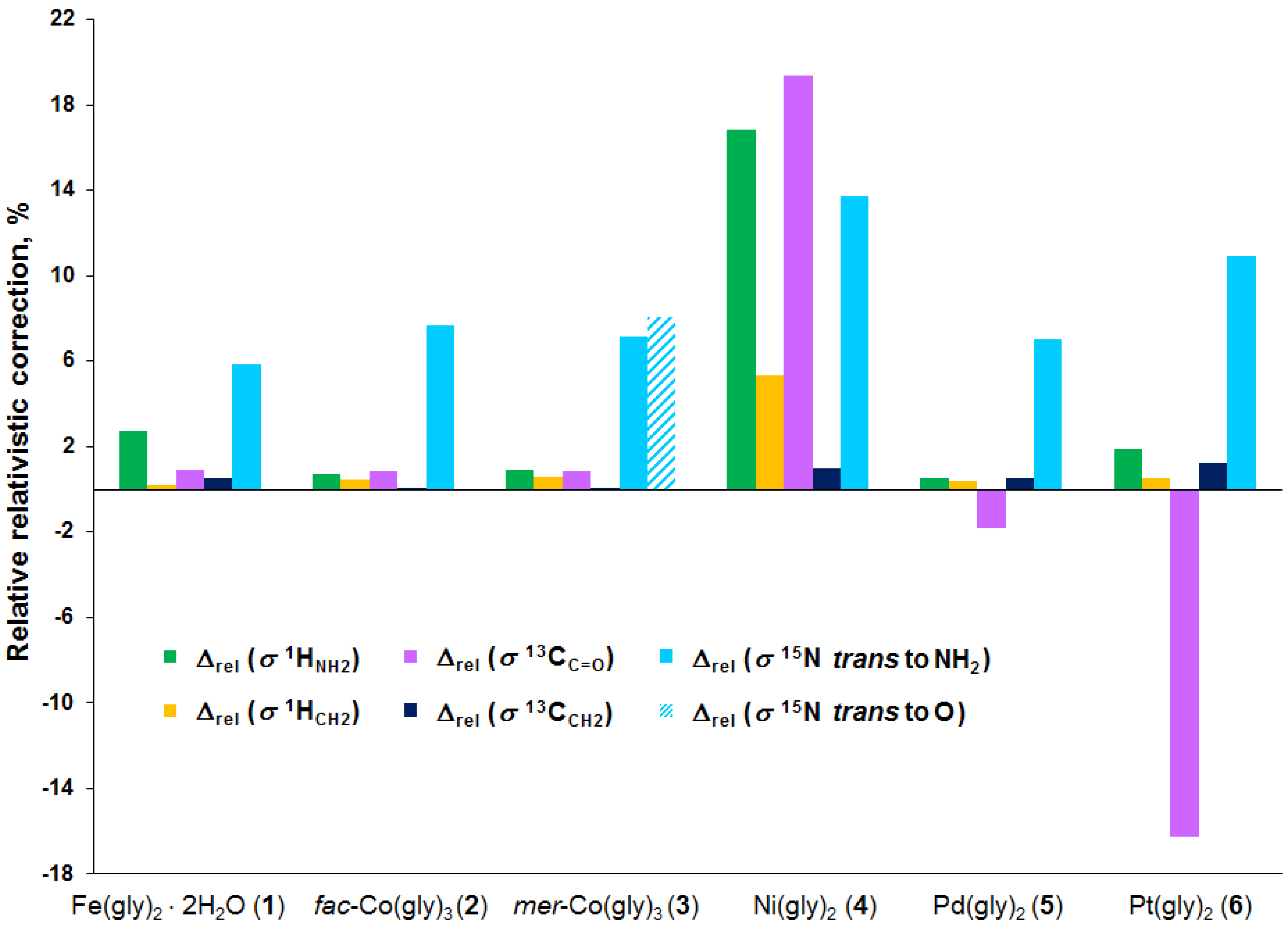
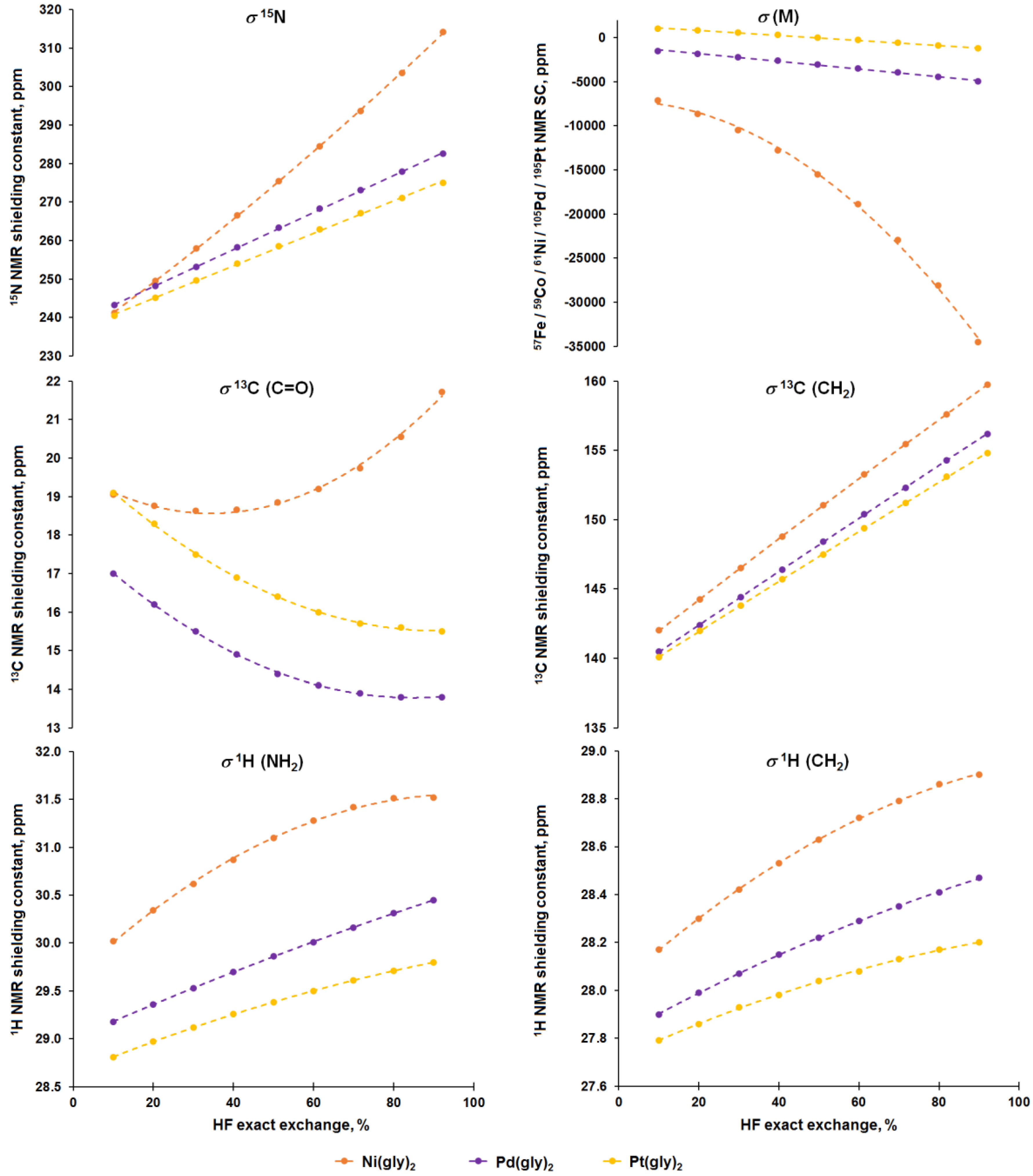
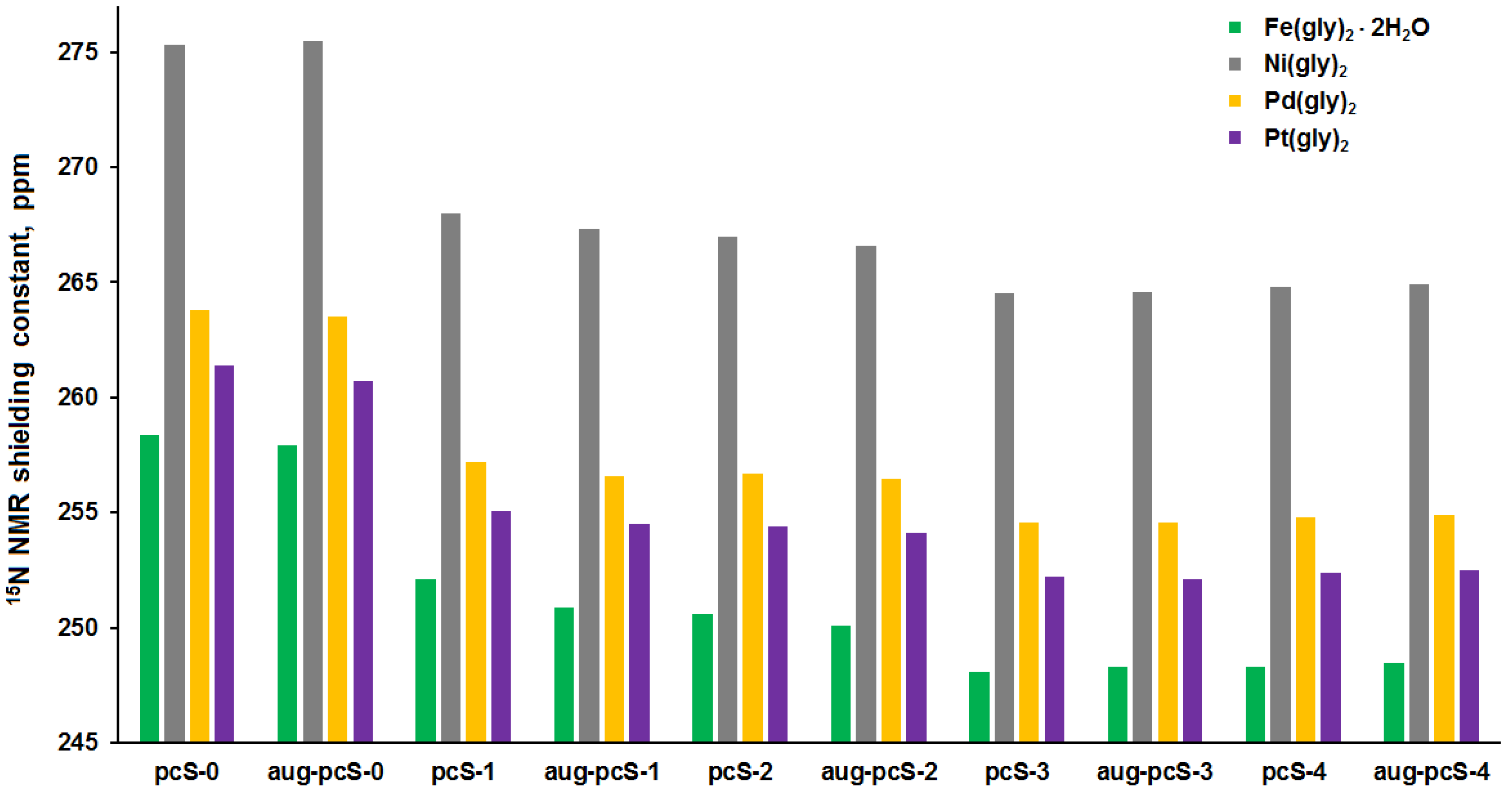
3.2. Analysis of Calculated Shielding Constants

Despite a fairly good agreement between the calculations of the geometric parameters performed at the CCSD and DFT levels (2cPBE0-DKH), to calculate the shielding constants, we used the CCSD geometries of the chelate complexes 1–6. For the calculation of the NMR shielding constants, the PBE0 functional was employed within the locally dense basis sets scheme, namely pc-1//aug-pcS-2//dyall.ae3z. At this, the pc-1 basis was set on the hydrogen atoms, the aug-pcS-2 basis was set on the nitrogen atoms, and dyall.ae3z was set on the metals. Using this computational scheme, NMR shielding constants were calculated both at the one-component non-relativistic and four-component relativistic levels within the formalism of the Dirac equation [23]. These results are presented in the form of the relative relativistic corrections to the shielding constants in Figure 7.
Based on the analysis of these data, one can conclude that in most cases, relativistic effects lead to a positive increase in the NMR shielding constants and thereby provide a relativistic highfield contribution to chemical shifts. The only exceptions are the calculated shielding constants of the carbonyl carbons in the palladium and platinum complexes, 5 and 6, respectively. For the complexes of iron (1) and cobalt (2, 3), relativistic contributions to the 1H and 13C shielding constants, as expected, turned out to be small. However, for the nickel complex (4), the values of the relativistic corrections were found to be unexpectedly large.
In addition, relativistic contributions to the anisotropy tensors were estimated for all the studied nuclei of glycinates 1–6 at the four-component relativistic level, see Supplementary Materials, Table S1. As in the case of the shielding constants, the relativistic effects on the anisotropy tensors for the metals and 15N turned out to be essential and amounted to about 650 and 34 ppm, respectively.
To explain this unusual manifestation of the HALA effect, a more detailed Canonical Molecular Orbitals (CMO) analysis is needed. In general, a more significant manifestation of the HALA effect in the shielding constants of the nitrogen atoms of all the complexes 1–6 as compared to the shielding constants of the other atoms was observed. This can be rationalized in terms of a stronger spin–orbit interaction between the complexing metal and nitrogen atom in the α-position.
Calculated relativistic corrections to the NMR shielding constants of 57Fe, 59Co, 61Ni, 105Pd, and 195Pt in the complexes 1–6 are presented in Figure 8. These data demonstrate a significant difference between the results of the non-relativistic and the four-component relativistic levels of the theory. It follows that in practice, it is necessary to take into account the relativistic contributions to the shielding constant (and, accordingly, to the chemical shift) of most metals. Such corrections, even for the relatively light metals of Period 4, are about 500 to 800 ppm, while for platinum, they can be up to an enormous 4300 ppm.
At present, theoretical studies of NMR shielding constants at the relativistic level are performed only within the framework of the electron density functional theory. This is because ab initio relativistic calculations require enormous computing resources and are therefore rarely used for medium-sized and even small molecules.
Since we used the PBE0 functional to calculate the shielding constants in this work, it was decided to check the influence of the contribution of the HF admixture to the value of the shielding constants, and we did this by creating an analogy whereby such a procedure was applied to the geometric parameters. For the square planar complexes 4–6 under consideration, the fraction of the exact-exchange admixture into the DFT functional was varied from 10 to 90%. Then, a number of the resulting hybrid functionals were used to calculate the corresponding shielding constants.
Shown in Figure 9 are the values of the 1H, 13C, 15N, 61Ni, 105Pd, and 195Pt shielding constants versus the contribution of HF to the PBE0 functional. As can be seen, in the case of the 15N shielding constants, the contributions of the HF exact exchange are essentially highfield being of about 0.4–0.9 ppm for every 1% of the exact exchange. Additionally, the total increase in the shielding along with the corresponding increase in the exact-exchange admixture was up to 20–30% of the initial value of the shielding constant. In this case, the shielding constants of methylene and amino protons changed less significantly, which provided a minimum sensitivity of 5%. A similar pattern was also observed for the carbons of both the methylene and carbonyl groups.
The shielding constants of the considered metals provided quite different dependences on the fraction of the exact-exchange admixture. For the Pd and Pt nuclei, the increase in the proportion of HF in PBE resulted in a moderate linear deshielding of about 30–40 ppm for each 1% of the exact exchange. However, for the Ni nucleus, there was a more pronounced deshielding of about 330 ppm for every 1% of the exact exchange. It followed that generally, considering the fraction of the HF exact exchange in the hybrid functional that was being used to calculate the shielding constants (chemical shifts) was of major importance only for the metals and their nearest surroundings (i.e., atoms in the α-position to the metals).
At the final stage of this study, we examined the influence of the quality of the basis set on the variations in the shielding constant values of the nitrogen nuclei. Since the 15N nucleus is especially sensitive to the process of coordination of the nitrogen-containing ligands with the transition metal, it appeared to be the most informative NMR probe for the structural studies of glycinates 1–6 and related systems. The testing of the dependence of the level of splitting of the basis set on the changes in the NMR shielding constants was carried out for the 15N nucleus of the amino group of the glycinates.
Based on the results of our previous studies [5,6,24], we chose a family of Jensen’s basis sets with a degree of splitting varying from 1 to 5, both with and without diffuse functions at each level, pcS-n and aug-pcS-n (n = 0–4), which resulted in as many as 10 basis sets schemes, see Figure 10.
The analysis of these data suggested that an essential improvement in the accuracy of the calculated 15N shielding constants of the studied glycinates began at the pcS-1/aug-pcS-1 level. At that, almost no changes in the values of the shielding constants were observed for the pcS-3 to aug-pcS-4 basis sets. It should also be noted that the 15N NMR shielding constants of nitrogen bonded to the iron(II) and nickel atoms in 1 and 4 differed in the explicit shielding/deshielding effects, respectively, when applying any of the basis set schemes. The information about such deviations can be used in structural studies of the related nitrogen-containing transition metal complexes.

4. Conclusions

Relativistic effects of the values of the shielding constants of 1H, 13C, 15N, 57Fe, 59Co, 61Ni, 105Pd, and 195Pt nuclei were studied at the four-component relativistic level as compared to the non-relativistic calculations in the series of biologically important Fe(II), Co(III), Ni, Pd, and Pt glycinates. The influence of the spin–orbit interaction on the salient geometric parameters of the studied chelates were evaluated at the two-component relativistic level. The marked difference in bond lengths was established for the different levels of theory. The M-N bond lengths calculated at the CCSD level in most cases differed significantly from those derived from the X-ray experiment. The results of the optimization at the DFT-PBE0 level was very much the same as the CCSD results, with the former being 1–2 orders of magnitude less computationally demanding. At the DFT level, the PBE0 functional resulted in the smallest values of the Normalized Mean Absolute Deviations for all three geometric parameters as compared to the other DFT functionals. The difference in the geometric parameters calculated at the non-relativistic (PBE0/ATZP) and two-component relativistic (2cPBE0-DKH/ATZP) levels increased with the atomic number of the element. For the relatively light atoms Fe, Co, and Ni, it ranged from 0.1 to 0.6%; for the heavier Pd it was 0.9 to 1.9%; and for the heavy Pt it was as much as 1.8 to 4.2%.
The influence of the proportion of the exact-exchange admixture on the geometric parameters of the studied complexes was determined using the PBE functional. For the complexes of iron and platinum, the value of about 33–38% of the exact exchange was optimal, while for the chelates of nickel and palladium, this value was approximately 15–20%. The shielding constants of the considered metals provided quite different dependences on the fraction of the exact-exchange admixture. Thus, for the Pd and Pt nuclei, the increase in the proportion of HF in PBE resulted in a moderate linear deshielding of about 30–40 ppm for each 1% of the exact exchange. However, for the Ni nucleus, a more pronounced deshielding of about 330 ppm for every 1% of the exact exchange was established.
The influence of the quality of the basis set on the 15N NMR shielding constants was established. An essential improvement in the accuracy of the calculated 15N shielding constants of the studied glycinates was found starting from the pcS-1/aug-pcS-1 level, while increasing the quality of the basis sets from pcS-3 to aug-pcS-4 surprisingly provided no further improvement.
The relativistic effects in most cases led to a positive increase in the NMR shielding constants and thereby provided a relativistic highfield contribution to the chemical shifts. For the complexes of iron and cobalt, the relativistic contributions to the 1H and 13C shielding constants, as expected, turned out to be small. However, for the heavier metals, the values of the relativistic corrections turned out to be much larger.

Supplementary Materials

The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/magnetochemistry9030083/s1: Cartesian coordinates (Angstroms) of 1–6, optimized at the CCSD/TZP level; Figure S1: Normalized Absolute Deviation (%) of M-N and M-O bond lengths of glycinates 1–6, obtained at non-relativistic (PBE0/ATZP) and relativistic (2cPBE0-DKH/ATZP) levels relative to CCSD geometry. Table S1: Relativistic corrections (ppm) to the 1H, 13C, 15N 57Fe, 59Co, 61Ni, 105Pd and 195Pt anisotropy tensors of 1–6, evaluated at the (4c)PBE0/pc-1//aug-pcS-2//dyall.ae3z level.

Author Contributions

Investigation, data curation, validation, and formal analysis, D.O.S.; conceptualization, methodology, software, and writing—original draft preparation, V.A.S.; supervision and project administration, L.B.K. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Russian Science Foundation, grant number 21-73-00182.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

All the calculations were performed at the Irkutsk Supercomputer Center of the Siberian Branch of the Russian Academy of Sciences using the HPC cluster “Academician V.M. Matrosov” (http://hpc.icc.ru, accessed on 15 March 2023) and at the A.E. Favorsky Irkutsk Institute of Chemistry using the facilities of the Baikal Analytical Center (http://ckp-rf.ru/ckp/3050, accessed on 15 March 2023).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Nomura, Y.; Takeuchi, Y. Substituent effects in aromatic proton NMR spectra. III substituent effects caused by halogens. Tetrahedron Lett. 1969, 10, 639–642. [Google Scholar] [CrossRef]
  2. Vícha, J.; Novotný, J.; Komorovsky, S.; Straka, M.; Kaupp, M.; Marek, M. Relativistic heavy-neighbor-atom effects on NMR shifts: Concepts and trends across the Periodic Table. Chem. Rev. 2020, 120, 7065–7103. [Google Scholar] [CrossRef] [PubMed]
  3. Rusakova, I.L.; Rusakov, Y.Y. Relativistic effects from heavy main group p-elements on the NMR chemical shifts of light atoms: From pioneering studies to recent advances. Magnetochemistry 2023, 9, 24. [Google Scholar] [CrossRef]
  4. Rusakova, I.L. Quantum Chemical Approaches to the Calculation of NMR Parameters: From Fundamentals to Recent Advances. Magnetochemistry 2022, 8, 50. [Google Scholar] [CrossRef]
  5. Samultsev, D.O.; Semenov, V.A.; Krivdin, L.B. Four-component relativistic calculations of NMR shielding constants of the transition metal complexes. Part 1: Pentaammines of cobalt, rhodium, and iridium. Magn. Reson. Chem. 2022, 60, 463–468. [Google Scholar] [CrossRef]
  6. Samultsev, D.O.; Semenov, V.A.; Rusakova, I.L.; Krivdin, L.B. Four-component relativistic calculations of NMR shielding constants of the transition metal complexes. Part 2: Nitrogen-coordinated complexes of cobalt. Int. J. Mol. Sci. 2022, 23, 13178. [Google Scholar] [CrossRef]
  7. Jorge, F.E.; Canal Neto, A.; Camiletti, G.G.; Machado, S.F. Contracted Gaussian basis sets for Douglas–Kroll–Hess calculations: Estimating scalar relativistic effects of some atomic and molecular properties. J. Chem. Phys. 2009, 130, 064108. [Google Scholar] [CrossRef]
  8. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B. GAUSSIAN 09, Revision, C.01; Gaussian, Inc.: Wallingford, CT, USA, 2009; Available online: http://www.gaussian.com (accessed on 15 March 2023).
  9. Hess, B.A. Relativistic electronic-structure calculations employing a two-component no-pair formalism with external-field projection operators. Phys. Rev. A 1986, 33, 3742–3748. [Google Scholar] [CrossRef] [Green Version]
  10. Barca, G.M.J.; Bertoni, C.; Carrington, L.; Datta, D.; De Silva, N.; Emiliano Deustua, J.; Fedorov, D.G.; Gour, J.R.; Gunina, A.O.; Guidez, E.; et al. Recent developments in the general atomic and molecular electronic structure system. J. Chem. Phys. 2020, 152, 154102. [Google Scholar] [CrossRef] [Green Version]
  11. Jensen, H.J.A.; Bast, R.; Saue, T.; Visscher, L. DIRAC16, Revision 2016. Available online: http://www.diracprogram.org (accessed on 15 March 2023).
  12. Adamo, C.; Barone, V. Toward chemical accuracy in the computation of NMR shieldings: The PBE0 model. Chem. Phys. Lett. 1998, 298, 113–119. [Google Scholar] [CrossRef]
  13. Dyall, K.G. Relativistic and nonrelativistic finite nucleus optimized double zeta basis sets for the 4p, 5p and 6p elements. Theor. Chem. Acc. 1998, 99, 366–371. [Google Scholar] [CrossRef]
  14. Dyall, K.G. Relativistic and nonrelativistic finite nucleus optimized triple-zeta basis sets for the 4p, 5p and 6p elements. Theor. Chem. Acc. 2002, 108, 335–340. [Google Scholar] [CrossRef]
  15. Jensen, F. Basis set convergence of nuclear magnetic shielding constants calculated by density functional methods. J. Chem. Theory Comp. 2008, 4, 719–727. [Google Scholar] [CrossRef] [PubMed]
  16. Bernal, I.; Somoza, F. Experimental Crystal Structure Determination; CCDC 645775; Cambridge Crystallographic Data Centre: Cambridge, UK, 2009. [Google Scholar] [CrossRef]
  17. Gu, K.-Q.; Sun, Y.X.; Zhang, R.; Zhang, N.W.; Che, H.W. Tris(glycinato-κ2N,O)cobalt(III). Acta Cryst. Sect. E Struct. Rep. Online 2007, 63, m740. [Google Scholar] [CrossRef]
  18. Jungen, S.; Chen, P. Alkyl Radical Generation by an Intramolecular Homolytic Substitution Reaction between Iron(II) and Trialkylsulfonium Groups. Chem. Eur. J. 2018, 24, 11008. [Google Scholar] [CrossRef]
  19. Wang, Z.-L.; Zhang, Z.-B. A monoclinic polymorph of bis(2-amino acetato)nickel(II) monohydrate. Acta Cryst. 2006, E62, m2546. [Google Scholar] [CrossRef]
  20. Baidina, I.A.; Podberezskaya, N.V.; Borisov, S.V.; Golubovskaya, E.V. Crystal structure of the β-modification of palladium(II)-trans-diglycinate. J. Struct. Chem. 1982, 23, 241–244. [Google Scholar] [CrossRef]
  21. Freeman, H.C.; Golomb, M.L. The crystal structure of trans-bisglycinatoplatinum(II), Pt(NH2CH2COO)2. Acta Cryst. 1969, B25, 1203. [Google Scholar] [CrossRef] [Green Version]
  22. Perdew, J.P.; Schmidt, K. Jacob’s ladder of density functional approximations for the exchange-correlation energy. AIP Conf. Proc. 2001, 577, 1. [Google Scholar] [CrossRef]
  23. Manninen, P.; Lantto, P.; Vaara, J.; Ruud, K. Perturbational ab initio calculations of relativistic contributions to nuclear magnetic resonance shielding tensors. J. Chem. Phys. 2003, 119, 2623–2637. [Google Scholar] [CrossRef]
  24. Semenov, V.A.; Samultsev, D.O.; Rusakova, I.L.; Krivdin, L.B. Computational multinuclear NMR of platinum complexes: A relativistic four-component study. J. Phys. Chem. A 2019, 123, 4908–4920. [Google Scholar] [CrossRef] [PubMed]
Magnetochemistry 09 00083 g001 550
Figure 1. Equilibrium geometries of iron(II) (1), cobalt(III) (2,3), nickel (4), palladium (5), and platinum (6) glycinates, optimized at the CCSD/TZP level. Bond lengths are given in angstroms, while bond angles are in degrees.
Figure 1. Equilibrium geometries of iron(II) (1), cobalt(III) (2,3), nickel (4), palladium (5), and platinum (6) glycinates, optimized at the CCSD/TZP level. Bond lengths are given in angstroms, while bond angles are in degrees.
Magnetochemistry 09 00083 g001
Magnetochemistry 09 00083 g002 550
Figure 2. Superimposed structures of glycinates 1–6 related to their geometries optimized at the HF, DFT(PBE0), MP2, and CCSD levels, as compared to the X-ray data.
Figure 2. Superimposed structures of glycinates 1–6 related to their geometries optimized at the HF, DFT(PBE0), MP2, and CCSD levels, as compared to the X-ray data.
Magnetochemistry 09 00083 g002
Magnetochemistry 09 00083 g003 550
Figure 3. M-N bond lengths (Å) of 1–6, optimized at the HF, DFT(PBE0), MP2, and CCSD levels, as compared to their X-ray geometries. Dotted lines denote the CCSD values.
Figure 3. M-N bond lengths (Å) of 1–6, optimized at the HF, DFT(PBE0), MP2, and CCSD levels, as compared to their X-ray geometries. Dotted lines denote the CCSD values.
Magnetochemistry 09 00083 g003
Magnetochemistry 09 00083 g004 550
Figure 4. Normalized Mean Absolute Deviations (%) of salient geometric parameters of 1–6 optimized at the DFT level using different functionals from experimental X-ray geometry (bottom) and that calculated at the CCSD level (top).
Figure 4. Normalized Mean Absolute Deviations (%) of salient geometric parameters of 1–6 optimized at the DFT level using different functionals from experimental X-ray geometry (bottom) and that calculated at the CCSD level (top).
Magnetochemistry 09 00083 g004
Magnetochemistry 09 00083 g005 550
Figure 5. The M-N bond length (Å) of glycinates 1, 4–6 calculated at the PBEx/ATZP level as a function of the amount of the exact-exchange admixture as compared to the CCSD equilibrium geometries.
Figure 5. The M-N bond length (Å) of glycinates 1, 4–6 calculated at the PBEx/ATZP level as a function of the amount of the exact-exchange admixture as compared to the CCSD equilibrium geometries.
Magnetochemistry 09 00083 g005
Magnetochemistry 09 00083 g006 550
Figure 6. Normalized Absolute Difference (%) of salient geometric parameters of glycinates 1–6 evaluated at the non-relativistic (PBE0/ATZP) and relativistic (2cPBE0-DKH/ATZP) levels.
Figure 6. Normalized Absolute Difference (%) of salient geometric parameters of glycinates 1–6 evaluated at the non-relativistic (PBE0/ATZP) and relativistic (2cPBE0-DKH/ATZP) levels.
Magnetochemistry 09 00083 g006
Magnetochemistry 09 00083 g007 550
Figure 7. Relative relativistic corrections (%) to the 1H, 13C, and 15N shielding constants of 1–6, evaluated at the 4cPBE0/pc-1//aug-pcS-2 level. Relativistic corrections are evaluated as percentages of the shielding constants values of the corresponding nuclei calculated at the non-relativistic level using the equation Δrel (%) = (σrel − σnon-rel)/σnon-rel × 100%.
Figure 7. Relative relativistic corrections (%) to the 1H, 13C, and 15N shielding constants of 1–6, evaluated at the 4cPBE0/pc-1//aug-pcS-2 level. Relativistic corrections are evaluated as percentages of the shielding constants values of the corresponding nuclei calculated at the non-relativistic level using the equation Δrel (%) = (σrel − σnon-rel)/σnon-rel × 100%.
Magnetochemistry 09 00083 g007
Magnetochemistry 09 00083 g008 550
Figure 8. Relativistic corrections (ppm) to the 57Fe, 59Co, 61Ni, 105Pd, and 195Pt shielding constants of 1–6, evaluated at the 4cPBE0/dyall.ae3z level.
Figure 8. Relativistic corrections (ppm) to the 57Fe, 59Co, 61Ni, 105Pd, and 195Pt shielding constants of 1–6, evaluated at the 4cPBE0/dyall.ae3z level.
Magnetochemistry 09 00083 g008
Magnetochemistry 09 00083 g009 550
Figure 9. The 1H, 13C, 15N, 61Ni, 105Pd, and 195Pt NMR shielding constants of 4–6 calculated at the PBEx//pc-1//aug-pcS-2//dyall.ae3z level with various amounts of the exact-exchange admixture.
Figure 9. The 1H, 13C, 15N, 61Ni, 105Pd, and 195Pt NMR shielding constants of 4–6 calculated at the PBEx//pc-1//aug-pcS-2//dyall.ae3z level with various amounts of the exact-exchange admixture.
Magnetochemistry 09 00083 g009
Magnetochemistry 09 00083 g010 550
Figure 10. The 15N NMR shielding constants (ppm) of glycinates 1, 4–6, calculated at the PBE38/(aug-)pcS-n level using different Jensen’s basis sets on the nitrogen atom.
Figure 10. The 15N NMR shielding constants (ppm) of glycinates 1, 4–6, calculated at the PBE38/(aug-)pcS-n level using different Jensen’s basis sets on the nitrogen atom.
Magnetochemistry 09 00083 g010
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Samultsev, D.O.; Semenov, V.A.; Krivdin, L.B. Four-Component Relativistic Calculations of NMR Shielding Constants of the Transition Metal Complexes—Part 3: Fe, Co, Ni, Pd, and Pt Glycinates. Magnetochemistry 2023, 9, 83. https://doi.org/10.3390/magnetochemistry9030083

AMA Style

Samultsev DO, Semenov VA, Krivdin LB. Four-Component Relativistic Calculations of NMR Shielding Constants of the Transition Metal Complexes—Part 3: Fe, Co, Ni, Pd, and Pt Glycinates. Magnetochemistry. 2023; 9(3):83. https://doi.org/10.3390/magnetochemistry9030083

Chicago/Turabian Style

Samultsev, Dmitry O., Valentin A. Semenov, and Leonid B. Krivdin. 2023. "Four-Component Relativistic Calculations of NMR Shielding Constants of the Transition Metal Complexes—Part 3: Fe, Co, Ni, Pd, and Pt Glycinates" Magnetochemistry 9, no. 3: 83. https://doi.org/10.3390/magnetochemistry9030083

APA Style

Samultsev, D. O., Semenov, V. A., & Krivdin, L. B. (2023). Four-Component Relativistic Calculations of NMR Shielding Constants of the Transition Metal Complexes—Part 3: Fe, Co, Ni, Pd, and Pt Glycinates. Magnetochemistry, 9(3), 83. https://doi.org/10.3390/magnetochemistry9030083

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop