Magnetic-Moment-Induced Metal–Insulator Transition in ThMnXN (X = As, P): A First Principles Study
Abstract
1. Introduction
2. Computational Methods
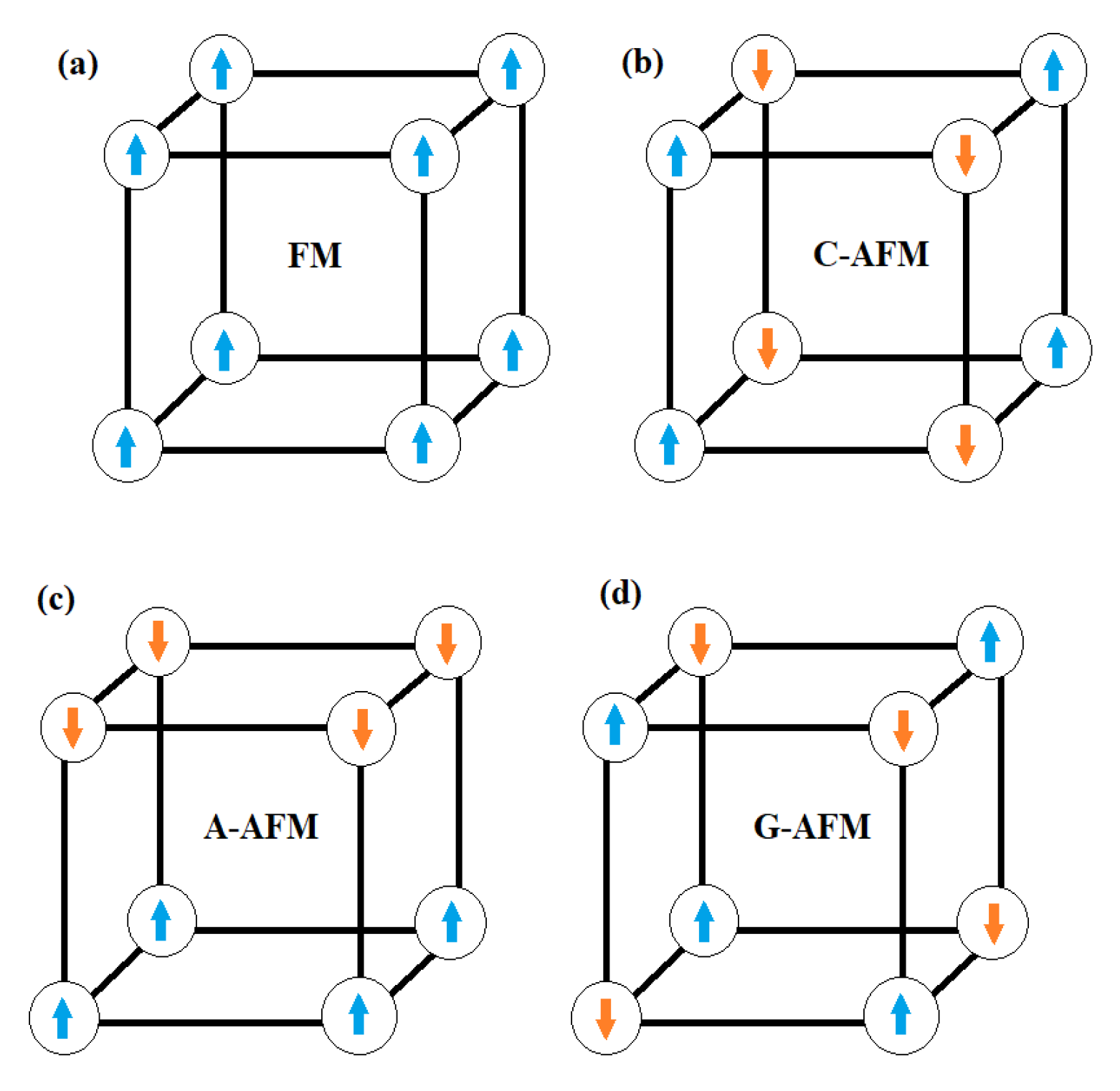
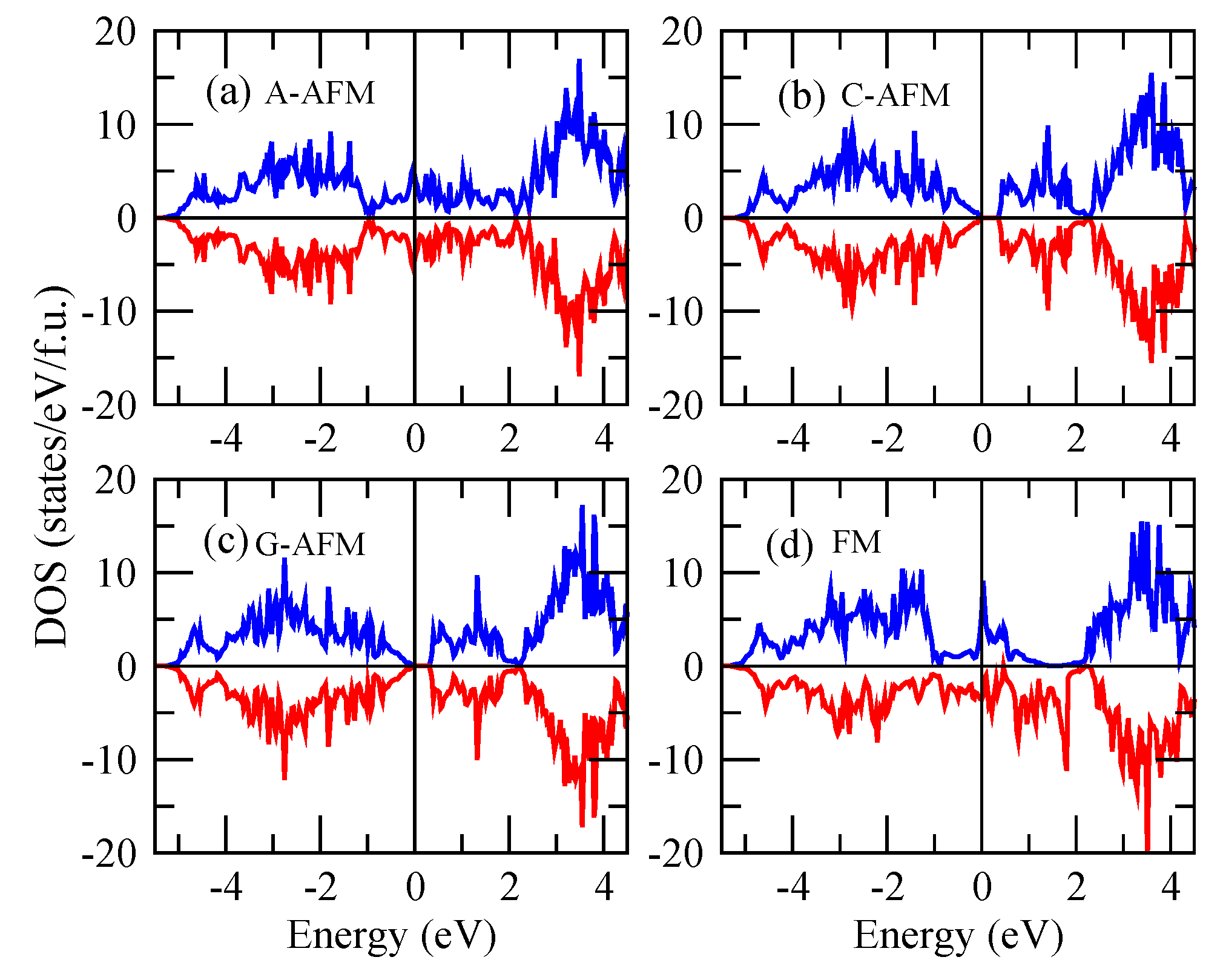
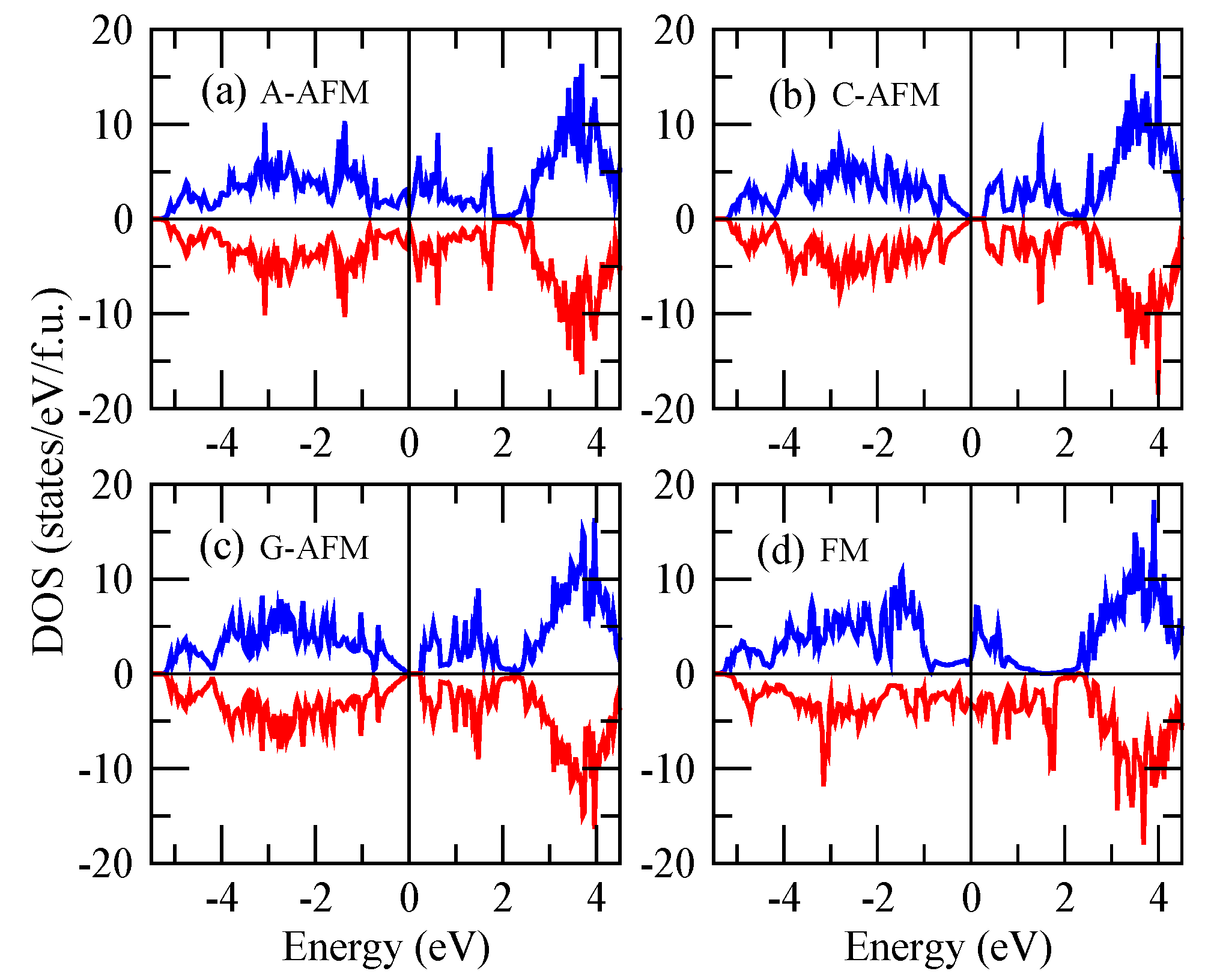
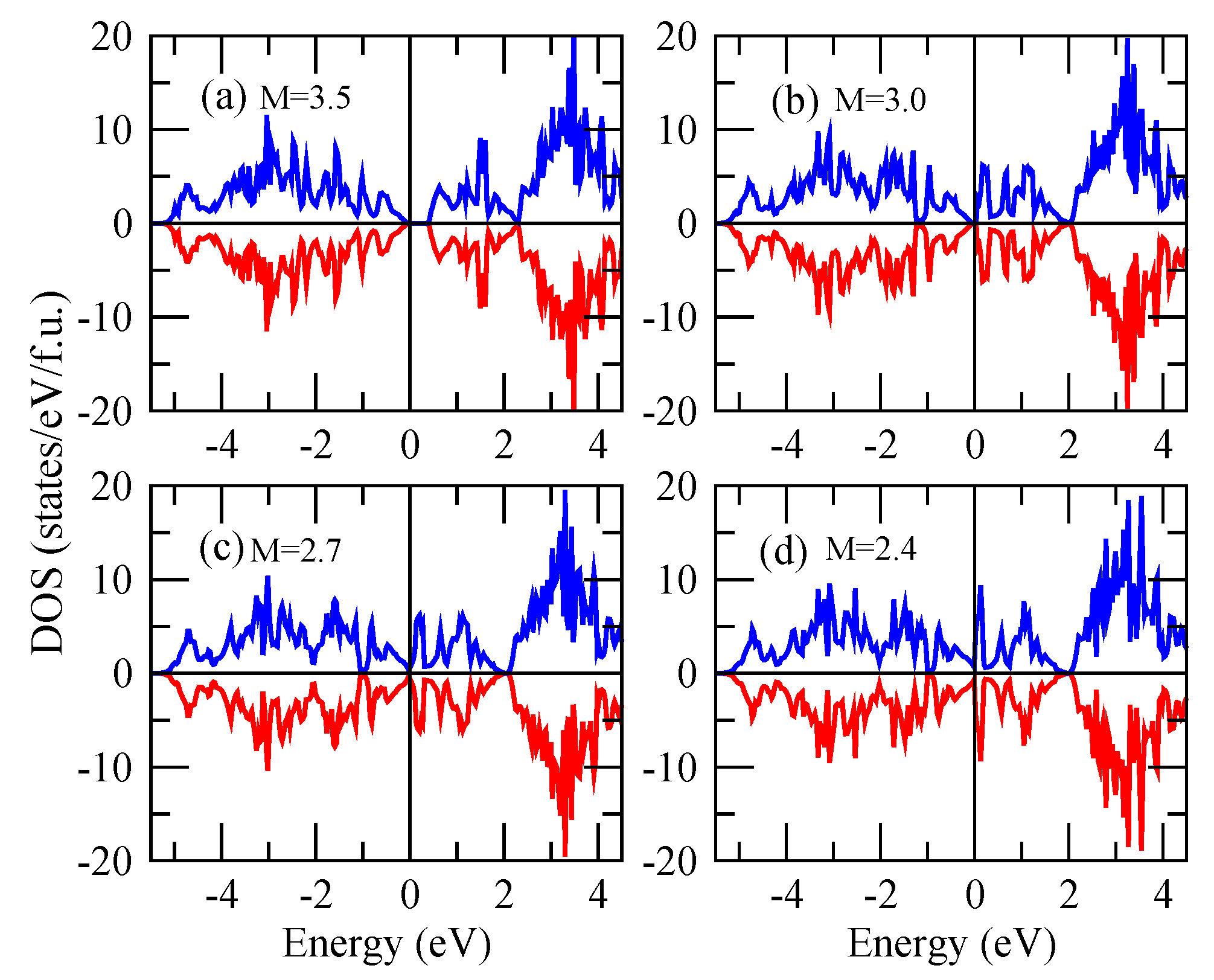
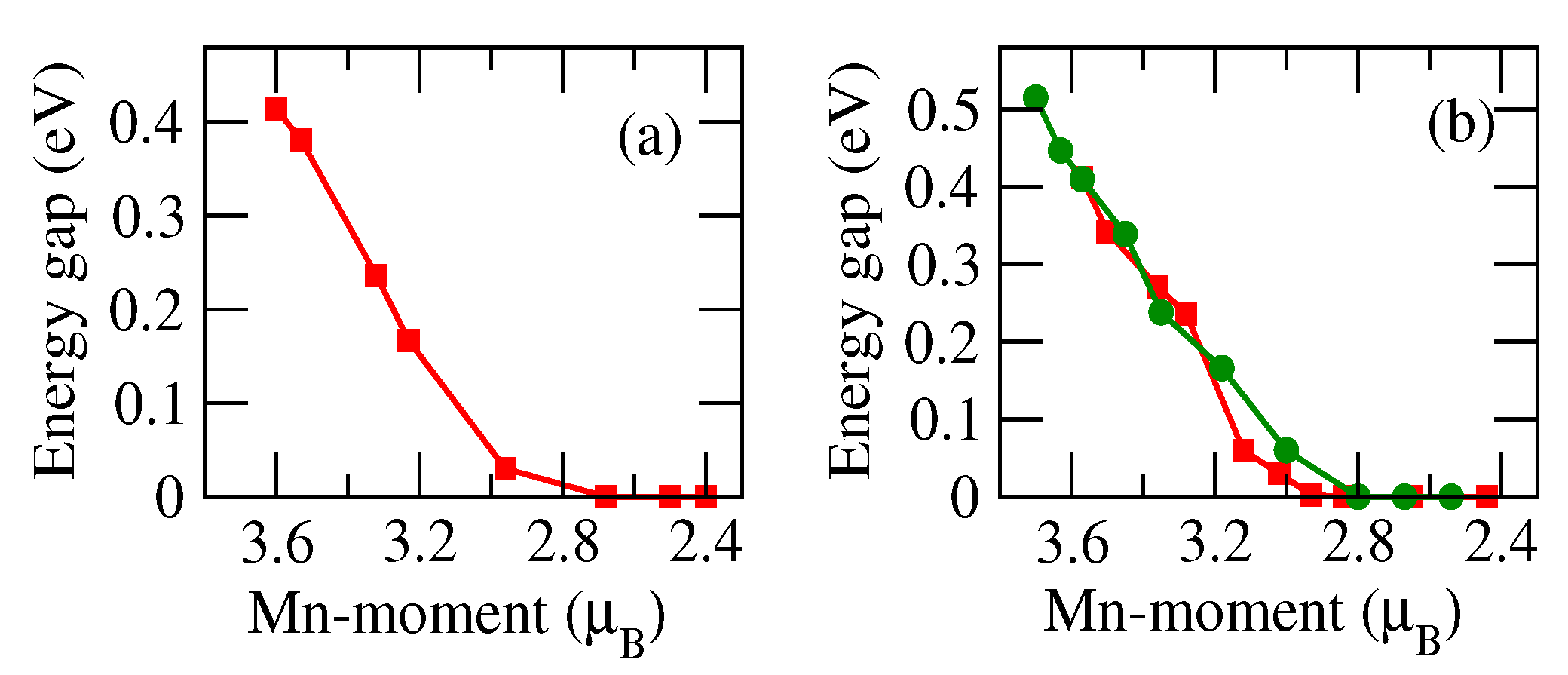
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Park, S.W.; Mizoguchi, H.; Kodama, K.; Shamoto, S.; Otomo, T.; Matsuishi, S.; Kamiya, T.; Hosono, H. Magnetic Structure and Electromagnetic Properties of LnCrAsO with a ZrCuSiAs-type Structure (Ln = La, Ce, Pr, and Nd). Inorg. Chem. 2013, 52, 13363–13368. [Google Scholar] [CrossRef]
- McGuire, M.A.; Garlea, V.O. Short- and long-range magnetic order in LaMnAsO. Phys. Rev. B 2016, 93, 054404. [Google Scholar] [CrossRef]
- Yanagi, H.; Kawamura, R.; Kamiya, T.; Kamihara, Y.; Hirano, M.; Nakamura, T.; Osawa, H.; Hosono, H. Itinerant ferromagnetism in the layered crystals LaCoOX (X = P, As). Phys. Rev. B 2008, 77, 224431. [Google Scholar] [CrossRef]
- Ohta, H.; Yoshimura, K. Magnetic properties of LCoAsO (L = La–Gd). Phys. Rev. B 2009, 80, 184409. [Google Scholar] [CrossRef]
- Prando, G.; Bonfa, P.; Profeta, G.; Khasanov, R.; Bernardini, F.; Mazzani, M.; Bruning, E.M.; Pal, A.; Awana, V.P.S.; Grafe, H.J.; et al. Common effect of chemical and external pressures on the magnetic properties of RCoPO (R = La, Pr). Phys. Rev. B 2013, 87, 064401. [Google Scholar] [CrossRef]
- Watanabe, T.; Yanagi, H.; Kamiya, T.; Kamihara, Y.; Hiramatsu, H.; Hirano, M.; Hosono, H. Nickel-Based Oxyphosphide Superconductor with a Layered Crystal Structure, LaNiOP. Inorg. Chem. 2007, 46, 7719–7721. [Google Scholar] [CrossRef]
- Wang, C.; Wang, Z.-C.; Mei, Y.-X.; Li, Y.-K.; Li, L.; Tang, Z.-T.; Liu, Y.; Zhang, P.; Zhai, H.-F.; Xu, Z.-A.; et al. A New ZrCuSiAs-Type Superconductor: ThFeAsN. J. Am. Chem. Soc. 2016, 138, 2170–2173. [Google Scholar] [CrossRef]
- Wang, Z.-C.; Shao, Y.-T.; Wang, C.; Wang, Z.; Xu, Z.-A.; Cao, G.-H. Enhanced superconductivity in ThNiAsN. Europhys. Lett. 2017, 118, 57004. [Google Scholar] [CrossRef]
- Shiroka, T.; Shang, T.; Wang, C.; Cao, G.-H.; Eremin, I.; Ott, H.-R.; Mesot, J. High-Tc superconductivity in undoped ThFeAsN. Nat. Commun. 2017, 8, 156. [Google Scholar] [CrossRef]
- Sen, S.; Guo, G.-Y. Pressure induced Lifshitz transition in ThFeAsN. Phys. Rev. Mater. 2020, 4, 104802. [Google Scholar] [CrossRef]
- Sen, S.; Guo, G.-Y. Electronic structure, lattice dynamics, and magnetic properties of ThXAsN (X=Fe,Co,Ni) superconductors: A first-principles study. Phys. Rev. B 2020, 102, 224505. [Google Scholar] [CrossRef]
- Yang, Y.; Feng, S.-Q.; Lu, H.-Y.; Gu, L.-T.; Chen, Z.-P. Electronic Properties and Lattice Dynamics Studies of the Nickel-Based Superconductor ThNiAsN. J. Supercond. Nov. Magn. 2018, 31, 3153–3158. [Google Scholar] [CrossRef]
- Zhang, F.; Li, B.; Ren, Q.; Mao, H.; Xia, Y.; Hu, B.; Liu, Z.; Wang, Z.; Shao, Y.; Feng, Z.; et al. ThMnPnN (Pn = P, As): Synthesis, Structure, and Chemical Pressure Effects. Inorg. Chem. 2020, 59, 2937–2944. [Google Scholar] [CrossRef] [PubMed]
- Corkett, A.J.; Free, D.G.; Clarke, S.J. Spin-reorientation transition in CeMnAsO. J. Clarke Inorg. Chem. 2015, 54, 1178–1184. [Google Scholar] [CrossRef] [PubMed]
- Marcinkova, A.; Hansen, T.; Curfs, C.; Margadonna, S.; Bos, J.-W. Nd-induced Mn spin-reorientation transition in NdMnAsO. Phys. Rev. B 2010, 82, 174438. [Google Scholar] [CrossRef]
- Kimber, S.; Hill, A.; Zhang, Y.-Z.; Jeschke, H.; Valentí, R.; Ritter, C.; Schellenberg, I.; Hermes, W.; Pöttgen, R.; Argyriou, D.N. Local moments and symmetry breaking in metallic PrMnSbO. Phys. Rev. B 2010, 82, 100412. [Google Scholar] [CrossRef]
- Satya, A.T.; Mani, A.; Arulraj, A.; Chandrashekar, N.V.; Vinod, K.; Sundar, C.S.; Bharathi, A. Pressure-induced metallization of BaMn2As2. Phys. Rev. B 84, 180515(R); Erratum in Phys. Rev. B 2012, 85, 019901. [Google Scholar] [CrossRef]
- Sen, S.; Kabbour, H. Pressure induced magnetic and structural transitions in ThMnAsN: An ab-initio study. arXiv 2022, arXiv:2207.00977. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558. [Google Scholar] [CrossRef]
- Bloch, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Perdew, J.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Dudarev, S.L.; Botton, G.A.; Savrasov, S.Y.; Humphreys, C.J.; Sutton, A.P. Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+U study. Phys. Rev. B 1998, 57, 1505. [Google Scholar] [CrossRef]
- Yu, K.; Carter, E.A. Communication: Comparing ab initio methods of obtaining effective U parameters for closed-shell materials. J. Chem. Phys. 2014, 140, 121105. [Google Scholar] [CrossRef]
- Cococcioni, M.; de Gironcoli, S. Linear response approach to the calculation of the effective interaction parameters in the LDA+U method. Phys. Rev. B 2005, 71, 035105. [Google Scholar] [CrossRef]
- Kulik, H.J.; Cococcioni, M.; Scherlis, D.A.; Marzari, N. Density Functional Theory in Transition-Metal Chemistry: A Self-Consistent Hubbard U Approach. Phys. Rev. Lett. 2006, 97, 103001. [Google Scholar] [CrossRef]
- Mosey, N.J.; Carter, E.A. Ab initio evaluation of Coulomb and exchange parameters for DFT+U calculations. Phys. Rev. B 2007, 76, 155123. [Google Scholar] [CrossRef]
- Mosey, N.J.; Liao, P.; Carter, E.A. Rotationally invariant ab initio evaluation of Coulomb and exchange parameters for DFT+U calculations. J. Chem. Phys. 2008, 129, 14103. [Google Scholar] [CrossRef] [PubMed]
- Aryasetiawan, F.; Karlsson, K.; Jepsen, O.; Schönberger, U. Calculations of Hubbard U from first-principles. Phys. Rev. B 2006, 74, 125106. [Google Scholar] [CrossRef]
- Miyake, T.; Aryasetiawan, F. Screened Coulomb interaction in the maximally localized Wannier basis. Phys. Rev. B 2008, 77, 085122. [Google Scholar] [CrossRef]
- Şaşíoğlu, E.; Friedrich, C.; Blügel, S. Effective Coulomb interaction in transition metals from constrained random-phase approximation. Phys. Rev. B 2011, 83, 121101. [Google Scholar] [CrossRef]
- Wang, L.; Maxisch, T.; Ceder, G. Oxidation energies of transition metal oxides within the GGA+U framework. Phys. Rev. B 2006, 73, 195107. [Google Scholar] [CrossRef]


| ThMnAsN | ThMnPN | |||
|---|---|---|---|---|
| Magnetic | Energy | Mn Moment | Energy | Mn Moment |
| Order | (meV/f.u.) | () | (meV/f.u.) | () |
| NM | 0 | 0 | 0 | 0 |
| FM | −317.8 | 2.39 | −332.8 | 2.03 |
| A-AFM | −322.3 | 2.69 | −332.1 | 1.91 |
| C-AFM | −781.1 | 3.52 | −701.7 | 3.34 |
| G-AFM | −780.3 | 3.52 | −700.9 | 3.34 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sen, S.; Ghosh, H. Magnetic-Moment-Induced Metal–Insulator Transition in ThMnXN (X = As, P): A First Principles Study. Magnetochemistry 2023, 9, 16. https://doi.org/10.3390/magnetochemistry9010016
Sen S, Ghosh H. Magnetic-Moment-Induced Metal–Insulator Transition in ThMnXN (X = As, P): A First Principles Study. Magnetochemistry. 2023; 9(1):16. https://doi.org/10.3390/magnetochemistry9010016
Chicago/Turabian StyleSen, Smritijit, and Haranath Ghosh. 2023. "Magnetic-Moment-Induced Metal–Insulator Transition in ThMnXN (X = As, P): A First Principles Study" Magnetochemistry 9, no. 1: 16. https://doi.org/10.3390/magnetochemistry9010016
APA StyleSen, S., & Ghosh, H. (2023). Magnetic-Moment-Induced Metal–Insulator Transition in ThMnXN (X = As, P): A First Principles Study. Magnetochemistry, 9(1), 16. https://doi.org/10.3390/magnetochemistry9010016







