Steady-State and Dynamic Rheological Properties of a Mineral Oil-Based Ferrofluid
Abstract
:1. Introduction
2. Experiment
2.1. Materials
2.2. Preparation Process
3. Results and Discussion
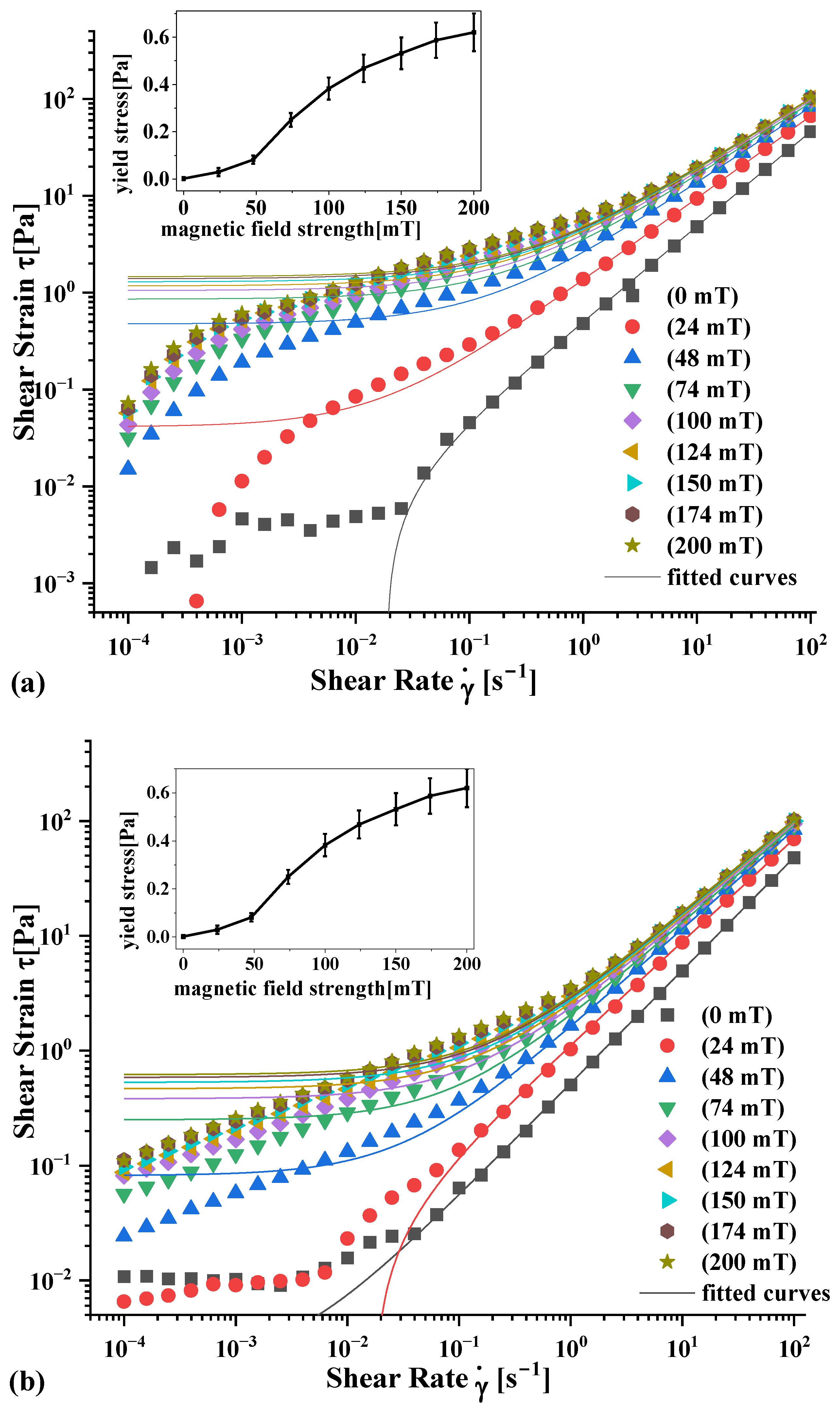
3.1. Static and Dynamic Yield Stresses Analysis
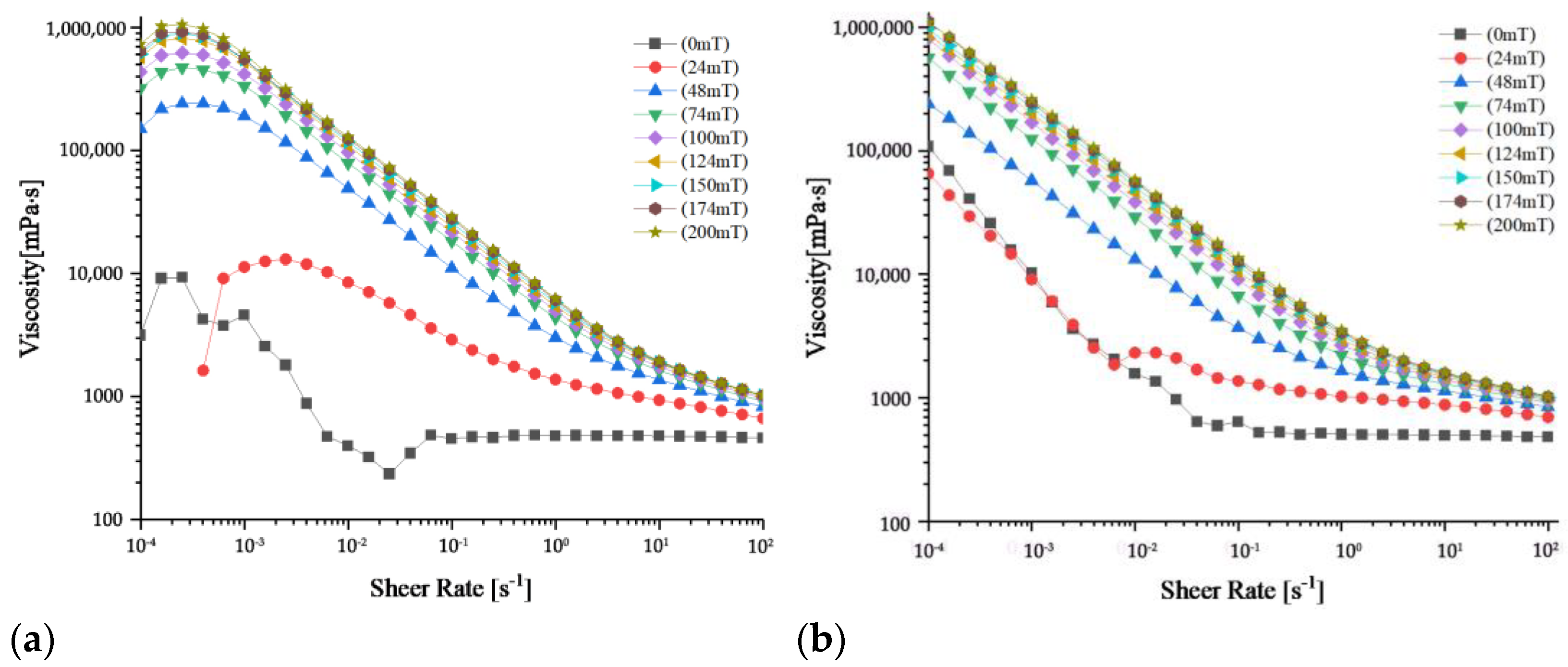
3.2. Viscosity Analysis
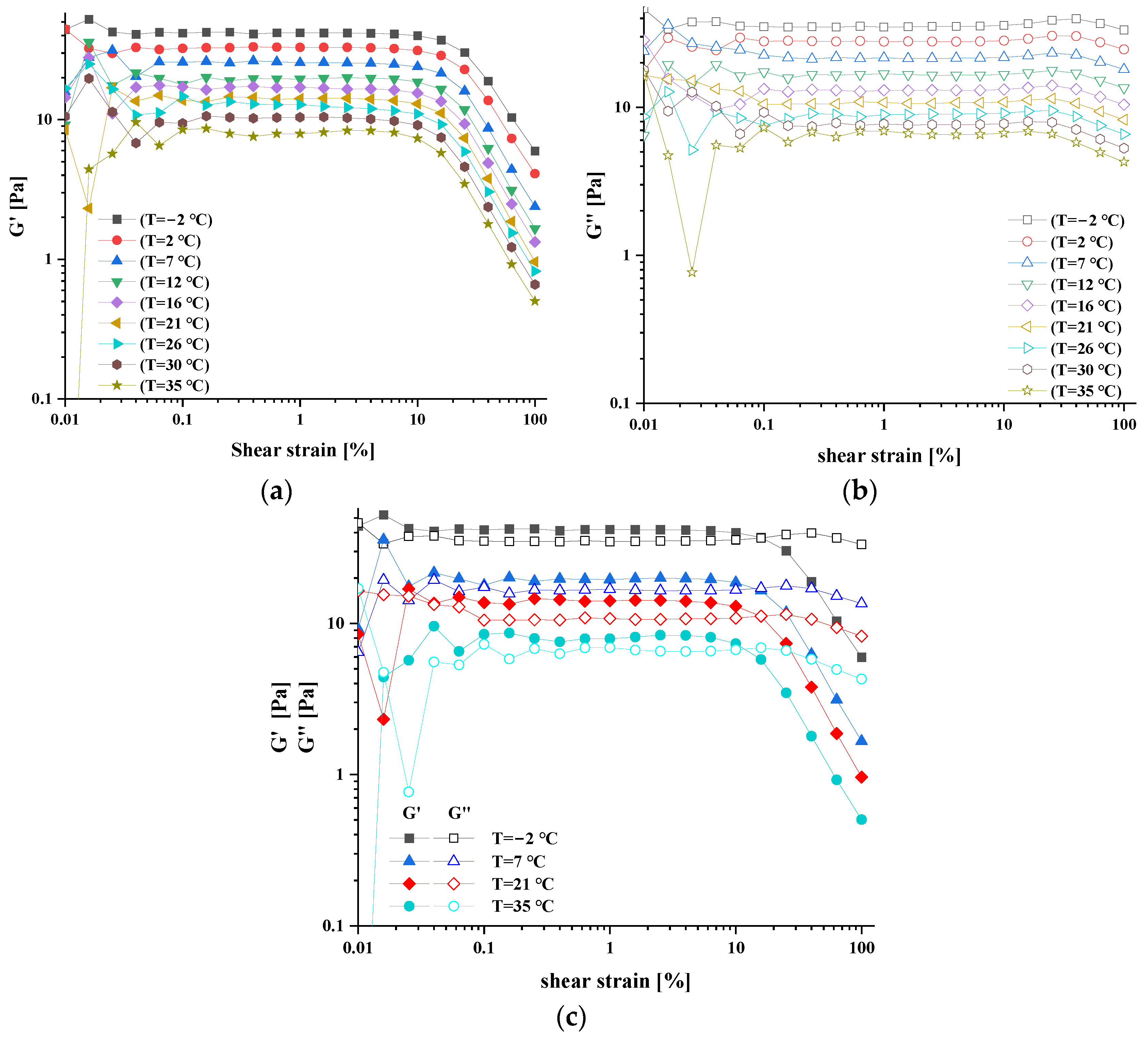
3.3. Viscoelastic Behavior of FFs
3.3.1. Amplitude Scanning Analysis
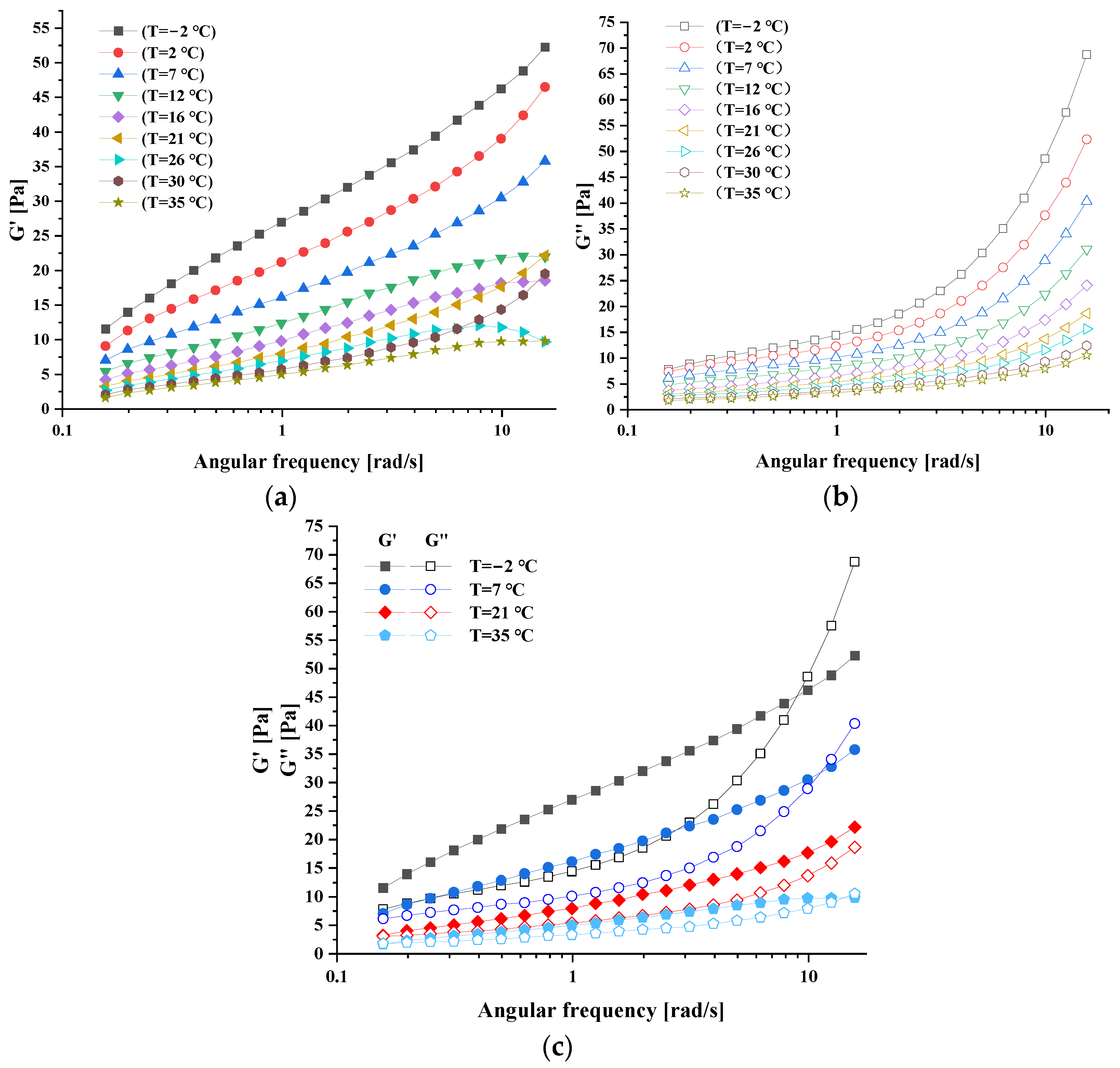
3.3.2. Frequency Scanning Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ronzova, A.; Sedlacik, M.; Cvek, M. Magnetorheological fluids based on core–shell carbonyl iron particles modified by various organosilanes: Synthesis, stability and performance. Soft Matter. 2021, 17, 1299–1306. [Google Scholar] [CrossRef] [PubMed]
- Maurya, C.S.; Sarkar, C. Rheological response of soft flake-shaped carbonyl iron water-based MR fluid containing iron nanopowder with hydrophilic carbon shell. Rheol. Acta 2021, 60, 277–290. [Google Scholar] [CrossRef]
- Pathak, S.; Jain, K.; Kumar, P.; Wang, X.; Pant, R.P. Improved thermal performance of annular fin-shell tube storage system using magnetic fluid. Appl. Energy 2019, 239, 1524–1535. [Google Scholar] [CrossRef]
- Pathak, S.; Zhang, R.; Gayen, B.; Kumar, V.; Zhang, H.; Pant, R.P.; Wang, X. Ultra-low friction self-levitating nanomagnetic fluid bearing for highly efficient wind energy harvesting. Sustain. Energy Technol. Assess. 2022, 52, 102024. [Google Scholar] [CrossRef]
- Pathak, S.; Zhang, R.; Bun, K.; Zhang, H.; Gayen, B.; Wang, X. Development of a novel wind to electrical energy converter of passive ferrofluid levitation through its parameter modelling and optimization. Sustain. Energy Technol. Assess. 2021, 48, 101641. [Google Scholar] [CrossRef]
- Pathak, S.; Jain, K.; Kumar, V.; Pant, R.P. Magnetic fluid based high precision temperature sensor. IEEE Sens. J. 2017, 17, 2670–2675. [Google Scholar] [CrossRef]
- Li, Z.; Li, D.; Chen, Y.; Yang, Y.; Yao, J. Influence of viscosity and magnetoviscous effect on the performance of a magnetic fluid seal in a water environment. Tribol. Trans. 2018, 61, 367–375. [Google Scholar] [CrossRef]
- Cvek, M.; Mrlik, M.; Pavlinek, V. A rheological evaluation of steady shear magnetorheological flow behavior using three-parameter viscoplastic models. J. Rheol. 2016, 60, 687–694. [Google Scholar] [CrossRef]
- Maurya, C.S.; Sarkar, C. Rheological and creep and recovery behavior of carbonyl iron water-based magnetorheological gel using laponite as an additive and oleic acid as a surfactant. Rheol. Acta 2022, 61, 99–110. [Google Scholar] [CrossRef]
- Zhu, S.; Li, D.; Wang, Z. Research on FF seal and mechanical seal combined sealing technology. Funct. Mater. 2017, 48, 2192–2196. [Google Scholar]
- Kumar, V.; Rana, A.; Yadav, M.S.; Pant, R.P. Size-induced effect on nano-crystalline CoFe2O4. J. Magn. Magn. Mater. 2008, 320, 1729–1734. [Google Scholar] [CrossRef]
- Noorjahan, G.A.; Jain, K.; Pathak, S.; Pant, R.P. Dipolar interaction and magneto-viscoelasticity in nanomagnetic fluid. Nanosci. Nanotechnol. 2017, 17, 1–6. [Google Scholar] [CrossRef]
- Li, Z.; Yao, J.; Li, D. Research on the rheological properties of a perfluoropolyether based ferrofluid. J. Magn. Magn. Mater. 2017, 424, 33–38. [Google Scholar] [CrossRef]
- Paul, G.; Das, P.K.; Manna, I. Synthesis, characterization and studies on magneto-viscous properties of magnetite dispersed water based nanofluids. J. Magn. Magn. Mater. 2016, 404, 29–39. [Google Scholar] [CrossRef]
- Bai, L.; Zhang, Z.L.; Xu, L.F. Preparation and properties of Fe3O4@SiO2 silicone oil based FF. J. Funct. Mater. 2017, 48, 11103–11107. [Google Scholar]
- Kim, D.K.; Zhang, Y.; Kehr, J.; Klason, T.; Bjelke, B.; Muhammed, M. Characterization and MRI study of surfactant-coated superparamagnetic nanoparticles administered into the rat brain. J. Magn. Magn. Mater. 2001, 225, 256–261. [Google Scholar] [CrossRef]
- Li, D. Research on the Theory and Application of Magnetic Fluid; Northern Jiaotong University: Beijing, China, 1996; pp. 24–28. [Google Scholar]
- Dinkgreve, M.; Paredes, J.; Denn, M.M.; Bonn, D. On different ways of measuring “the” yield stress. J. Non-Newton. Fluid Mech. 2016, 238, 233–241. [Google Scholar] [CrossRef]
- Wang, G.; Ma, Y.; Tong, Y.; Dong, X. Synthesis, characterization and magnetorheological study of 3-aminopropyltriethoxysilane-modified Fe3O4 nanoparticles. Smart Mater. Struct. 2016, 25, 035028. [Google Scholar] [CrossRef]
- de Vicente, J.; Vereda, F.; Segovia-Gutiérrez, J.P.; del Puerto Morales, M.; Hidalgo-Álvarez, R. Effect of particle shape in magnetorheology. J. Rheol. 2010, 54, 1337–1362. [Google Scholar] [CrossRef]
- Mishra, A.; Pathak, S.; Kumar, P.; Singh, A.; Jain, K.; Chaturvedi, R.; Singh, D.; Basheed, G.A.; Pant, R.P. Measurement of static and dynamic magneto-viscoelasticity in facile varying pH synthesized CoFe2O4-based magnetic fluid. IEEE Trans. Magn. 2019, 55, 1–7. [Google Scholar] [CrossRef]
- Fan, Y.; Xie, L.; Yang, W.; Sun, B. Magnetic field dependent viscoelasticity of a highly stable magnetorheological fluid under oscillatory shear. J. Appl. Phys. 2021, 129, 204701. [Google Scholar] [CrossRef]
- Zhu, Y.; Ivey, M.L.; Sheaffer, P.; Pousset, J.; Liu, J. Magnetic field-induced phase transitions in ferrofluid emulsion. Int. J. Mod. Phys. B 1996, 10, 2973–2981. [Google Scholar] [CrossRef]
- Lacoste, D.; Lubensky, T.C. Phase transitions in a ferrofluid at magnetic-field-induced microphase separation. Phys. Rev. E 2001, 64, 041506. [Google Scholar] [CrossRef] [Green Version]

| Kinematical Viscosity mPa·s (40 °C) | Flash Point °C | Pour Point °C | Density g/cm3 (25 °C) |
|---|---|---|---|
| 32 | 208 | −31 | 0.865 |
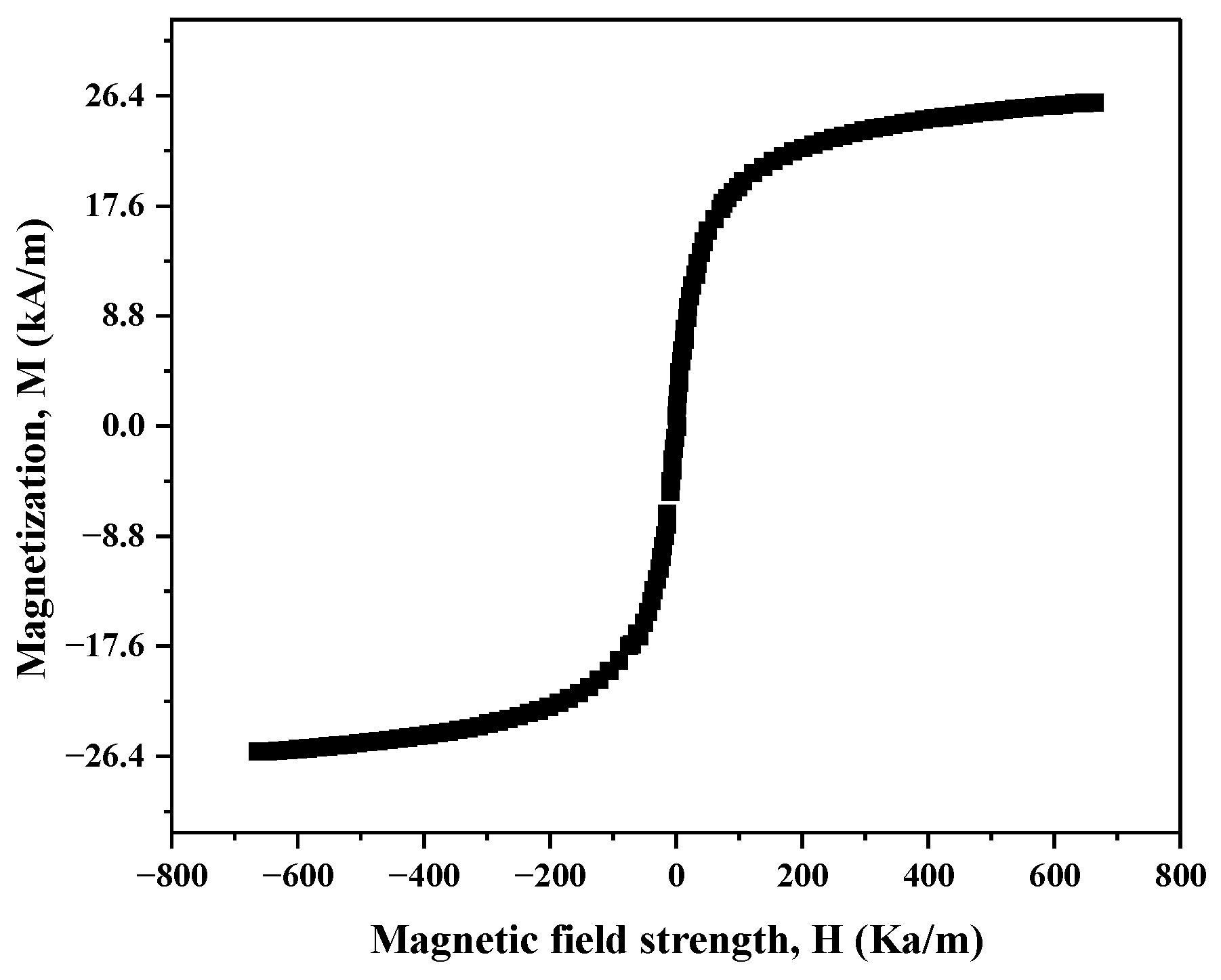
| Density g/cm3 (25 °C) | Zero Magnetic Field Viscosity mPa·s (40 °C) | Saturation Magnetization kA/m | Particle Volume Fraction % |
|---|---|---|---|
| 1.249 | 341.4 | 24.45 | 7.26 |
| Fitting Parameter/M.F. | Static Parameter | Dynamic Parameter | ||||||
|---|---|---|---|---|---|---|---|---|
[Pa] | n | R2 | [Pa] | n | R2 | |||
| 0 mT | 0.01 | 0.51 | 0.98 | 1 | 0.002 | 0.52 | 0.98 | 0.9999 |
| 24 mT | 0.04 | 1.33 | 0.85 | 0.9999 | 0.03 | 1.14 | 0.89 | 0.9999 |
| 48 mT | 0.48 | 2.15 | 0.79 | 0.9997 | 0.08 | 1.55 | 0.88 | 0.9999 |
| 74 mT | 0.86 | 2.68 | 0.76 | 0.9992 | 0.25 | 1.81 | 0.85 | 0.9999 |
| 100 mT | 1.05 | 2.92 | 0.76 | 0.999 | 0.38 | 2.00 | 0.84 | 0.9999 |
| 124 mT | 1.17 | 3.16 | 0.75 | 0.9989 | 0.47 | 2.14 | 0.83 | 0.9998 |
| 150 mT | 1.29 | 3.21 | 0.75 | 0.9986 | 0.53 | 2.24 | 0.82 | 0.9997 |
| 174 mT | 1.39 | 3.26 | 0.74 | 0.9983 | 0.59 | 2.31 | 0.82 | 0.9997 |
| 200 mT | 1.46 | 3.32 | 0.74 | 0.9982 | 0.62 | 2.36 | 0.82 | 0.9997 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Meng, Y.; Li, Z.; Dong, J.; Cui, H. Steady-State and Dynamic Rheological Properties of a Mineral Oil-Based Ferrofluid. Magnetochemistry 2022, 8, 100. https://doi.org/10.3390/magnetochemistry8090100
Wang H, Meng Y, Li Z, Dong J, Cui H. Steady-State and Dynamic Rheological Properties of a Mineral Oil-Based Ferrofluid. Magnetochemistry. 2022; 8(9):100. https://doi.org/10.3390/magnetochemistry8090100
Chicago/Turabian StyleWang, Hujun, Yuan Meng, Zhenkun Li, Jiahao Dong, and Hongchao Cui. 2022. "Steady-State and Dynamic Rheological Properties of a Mineral Oil-Based Ferrofluid" Magnetochemistry 8, no. 9: 100. https://doi.org/10.3390/magnetochemistry8090100
APA StyleWang, H., Meng, Y., Li, Z., Dong, J., & Cui, H. (2022). Steady-State and Dynamic Rheological Properties of a Mineral Oil-Based Ferrofluid. Magnetochemistry, 8(9), 100. https://doi.org/10.3390/magnetochemistry8090100







