Abstract
An experimental study of the rotational magnetocaloric effect in Ni(en)(H2O)4SO4∙2H2O (en = ethylenediamine) single crystal is presented. The study was carried out at temperatures above 2 K and was associated with adiabatic crystal rotation between the easy plane and hard axis in magnetic fields up to 7 T. The magnetocaloric properties of the studied system were investigated by isothermal magnetization measurement. The experimental observations were completed with ab initio calculations of the anisotropy parameters. A large rotational magnetic entropy change ≈12 Jkg−1K−1 and ≈16.9 Jkg−1K−1 was achieved in 5 T and 7 T, respectively. The present study suggests a possible application of this material in low-temperature refrigeration since the adiabatic rotation of the single crystal in 7 T led to a cooldown of the sample from the initial temperature of 4.2 K down to 0.34 K. Finally, theoretical calculations show that S = 1 Ni(II)-based systems with easy-plane anisotropy can have better rotational magnetocaloric properties than costly materials containing rare-earth elements in their chemical structures.
1. Introduction
Recently, the magnetocaloric effect (MCE) has become a focus of the physical and material science community [1,2,3,4,5,6,7,8]. The effort is motivated by a search for a more efficient and environmentally friendly alternative for refrigeration and air conditioning. The magnetic coolant represents one of the crucial components of a magnetic refrigerator. Apart from a pronounced magnetocaloric response, it must also meet specific criteria, e.g., a large density of magnetic entropy, nearly zero magnetic hysteresis, very small thermal hysteresis, small specific heat, large thermal conductivity, high chemical stability, low cost, availability, and simple sample synthesis [9].
The conventional MCE is based on the heating (normal MCE) or cooling (inverse MCE) of the system exposed to an increasing external magnetic field. Two parameters are essential for the quantitative expression of MCE, namely, the isothermal magnetic entropy change (ΔSM) and the adiabatic temperature change (ΔTad) [4,10]. The mentioned parameters are influenced by the magnitude of external magnetic field change. Obviously, the efficient magnetic refrigerants for active MCE should have the given parameters in the relevant temperature and magnetic field ranges as large as possible. Designing materials with a large density of magnetic ions while keeping magnetic coupling weak [11,12] as well as tailoring critical behavior [13] have become conventional approaches in tuning magnetocaloric properties. Alternatively, properties of spin liquids in quantum spin chains [14] and localized excitations in geometrically frustrated magnets proved an enhanced magnetocaloric effect in these systems.
In addition, in recent years, the topic of the rotational magnetocaloric effect has come to the forefront in the field of magnetic cooling [15,16,17,18,19,20,21,22,23,24,25,26,27]. The cooling of the sample is obtained by a simple rotation of the magnetocaloric material in a constant magnetic field from the easy to hard magnetization axis. The rotation of a magnetocaloric material changes its entropy, referred to as a rotational entropy change, ΔSR. A large value of ΔSR causes a significant temperature change during the rotation of the sample, and therefore the presence of the magnetic anisotropy of the system is a necessary condition for the observation of a large rotational MCE. It is important to note that all investigated systems with large rotational MCE contained rare-earth elements in their chemical structures. However, the single crystal preparation of these materials is money-, time-, and energy-consuming. For this reason, the given materials may not meet the important criteria for selecting appropriate magnetic refrigerants. It should be noted that the magnetocaloric properties of financially affordable S = 1 Ni(II)-based systems have been studied. Their properties can be tuned by magnetic dimensionality, exchange coupling, and single-ion anisotropy [28,29,30]. If the S = 1 Ni(II)-based systems are described within a model of a spin-1 paramagnet in a crystal field with a spin Hamiltonian , where D and E represent uniaxial and in-plane anisotropy parameters, respectively, an inverse MCE can be observed for the easy-plane anisotropy [31]. Thus, considering the combination of normal and inverse MCE, a large rotational MCE can be expected, comparable to the rotational MCE observed in materials containing rare-earth elements in their chemical structures.
The title compound Ni(en)(H2O)4SO4∙2H2O (en = ethylenediamine) (NEHS) has been identified as a spin-1 paramagnet with the nonmagnetic ground state introduced by the easy-plane anisotropy D/kB = 11.6 K with E/D = 0.1 and negligible exchange interactions J ≈ 0 [32]. Analysis of the specific heat in zero magnetic field indicated the absence of a phase transition to a magnetically ordered state below 1.8 K as a direct consequence of the dominant influence of the crystal field on the magnetic properties of the studied system.
This work presents an experimental study of the rotational MCE in NEHS single crystal at temperatures above 2 K, associated with adiabatic crystal rotation between the easy plane and hard axis in magnetic fields up to 7 T. The experimental observations are completed with ab initio calculations of the anisotropy parameters. Besides that, theoretical simulations of the rotational MCE in the S = 1 paramagnet were performed, and the simulations were compared with experimental data. Based on the present results, the design of better magnetocaloric properties of financially affordable S = 1 Ni(II)-based systems is discussed.
2. Materials and Methods
The crystal structure of NEHS is a monoclinic, space group C 2/c with the unit cell parameters a = 9.523 Å, b = 12.185 Å, c = 11.217 Å, β = 107.3°; and Z = 4 [33]. The crystal structure consists of [Ni(en)(H2O)4]2+ cations, [SO4]2− anions, and two molecules of water. These units are connected by a large number of hydrogen bonds [33]. NEHS single crystals were prepared in the form of blue prisms from an aqueous solution of nickel sulphate and en in stoichiometric amounts.
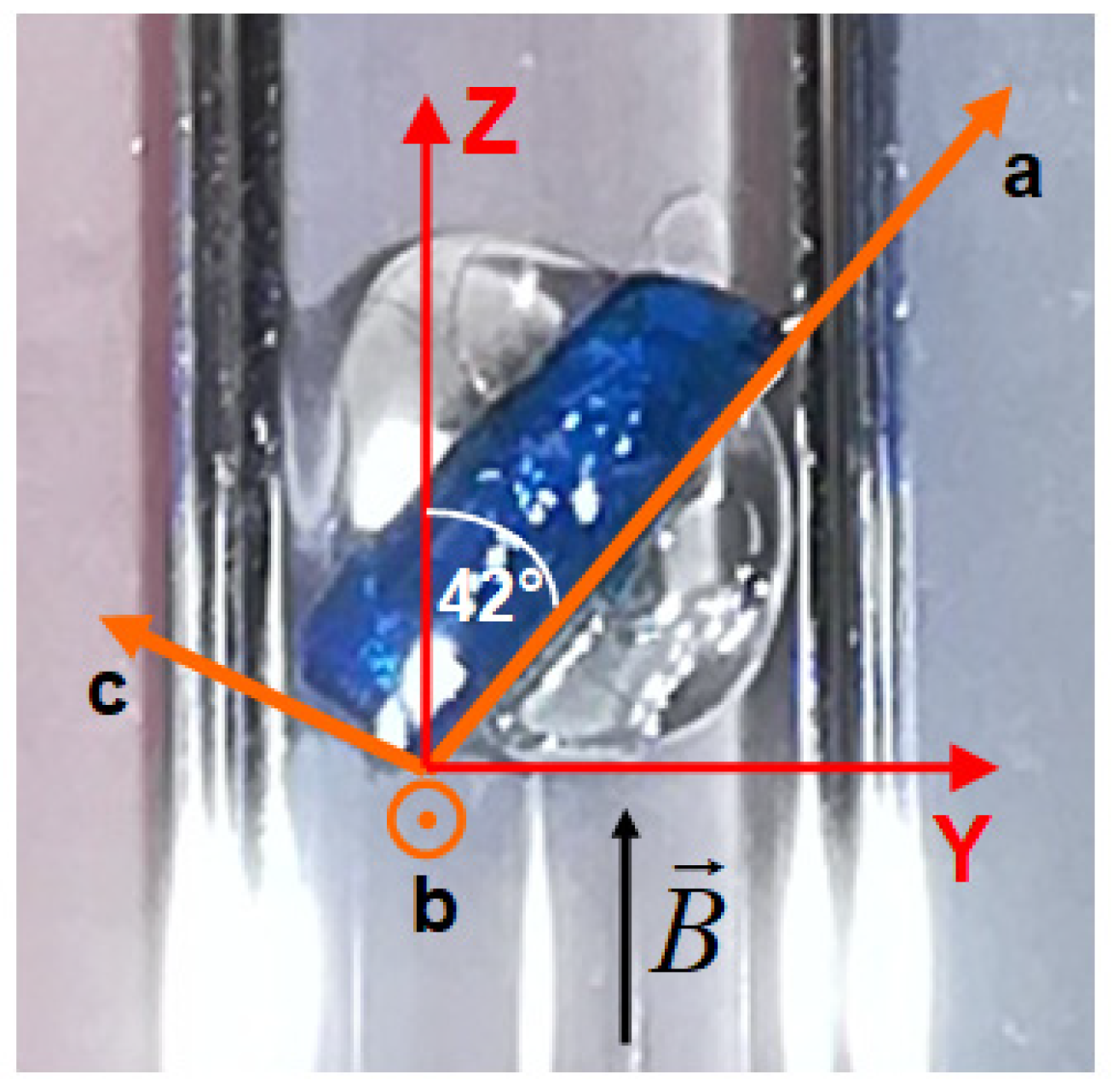
Isothermal magnetization curves were measured in a commercial superconducting quantum device (SQUID) magnetometer in magnetic fields up to 7 T in the temperature range from 2 K to 20 K. A single crystal of NEHS glued to a quartz holder with a mass of 2.58 mg and dimensions 3 × 1 × 0.3 mm3 was used (Figure 1).
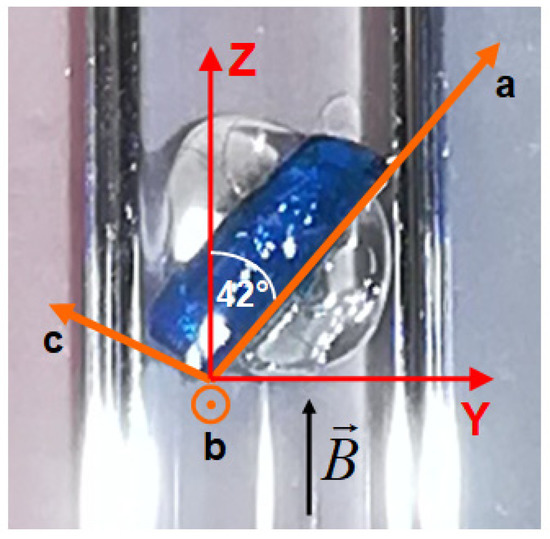
Figure 1.
A photograph of the NEHS single crystal glued to a quartz holder for the orientation B || Z with a schematic illustration of the direction of the local anisotropy and crystallographic axes.
Ab initio calculations were performed using the computational package ORCA 5.0.1 [34]. The estimates of single-ion anisotropy parameters were based on the state-averaged complete-active-space self-consistent field wave functions (SA-CASSCF) with tight SCF convergence criteria, including the following N-electron valence second-order perturbation theory (NEVPT2) [35,36,37,38,39]. The active space was defined on metal-based d-orbitals for Ni(II) as CAS(8,5) and CAS(8,10). The state averaged approach was used with all 10 triplet and 15 singlet states equally weighted. The ZFS parameters were calculated through the quasi-degenerate perturbation theory [40,41,42]. Relativistic effects were taken into account by using the zeroth-order regular approximation [43,44] together with the corresponding segmented all-electron relativistic contracted version of the triple-ζ basis set Def2-TZVP [45] for all atoms. The calculations utilized the RI approximation and the chain-of-spheres (RIJCOSX) approximation to exact exchange [46,47,48].
3. Results
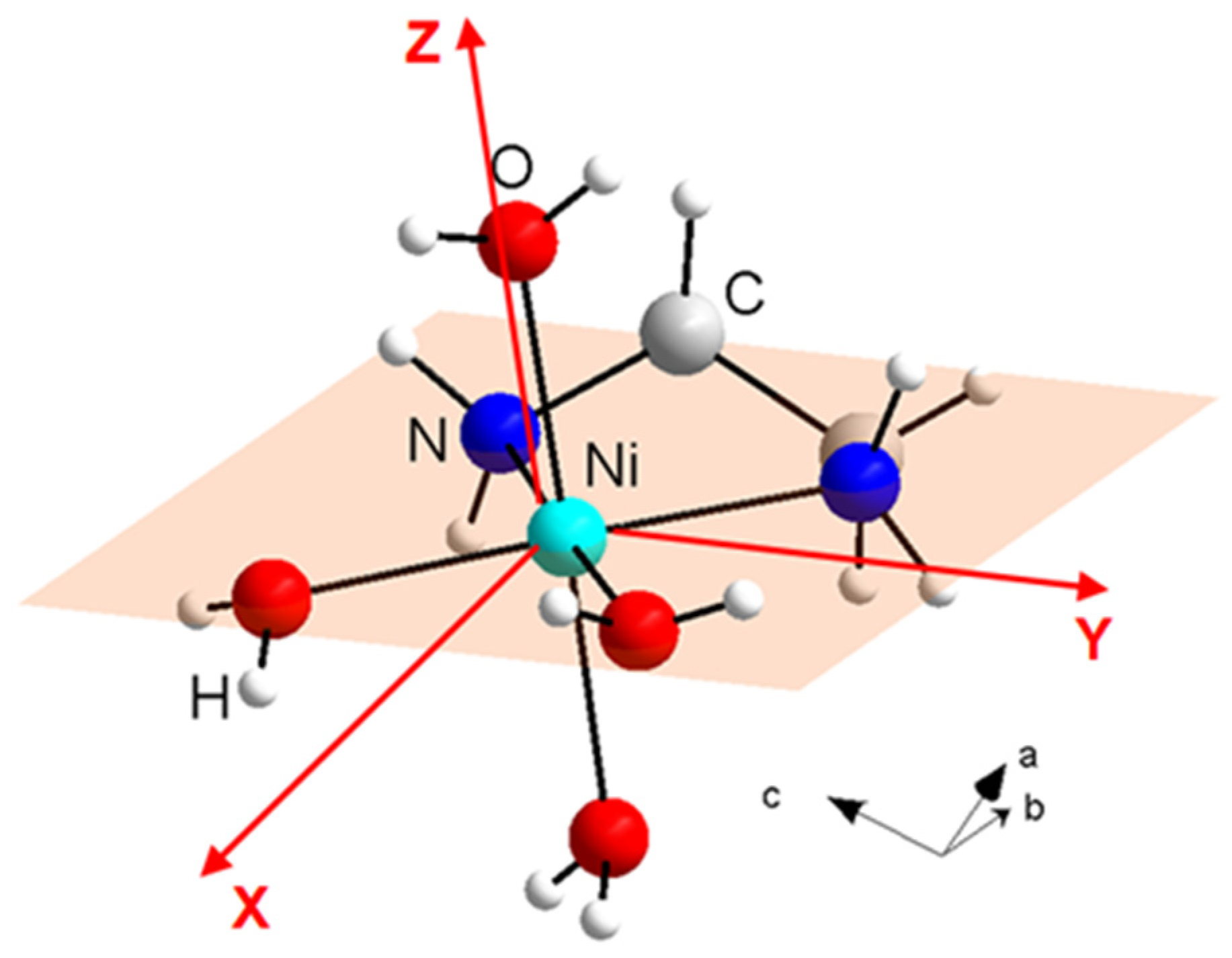
The single-ion anisotropy parameters, together with the orientations of local anisotropy axes of Ni(II) ions in NEHS [33], were predicted using ab initio calculations in ORCA on [Ni(en)(H2O)4]2+ cation using atom positions as obtained from X-ray diffraction. The SA-CASSCF/NEVPT2 calculations yielded crystal field parameters D/kB = 11.5 K, E/D = 0.07 with an average g-factor g = 2.22. This result is in excellent agreement with the values obtained from the analysis of the heat capacity in the zero magnetic field [32]. The crystal structure of a [Ni(en)(H2O)4]2+ cation with the schematic orientation of the equatorial plane of the octahedron and local anisotropy axes predicted by SA-CASSCF/NEVPT2 calculations is shown in Figure 2. It can be seen that the local anisotropy Z-axis is parallel to the direction of the bond between the nickel ion and oxygen, which corresponds to the axis of the octahedron. On the other hand, the local anisotropy axes X and Y are located within the equatorial plane of the octahedron, with the X-axis passing along the bisector axis of the oxygen–nickel–oxygen angle while the Y-axis is oriented along the bisector axis of the oxygen–nickel–nitrogen angle.
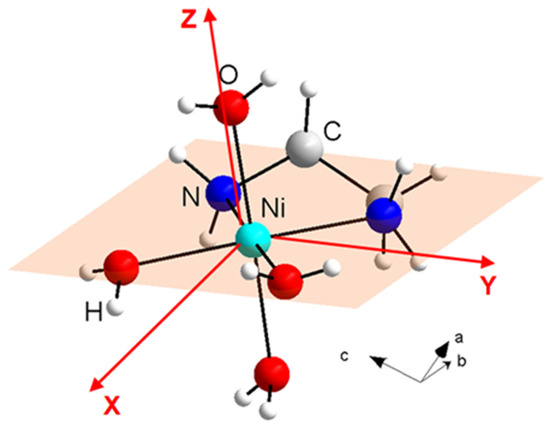
Figure 2.
The crystal structure of [Ni(en)(H2O)4]2+ cation in NEHS with the schematic orientation of the equatorial plane of the octahedron and local anisotropy axes determined by ORCA calculations.
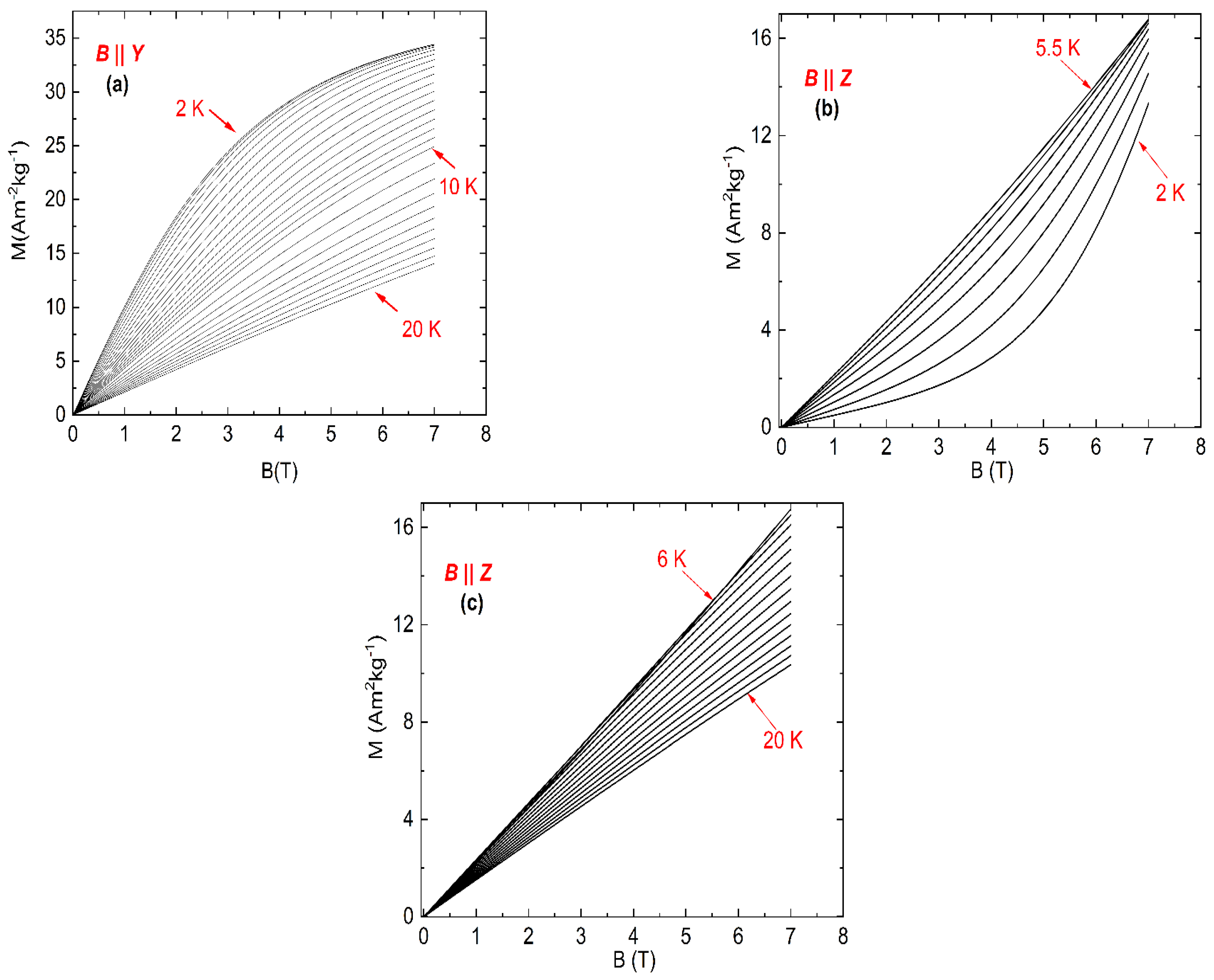
The field dependence of the magnetization of NEHS for the magnetic field parallel to the Y-axis is shown in Figure 3a. It can be seen that the value of the magnetization increases with increasing magnetic field for each temperature, but the magnetization does not reach its saturation value even at the lowest measured temperatures. On the other hand, the magnetization decreases with increasing temperature for all magnetic fields, which implicates a normal magnetocaloric effect for the orientation B || Y.
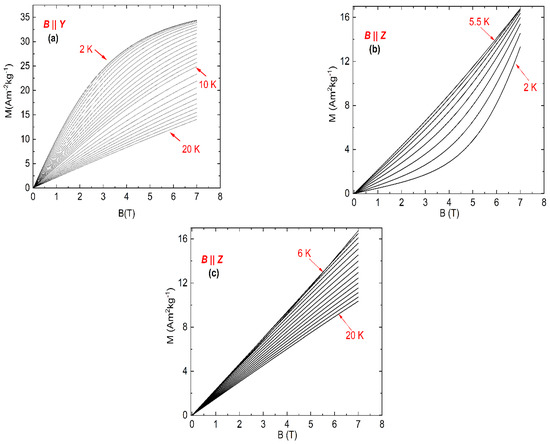
Figure 3.
Magnetic-field dependence of the magnetization of NEHS for B || Y (a) and B || Z (b,c), temperature steps ΔT = 0.5 K and 1 K for intervals 2–10 and 11–20 K, respectively.
A different situation was observed for the field dependence of the magnetization in the magnetic field parallel to the Z-axis (Figure 3b,c). The value of the magnetization increases with increasing magnetic field for each temperature, but at temperatures between 2 and 5.5 K the magnetization increases with increasing temperature. At higher temperatures the isothermal magnetization curves for B || Z show the same behavior as the data for the orientation B || Y.
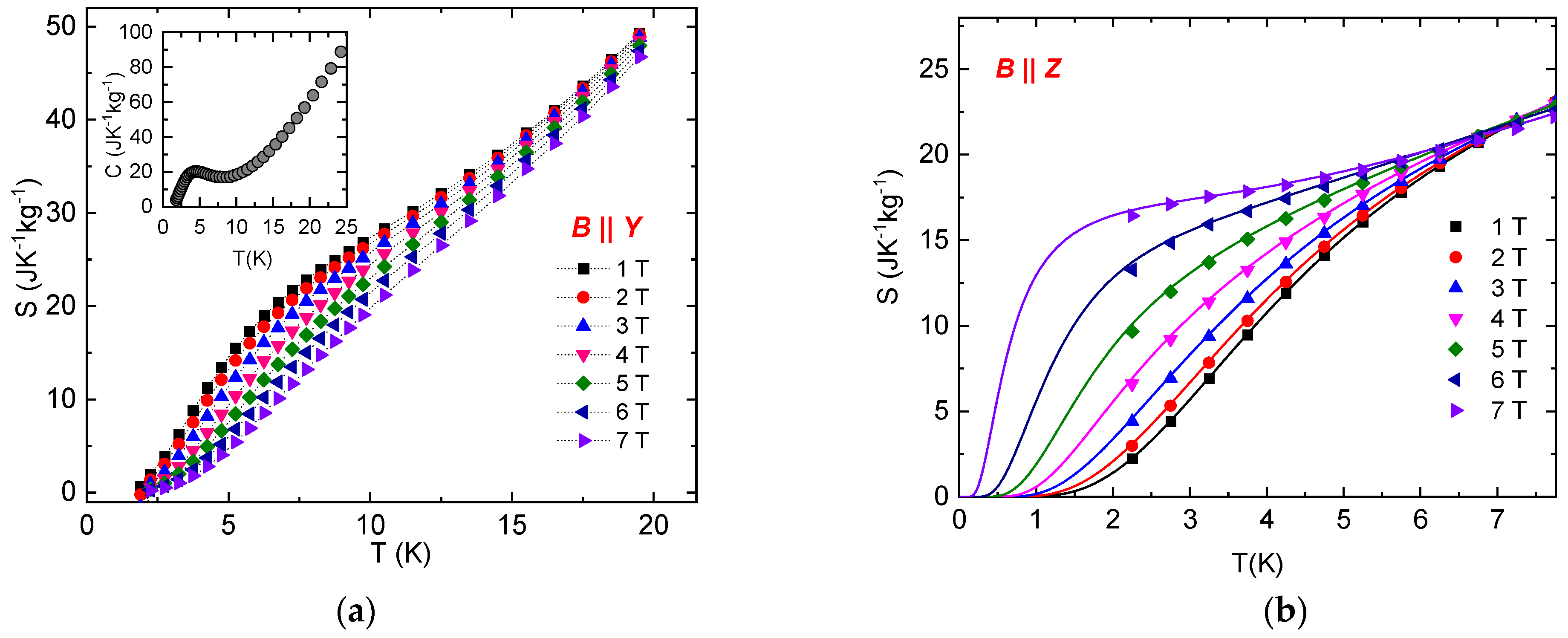
For the analysis of the magnetocaloric effect of the system NEHS in both mentioned orientations, the magnetic entropy change was calculated using the Maxwell relation [49]:
where ΔB = Bi − Bf, while Bf and Bi stand for the final and initial magnetic fields, respectively. Due to the real conditions of the experiment, relation (1) can be replaced by:
where Mj+1 and Mj are the magnetization values measured in the magnetic field B at temperatures Tj+1 and Tj, respectively. The temperature dependence of the magnetic entropy change (Equation (2)) calculated for several Bf values and Bi = 0 T for the orientations B || Y and B || Z is shown in Figure 4. It can be seen that the normal MCE has been observed for the orientation B || Y in a whole range of temperatures and magnetic fields. The maximum value of –ΔSM is shifted towards high temperatures with increasing magnetic fields. A large magnetocaloric effect is observed around 6 K (−ΔSmax = 10.9 Jkg−1K−1 for 7 T). However, an interesting situation is observed in the temperature dependence of –ΔSM for the orientation B || Z. Approximately below 7 K, an inverse magnetocaloric effect is observed for all magnetic field values, with −ΔSM decreasing with increasing magnetic field. On the other hand, the temperature dependence of −ΔSM above 7 K has a similar tendency as the data in the orientation B || Y. Large inverse magnetocaloric effect is observed around 2 K (−ΔSmax = −14.5 Jkg−1K−1 for 7 T). Further analysis of the experimental data was performed using the model of the S = 1 paramagnet, including single-ion anisotropy with D/kB = 11.6 K, E/D = 0.1, and g = 2.16 as obtained from the previous analysis of specific heat and susceptibility [32]. Corresponding theoretical prediction of the temperature dependence of −ΔSM for both field orientations is in excellent agreement with experimental data (Figure 4).
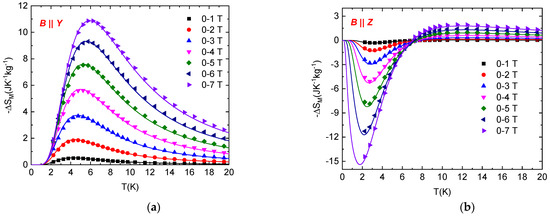
Figure 4.
Temperature dependence of the isothermal entropy change in NEHS at different magnetic fields for B || Y (a) and B || Z (b). Symbols represent –ΔSM values obtained from experimental magnetization curves; solid lines represent –ΔSM values calculated for the S = 1 paramagnet with E/D = 0.1, D/kB = 11.6 K and g = 2.16.
Figure 4.
Temperature dependence of the isothermal entropy change in NEHS at different magnetic fields for B || Y (a) and B || Z (b). Symbols represent –ΔSM values obtained from experimental magnetization curves; solid lines represent –ΔSM values calculated for the S = 1 paramagnet with E/D = 0.1, D/kB = 11.6 K and g = 2.16.
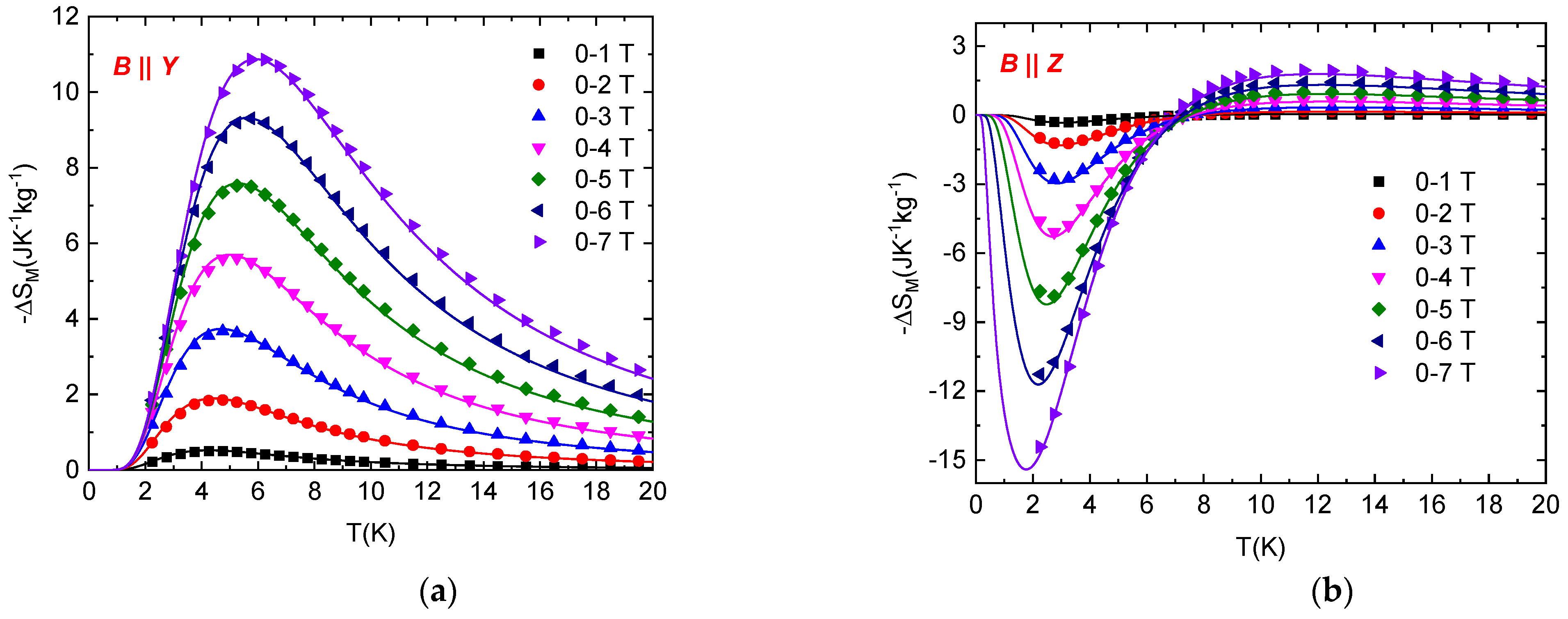
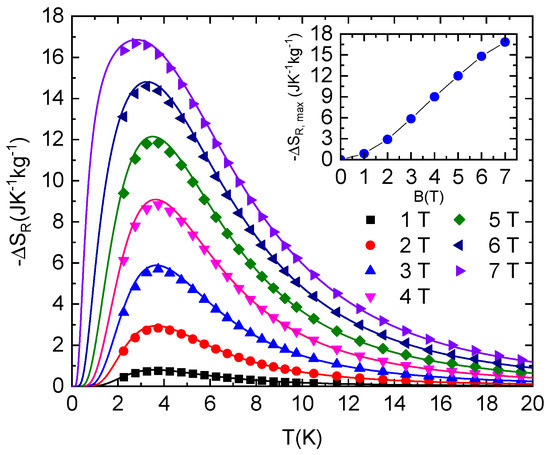
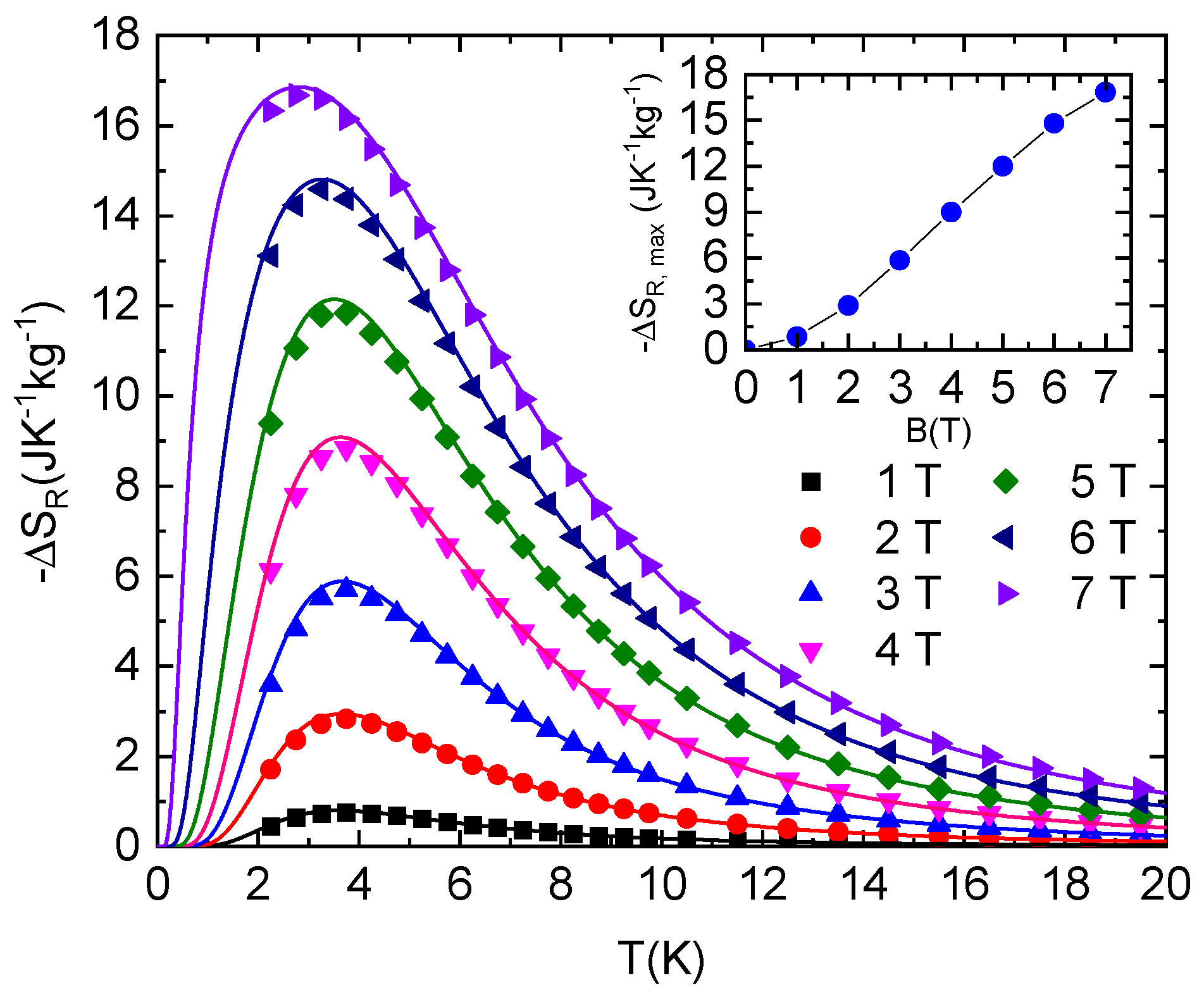
Figure 5.
Isothermal entropy changes resulting from the rotation of NEHS single crystal between the Y and Z axes in constant magnetic fields (symbols). Lines represent –ΔSR values calculated for the S = 1 paramagnet with E/D = 0.1, D/kB = 11.6 K and g = 2.16. Inset: Field dependence of −ΔSR,max.
Figure 5.
Isothermal entropy changes resulting from the rotation of NEHS single crystal between the Y and Z axes in constant magnetic fields (symbols). Lines represent –ΔSR values calculated for the S = 1 paramagnet with E/D = 0.1, D/kB = 11.6 K and g = 2.16. Inset: Field dependence of −ΔSR,max.
The isothermal rotational entropy change as a result of the isothermal rotation of NEHS single crystal in constant magnetic field from the initial sample position B || Z to the position B || Y yields from the relation:
The resulting isothermal rotational entropy change is shown in Figure 5. The maximal value of −ΔSR,max increases with increasing magnetic field and is shifted to lower temperatures. However, high values, −ΔSR ≈ 12 Jkg−1K−1 and −ΔSR ≈ 16.9 Jkg−1K−1, are achieved in 5 T and 7 T, respectively. It should be mentioned again that the temperature dependence of −ΔSR is in excellent agreement with the theoretical prediction.
The temperature dependence of the total (i.e., magnetic and lattice) entropy in NEHS was used for the calculation of the adiabatic temperature change −ΔTad,R, associated with sample rotation in constant magnetic field from the initial sample position B || Y to the position B || Z under adiabatic conditions. The total entropy in the zero magnetic field was calculated from the experimental specific heat data from Ref. [32]. The temperature dependence of the total entropy in different magnetic fields for both orientations was calculated as the difference between the total entropy of NEHS in zero magnetic field and the absolute values of ΔSM obtained from experimental magnetization curves (Figure 6). The unavailable experimental d of the total entropy in magnetic fields below 2 K for B || Z were approximated with the model of total entropy for the S = 1 paramagnet with E/D = 0.1, D/kB = 11.6 K, g = 2.16 with included lattice entropy of NEHS taken from Ref. [32]. It can be seen that the mentioned model perfectly describes the experimental d of the total entropy in magnetic fields for B || Z.
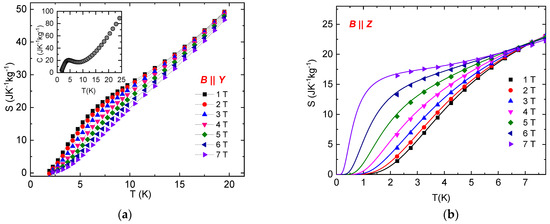
Figure 6.
Temperature dependence of the total (i.e., magnetic and lattice) entropy in NEHS at different magnetic fields for B || Y (a) and B || Z (b). Symbols represent the total entropy calculated as the difference between the total entropy of NEHS in zero magnetic field (calculated from the experimental specific heat) and the absolute values of ΔSM obtained from experimental magnetization curves. Lines represent the total entropy for the S = 1 paramagnet with E/D = 0.1, D/kB = 11.6 K, g = 2.16 with included lattice entropy of NEHS. Inset: Temperature dependence of specific heat of NEHS in zero magnetic field taken from Ref. [32].
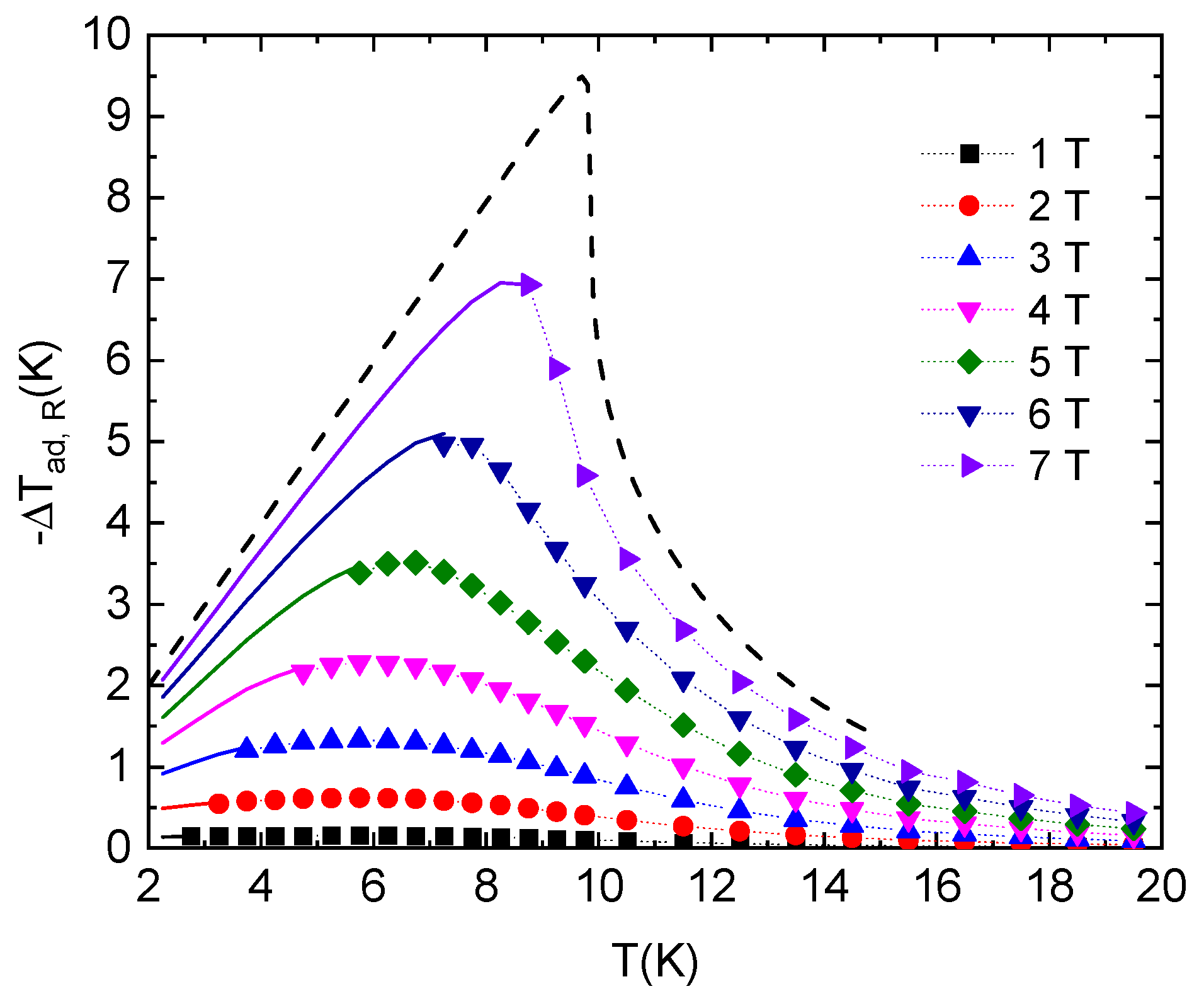
The temperature dependence of the adiabatic temperature change −ΔTad,R, calculated from the total entropy, is shown in Figure 7. The maximal value of −ΔTad,R is shifted to higher temperatures with an increasing magnetic field. Rotation of the crystal from position B || Y to position B || Z in 5 T and 7 T at the initial temperature of 6.5 K and 8.4 K leads to −ΔTad,R ≈ 3.55 K and 6.95 K, respectively. If the initial temperature of 4.2 K is considered, the rotation of the crystal in conditions mentioned above in 5 and 7 T leads to cooling of the samples to 1.4 K and 0.34 K, respectively, which suggests the applicability of this material in low-temperature refrigeration. Examples of conventional and rotational magnetocaloric properties of selected magnetic refrigerants compared with the studied system NEHS are given in Table 1. One can conclude that NEHS is not a very suitable material in conventional magnetocaloric applications; however, in rotational MCE it is competitive with expensive materials containing rare-earth metal ions.
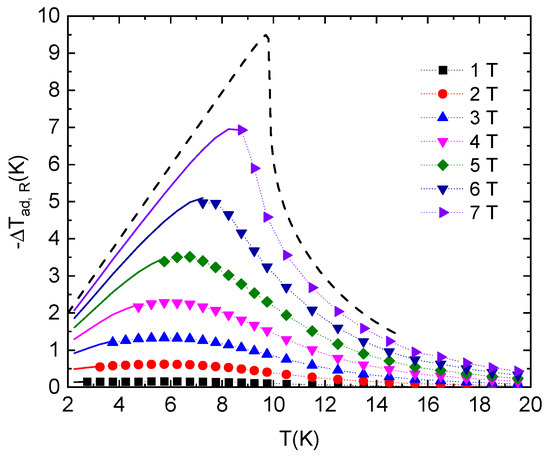
Figure 7.
Adiabatic temperature change as a function of the initial temperature, i.e., cooling NEHS single crystal during the adiabatic rotation from the position B || Y to the orientation B || Z in the constant magnetic fields (symbols). Lines represent the results of the extrapolation of total entropy data for orientation B || Z below 2 K. The dashed line represents the theoretical prediction of the adiabatic temperature change in the mentioned rotation conditions for NEHS single crystal in the critical magnetic field Bc (see text below).

Table 1.
Examples of conventional and rotational magnetocaloric properties of selected potential refrigerants.
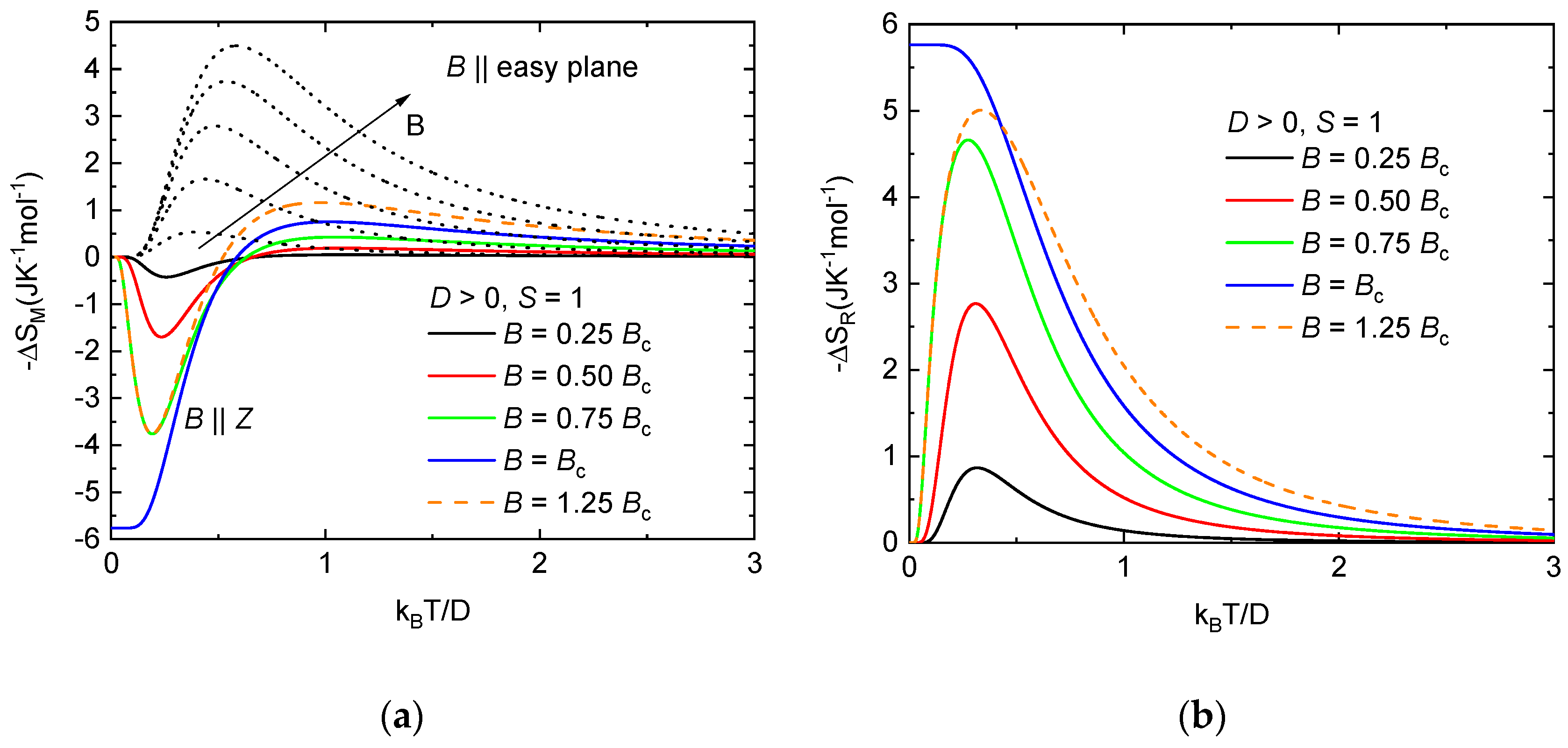
As already mentioned, the system NEHS was identified as a spin-1 paramagnet with the nonmagnetic ground state induced by the easy-plane anisotropy with D/kB = 11.6 K and E/D = 0.1. For this system, there is a critical value of the magnetic field Bc equal to when the energy levels cross, and the character of the ground state changes. For the description of the rotational magnetocaloric effect of the S = 1 paramagnet with easy-plane anisotropy, the temperature dependence of the isothermal entropy change was calculated for magnetic fields applied parallel and perpendicular to the easy plane. For simplicity, only parameter D was considered. It can be seen (Figure 8a) that the normal MCE is observed for orientation B || easy plane in the whole range of temperatures and magnetic fields. The maximum value of −ΔSM is shifted towards low temperatures with decreasing magnetic field. Different behavior is observed for magnetic fields parallel to the hard axis. For temperatures kBT/D < 0.5, an inverse magnetocaloric effect is observed for all considered magnetic field values, while the –ΔSM acquires the maximum value equal to ≈−5.76 Jmol−1K−1 in the critical magnetic field. However, the magnitude of the inverse magnetocaloric effect begins to decrease with magnetic fields above Bc at temperatures below kBT/D ≈ 0.5. Normal MCE is observed at temperatures above kBT/D ≈ 0.5 for all values of the magnetic field, while −ΔSM is larger with the increasing magnetic field. The resulting isothermal rotational entropy change for the mentioned model is shown in Figure 8b. The largest rotational MCE is observed in the critical magnetic field, −ΔSR ≈ 5.76 Jmol−1K−1, at temperatures below kBT/D ≈ 0.15. In higher magnetic fields exceeding Bc, the isothermal rotational entropy change decreases and the maximum of −ΔSR is shifted to higher temperatures.
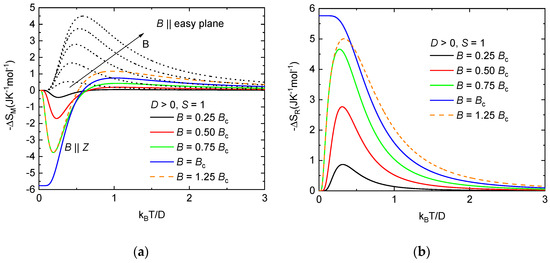
Figure 8.
(a)Temperature dependence of the isothermal entropy change for the S = 1 paramagnet with easy-plane anisotropy for B || easy plane (dotted lines) and B || Z (solid lines) at different magnetic fields; (b) isothermal entropy changes resulting from the rotation of S = 1 paramagnet with easy-plane anisotropy between the easy plane and hard axis in constant magnetic fields. The critical magnetic field Bc was calculated using relation Bc = D/(gμB).
The critical field for NEHS can be estimated as Bc ≈ 7.95 T. The theoretical prediction of the temperature dependence of the adiabatic temperature change −ΔTad,R for this magnetic field value was calculated, as depicted in Figure 7. Apparently, in the critical field the −ΔTad,R reaches a maximum at T = 9.7 K and −ΔTad,R ≈ 9.5 K. At liquid helium temperatures (i.e., the initial temperature of 4.2 K), the rotation leads to −ΔTad,R ≈ 4.18 K, suggesting the applicability of this material in low-temperature cooling at the critical magnetic field.
The aforementioned theoretical calculations show that the largest rotational magnetocaloric effect is observed at the critical magnetic field Bc. If Bc is equal to 1, 2, 3, 4, 5, or 6 T, the parameter D/kB must be equal to 1.45, 2.90, 4.35, 5.81, 7.26, and 8.71 K, respectively, to achieve a similar effect for spin-1 systems with easy-plane anisotropy (neglecting in-plane anisotropy parameter E).
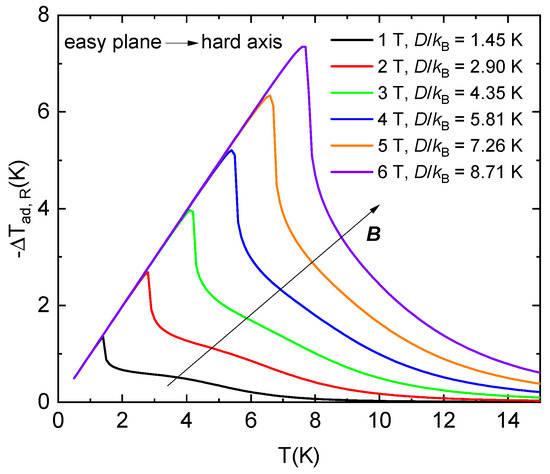
Figure 9.
Theoretical prediction of an adiabatic temperature change as a function of the initial temperature, i.e., cooling of the S = 1 paramagnet with the stated values of single-ion anisotropy and g = 2.16 during the adiabatic rotation from the easy plane to the hard axis in the constant critical magnetic fields. The lattice specific heat of NEHS was considered in the calculations.
Figure 9.
Theoretical prediction of an adiabatic temperature change as a function of the initial temperature, i.e., cooling of the S = 1 paramagnet with the stated values of single-ion anisotropy and g = 2.16 during the adiabatic rotation from the easy plane to the hard axis in the constant critical magnetic fields. The lattice specific heat of NEHS was considered in the calculations.
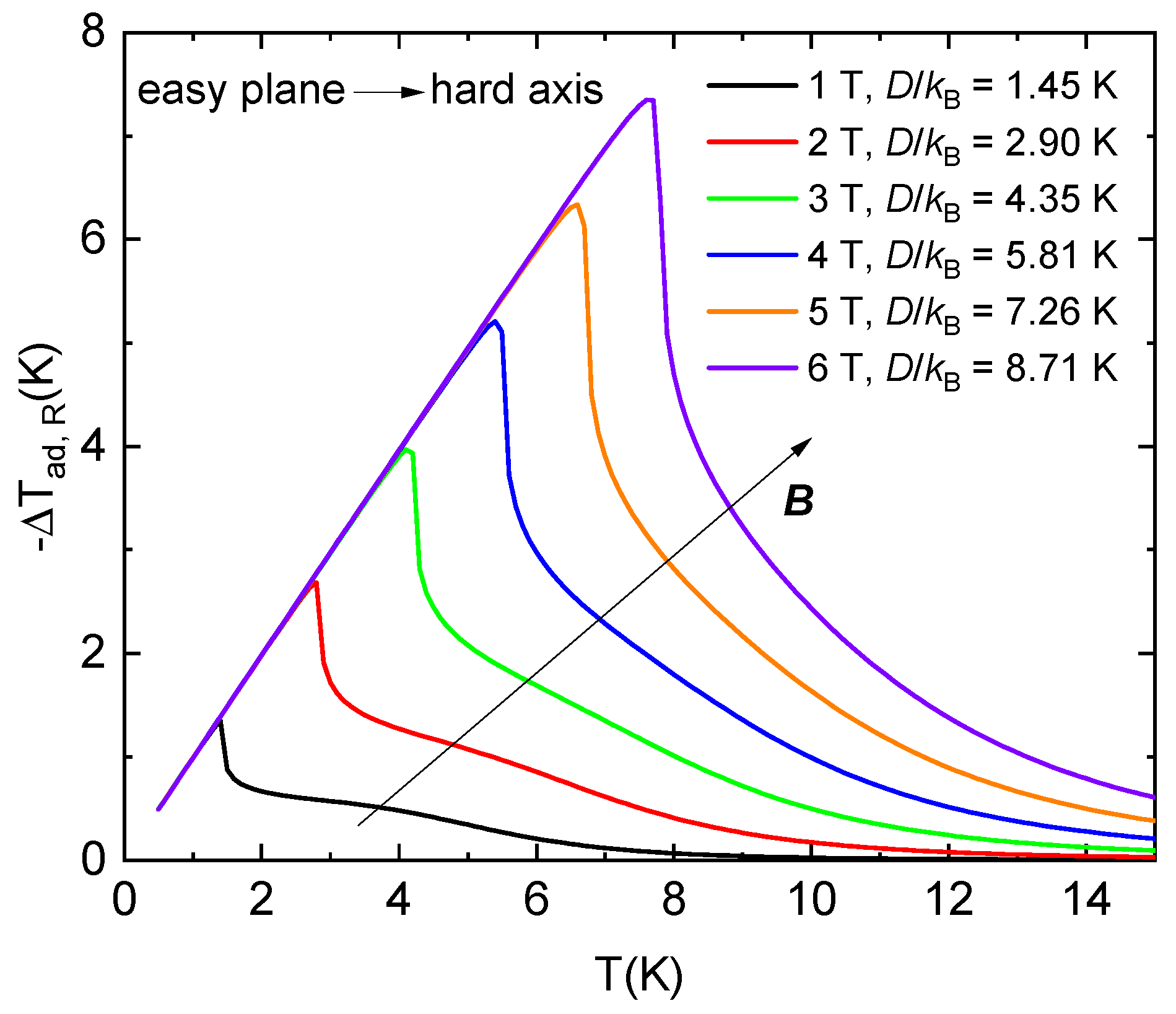
Suppose the considered systems have a lattice specific heat comparable to the NEHS system. In that case, it is possible to calculate the adiabatic temperature change as a function of the initial temperature during the rotation of a single crystal from the easy plane to the hard axis in adiabatic conditions in the mentioned critical magnetic fields (Figure 9). The maximal values of −ΔTad,R shift to higher temperatures with increasing critical magnetic fields, and the rotation leads to −ΔTad,R ≈ 4.18 K at an initial temperature of 4.2 K for critical magnetic fields higher than 3 T.
To date, the largest rotational MCE has been observed in the system of HoNiSi in the magnetic field 5 T, where −ΔSR = 26.7 Jkg−1K−1 [51]. Theoretical calculations show that the same value of rotational magnetic entropy change in the magnetic field of 5 T has a spin-1 magnet with a nonmagnetic ground state introduced by easy-plane anisotropy with D/kB = 7.26 K and with a molecular mass of 215.73 g.mol−1. Such theoretical estimates could help find financially affordable S = 1 Ni(II)-based systems with better magnetocaloric properties than materials containing rare-earth elements in their chemical structures.
4. Conclusions
This work presents an experimental study of the rotational magnetocaloric effect in Ni(en)(H2O)4SO4∙2H2O single crystal at temperatures above 2 K, associated with adiabatic crystal rotation between the easy plane and hard axis in magnetic fields up to 7 T. The magnetocaloric properties of the studied system were investigated by isothermal magnetization measurement. The experimental observations were completed with ab initio calculations of the anisotropy parameters. The calculations enabled determination of the single-ion anisotropy parameters together with the orientations of local anisotropy axes of Ni(II) ions. The calculated values of the single-ion anisotropy parameters are in excellent agreement with the values obtained from previous analysis of heat capacity. A large rotational magnetic entropy change ≈12 Jkg−1K−1 and ≈16.9 Jkg−1K−1 was achieved in 5 and 7 T, respectively.
The present study reveals that adiabatic rotation of the crystal in 7 T starting at the initial temperature of 4.2 K leads to the cooling of the sample down to 0.34 K, which suggests a possible application of this material in low-temperature refrigeration.
Finally, our simulations show that S = 1 Ni(II)-based systems with easy-plane anisotropy can have better rotational magnetocaloric properties than costly materials containing rare-earth elements in their chemical structures.
Author Contributions
Conceptualization, R.T. and P.D.; Investigation, R.T., P.D. and V.T.; software, E.Č.; Writing—Original Draft Preparation, R.T.; Writing—Review and Editing, V.T., E.Č., A.O. and M.O.; Visualization, R.T. and P.D.; Funding Acquisition, M.O. and A.F. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Slovak Research and Development Agency Projects numbers APVV-18-0197, APVV-14-0073, and APVV-SK-BY-RD-19-0008 and VEGA Grants No. 1/0426/19, 1/0132/22 of the Scientific Grant Agency of the Ministry of Education, Science, Research and Sport of the Slovak Republic.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All the data needed to evaluate the conclusions are presented in this paper.
Acknowledgments
Material support from U.S. Steel Košice s.r.o. is greatly acknowledged.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Spichkin, Y.I.; Zvezdin, A.K.; Gubin, S.P.; Mischenko, A.S.; Tishin, A.M. Magnetic Molecular Clusters as Promising Materials for Refrigeration in Low-Temperature Regions. J. Phys. D Appl. Phys. 2001, 34, 1162–1166. [Google Scholar] [CrossRef]
- Sessoli, R. Chilling with Magnetic Molecules. Angew. Chem.-Int. Ed. 2012, 51, 43–45. [Google Scholar] [CrossRef] [PubMed]
- Tegus, O.; Brück, E.; Buschow, K.H.J.; de Boer, F.R. Transition-Metal-Based Magnetic Refrigerants for Room-Temperature Applications. Nature 2002, 415, 150–152. [Google Scholar] [CrossRef]
- Pecharsky, V.K.; Gschneidner, K.A. Magnetocaloric Effect and Magnetic Refrigeration. J. Magn. Magn. Mater. 1999, 200, 44–56. [Google Scholar] [CrossRef]
- Barclay, J.A.; Steyert, W.A. Materials for Magnetic Refrigeration between 2 K and 20 K. Cryogenics 1982, 22, 73–80. [Google Scholar] [CrossRef]
- Kuz’min, M.D.; Tishini, A.M. Magnetic Refrigerants for the 4.2-20 k Region: Garnets or Perovskites? J. Phys. D Appl. Phys. 1991, 24, 2039–2044. [Google Scholar] [CrossRef]
- Franco, V.; Blázquez, J.S.; Ipus, J.J.; Law, J.Y.; Moreno-Ramírez, L.M.; Conde, A. Magnetocaloric Effect: From Materials Research to Refrigeration Devices. Prog. Mater. Sci. 2018, 93, 112–232. [Google Scholar] [CrossRef]
- Pęczkowski, P.; Łuszczek, M.; Szostak, E.; Muniraju, N.K.C.; Krztoń-Maziopa, A.; Gondek, Ł. Superconductivity and Appearance of Negative Magnetocaloric Effect in Ba1–XKxBiO3 Perovskites, doped by Y, La and Pr. Acta Mater. 2022, 222, 117437. [Google Scholar] [CrossRef]
- Alahmer, A.; Al-Amayreh, M.; Mostafa, A.O.; Al-Dabbas, M.; Rezk, H. Magnetic Refrigeration Design Technologies: State of the Art and General Perspectives. Energies 2021, 14, 4662. [Google Scholar] [CrossRef]
- Tishin, A.M.; Spichkin, Y.I. The Magnetocaloric Effect and Its Applications; CRC Press: Boca Raton, FL, USA, 2003; p. 475. [Google Scholar]
- Shen, B.G.; Sun, J.R.; Hu, F.X.; Zhang, H.W.; Cheng, Z.H. Recent Progress in Exploring Magnetocaloric Materials. Adv. Mater. 2009, 21, 4545–4564. [Google Scholar] [CrossRef]
- Langley, S.K.; Chilton, N.F.; Moubaraki, B.; Hooper, T.; Brechin, E.K.; Evangelisti, M.; Murray, K.S. Molecular Coolers: The Case for [CuII5GdIII4]. Chem. Sci. 2011, 2, 1166–1169. [Google Scholar] [CrossRef]
- Franco, V.; Conde, A. Scaling Laws for the Magnetocaloric Effect in Second Order Phase Transitions: From Physics to Applications for the Characterization of Materials. Int. J. Refrig. 2010, 33, 465–473. [Google Scholar] [CrossRef]
- Honecker, A.; Wessel, S. Magnetocaloric Effect in Quantum Spin-s Chains. Condens. Matter Phys. 2009, 12, 399–410. [Google Scholar] [CrossRef][Green Version]
- Wu, Y.D.; Qin, Y.L.; Ma, X.H.; Li, R.W.; Wei, Y.Y.; Zi, Z.F. Large Rotating Magnetocaloric Effect at Low Magnetic Fields in the Ising-like Antiferromagnet DyScO3 Single Crystal. J. Alloy. Compd. 2019, 777, 673–678. [Google Scholar] [CrossRef]
- Ruan, M.Y.; Li, Y.H.; Wang, L.; Ouyang, Z.W.; Chen, H.S.; Zheng, Y.Z. Large Rotational Magnetocaloric Effect in GdVO4 Single Crystal. Solid State Commun. 2020, 320, 114018. [Google Scholar] [CrossRef]
- Balli, M.; Jandl, S.; Fournier, P.; Dimitrov, D.Z. Giant Rotating Magnetocaloric Effect at Low Magnetic Fields in Multiferroic TbMn2O5 Single Crystals. Appl. Phys. Lett. 2016, 108, 102401. [Google Scholar] [CrossRef]
- Balli, M.; Jandl, S.; Fournier, P.; Gospodinov, M.M. Anisotropy-Enhanced Giant Reversible Rotating Magnetocaloric Effect in HoMn2O5 Single Crystals. Appl. Phys. Lett. 2014, 104, 232402. [Google Scholar] [CrossRef]
- Balli, M.; Mansouri, S.; Jandl, S.; Fournier, P.; Dimitrov, D.Z. Large Rotating Magnetocaloric Effect in the Orthorhombic DyMnO3 Single Crystal. Solid State Commun. 2016, 239, 9–13. [Google Scholar] [CrossRef]
- Balli, M.; Jandl, S.; Fournier, P.; Vermette, J.; Dimitrov, D.Z. Unusual Rotating Magnetocaloric Effect in the Hexagonal ErMnO3 Single Crystal. Phys. Rev. B 2018, 98, 184414. [Google Scholar] [CrossRef]
- Moon, J.Y.; Kim, M.K.; Oh, D.G.; Kim, J.H.; Shin, H.J.; Choi, Y.J.; Lee, N. Anisotropic Magnetic Properties and Giant Rotating Magnetocaloric Effect in Double-Perovskite T B2CoMnO6. Phys. Rev. B 2018, 98, 174424. [Google Scholar] [CrossRef]
- Jia, Y.; Namiki, T.; Kasai, S.; Li, L.; Nishimura, K. Magnetic Anisotropy and Large Low Field Rotating Magnetocaloric Effect in NdGa Single Crystal. J. Alloy. Compd. 2018, 757, 44–48. [Google Scholar] [CrossRef]
- Zhao, X.; Zheng, X.; Qi, J.; Luo, X.; Ma, S.; Rehman, S.U.; Ren, W.; Chen, C.; Zhong, Z. Anisotropic Magnetocaloric Effect and Magnetoresistance in Antiferromagnetic HoNiGe3 Single Crystal. Intermetallics 2021, 138, 107307. [Google Scholar] [CrossRef]
- Orendáč, M.; Gabáni, S.; Gažo, E.; Pristáš, G.; Shitsevalova, N.; Siemensmeyer, K.; Flachbart, K. Rotating Magnetocaloric Effect and Unusual Magnetic Features in Metallic Strongly Anisotropic Geometrically Frustrated TmB4. Sci. Rep. 2018, 8, 10933. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Li, Y.; Liu, E.; Ke, Y.; Jin, J.; Long, Y.; Shen, B. Giant Rotating Magnetocaloric Effect Induced by Highly Texturing in Polycrystalline DyNiSi Compound. Sci. Rep. 2015, 5, 11929. [Google Scholar] [CrossRef] [PubMed]
- Tkáč, V.; Orendáčová, A.; Čižmár, E.; Orendáč, M.; Feher, A.; Anders, A.G. Giant Reversible Rotating Cryomagnetocaloric Effect in KEr(MoO4)2 Induced by a Crystal-Field Anisotropy. Phys. Rev. B—Condens. Matter Mater. Phys. 2015, 92, 024406. [Google Scholar] [CrossRef]
- Tarasenko, R.; Tkáč, V.; Orendáčová, A.; Orendáč, M.; Feher, A. Experimental Study of the Rotational Magnetocaloric Effect in KTm(MoO4)2. Phys. B Condens. Matter 2018, 538, 116–119. [Google Scholar] [CrossRef]
- Tarasenko, R.; Orendáčová, A.; Čižmár, E.; Orendáč, M.; Potočňák, I.; Feher, A. Experimental Study of the Magnetocaloric Effect in Ni(en)(H2O)4SO4·2H2O—An S = 1 Molecular Magnet with Easy-Plane Anisotropy. Acta Phys. Pol. A 2017, 131, 904–906. [Google Scholar] [CrossRef]
- Ráczová, K.; Cižmár, E.; Feher, A. Magnetocaloric Effect in NiCl2(bipy) at Low Temperatures. Acta Phys. Pol. A 2017, 131, 922–924. [Google Scholar] [CrossRef]
- Orendáč, M.; Tarasenko, R.; Tkáč, V.; Orendáčová, A.; Sechovský, V. Specific Heat Study of the Magnetocaloric Effect in the Haldane-Gap S=1 Spin-Chain Material [Ni(C2H8N2)2NO2](BF4). Phys. Rev. B 2017, 96, 094425. [Google Scholar] [CrossRef]
- Kokorina, E.E.; Medvedev, M.V. Inverse Magnetocaloric Effect in the Uniaxial Paramagnet with Non-Kramers Ions. Phys. Met. Metallogr. 2017, 118, 217–226. [Google Scholar] [CrossRef]
- Tarasenko, R.; Orendáčová, A.; Tibenská, K.; Potočňák, I.; Kajňaková, M.; Vlček, A.; Orendáč, M.; Feher, A. [Ni(en)(H2O)4][SO4]·2H2O—An S = 1 Molecular Magnet with Easy-Plane Anisotropy. Acta Phys. Pol. A 2008, 113, 481–484. [Google Scholar] [CrossRef]
- Healy, P.C.; Patrick, J.M.; White, A.H. Crystal Structure of Tetraaqua(Ethylenediamine)Nickel(II) Sulfate Dihydrate and of Tetraaqua(2,2′-bipyridyl)Nickel(II) Sulfate Dihydrate. Aust. J. Chem. 1984, 37, 921–928. [Google Scholar] [CrossRef]
- Neese, F.; Wennmohs, F.; Becker, U.; Riplinger, C. The ORCA Quantum Chemistry Program Package. J. Chem. Phys. 2020, 152, 224108. [Google Scholar] [CrossRef]
- Atanasov, M.; Ganyushin, D.; Pantazis, D.A.; Sivalingam, K.; Neese, F. Detailed Ab Initio First-Principles Study of the Magnetic Anisotropy in a Family of Trigonal Pyramidal Iron(II) Pyrrolide Complexes. Inorg. Chem. 2011, 50, 7460–7477. [Google Scholar] [CrossRef] [PubMed]
- Angeli, C.; Cimiraglia, R.; Evangelisti, S.; Leininger, T.; Malrieu, J.P. Introduction of N-Electron Valence States for Multireference Perturbation Theory. J. Chem. Phys. 2001, 114, 10252. [Google Scholar] [CrossRef]
- Angeli, C.; Cimiraglia, R.; Malrieu, J.P. N-Electron Valence State Perturbation Theory: A Spinless Formulation and an Efficient Implementation of the Strongly Contracted and of the Partially Contracted Variants. J. Chem. Phys. 2002, 117, 9138. [Google Scholar] [CrossRef]
- Angeli, C.; Borini, S.; Cestari, M.; Cimiraglia, R. A Quasidegenerate Formulation of the Second Order N-Electron Valence State Perturbation Theory Approach. J. Chem. Phys. 2004, 121, 4043. [Google Scholar] [CrossRef] [PubMed]
- Neese, F. Calculation of the Zero-Field Splitting Tensor on the Basis of Hybrid Density Functional and Hartree-Fock Theory. J. Chem. Phys. 2007, 127, 164112. [Google Scholar] [CrossRef] [PubMed]
- Ganyushin, D.; Neese, F. First-Principles Calculations of Zero-Field Splitting Parameters. J. Chem. Phys. 2006, 125, 024103. [Google Scholar] [CrossRef] [PubMed]
- Neese, F. Efficient and Accurate Approximations to the Molecular Spin-Orbit Coupling Operator and Their Use in Molecular g-Tensor Calculations. J. Chem. Phys. 2005, 122, 034107. [Google Scholar] [CrossRef]
- Maurice, R.; Bastardis, R.; de Graaf, C.; Suaud, N.; Mallah, T.; Guihéry, N. Universal Theoretical Approach to Extract Anisotropic Spin Hamiltonians. J. Chem. Theory Comput. 2009, 5, 2977–2984. [Google Scholar] [CrossRef] [PubMed]
- van Lenthe, E.; Baerends, E.J.; Snijders, J.G. Relativistic Regular Two-component Hamiltonians. J. Chem. Phys. 1998, 99, 4597. [Google Scholar] [CrossRef]
- van Wüllen, C. Molecular Density Functional Calculations in the Regular Relativistic Approximation: Method, Application to Coinage Metal Diatomics, Hydrides, Fluorides and Chlorides, and Comparison with First-Order Relativistic Calculations. J. Chem. Phys. 1998, 109, 392. [Google Scholar] [CrossRef]
- Schäfer, A.; Huber, C.; Ahlrichs, R. Fully Optimized Contracted Gaussian Basis Sets of Triple Zeta Valence Quality for Atoms Li to Kr. J. Chem. Phys. 1998, 100, 5829. [Google Scholar] [CrossRef]
- Neese, F.; Wennmohs, F.; Hansen, A.; Becker, U. Efficient, Approximate and Parallel Hartree–Fock and Hybrid DFT Calculations. A ‘Chain-of-Spheres’ Algorithm for the Hartree–Fock Exchange. Chem. Phys. 2009, 356, 98–109. [Google Scholar] [CrossRef]
- Weigend, F. Accurate Coulomb-Fitting Basis Sets for H to Rn. Phys. Chem. Chem. Phys. 2006, 8, 1057–1065. [Google Scholar] [CrossRef] [PubMed]
- Hellweg, A.; Hättig, C.; Höfener, S.; Klopper, W.; Hellweg, A.; Klopper, W.; Karlsruhe, F.; Hättig, C.; Höfener, S. Optimized Accurate Auxiliary Basis Sets for RI-MP2 and RI-CC2 Calculations for the Atoms Rb to Rn. Chem. Acc. 2007, 117, 587–597. [Google Scholar] [CrossRef]
- Gschneidner, A.; Pecharsky, V.K.; Tsokol, A.O. Recent Developments in Magnetocaloric Materials. Rep. Prog. Phys. 2005, 68, 1479–1539. [Google Scholar] [CrossRef]
- Wu, Y.D.; Duan, W.W.; Li, Q.Y.; Geng, W.; Zhang, C.; Lv, Q.Q.; He, L.; Chen, J.Q.; Hu, X.Y.; Qin, Y.L.; et al. Giant Conventional and Rotating Magnetocaloric Effects in TbScO3 Single Crystal. J. Alloy. Compd. 2022, 894, 162447. [Google Scholar] [CrossRef]
- Zhang, H.; Xing, C.; Zhou, H.; Zheng, X.; Miao, X.; He, L.; Chen, J.; Lu, H.; Liu, E.; Han, W.; et al. Giant Anisotropic Magnetocaloric Effect by Coherent Orientation of Crystallographic Texture and Rare-Earth Ion Moments in HoNiSi Ploycrystal. Acta Mater. 2020, 193, 210–220. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).