Abstract
The present article is a short overview of the theoretical modeling of spin transitions in polymetallic compounds. As distinguished from many insightful reviews on this topic, the present work is focused on the nature of cooperative interaction of the metal clusters in molecular crystals with emphasis at the physical role of molecular vibrations and phonons. The underlying model assumes that the cooperativity is triggered by phonons while the metal centers are coupled to molecular vibrations. It is demonstrated that the suggested model gives a satisfactory description of the observed spin transitions in mono-, bi- and tetranuclear compounds. In the framework of the described approach, we discuss the experimental data on spin crossover in the mononuclear [Fe(ptz)6](BF4)2, binuclear [{Fe(bt)(NCS)2}2bpym] and tetranuclear [Fe(tpa){N(CN)2}]4·(BF4)4·(H2O)2 compounds containing iron ions. The approach is also applied to the description of the charge-transfer-induced spin transition in the [{(Tp)Fe(CN)3}{Co-(PY5Me2)}](CF3SO3) complex.
1. Introduction
The term “spin transitions” joins two types of phenomena: spin crossover (SCO) [1] and charge-transfer-induced spin transitions [2] (CTIST). The phenomenon of SCO was discovered almost one hundred years ago [3,4] and refers to the change of the ground spin state of transition metal ions with the electronic configuration from the low-spin (ls) state to the high spin (hs) one under action of temperature, light or external pressure (see review papers [1,5,6,7]). Last years, many works were devoted to binuclear [8,9,10,11], trinuclear [12,13,14] and tetranuclear [15,16,17,18,19] iron(II) SCO systems. SCO can take place if the molecular unit of a crystal cell has at least one ion with the electronic configuration and closely spaced low-spin (ls) and high-spin (hs) levels of this ion.
In the case of CTIST, two ions, a donor and an acceptor of an electron, are involved in the spin transition. However, in most cases the donor ion possessing a carbon or a mixed carbon–nitrogen surrounding with a predominant number of carbons or at least with a half number of carbons in the first coordination sphere, which create a strong crystal field, acquires a higher oxidation degree, and its spin changes on ½, while the ion, surrounded by nitrogen atoms (intermediate crystal field) and accepting the electron, undergoes a transition from its ls state to the hs one (see review [20]).
In the field of SCO, the study started from mononuclear systems and then passed to polynuclear ones, while CTIST was first observed in the Prussian blue analogue of K0.14Co[Fe(CN)6]0.71·4.93H2O stoichiometry [2]. Then a series of low-dimensional Fe/Co cyanide complexes demonstrating thermally or photo-induced metal to metal electron transfer was reported [21,22,23]. As an example of Fe/Co complexes, the dinuclear cyanide-bridged [{(Tp)Fe(CN)3}{Co-(PY5Me2)}](CF3SO3)·2DMF complex is to be mentioned [24].
The pioneering idea of the coupling of the SCO ions via phonon field as a source of cooperativity was first proposed by Sasaki and Kambara [25,26]. The vibrational spectra of molecular crystals contain along the phonons (interrelated to intermolecular vibrations) the distinct branches of localized (molecular) vibrations directly coupled to the electronic shells of SCO ions. This circumstance essentially complicates the theory of cooperative phenomena, but the development of a more common model represents an emerging challenge and, as we will demonstrate, gives new physical results. Spin transitions induced by electron transfer in SCO and CTIST cases, can be described in the frames of the unique approach [27,28,29,30] that takes into account both molecular vibrations and phonons. These branches of the whole vibrational spectrum of molecular crystal play essentially different physical roles in SCO transitions. While molecular vibrations form the energy pattern, the cooperativity in the whole crystal is assured by the electron–phonon interaction. An imaginative classical picture (Figure 1) describing the interactions responsible for spin transitions in molecular crystals can be presented by two types of springs with different force constants: the stiffer spring corresponds to the coupling of the ions with molecular vibrations, while the softer one describes the cooperative interaction through acoustic modes between the structural units undergoing the spin transition [27].
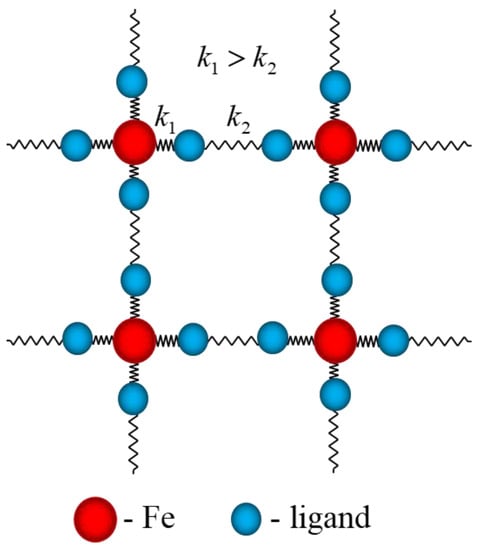
Figure 1.
Schematic image of molecular SCO crystals: the elastic interactions in the crystal corresponding to intra- and intermolecular vibrations are represented by springs with different rigidity and .
A concise description of the abovementioned approach [27,28,29,30] and its applications to different systems with labile electronic states is one of the aims of the present mini-review, that focuses on the possible types of spin transitions in mono-, di- and tetranuclear SCO iron(II) systems and in binuclear Fe–Co compounds demonstrating CTIST [24].
2. Background of the Model
The examination of spin crossover in mono-, bi- and tetranuclear iron(II) compounds [9,17,31] as well as of CTIST in the dinuclear cyanide-bridged [{(Tp)Fe(CN)3}{Co-(PY5Me2)}] (CF3SO3)·2DMF complex [24] is based on the abovementioned approach recently elaborated in Refs. [27,28,29,30]. The quintessence of this approach consists of the following. The systems demonstrating spin transitions represent molecular crystals. In these crystals, one can distinguish two types of vibrations playing different physical roles in the phenomenon of spin transitions: molecular modes that are localized and confined by the metal ion strongly coupled to its ligand surrounding and phonons that are interrelated with the relatively weak intermolecular interactions and therefore spread out over the crystal lattice. The interaction of the SCO ion with the molecular modes is dominant, because in molecular crystals, the intermolecular interactions are very weak as compared to the intramolecular ones and their thermal modulation can mainly give rise to the coupling with small energy acoustic long-wave vibrations. Thus, one can assume that the molecular vibrations are weakly disturbed by the vibrations arising from the interactions which unite the molecules in the crystal, and the ligands of the iron(II) ions in spin crossover compounds or of the Co-ion in the compound demonstrating CTIST participate both in the molecular and crystalline displacements. The symmetry adapted coordinates of the ligand surrounding can be represented as the normalized linear superposition of the coordinates of molecular (first term) and crystalline (second term) vibrations:
The dimensionless parameter characterizes the weight of the phonon-induced displacements in the full vibrational coordinate and it is assumed to be small as compared with unity because normally the molecular vibrations are weakly disturbed by the intermolecular interactions in systems undergoing spin transitions. The representation of the configurational coordinate in this form was suggested by Hizhnyakov et al. [32,33,34] and applied to the problems of relaxation in Jahn–Teller centers and resonance Raman scattering. In Equation (1), is the coordinate of the molecular full-symmetric (A1) mode for the j-th iron ion in n-th SCO complex, the index j = 1, 1−2, 1–4 for mono-, bi- and tetranuclear SCO Fe(II) compounds, for the Co ion in the n-th Fe–Co complex is the position vector of the Co ion, in this case j = 1 and the coordinate refers to the molecular full-symmetric (A1) mode of the cobalt ion. in Equation (1) represent the dimensionless vibrational coordinates of the phonons with the frequencies , is the phonon wave vector, the symbol denotes the branch of the phonon mode, and finally, is the number of ions or clusters in the crystal. The values
are known as Van Vleck coefficients, which perform the unitary transformation from the symmetry adapted displacements of the ligand surroundings to the normal coordinates of the phonons. Index k enumerates the ligands of the ion which occupies the position n, are the position vectors of these ligands, the coefficients describe the transformation from the Cartesian displacements to the full-symmetric coordinate, are the phonon polarization vectors, . The dimensionless parameter characterizes the weight of the phonon-induced displacements in the full vibrational coordinate.
3. Mononuclear Spin Crossover Systems
One can deduce (see details in Ref. [27]) that the Hamiltonian of electron–vibrational interaction for a crystal containing a single spin crossover ion in the unit cell includes both molecular and crystal vibrations:
where, and are the phonon creation and annihilation operators, the values are expressed in the matrix form [27]:
Here and are the dimensionless coordinates of the full-symmetric molecular vibrations in the hs and ls states of the SCO ion in the position n, and are the frequencies of molecular vibrations. The elements of the diagonal matrix are 1 and 0, while of 0 and 1 for the hs and ls states, correspondingly. The meaning of the parameter is determined by Equation (1).
The Hamiltonian of the crystal, containing mononuclear SCO units, looks as follows:
where the first two terms describe the free molecular vibrations in the ls and hs states and the coupling of the spin crossover ions with these vibrations, and are the constants characterizing this coupling, is the energy gap between the ground (ls) and excited (hs) crystal field terms of the SCO ion, the third term describes the free phonons and the last one the interaction of phonons with molecular modes (see Equation (3) and Ref. [27]).
The next step includes the shift transformation proposed by Kanamori [35] in the theory of cooperative Jahn–Teller effect [36] and further on developed by Kaplan and Vekhter [37]. This transformation excludes phonon variables and gives rise to the cooperative interaction of the centers derived in [27] and expressed by the following equation:
here the parameters (i = hs, ls), which enter in Equation (6), represent products of the electronic matrices and the coordinates of the full-symmetric molecular vibrations in the low- and high-spin states.
Then, the mean field approximation is applied in order to reduce the many-body problem to the single-site one (see details in Ref. [27]). The effective parameter of cooperative interaction is obtained as:
The expression (7) is derived, using the simplest dispersion law for the acoustic phonons and neglecting the difference between the longitudinal and transversal speeds of sound . Actually, Equation (7) connects the parameters of cooperative interaction with the intrinsic parameters of the crystal. Here are the metal–ligand distances in these states, is the maximal phonon frequency, c is the speed of sound. Parameter (introduced in Ref. [27]) can be evaluated from lattice dynamics simulation of molecular crystals [38].
Several sample calculations for mononuclear spin crossover systems have been performed [27] using the numerical values of the parameters for Fe(II) SCO compounds taken from the classical paper of Gütlich and coworkers [39]: , , = /Å2, /Å2, = 2.0 Å, = 2.2 Å, [39], [39] [31], and the constants of interaction with the molecular vibrations in the ls and hs states: , [27] expressed through the above given crystal field parameters and . It should be mentioned that the Debye frequency of the acoustic lattice vibrations was evaluated in [39] from their parabolic dependence on the wave vector in the center of the Brillouin zone. This frequency is small because it is interrelated with the relative displacements of heavy metal centers. With the aid of Equation (7), the ratio of the parameters of cooperative interactions was estimated as: :: = 1.59:1.26:1. It should also be noticed that the relation between the values of , , provides a possibility to vary only one of these parameters. The performed examination shows that mononuclear SCO compounds can demonstrate three types of spin transitions: gradual, abrupt and those accompanied by a hysteresis loop. Depending on the internal parameters of the system, these transitions can occur even in the room temperature range.
Finally, the model was applied to the description of spin crossover in the [Fe(ptz)6](BF4)2 compound. From Figure 2, one can see that the accepted model well describes the observed χT of [Fe(ptz)6](BF4)2 in the whole temperature interval, namely, the gradual increase of χT in the range 100–129 K, the hysteresis loop between 129 and 135 K and the slow growth above 135 K.
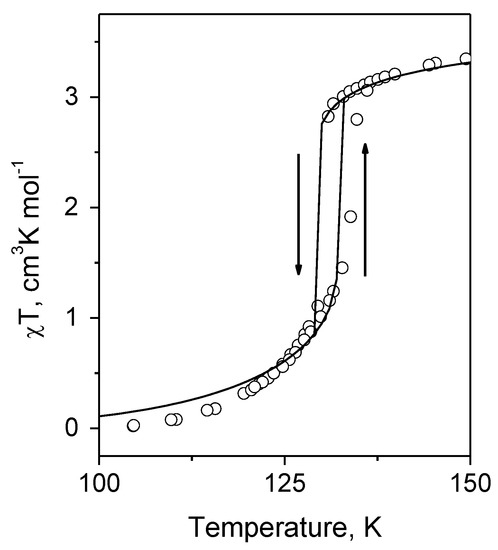
Figure 2.
χT vs. T dependence for the [Fe(ptz)6](BF4)2 crystal: circles—experimental data [31], solid line—theoretical curve calculated with Δhl = 460 cm−1, = 4.19 cm−1 and .
4. Binuclear Spin Crossover Systems
The summary of experimental results [8,9,10,11] (see refs in [28]) allows us to conclude that three types of spin transitions can occur in binuclear spin crossover systems: (i) gradual, abrupt or accompanied by a hysteresis loop transitions in which both ions pass simultaneously from the ls–ls state to the hs–hs one; (ii) two-step transitions with a plateau; (iii) two-step transitions with a hysteresis loop in one of the steps or displaying wide thermal hysteresis loops in the lower and the upper steps. Several earlier approaches for the description of the variety of spin transitions in binuclear systems are concisely discussed in Ref. [28]. The microscopic model of SCO in binuclear systems developed in [28] takes into account the vibrational spectra, intra- and intercluster interactions and describes all types of the observed spin transitions. The principal difference from the model for mononuclear SCO compounds is the account of the intracluster interactions in the three possible configurations of the dimer: (1) ls–ls; (2) ls–hs, hs–ls; (3) hs–hs.
The interaction Hamiltonian of the crystal containing binuclear clusters as structural units is obtained in the following form:
where , and i, j number the clusters in the crystal and the ions inside the cluster, respectively, the position of the i-th SCO ion in the -th cell is determined by the vector The first three terms in Equation (8) refer to the cooperative coupling, while the last term describes the Coulomb interaction of the ions inside each cluster, depending on the states of the cluster ions a and b three parameters , [9,28] are involved in the model. The notations in Equation (7) are the following: (ks = hs, ls; i = 1, 2), as in the case of mononuclear clusters, the diagonal matrices and of the dimension possess the non-vanishing matrix elements
where and numerate the hs and ls states, and are the dimensionless full-symmetric displacements of the nearest surrounding of the -th SCO ion in the -th cluster in the and states, respectively. Within the long wave approximation, the parameters do not depend on the indices and (Equation (8)). The total Hamiltonian contains the contribution of non-interacting clusters that in its turn includes the free molecular vibrations in the ls and hs states, the coupling of the SCO ions with these vibrations as well as the Hamiltonian of free phonons. Then the mean field approximation is applied [28]. The parameters of the cooperative interaction are assumed to obey the same relation :: = 1.59:1.26:1 as for mononuclear systems.
The model was applied to the description of the observed spin transformation in the [{Fe(bt)(NCS)2}2bpym] crystal (Figure 3) containing as a structural unit iron(II) dimers. The theoretical consideration reproduces the observed two-step transition. The experimental curve was described quite well using the following set of parameters: Δhl = 1540 cm−1, δ = 170 cm−1, = 9.08 cm−1, gav = 2.124 and the abovementioned ratio between the parameters , and . Since the observed product as a function of temperature does not tend to zero at T→0, it was assumed that initially some of the iron ions are in the hs state, the fraction of these ions was determined as y = 7.25% under the assumption that they are uniformly distributed between the binuclear clusters. The inset in Figure 2 shows the populations n0, n1 and n2 of cluster configurations with 0, 1 and 2 ions in the hs state. It is seen that up to T = 125 K, the main part of ions is in the ls state, the number of dimers with one ion in the hs state is quite low. In the range of temperatures in between 150–200 K the biggest is the number of clusters with one ion in the hs state. It is worth noting that the non-pronounced step in the temperature dependence of the product is observed, namely, in this range at about 175 K. At temperatures higher than 200 K, binuclear clusters with two hs ions dominate and are responsible for the second observed step in the thermal behavior of the χT product. At the same time, the number of clusters in which only one ion is in the hs state is a bit larger than the initial one at T < 100 K. The suggested model [28] of spin transitions in binuclear systems reproduces all observable types of these transitions and describes quite well the spin transformation in the [{Fe(bt)(NCS)2}2bpym] compound.
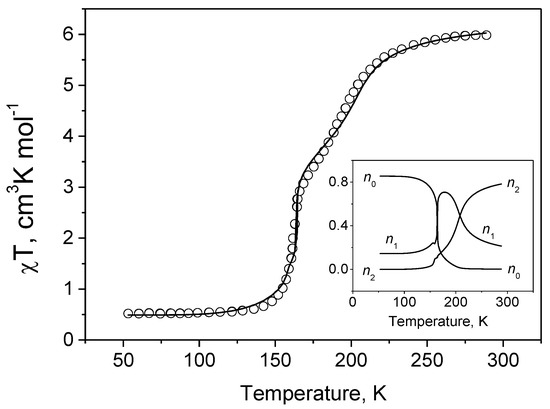
Figure 3.
χT vs. T dependence for the [{Fe(bt)(NCS)2}2bpym] crystal: symbols—experimental data [9], solid line—theoretical curve calculated with Δhl = 1540 cm−1, δ = 170 cm−1, = 9.08 cm−1 and gav = 2.124. The fraction of ions that do not participate in the spin transition and that are always in hs configuration is y = 7.25%. The inset is the thermal variation of the population of different cluster configurations (subscripts indicate the number of Fe ions in hs state).
5. Spin Crossover in Tetranuclear Systems
Recently, polynuclear SCO compounds have attracted attention because the variety of new types of intracluster interactions leads to interesting features in their magnetic behavior. Among the polynuclear SCO compounds the class of tetranuclear square Fe(II) complexes should be mentioned, since these systems demonstrate spectacular types of the temperature dependence of the hs fraction: (i) one-step transitions in which two ions located along the side of the square pass from the ls state to the hs one, while the other two ions remain in the hs state in the whole temperature range [15]; (ii) two-step transitions with the following order of configurations (4ls)→(3ls,1hs)→(2ls,2hs), in the latter configuration the ions in the same spin state are located along the diagonal of the square [40]; (iii) two-step transitions between 4 Fe ions in the ls state and all these ions in the hs state with the plateau between steps arising from the configuration with two ls and two hs ions also located along the diagonal of the square [17].
The previous models of spin transitions in polynuclear cluster systems are summarized in Ref. [29]. Two points in the model under discussion require changes in comparison with the consideration of mono- and binuclear clusters. These are the number of configurations with a different ratio of hs and ls ions and the number of intracluster interactions in the configurations, in which more ions are involved. The strengths of the intracluster interactions also depend on the geometrical structure of the cluster and number of participating SCO ions.
Possible distributions of the hs and ls ions and multiplicities of the corresponding configurations in a tetranuclear square are shown in Figure 4.
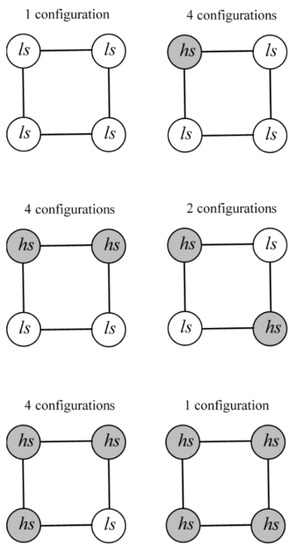
Figure 4.
Possible distributions of hs and ls ions in a tetranuclear square SCO cluster.
The total energies of the Coulomb interactions are denoted by , where symbols i, j denote the types of interacting ions (hs or ls) and the superscript l is used to discriminate location of the interacting ions (along the side (l = s) or the diagonal of the square (l = d)). For each electronic configuration the energies (fi = ls, hs) of intracluster interactions can be expressed in terms of the parameters . Due to intracluster interactions, the effective energy gap between the configurations ls-ls-ls-ls and hs-hs-hs-hs is determined as follows:
The energy shifts from the equidistant positions for other cluster configurations (with n = 1, 2 or 3 hs ions) can be found as
where the parameters , , and refer to the cluster configurations hs-ls-ls-ls, hs-hs-ls-ls, hs-ls-hs-ls and hs-hs-hs-ls, respectively. As can be seen the effect of intracluster interactions can be described in terms of the two parameters and . The energies of the system in the mean field approximation are given in Ref. [29].
For the tetranuclear systems, all 15 vibrational modes of the complex consisting of the iron ion and 6 surrounding nitrogen ligands are to be taken into account. The corresponding energies of these modes were taken from Ref. [41]. The energies of the full-symmetric vibrations obtained in [41] are 97 cm−1 and 151 cm−1 for the hs and ls configurations, respectively. The new frequencies employed in calculations led to the redetermination of the ratio between the parameters of cooperative interaction as compared with that employed above for mono- and binuclear spin crossover systems: :: 3.22:1.79:1. The system of self-consistent equations for the order parameters can be found in Ref. [29].
The account in the model of the interactions mentioned so far allows us to reproduce the observed types of nontrivial spin crossover behavior peculiar for tetranuclear systems. To demonstrate the efficiency of the model, we analyze the magnetic properties of the tetranuclear [Fe(tpa){N(CN)2}]4·(BF4)4·(H2O)2 compound. From Figure 5, it is seen that the model gives quite a good description of the experimental data with the set of parameters representing a part of the figure caption. The course of the spin transformation in this compound can be easily followed analyzing the temperature dependence of the populations of configurations with different number of iron(II) ions in the hs state. Up to 150 K, the majority of Fe4 clusters are in the ls state, that is confirmed by the plateau observed in the experimental curve in the range 100–160 K then the number of two hs ions situated along the diagonal of the square significantly increases and achieves its maximum value at about 250 K. Namely, this increase provokes the step in the temperature dependence of the effective magnetic moment μeff in the range 210–250 K. At temperatures higher than 325 K, clusters with 4 hs ions dominate. At the same time, in this temperature range there exists a non-negligible amount of clusters with two or three hs ions. Therefore, the observed effective magnetic moment does not achieve its maximum value corresponding to four iron(II) ions in the hs state. Here, it is worth noting that in polynuclear spin crossover compounds the interplay between the intra- and intercluster interactions plays a crucial role in the type and temperature of the spin transformation.
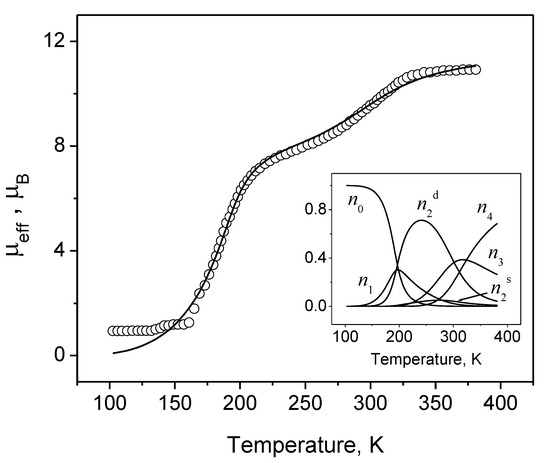
Figure 5.
μeff vs. T dependence for the [Fe(tpa){N(CN)2}]4·(BF4)4·(H2O)2: symbols—experimental data [17], solid line—theoretical curve calculated with Δhl = 5800 cm−1, δs = 280 cm−1, δd = −320 cm−1, = 2.46 cm−1 and gav = 2.37. The inset shows the thermal variation of the populations of different cluster configurations.
6. Charge-Transfer-Induced Spin Transition in Binuclear {Fe(μ − CN)Co} Complexes
Photochemically induced metal-to-metal CTIST of diamagnetic ls-FeII−CN−ls-CoIII units into paramagnetic ls-FeIII–CN–hs-CoII ones was observed in the Prussian Blue analogue (PBA) of K0.14Co[Fe(CN)6]0.71·4.93H2O stoichiometry [2]. In the present section, it is demonstrated how the approach above, applied to mono-, bi- and tetranuclear spin crossover systems, can be generalized to the case of molecular crystals comprising as a structural unit binuclear cyanide-bridged iron-cobalt systems exhibiting CTIST. As an example, the spin transformation in the [{(Tp)Fe(CN)3}{Co-(PY5Me2)}](CF3SO3) [24] compound is discussed.
The model suggested in Ref. [30] takes into account the vibronic coupling as it was described in previous sections and the following two configurations: (I) ls-CoIII−ls-FeII and (II) hs-CoII−ls-FeIII. The following states were taken into consideration: the ground non-degenerate state arising from the ls-CoIII−ls-FeII configuration and two groups of excited states. The first group of excited states, formed by the direct product of two ground Kramers doublets belonging to the ls-FeIII and hs-CoII ions, has the degeneracy = 4 and it is separated from the ground ls-CoIII−ls-FeII state by the energy gap . The second group of the cluster excited states arising from the ground Kramers doublet of the ls-FeIII ion and the quadruplet of the hs-CoII ion possesses the energy and the degeneracy = 8, where the parameter of spin–orbit coupling is about −180 cm−1 for the hs-CoII ion. The magnetic exchange interaction is omitted. Only the ground Kramers doublet of the ls-FeIII ion is taken into account because the excited quadruplet of this ion is much higher in energy due to large spin–orbital coupling, = −486 cm−1 [42].
From the structural and magnetic data on the [{(Tp)Fe(CN)3}{Co-(PY5Me2)}](CF3SO3) compound [24] it follows that with temperature rise, the Fe–ligand distances are almost constant in the whole temperature range, while the first coordination sphere of Co ion significantly increases with temperature. From this, it follows that the transformation ls-CoIII hs-CoII assures the cooperativity of the transition. Correspondingly, in the model there are taken into consideration the single state arising from configuration ls-CoIII−ls-FeII and 12 above mentioned states of the hs-CoII–ls-FeIII configuration. Further on, these configurations will be referred to as the ls and hs ones, respectively. The problem is solved in the mean field approximation (see Ref. [30]).
In the numerical calculations, the following values of the parameters were employed: = 420 cm−1 [30], = 2408 cm−1 [30], = 390 cm−1 [43], = 200 cm−1 [39], = 92 cm−1, = 108 cm−1 [30]. The procedure of the calculation of the vibronic coupling constants and is described in detail in Ref. [30]. The parameters and are evaluated with the use of Equation (7). The Debye frequency is calculated as [44]:
where Ω0 is the unit cell volume and c is the speed of sound. For Ω0 = 5126.3 Å3 [24] and c = 2 × 105 cm/s one obtains = 24 cm−1 [30]. It is seen that the Debye frequency calculated in this way is practically the same as that presented in [39] and used above for the description of SCO Fe(II) complexes. One easily finds the following ratio between the parameters of cooperative interaction : = 1.549:1.245:1. This relation allows us to use only one fitting parameter instead of three independent parameters. A weak exchange interaction through the cyanide bridge in the pair − can be neglected.
Within the framework of the developed model [30], the analysis of the magnetic properties of the [{(Tp)Fe(CN)3}{Co-(PY5Me2)}](CF3SO3) compound [24] is performed. Since at very low temperatures the observed χT product has a non-vanishing value, it means that from the very beginning a part of binuclear complexes is in the ls-FeIII−hs-CoII state. Therefore, the χT product is calculated as , where the hs fraction = and describes the magnetic behavior of the ls-FeIII−hs-CoII complex. The exchange interaction of the ls-FeIII and hs-CoII ions is neglected; therefore, the magnetic susceptibility of the hs fraction can be presented as a sum of the susceptibilities of the ls-FeIII and hs-CoII ions. Here, it should be mentioned that for the correct description of the magnetic behavior of the compound under examination it is necessary to take into consideration the excited energy levels for both the ls-FeIII and the hs-CoII ions neglected at the previous stage. For example, the mixing of the ground Kramers doublet of the ls-FeIII ion with the excited quadruplet by the external magnetic field results in the temperature independent paramagnetism significant for the correct interpretation of the magnetic behavior. The detailed description of this procedure can be found in Ref. [30].
Finally, the elaborated model is applied to the explication of CTIST which takes place in the [{(Tp)Fe(CN)3}{Co-(PY5Me2)}](CF3SO3) complex (Figure 6).
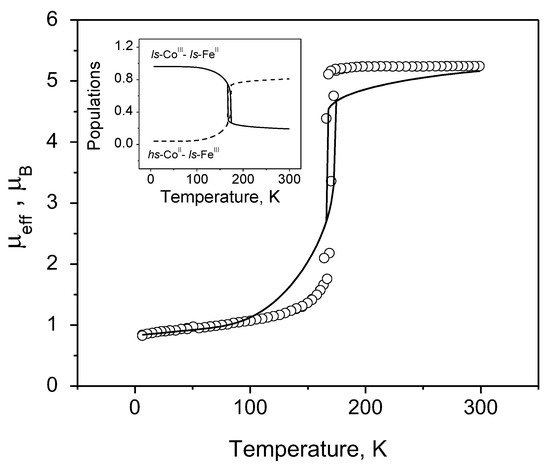
Figure 6.
μeff vs. T dependence for the [{(Tp)Fe(CN)3}{Co-(PY5Me2)}](CF3SO3) complex: symbols—experimental data [24], solid line—theoretical curve calculated with Δhl = 410 cm−1, = 1.435 cm−1 and yhs = 4.0%. The inset is the thermal variation of the population of different complex configurations.
It is seen that the model describes quite well all the characteristic features of the observed curve and, namely, the width of observed hysteresis loop and the position of this loop in the temperature scale, the plateau at temperatures higher than 175 K, the slow increase in the effective magnetic moment in the range of 4–150 K as well as the relative number of clusters that are initially in the hs state. A good coincidence is observed between the calculated and observed [24] values of the effective magnetic moment. The inset in Figure 6 provides information about the populations of the configurations involved in the transformation in the wide temperature range.
7. Concluding Remarks
We have presented a short overview of the theoretical modeling of spin transitions in polymetallic compounds. The emphasis is made on the two main issues: (1) the problem of cooperative interaction of the metal clusters in crystal via phonons coupled to molecular vibrations, and (2) discussion of the origin, basic interactions and main peculiarities of spin transitions in polynuclear compounds in the crystalline phase for which the molecular vibrations constitute a pronounced part of the vibrational spectrum. The suggested model explicitly involves the physical mechanism of cooperativity and gives a satisfactory description of the observed spin transitions in mono-, bi- and tetranuclear compounds. In the framework of the described approach, we have discussed the experimental data on spin crossover in the mononuclear [Fe(ptz)6](BF4)2, binuclear [{Fe(bt)(NCS)2}2bpym] and tetranuclear [Fe(tpa){N(CN)2}]4·(BF4)4·(H2O)2 compounds based on iron ions. The approach is also applied to the description of the charge-transfer-induced spin transition in the [{(Tp)Fe(CN)3}{Co-(PY5Me2)}](CF3SO3) complex.
Author Contributions
The contributions of all authors in this review are equal. All authors have read and agreed to the published version of the manuscript.
Funding
National Agency for Research and Development of Moldova, Ministry of Science and Higher Education of the Russian Federation.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
S.K. and S.O. are grateful to the National Agency for Research and Development of Moldova for financial support (Project No. 20.80009.5007.19). Financial support from the Ministry of Science and Higher Education of the Russian Federation (the state assignment no. AAAA-A19-119092390079-8) is acknowledged.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| spin crossover | SCO |
| charge-transfer-induced spin transitions | CTIST |
| high-spin ion | hs ion |
| low-spin ion | ls ion |
References
- Gütlich, P.; Garsia, Y.; Goodwin, H.A. Spin crossover phenomena in Fe(II) complexes. Chem. Soc. Rev. 2000, 29, 419–427. [Google Scholar] [CrossRef]
- Sato, O.; Iyoda, T.; Fujishima, A.; Hashimoto, K. Photoinduced Magnetization of a Cobalt-Iron Cyanide. Science 1996, 272, 704–705. [Google Scholar] [CrossRef] [PubMed]
- Cambi, L.; Szego, L. Über die magnetische Susceptibilität der komplexen Verbindungen. Ber. Dtsch. Chem. Ges. 1931, 64, 2591–2598. [Google Scholar] [CrossRef]
- Cambi, L.; Szego, L. Über die magnetische Susceptibilität der komplexen Verbindungen (II. Mitteil.). Ber. Dtsch. Chem. Ges. 1933, 66, 656–661. [Google Scholar] [CrossRef]
- Gaspar, A.B.; Ksenofontov, V.P.; Serdyuk, M.; Gutlich, P. Multifunctionality in spin crossover materials. Coord. Chem. Rev. 2005, 249, 2661–2676. [Google Scholar] [CrossRef]
- Bousseksou, A.; Molnar, G.; Salmon, L.; Nicolazzi, W. Molecular spin crossover phenomenon: Recent achievements and prospects. Chem. Soc. Rev. 2011, 40, 3313–3335. [Google Scholar] [CrossRef]
- Brooker, S. Spin crossover with thermal hysteresis: Practicalities and lessons learnt. Chem. Soc. Rev. 2015, 44, 2880–2892. [Google Scholar] [CrossRef] [Green Version]
- Real, J.A.; Zarembowitch, J.; Kahn, O.; Solans, X. Magnetic Interaction and Spin Transition in Iron(II) Dinuclear Compounds. Crystal Structure of (μ-2,2′-Bipyrimidine)bis[(2,2′-Bipyrimidine)bis-(Thiocyanato)Iron(II)]. Inorg. Chem. 1987, 26, 2939–2943. [Google Scholar] [CrossRef]
- Real, J.A.; Bolvin, H.; Bousseksou, A.; Dworkin, A.; Kahn, O.; Varret, F.; Zarembowitch, J. Two-Step Spin Crossover in the New Dinuclear Compound [Fe(bt)(NCS)2]2bpym, with bt = 2,2′-bi-2-Thiazoline and bpym = 2,2′-Bipyrimidine: Experimental Investigation and Theoretical Approach. J. Am. Chem. Soc. 1992, 114, 4650–4658. [Google Scholar] [CrossRef]
- Ksenofontov, V.; Gaspar, A.B.; Niel, V.; Reiman, S.; Real, J.A.; Gütlich, P. On the Nature of the Plateau in Two-Step Dinuclear Spin-Crossover Complexes. Chem. Eur. J. 2004, 10, 1291–1298. [Google Scholar] [CrossRef]
- Bousseksou, A.; Molnar, G.; Real, J.A.; Tanaka, K. Spin Crossover and Photomagnetism in Dinuclear Iron(II) Compounds. Coord. Chem. Rev. 2007, 251, 1822–1833. [Google Scholar] [CrossRef]
- Klein, Y.M.; Sciortino, N.F.; Housecroft, C.E.; Kepert, C.J.; Neville, S.M. Structure and Magnetic Properties of the Spin Crossover Linear Trinuclear Complex [Fe3(furtrz)6(ptol)2(MeOH)4]·4(ptol)·4(MeOH) (furtrz: Furanylidene-4H-1,2,4-triazol-4-amine ptol: P-tolylsulfonate). Magnetochemistry 2016, 2, 7. [Google Scholar] [CrossRef] [Green Version]
- Pitalla, N.; Thetiot, F.; Charles, C.; Triki, S.; Boukheddaden, K.; Chastanet, G.; Marchivie, M. Unprecedented trinuclear FeII triasole-based complex exhibiting a concerted and complete sharp spin transition above room temperature. Chem. Commun. 2017, 53, 8356–8359. [Google Scholar] [CrossRef] [PubMed]
- Romanini, M.; Wang, Y.; Gürpinar, K.; Ornelas, G.; Lloveras, P.; Zhang, Y.; Zheng, W.; Barrio, M.; Aznar, A.; Gràcia-Condal, A.; et al. Giant and Reversible Barocaloric Effect in Trinuclear Spin-Crossover Complex Fe 3 (bntrz) 6 (tcnset) 6. Adv. Mater. 2021, 33, 2008076. [Google Scholar] [CrossRef]
- Wu, D.-Y.; Sato, O.; Einaga, Y.; Duan, C.-Y. A Spin-Crossover Cluster of Iron(II) Exhibiting a Mixed-Spin Structure and Synergy between Spin Transition and Magnetic Interaction. Angew. Chem. Int. Ed. 2009, 48, 1475–1478. [Google Scholar] [CrossRef]
- Matsumoto, T.; Newton, G.N.; Shiga, T.; Hayami, S.; Matsui, Y.; Okamoto, H.; Kumai, R.; Murakami, Y.; Oshio, H. Programmable spinstate switching in a mixed-valence spin-crossover iron grid. Nat. Commun. 2014, 5, 3865. [Google Scholar] [CrossRef] [Green Version]
- Wei, R.-J.; Huo, Q.; Tao, J.; Huang, R.-B.; Zheng, L.-S. Spin-Crossover Fe4II Squares: Two-Step Complete Spin Transition and Reversible Single-Crystal-to-Single-Crystal Transformation. Angew. Chem. Int. Ed. 2011, 50, 8940–8943. [Google Scholar] [CrossRef] [Green Version]
- Steinert, M.; Schneider, B.; Dechert, S.; Demeshko, S.; Meyer, F. Spin-State Versatility in a Series of Fe4 [2 × 2] Grid Complexes: Effects of Counteranions, Lattice Solvent and Intramolecular Cooperativity. Inorg. Chem. 2016, 55, 2363–2373. [Google Scholar] [CrossRef] [Green Version]
- Dhers, S.; Mondal, A.; Aguilà, D.; Ramirez, J.; Vela, S.; Dechambernoit, P.; Rouzièrs, M.; Nitschke, J.R.; Clèrac, R.; Lehn, J.-M. Spin State Chemistry: Modulation of Ligand pKa by Spin State Switching in a [2 × 2] Iron(II) Grid-Type Complex. J. Am. Chem. Soc. 2018, 140, 8218–8227. [Google Scholar] [CrossRef] [Green Version]
- Aguilà, D.; Prado, Y.; Koumousi, E.S.; Mathonière, C.; Clérac, R. Switchable Fe/Co Prussian blue networks and molecular analogues. Chem. Soc. Rev. 2016, 45, 203–224. [Google Scholar] [CrossRef] [Green Version]
- Berlinguette, C.P.; Dragulescu-Andrasi, A.; Sieber, A.; Galan-Mascaros, J.R.; Güdel, H.-U.; Achim, C.; Dunbar, K.R. A Charge-Transfer-Induced Spin Transition in the Discrete Cyanide-Bridged Complex {[Co(tmphen)2]3[Fe(CN)6]2}. J. Am. Chem. Soc. 2004, 126, 6222–6223. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Clérac, R.; Roubeau, O.; Harte, E.; Mathonière, C.; Le Bris, R.; Holmes, S.M. Magnetic and Optical Bistability Driven by Thermally and Photoinduced Intramolecular Electron Transfer in a Molecular Cobalt−Iron Prussian Blue Analogue. J. Am. Chem. Soc. 2008, 130, 252–258. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, D.; Clérac, R.; Kalisz, M.; Mathonière, C.; Holmes, S.M. Reversible Thermally and Photoinduced Electron Transfer in a Cyano-Bridged {Fe2Co2} Square Complex. Angew. Chem. Int. Ed. 2010, 122, 3840–3844. [Google Scholar] [CrossRef]
- Koumousi, E.S.; Jeon, I.-R.; Gao, Q.; Dechambenoit, P.; Woodruff, D.N.; Merzeau, P.; Buisson, L.; Jia, X.; Li, D.; Volatron, F.; et al. Metal-to-Metal Electron Transfer in Co/Fe Prussian Blue Molecular Analogues: The Ultimate Miniaturization. J. Am. Chem. Soc. 2014, 136, 15461–15464. [Google Scholar] [CrossRef]
- Sasaki, N.; Kambara, T.J. Theory of cooperative high-spin ↔ low-spin transitions in iron (III) compounds induced by the molecular distortions. Chem. Phys. 1981, 74, 3472–3481. [Google Scholar] [CrossRef]
- Sasaki, N.; Kambara, T. Theory of the two-step spin conversion induced by the cooperative molecular distortions in spin-crossover compounds. Phys. Rev. B 1989, 40, 2442–2449. [Google Scholar] [CrossRef] [PubMed]
- Palii, A.; Ostrovsky, S.; Reu, O.; Tsukerblat, B.; Decurtins, S.; Liu, S.-X.; Klokishner, S. Microscopic theory of cooperative spin crossover: Interaction of molecular modes with phonons. J. Chem. Phys. 2015, 143, 084502. [Google Scholar] [CrossRef]
- Palii, A.; Ostrovsky, S.; Reu, O.; Tsukerblat, B.; Decurtins, S.; Liu, S.-X.; Klokishner, S. Diversity of Spin Crossover Transitions in Binuclear Compounds: Simulation by Microscopic Vibronic Approach. J. Phys. Chem. C 2016, 120, 14444–14453. [Google Scholar] [CrossRef]
- Ostrovsky, S.; Palii, A.; Decurtins, S.; Liu, S.-X.; Klokishner, S. Microscopic Approach to the Problem of Cooperative Spin Crossover in Polynuclear Cluster Compounds: Application to Tetranuclear Iron(II) Square Complexes. J. Phys. Chem. C 2018, 122, 22150–22159. [Google Scholar]
- Klokishner, S.; Ostrovsky, S. Modeling of electron transfer phenomenon in the dinuclear {Fe(μ−CN)Co} complexes. J. Appl. Phys. 2021, 129, 113901. [Google Scholar] [CrossRef]
- Jung, J.; Schmitt, G.; Wiehl, L.; Hauser, A.; Knorr, K.; Spiering, H.; Gutlich, P. The cooperative spin transition in [FexZn1−x(ptz)6](BF4)2: II. Structural properties and calculation of the elastic interaction. Z. Phys. B 1996, 100, 523–534. [Google Scholar] [CrossRef]
- Hizhnyakov, V.; Pae, K.; Vaikjarv, T. Optical Jahn−Teller effect in the case of local modes and phonons. Chem. Phys. Lett. 2012, 525–526, 64–68. [Google Scholar] [CrossRef]
- Pae, K.; Hizhnyakov, V. Nonadiabaticity in a Jahn-Teller system probed by absorption and resonance Raman scattering. J. Chem. Phys. 2013, 138, 104103. [Google Scholar] [CrossRef] [PubMed]
- Pae, K.; Hizhnyakov, V. Quantum friction of pseudorotation in Jahn-Teller System: Passage through conical intersection. J. Chem. Phys. 2016, 145, 064108. [Google Scholar] [CrossRef]
- Kanamori, J. Crystal Distortion in Magnetic Compounds. J. Appl. Phys. 1960, 31, S14–S23. [Google Scholar] [CrossRef]
- Gehring, G.A.; Gehring, K.A. Co-operative Jahn-Teller effects. Rep. Prog. Phys. 1975, 38, 1. [Google Scholar] [CrossRef]
- Kaplan, M.D.; Vekhter, B.G. Cooperative Phenomena in Jahn-Teller Crystals; Plenum: New York, NY, USA, 1995. [Google Scholar]
- Califano, S.; Schettino, V.; Neto, N. Lattice Dynamics of Molecular Crystals; Springer: Berlin, Germany, 1981. [Google Scholar]
- Jung, J.; Spiering, H.; Yu, Z.; Gutlich, P. The debye-waller factor in spincrossover molecular crystals: A mössbauer study on [FexZn1−x(ptz)6](BF4)2. Hyperfine Interact. 1995, 95, 107. [Google Scholar] [CrossRef]
- Nihei, M.; Ui, M.; Yokota, M.; Han, L.; Madda, A.; Kishida, H.; Okamoto, H.; Oshio, H. Two-Step Spin Conversion in a Cyanide-Bridged Ferrous Square. Angew. Chem. Int. Ed. 2005, 44, 6484–6487. [Google Scholar] [CrossRef]
- Ronayne, K.L.; Paulsen, H.; Höfer, A.; Dennis, A.C.; Wolny, J.A.; Chumakov, A.I.; Schünemann, V.; Winkler, H.; Spiering, H.; Bousseksou, A.; et al. Vibrational spectrum of the spin crossover complex [Fe-(phen)2(NCS)2] studied by IR and Raman spectroscopy, nuclear inelastic scattering and DFT calculations. Phys. Chem. Chem. Phys. 2006, 8, 4685–4693. [Google Scholar]
- Abragam, A.; Bleaney, B. Electron Paramagnetic Resonance of Transition Ions; Clarendon Press: Oxford, UK, 1970. [Google Scholar]
- Rury, A.S.; Goodrich, I.E.; Galinato, M.G.I.; Lehnert, N.; Sension, R.J. Ligand Recruitment and Spin Transitions in the Solid-State Photochemistry of Fe(III)TPPCl. J. Phys. Chem. A 2012, 116, 8321–8333. [Google Scholar] [CrossRef]
- Ansel’m, A. Introduction to Semiconductor Theory; Mir Publishers: Moscow, Russia, 1981; (In Russian). Elglish Translation: Prenctice-Hall, 1981; ISBN1 10: 0134960343. ISBN2 13: 978-0134960340. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).