Effect of Substrate on One-Dimensional Multiferroic Properties

Abstract

We present a theoretical study of the substrate influence on the electrical and magnetic properties of a one-dimensional multiferroic. We used a one-dimensional axial next-nearest neighbor Ising model (1D ANNNI model). The effect of the substrate was modeled using the periodic Frenkel–Kontorova potential. It is shown that the periodic potential of the substrate reduces the polarization of the multiferroic at low temperatures. The substrate potential significantly affects the structural changes near the magnetic phase transition temperature.

1. Introduction

In recent years, composites of ferromagnetic (FM), antiferromagnetic (AFM), and ferroelectric (FE) materials have received considerable attention due to their wide use in spintronic devices. Such heterostructures can be created from bilayers of FM and FE structures, which enable controlling the magnetic and electrical properties by the strain along the surface [1,2]. Reference [3] showed the strong influence of deformations caused by the structural phase transition in the BaTiO${}_3$ FE substrate on the magnetic properties of the La${}_{0.7}$Sr${}_{0.3}$MnO${}_6$ ferromagnet. The substrate influence can be significant in the boundary layer of the magnet only. Thus, a noticeable change in material properties because of the substrate can be expected for 2D or 1D materials. Thin film is an example of a 2D multiferroic and the Ca${}_3$CoMnO${}_6$ compound is an example of a 1D multiferroic [4].

Ca${}_3$CoMnO${}_6$ has a rhombohedral structure (crystallographic group R$\overline{3}$c), similar to K${}_4$CdCl${}_6$. It contains parallel CoMnO${}_6$ chains consisting of an alternating CoO${}_6$ trigonal prism and MnO${}_6$ octahedron along the c axis. Ca${}^{2+}$ ions separate the CoMnO${}_6$ chains, which form a triangular lattice in the $ab$ plane [4,5,6]. Ca${}_3$CoMnO${}_6$ belongs to type II multiferroic in Chomsky’s classification [7]. The alternation of Co${}^{2+}$ and Mn${}^{4+}$ ions along the CoMnO${}_6$ chain breaks the spatial symmetry, leading to unusual physical properties, such as magnetization tunneling, electric polarization due to magnetostriction [8], magnetoelectric interaction [9], etc.

The ground state of the magnetic lattice is up–up–down–down if the competing interactions parameter is $|J_{AF}/J_{FM}|>1/2$ [10]. The exchange interaction shortens the distances between parallel spins and increases between anti-parallel ones. This leads to the electric polarization appearance in the up–up–down–down magnetic structure.

References [11,12] confirmed the occurrence of ferroelectricity as a result of a change in the Co-Mn distances and up–up–down–down magnetic ordering with the help of density functional theory and ab initio calculation of the electronic structure. Experimental work [13] revealed ferroelectricity in the Ca${}_3$Co${}_{2-x}$Mn${}_x$O${}_6$ crystal ($x\approx 0.96$). The authors of [14] presented the original microscopic model of up–up–down–down structure formation in type II multiferroics by using the renormalization group method. Subsequent works showed that the long-range spin order is retained only for Ca${}_3$Co${}_{1+x}$Mn${}_{1-x}$O${}_6$ [15], while the long-range order disappears and the macroscopic polarization weakens on defect-free Ca${}_3$CoMnO${}_6$ [16]. Reference [17] showed the relaxor nature of the ferroelectric phase transition, which implied the existence of polar nanoregions [18]. The doped Ca${}_{2.7}$Sr${}_{0.3}$CoMn${}_{1-x}$Fe${}_x$O${}_6$ compound demonstrates a rather large magnetoelectric (ME) interaction coefficient at room temperature (about 1.7 mV/cm · Oe) and a decrease in the band gap from 2.25 to 1.8 eV [19], which allows its potential application in sensors, filters, and various actuators working in the mid-frequency range.

In this work, we studied the effect of the substrate on the magnetic and electrical properties of a one-dimensional multiferroic. The study was performed by using the Monte Carlo simulation. We applied the ANNNI Ising model for a one-dimensional multiferroic and the periodic Frenkel–Kontorova potential [20] to simulate the effect of the substrate. We found that the substrate significantly affects the structural changes near the magnetic phase transition temperature and reduces the polarization of the multiferroic at low temperatures.

2. Materials and Methods

We considered a model with competing FM nearest neighbor interactions $J_{FM}$ and AFM next neighbor interactions $J_{AF}$. The distance dependencies of the FM and AFM exchange integrals can be presented as linear approximations [21]:

$$J_{FM}\left(r_{i,i+1}\right)=J_{F{M}_0}exp\left(\eta \frac{r_{i,i+1}-r_0}{r_0}\right)\approx J_{F{M}_0}\left(1+\eta \frac{r_{i,i+1}-r_0}{r_0}\right)=J_{F{M}_0}[1+\eta (d_{i+1}-d_i)]$$

(1)

$$J_{AF}\left(r_{i,i+2}\right)=J_{A{F}_0}exp\left(\eta \frac{r_{i,i+2}-2r_0}{2r_0}\right)=J_{A{F}_0}\left[1+\frac{\eta }{4}(d_{i+2}-d_i)\right],$$

(2)

where $J_{F{M}_0}$ and $J_{A{F}_0}$ are the FM and AFM exchange integrals in the absence magnetostriction, ($J_{F{M}_0}>0$, $J_{A{F}_0}<0$), $r_0$ is the interatomic distance in the ground state, $\eta$ is the magnetostriction coefficient ($\eta <0$), $r_{ij}$ is the distance between i and $j=i+1,i+2$ ions, and $d_i$ is the displacement of the i-ion from the initial position normalized to $r_0$.

To simplify the simulation, we will assume that only every even ion in the chain moves. This is true for chains with alternating atoms of two types. The magnitude of the AFM interaction for various atoms will be different due to the various magnetic moments. We take the relative values of magnetic moments for the CoMnO${}_6$ chain, where the magnetic moment of Mn ions is three times larger than the magnetic moment of Co, i.e., ($J_{A{F}_{\mathrm{Mn}}}=9J_{A{F}_{\mathrm{Co}}}$) [13]. The Mn ions are taken as immobile ($d_{\mathrm{Mn}}=0$). We use the periodic Frenkel–Kontorova potential to model the substrate influence. Then the Hamiltonian is:

$$H=H_{FM}+H_{AF}+H_M+H_E+H_{el}+H_{FK}$$

(3)

$$\begin{array}{cc}\hfill H_{FM}=& -\sum _{\langle i,j\rangle }{J}_{FM}\left(r_{i,j}\right)S_i{S}_j;H_{AF}=-\sum _{[i,k]}^{\mathrm{Mn}}{J}_{A{F}_{\mathrm{Mn}}}{S}_i{S}_j-\sum _{[i,k]}^{\mathrm{Co}}{J}_{A{F}_{\mathrm{Co}}}\left(r_{i,j}\right)S_i{S}_j;\hfill \\ & H_M=-hg{\mu }_B\sum _i{S}_i;H_E=-E\sum _{i}q{d}_i;H_{el}=\frac{1}{2}k\sum _i{d}_i^2;\hfill \\ & H_{FK}=-{\alpha }_{FK}\sum _{i}cos\left(\frac{2\pi (i+d_i)}{b_{FK}}\right),\hfill \end{array}$$

where $H_{FM}$ and $H_{AF}$ are the competing FM and AFM interactions, the angle brackets denote the summation over the pairs of nearest neighbors, and the square brackets denote the summation over pairs of next-nearest neighbors. $H_M$ and $H_E$ are the energies of the magnetic and electric fields, respectively, h is the external magnetic field, g is the Landé factor, ${\mu }_B$ is the Bohr magneton, E is the external electric field, and q is the charge of moving ions ($q=2$ for Co). $H_{el}$ is the elastic energy, where k is the elasticity coefficient, $H_{FK}$ describes the periodic potential of the substrate, ${\alpha }_{FK}$ and $b_{FK}$ are the amplitude and the period of the potential. We take the Boltzmann constant as a unit, so the temperature is measured in units of energy.

The simulation parameters are presented in

Table 1. The simulation parameters.

Parameter	Value	Parameter	Value
$J_{F{M}_0}$	360	$\eta$	−8
$J_{A{F}_{\mathrm{Mn}}}$	−262.8	k	136,000
$J_{A{F}_{{\mathrm{Co}}_0}}$	−29.2	g	2

. We selected them to provide the qualitative agreement with experiment [13].

The simulation was carried out on a chain of length L = 4000 with periodic boundary conditions. For each temperature value, the system came to the state of thermodynamic equilibrium during $3\times {10}^5$ Monte Carlo (MC) steps. Thermodynamic parameters were calculated during the next $5\times {10}^4$ MC steps.

The electrical susceptibility of a chain was calculated according to the statistical fluctuation [22]:

$${\chi }_e=\frac{\langle P^2\rangle -{\langle P\rangle }^2}{T}.$$

(4)

The dielectric constant is determined as:

$$\epsilon ={\chi }_e+1.$$

(5)

3. Results

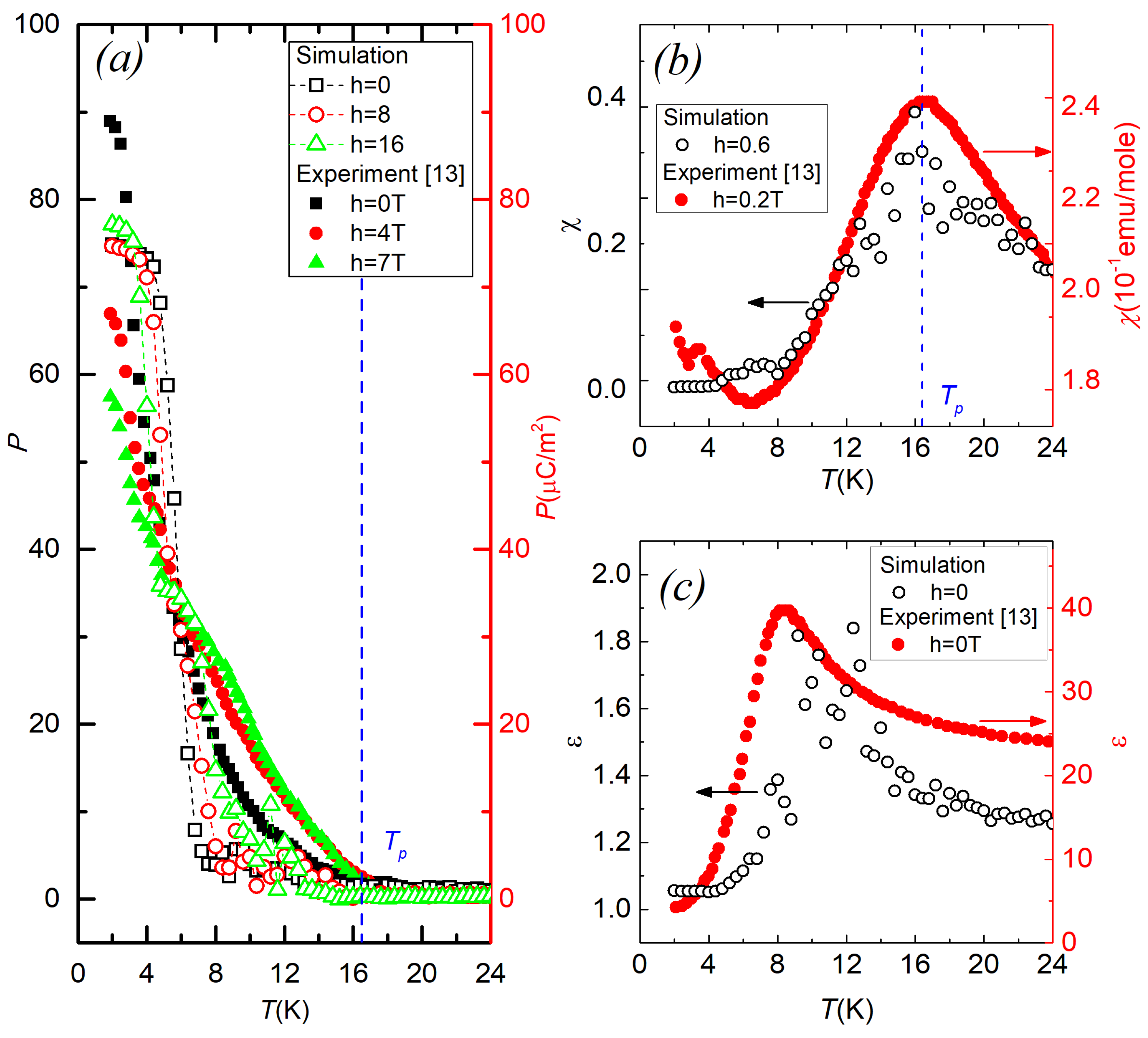
Figure 1 shows the calculated temperature dependencies of the polarization P (Figure 1a), magnetic susceptibility ($\chi =M/h$) (Figure 1b), permittivity $\epsilon$ (Figure 1c) without the substrate influence, and the corresponding experimental curves for Ca${}_3$Co${}_{2-x}$Mn${}_x$O${}_6$ ($x=0.96$) [22]. A comparison of simulation results with experimental data indicates their qualitative agreement.

The broad peak of the $\chi \left(T\right)$ indicates the presence of a phase transition from the AFM to the paramagnetic phase at $T_p\approx 16$. One can see the decrease in electric polarization below this temperature. The inclusion of a magnetic field reduces the polarization at $T<6$ and increases it at a higher temperature. The experimental curves [13] demonstrate similar behavior and confirm the results of simulations.

Figure 2 shows the electric polarization change under the influence of the periodic potential of the substrate in the presence and the absence of an external magnetic field. We considered the cases when the period of the substrate potential was larger and smaller by 5% than the interatomic distance $r_0$. It can be seen that the substrate potential reduces the macroscopic polarization proportionally to the amplitude. However, the deviation of the potential period less or higher than the lattice constant reduces the polarization similarly.

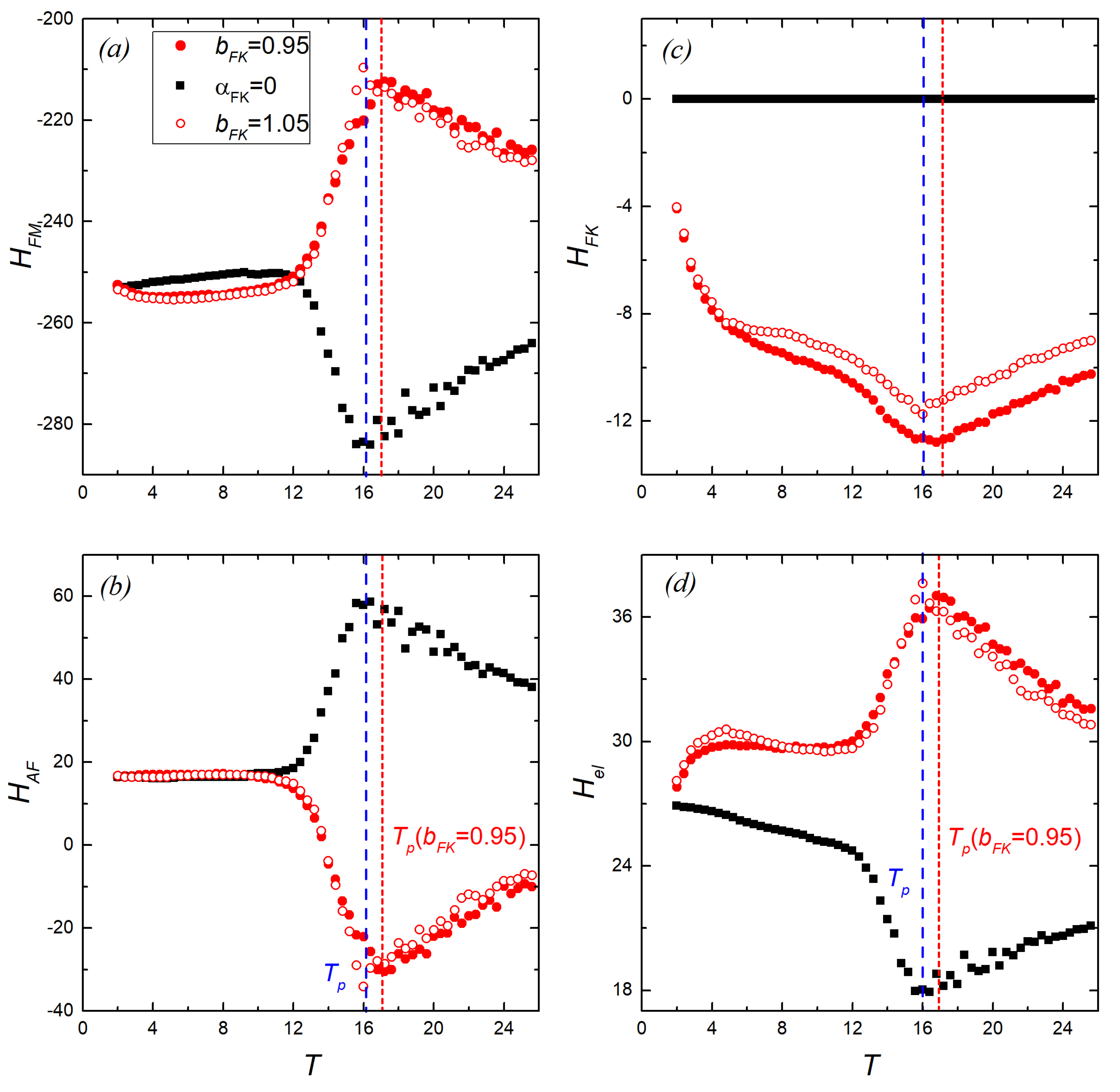
We analyzed the energy components by themselves for further study of the magnetic and electrical parameters of the system. We chose the FM and AFM interactions $H_{FM}$ and $H_{AF}$, the influence energy of the substrate $H_{FK}$, and the elastic energy $H_{el}$ as the main components.

Figure 3 shows the temperature dependencies of these components without and with the substrate when the period of the substrate potential is smaller (Figure 3(filled circles)) and larger (Figure 3(opened circles)) than the interatomic distance by $5\%$. The $H_{FM}$ and $H_{AF}$ dependencies have singularities at the transition temperature $T_p$, which indicates that the magnetic structure is destroyed. Note that $T_p$ shifts slightly higher with a decrease in the potential period ($b_{FK}=0.95$). Identical change in the phase transition temperature was observed for 2D magnets in [23]. At a temperature $T<12$, $H_{FM}$ and $H_{AF}$ are almost the same in the presence and absence of the substrate potential. However, the dependencies of these components change dramatically at temperatures above 12. Near $T_p$, $H_{FM}$ and $H_{AF}$ change the type of extremum: a maximum instead of a minimum and vice versa. This indicates a change in the balance of FM/AFM interactions, i.e., toward the AFM interaction with the presence of the substrate potential and toward the FM interaction without it.

The behavior of $H_{el}$ also changes with the substrate potential. Instead of a minimum at $T_p$ in the absence of the potential, it demonstrates a maximum (Figure 3d). The $H_{FK}$ energy has a minimum at $T_p$ (Figure 3c), suggesting that a system has the minimum displacements at $T_p$ without the substrate and the maximum displacements when the substrate appears. However, the growth of macroscopic polarization at $T_p$ does not take place with the substrate potential (Figure 2). To explain this, let us consider the evolution of the magnetic subsystem in detail.

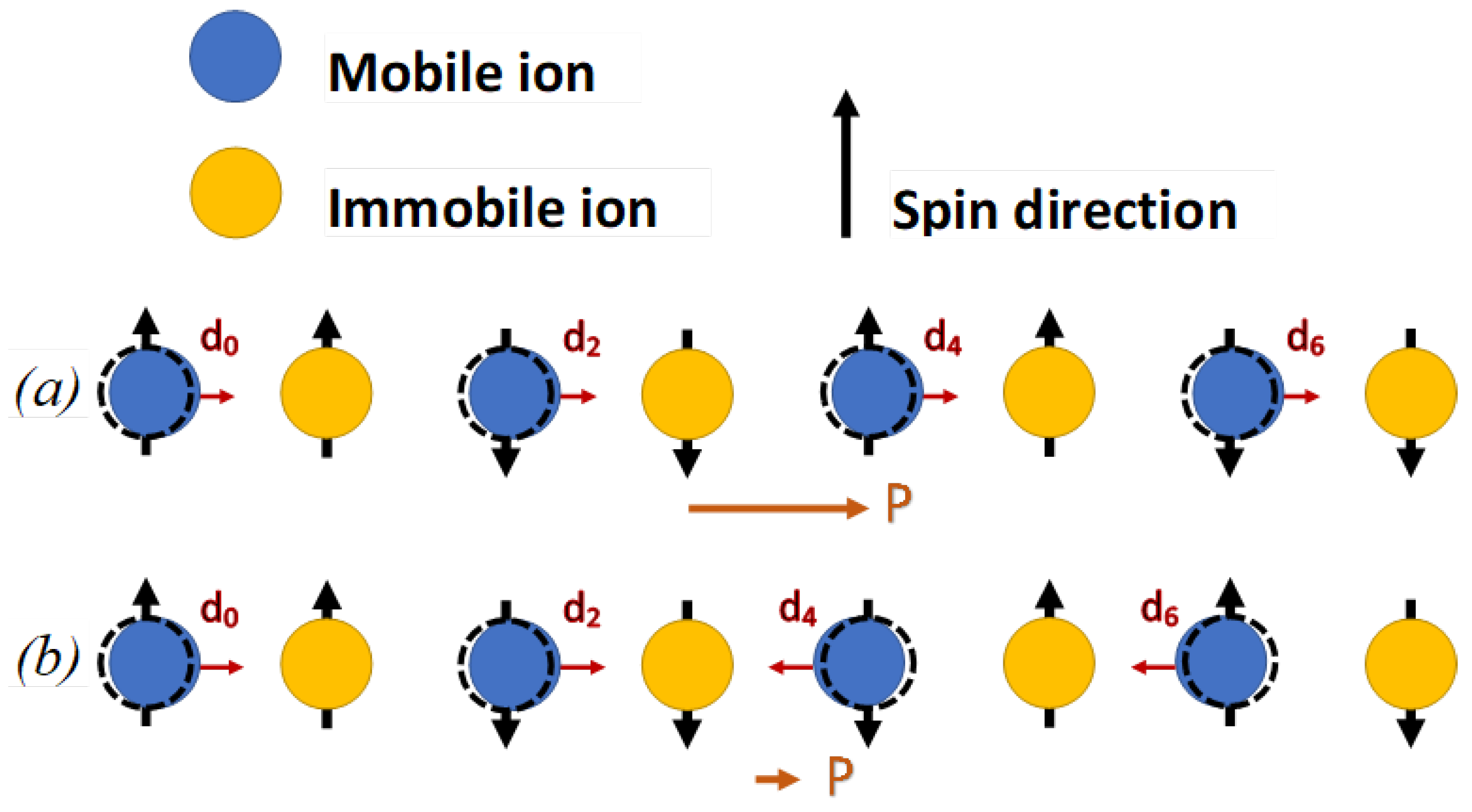
Figure 4 shows the formation mechanism of microscopic polarization when the distances between parallel spins decrease and the distances between anti-parallel spins increase. The magnetic domain with an odd number of spins contributes to the formation of shifts in opposite directions (Figure 4b), thereby reducing the macroscopic polarization.

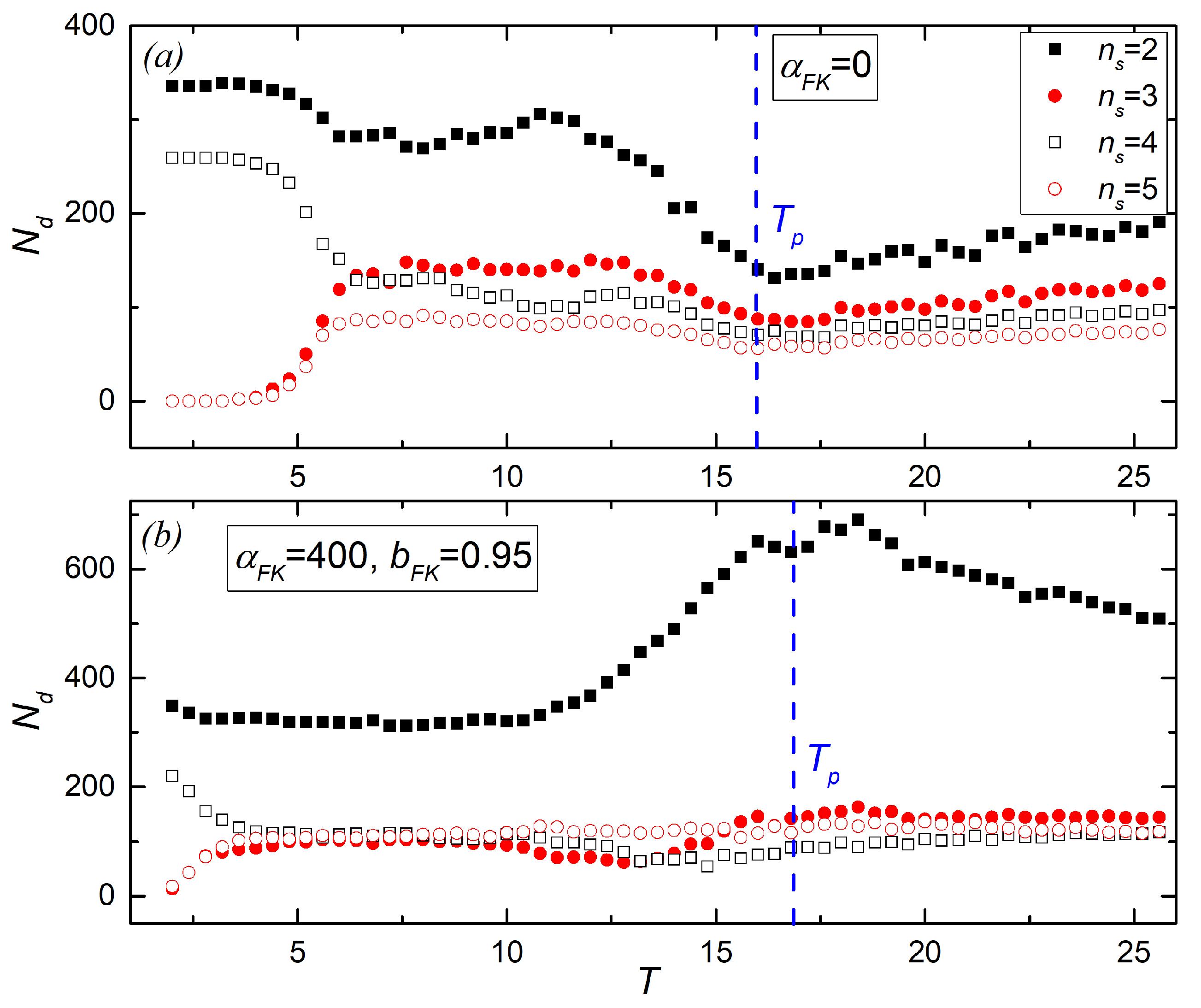
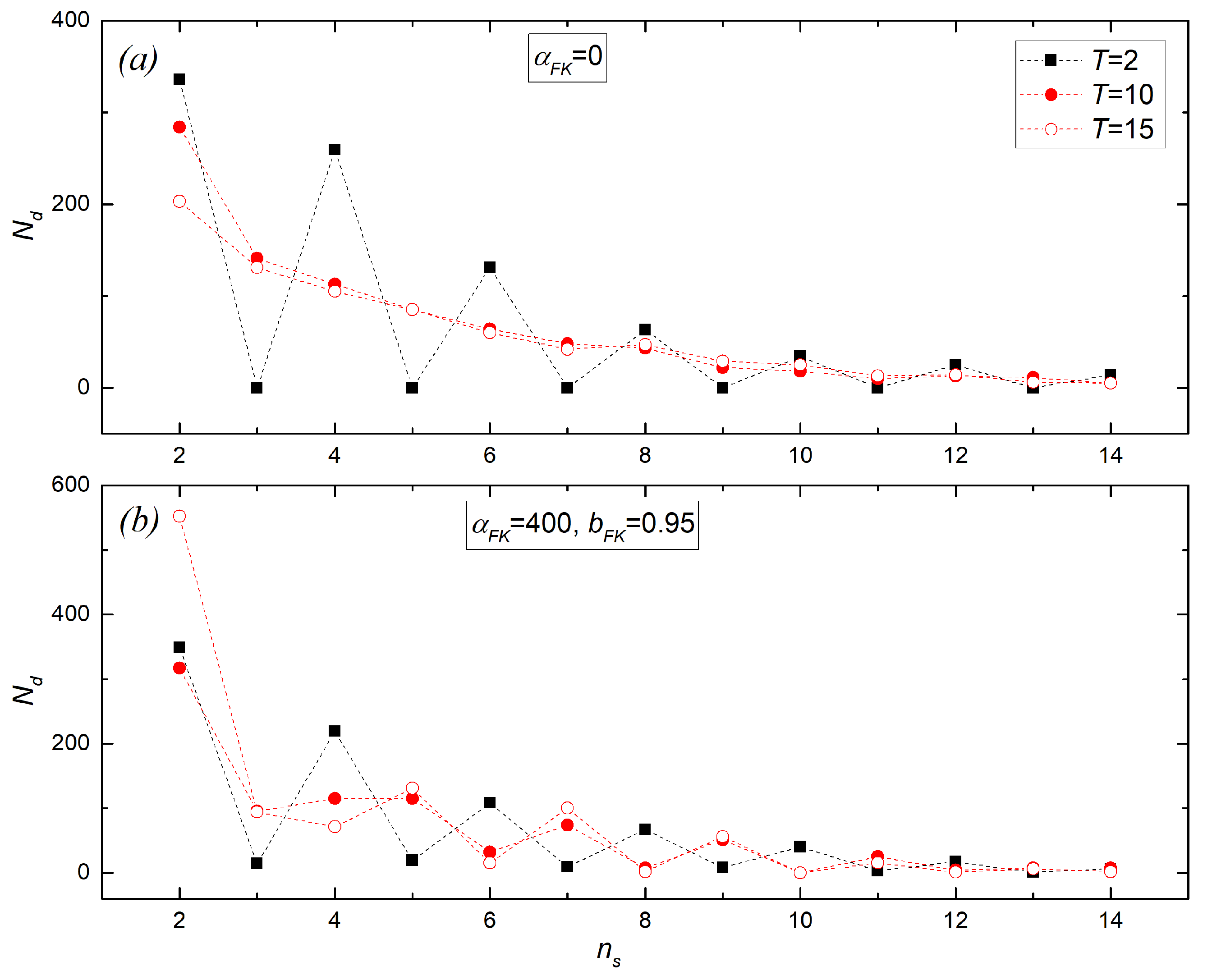
Therefore, we study the distribution of magnetic domains with even and odd numbers of spins. Let us consider the number of magnetic domains $N_d\left(n_s\right)$, where the length of magnetic domains $n_s$ is the number of neighboring spins lined in one direction. Figure 5 shows the distribution of magnetic domains with $n_s=2.5$ as the function of the temperature.

Figure 5a shows the case without substrate influence. At low temperatures ($T<4$), the system contains domains with lengths of two and four spins, while there are no domains with lengths of three and five. In this region, the macroscopic polarization has a maximum. With an increase in temperature, domains with an odd number of spins appear, and there are fewer domains with an even number of spins. In this area, the polarization decreases (Figure 2). A significant decrease of $N_d$(2) occurs near the phase transition temperature. The substrate potential lowers the temperature at which $N_d\left(3\right)\approx N_d\left(4\right)\approx N_d\left(5\right)$. The behavior of $N_d$(2) with the substrate potential is very different at $T>10$ (Figure 5b). It grows to $T_p$, and the number of domains with odd $n_s$ increases near $T_p$.

Figure 6 shows the distribution of $N_d$ at different temperatures. Without substrate potential (Figure 6a), only domains with even $n_s$ are present in the system at T = 2. The curve becomes smooth as the temperature rises, and domains with odd $n_s$ appear. The substrate potential changes the behavior of $N_d$ at higher temperatures. At T = 10, the number of domains with odd $n_s$ increases, and it becomes higher than the number with even $n_s$. At T = 15, $N_d$(2) increases significantly. This can be explained by the AFM interaction increase and the FM interaction decrease near $T_p$, as shown in Figure 3a,b. Thus, the polarization of the system does not increase significantly despite a visible increase of $N_d$(2) near $T_p$. Displacements formed by magnetic domains with even $n_s$ are compensated by oppositely directed displacements formed by domains with odd $n_s$.

4. Conclusions

In this work, we studied the influence of the periodic substrate potential on the behavior of the thermodynamic parameters of a quasi-one-dimensional multiferroic. We investigated the case of a little deviation of the potential period from the interatomic distance in a spin chain of multiferroic. The discrepancy between the period of the substrate potential and the interatomic distance leads to a change in the space between atoms and, as a consequence, a change in the exchange integrals. The analysis of the individual energy components of the system showed a change in the balance of FM/AFM interactions when the substrate potential appeared. Near the magnetic phase transition, the AFM interaction starts to increase, while the FM interaction becomes weaker. The elastic component of the energy also changes its behavior when the substrate potential appears: the energy maximum appears instead of the minimum at the phase transition point. At this point, the displacements of spins from the equilibrium position are the largest. This leads to an increase in the number of magnetic domains with a length of two spins, which contributes to the creation of microscopic polarization, as well as domains with odd lengths, which contribute to the appearance of an oppositely directed polarization. As a result, macroscopic polarization does not change significantly.