An Improved 3D Magnetization Inversion Based on Smoothness Constraints in Spherical Coordinates
Abstract
1. Introduction
2. Methodology
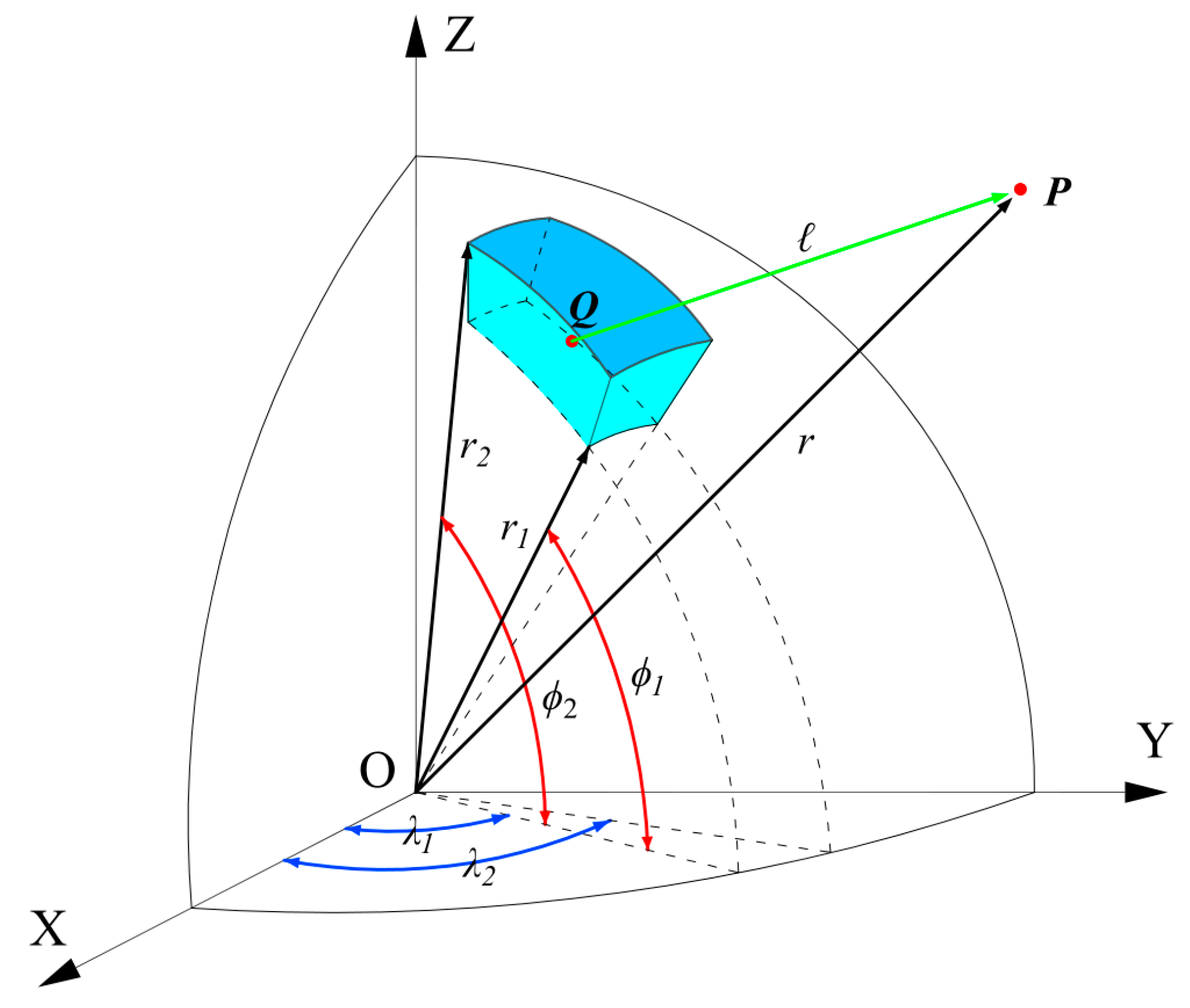
2.1. Forward Modeling in Spherical Coordinates
2.2. Occam Inversion Method
2.3. Improved Inversion Method
3. Synthesis Model Analysis
3.1. Models’ Geometry and Magnetic Parameters
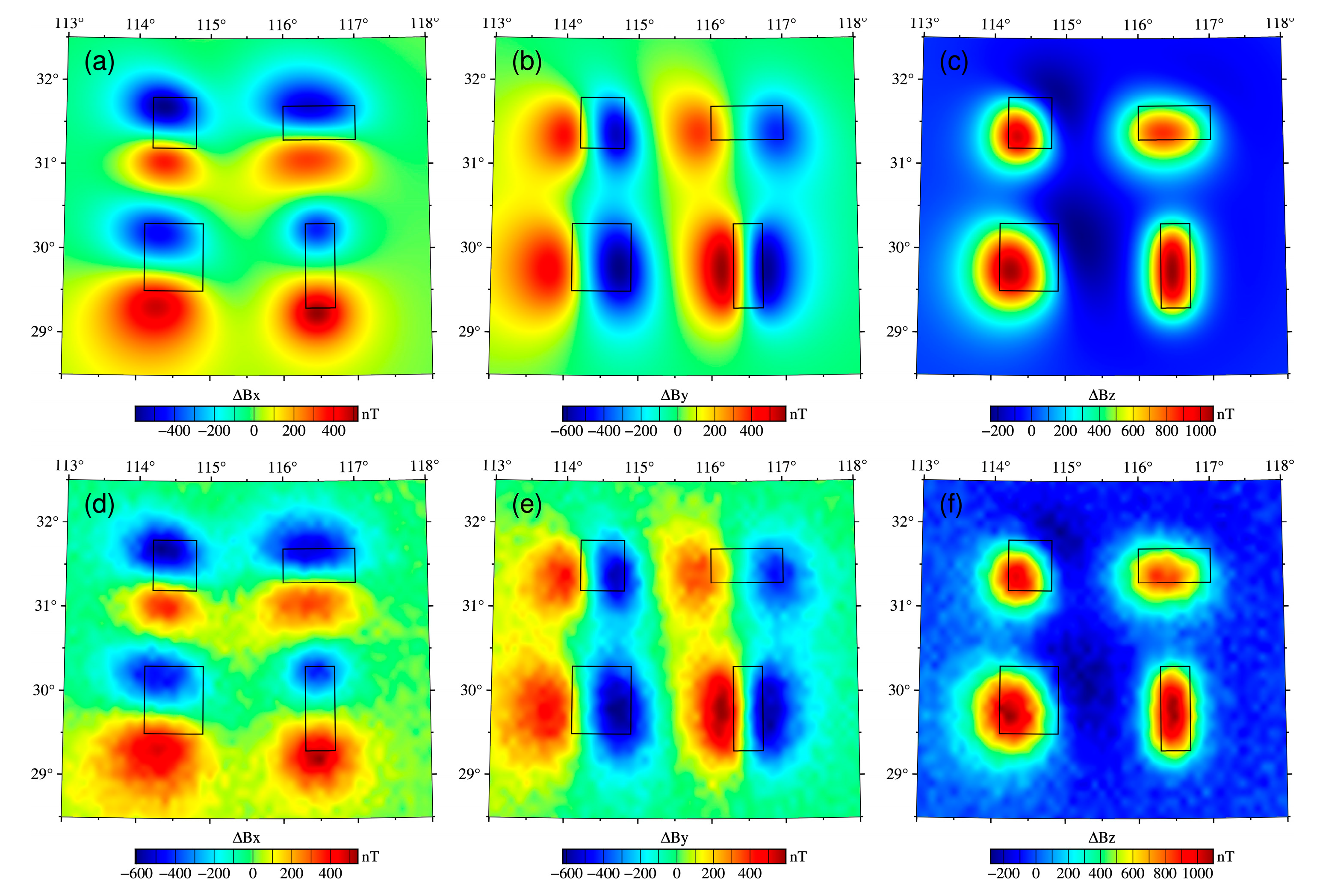
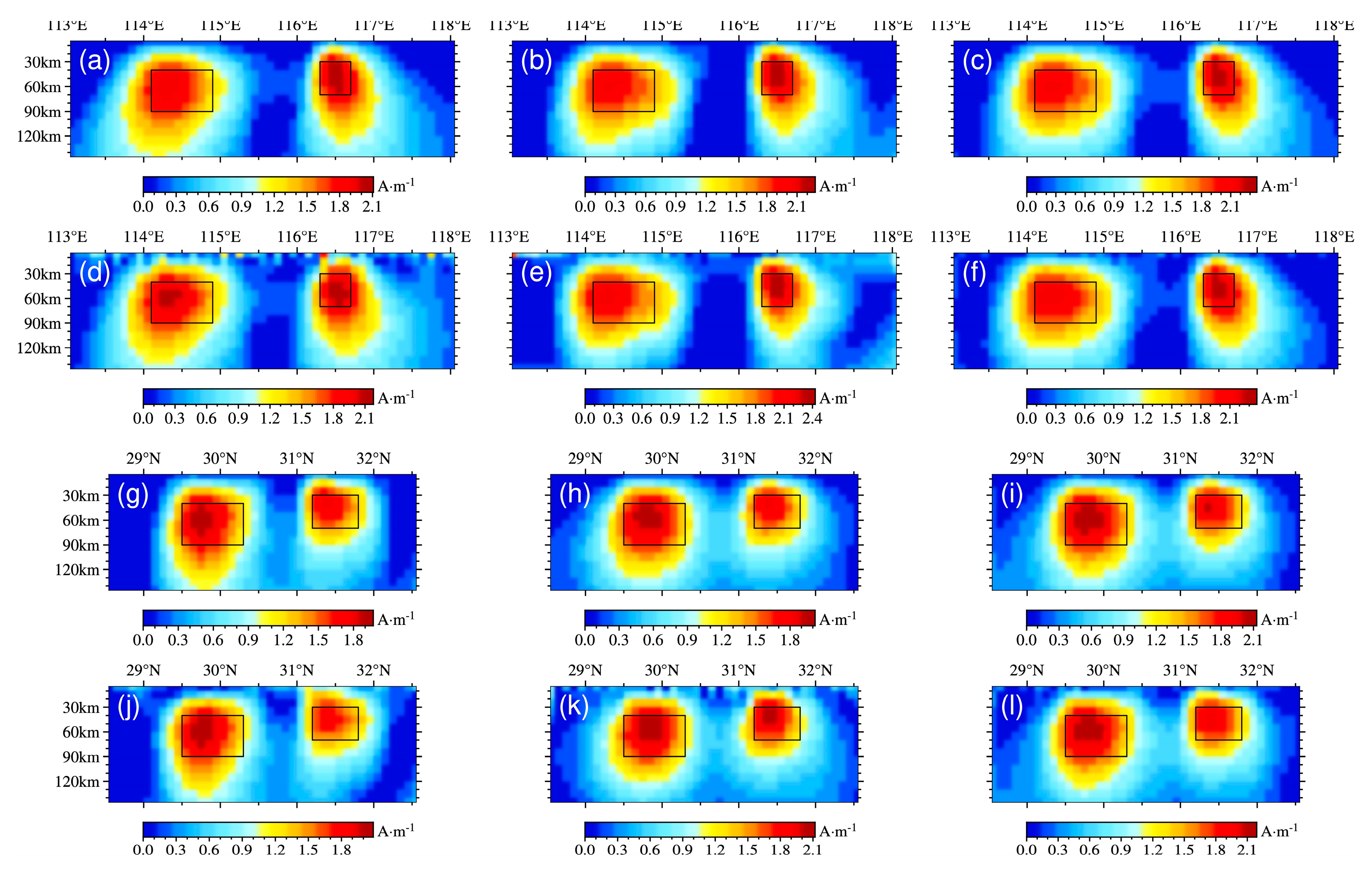
3.2. Analysis of Inversion Results
3.2.1. Synthesis Model of the Same Magnetic Parameters
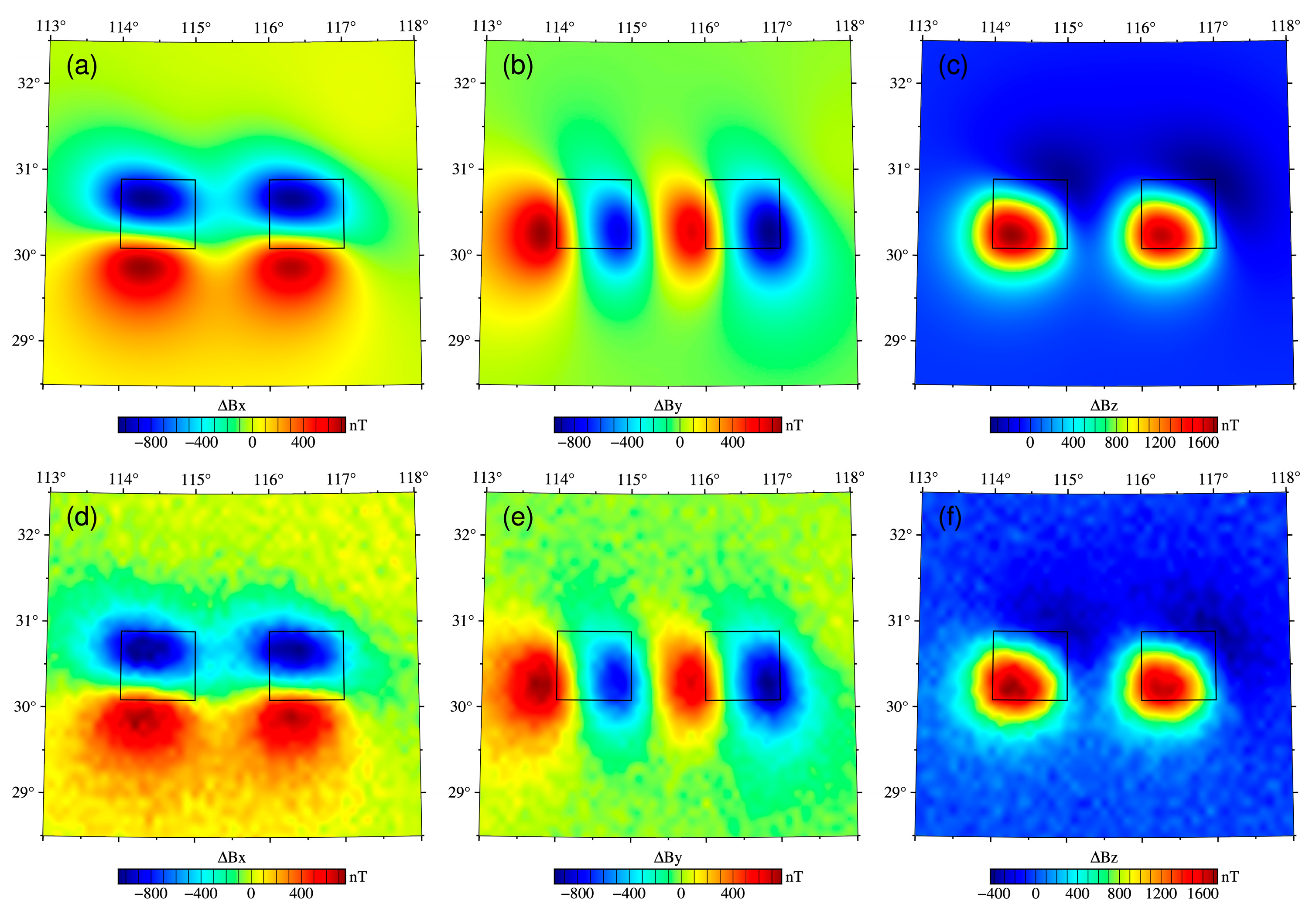

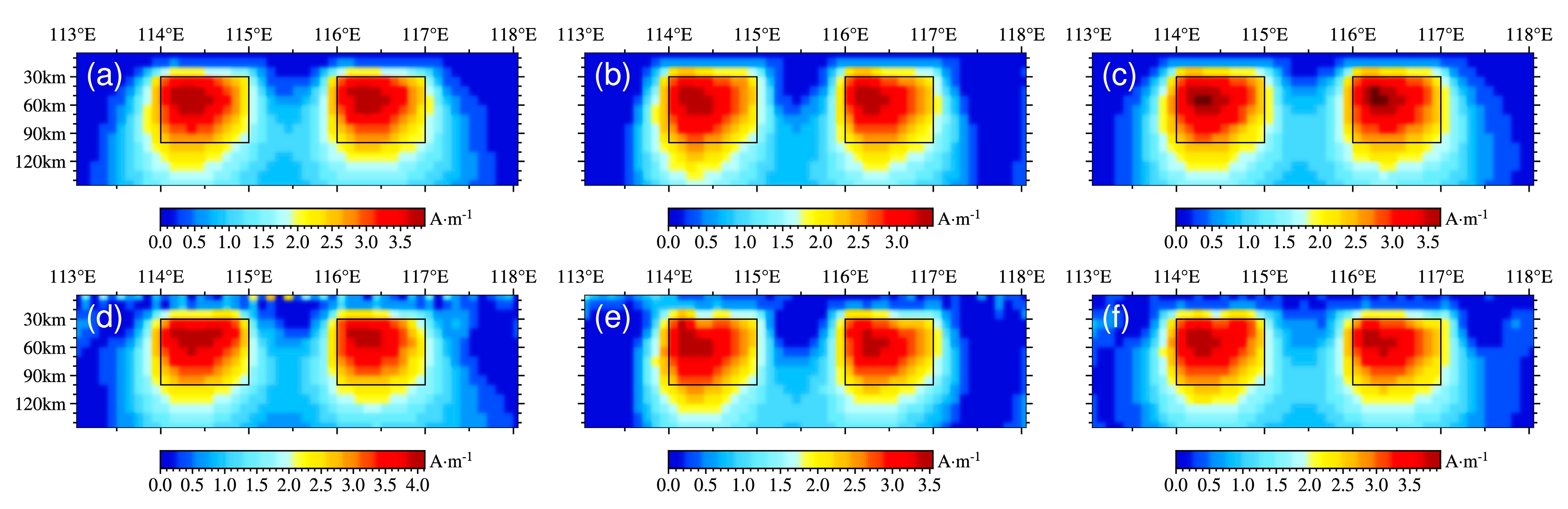
3.2.2. Synthesis Model of Different Magnetic Parameters
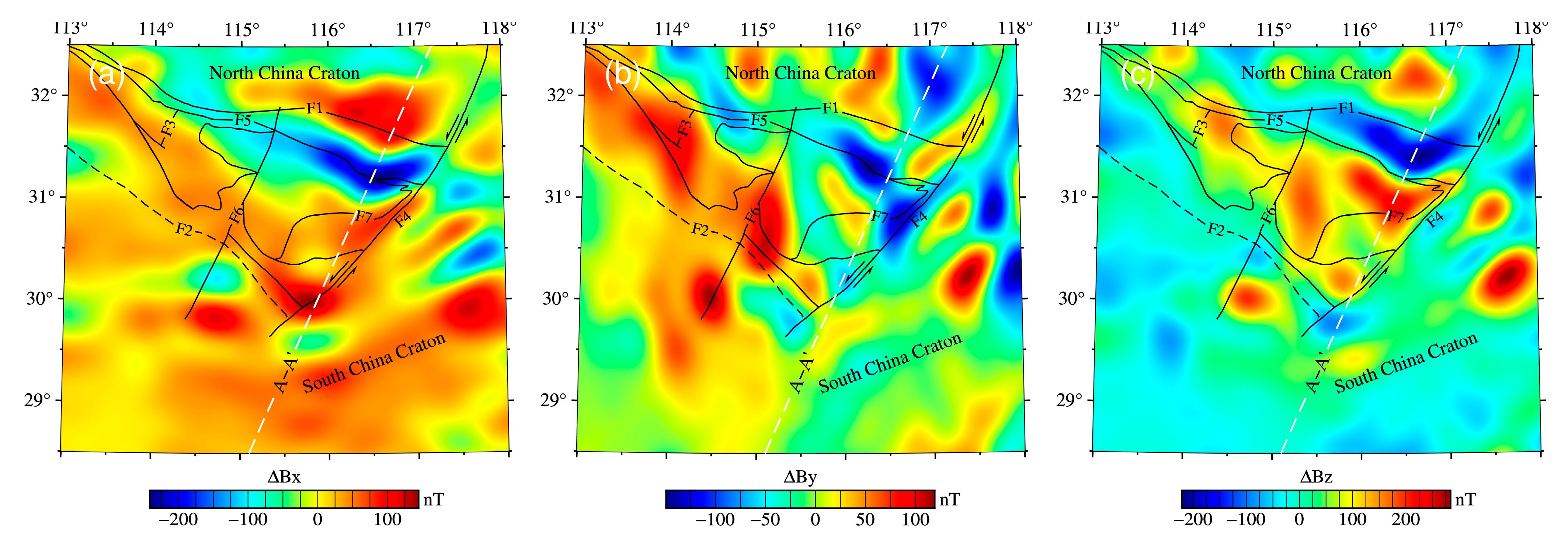
4. Magnetic Data Tests
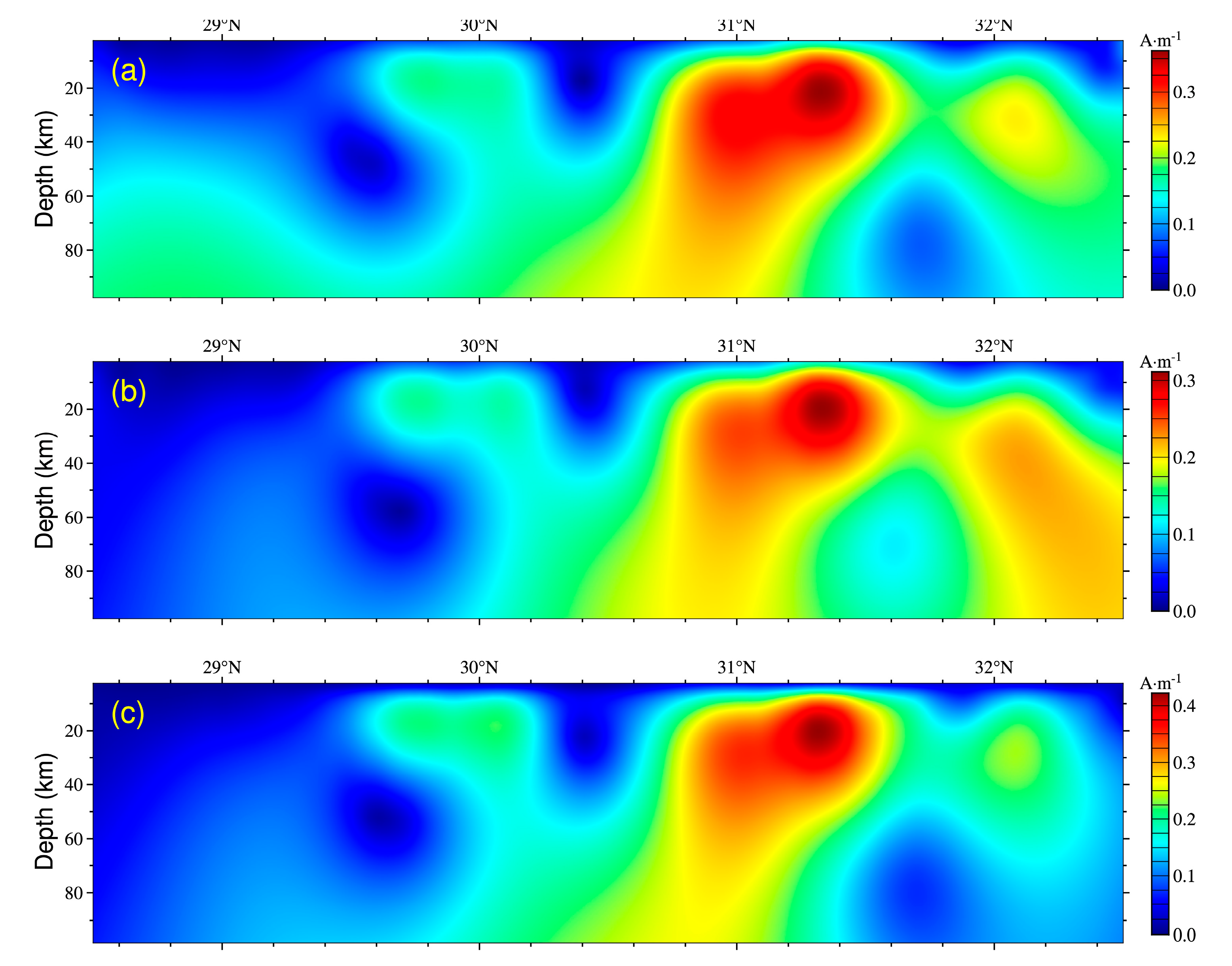
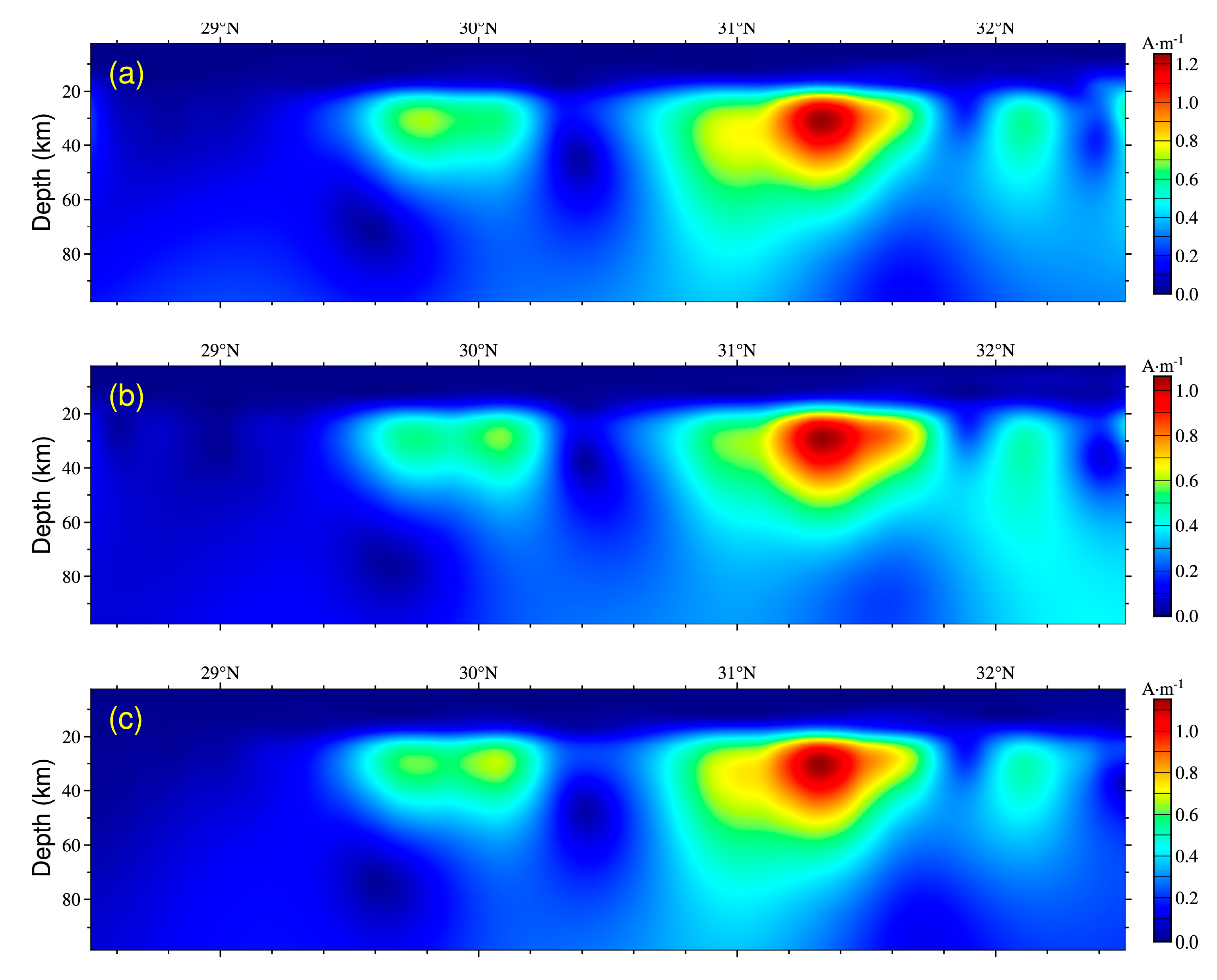
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Eppelbaum, L.; Katz, Y. A new regard on the tectonic map of the Arabian–African region inferred from the satellite gravity analysis. Acta Geophys. 2017, 65, 607–626. [Google Scholar] [CrossRef]
- Gao, G.; Kang, G.; Bai, C.; Li, G. Distribution of the crustal magnetic anomaly and geological structure in Xinjiang, China. J. Asian Earth Sci. 2013, 77, 12–20. [Google Scholar] [CrossRef]
- Nair, N.; Anand, S.P.; Rajaram, M.; Rao, P.R. A relook into the crustal architecture of Laxmi ridge, northeastern Arabian sea from geopotential data. J. Earth Syst. Sci. 2015, 124, 613–630. [Google Scholar] [CrossRef][Green Version]
- Li, C.; Wang, J. Variations in Moho and Curie depths and heat flow in eastern and Southeastern Asia. Mar. Geophys. Res. 2016, 37, 1258. [Google Scholar] [CrossRef]
- Idárraga-García, J.; Vargas, C.A. Depth to the bottom of magnetic layer in South America and its relationship to Curie isotherm, Moho depth and seismicity behavior. J. Geod. Geodyn. 2018, 9, 93–107. [Google Scholar] [CrossRef]
- Wen, L.; Kang, G.; Bai, C.; Gao, G. Studies on the relationships of the curie surface with heat flow and crustal structures in Yunnan province, China, and its adjacent areas. Earth Planets Space 2019, 71, 85. [Google Scholar] [CrossRef]
- Lelièvre, P.G.; Oldenburg, D.W. A 3d total magnetization inversion applicable when significant, complicated remanence is present. Geophysics 2009, 74, L21–L30. [Google Scholar] [CrossRef]
- Du, J.; Chen, C.; Liang, Q.; Wang, H.; Li, Y.; Lane, R. 3-d inversion of regional magnetic data in spherical coordinates and its preliminary application in Australia. In Proceedings of the 23rd International Geophysical Conference and Exhibition, Melbourne, Australia, 11–14 August 2013. [Google Scholar]
- Liu, S.; Hu, X.; Zhang, H.; Geng, M.; Zuo, B. 3d magnetization vector inversion of magnetic data: Improving and comparing methods. Pure Appl. Geophys. 2017, 174, 4421–4444. [Google Scholar] [CrossRef]
- Liu, S.; Hu, X.; Zuo, B.; Zhang, H.; Geng, M.; Ou, Y.; Yang, T.; Vatankhah, S. Susceptibility and remanent magnetization inversion of magnetic data with a priori information of the köenigsberger ratio. Geophys. J. Int. 2020, 221, 1090–1109. [Google Scholar] [CrossRef]
- Wang, M.Y.; Di, Q.Y.; Xu, K.; Wang, R. Magnetization vector inversion equations and forword and inversed 2-d model study. Chin. J. Geophys. 2004, 47, 528–534. [Google Scholar] [CrossRef]
- Liu, S.; Hu, X.; Liu, T.; Feng, J.; Gao, W.; Qiu, L. Magnetization vector imaging for borehole magnetic data based on magnitude magnetic anomaly. Geophysics 2013, 78, D429–D444. [Google Scholar] [CrossRef]
- Li, Y.; Shearer, S.E.; Haney, M.M.; Dannemiller, N. Comprehensive approaches to 3d inversion of magnetic data affected by remanent magnetization. Geophysics 2010, 75, L1–L11. [Google Scholar] [CrossRef]
- Liu, S.; Hu, X.; Xi, Y.; Liu, T.; Xu, S. 2d sequential inversion of total magnitude and total magnetic anomaly data affected by remanent magnetization. Geophysics 2015, 80, K1–K12. [Google Scholar] [CrossRef]
- Liang, Q.; Chen, C.; Li, Y. 3-d inversion of gravity data in spherical coordinates with application to the grail data. J. Geophys. Res. Planets 2014, 119, 1359–1373. [Google Scholar] [CrossRef]
- Wang, H.; Li, Y.; Chen, C. 3d joint inversion of magnetic amplitude and gravity gradiometry data in spherical coordinates. In Proceedings of the SEG New Orleans Annual Meeting, New Orleans, LA, USA, 5–9 August 2015; SEG Technical Program Expanded Abstracts. pp. 1553–1557. [Google Scholar]
- Zhang, Y.; Wu, Y.; Yan, J.; Wang, H.; Rodriguez, J.A.P.; Qiu, Y. 3d inversion of full gravity gradient tensor data in spherical coordinate system using local north-oriented frame. Earth Planets Space 2018, 70, 58. [Google Scholar] [CrossRef]
- Zhao, G.; Chen, B.; Uieda, L.; Liu, J.; Kaban, M.K.; Chen, L.; Guo, R. Efficient 3-d large-scale forward modeling and inversion of gravitational fields in spherical coordinates with application to lunar mascons. J. Geophys. Res. Solid Earth 2019, 124, 4157–4173. [Google Scholar] [CrossRef]
- Li, Y.G.; Oldenburg, D.W. 3-d inversion of magnetic data. Geophysics 1996, 61, 394–408. [Google Scholar] [CrossRef]
- Li, Y.; Oldenburg, D.W. Separation of regional and residual magnetic field data. Geophysics 1998, 63, 431–439. [Google Scholar] [CrossRef]
- Portniaguine, O.; Zhdanov, M.S. Focusing geophysical inversion images. Geophysics 1999, 64, 874–887. [Google Scholar] [CrossRef]
- Zhdanov, M.S.; Ellis, R.; Mukherjee, S. Three-dimensional regularized focusing inversion of gravity gradient tensor component data. Geophysics 2004, 69, 925–937. [Google Scholar] [CrossRef]
- Asli, M.; Marcotte, D.; Chouteau, M. Direct inversion of gravity data by cokriging. In Geostat2000, Proceedings of the International Geostatistics Congress, Rio de Janeiro, Brazil, 6–17 August 2000; Springer: Cape Town, South Africa, 2000. [Google Scholar]
- Geng Meixia, G.M.; Huang Danian, H.D.; Yang Qingjie, Y.Q.; Liu Yinping, L.Y. 3d inversion of airborne gravity-gradiometry data using cokriging. Geophysics 2014, 79, G37–G47. [Google Scholar] [CrossRef]
- Krahenbuhl, R.A.; Li, Y. Inversion of gravity data using a binary formulation. Geophys. J. Int. 2006, 167, 543–556. [Google Scholar] [CrossRef]
- Zhdanov, M.S.; Cox, L.H. Multinary inversion for tunnel detection. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1100–1103. [Google Scholar] [CrossRef]
- Sun, J.; Li, Y. Multidomain petrophysically constrained inversion and geology differentiation using guided fuzzy c-means clustering. Geophysics 2015, 80, D1–D18. [Google Scholar] [CrossRef]
- Constable, S.C.; Parker, R.L.; Constable, C.G. Occam’s inversion; A practical algorithm for generating smooth models from electromagnetic sounding data. Geophysics 1987, 52, 289–300. [Google Scholar] [CrossRef]
- Tikhonov, A.N.; Arsenin, V.Y. Solutions of Ill-Posed Problems; American Mathematical Society: Ann Arbor, MI, USA, 1977. [Google Scholar]
- Moghadas, D.; Engels, M.; Schwalenberg, K. 1d joint multi-offset inversion of time-domain marine controlled source electromagnetic data. Geophys. Prospect. 2015, 63, 1334–1354. [Google Scholar] [CrossRef]
- Tian, Y.; Wang, Y. Inversion of the density structure of the lithosphere in the north China craton from goce satellite gravity gradient data. Earth Planets Space 2018, 70, 173. [Google Scholar] [CrossRef]
- Lesur, V.; Gubbins, D. Using geomagnetic secular variation to separate remanent and induced sources of the crustal magnetic field. Geophys. J. Int. 2000, 142, 889–897. [Google Scholar] [CrossRef][Green Version]
- Hulot, G.; Olsen, N.; Thébault, E.; Hemant, K. Crustal concealing of small-scale core-field secular variation. Geophys. J. Int. 2009, 177, 361–366. [Google Scholar] [CrossRef]
- Hemant, K.; Maus, S. Why no anomaly is visible over most of the continent–ocean boundary in the global crustal magnetic field. Phys. Earth Planet. Inter. 2005, 149, 321–333. [Google Scholar] [CrossRef]
- Hemant, K.; Mitchell, A. Magnetic field modelling and interpretation of the Himalayan–Tibetan plateau and adjoining north indian plains. Tectonophysics 2009, 478, 87–99. [Google Scholar] [CrossRef]
- Gao, G.; Kang, G.; Li, G.; Bai, C. Crustal magnetic anomaly in the ordos region and its tectonic implications. J. Asian Earth Sci. 2015, 109, 63–73. [Google Scholar] [CrossRef]
- Vonfrese, R.R.B.; Hinze, W.; Braile, L.; Luca, A. Spherical-earth gravity and magnetic anomaly modeling by gauss-legendre quadrature integration. J. Geophys. Z. Geophys. 1981, 49, 234–242. [Google Scholar]
- Asgharzadeh, M.F.; von Frese, R.R.B.; Kim, H.R. Spherical prism magnetic effects by gauss-legendre quadrature integration. Geophys. J. Int. 2008, 173, 315–333. [Google Scholar] [CrossRef]
- Du, J.; Chen, C.; Lesur, V.; Lane, R.; Wang, H. Magnetic potential, vector and gradient tensor fields of a tesseroid in a geocentric spherical coordinate system. Geophys. J. Int. 2015, 201, 1977–2007. [Google Scholar] [CrossRef]
- Blakely, R.J. Potential Theory in Gravity and Magnetic Applications, 1st ed.; Cambridge University Press: New York, NY, USA, 1995; pp. 91–93. [Google Scholar]
- Heiskanen, W.A.; Moritz, H. Physical Geodesy; W.H. Freeman and Company: San Francisco, CA, USA; London, UK, 1967; pp. 46–48. [Google Scholar]
- Ku, C.C. A direct computation of gravity and magnetic anomalies caused by 2- and 3-dimensional bodies of arbitrary shape and arbitrary magnetic polarization by equivalent-point method and a simplified cubic spline. Geophysics 1977, 42, 610–622. [Google Scholar] [CrossRef]
- Asgharzadeh, M.F.; von Frese, R.R.B.; Kim, H.R.; Leftwich, T.E.; Kim, J.W. Spherical prism gravity effects by gauss-legendre quadrature integration. Geophys. J. Int. 2007, 169, 1–11. [Google Scholar] [CrossRef]
- Heck, B.; Seitz, K. A comparison of the tesseroid, prism and point-mass approaches for mass reductions in gravity field modelling. J. Geodesy 2007, 81, 121–136. [Google Scholar] [CrossRef]
- Uieda, L.; Barbosa, V.C.F.; Braitenberg, C. Tesseroids: Forward-modeling gravitational fields in spherical coordinates. Geophysics 2016, 81, F41–F48. [Google Scholar] [CrossRef]
- Li, Y.G. 3-d inversion of gravity gradiometer data. In Proceedings of the Paper Presented at the 2001 SEG Annual Meeting, San Antonio, TX, USA, 9–14 September 2001. [Google Scholar]
- Joulidehsar, F.; Moradzadeh, A.; Doulati Ardejani, F. An improved 3d joint inversion method of potential field data using cross-gradient constraint and lsqr method. Pure Appl. Geophys. 2018, 175, 4389–4409. [Google Scholar] [CrossRef]
- Pilkington, M. 3-d magnetic imaging using conjugate gradients. Geophysics 1997, 62, 1132–1142. [Google Scholar] [CrossRef]
- Li, Y.; Yang, Y. Gravity data inversion for the lithospheric density structure beneath north China craton from egm 2008 model. Phys. Earth Planet. Inter. 2011, 189, 9–26. [Google Scholar] [CrossRef]
- Chen, S.H.; Zhu, Z.Q.; Lu, G.Y.; Cao, S.J. Inversion of gravity gradient tensor based on preconditioned conjugate gradient. J. Cent. South Univ. (Sci. Technol.) 2013, 44, 619–625, (In Chinese with English abstract). [Google Scholar]
- Last, B.J.; Kubik, K. Compact gravity inversion. Geophysics 1983, 48, 713–721. [Google Scholar] [CrossRef]
- Guillen, A.; Menichetti, V. Gravity and magnetic inversion with minimization of a specific functional. Geophysics 1984, 49, 1354–1360. [Google Scholar] [CrossRef]
- Silva, J.B.C.; Medeiros, W.E.; Barbosa, V.C.F. Gravity inversion using convexity constraint. Geophysics 2000, 65, 102–112. [Google Scholar] [CrossRef]
- Ames, L.; Tilton, G.R.; Zhou Gaozhi, Z.G. Timing of collision of the Sino-Korean and Yangtse cratons; U-pb zircon dating of coesite-bearing eclogites. Geology 1993, 21, 339–342. [Google Scholar] [CrossRef]
- Hacker, B.R.; Ratschbacher, L.; Liou, J.G. Subduction, collision and exhumation in the ultrahigh-pressure Qinling-Dabie orogen. Geol. Soc. Lond. Spec. Publ. 2004, 226, 157–175. [Google Scholar] [CrossRef]
- Zhang, H.; Gao, S.; Zhong, Z.; Zhang, B.; Zhang, L.; Hu, S. Geochemical and sr–nd–pb isotopic compositions of cretaceous granitoids: Constraints on tectonic framework and crustal structure of the Dabieshan ultrahigh-pressure metamorphic belt, China. Chem. Geol. 2002, 186, 281–299. [Google Scholar] [CrossRef]
- Wang, C.; Zeng, R.; Mooney, W.D.; Hacker, B.R. A crustal model of the ultrahigh-pressure Dabie Shan orogenic belt, China, derived from deep seismic refraction profiling. J. Geophys. Res. Solid Earth 2000, 105, 10857–10869. [Google Scholar] [CrossRef]
- Yang, Y.; Li, Y. Crustal structure of the Dabie orogenic belt (eastern China) inferred from gravity and magnetic data. Tectonophysics 2018, 723, 190–200. [Google Scholar] [CrossRef]
- Xu, Y.X.; Zhang, S.; Griffin, W.L.; Yang, Y.J.; Yang, B.; Luo, Y.H.; Zhu, L.P.; Afonso, J.C.; Lei, B.H. How did the Dabie orogen collapse? Insights from 3-d magnetotelluric imaging of profile data. J. Geophys. Res. Solid Earth 2016, 121, 5169–5185. [Google Scholar] [CrossRef]
- Purucker, M.E.; Whaler, K.A. Crustal magnetism. Treatise Geophys. 2007, 5, 195–235. [Google Scholar]
- Shutong, X.; Wen, S.; Yican, L.; Laili, J.; Shouyuan, J.; Okay, A.I.; Sengor, A.M.C. Diamond from the Dabie Shan metamorphic rocks and its implication for tectonic setting. Science 1992, 256, 80–82. [Google Scholar] [CrossRef]
- Chopin, C. Ultrahigh-pressure metamorphism: Tracing continental crust into the mantle. Earth Planet. Sci. Lett. 2003, 212, 1–14. [Google Scholar] [CrossRef]
- Faure, M.; Lin, W.; Schärer, U.; Shu, L.; Sun, Y.; Arnaud, N. Continental subduction and exhumation of uhp rocks. Structural and geochronological insights from the Dabieshan (east China). Lithos 2003, 70, 213–241. [Google Scholar] [CrossRef]
- Wang, J.; Deng, S. Emplacement age for the mafic-ultramafic plutons in the northern Dabie Mts. (Hubei): Zircon U-Pb, Sm-Nd and 40Ar/39Ar dating. Sci. China Ser. D Earth Sci. 2002, 45, 1. [Google Scholar] [CrossRef]
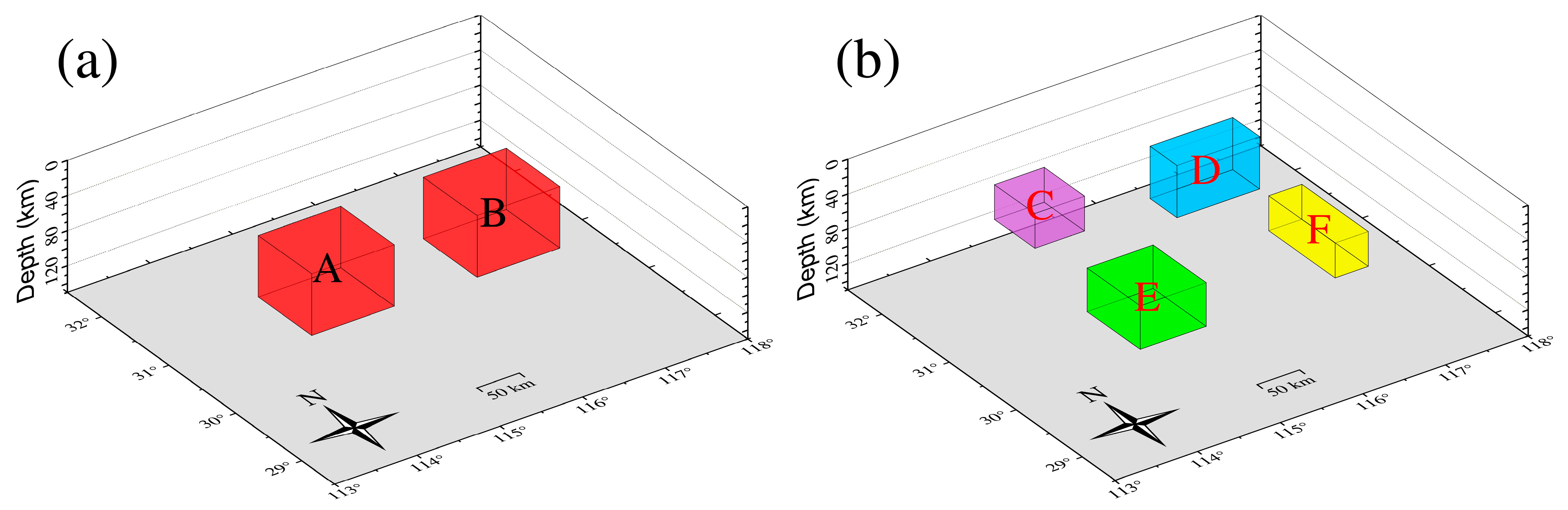
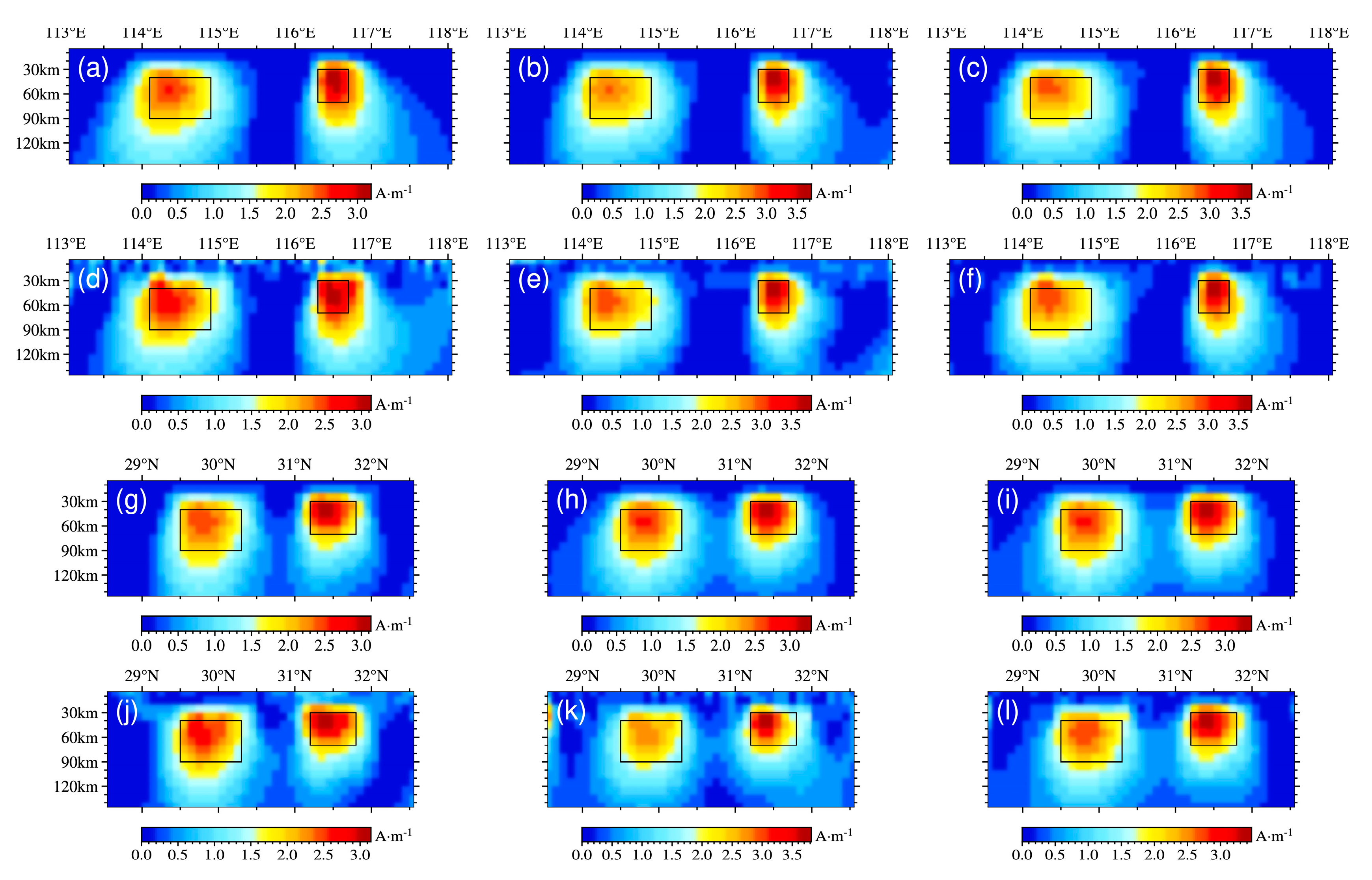

| Model Id | Longitude | Latitude | Depth | Inclination | Declination |
|---|---|---|---|---|---|
| A | 114.0–115.0 | 30.1–30.9 | 30–100 | 45 | 45 |
| B | 116.0–117.0 | 30.1–30.9 | 30–100 | 45 | 45 |
| C | 114.2–114.8 | 31.2–31.8 | 30–70 | 45 | 45 |
| D | 116.0–117.0 | 31.3–31.7 | 40–100 | 60 | 45 |
| E | 114.1–114.9 | 29.5–30.3 | 40–90 | 45 | 60 |
| F | 116.3–116.7 | 29.3–30.3 | 30–70 | 90 | 30 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Lu, G.; Zhu, Z.; Cao, S. An Improved 3D Magnetization Inversion Based on Smoothness Constraints in Spherical Coordinates. Magnetochemistry 2022, 8, 157. https://doi.org/10.3390/magnetochemistry8110157
Zhang L, Lu G, Zhu Z, Cao S. An Improved 3D Magnetization Inversion Based on Smoothness Constraints in Spherical Coordinates. Magnetochemistry. 2022; 8(11):157. https://doi.org/10.3390/magnetochemistry8110157
Chicago/Turabian StyleZhang, Liang, Guangyin Lu, Ziqiang Zhu, and Shujin Cao. 2022. "An Improved 3D Magnetization Inversion Based on Smoothness Constraints in Spherical Coordinates" Magnetochemistry 8, no. 11: 157. https://doi.org/10.3390/magnetochemistry8110157
APA StyleZhang, L., Lu, G., Zhu, Z., & Cao, S. (2022). An Improved 3D Magnetization Inversion Based on Smoothness Constraints in Spherical Coordinates. Magnetochemistry, 8(11), 157. https://doi.org/10.3390/magnetochemistry8110157






