On the Concurrent Bipartite Entanglement of a Spin-1 Heisenberg Diamond Cluster Developed for Tetranuclear Nickel Complexes

Abstract

The bipartite entanglement of a quantum spin-1 Heisenberg diamond cluster in the presence of the external magnetic field is quantified through the negativity, which is calculated for spin pairs from a diagonal and a side of the diamond spin cluster taking into consideration two different coupling constants. The magnetic field may cause a few crossings of energy levels of the spin-1 Heisenberg diamond cluster, which is responsible at low enough temperatures for a stepwise dependence of the negativity on the magnetic field accompanied with a drop of the negativity at respective magnetic-field-driven transitions due to emergence of mixed states. It is shown that the bipartite entanglement between spin pairs on a diagonal and a side of the diamond spin cluster is concurrent although they may eventually become both nonzero albeit not fully saturated. It is predicted that the tetranuclear nickel complex [Ni${}_4$($\mu$-CO${}_3$)${}_2$(aetpy)${}_8$](ClO${}_4$)${}_4$ (aetpy = 2-aminoethyl-pyridine), which represents an experimental realization of the spin-1 Heisenberg diamond cluster with two different antiferromagnetic coupling constants, exhibits a substantial bipartite entanglement between two spin-1 Ni${}^{2+}$ magnetic ions from a shorter diagonal of the diamond spin cluster up to temperatures approximately about 50 K and up to magnetic fields about 70 T.

1. Introduction

Entanglement is one of the most striking characteristics of quantum physics and it has attracted much attention since its emergence. An extraordinary correlation and instant action at distance, which exist between entangled particles, does not have any classical counterpart. Retrospectively, it recalls the challenge of some fundamental assumptions of physics [1,2], which led to the violation of locality principle that does not hold for quantum-mechanical systems [3,4].

It is supposed that the entanglement is proficient for the development of novel quantum technologies such as quantum computers and quantum information processing [5,6]. Since the second quantum revolution came to existence, it became advantageous to investigate quantum spin systems, which may also promote development of quantum computers, quantum memory devices, quantum information processing and so on. A crucial issue concerned with a quantum computer that outperforms a classical computer both in precision and speed of calculations [7] is to exploit qubits as primary building blocks of hardware as well as suitable quantum algorithms [8,9].

Initially, the entanglement was believed to exist just within the atomic scale, because the systems with constituents at larger scales are exposed to interaction with the environment being the source of a quantum decoherence [10]. In contrast, current theoretical and experimental studies indicate the presence of entanglement at nonzero temperatures in solid-state magnetic materials. From this perspective, there has been a great interest and effort to search for molecular magnetic materials for which entanglement survives in common environmental circumstances, such as high temperature, magnetic field and can be manipulated by the standard experimental techniques such as a pulsed electron spin resonance [11,12,13,14,15]. The search for advanced molecular magnetic materials that would retain their quantum-mechanical features up to sufficiently high (at best room) temperature is thus of principal importance for development of novel technologies based on fully quantum grounds [12,13,14,15].

The quantum Heisenberg spin model and its various modifications offer comprehensive description of magnetic properties as well as quantum entanglement of molecular magnetic materials, which can be viewed from the magnetic point of view as experimental representatives of quantum Heisenberg spin dimers [16], quantum Heisenberg spin clusters [17] or even quantum Heisenberg spin chains [18]. To date, the entanglement of various spin-1/2 quantum systems have been studied abundantly from different perspectives [19,20,21,22,23,24,25], while the state-of-the-art knowledge of entanglement of quantum systems with higher spin sizes is compared to this much less developed and is far from being fully understood [26,27,28,29]. The bipartite as well as multipartite entanglement of a spin-1/2 Heisenberg tetramer with different spatial configurations was for instance detailed studied through two measures of entanglement referred to as the concurrence and fidelity [30,31].

In this article, we will comprehensively examine a bipartite entanglement of the spin-1 Heisenberg diamond cluster, which is designed as the appropriate model system of tetranuclear nickel complexes. To this end, we will calculate the negativity for spin pairs along a diagonal and a side of the spin-1 Heisenberg diamond cluster, which may also serve as a measure of quantum and thermal entanglement for pure as well as mixed states, respectively. The main goal of the present study is to investigate a concurrent bipartite entanglement emergent along a diagonal and a side of the spin-1 Heisenberg diamond cluster as well as its persistence with respect to rising temperature and magnetic field.

This paper is organized as follows. In Section 2, we will introduce a spin-1 Heisenberg diamond cluster and obtain the exact solution for the negativity. In Section 3, we demonstrate typical dependencies of the negativity as a function of temperature and magnetic field for a few different values of the coupling constant ratio. Our conjecture about the negativity of the tetranuclear nickel complex [Ni${}_4$($\mu$-CO${}_3$)${}_2$(aetpy)${}_8$](ClO${}_4$)${}_4$ (aetpy = 2-aminoethyl-pyridine) serving as an experimental realization of the spin-1 Heisenberg diamond cluster is presented in Section 4. Finally, the conclusion and summary of the most important findings are presented in Section 5. Some technical details concerning with the calculation procedure are presented in Appendix A, Appendix B and Appendix C.

2. Model and Method

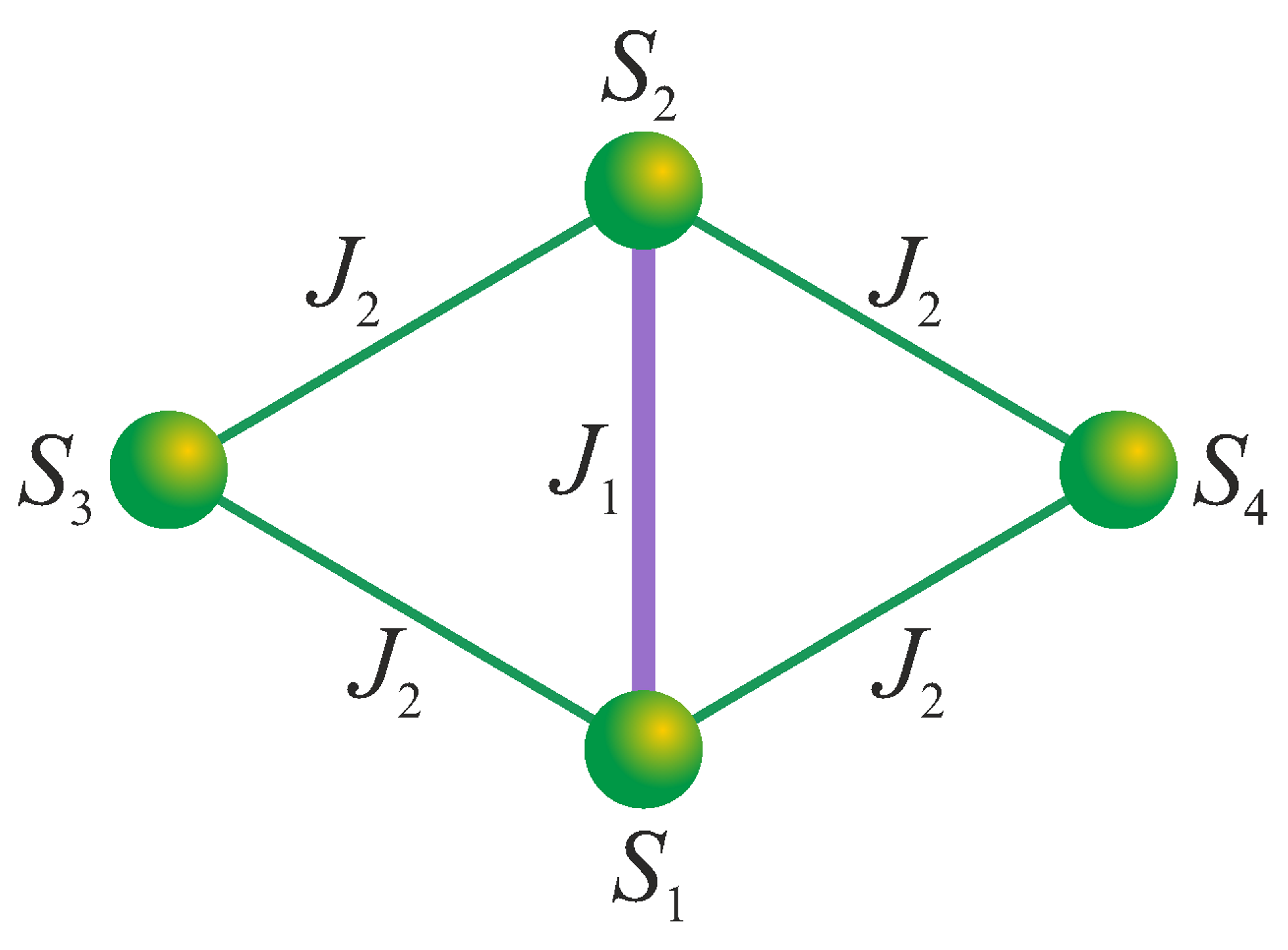
In the present paper, we will investigate in detail a quantum and thermal entanglement of the spin-1 Heisenberg diamond cluster defined through the Hamiltonian:

$$\begin{array}{c}\hfill \widehat{H}=J_1{\widehat{\mathbf{S}}}_1·{\widehat{\mathbf{S}}}_2+J_2({\widehat{\mathbf{S}}}_1+{\widehat{\mathbf{S}}}_2)·({\widehat{\mathbf{S}}}_3+{\widehat{\mathbf{S}}}_4)-h\sum _{i=1}^4{\widehat{S}}_i^z,\end{array}$$

(1)

which relates to a magnetic structure of the diamond spin cluster schematically illustrated in Figure 1 and previously referred to also as the butterfly tetramer [32,33]. The diamond spin cluster involves four spin-1 operators ${\widehat{\mathbf{S}}}_i$$(i=1–4)$, which are coupled together through two different coupling constants $J_1$ and $J_2$ along the shorter diagonal (the body of butterfly) and the side (wings of the butterfly) of the diamond spin cluster, respectively, (see Figure 1). The first and second terms of the Hamiltonian (1) of the spin-1 Heisenberg diamond cluster are thus connected to the relevant exchange interactions $J_1$ and $J_2$, while the last term is the Zeeman’s term $h=g{\mu }_{\mathrm{B}}B$ that determines an energy of magnetic spin moments in an external magnetic field B (g is the Landé g-factor and ${\mu }_{\mathrm{B}}$ is Bohr magneton). It is worthwhile to remark that no single-ion anisotropy is considered in the Hamiltonian (1), because the single-ion anisotropy of spin-1 Ni${}^{2+}$ magnetic ions is negligible within the tetranuclear molecular-based magnetic material [Ni${}_4$($\mu$-CO${}_3$)${}_2$(aetpy)${}_8$](ClO${}_4$)${}_4$ serving as an experimental realization of the spin-1 Heisenberg diamond cluster [32,33].

By introducing two composite spin operators ${\widehat{\mathbf{S}}}_{12}={\widehat{\mathbf{S}}}_1+{\widehat{\mathbf{S}}}_2$, ${\widehat{\mathbf{S}}}_{34}={\widehat{\mathbf{S}}}_3+{\widehat{\mathbf{S}}}_4$ and the total spin operator ${\widehat{\mathbf{S}}}_T={\widehat{\mathbf{S}}}_{12}+{\widehat{\mathbf{S}}}_{34}$ together with its z-component ${\widehat{S}}_T^z={\widehat{S}}_{12}^z+{\widehat{S}}_{34}^z$ within the Kambe projection method [34,35], the Hamiltonian (1) of the spin-1 Heisenberg diamond cluster can be alternatively rewritten into the following equivalent form:

$$\begin{array}{c}\hfill \widehat{H}=\frac{J_1}{2}({\widehat{\mathbf{S}}}_{12}^2-4)+\frac{J_2}{2}({\widehat{\mathbf{S}}}_T^2-{\widehat{\mathbf{S}}}_{12}^2-{\widehat{\mathbf{S}}}_{34}^2)-h{\widehat{S}}_T^z.\end{array}$$

(2)

The energy eigenvalues of the spin-1 Heisenberg diamond cluster can be accordingly expressed within the Kambe coupling scheme [34,35] in terms of four possible quantum spin numbers $S_{12}$, $S_{34}$, $S_T$ and $S_T^z$:

$$\begin{array}{c}\hfill E=\frac{J_1}{2}[S_{12}(S_{12}+1)-4]+\frac{J_2}{2}[S_T(S_T+1)-S_{12}(S_{12}+1)-S_{34}(S_{34}+1)]-h{S}_T^z.\end{array}$$

(3)

A complete set of the energy eigenvalues of the spin-1 Heisenberg diamond cluster was exactly calculated in Reference [36], to which readers interested in further details are referred. For the sake of completeness, all possible lowest-energy eigenvectors of the spin-1 Heisenberg diamond cluster are listed in Appendix A. The primary goal of the present work is to compare a relative strength of bipartite entanglement emergent within the spin-1 Heisenberg diamond cluster between the spin pair $S_1$–$S_2$ on the diagonal (body) and the spin pair $S_1$–$S_3$ on the side (wing) of the diamond spin cluster (butterfly spin tetramer). It is quite clear that the bipartite entanglement within the spin pair $S_1$–$S_3$ is inherent to another three structurally identical spin pairs $S_1$–$S_4$, $S_2$–$S_4$, and $S_2$–$S_3$ as well.

To quantify a degree of the bipartite entanglement within the spin-1 Heisenberg diamond cluster one may adapt according to the Peres-Horodecki criterion the quantity negativity [37,38,39]. The first step required for calculation of the negativity is to derive an explicit form of the overall density operator:

$$\begin{array}{c}\hfill \widehat{\rho }=\frac{1}{Z}\exp (-\beta \widehat{H})=\frac{1}{Z}\sum _{i=1}^{81}\exp (-\beta E_i)|{\psi }_i\rangle \langle {\psi }_i|,\end{array}$$

(4)

where $\beta =1/\left(k_{\mathrm{B}}T\right)$, $k_{\mathrm{B}}$ is the Boltzmann’s constant and T is the absolute temperature. Moreover, $E_i$ and $|{\psi }_i\rangle$ are the respective eigenvalues and eigenvectors of the Hamiltonian (1) obtained by solving the eigenvalue problem $\widehat{H}|{\psi }_i\rangle =E_i|{\psi }_i\rangle$ and Z is the relevant partition function $Z={\sum }_i\exp (-\beta E_i)$. In the second step one traces out in the overall density operator (4) degrees of freedom of two spins, say $S_3$ and $S_4$, in order to obtain the reduced density operator for the other two spins ${\widehat{\rho }}_{12}={Tr}_{S_3}{Tr}_{S_4}\widehat{\rho }$. The third step lies in deriving the matrix representation of the reduced density operator ${\rho }_{12}=\langle S_1^z,S_2^z|\widehat{{\rho }_{12}}|S_1^{z^{\prime }},S_2^{z^{\prime }}\rangle$ in the standard basis of vectors $|S_1^z,S_2^z\rangle$. In the fourth step one performs a partial transposition with respect to one of two remaining spins (e.g., $S_2$) in order to derive the partially transposed density matrix ${\rho }_{12}^{T_2}=\langle S_1^z,S_2^z|\widehat{\rho }|S_1^{z^{\prime }},S_2^{z^{\prime }}{\rangle }^{T_2}=\langle S_1^z,S_2^{z^{\prime }}|\widehat{\rho }|S_1^{z^{\prime }},S_2^z\rangle$. The fifth final step consists of finding eigenvalues of the partially transposed density matrix, since the negativity $\mathcal{N}$ is according to the formula put forward by Vidal and Werner [39] defined by a sum of absolute values of negative eigenvalues of the partially transposed density matrix:

$$\begin{array}{c}\hfill \mathcal{N}=\sum _{{\lambda }_i<0}\left|{\lambda }_i\right|=\sum _i\frac{|{\lambda }_i|-{\lambda }_i}{2}.\end{array}$$

(5)

The eigenvalue problem for the spin-1 Heisenberg diamond cluster was solved in Reference [36] and hence, one may directly proceed to an investigation of the bipartite entanglement quantified through the negativity. It is noteworthy that the spin-1 Heisenberg diamond cluster defined through the Hamiltonian (1) has 81 eigenstates and its density matrix is also of the same dimension. On the other hand, the reduced density matrix obtained after tracing out degrees of freedom of two spins is only of dimension nine. It was shown in Reference [36] that the eigenvectors of the spin-1 Heisenberg diamond cluster given by the Hamiltonian (1) can be displayed in the form $|\psi \rangle =|S_T,S_{12},S_{34},S_T^z\rangle$, which can be expressed as a linear combination of standard basis state vectors $|\psi \rangle ={\sum }_{S_1^z}{\sum }_{S_2^z}{\sum }_{S_3^z}{\sum }_{S_4^z}{c}_{S_1^z,S_2^z,S_3^z,S_4^z}|S_1^z,S_2^z,S_3^z,S_4^z\rangle$.

For illustration, let us calculate the negativity for the spin pair $S_1$–$S_2$. In the first step, one needs to obtain the reduced density operator ${\widehat{\rho }}_{12}$ of the spin pair $S_1$–$S_2$ by performing a partial trace over the state vectors $|S_3^z,S_4^z\rangle$ of the other two spins:

$$\begin{array}{c}\hfill {\widehat{\rho }}_{12}=\frac{1}{Z}\sum _{S_3^z}\sum _{S_4^z}\sum _{i=1}^{81}\langle S_3^z,S_4^z|{\psi }_i\rangle \langle {\psi }_i|S_3^z,S_4^z\rangle {\mathrm{e}}^{-\beta E_i}.\end{array}$$

(6)

The individual elements of the reduced density matrix, which corresponds to the reduced density operator (6), can be calculated according to the formula:

$$\begin{array}{c}\hfill \langle S_1^z,S_2^z|{\widehat{\rho }}_{12}|S_1^{z^{\prime }},S_2^{z^{\prime }}\rangle =\frac{1}{Z}\sum _{S_3^z}\sum _{S_4^z}\sum _{i=1}^{81}\langle S_1^z,S_2^z,S_3^z,S_4^z|{\psi }_i\rangle \langle {\psi }_i|S_1^{z^{\prime }},S_2^{z^{\prime }},S_3^z,S_4^z\rangle {\mathrm{e}}^{-\beta E_i},\end{array}$$

(7)

whereby the overall reduced density matrix reads as follows:

$${\rho }_{12}=\begin{array}{cc}\hfill & \begin{array}{lllllllll}\hspace{1em}|1,1\rangle \hfill & \hspace{1em}|1,0\rangle \hfill & |1,-1\rangle \hfill & |0,1\rangle \hfill & |0,0\rangle \hfill & |0,-1\rangle \hfill & |-1,1\rangle \hfill & |-1,0\rangle \hfill & |-1,-1\rangle \hfill \end{array}\hfill \\ \begin{array}{c}\hfill \langle 1,1|\hfill \\ \hfill \langle 1,0|\hfill \\ \hfill \langle 1,-1|\hfill \\ \hfill \langle 0,1|\hfill \\ \hfill \langle 0,0|\hfill \\ \hfill \langle 0,-1|\hfill \\ \hfill \langle -1,1|\hfill \\ \hfill \langle -1,0|\hfill \\ \hfill \langle -1,-1|\hfill \end{array}\hfill & \left(\begin{array}{ccccccccc}{\rho }_{11}& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& {\rho }_{22}& 0& {\rho }_{24}& 0& 0& 0& 0& 0\\ 0& 0& {\rho }_{33}& 0& {\rho }_{35}& 0& {\rho }_{37}& 0& 0\\ 0& {\rho }_{42}& 0& {\rho }_{44}& 0& 0& 0& 0& 0\\ 0& 0& {\rho }_{53}& 0& {\rho }_{55}& 0& {\rho }_{57}& 0& 0\\ 0& 0& 0& 0& 0& {\rho }_{66}& 0& {\rho }_{68}& 0\\ 0& 0& {\rho }_{73}& 0& {\rho }_{75}& 0& {\rho }_{77}& 0& 0\\ 0& 0& 0& 0& 0& {\rho }_{86}& 0& {\rho }_{88}& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& {\rho }_{99}\end{array}\right)\hfill \end{array}.$$

(8)

An explicit form of individual elements of the reduced density matrix (8) is for brevity quoted in Appendix B. If one performs a partial transpose $T_2$ of the reduced density matrix (8) with respect to the states of the second spin $S_2$ one acquires the partially transposed reduced density matrix:

$$\begin{array}{c}\hfill {\rho }_{12}^{T_2}=\langle S_1^z,S_2^z|{\rho }_{12}{|S_1^{z^{\prime }},S_2^{z^{\prime }}\rangle }^{T_2}=\frac{1}{Z}\sum _{S_3^z}\sum _{S_4^z}\sum _{i=1}^{81}\langle S_1^z,S_2^{z^{\prime }},S_3^z,S_4^z|{\psi }_i\rangle \langle {\psi }_i|S_1^{z^{\prime }},S_2^z,S_3^z,S_4^z\rangle {\mathrm{e}}^{-\beta E_i},\end{array}$$

which has the following matrix representation:

$$\begin{array}{c}\hfill {\rho }_{12}^{T_2}=\left(\begin{array}{ccccccccc}{\rho }_{11}& 0& 0& 0& {\rho }_{24}& 0& 0& 0& {\rho }_{37}\\ 0& {\rho }_{22}& 0& 0& 0& {\rho }_{35}& 0& 0& 0\\ 0& 0& {\rho }_{33}& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& {\rho }_{44}& 0& 0& 0& {\rho }_{57}& 0\\ {\rho }_{24}& 0& 0& 0& {\rho }_{55}& 0& 0& 0& {\rho }_{68}\\ 0& {\rho }_{35}& 0& 0& 0& {\rho }_{66}& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& {\rho }_{77}& 0& 0\\ 0& 0& 0& {\rho }_{57}& 0& 0& 0& {\rho }_{88}& 0\\ {\rho }_{37}& 0& 0& 0& {\rho }_{68}& 0& 0& 0& {\rho }_{99}\end{array}\right).\end{array}$$

(9)

In the last step of our calculation one diagonalizes the partially transposed reduced density matrix (9) by solving the eigenvalue problem $\det |{\rho }_{12}^{T_2}-\lambda |=0$. According to Equation (5), the sum of negative eigenvalues of the partially transposed reduced density matrix (9) then determines the negativity. It directly follows from the block diagonal form of the partially transposed density matrix (9) that two elements ${\rho }_{33}$ and ${\rho }_{77}$ on the main diagonal are decoupled from all other matrix elements and they directly represent two eigenvalues. The remaining eigenvalues can be found by solving two quadratic equations and one cubic equation pertinent to three orthogonal blocks of the partially transposed density matrix (9). A complete set of the eigenvalues of the partially transposed density matrix (9) reads:

$$\begin{array}{cc}\hfill {\lambda }_1& ={\rho }_{33},{\lambda }_2={\rho }_{77},\hfill \\ \hfill {\lambda }_3& =\frac{1}{2}\left[{\rho }_{22}+{\rho }_{66}+\sqrt{{({\rho }_{22}-{\rho }_{66})}^2+4{\rho }_{35}^2}\right],{\lambda }_4=\frac{1}{2}\left[{\rho }_{44}+{\rho }_{88}+\sqrt{{({\rho }_{44}-{\rho }_{88})}^2+4{\rho }_{57}^2}\right],\hfill \\ \hfill {\lambda }_5& =\frac{1}{2}\left[{\rho }_{22}+{\rho }_{66}-\sqrt{{({\rho }_{22}-{\rho }_{66})}^2+4{\rho }_{35}^2}\right],{\lambda }_6=\frac{1}{2}\left[{\rho }_{44}+{\rho }_{88}-\sqrt{{({\rho }_{44}-{\rho }_{88})}^2+4{\rho }_{57}^2}\right],\hfill \\ \hfill {\lambda }_n& =-\frac{a}{3}+2\mathrm{sgn}\left(q\right)\sqrt{p}cos\left[\frac{\varphi +2\pi (n-7)}{3}\right],n=7,8,9,\hfill \end{array}$$

where the parameters determining three cubic roots are defined as follows:

$$\begin{array}{cc}\hfill a& =-\left({\rho }_{11}+{\rho }_{55}+{\rho }_{99}\right),\hfill \\ \hfill b& ={\rho }_{11}{\rho }_{55}+{\rho }_{55}{\rho }_{99}+{\rho }_{11}{\rho }_{99}-\left({\rho }_{24}^2+{\rho }_{37}^2+{\rho }_{68}^2\right),\hfill \\ \hfill c& ={\rho }_{11}{\rho }_{68}^2+{\rho }_{55}{\rho }_{37}^2+{\rho }_{99}{\rho }_{24}^2-{\rho }_{11}{\rho }_{55}{\rho }_{99}-2{\rho }_{24}{\rho }_{37}{\rho }_{68},\hfill \\ \hfill p& =\frac{a^2}{9}-\frac{b}{3},\hfill \\ \hfill q& =-{\left(\frac{a}{3}\right)}^3+\frac{ab}{6}-\frac{c}{2},\hfill \\ \hfill \varphi & =arctan\left(\frac{\sqrt{p^3-q^2}}{q}\right).\hfill \end{array}$$

It is quite evident that the eigenvalues ${\lambda }_1$, ${\lambda }_2$, ${\lambda }_3$ and ${\lambda }_4$ are always positive. In addition, the detailed numerical analysis reveals the same feature also for the eigenvalue ${\lambda }_9$. Those five positive eigenvalues of the partially transposed reduced density matrix (9) thus do not contribute to the negativity. On the other hand, the eigenvalues ${\lambda }_5$, ${\lambda }_6$, ${\lambda }_7$ and ${\lambda }_8$ may be negative and they thus determine the negativity (5).

As could be expected, the matrix representation of the reduced density matrix (7) turns out to be identical with the one of the spin-1 Heisenberg dimer [40], whereby it only differs through a more complex form of the individual matrix elements explicitly quoted in Appendix B. Before ending this section, it should be emphasized that the same calculation procedure can be repeated for the negativity measuring a bipartite entanglement of the spin pair $S_1$–$S_3$ with exception of that a partial trace is performed over states of the spins $S_2$ and $S_4$ in order to obtain the reduced density operator ${\widehat{\rho }}_{13}$. Bearing all this in mind, all formulas presented in above for the negativity remain valid and one only needs to consider different elements of the partially transposed reduced density matrix ${\rho }_{13}^{T_3}$ explicitly quoted in Appendix C.

3. Results and Discussions

In this section, we will present and discuss the most interesting results for the bipartite entanglement of the spin-1 Heisenberg diamond cluster, which will be quantified through the negativity calculated for two different spin pairs $S_1$–$S_2$ and $S_1$–$S_3$, respectively. Let us first proceed to an investigation of the bipartite quantum entanglement between aforementioned spin pairs at zero temperature. It was shown in Reference [36] that the spin-1 Heisenberg diamond cluster has up to five or eight different ground states depending on whether the exchange interaction $J_1$ along the shorter diagonal of the diamond spin cluster is ferromagnetic $J_1<0$ or antiferromagnetic $J_1>0$, respectively. Generally, the density operator (4) reduces in a zero-temperature limit to a relatively simple projection operator $\widehat{\rho }=|\psi \rangle \langle \psi |$ ascribed to the relevant ground-state eigenvector, from which one can readily calculate the negativity. For completeness, we listed an explicit form of all ground-state eigenvectors $|S_T,S_{12},S_{34}\rangle$ in Appendix A. It should be pointed out that the z-component of the total spin necessarily equals to the total spin $S_T^z=S_T$ within all possible ground states at nonzero magnetic fields and thus, the ground-state eigenvectors may be unambiguously characterized through the set of only three quantum spin numbers $S_T$, $S_{12}$ and $S_{34}$.

For illustration, we will present hereafter a few calculation details for the negativity of the spin pair $S_1$–$S_2$ within the ground state $|1,1,2\rangle$, while the calculation of the negativity for all other ground states is quite analogous and will be therefore omitted for the sake of brevity. If the negativity is calculated for the spin pair $S_1$–$S_2$, the basis state vectors $|S_1^z,S_2^z,S_3^z,S_4^z\rangle$ should be split into the product state $|S_1^z,S_2^z,S_3^z,S_4^z\rangle =|S_1^z,S_2^z\rangle \otimes |S_3^z,S_4^z\rangle$ and the relevant ground-state eigenvector can be consequently written as their linear combination $|S_T,S_{12},S_{34}\rangle ={\sum }_{S_1^z}{\sum }_{S_2^z}{\sum }_{S_3^z}{\sum }_{S_4^z}{c}_{S_1^z,S_2^z,S_3^z,S_4^z}|S_1^z,S_2^z\rangle \otimes |S_3^z,S_4^z\rangle$. More concretely, the ground-state eigenvector $|1,1,2\rangle$ acquires the following explicit form:

$$\begin{array}{cc}\hfill |1,1,2\rangle & =\sqrt{\frac{3}{10}}(|-1,0\rangle -|0,-1\rangle )\otimes |1,1\rangle +\sqrt{\frac{3}{40}}(|1,-1\rangle -|-1,1\rangle )\otimes (|0,1\rangle -|1,0\rangle )\hfill \\ \hfill & -\frac{1}{\sqrt{120}}(|1,0\rangle -|0,1\rangle )\otimes (|1,-1\rangle +|-1,1\rangle +2|0,0\rangle ),\hfill \end{array}$$

from which the total density operator is obtained as the projection operator $\widehat{\rho }=|1,1,2\rangle \langle 1,1,2|$. The reduced density operator ${\widehat{\rho }}_{12}$ for the spin pair $S_1$–$S_2$ then results from Equation (6) after summing over all possible spin values for the spins $S_3^z$ and $S_4^z$:

$$\begin{array}{cc}\hfill {\widehat{\rho }}_{12}& =\sum _{S_3^z}\sum _{S_4^z}\langle S_3^z,S_4^z|\widehat{\rho }|S_3^z,S_4^z\rangle =\frac{3}{10}\left(|-1,0\rangle -|0,-1\rangle \right)\left(\langle -1,0|-\langle 0,-1|\right)\hfill \\ \hfill & +\frac{3}{20}\left(|1,-1\rangle -|-1,1\rangle \right)\left(\langle 1,-1|-\langle -1,1|\right)+\frac{1}{20}\left(|1,0\rangle -|0,1\rangle \right)\left(\langle 1,0|-\langle 0,1|\right),\hfill \end{array}$$

which has the following matrix representation:

$${\rho }_{12}=\begin{array}{cc}\hfill & \begin{array}{ccccccccc}\hfill |1,1\rangle \hfill & \hfill |1,0\rangle \hfill & \hfill |1,-1\rangle \hfill & \hfill |0,1\rangle \hfill & \hfill |0,0\rangle \hfill & \hfill |0,-1\rangle \hfill & \hfill |-1,1\rangle \hfill & \hfill |-1,0\rangle \hfill & \hfill |-1,-1\rangle \hfill \end{array}\hfill \\ \begin{array}{c}\hfill \langle 1,1|\hfill \\ \hfill \langle 1,0|\hfill \\ \hfill \langle 1,-1|\hfill \\ \hfill \langle 0,1|\hfill \\ \hfill \langle 0,0|\hfill \\ \hfill \langle 0,-1|\hfill \\ \hfill \langle -1,1|\hfill \\ \hfill \langle -1,0|\hfill \\ \hfill \langle -1,-1|\hfill \end{array}\hfill & \left(\begin{array}{ccccccccc}0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& \frac{1}{20}& 0& -\frac{1}{20}& 0& 0& 0& 0& 0\\ 0& 0& \frac{3}{20}& 0& 0& 0& -\frac{3}{20}& 0& 0\\ 0& -\frac{1}{20}& 0& \frac{1}{20}& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& \frac{3}{10}& 0& -\frac{3}{10}& 0\\ 0& 0& -\frac{3}{20}& 0& 0& 0& \frac{3}{20}& 0& 0\\ 0& 0& 0& 0& 0& -\frac{3}{10}& 0& \frac{3}{10}& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right)\hfill \end{array}.$$

(10)

If the reduced density matrix (10) is partially transposed $T_2$ with respect to the states of the second spin $S_2$ one obtains the following representation of the partially transposed reduced density matrix:

$$\begin{array}{c}\hfill {\rho }_{12}^{T_2}=\left(\begin{array}{ccccccccc}0& 0& 0& 0& -\frac{1}{20}& 0& 0& 0& -\frac{3}{20}\\ 0& \frac{1}{20}& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& \frac{3}{20}& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& \frac{1}{20}& 0& 0& 0& 0& 0\\ -\frac{1}{20}& 0& 0& 0& 0& 0& 0& 0& -\frac{3}{10}\\ 0& 0& 0& 0& 0& \frac{3}{10}& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& \frac{3}{20}& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& \frac{3}{10}& 0\\ -\frac{3}{20}& 0& 0& 0& -\frac{3}{10}& 0& 0& 0& 0\end{array}\right).\end{array}$$

(11)

The negativity can be now straightforwardly calculated by a diagonalization of the partially transposed reduced density matrix (11). By inspection, it can be found that there are eight positive eigenvalues, six of them emerge on the main diagonal ${\lambda }_{1,2}=\frac{3}{20}$, ${\lambda }_{3,5}=\frac{1}{20}$, ${\lambda }_{4,6}=\frac{3}{10}$, while other two positive eigenvalues ${\lambda }_8=0.039$ and ${\lambda }_9=0.317$ are roots of a cubic equation. From this perspective, there is just one negative eigenvalue ${\lambda }_7=-0.357$ of the partially transposed reduced density matrix (11), which in turn determines according to Equation (5) the negativity ${\mathcal{N}}_{12}=0.357$. The negativity for the remaining ground states can be obtained in a similar fashion and we therefore only present the final outcomes in

Table 1. The calculated values of the negativity ${\mathcal{N}}_{12}$ and ${\mathcal{N}}_{13}$ for all available ground states of the spin-1 Heisenberg diamond cluster.

Ground State	Analytical Result	Numerical Value
$|4,2,2\rangle$	${\mathcal{N}}_{12}$ = 0	${\mathcal{N}}_{12}$ = 0
	${\mathcal{N}}_{13}$ = 0	${\mathcal{N}}_{13}$ = 0
$|3,2,2\rangle$	${\mathcal{N}}_{12}$ = $\frac{1}{2\sqrt{2}}-\frac{1}{4}$	${\mathcal{N}}_{12}$ = 0.103
	${\mathcal{N}}_{13}$ = $\frac{1}{2\sqrt{2}}-\frac{1}{4}$	${\mathcal{N}}_{13}$ = 0.103
$|3,1,2\rangle$	${\mathcal{N}}_{12}$ = $\frac{1}{2}$	${\mathcal{N}}_{12}$ = 0.5
	${\mathcal{N}}_{13}$ = 0	${\mathcal{N}}_{13}$ = 0
$|2,2,2\rangle$	${\mathcal{N}}_{12}$ = $\frac{\sqrt{145}-9}{42}-\frac{10}{63}-\frac{\sqrt{367}}{63}cos(\frac{\varphi +2\pi }{3})$, $\varphi =arctan(\sqrt{\frac{{367}^3}{{6578}^2}-1})$	${\mathcal{N}}_{12}$ = 0.096
	${\mathcal{N}}_{13}$ = $\frac{\sqrt{769}-25}{84}-\frac{13}{126}-\frac{\sqrt{1993}}{126}cos(\frac{\varphi +2\pi }{3})$, $\varphi =arctan(\sqrt{\frac{{1993}^3}{{\mathrm{66,995}}^2}-1})$	${\mathcal{N}}_{13}$ = 0.174
$|2,0,2\rangle$	${\mathcal{N}}_{12}$ = 1	${\mathcal{N}}_{12}$ = 1
	${\mathcal{N}}_{13}$ = 0	${\mathcal{N}}_{13}$ = 0
$|1,2,2\rangle$	${\mathcal{N}}_{12}$ = $-\frac{2}{15}-\frac{\sqrt{58}}{30}cos(\frac{\varphi +2\pi }{3})$, $\varphi =arctan(\sqrt{\frac{{29}^3}{2{(83)}^2}-1})$	${\mathcal{N}}_{12}$ = 0.042
	${\mathcal{N}}_{13}$ = $\frac{\sqrt{13}}{10}-\frac{1}{3}-\frac{\sqrt{1180}}{120}cos(\frac{\varphi +2\pi }{3})$, $\varphi =arctan(\sqrt{\frac{{295}^3}{{3034}^2}-1})$	${\mathcal{N}}_{13}$ = 0.239
$|1,1,2\rangle$	${\mathcal{N}}_{12}$ = $\frac{\sqrt{23}}{5\sqrt{6}}cos\left(\frac{\varphi }{3}\right)$, $\varphi =arctan\left(\sqrt{\frac{2{\left(23\right)}^3}{3^7}-1}\right)$	${\mathcal{N}}_{12}$ = 0.357
	${\mathcal{N}}_{13}$ = $\frac{7}{60}$	${\mathcal{N}}_{13}$ = 0.116
$|0,2,2\rangle$	${\mathcal{N}}_{12}$ = 0	${\mathcal{N}}_{12}$ = 0
	${\mathcal{N}}_{13}=\frac{1}{3}$	${\mathcal{N}}_{13}$ = 0.333

in the form of their exact analytical results as well as numerical values.

Zero-temperature density plots of the negativity shown in Figure 2 in the interaction ratio $J_2/J_1$ versus magnetic field $h/J_1$ plane are in a perfect agreement with the ground-state phase diagram reported previously in Reference [36]. Figure 2a,b shows the density plot of the negativity ${\mathcal{N}}_{12}$ ascribed to the spin pair $S_1$–$S_2$, while Figure 2c,d displays the density plots of the negativity ${\mathcal{N}}_{13}$ ascribed to the spin pair $S_1$–$S_3$. Figure 2a,c refers to the spin-1 Heisenberg diamond cluster with the antiferromagnetic interaction $J_1>0$, while Figure 2b,d refers to the particular case with the ferromagnetic interaction $J_1<0$.

It is obvious from Figure 2a that the strongest quantum entanglement of the spin pair $S_1$–$S_2$ can be found within the ground state $|2,0,2\rangle$, which appears only for the antiferromagnetic interaction $J_1>0$. It is worthwhile to remark that the ground states $|2,0,2\rangle$ and $|3,1,2\rangle$ have useful representation within the valence-bond-solid picture where a spin-1 particle is symmetrically decomposed into two spin-1/2 entities. The couple of spins $S_1$ and $S_2$ create two singlets within the ground state $|2,0,2\rangle$ and the negativity accordingly acquires the highest possible value ${\mathcal{N}}_{12}=1$. If the eigenvector $|3,1,2\rangle$ becomes the relevant ground state upon increasing of the magnetic field, then, one of two singlet bonds breaks and transforms into a fully polarized state with zero entanglement. This argumentation is consistent with the observed value of the negativity ${\mathcal{N}}_{12}=1/2$, which evidently acquires a half of its maximal value within the ground state $|3,1,2\rangle$. Upon further increase of the magnetic field the other singlet bond also breaks and consequently, there is no entanglement ${\mathcal{N}}_{12}=0$ within the ground state $|4,2,2\rangle$ with regard to its separable character. It should be also pointed out that all three ground states $|2,0,2\rangle$, $|3,1,2\rangle$ and $|4,2,2\rangle$ can be expressed solely in terms of a linear combination of basis state vectors ${\sum }_{S_1^z}{\sum }_{S_2^z}|S_1^z,S_2^z,1,1\rangle$ and hence, there is no bipartite entanglement between the spin from the main body ($S_1$ or $S_2$) and the spin from wing ($S_3$ or $S_4$) of the diamond spin cluster in concordance with zero value of the negativity ${\mathcal{N}}_{13}=0$, see Figure 2c.

Contrary to this, one may detect a striking concurrent bipartite entanglement within the ground state $|1,1,2\rangle$ emergent at higher values of the interaction ratio $J_2/J_1$ and low enough magnetic fields, where the nonzero negativity ${\mathcal{N}}_{12}=0.357$ is found not only for the spin pair $S_1$–$S_2$ but also ${\mathcal{N}}_{13}=0.116$ for the spin pair $S_1$–$S_3$. Another quantum ground state $|0,2,2\rangle$, which appears at low enough magnetic fields either if the antiferromagnetic interaction $J_2>0$ along sides of the diamond spin cluster is sufficiently strong or the coupling constant along the shorter diagonal of the diamond spin cluster becomes ferromagnetic $J_1<0$, contrarily shows absence of the bipartite entanglement ${\mathcal{N}}_{12}=0$ within the spin pair $S_1$–$S_2$ and its presence ${\mathcal{N}}_{13}=1/3$ within the spin pair $S_1$–$S_3$. Another three ground states $|1,2,2\rangle$, $|2,2,2\rangle$ and $|3,2,2\rangle$ consecutively evolve above the ground state $|0,2,2\rangle$ upon rising of the magnetic field. The general feature of the ground states $|S_T,2,2\rangle$ with $S_T=0–3$ is that the bipartite entanglement is progressively suppressed within the spin pair $S_1$–$S_2$ at the expense of a gradual reinforcement of the bipartite entanglement within the spin pair $S_1$–$S_3$ as the quantum spin number $S_T$ increases. Remarkably, the concurrent bipartite entanglement of equal strength ${\mathcal{N}}_{12}={\mathcal{N}}_{13}\approx 0.103$ exists in the ground state $|3,2,2\rangle$ where the spin pairs $S_1$–$S_2$ and $S_1$–$S_3$ are equally entangled.

Bearing all this in mind, the spin pair $S_1$–$S_3$ is subject to the strongest bipartite entanglement within the ground state $|0,2,2\rangle$ though the achieved value of the negativity ${\mathcal{N}}_{13}=1/3$ is three times smaller than the maximally allowed value (see Figure 2c). It is quite clear from Figure 2d that all aforementioned generic features of the measure of the bipartite entanglement ${\mathcal{N}}_{13}=1/3$ for the spin pair $S_1$–$S_3$ are still preserved also for the spin-1 Heisenberg diamond cluster with the ferromagnetic coupling constant $J_1<0$.

Before going to discussion of a thermal entanglement of the spin-1 Heisenberg diamond cluster, it should be pointed out that we will consider a few different values of the interaction ratio to cover all possibilities of magnetic-field-driven changes of the bipartite entanglement as implied by the ground-state phase diagram shown in Figure 2. To this end, Figure 3 shows the magnetic-field dependence of the negativity ${\mathcal{N}}_{12}$ inherent to the spin pair $S_1$–$S_2$ of the spin-1 Heisenberg diamond cluster by considering four different values of temperature and six selected values of the interaction ratio. The most interesting feature of the magnetic-field dependence of the negativity ${\mathcal{N}}_{12}$ is consistence of the negativity plateaus and their respective magnetic-field ranges with the ground-state phase diagram. At low enough temperatures (close to zero degrees) one indeed observes a remarkable stepwise dependence of the negativity on the magnetic field. Besides, the negativity ${\mathcal{N}}_{12}$ may unexpectedly exhibit a highly non-monotonous dependence on the magnetic field due to extraordinarily wide variety of the ground states with very different strength of the bipartite entanglement. As could be expected, the negativity smears out on the temperature rise and the sharp stepwise dependencies of the negativity become smoother [41]. At magnetic-field-driven transitions between two ground states with nonzero bipartite entanglement the negativity ${\mathcal{N}}_{12}$ drops down to a local minimum, which always lies below smaller value among two different values of the negativity ascribed to two coexistent ground states. The observation of these peculiar minima of the negativity ${\mathcal{N}}_{12}$ can be attributed to the fact that the spin-1 Heisenberg diamond cluster is in a pure state within all ground states, but it necessarily acquires a mixed state at the respective magnetic-field-induced transition. With regard to this, two eigenvectors equally contribute to the density matrix and the value of the negativity drops down.

Let us verify presence of the local minima of the negativity by considering some particular examples of the magnetic-field-driven change of the ground state. To this end, we will rigorously calculate the local minimum of the negativity ${\mathcal{N}}_{12}$ at the magnetic-field-induced transition between the ground states $|2,0,2\rangle$ and $|3,1,2\rangle$ (see for instance the magnetic-field dependence of ${\mathcal{N}}_{12}$ for $J_2/J_1=0.5$ around $h/J_1=2.0$ in Figure 3c). The density operator corresponding to the mixed state at this magnetic-field-induced transition can be defined as:

$$\begin{array}{c}\hfill \widehat{\rho }=\frac{1}{2}(|2,0,2\rangle \langle 2,0,2|+|3,1,2\rangle \langle 3,1,2|).\end{array}$$

(12)

According to Equation (6), the reduced density operator ascribed to the spin pair $S_1$–$S_2$ follows from the formula:

$$\begin{array}{c}\hfill {\widehat{\rho }}_{12}=\frac{1}{2}\sum _{S_3^z}\sum _{S_4^z}\langle S_3^z,S_4^z|(|2,0,2\rangle \langle 2,0,2|+|3,1,2\rangle \langle 3,1,2|)|S_3^z,S_4^z\rangle ,\end{array}$$

(13)

which gives the following explicit form of the reduced density operator for the spin pair $S_1$–$S_2$ after doing all necessary algebraic manipulations:

$$\begin{array}{cc}\hfill {\widehat{\rho }}_{12}& =\frac{1}{6}(|1,-1\rangle +|-1,1\rangle -|0,0\rangle )\otimes (\langle 1,-1|+\langle -1,1|-\langle 0,0|)\hfill \\ \hfill & +\frac{1}{4}(|1,0\rangle -|0,1\rangle )\otimes (\langle 1,0|-\langle 0,1|).\hfill \end{array}$$

(14)

The reduced density matrix for the spin pair $S_1$–$S_2$ is then given by:

$${\rho }_{12}=\begin{array}{cc}\hfill & \begin{array}{lllllllll}\hspace{1em}|1,1\rangle \hfill & \hspace{1em}|1,0\rangle \hfill & |1,-1\rangle \hfill & \hspace{1em}|0,1\rangle \hfill & \hspace{0.5em}|0,0\rangle \hfill & |0,-1\rangle \hfill & |-1,1\rangle \hfill & |-1,0\rangle \hfill & |-1,-1\rangle \hfill \end{array}\hfill \\ \begin{array}{c}\hfill \langle 1,1|\hfill \\ \hfill \langle 1,0|\hfill \\ \hfill \langle 1,-1|\hfill \\ \hfill \langle 0,1|\hfill \\ \hfill \langle 0,0|\hfill \\ \hfill \langle 0,-1|\hfill \\ \hfill \langle -1,1|\hfill \\ \hfill \langle -1,0|\hfill \\ \hfill \langle -1,-1|\hfill \end{array}\hfill & \left(\begin{array}{ccccccccc}0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& \frac{1}{4}& 0& -\frac{1}{4}& 0& 0& 0& 0& 0\\ 0& 0& \frac{1}{6}& 0& -\frac{1}{6}& 0& \frac{1}{6}& 0& 0\\ 0& -\frac{1}{4}& 0& \frac{1}{4}& 0& 0& 0& 0& 0\\ 0& 0& -\frac{1}{6}& 0& \frac{1}{6}& 0& -\frac{1}{6}& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& \frac{1}{6}& 0& -\frac{1}{6}& 0& \frac{1}{6}& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right)\hfill \end{array},$$

which provides the following partially transposed density matrix if one performs the partial transposition $T_2$ with respect to the states of the spin $S_2$

$$\begin{array}{c}\hfill {\rho }_{12}^{T_2}=\left(\begin{array}{ccccccccc}0& 0& 0& 0& -\frac{1}{4}& 0& 0& 0& \frac{1}{6}\\ 0& \frac{1}{4}& 0& 0& 0& -\frac{1}{6}& 0& 0& 0\\ 0& 0& \frac{1}{6}& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& \frac{1}{4}& 0& 0& 0& -\frac{1}{6}& 0\\ -\frac{1}{4}& 0& 0& 0& \frac{1}{6}& 0& 0& 0& 0\\ 0& -\frac{1}{6}& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& \frac{1}{6}& 0& 0\\ 0& 0& 0& -\frac{1}{6}& 0& 0& 0& 0& 0\\ \frac{1}{6}& 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right).\end{array}$$

(15)

The partially transposed density matrix (15) has three negative eigenvalues contributing to the negativity ${\mathcal{N}}_{12}$, which acquires according to Equation (5) the value ${\mathcal{N}}_{12}=0.422$ that is much smaller than the values ${\mathcal{N}}_{12}=1$ and $1/2$ corresponding to the pure states $|2,0,2\rangle$ and $|3,1,2\rangle$, respectively. In agreement with this argumentation, the negativity actually falls down at the magnetic-field-driven transition between the ground states $|2,0,2\rangle$ and $|3,1,2\rangle$ from its largest possible value ${\mathcal{N}}_{12}=1$ pertinent to the pure state $|2,0,2\rangle$ to the local minimum ${\mathcal{N}}_{12}=0.422$ corresponding to the mixed state made of two eigenvectors $|2,0,2\rangle$ and $|3,1,2\rangle$ before it reaches the other stationary value ${\mathcal{N}}_{12}=1/2$ inherent to the pure state $|3,1,2\rangle$ (see the relevant behavior of ${\mathcal{N}}_{12}$ around $h/J_1=2.0$ in Figure 3c). It is noteworthy that the final outcomes of the analogous calculation of the negativity for the mixed states of the spin-1 Heisenberg diamond cluster realized at different magnetic-field-driven transitions are summarized in

Table 2. Numerical values of the negativity ${\mathcal{N}}_{12}$ and ${\mathcal{N}}_{13}$, which correspond to the mixed states realized at different magnetic-field-driven transitions of the spin-1 Heisenberg diamond cluster.

Coexistent Ground States	${\mathcal{N}}_{12}$	${\mathcal{N}}_{13}$
$|3,2,2\rangle$/$|2,2,2\rangle$	0.054	0.227
$|2,2,2\rangle$/$|1,2,2\rangle$	0.015	0.171
$|1,2,2\rangle$/$|0,2,2\rangle$	0	0.102
$|0,2,2\rangle$/$|1,1,2\rangle$	0	0.080
$|1,1,2\rangle$/$|2,0,2\rangle$	0.307	0
$|2,0,2\rangle$/$|3,1,2\rangle$	0.422	0

.

The similar argumentation can be also applied in order to explain an intriguing magnetic-field-induced rise of the negativity ${\mathcal{N}}_{12}$ observable in a close vicinity of zero magnetic field (see for instance Figure 3a for $J_2/J_1=-0.7$). It could be naively expected from the ground-state phase diagram shown in Figure 2a that the negativity should achieve for the interaction ratio $J_2/J_1=-0.7$ the constant value ${\mathcal{N}}_{12}=1/2$ in the magnetic-field range $h/J_1\in (0,0.6)$ inherent to the ground state $|3,1,2\rangle$, but a true zero-field asymptotic limit of the negativity at low enough temperatures turns out to be much smaller ${\mathcal{N}}_{12}=1/3$. The mysterious lower value of the negativity ${\mathcal{N}}_{12}=1/3$ can be attributed to a zero-field ground-state degeneracy, which is immediately lifted by Zeeman’s splitting of energy levels when applying any nonzero magnetic field. One actually finds in the limit of zero magnetic field a seven-fold degenerate ground state $|3,1,2,S_T^z\rangle$ with seven possible values of the z-component of the total spin $S_T^z=0,\pm 1,\pm 2,\pm 3$, while the unique ground state $|3,1,2,3\rangle$ with the highest possible value of the z-component of the total spin $S_T^z=S_T=3$ is favorable for the arbitrarily small nonzero magnetic field. Consequently, the density operator corresponding to the mixed state composed from seven eigenvectors $|3,1,2,S_T^z\rangle$ with $S_T^z=0,\pm 1,\pm 2,\pm 3$ being degenerate at zero magnetic field should be calculated according to the formula:

$$\begin{array}{c}\hfill {\widehat{\rho }}_{12}=\frac{1}{7}\sum _{S_T^z=0,\pm 1,\pm 2,\pm 3}|3,1,2,S_T^z\rangle \langle 3,1,2,S_T^z|.\end{array}$$

(16)

With the help of the density operator (16) one may consecutively obtain the negativity ${\mathcal{N}}_{12}=1/3$ pertinent to the mixed state constituted by seven degenerate eigenvectors $|3,1,2,S_T^z\rangle$ by following the same steps as previously used for the mixed states emergent at magnetic-field-driven transitions. Owing to this fact, the negativity shows a steep increase upon rising of the magnetic field at low enough temperatures, because the mixed state with a smaller degree of the bipartite entanglement is due to Zeeman splitting of energy levels replaced at any nonzero magnetic field with the unique pure state with a higher degree of the bipartite entanglement.

Next, let us make a few comments on typical magnetic-field dependencies of the negativity ${\mathcal{N}}_{13}$, which quantifies a strength of the bipartite entanglement of the spin pair $S_1$–$S_3$ of the spin-1 Heisenberg diamond cluster. Figure 4 elaborates all nontrivial scenarios of the magnetic-field variations of the negativity ${\mathcal{N}}_{13}$ compiled according to the ground-state phase diagrams shown in Figure 2c,d. Unlike the previous cases discussed for the bipartite entanglement of the spin pair $S_1$–$S_2$, the negativity ${\mathcal{N}}_{13}$ mostly shows at sufficiently low temperatures a stepwise decline upon increasing of the magnetic field. The most notable exception to this rule concerns with a rather limited magnetic-field range slightly above the magnetic-field-driven transition between the ground states $|0,2,2\rangle$ and $|1,1,2\rangle$, where one detects strengthening of the negativity ${\mathcal{N}}_{13}$ with increasing of the magnetic field (Figure 4b). It is worth mentioning that this unusual feature can be found also for other magnetic-field-induced transitions between the ground states $|S_T,2,2\rangle$ and $|S_T+1,2,2\rangle$, however, the striking rise of the negativity ${\mathcal{N}}_{13}$ induced by the magnetic field is in this case much less pronounced.

The formerly derived exact results for the negativities ${\mathcal{N}}_{12}$ and ${\mathcal{N}}_{13}$ of the spin pairs $S_1$–$S_2$ and $S_1$–$S_3$ of a spin-1 Heisenberg diamond cluster can be also employed in order to construct the particular form of finite-temperature phase diagrams, which delimit the parameter region with nonzero bipartite entanglement from that one without the bipartite entanglement. To this aim, we depict, in Figure 5 and Figure 6, the density plots of the negativities ${\mathcal{N}}_{12}$ and ${\mathcal{N}}_{13}$ in the temperature versus magnetic field ($k_{\mathrm{B}}T/J_1-h/J_1$) plane for a few selected values of the interaction ratio. It can be observed from Figure 5 and Figure 6 that the ground states with nonzero bipartite entanglement remain thermally entangled at least up to moderate temperatures $k_{\mathrm{B}}T/J_1\approx 0.4$, but in a few cases the bipartite thermal entanglement persists up to much higher temperatures $k_{\mathrm{B}}T/J_1\approx 1.0$ comparable with the coupling constants. It is quite evident from Figure 5 and Figure 6, moreover, that the established finite-temperature phase diagrams decisively verify presence of all ground states with nonzero bipartite entanglement through the parameter region with the shape of domes, which are sharply delimited from each other due to substantial differences in a strength of the bipartite entanglement of individual ground states.

4. Bipartite Entanglement in the Tetranuclear Molecular Compound {Ni${}_4\}$

In this section, we will comprehensively explore the bipartite entanglement of the tetranuclear nickel complex [Ni${}_4$($\mu$-CO${}_3$)${}_2$(aetpy)${}_8$](ClO${}_4$)${}_4$ (aetpy = 2-aminoethyl-pyridine) [32,33] hereafter abbreviated as {Ni${}_4$}, which affords an experimental realization of the spin-1 Heisenberg diamond cluster given by the Hamiltonian (1). A part of the crystal structure of the molecular compound {Ni${}_4$} involving the complex cation [Ni${}_4$($\mu$-CO${}_3$)${}_2$(aetpy)${}_8$]${}^{4+}$ is displayed in Figure 7, whereas crystallographic positions of hydrogen atoms and perchlorate ClO${}_4^{-}$ counter anions were omitted for better clarity. The complex cation consists of four octahedrally coordinated spin-1 Ni${}^{2+}$ ions, which are responsible for magnetic properties of the tetranuclear complex {Ni${}_4$}. All four Ni${}^{2+}$ ions are coordinated by two (ethylamino)pyridine bidentate groups, which simultaneously serve as blocking ligands precluding extension of this zero-dimensional magnetic structure into a more extended one. The molecular complex {Ni${}_4$} consequently has a magnetic structure of the spin-1 Heisenberg diamond cluster, in which two spin-1 Ni${}^{2+}$ ions from a shorter diagonal of the diamond cluster interact via double-oxygen superexchange pathways while other two spin-1 Ni${}^{2+}$ ions from a side of the diamond cluster interact via superexchange pathway mediated by a carbonate bridge [32]. High-field magnetization data recorded for the molecular compound {Ni${}_4$} were successfully interpreted by the spin-1 Heisenberg diamond cluster with the coupling constants $J_1/k_{\mathrm{B}}=41.4$ K and $J_2/k_{\mathrm{B}}=9.2$ K when adopting the notation introduced in the Hamiltonian (1) [36]. The tetranuclear molecular compound {Ni${}_4$} consequently belongs to geometrically frustrated quantum spin systems, whereby the gyromagnetic factor of the spin-1 Ni${}^{2+}$ ions was determined as $g=2.2$ [33].

By adapting the aforementioned set of the coupling constants one finds that the interaction ratio $J_2/J_1=9.2/41.4\approx 0.22$ falls into the parameter region of the ground-state phase diagram (see Figure 3b), where the bipartite entanglement within the spin pair $S_1$–$S_2$ acquires its maximum value ${\mathcal{N}}_{12}=1$ due to the ground state $|2,0,2\rangle$ in the magnetic-field range from $h/J_1=0$ to $h/J_1=1.44$, then it reduces to a half of its maximum value ${\mathcal{N}}_{12}=1/2$ owing to the ground state $|3,1,2\rangle$ in the magnetic-field range from $h/J_1=1.44$ to $h/J_1=2.44$ before it finally tends to zero due to the ground state $|4,2,2\rangle$. By contrast, the bipartite entanglement within the spin pair $S_1$–$S_3$ is zero in the parameter space pertinent to the coupling ratio $J_2/J_1\approx 0.22$. To illustrate the case, the negativity ${\mathcal{N}}_{12}$ of the molecular compound {Ni${}_4$} is depicted in Figure 8a as a function of the magnetic field at a few different temperatures when translating dimensionless magnetic field and temperature into the standard SI units. Figure 8a bears evidence to the fact that the molecular complex {Ni${}_4$} has the highest possible value of the negativity ${\mathcal{N}}_{12}=1$ to $B\approx 40$ T, then the negativity falls down to the intermediate value ${\mathcal{N}}_{12}=1/2$ in the magnetic-field range from $B\approx 40$ T to $B\approx 70$ T before it finally goes to zero at the saturation magnetic field $B\approx 70$ T. It is also noteworthy that the tetranuclear complex {Ni${}_4$} provides a useful platform for an experimental testing of a transient reduction of the bipartite entanglement observable slightly above the magnetic-field-driven transition between the ground states $|2,0,2\rangle$ and $|3,1,2\rangle$, which is followed by a peculiar strengthening of the bipartite entanglement invoked by a successive increase of the magnetic field.

Last but not least, the negativity ${\mathcal{N}}_{12}$ of the molecular compound {Ni${}_4$} is plotted in Figure 8b in the form of a density plot in temperature versus magnetic field plane. A few contour lines of the negativity ${\mathcal{N}}_{12}$ were also added to the relevant density plot in order to more easily identify steep changes of the bipartite entanglement. It should be stressed that the eigenstate $|1,1,2\rangle$ is for the interaction ratio $J_2/J_1\approx 0.22$ relatively close in energy to the zero-field ground state $|2,0,2\rangle$, which implies a strong role of thermal fluctuations upon suppression of the bipartite entanglement at zero magnetic field. The most sudden drop of the negativity ${\mathcal{N}}_{12}$ naturally occurs close to the magnetic-field-induced transition between two valence-bond-solid ground states $|2,0,2\rangle$ and $|3,1,2\rangle$. It can be also concluded from Figure 8b that the bipartite entanglement of the tetranuclear nickel compound {Ni${}_4$} persists up to roughly $T\approx 50$ K and $B\approx 70$ T, which are superior with respect to the ones reported for the dinuclear nickel complex NAOC studied in our previous work [40].

5. Conclusions

In the present paper, we rigorously studied the negativity as a measure of the bipartite entanglement between two crystallographically inequivalent spin pairs of the spin-1 Heisenberg diamond cluster by making use of the method of a full exact analytical diagonalization. It was shown that the bipartite entanglement between two considered spin pairs $S_1$–$S_2$ and $S_1$–$S_3$ from a shorter diagonal and a side of the diamond spin cluster is concurrent, i.e., the higher is one out of two measures, the smaller is the second one. The perfect bipartite entanglement, i.e., the highest possible value of the negativity, has been found for the spin pair $S_1$–$S_2$ in the valence-bond-solid ground state $|2,0,2\rangle$, in which the couple of spins from a shorter diagonal create a singlet effectively decoupling the exchange interaction with other two spins. In general, the negativity displays at sufficiently low temperatures a stepwise dependence on the magnetic field, which is accompanied with a substantial drop of the negativity at magnetic-field-driven transitions between two ground states with nonzero bipartite entanglement. Moreover, it was demonstrated that the negativity can be surprisingly reinforced by the external magnetic field, which replaces due to Zeeman’s splitting of energy levels a mixed state inherent to a degenerate zero-field ground state through a unique ground state.

The calculated measures of the bipartite entanglement were subsequently applied to the tetranuclear molecular compound {Ni${}_4$}, which represents an experimental realization of the spin-1 Heisenberg diamond cluster. Adopting the estimated values of both coupling constants determined by a theoretical fitting of the magnetometry measurements one may conclude that the tetranuclear complex {Ni${}_4$} exhibits a nontrivial bipartite entanglement only between two spin-1 Ni${}^{2+}$ ions from a shorter diagonal of the diamond spin cluster. At low enough temperatures and magnetic fields below $B\approx 40$ T the molecular compound {Ni${}_4$} displays the strongest possible bipartite entanglement ${\mathcal{N}}_{12}=1$ within the valence-bond-solid ground state $|2,0,2\rangle$, while the negativity drops down to a half of its maximum value in the magnetic-field range between $B\approx 40$ T and 70 T due to the other valence-bond-solid ground state $|3,1,2\rangle$. Besides, it was found that the bipartite entanglement of the molecular compound {Ni${}_4$} generally persists up to moderate temperatures $T\approx 50$ K.

Bearing all this in mind, the tetranuclear molecular complex {Ni${}_4$} represents an intriguing platform for experimental testing of a persistence of the bipartite entanglement with respect to rising temperature and magnetic field. Although the physical quantity negativity cannot be directly measured, all elements of the density matrix unambiguously determining also the negativity may be alternatively expressed in terms of local observables such as the magnetization, pair correlation functions and quadrupolar moment by following the same approach as envisaged for the heterodinuclear molecular complexes [16]. The experimental data acquired from standard magnetometry measurements in combination with inelastic neutron scattering or nuclear magnetic resonance experiments thus pave the way towards indirect experimental determination of the negativity serving as a measure of the bipartite thermal entanglement. It is also quite evident that any pronounced feature of some local observable, such as presence of an intermediate plateau in a low-temperature magnetization curve, will be accordingly carried over the relevant behavior of the negativity as well.