Abstract
The strain-magnetooptical properties of single crystals of the ferrimagnetic spinel CoFe2O4, which reflect a correlation between optical properties (magnetoabsorption and magnetoreflection) and magnetostriction, have been studied in the infrared spectral range. The conditions for the observation of the strain-magnetooptics are specified and physical mechanisms responsible for these effects in the spinel are explained.
1. Introduction
During the last century, spintronics, which deals with the spin-dependent transfer of charge carriers in solids, has been extensively developed. Recently, a new branch of spintronics, straintronics, has emerged [1,2,3,4], studying the effect of elastic deformations caused by external fields on the physical properties of various objects, including materials with a magnetic order.
The reflection and absorption of light in magnetic materials depend on magnetic fields and elastic deformations, which makes optical experiments an effective tool for studying electronic, spin, and lattice subsystems, as well as interactions between them ([5,6] and references therein). The fundamental magnetooptical (MO) effects in ferro- and ferrimagnets are observed in the range of fundamental absorption near the Curie temperature TC. In this temperature range, the application of a magnetic field gives rise to a significant change in magnetization and thus affects the positions of energy bands. In a magnetically ordered phase, magnetization varies slightly at T << TC and, therefore, MO effects are expected to be weak. However, recent experimental data [7] showed that the magnetoreflection and magnetotransmission of nonpolarized light in the ferromagnetic spinel CoFe2O4 at T << TC are sizeable and essentially depend on orientation of the magnetic field applied, thus demonstrating a direct relation with magnetostriction, which is large in this compound [8]. Note that in the case of CoFe2O4, the contribution of magnetostriction to the magnetic anisotropy is anomalously large as well [8].
A close interplay between MO and magnetoelastic properties in ferrite spinel materials with anomalously strong magnetostriction indicates that such compounds should be considered a special class of optical materials and in the corresponding field of magnetooptics can be classified as strain-magnetooptics. The literature is scanty for strain-magnetooptic properties of different materials and only CoFe2O4 has been studied so far. However, the matter in question is the discovery of similar properties in magnetostrictive magnetic materials of other compositions.
In the current work, we review the results of investigations of optical, magnetic and magnetoelastic properties, as well as the effect of magnetostriction on the absorption and reflection of nonpolarized light in the IR spectral range at different orientations of magnetic fields with respect to single crystals of CoFe2O4.
2. Materials and Methods
Single crystals of CoFe2O4 were grown by crucibleless floating-zone melting with radiation heating in the Institute of Metal Physics UB of RAS. The details of the method can be found in [9]. The magnetic and magnetostrictive properties of the cobalt ferrites are not only determined by the basic composition, but also by structural characteristics, induced uniaxial anisotropy and cation distributions influenced by the route of ferrite production. Inset in Figure 1a is a schematic of the crystal lattice of a single-crystal inversed spinel AB2O4, space symmetry group Fd3m, cubic syngony Oh7. In an ideal two-sublattice ferrimagnet CoFe2O4, ions of 3d elements are distributed over sublattices, accounting for their valence, as follows:
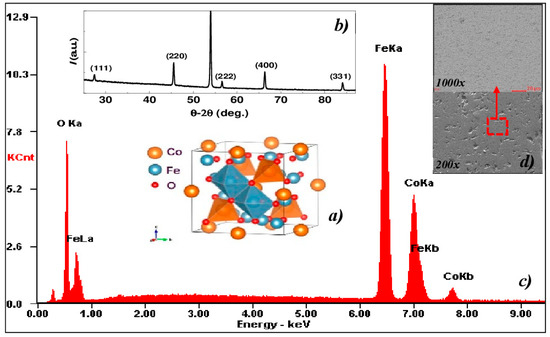
Figure 1.
(a) Data of X-ray spectral microanalysis for the single-crystal CoFe2O4 at T = 295 K, (b) model of crystal lattice of ferrite spinel, (c) data of X-ray analysis in large angles (θ–2θ), (d) electron microscopy pattern of the crystal surface with a magnification of 200× and 1000× (red-selected area).
Ions Co2+ are located at A-sites of octahedra, whereas Fe3+ exists in equal numbers at B–sites of octahedra and tetrahedra [10]. According to the X-ray data (Figure 1b), the lattice parameter makes up a0 = 8.38 Å, which is close to the previous reported values a0 = 8.39 Å [11]. Samples of different thickness were cut from single crystals in the form of thin plates with plane (001). The plate surface was mechanically ground and polished with diamond pastes with a grain size that was gradually decreased to 0.5 µm. The comparison of chemical composition of the samples with the etalon value was conducted at different surface spots by reference-free X-ray spectral microanalysis with the help of an Inspect F scanning electron microscope equipped by an energy-dispersion X-ray spectrometer EDAX. The accelerating voltage was 20 kV. A typical EDAX spectrum of the single crystal is shown on Figure 1c. According to the data of X-ray diffraction and electron microscopy, the samples were single-phase with a composition corresponding to the nominal one within the instrumental error (~1%); no other phases and impurities were detected. Note that the precise determination of the amount of oxygen in CoFe2O4 by the method of X-ray microanalysis is difficult because of the small oxygen mass. The images of the sample surface obtained by the scanning microscope with different magnifications are shown in Figure 1d. The roughness of the sample surface was registered to be less than 1 µm. Thus, it meets the conditions and is suitable for the determination of specular reflection in the infrared spectral range.
The optical and magnetooptical properties of the samples were measured using a prism spectrometer in a wavelength range of 1 μm ≤ λ ≤ 30 μm at a temperature range of 80 to 300 K in magnetic fields up to H = 7.5 kOe.
The specular reflection of single crystals is defined as R = IS/IAl, where IS and IAl are the intensities of nonpolarized light reflected from a sample and Al mirror at an angle of 7° to the normal of the sample surface. The samples had the shape of a thin plate with the dimensions 4 × 4 mm2 and thickness d = 400 µm. The transmission was defined as t = YS/Yo, where YS and Yo are the intensities of the incident and transmitted nonpolarized light. This was measured on a plate with d = 100 µm and normal light incidence. In the wavelength range 2.5 ≤ λ ≤ 5 μm, the transmission of the samples did not exceed 10%. Thus, when calculating the absorption coefficient α(λ,H,T), a simple expression can be used:
Registration of R and t was fulfilled in the absence and presence of the external magnetic fields. The relative error of determination of R, t and α did not exceed 0.25%. Magnetoreflection of CoFe2O4 was determined as ΔR/R = (RH − R0)/R0, magnetoabsorption as Δα/α = (αH − α0)/α0 and the magnetorefractive effect as Δn/n = (nH − n0)/n0, where R0,H, t0,H, α0,H and n0,H are the coefficients of specular reflection, transmission, absorption and index of refraction of light in the absence and presence of a magnetic field, respectively. Magnetooptical measurements were carried out in two experimental geometries: (1) Faraday configuration, where the magnetic field is directed perpendicular to the plate plane and aligned with the direction of light propagation, and (2) Voigt configuration, where the magnetic field is lying in the plate plane perpendicular to the direction of light propagation. Specific Faraday rotation (Faraday effect -F) was measured using a single-beam technique at an angle θ = 45° between polarization planes of the polarizer and analyzer. The contribution of light ellipticity to the Faraday effect was ignored in view of the smallness of these corrections.
The magnetization of the samples was measured at room temperature in fields up to 17 kOe on a vibrating sample magnetometer “LakeShore 7400” at the Collaborative Access Center “Testing Center of Nanotechnology and Advanced Materials” IMP UB of RAS. Magnetostriction (Δl/l) measurements were carried out by the tensometric method [8] with a strain gauge (FLA-1-11, Tokyo Co, Japan.) in a bridge circuit upon the homogeneously magnetized ferrite plate with thickness d = 400 µm. Following this method, the external magnetic field was applied in the sample plane along and perpendicular to the [100] single-crystal axis and a gauge direction.
3. Magnetization
It is well known that CoFe2O4 is a ferrimagnetic material. The magnetic moments of cations in the A- and B-sites are aligned antiparallel with respect to one another, yielding a total moment of spins with ferrimagnetic ordering. In the inversed ferrites, half the Fe3+ with magnetic moment 5μB was placed in A-sites and the other half in B-sites. Their moments are mutually compensated and the net moment of ferrite was due to the moment of 3μB of Co2+ in the B-site. The general formula of the net magnetic moment per formula unit of spinel ferrite as a function of inversion degree x may be written as: μ = μB-sites–μA-sites= (7–4x)(μB), where μ is the net moment of the material, and μB-sites and μA-sites are moments of cations in B and A-sites, respectively [12]. Thus, the cation distribution affects the magnetic properties of the ferrite.
In Figure 2a, field dependences of magnetization M(H) at T = 295 K are shown for different field orientations relative to the crystallographic axes. At H||[100], where [100] is the easy-magnetization axis [13], the magnetization is saturated at H ≈ 3 kOe and a further paraprocess takes place, with a linear growth up to MS = 82 emu/g at H = 15 kOe. This magnetization value lies in close proximity to the data reported for single crystals and films of CoFe2O4 [11,13]. A similar dependence M(H) was also observed in the case of H⊥[100]. If the magnetic field is oriented at an angle φ = 45° to the axis [100], which matches to H||[110], the magnetization curve displays two steps. The extrema of the first derivative dM/dH at H ≈ 1.5 kOe and H ≈ 2.8 kOe (Figure 2) correspond to the appearance of the steps in M(H). The condition dM/dH = 0 fulfilled at H ≈ 3.9 kOe corresponds to the saturation state, with MS~78 emu/g. A step in M(H) at H||[111] was detected earlier in non-stoichiometric Co0.8Fe2.2O4 at the field H~70 kOe in [12]. This step was followed by a jump in magnetostriction and was ascribed to the anisotropy-driven transition caused by a rotation of the magnetization vector jumping over an energy barrier. In stoichiometric single crystals of CoFe2O4, the step is formed already in relatively small fields H~8 kOe [14]. In our experiments, the step was registered in H~1.5 kOe at room temperature and it was supposed to be caused by the distortions of the cubic symmetry of the CoFe2O4 crystal lattice at H||[110]. Indeed, the anisotropic energy for a cubic crystal can be written as:
where αx,y,z are the directional cosines of the magnetization vector. The z axis is directed along the normal to the plate surface, i.e., along the [001] direction.
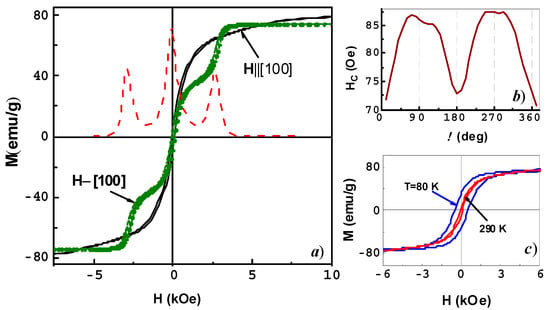
Figure 2.
Field dependences of (a) magnetization M(H) for the single-crystal CoFe2O4 at T = 295 K in H||[100] (solid line) and H||[110] (open symbols). First derivative of magnetization dM/dH is given by the red dashed line. (b) The angle dependence of the coercivity HC on the magnetic field direction relative to the [100] crystal axis and (c) the hysteresis loops M(H) in small fields at T = 80 K and 295 K.
Since the magnetization vector rotates in plane (001), we have αz = 0. In this case, magnetization projection MH onto the magnetic field direction in our experiment (H < HA is applied in the plane of the sample) is the solution to the equation:
where mH = MH/MS, MS being the saturation magnetization and HA = 2K1/MS is the anisotropy field.
Evidently, no steps are described by Equation (3), which supports the assignment of the step at H||[110] to the distortions of the crystal symmetry in our crystal.
It should be noted the coercive fields of a single crystal are much smaller than those measured on polycrystalline materials, because there is no influence of grain size and grain boundaries in a single crystal. The coercivity of the crystal was HC ≈ 80 Oee at T = 295 K, which was close to reported data [11]; however, it depends on the orientation of the magnetic field relative to the crystallographic axes (Figure 2b). Such behavior of HC reflects the cubic anisotropy of the CoFe2O4 single crystal [8]. The value of HC is controlled by the cation distribution on the surface and in the bulk of a single crystal and can be lowered by annealing and subsequent etching of the sample [8,12]. Decreasing the temperature to 80 K increases HC to ~500 Oe (Figure 2c), while the saturation magnetization of the CoFe2O4 crystal is virtually unchanged. This indicates the complex competing nature of the contributions of the magnetocrystalline and magnetoelastic energies to the magnetic anisotropy of the crystal. Additional contributions from both the shape and growth anisotropy of the crystal, as well as the error in the orientation of the crystal, lead to smearing and the inaccurate reproduction of the positions of the maxima of the observed angular dependences of the magnetization (Figure 2b).
4. Magnetostriction
Magnetostriction is an intrinsic property of magnetic materials. Due to the magnetic exchange, these materials change their shape when a magnetic field is applied. Magnetostriction is based on the coupling of the magnetic moment to the lattice. In a single crystal, magnetostriction is a tensor property which depends on the crystal structure and symmetry of the lattice [8,10,12]. Figure 3 shows the field dependences of magnetostriction Δl/l measured along the [100] axis. The obtained value (Δl/l)100 exceeds those for nonstoichiometric and alloyed single crystals, but is lower in magnitude as compared to the magnetostriction of crystals annealed in magnetic field [8,12,15,16]. The magnetization hysteresis due to the defects in the CoFe2O4 crystals was accompanied by a weak hysteresis of magnetostriction. At T = 295 K << TC = 812 K, in the region of paraprocess, the magnetization almost did not change, which indicates that the volume of magnetostriction was small and can be neglected.
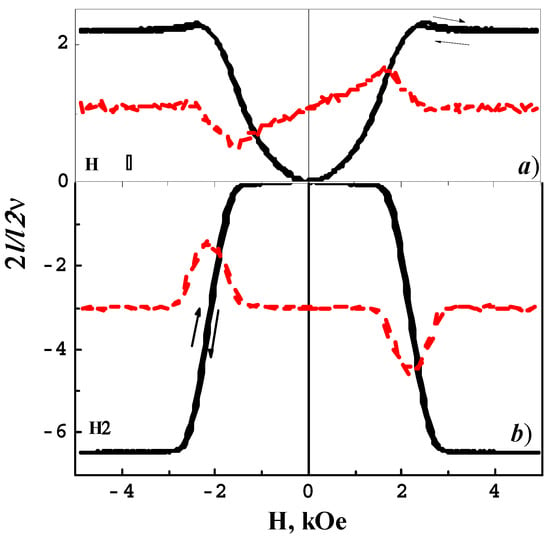
Figure 3.
Field dependences of perpendicular (a): (H⊥[100]) and longitudinal (b): (H||[100]) magnetostriction (Δl/l)100 and first derivatives of magnetostriction (dashed red lines) for the single-crystal CoFe2O4 at T = 295 K.
In the case of a cubic ferromagnet, the relative elongation along the axis specified by direction cosines βx,y,z can be defined as [17]:
Δl/l = (3/2) λ100(αx2βx2+ αy2βy2+ αz2βz2 − 1/3) + 3 λ111(αxαyβxβy + αyαzβyβz + αzαxβzβx)
In this study, the measurements of Δl/l were performed along the x-axis in the in-plane magnetic field; therefore, αz = βy= βz = 0, βx = 1. Consequently, (Δl/l)100 = λ100 at H||[100] and (Δl/l)100 = −λ100/2 at H⊥[100]. Indeed, the magnetostriction (Δl/l)100 for studied crystals of CoFe2O4 has the opposite sign in the case of H||[100] and H⊥[100]. The first derivative of magnetostriction (dashed lines in Figure 3) demonstrates saturation in a field HS ≥ 3 kOe, which is close to the saturation field (Figure 2). The maximal magnetostriction value at H||[100] makes up (Δl/l)100 ≈ −624·10−6. This is almost three times as high as (Δl/l)100 ≈ +221·10−6 at H⊥[100]. The obtained discrepancy, as well as the steps on the M(H) curve, point out to the distortions of the cubic crystal structure.
At H||[100], the (Δl/l)100 sharply grew starting with only H = 1.6 kOe. When H⊥[100], the growth of (Δl/l)100 was observed from H = 0 by the power law. The peculiarities of the magnetostriction of the crystal manifest clearly through the different behavior of the first derivatives of (Δl/l)100 with extremes near 1.6 kOe (Figure 3). The small values of (Δl/l)100 at H < 1.6 kOe were accounted for by the fact that the growth of domains with the magnetization aligned with field was compensated by a decrease in the size of domains with opposite magnetization. Meanwhile the total magnetic moment of the sample gradually increased.
It is commonly accepted that in cubic ferrimagnets the magnetostriction contribution ΔK to the magnetic anisotropy constant K1 does not exceed several percent [8,18,19]. According to Bonnenberg and colleagues [16], the magnetostriction contribution to K1 is given by:
where the elastic constants for CoFe2O4 make up c11 = 2.57·1012 erg/cm3, c12 = 1.5·1012 erg/cm3 and c44 = 0.85 × 1012 erg/cm3 [20].
Given λ111 = 120 × 10−6 [8] and λ100 = −654 × 10−6, we can calculate ΔK ≈ 1 × 106 erg/cm3. Taking the data of Figure 2a, we obtain K1 ≈ 2 × 106 erg/cm3. Thus, in our case, the magnetostriction contribution to the magnetic anisotropy constant ΔK/K1 of CoFe2O4 crystal makes up ~1/2, which is anomalously large.
5. Optical Properties
The spectrum of specular reflection R for a single crystal of CoFe2O4 (Figure 4a) was formed by the absorption edge in the short-wave range at λ < 2 µm. Furthermore, a weak band at λ < 3 µm, a frequency-independent (dispersionless) interval (R~14.7%) in the range 3 µm < λ< 12 µm and phonon bands at wavelength λ = 16.4 µm (E1 = 609 cm−1) and λ = 24.2 µm (E2 = 413 cm−1) [21] were also observed.
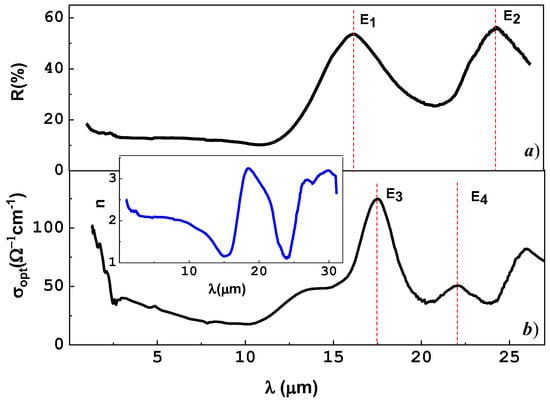
Figure 4.
Spectra of (a) reflectivity R and (b) optical conductivity σopt for the single-crystal CoFe2O4. In inset, spectrum of refraction index n for the single-crystal CoFe2O4 at T = 295 K. Spectra of σopt and n were calculated by the Kramers–Kronig method.
The band E1 with symmetry T1u arises due to Co–O ion oscillations in the octahedral sublattice [22], whereas E2(T1u) is predominantly related to the oxygen-ion oscillations in the tetrahedral sublattice [23]. The short-wave edges of the bands E1 и E2 were distorted by the contribution of weak additional bands. The room-temperature resistivity of the samples was about ~105 Ω∙cm, hence, free charge carriers do not contribute to the reflection spectrum. This fact helped to simplify the application of the Kramers–Kronig method for processing the spectra of optical conductivity σopt (light absorption) and the calculation of refraction indices from the reflection spectra [24]. In the spectrum of σopt (Figure 4b), additional phonon bands at λ = 22 µm (E3 = 455 cm−1) and λ = 17.7 µm (E4 = 565 cm−1) become distinctly pronounced, which corresponds to data reported by Bujakiewicz-Koronska et al. [23]. In the vicinity of the fundamental absorption edge at λ~3 µm, the impurity-absorption band appears in the spectrum of σopt (Figure 4b), which was ascribed in to elastic modes [25].
In the determination of the refraction index n of the single-crystal CoFe2O4, an important part was played by the dispersionless interval of R(λ). In the case of normal light incidence, it can be estimated from n∞ = (1 + √R)/(1 − √R) ≈ 2.04. In the range 3 µm < λ< 12 µm, it varies within the limits 1.8 < n < 2 (inset on Figure 4). These values are less than n = 2.2 as obtained in [21], but exceed n = 1.72 for a classical spinel. The spectral ranges with strong n dispersion at λ < 3 µm and λ > 12 µm reflect impurity absorption and the phonon spectrum, respectively. Our spectra of R, σopt and n for the single CoFe2O4 crystal (Figure 4) supplement and rectify the reported data from [21,26].
The measured absorption spectrum of CoFe2O4 α(λ) agrees well with the spectrum of optical conductivity (Figure 4 and Figure 5). A sharp growth of α at λ < 2 µm was provided by the fundamental absorption edge at λ~0.95 µm (Eg = 1.18 eV) connected with indirect transitions from the hybridized dCo + pO– states of valence band at the X point of Brillion zone to the dFe– state of the conduction band at the Γ point [27]. While temperature decreases to 80 K (inset in Figure 5), the absorption edge shifts toward the shorter wavelengths by 0.1 µm (+0.08 eV); this value is in close proximity to that for films from [28,29].
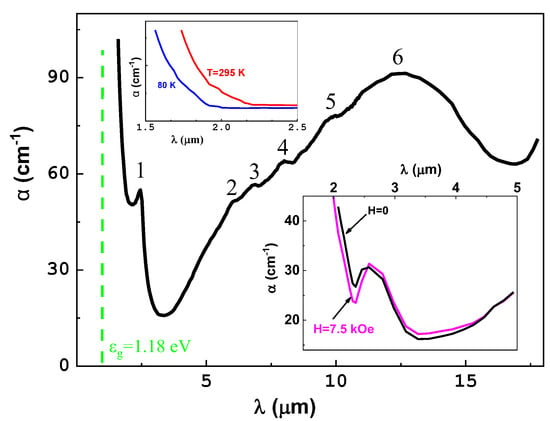
Figure 5.
Spectrum of light absorption α for the single-crystal CoFe2O4 at T = 295 K. Left inset— blue shift of the absorption edge on cooling; right inset—the absorption spectra α(λ) in zero and non-zero magnetic field H = 7.5 kOe.
At λ1 = 2.6 µm (0.48 eV), the spectrum exhibited band 1, which was also presented in the spectra of σopt (Figure 4b) and was conditioned by the impurity absorption. In [30], it was established that oxygen surrounding the ions Co2+ and Fe3+ endures octahedral distortions, stronger in the case of Co2+. We suppose that band 1 can be formed by transitions from the valence band to the states VO (oxygen vacancy) +3d(Fe3+) and VO+3d(Co2+), similar to the impurity absorption in single crystal of Hg(Cd)Cr2Se4 [31]. On decreasing temperature, the intensity of band 1 also decreased (left inset in Figure 5), which was related to the temperature-induced shift of the absorption edge. In the wavelength range 3 < λ < 15 µm, the absorption spectrum exhibited a broad band with a maximum at λ6 = 12.5 µm (0.1 eV) and a fine structure consisting of small bands centered at λ2 = 6.1 µm (0.2 eV), λ3 = 7 µm (0.17eV), λ4 = 8.4 µm (0.14 eV) and λ5 = 10 µm (0.12 eV) (Figure 5). Cooling CoFe2O4 crystals to T = 80 K resulted in better resolution of the fine structure (data not shown). The positions of these bands are close to those of the impurity bands, which were observed in the spectrum of CoFe2O4 crystals doped by ions of Zn, Zr or Cd [26]. The increase in the absorption at λ > 15 µm was attributed to the phonon spectrum.
The inset in Figure 5 shows that the magnetic field of 7.5 kOe led to a small blue shift of the absorption edge (~10 meV) at T = 295 K. There are no free charge carriers in CoFe2O4, so the value exchange interaction and the shift of the absorption edge were significantly lower in comparison with, for example, the ferromagnetic spinel Hg(Cd)Cr2Se4 [32]. Another important finding was the detection of the red shift of the MIR-band at λ = 2.6 µm (~15 meV) under the same conditions (right inset in Figure 5). The field sensitivity of the MIR band confirms the connection of this band to the 3d(Fe3+) and 3d(Co2+) states, as in the case of donor states in Hg(Cd)Cr2Se4 formed by vacancies of VSe+Cr2+ [32]. The effect of magnetic field also leads to an insignificant shift and change in intensity of the impurity bands in this range. Thus, in single-crystal CoFe2O4, the magnetic field influences not only the absorption edge but the impurity-absorption bands as well. This effect can be traced more distinctly when analyzing magnetoreflection and magnetoabsorption spectra.
6. Magnetooptical Properties
In a magnetic field exceeding the saturation field (HS =3 kOe), the coefficients of reflection, absorption, and refraction of CoFe2O4 were changed, i.e., MO effects manifest themselves in the IR range [7,32]. The coefficients R and α depend on both the magnetic field strength and its direction relative to the crystallographic axes of the sample.
Let us treat the case when magnetization vector lies in the plane (001). For the nonpolarized light, the dependence of α on the field direction for a sample in the single-domain state can be written in the form
where A and B depend on the light wavelength, temperature, and field strength H; |B| << A, φ is the angle between axis [100] and magnetization direction.
If the field is applied to a multi-domain sample, the is replaced by , where means averaging over magnetization directions in a multi-domain structure. In the common case, the magnetoabsorption of light Δα/α can then be written in the form:
where ΔA(H) = A(H) − A(H = 0) << A(H = 0).
If the field applied exceeds Hs, . In a case in which ΔA and B are the same order of magnitude, the strong dependence of Δα/α, as well as ΔR/R and Δn/n on the angle φ can be observed.
As shown in Figure 6, the spectral shape and the value of magnetoreflection essentially depend on orientation of magnetic field relative to the crystallographic axes. In the range λ < 1.5 µm, the dependence ΔR/R(λ) demonstrates a growth connected with the shift of the fundamental absorption edge under the action of the field independently of its direction. An intense band ΔR/R at λ~2.9 µm, weak bands at λ~6 µm and a feature at λ~ 10–12 µm arise due to changes in the intensity and position of the impurity-absorption bands (Figure 6a). At H||[100], the value of ΔR/R was almost twice as high as at H⊥[100] and can reach ~4%. In the case of H||[110], magnetoreflection tends to zero within the accuracy of experiments. Features of ΔR/R at λ > 16 µm were ascribed to the impact of magnetic field on the phonon spectrum. More distinctly they are pronounced in the changes of Raman spectra for the CoFe2O4 single crystal under application of an external magnetic field (inset in Figure 6). This is a direct evidence of a close interplay of phonon and magnetic subsystems, which was earlier observed in [33].
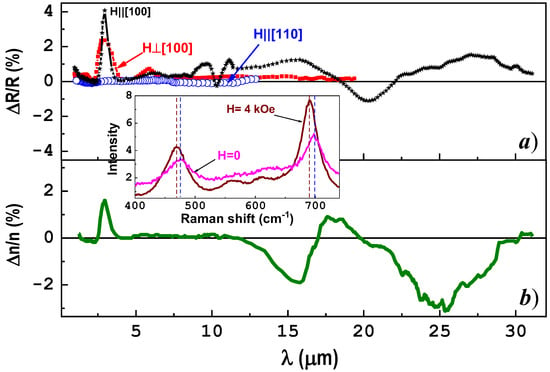
Figure 6.
Spectra of (a) magnetoreflection ΔR/R for the single-crystal CoFe2O4 at different orientations of magnetic field relative to the crystal axes at T = 295 K and (b) magnetorefractive effect Δn/n in the field H = 3.6 kOe. Inset: Raman shift taken at the in-plane magnetic field 4 kOe applied along [100] direction and at zero field (dashed lines are guided for eye).
The presence of a weakly dispersed spectral part of n(λ) (Figure 4c) was helpful in the determination of the magnetorefractive effect (Δn/n). The maximum of Δn/n~ +1.5 × 10−3 in CoFe2O4 at H||[100] (Figure 6b) is, for example, higher by an order of magnitude than the theoretically predicted Δn/n for the orthoferrite YFeO3, whose magnetostriction is also lower by almost an order of magnitude than that of CoFe2O4 [6]. Thus, we can suggest that the higher value of Δn/n for CoFe2O4 can be accounted for by its pronounced magnetoelastic properties.
Figure 7 demonstrates the very complicated shape of magnetoabsorption spectra Δα/α in CoFe2O4. It is worth noting the close correlation between the peculiarities in Δα/α and the absorption spectra (Figure 5). These peculiarities arise due to shifting of the fundamental absorption edge and changes in the intensity and position of impurity-absorption bands under the action of a magnetic field.
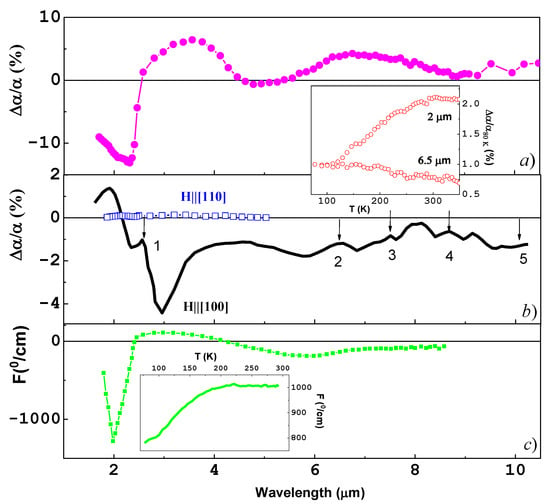
Figure 7.
Spectra of magnetoabsorption Δα/α for the single-crystal CoFe2O4 at H = 7.5 kOe: (a) in the Faraday configuration, (b) in the Voigt configuration (arrows indicate positions of absorption bands), and (c) spectrum of Faraday effect (F) at H = 7.5 kOe and T = 295 K. Upper inset presents temperature dependences of Δα/α80 K at λ = 2 μm and 6.5 μm; lower inset—temperature dependences of F at λ= 2 μm.
According to the data on the band structure of CoFe2O4 [27,28], the changes of absorption coefficient in the magnetic field were caused by crystal distortion along the fourth-order axis induced by magnetostriction. Let us estimate Δα/α resulting from the changes in the energy of the absorption edge due to magnetoelastic deformations. As mentioned above, in the case of linear magnetostriction, the crystal volume did not change and, therefore, the shift of the conduction band bottom located at the Γ point of the Brillouin zone is equal to zero. The top of valence band is located at the X point. Therefore, in fields, which are above the saturation field and directed along [100] crystal axis, the shift of the valence band edge can be estimated as Δεν = Ξu|λ100|, where Ξu is the deformation potential. The magnetoabsorption is then Δα/α = [α(E +Δεν) − α(E)]/α(E) ≈ (dln α(E)/dE) × Δεν. In the region of the absorption edge for α = 105 cm−1 at E ≈ 2 eV [30], the first derivative is ∼0.6 eV−1. The value of |Ξu| makes up 10–20 eV [34], |λ100| ≈ 6 × 10−4 at room temperature [8]. Hence, in the vicinity of the absorption edge, the value Δα/α should be about 1%. This estimated value of Δα/α is close to the experimental data for the case of a Voigt configuration (Figure 7b) and smaller by an order of magnitude than that in the case of a Faraday configuration (Figure 7a).
Such a difference can be caused by an additional contribution of “parasitic” mechanical stresses, which arise in the Faraday configuration and lead to a poorly controlled deformation of the sample and overestimation of the data gained. In the Voigt configuration, when the field lies in the sample plane, such stresses are minimal.
Unlike in the Faraday configuration, in the Voigt configuration the positions of impurity-absorption bands are well distinguished and are shown by arrays (Figure 7b). In accordance with (7), the values of Δα/α and ΔR/R essentially depend on the field direction relative to the crystallographic axes. In the case of H||[100], the magnetoabsorption reaches its maximal values, for instance, at room temperature Δα/α~5% at λ~2.9 µm. Upon cooling to 80 K, the value of Δα/α is enhanced to 12%. However, in the case H||[110], the values of Δα/α and ΔR/R were almost close to zero (Figure 6a and Figure 7b). Thus, in the magnetostrictive spinel CoFe2O4, the shape of the Δα/α and ΔR/R spectra was controlled by the angle between axis [100] and magnetization direction.
The magnetoabsorption and magnetoreflection effects occur in natural light and have nothing in common with traditional MO effects in polarized light—say, Faraday (F) and Kerr effects, respectively. However, as shown in Section 5, F can contribute to Δα/α if the light is partially polarized in the optical setup. In view of this, in Figure 7c, the spectrum of specific F for CoFe2O4 at T = 295 K is shown. It was formed by a deep negative extreme at λ = 1.9 µm with F ≈ −1300°/cm ascribed to transitions from the Co2+ to Fe3+ state [35]. In the range of 2 < λ< 9 µm, the spectrum of Faraday rotation has a positive maximum F~ +120 °/cm at λ ≈ 3 µm and negative one F ~−200 °/cm at λ ≈ 6 µm. The complicated spectral shape of the Faraday effect in the middle IR range is by no means characteristic of a spinel [36] and is likely due to the impurity states and contribution of the frequency-independent F.
The temperature dependences Δα/α(T) and F(T) reflect the behavior of the optical gap (εg) and magnetic anisotropy constant for CoFe2O4 [37]. Blue shift of the absorption edge upon cooling the crystal leads to a decrease in the effects (insets in Figure 7). At λ = 6.5 µm, the influence of the absorption edge on Δα/α was essentially reduced, which results in the appearance of a weak reverse temperature course in the range of impurity absorption. The plateau on the dependences Δα/α(T) and F(T) at T < 120 K is probably traceable to the anisotropy constants being temperature independent [38].
7. Strain-Magnetooptics: Close Connection between Magnetooptical Effects and Magnetostriction in CoFe2O4
7.1. Voigt Configuration
In the magnetostrictive ferrite spinel CoFe2O4, there is a strong correlation between the field dependencies of magnetostriction and those of magnetoreflection and magnetoabsorption (magnetotransmission), so one can say that strain-magnetooptics is a special part of magnetooptics. This correlation exists at different orientations of magnetic field relative to the crystal surface, as well as crystallographic axes of the samples. Figure 8 presents the field dependences of magnetostriction (Δl/l)100, ΔR/R and Δα/α in the Voigt configuration at various directions of the magnetic field in the vicinity of impurity-absorption band 1 at λ = 2.7 µm.
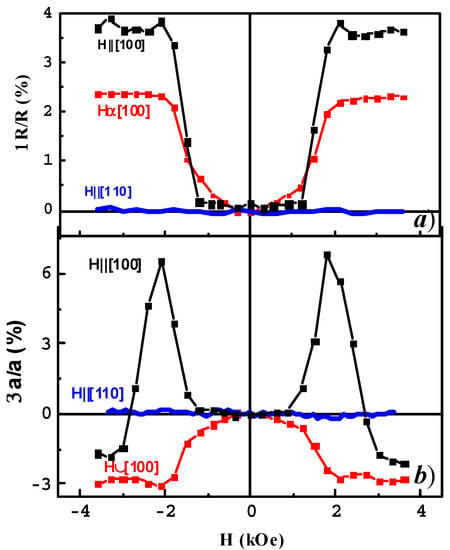
Figure 8.
Field dependences of (a) magnetoreflection ΔR/R and (b) magnetoabsorption Δα/α for the single-crystal CoFe2O4 at λ = 2.7 µm and T = 295 K for different orientations of magnetic field.
Comparing Figure 3a and Figure 8a, we see that in the case of H||[100], the course of plots ΔR/R(H) and Δα/α(H) was similar to that of Δl/l(H) with the values of ΔR/R and Δα/α being close to zero at H < 1 kOe. In fields higher than ~1.6 kOe, the MO effects change drastically with the subsequent saturation, which was similar to the (Δl/l)100 behavior; see Figure 3. The extremes of the first derivatives of Δα/α(H) and ΔR/R(H) (not shown) coincide in positions with those of (Δl/l)100, which can confirm the interplay of these MO effects in natural light with the magnetostriction of CoFe2O4.
In the case of H⊥[100], a gradual growth of ΔR/R and Δα/α values was observed with an increasing field, starting from the zero point, which was similar to the behavior of Δl/l(H). The effects become saturated in the same fields as in the case of H||[100]. As aforementioned, at H⊥|[100] the magnetostriction should be twice as low as at H||[100] − (Δl/l)100 = −λ100/2. Correspondingly, the values of ΔR/R and Δα/α were saturated and approximately twice as low as in the case of H||[100] (Figure 8).
In the case of H||[110], the effects ΔR/R and Δα/α are virtually absent within the experimental error up to H = 3.6 kOe, although the magnetization was close to its saturation value at that field. This indicates that our MO effects are not determined by the magnetization value. When H > 2.8 kOe, the magnetic moment of the sample is parallel to the field direction, so that α2x = 1/2 was substituted in Formula (4). If we take λ111 = +120·10−6 [8], a simple estimate shows that at H||[110] the magnetostriction is about (Δl/l)110 = −70 × 10−6, which is almost one order of magnitude less than in the case of H||[100], when (Δl/l)100 ≈ −630 × 10−6. It can be concluded that there should be a direct relation between magnetoreflection and magnetoabsorption of light and magnetostriction that could explain the low values of ΔR/R and Δα/α at H||[110].
The field dependences ΔR/R(H) and Δα/α(H) of single CoFe2O4 crystals displayed virtually no hysteresis. However, in the case of a highly defective structure, a strong hysteresis can appear on ΔR/R(H), Δα/α(H) and magnetostriction, as was observed, e.g., in films of CoFe2O4 [39]. A more detailed pattern of the behavior of the field dependences of the Δα/α(H) and ΔR/R(H) at different wavelengths is presented in Figure 9. The data are given for the orientation H||[100] and T = 295 K. At all points of the spectrum, the growth of effects is seen to begin at H > 1.6 kOe, with the following saturation of effects at H > 2.5 kOe. The course of plots Δα/α(H) and ΔR/R(H) is controlled by both displacement of spectra under magnetic fields and changes in the coefficients of absorption and reflectance. In the vicinity of the impurity-absorption band 1 (points A and B), solely the reflection intensity was changed and the behavior of ΔR/R(H) was similar to the field dependences of magnetostriction (Figure 3 and Figure 8a). However, in the case of magnetoabsorption, changing the intensity and simultaneously shifting the impurity-absorption band are resulted in the appearance of a maximum of Δα/α(H) at ~1.9 kOe and a sign reversal in the field corresponding to the extreme of the first derivatives for (Δl/l)100. At other points of the impurity absorption, say, C, D, E and F, the intensity changes and spectral shift under the action of magnetic field were observed for both Δα/α and ΔR/R effects. A similar process of formation of Δα/α and ΔR/R spectra depending on magnetic field was previously described for manganites in [40].
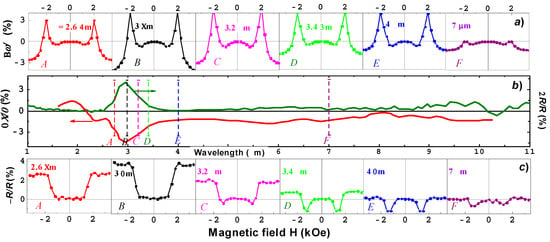
Figure 9.
Field dependences of (a) magnetoabsorption Δα/α and (c) magnetoreflection ΔR/R of the single-crystal CoFe2O4 at H||[100] and T = 295 K for different wavelengths, (b) spectra of magnetoabsorption Δα/α (less ordinate axis) and magnetoreflection ΔR/R (right ordinate axis) in the field 3.5 kOe.
The obtained sensitivity of the impurity-absorption bands to the magnetoelastic properties and orientation of the field relative to crystallographic axes indicates that impurities occupy low-symmetry positions in the unit cell, predominantly in the B-sublattice. In [28], it was shown that distortion of the B sublattice that contains Co2+ and Fe3+ ions in octahedral sites results in changes in the electronic states mostly Co2+. Therefore, the magnetic-field-induced changes in the coefficients of light absorption and reflection in the IR spectral range result from the changes of electron states of Co2+ ions due to magnetoelastic deformation of the spinel crystals.
7.2. Faraday Configuration
Let us now compare the behavior of the Faraday effect F and Δα/α(H), measured in natural light. The field dependences of F and Δα/α are given in Figure 10. The F(H) plot shows that the Faraday effect (and hence magnetization) in CoFe2O4 crystals monotonously grows with the field and becomes saturated when the field is somewhat above 4πMs ≈ 5 kG, which can be explained by the contribution of demagnetizing factor for a sample in the form of thin plate. On the Δα/α(H) dependence, however, a noticeable rise of the effect starts at H~2 kOe. Such behavior of Δα/α(H) near the absorption edge (λ = 2.3 µm) and in the range of impurity absorption (λ = 6.5 µm) resembles the field dependence of magnetostriction at H⊥[100], in the sense that the Δα/α appears only if the field is sufficiently large. Therefore, it is reasonable to think that the Δα/α(H) dependence in Faraday configuration is connected not only with the demagnetizing field but also with magnetostriction.
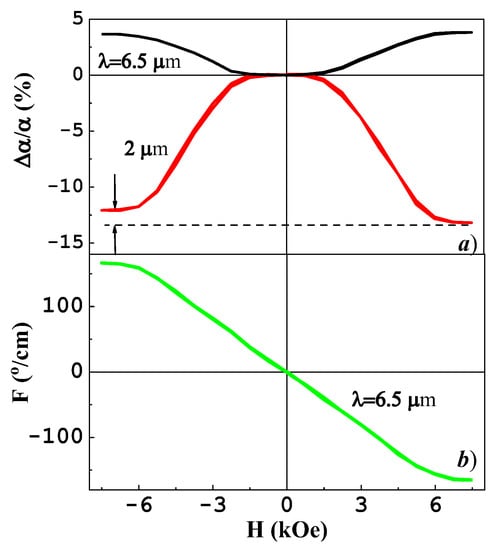
Figure 10.
Field dependences of (a) magnetoabsorption Δα/α and (b) Faraday rotation F for the single-crystal CoFe2O4 at different wavelengths and T = 295 K. Arrows indicate the asymmetry of Δα/α(H) dependences.
In the Voigt configuration, the hysteresis of Δα/α(H) is virtually absent. On the contrary, in the Faraday configuration, a weak loop was observed, which can be explained by the appearance of additional contributions of “parasite” mechanical stresses that lead to a poorly controlled deformation of the sample. No detectable contribution of linear MO effects to Δα/α(H) and ΔR/R(H) were found in the Voigt configuration. In the Faraday configuration, the contribution of F to the magnetoabsorption manifests itself in the asymmetry of the branches of curves Δα/α(H) upon changing the field direction though the magnetoabsorption effect is even with respect to the magnetic field (Figure 10a).
It is important that the asymmetry of Δα/α(H) corresponds to the sign of F. The estimation of the F values at room temperature, accounting for Malus’s law and partial polarization of light P in the optical setup (P ≈ 0.1), gives F ≈ −450 °/cm, +150 °/cm, and −400 °/cm at λ = 2.3 µm, 3.3 µm and 6.5 µm, respectively, in the saturation field H = 6.5 kOe. Thus, the estimated contribution of the Faraday effect to the magnetoabsorption did not exceed 1/6 of the experimental value of Δα/α.
8. Conclusions
The study of the magnetic, magnetoelastic, optical and magnetooptical properties of single crystals of the ferromagnetic spinel CoFe2O4 highlighted the peculiarities related to the interplay of magnetoelastic and magnetooptical properties of the material. These peculiarities are pronounced in the effects of magnetoreflection and magnetoabsorption (~6% in H~3.5 kOe) of the natural (nonpolarized) light in the infrared spectral range from 1 µm to 30 µm.
It was shown that the strain-magnetooptical properties of CoFe2O4 manifest themselves as a correlation of the field dependences of magnetostriction, magnetoreflection and magnetoabsorption. These effects reach large values in the IR range and were ascribed to the sensitivity of the fundamental absorption edge and impurity-absorption bands to magnetoelastic properties of the crystal. The correlation takes place at different orientations of the magnetic field relative to the crystal surface—in the Faraday and Voigt geometries of experiment—and to the crystallographic axes. In the Faraday configuration, a contribution of the Faraday effect to the magnetoabsorption was observed due to the partial polarization of light in the optical setup. The features of the field dependences of magnetoreflection and magnetoabsorption in the Faraday configuration was related to the additional contribution of mechanical stresses.
The anomalously large (on the order of 50%) contribution of magnetostriction to the magnetic anisotropy constant K1 is responsible for the strain-magnetooptical effects in CoFe2O4. The effect of magnetostriction on the magnetooptical properties of CoFe2O4 was found to be indirect. Due to the magnetostriction, an external magnetic field gives rise to B-sublattice distortion and thereby changes the electronic states of Co2+ ions, which in turn results in the observed changes in the absorption spectrum.
Finally, the results of investigations of the strain-magnetooptics in ferromagnetic CoFe2O4 single crystals are imperative in understanding and studying similar properties in magnetostrictive magnetic materials of other compositions.
Author Contributions
All authors contributed to the study conception, design, data collection and analysis, V.B., N.B., S.N., D.S. and A.N. The first draft of the manuscript was written by Y.S. and A.T. commented on previous versions of the manuscript. All authors read and approved the final manuscript.
Funding
The work was carried out within the framework of the state task of the Ministry of Education and Science of the Russian Federation (subject “Spin” No. 122021000036-3).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors are grateful to E.I. Patrakov for conducting electron microscopy and local X-ray spectroscopy study. The magnetic measurements were carried out at the Center for Collective use of the IMP UB of RAS.
Conflicts of Interest
The authors have no competing interests to declare that are relevant to the content of this article. All data generated or analyzed during this study are included in this published article. Any supplementary data are available from the corresponding author on reasonable request.
References
- Bukharaev, A.A.; Zvezdin, A.K.; Pyatakov, A.P.; Fetisov, Y.K. Straintronics: A new trend in micro- and nanoelectronics and materials science. Physics-Uspekhi 2018, 61, 1175. [Google Scholar] [CrossRef]
- Roy, K. Ultra-low-energy straitronics using multiferroic composites. Proc. SPIE 2014, VII, 91670U. [Google Scholar]
- Ustinov, A.B.; Kolkov, P.I.; Nikitin, A.A.; Kalinikos, B.A.; Fetisov, Y.K.; Srinivasan, G. Ferrite-ferroelectric phase shifters controlled by electric and magnetic fields. Tech. Phys. 2011, 56, 821. [Google Scholar]
- Sukhorukov, Y.; Telegin, A.; Bebenin, N.; Nosov, A.; Bessonov, V.; Buchkevich, A. Strain-magneto-optics of a magnetostrictive ferrimagnetic CoFe2O4. Solid State Commun. 2017, 263, 27–30. [Google Scholar] [CrossRef]
- Ferre, J.; Gehring, G. Linear optical birefringence of magnetic crystals. Rep. Prog. Phys. 1984, 47, 513–611. [Google Scholar] [CrossRef]
- Moskvin, A.S.; Latypov, D.G.; Gudkov, V.G. The nature of birefringence in and elasto-optical properties of ortho-ferrites. Fizika Tverdogo Tela 1988, 30, 413–419, (In Russian only). [Google Scholar]
- Sukhorukov, Y.P.; Telegin, A.V.; Bebenin, N.G.; Naumov, S.V.; Nossov, A.P. Strain-magneto-optics in CoFe2O4: Magneto-absorption in Voight geometry. J. Appl. Phys. 2020, 128, 195103. [Google Scholar] [CrossRef]
- Bozorth, R.M.; Tilden, E.F.; Williams, A.J. Anisotropy and magnetostriction of some ferrites. Phys. Rev. 1955, 99, 1788–1798. [Google Scholar] [CrossRef]
- Letyuk, L.M.; Balbashov, A.M.; Krutogin, D.G.; Gonchar, A.V.; Kudryashkin, I.G.; Saldunei, A.M. Technology of the Production of Magnetoelectronic Materials; Metalllurgiya: Moscow, Russia, 1994. (In Russian) [Google Scholar]
- Krupichka, S.; Pohomov, A.S. Physics of Ferrites and Related Magnetic Oxides; Mir: Moscow, Russia, 1976. [Google Scholar]
- Wang, W.H.; Ren, X. Flax growth of high-quality CoFe2O4 single crystals and their characterization. J. Cryst. Growth 2006, 289, 605–608. [Google Scholar] [CrossRef]
- Turtelli, R.S.; Kriegisch, M.; Atif, M.; Grössinger, R. Co-ferrite—A material with interesting magnetic properties. IOP Conf. Ser. Mater. Sci. Eng. 2014, 60, 012020. [Google Scholar] [CrossRef]
- Evtihiev, N.N.; Economov, N.A.; Krebs, A.B.; Zamjatina, N.A. Co-ferrite—New magnetooptic recording material. IEEE Trans. Magn. 1976, 12, 773–775. [Google Scholar] [CrossRef]
- Perthel, P.K.; Keilig, R.W. Monatsber; Deut. Akad. Wiss.: Berlin, Germany, 1963; Volume 5, pp. 109–125. [Google Scholar]
- Kambale, R.C.; Song, K.; Won, C.; Lee, K.; Hur, N. Magnetic and magnetostrictive behavior of Dy3+ doped CoFe2O4 single crystals grown by flux method. J. Cryst. Growth 2012, 340, 171–174. [Google Scholar] [CrossRef]
- Bonnenberg, D.; Boyd, E.L.; Calhoun, B.A.; Folen, V.J.; Gräper, W. Magnetic and Other Properties of Oxides and Related Compounds in “Landolt-Bornstein” Vol. III/4b; Hellwege, K.H., Hellwege, A.M., Eds.; Springer: Berlin/Heidelberg, Germany, 1970; pp. 367–391. [Google Scholar]
- Vonsovskii, S.V. Magnetism; Wiley: New York, NY, USA, 1974. [Google Scholar]
- Kittel, C. Physical theory of ferromagnetic domains. Rev. Mod. Phys. 1949, 21, 541–583. [Google Scholar] [CrossRef]
- Krinchik, G.S. Fizika Mgnitnykh Yavlenii (Physics of Magnetic Phenomena); Mosk. Gos. Univ.: Moscow, Russia, 1985. [Google Scholar]
- Li, Z.; Fisher, E.S.; Liu, J.Z.; Nevitt, M.V. Single-crystal elastic constants of Co-Al and Co-Fe spinels. J. Mater. Sci. 1991, 26, 2621–2624. [Google Scholar] [CrossRef]
- Danil’kevich, M.I.; Litvinivich, G.V.; Naumenko, V.I. IR reflection spectra and optical constants of cobalt ferrite—gallates. J. Appl. Spectrosc. 1976, 24, 38–43. [Google Scholar] [CrossRef]
- Waldron, R.D. Infrared Spectra of Ferrites. Phys. Rev. 1955, 99, 1727–1735. [Google Scholar] [CrossRef]
- Bujakiewicz-Korońska, R.; Hetmańczyk, Ł.; Garbarz-Glos, B.; Budziak, A.; Kalvane, A.; Bormanis, K.; Drużbicki, K. Low temperature measurements by infrared spectroscopy in CoFe2O4 ceramic. Open Phys. 2012, 10, 1137–1143. [Google Scholar] [CrossRef]
- Lucarini, V.; Peiponen, K.-E.; Saarinen, J.J.; Vartiainen, E.M. Kramers-Kronig Relations in Optical Materials Research; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2005. [Google Scholar]
- Rahman, A.; Gafur, A.; Sarker, A.R. Impact of doping on structural, electronic and optical properties of cobalt ferrite prepared by solid-state reaction. Int. J. Innov. Res. Adv. Eng. 2015, 2, 99–107. [Google Scholar]
- Rahman, M.A.; Hossain, M.M.; Islam, M.S.; Sarker, M.A.R. First-principle investigation of doping effects on electronic, elastic, thermal and optical properties of CoFe2O4. Appl. Res. J. 2015, 1, 127–136. [Google Scholar]
- Holinsworth, B.S.; Mazumdar, D.; Sims, H.; Sun, Q.-C.; Yurtisigi, M.K.; Sarker, S.K.; Gupta, A.; Butler, W.H.; Musfeldt, J.L. Chemical tuning of the optical band gap in spinel ferrites: CoFe2O4 vs. NiFe2O4. Appl. Phys. Lett. 2013, 103, 082406. [Google Scholar] [CrossRef]
- Rai, R.C.; Wilser, S.; Guminiak, M.; Cai, B.; Nakarmi, M.L. Optical and electronic properties of NiFe2O4 and CoFe2O4 thin films. Appl. Phys. A 2011, 106, 207–211. [Google Scholar] [CrossRef]
- Himcinschi, C.; Vrejoiu, I.; Salvan, G.; Fronk, M.; Talkenberger, A.; Zahn, D.R.T.; Rafaja, D.; Kortus, J. Optical and magneto-optical study of nickel and cobalt ferrite epitaxial thin films and submicron structures. J. Appl. Phys. 2013, 113, 084101. [Google Scholar] [CrossRef]
- Subías, G.; Cuartero, V.; García, J.; Blasco, J.; Pascarelli, S. Atomic-scale mechanisms for magnetostriction in CoFe2O4 and La0.5Sr0.5CoO3 oxides determined by differential x-ray absorption spectroscopy. Phys. Rev. B 2019, 100, 104420. [Google Scholar] [CrossRef]
- Auslender, M.I.; Barsukova, E.V.; Bebenin, N.G.; Gizhevskii, B.A.; Loshkareva, N.N.; Sukhorukov, Y.P.; Chebotaev, N.M. Absorption spectrum of n- and p-type single crystals of ferromagnetic semiconductor HgCr2Se4 in a magnetic field. Sov. Phys. JETP 1989, 68, 139–142. [Google Scholar]
- Sukhorukov, Y.P.; Telegin, A.V.; Bebenin, N.G.; Nosov, A.P.; Bessonov, V.D.; Buchkevich, A.A.; Patrakov, E.I. Magnetoreflection and magnetostriction in ferrimagnetic spinels CoFe2O4. JETP 2018, 126, 106. [Google Scholar] [CrossRef]
- Yu, T.; Shen, Z.X.; Shi, Y.; Ding, J. Cation migration and magnetic ordering in spinel CoFe2O4 powder: Micro-Raman scattering study. J. Phys. Cond. Matter 2002, 14, L613–L618. [Google Scholar] [CrossRef]
- Seeger, K. Semiconductor Physics; Springer: Berlin/Heidelberg, Germany, 2004; p. 538. [Google Scholar]
- Peeters, W.L.; Martens, J.W.D. Magneto-optical effects of aluminium and ferrous substituted cobalt ferrite. J. Appl. Phys. 1982, 53, 8178–8180. [Google Scholar] [CrossRef]
- Zanmarchi, G.; Bongers, P.F. Infrared Faraday rotation in ferrites. J. Appl. Phys. 1969, 40, 1230–1231. [Google Scholar] [CrossRef]
- Kriegisch, M.; Ren, W.; Sato-Turelli, R.; Muller, H.; Grossinger, R.; Zhang, Z. Field-induced magnetic transition in cobalt-ferrite. J. Appl. Phys. 2012, 111, 07E308. [Google Scholar] [CrossRef]
- Ahrenkiel, R.K.; Moser, F.; Carnall, E.; Martin, T.; Pearlman, D.; Lyu, S.L.; Coburn, T.; Lee, T.H. Hot-pressed CdCr2S4: An efficient magneto-optic material. Appl. Phys. Lett. 1971, 18, 171. [Google Scholar]
- Guchhait, S.; Aireddy, H.; Das, A.K. The emergence of high room temperature in-plane and out-of-plane magnetostriction in polycrystalline CoFe2O4 film. Sci. Rep. 2021, 11, 22890. [Google Scholar] [CrossRef] [PubMed]
- Granovskii, A.B.; Sukhorukov, Y.P.; Telegin, A.V.; Bessonov, V.D.; Gan’Shina, E.A.; Kaul’, A.R.; Korsakov, I.E.; Gorbenko, O.Y.; González, J. Giant magnetorefractive effect in La0.7Ca0.3MnO3 films. J. Exp. Theor. Phys. 2011, 112, 77–86. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).