Magnetic, Electric and Optical Properties of Ion Doped CuCr2O4 Nanoparticles
Abstract
1. Introduction
2. The Model
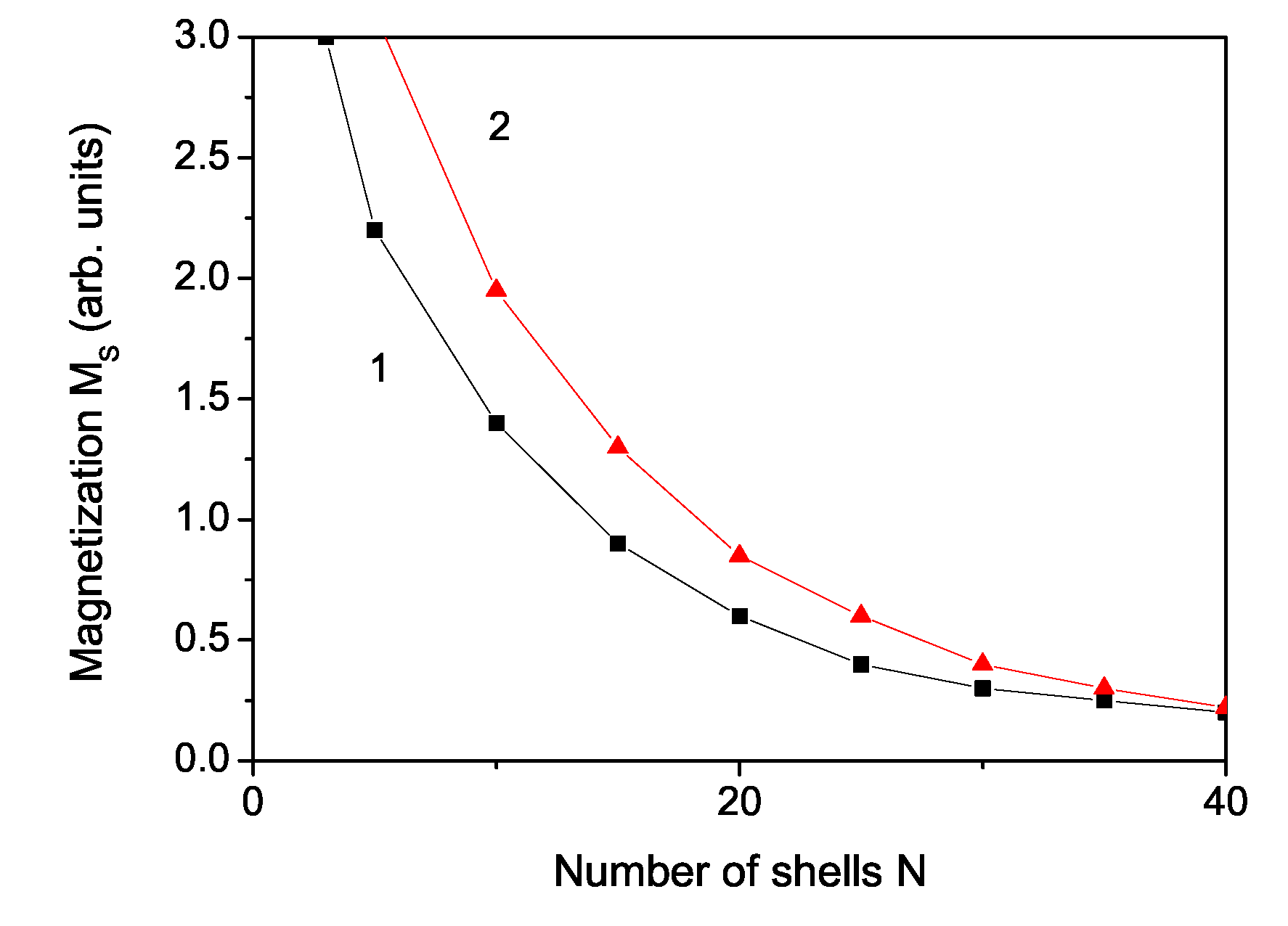
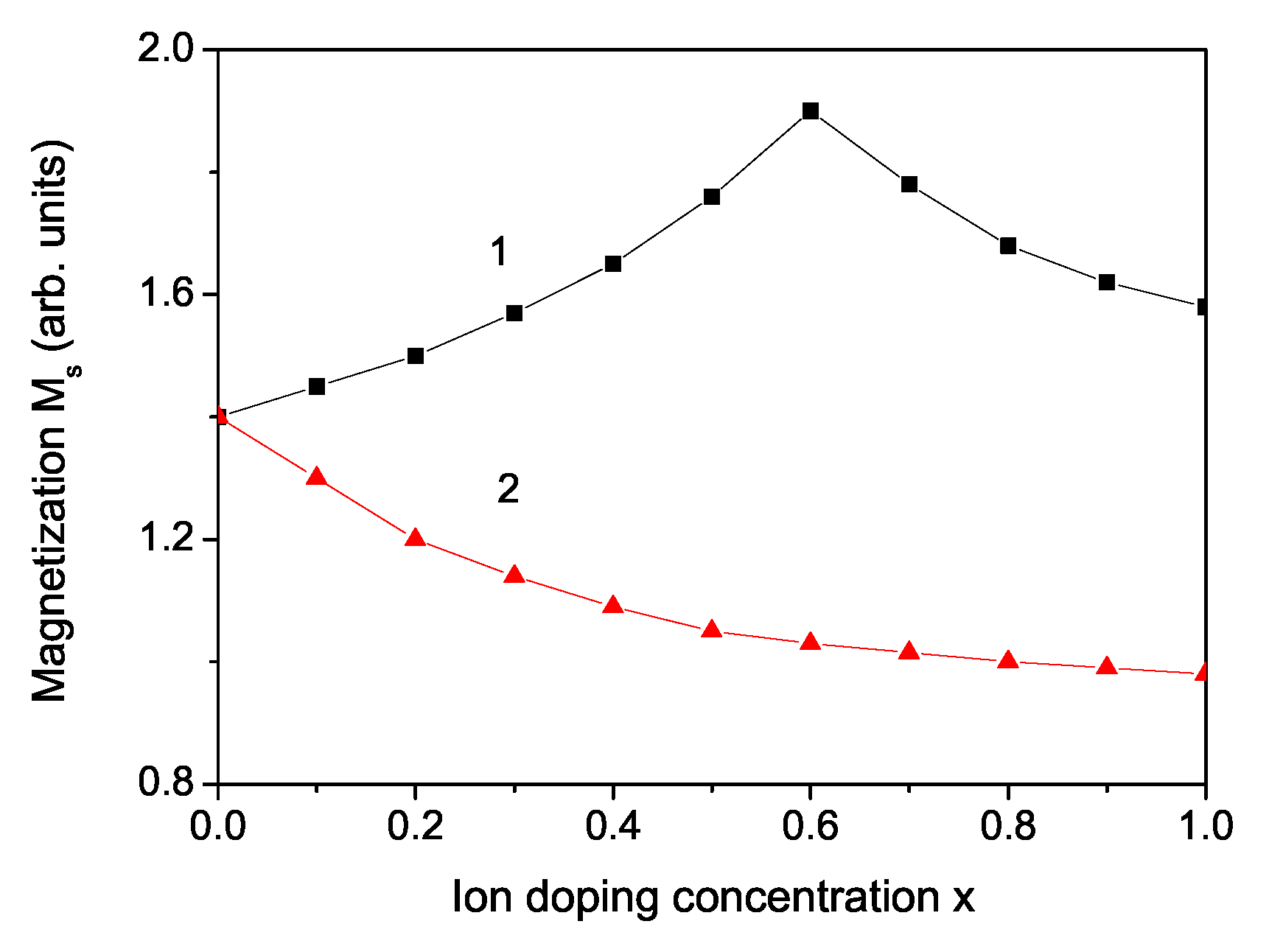
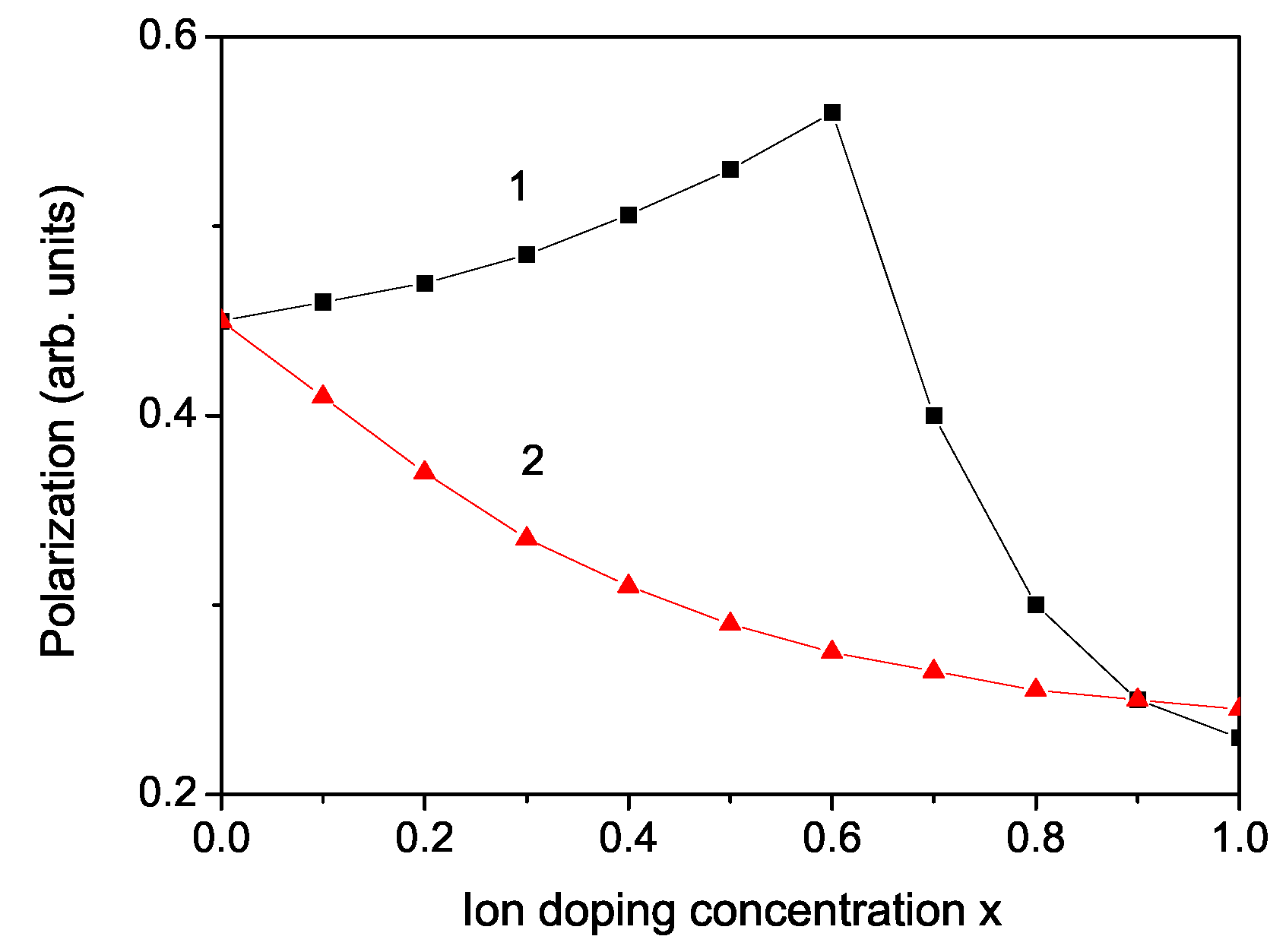
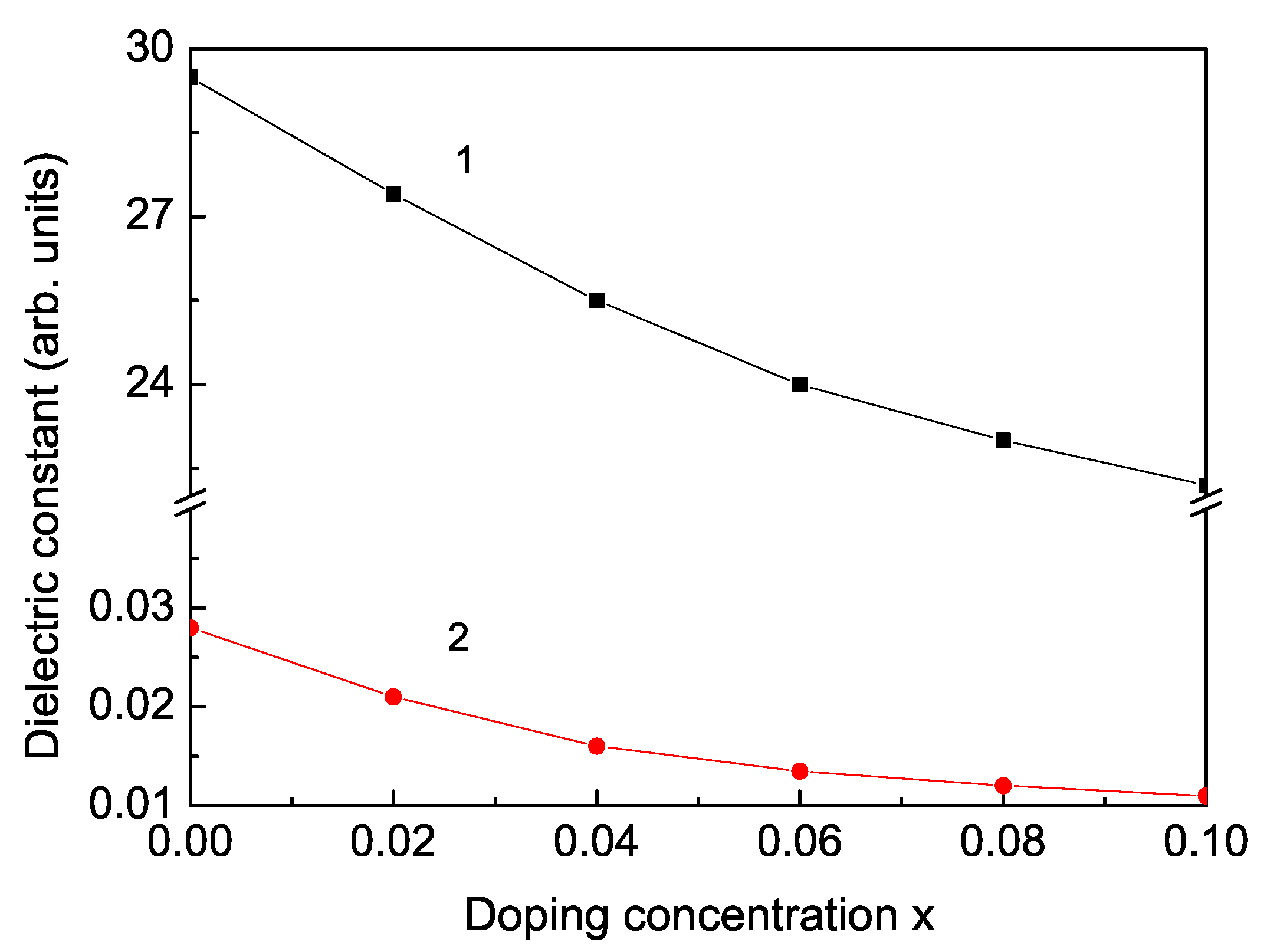
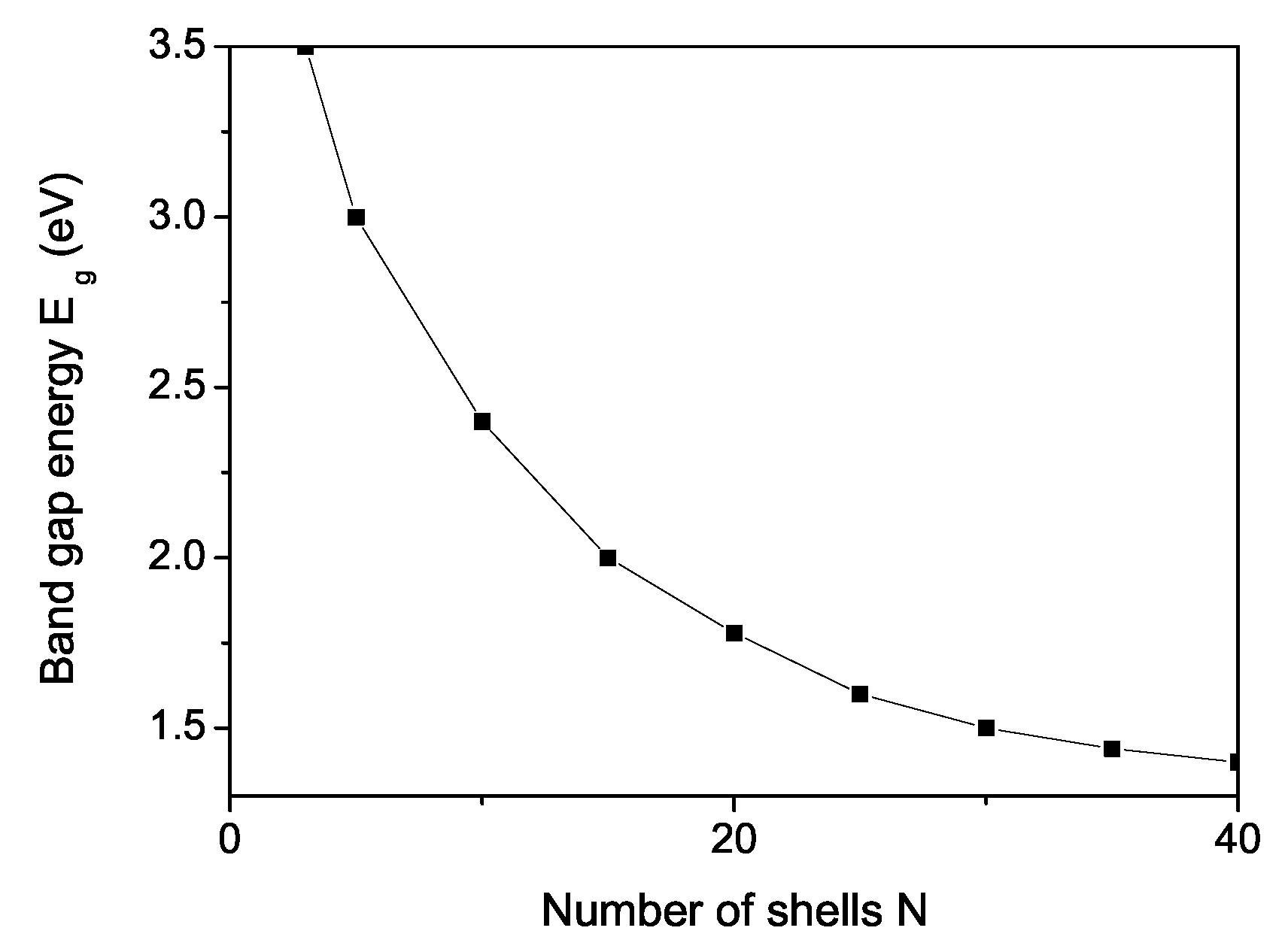
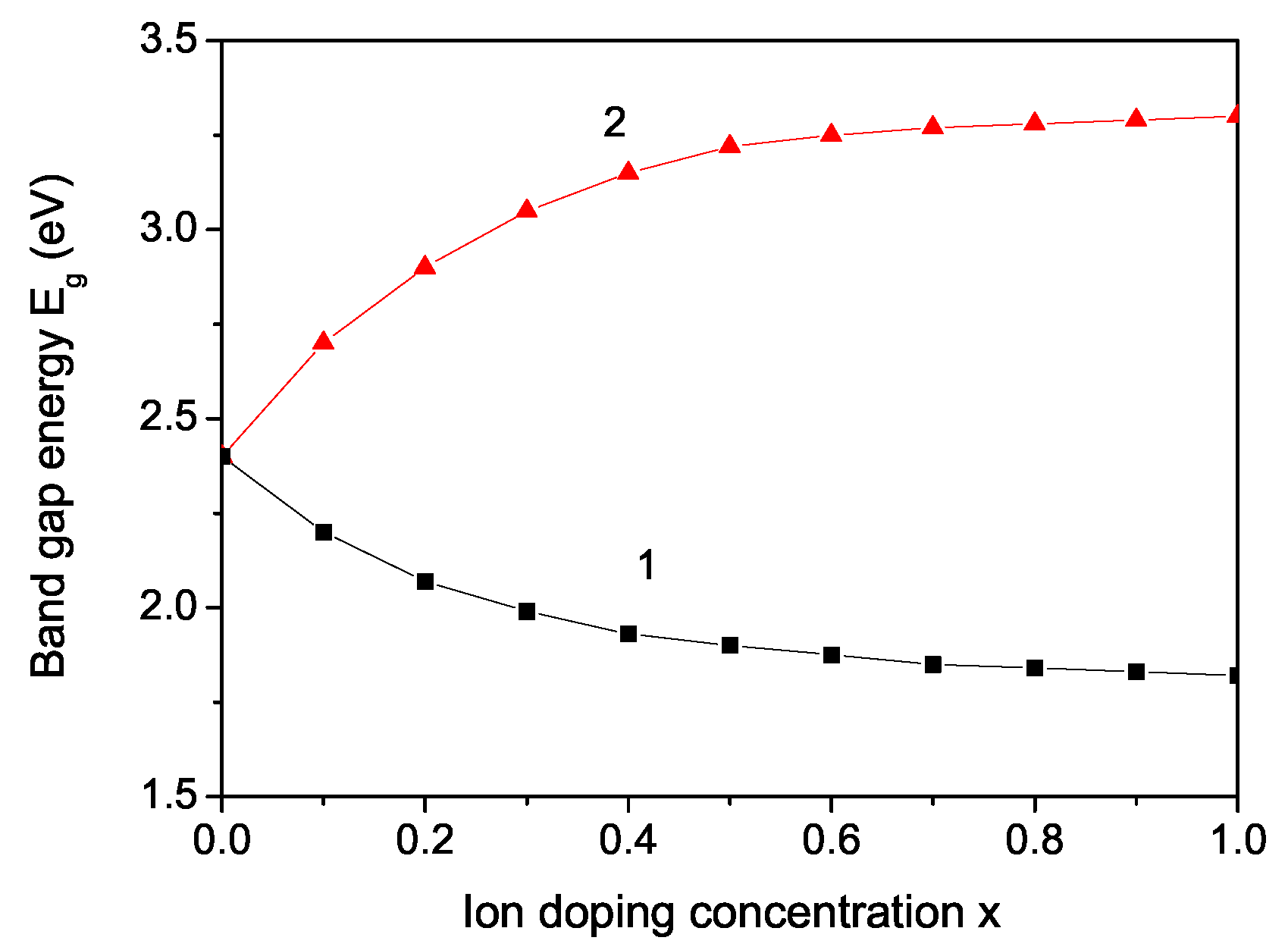
3. Numerical Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Prasad, R.; Singh, P. Applications and Preparation Methods of Copper Chromite Catalysts: A Review. Bull. Chem. React. Eng. Catal. 2011, 6, 63–113. [Google Scholar] [CrossRef]
- Kanti, P.K.; Chereches, E.I.; Minea, A.A.; Sharma, K.V. Experiments on thermal properties of ionic liquid enhanced with alumina nanoparticles for solar applications. J. Therm. Anal. Calorim. 2022. [Google Scholar] [CrossRef]
- Gurgel, T.T.; Buzinaro, M.A.; Moreno, N.O. Magnetization Study in CuCr2O4 Spinel Oxide. J. Supercond. Nov. Magn. 2013, 26, 2557–2559. [Google Scholar] [CrossRef]
- Tripathi, T.S.; Yadav, C.S.; Karppinen, M. Transparent ferrimagnetic semiconducting CuCr2O4 thin films by atomic layer deposition. APL Mater. 2016, 4, 046106. [Google Scholar] [CrossRef]
- Iwata, J.M.; Chopdekar, R.V.; Wong, F.; Nelson-Cheeseman, B.B.; Arenholz, E.; Suzuki, Y. Enhanced Magnetization of CuCr2O4 Thin Films by Substrate-Induced Strain. J. Appl. Phys. 2009, 105, 07A905. [Google Scholar] [CrossRef]
- Ali, A.; Singh, Y. A magnetocaloric study on the series of 3d-metal chromites ACr2O4 where A = Mn, Fe, Co, Ni, Cu and Zn. J. Magn. Magn. Mater. 2020, 499, 166253. [Google Scholar] [CrossRef]
- Ye, Z.-G.; Crottaz, O.; Vaudano, F.; Kubel, F.; Tissot, P.; Schmid, K. Single crystal growth, structure refinement, ferroelastic domains and phase transitions of the hausmannite CuCr2O4. Ferroel. 1994, 162, 103. [Google Scholar] [CrossRef]
- Chatterjee, A.; Dey, J.K.; Majumdar, S.; Dippel, A.-C.; Gutowski, O.; Zimmermann, M.V.; Giri, S. Tuning of multiferroic order with Co doping in CuCr2O4: Interplay between structure and orbital order. Phys. Rev. Mater. 2019, 3, 104403. [Google Scholar] [CrossRef]
- Rajeswari, G.; Prabavathi, N.; Tamizhdurai, P.; Prakasam, A.; Kumar, G. Enhancement of the structure, solar cells and vibrational studies of undoped CuCr2O4 and La-doped CuCr2O4 semiconductor compounds. Heliyon 2022, 8, e09233. [Google Scholar] [CrossRef] [PubMed]
- Yadav, P.; Sharma, S.; Sau, T.; da Silva, I.; Lalla, N.P. Jahn-Teller and geometric frustration effects on the structural and magnetic ground states of substituted spinels (Ni,A)Cr2O4 (A = Mn/Cu). J. All. Compd. 2020, 826, 154139. [Google Scholar] [CrossRef]
- Singh, K.; Maignana, A.; Simon, C.; Martin, C. FeCr2O4 and CoCr2O4 spinels: Multiferroicity in the collinear magnetic state? Appl. Phys. Lett. 2011, 99, 172903. [Google Scholar] [CrossRef]
- Habibi, M.H.; Fakhri, F. Fabrication and Characterization of CuCr2O4 Nanocomposite by XRD, FESEM, FTIR, and DRS. Synth. React. Inorg. Met.-Org. Nano-Met. Chem. 2016, 46, 847. [Google Scholar] [CrossRef]
- Beshkar, F.; Zinatloo-Ajabshir, S.; Salavati-Niasari, M. Preparation and characterization of the CuCr2O4 nanostructures via a new simple route. J. Mater. Sci. Mater. Electron. 2015, 26, 5043. [Google Scholar] [CrossRef]
- Krause, M.; Sonnenberg, J.; Munnik, F.; Grenzer, J.; Huebner, R.; Garcia-Valenzuela, A.; Gemming, S. Formation, structure, and optical properties of copper chromite thin films for high-temperature solar absorbers. Materialia 2021, 18, 101156. [Google Scholar] [CrossRef]
- Lahmar, H.; Kebir, M.; Nasrallah, N.; Trari, M. Photocatalytic reduction of Cr(VI) on the new hetero-system CuCr2O4/ZnO. J. Mol. Catal. A Chem. 2012, 353–354, 74–79. [Google Scholar] [CrossRef]
- Ghorai, K.; Panda, A.; Hossain, A.; Bhattacharjee, M.; Chakraborty, M.; Bhattacharya, S.K.; Bera, P.; Kim, H.; Seikh, M.M.; Gayen, A. Anatase TiO2 decorated CuCr2O4 nanocomposite: A versatile photocatalyst under domestic LED light irradiation. Appl. Surf. Sc. 2021, 568, 150838. [Google Scholar] [CrossRef]
- Benrighi, Y.; Nasrallah, N.; Chaabane, T.; Belkacemi, H.; Bourkeb, K.W.; Kenfoud, H.; Baaloudj, O. Characterization and application of the spinel CuCr2O4 synthesized by sol–gel method for sunset yellow photodegradation. J. Sol.-Gel. Sc. Techn. 2022, 101, 390. [Google Scholar] [CrossRef]
- Soleimani, F.; Salehi, M.; Gholizadeh, A. Synthesis and characterization of new spinel Mn0.5Cu0.5Cr2O4 and degradation of Malachite Green from wastewater in comparison with CuCr2O4. Int. J. Nano Dimens. 2019, 10, 260–271. [Google Scholar]
- Nagaev, E.L. Spin Polaron Theory for Magnetic Semiconductors with Narrow Bands. Phys. Status Sol. B 1974, 65, 11. [Google Scholar] [CrossRef]
- Nolting, W. Theory of ferromagnetic semiconductors. Phys. Status Sol. B 1979, 96, 11. [Google Scholar] [CrossRef]
- Kochelaev, B.I. Spin-Phonon Interaction and the EPR Linewidth in La2CuO4 and Related Cuprates. J. Supercond. 1999, 12, 53. [Google Scholar] [CrossRef]
- Tserkovnikov, Y.A. Decoupling of chains of equations for two-time Green’s functions. Teor. Mat. Fiz. 1971, 7, 250. [Google Scholar] [CrossRef]
- Apostolova, I.N.; Apostolov, A.T.; Wesselinowa, J.M. Multiferroic and phonon properties of pure and ion doped CoCr2O4-Bulk and nanoparticles. J. All. Comp. 2021, 852, 156885. [Google Scholar] [CrossRef]
- Katsura, H.; Nagaosa, N.; Balatsky, A.V. Spin current and magnetoelectric effect in noncollinear magnets. Phys. Rev. Lett. 2005, 95, 057205. [Google Scholar] [CrossRef] [PubMed]
- Vaks, V.G. Introduction to the Microscopic Theory of Ferroelectrics; Nauka: Moscow, Russia, 1973; p. 158. (In Russian) [Google Scholar]
- Goryachev, E.; Kuzmin, E.V.; Ovchinnikov, S.G. Metal-insulator transition in the Hubbard model by the irreducible Green functions method. J. Phys. C 1982, 15, 1481. [Google Scholar] [CrossRef]
- Lawes, G.; Melot, B.; Page, K.; Ederer, C.; Hayward, M.A.; Proffen, T.; Seshadri, R. Dielectric anomalies and spiral magnetic order in CoCr2O4. Phys. Rev. B 2006, 74, 024413. [Google Scholar] [CrossRef]
- Kocsis, V.; Bordacs, S.; Varjas, D.; Penc, K.; Abouelsayed, A.; Kuntscher, C.A.; Ohgushi, K.K.; Tokura, Y.; Kezsmarki, I. Magnetoelasticity in ACr2O4 spinel oxides (A = Mn, Fe, Co, Ni, and Cu). Phys. Rev. B 2013, 87, 064416. [Google Scholar] [CrossRef]
- Wesselinowa, J.M.; Apostolov, A.T. Anharmonic effects in ferromagnetic semiconductors. J. Phys. Cond. Matter 1996, 8, 473–488. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, X.; Kan, X.; Feng, S.; Wang, W.; Liu, C.; Li, Y. Synthesis and Analysis of Zn-Substituted CoCr2O4 Spinel Oxide. J. Supercond. Novel Magn. 2022, 35, 753–762. [Google Scholar] [CrossRef]
- Hosseini, S.G.; Abazari, R.; Gavi, A. Pure CuCr2O4 nanoparticles: Synthesis, characterization and their morphological and size effects on the catalytic thermal decomposition of ammonium perchlorate. Solid State Sc. 2014, 37, 72–79. [Google Scholar]
- Ortuno-Lopez, M.B.; Sotelo-Lerma, M.; Mendoza-Galvana, A.; Ramirez-Bona, R. Optical band gap tuning and study of strain in CdS thin films. Vacuum 2004, 76, 181. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Apostolov, A.T.; Apostolova, I.N.; Wesselinova, J.M. Magnetic, Electric and Optical Properties of Ion Doped CuCr2O4 Nanoparticles. Magnetochemistry 2022, 8, 122. https://doi.org/10.3390/magnetochemistry8100122
Apostolov AT, Apostolova IN, Wesselinova JM. Magnetic, Electric and Optical Properties of Ion Doped CuCr2O4 Nanoparticles. Magnetochemistry. 2022; 8(10):122. https://doi.org/10.3390/magnetochemistry8100122
Chicago/Turabian StyleApostolov, Angel Todorov, Iliana Naumova Apostolova, and Jilia Mihailowa Wesselinova. 2022. "Magnetic, Electric and Optical Properties of Ion Doped CuCr2O4 Nanoparticles" Magnetochemistry 8, no. 10: 122. https://doi.org/10.3390/magnetochemistry8100122
APA StyleApostolov, A. T., Apostolova, I. N., & Wesselinova, J. M. (2022). Magnetic, Electric and Optical Properties of Ion Doped CuCr2O4 Nanoparticles. Magnetochemistry, 8(10), 122. https://doi.org/10.3390/magnetochemistry8100122






