Simulating Static and Dynamic Properties of Magnetic Molecules with Prototype Quantum Computers
Abstract
1. Introduction
2. Determining the Ground State of Heisenberg Chains by VQE
2.1. Variational Quantum Eigensolver
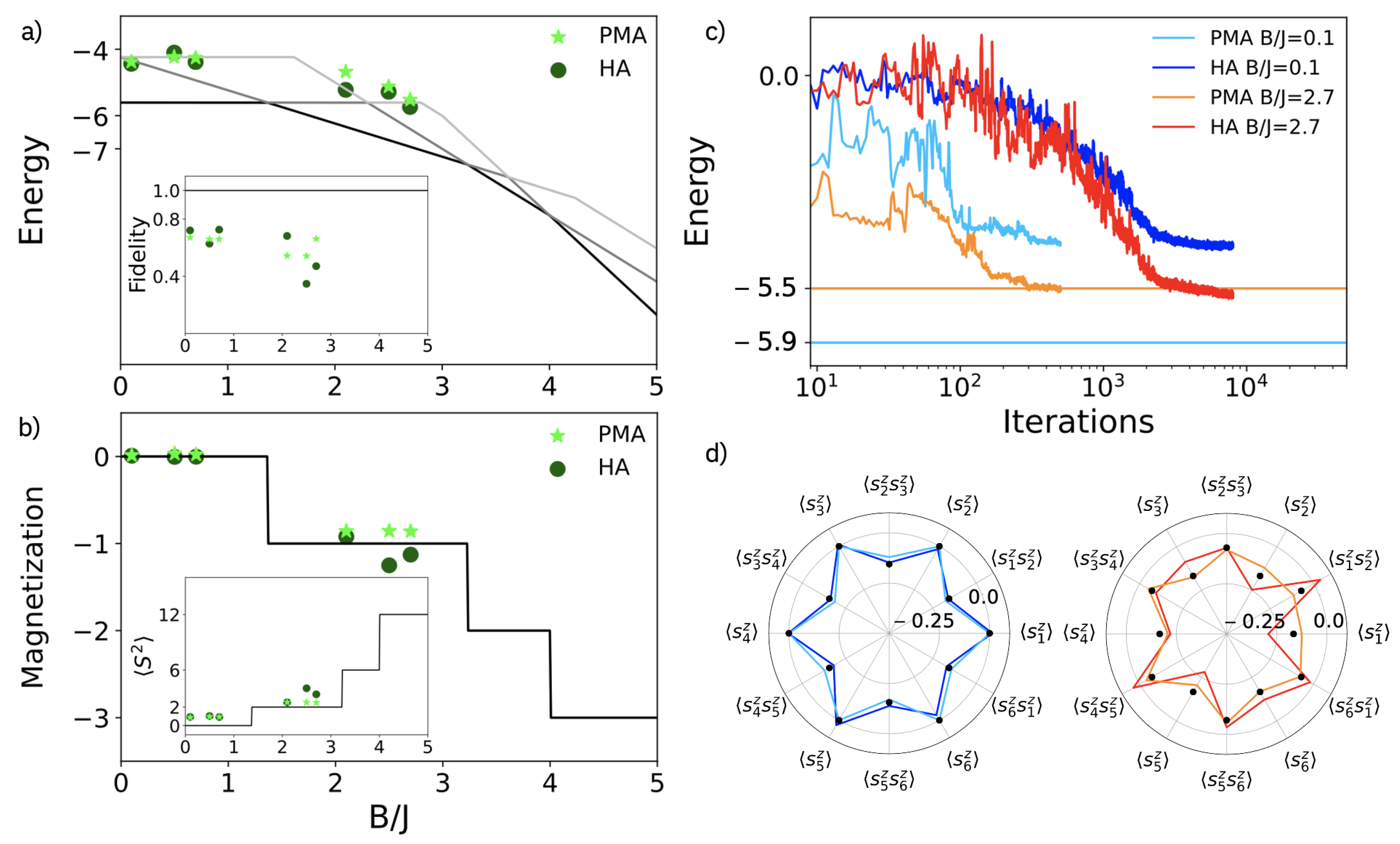
2.2. Heisenberg Spin Chains and Adapted Ansatz
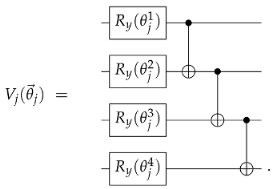
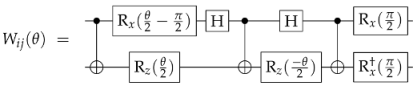
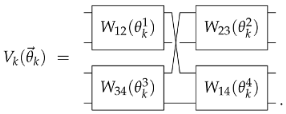
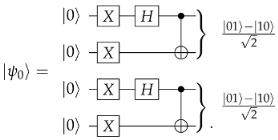
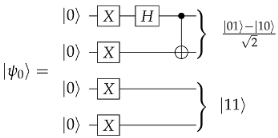
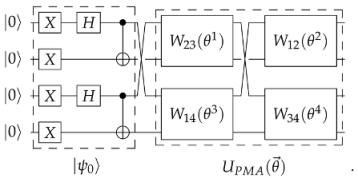
Effect of Noise
- finite relaxation () and coherence () times of the physical qubits, which typically lead to amplitude and phase damping effects;
- single- and 2-qubit gate errors (the latter being usually much higher), acting during the implementation of each quantum operation, due to both imperfections of the coherent qubit manipulation and additional incoherent effects (e.g., depolarizing Pauli noise);
- readout errors, associated with imperfect measurements and erroneous assignment of the outcome, which can be modeled, for example, as bit flip channels.
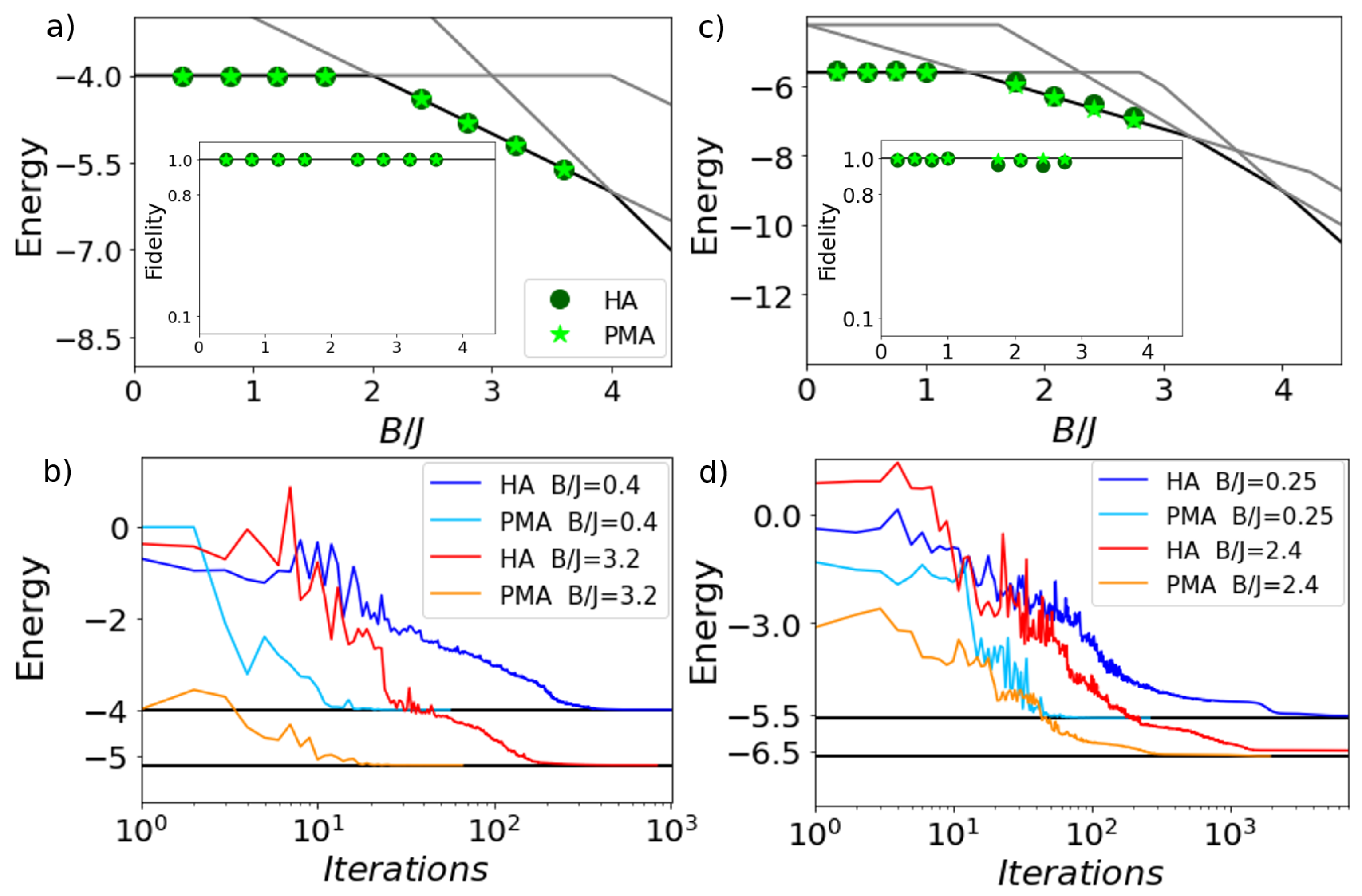
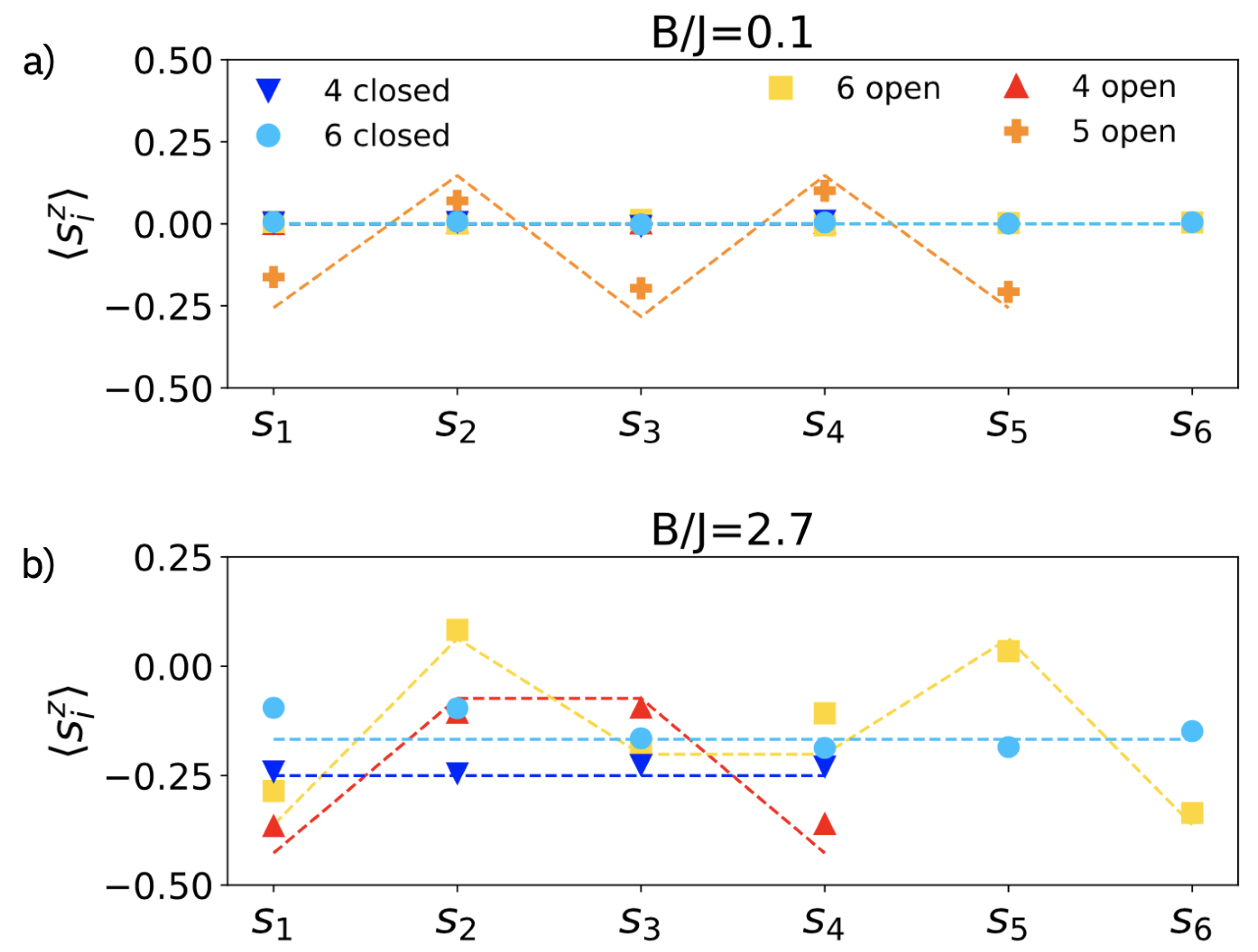
2.3. Finite-Size and Parity Effects
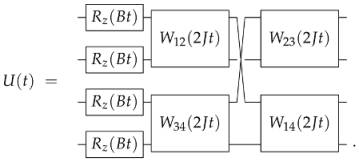
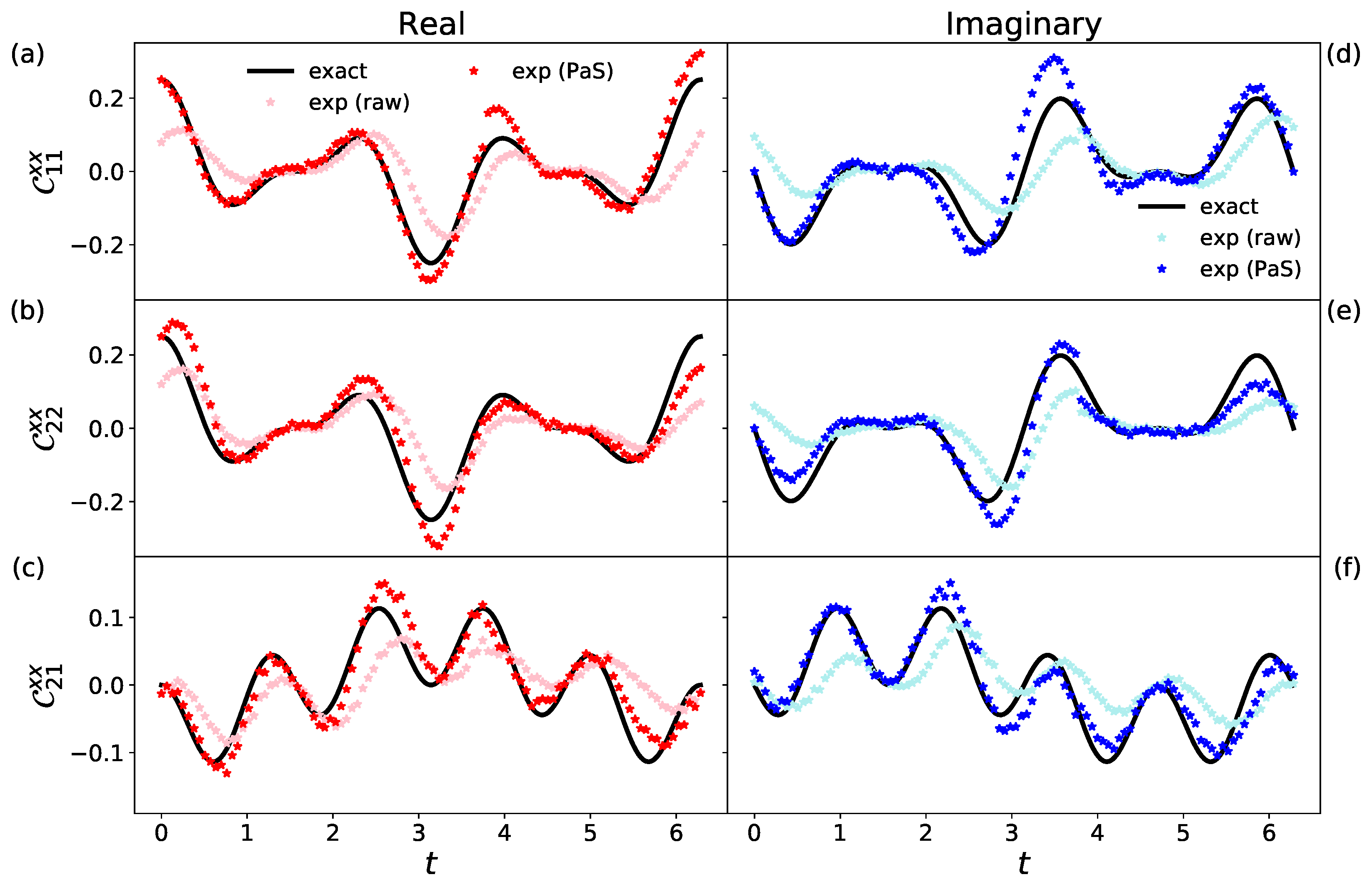
3. Dynamical Correlation Functions

4. Discussion and Conclusions
5. Materials and Methods
Simulations
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Troiani, F.; Affronte, M.; Carretta, S.; Santini, P.; Amoretti, G. Proposal for Quantum Gates in Permanently Coupled Antiferromagnetic Spin Rings without Need of Local Fields. Phys. Rev. Lett. 2005, 94, 190501. [Google Scholar] [CrossRef]
- Troiani, F.; Ghirri, A.; Affronte, M.; Carretta, S.; Santini, P.; Amoretti, G.; Piligkos, S.; Timco, G.; Winpenny, R.E.P. Molecular Engineering of Antiferromagnetic Rings for Quantum Computation. Phys. Rev. Lett. 2005, 94, 207208. [Google Scholar] [CrossRef] [PubMed]
- Luis, F.; Repollés, A.; Martínez-Pérez, M.J.; Aguilá, D.; Roubeau, O.; Zueco, D.; Alonso, P.J.; Evangelisti, M.; Camón, J.S.; Barrios, L.A.; et al. Molecular prototypes for spin-based CNOT and SWAP quantum gates. Phys. Rev. Lett. 2011, 107, 117203. [Google Scholar] [CrossRef] [PubMed]
- Santini, P.; Carretta, S.; Troiani, F.; Amoretti, G. Molecular Nanomagnets as Quantum Simulators. Phys. Rev. Lett. 2011, 107, 230502. [Google Scholar] [CrossRef]
- Wedge, C.J.; Timco, G.A.; Spielberg, E.T.; George, R.E.; Tuna, F.; Rigby, S.; McInnes, E.J.L.; Winpenny, R.E.; Blundell, S.J.; Ardavan, A. Chemical engineering of molecular qubits. Phys. Rev. Lett. 2012, 108, 107204. [Google Scholar] [CrossRef] [PubMed]
- Chiesa, A.; Whitehead, G.F.S.; Carretta, S.; Carthy, L.; Timco, G.A.; Teat, S.J.; Amoretti, G.; Pavarini, E.; Winpenny, R.E.P.; Santini, P. Molecular nanomagnets with switchable coupling for quantum simulation. Sci. Rep. 2014, 4, 7423. [Google Scholar] [CrossRef]
- Aguilà, D.; Barrios, D.; Velasco, V.; Roubeau, O.; Repollés, A.; Alonso, P.; Sesé, J.; Teat, S.; Luis, F.; Aromí, G. Heterodimetallic [LnLn’] lanthanide complexes: Toward a chemical design of two-qubit molecular spin quantum gates. J. Am. Chem. Soc. 2014, 136, 14215. [Google Scholar] [CrossRef]
- Ardavan, A.; Bowen, A.M.; Fernandez, A.; Fielding, A.J.; Kaminski, D.; Moro, F.; Muryn, C.A.; Wise, M.; Ruggi, A.; McInnes, E.J.L.; et al. Engineering coherent interactions in molecular nanomagnet dimers. NPJ Quantum Inf. 2015, 1, 15012. [Google Scholar]
- Zadrozny, J.M.; Niklas, J.; Poluektov, O.G.; Freedman, D.E. Millisecond Coherence Time in a Tunable Molecular Electronic Spin Qubit. ACS Cent. Sci. 2015, 1, 488. [Google Scholar]
- Shiddiq, M.; Komijani, D.; Duan, Y.; Gaita-Ariño, A.; Coronado, E.; Hill, S. Enhancing coherence in molecular spin qubits via atomic clock transitions. Nature 2016, 531, 348–351. [Google Scholar]
- Ferrando-Soria, J.; Moreno-Pineda, E.; Chiesa, A.; Fernandez, A.; Magee, S.A.; Carretta, S.; Santini, P.; Vitorica-Yrezabal, I.; Tuna, F.; McInness, E.J.L.; et al. A modular design of molecular qubits to implement universal quantum gates. Nat. Commun. 2016, 7, 11377. [Google Scholar] [CrossRef]
- Atzori, M.; Tesi, L.; Morra, E.; Chiesa, M.; Sorace, L.; Sessoli, R. Room-Temperature Quantum Coherence and Rabi Oscillations in Vanadyl Phthalocyanine: Toward Multifunctional Molecular Spin Qubits. J. Am. Chem. Soc. 2016, 138, 2154–2157. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.S.; Deng, Y.F.; Zheng, Y.Z. The Rise of Single-Ion Magnets as Spin Qubits. Magnetochemistry 2016, 2, 40. [Google Scholar] [CrossRef]
- Chiesa, A.; Santini, P.; Carretta, S. Supramolecular Complexes for Quantum Simulation. Magnetochemistry 2016, 2, 37. [Google Scholar] [CrossRef]
- Atzori, M.; Morra, E.; Tesi, L.; Albino, A.; Chiesa, M.; Sorace, L.; Sessoli, R. Quantum Coherence Times Enhancement in Vanadium(IV)-based Potential Molecular Qubits: The Key Role of the Vanadyl Moiety. J. Am. Chem. Soc. 2016, 138, 11234–11244. [Google Scholar] [CrossRef] [PubMed]
- Yu, C.J.; Graham, M.J.; Zadrozny, J.M.; Niklas, J.; Krzyaniak, M.D.; Wasielewski, M.R.; Poluektov, O.G.; Freedman, D.E. Long Coherence Times in Nuclear Spin-Free Vanadyl Qubits. J. Am. Chem. Soc. 2016, 138, 14678–14685. [Google Scholar] [CrossRef]
- Ferrando-Soria, J.; Magee, S.A.; Chiesa, A.; Carretta, S.; Santini, P.; Vitorica-Yrezabal, I.J.; Tuna, F.; Whitehead, G.F.S.; Sproules, S.; Lancaster, K.M.; et al. Swithcable interactions in molecular double qubits. Chem 2016, 1, 727–752. [Google Scholar] [CrossRef]
- Atzori, M.; Tesi, L.; Benci, S.; Lunghi, A.; Righini, R.; Taschin, A.; Torre, R.; Sorace, L.; Sessoli, R. Spin Dynamics and Low Energy Vibrations: Insights from Vanadyl- Based Potential Molecular Qubits. J. Am. Chem. Soc. 2017, 139, 4338–4341. [Google Scholar] [CrossRef]
- Godfrin, C.; Ferhat, A.; Ballou, R.; Klyatskaya, S.; Ruben, M.; Wernsdorfer, W.; Balestro, F. Operating Quantum States in Single Magnetic Molecules: Implementation of Grover’s Quantum Algorithm. Phys. Rev. Lett. 2017, 119, 187702. [Google Scholar] [CrossRef]
- Atzori, M.; Chiesa, A.; Morra, E.; Chiesa, M.; Sorace, L.; Carretta, S.; Sessoli, R. A two-qubit molecular architecture for electronmediated nuclear quantum simulation. Chem. Sci. 2018, 9, 6183. [Google Scholar] [CrossRef]
- Atzori, M.; Benci, S.; Morra, E.; Tesi, L.; Chiesa, M.; Torre, R.; Sorace, L.; Sessoli, R. Structural Effects on the Spin Dynamics of Potential Molecular Qubits. Inorg. Chem. 2018, 57, 731–740. [Google Scholar] [CrossRef]
- Hussain, R.; Allodi, G.; Chiesa, A.; Garlatti, E.; Mitcov, D.; Konstantatos, A.; Pedersen, K.; Renzi, R.D.; Piligkos, S.; Carretta, S. Coherent Manipulation of a Molecular Ln-Based Nuclear Qudit Coupled to an Electron Qubit. J. Am. Chem. Soc. 2018, 140, 9814–9818. [Google Scholar] [CrossRef]
- Gaita-Ariño, A.; Luis, F.; Hill, S.; Coronado, E. Molecular spins for quantum computation. Nat. Chem. 2019, 11, 301–309. [Google Scholar] [CrossRef] [PubMed]
- Atzori, M.; Sessoli, R. The Second Quantum Revolution: Role and Challenges of Molecular Chemistry. J. Am. Chem. Soc. 2019, 141, 11339. [Google Scholar] [CrossRef] [PubMed]
- Macaluso, E.; Rubín, M.; Aguilà, D.; Chiesa, A.; Barrios, J.I.M.; Alonso, P.J.; Roubeau, O.; Luis, F.; Aromí, G.; Carretta, S. A heterometallic [LnLn’Ln] lanthanide complex as a qubit with embedded quantum error correction. Chem. Sci. 2020, 11, 10337. [Google Scholar] [CrossRef]
- Wojnar, M.K.; Laorenza, D.W.; Schaller, R.D.; Freedman, D.E. Nickel(II) Metal Complexes as Optically Addressable Qubit Candidates. J. Am. Chem. Soc. 2020, 142, 14826–14830. [Google Scholar] [CrossRef] [PubMed]
- Chiesa, A.; Macaluso, E.; Petiziol, F.; Wimberger, S.; Santini, P.; Carretta, S. Molecular Nanomagnets as Qubits with Embedded Quantum-Error Correction. J. Phys. Chem. Lett. 2020, 11, 8610–8615. [Google Scholar] [CrossRef] [PubMed]
- Woodruff, D.N.; Winpenny, R.; Layfield, R.A. Lanthanide Single-Molecule Magnets. Chem. Rev. 2013, 113, 5110–5148. [Google Scholar] [CrossRef]
- Chiesa, A.; Guidi, T.; Carretta, S.; Ansbro, S.; Timco, G.A.; Vitorica-Yrezabal, I.; Garlatti, E.; Amoretti, G.; Winpenny, R.E.P.; Santini, P. Magnetic Exchange Interactions in the Molecular Nanomagnet Mn12. Phys. Rev. Lett. 2017, 119, 217202. [Google Scholar] [CrossRef]
- Goodwin, C.A.P.; Ortu, F.; Reta, D.; Chilton, N.F.; Mills, D.P. Molecular magnetic hysteresis at 60 kelvin in dysprosocenium. Nature 2017, 548, 439. [Google Scholar] [CrossRef]
- Guo, F.S.; Day, B.M.; Chen, Y.C.; Tong, M.L.; Mansikkamäki, A.; Layfield, R.A. Magnetic hysteresis up to 80 kelvin in a dysprosium metallocene single-molecule magnet. Science 2018, 362, 1400–1403. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.L.; Chen, Y.C.; Tong, M.L. Symmetry strategies for high performance lanthanide-based single-molecule magnets. Chem. Soc. Rev. 2018, 47, 2431–2453. [Google Scholar] [CrossRef]
- Chiesa, A.; Cugini, F.; Hussain, R.; Macaluso, E.; Allodi, G.; Garlatti, E.; Giansiracusa, M.; Goodwin, C.A.P.; Ortu, F.; Reta, D.; et al. Understanding magnetic relaxation in single-ion magnets with high blocking temperature. Phys. Rev. B 2020, 101, 174402. [Google Scholar] [CrossRef]
- Prokof’ev, N.V.; Stamp, P.C.E. Low-Temperature Quantum Relaxation in a System of Magnetic Nanomolecules. Phys. Rev. Lett. 1998, 80, 5794–5797. [Google Scholar] [CrossRef]
- Martínez-Pérez, M.J.; Cardona-Serra, S.; Schlegel, C.; Moro, F.; Alonso, P.J.; Prima-García, H.; Clemente-Juan, J.M.; Evangelisti, M.; Gaita-Ariño, A.; Sesé, J.; et al. Gd-Based Single-Ion Magnets with Tunable Magnetic Anisotropy: Molecular Design of Spin Qubits. Phys. Rev. Lett. 2012, 108, 247213. [Google Scholar] [CrossRef]
- Wernsdorfer, W.; Ohm, T.; Sangregorio, C.; Sessoli, R.; Mailly, D.; Paulsen, C. Observation of the Distribution of Molecular Spin States by Resonant Quantum Tunneling of the Magnetization. Phys. Rev. Lett. 1999, 82, 3903–3906. [Google Scholar] [CrossRef]
- Wernsdorfer, W.; Bhaduri, S.; Boskovic, C.; Christou, G.; Hendrickson, D.N. Spin-parity dependent tunneling of magnetization in single-molecule magnets. Phys. Rev. B 2002, 65, 180403. [Google Scholar] [CrossRef]
- Santini, P.; Carretta, S.; Amoretti, G.; Guidi, T.; Caciuffo, R.; Caneschi, A.; Rovai, D.; Qiu, Y.; Copley, J.R.D. Spin dynamics and tunneling of the Néel vector in the Fe10 magnetic wheel. Phys. Rev. B 2005, 71, 184405. [Google Scholar] [CrossRef]
- Schmidt, R.; Richter, J.; Schnack, J. Frustration effects in magnetic molecules. J. Magn. Magn. Mater. 2005, 295, 164–167. [Google Scholar] [CrossRef]
- Furukawa, Y.; Kiuchi, K.; Kumagai, K.I.; Ajiro, Y.; Narumi, Y.; Iwaki, M.; Kindo, K.; Bianchi, A.; Carretta, S.; Santini, P.; et al. Evidence of spin singlet ground state in the frustrated antiferromagnetic ring Cr8Ni. Phys. Rev. B 2009, 79, 134416. [Google Scholar] [CrossRef]
- Florek, W.; Antkowiak, M.; Kamieniarz, G. Sequences of ground states and classification of frustration in odd-numbered antiferromagnetic rings. Phys. Rev. B 2016, 94, 224421. [Google Scholar] [CrossRef]
- Florek, W.; Antkowiak, M.; Kamieniarz, G. The Kahn degenerate frustration points and the Lieb-Mattis level order in heterometallic wheel molecules with competing interactions. J. Magn. Magn. Mater. 2019, 487, 165326. [Google Scholar] [CrossRef]
- Prokof’ev, N.V.; Stamp, P.C.E. Theory of the spin bath. Rep. Prog. Phys. 2000, 63, 669–726. [Google Scholar] [CrossRef]
- Waldmann, O. Spin dynamics of finite antiferromagnetic Heisenberg spin rings. Phys. Rev. B 2001, 65, 024424. [Google Scholar] [CrossRef]
- Guidi, T.; Gillon, B.; Mason, S.A.; Garlatti, E.; Carretta, S.; Santini, P.; Stunault, A.; Caciuffo, R.; van Slageren, J.; Klemke, B.; et al. Direct observation of finite size effects in chains of antiferromagnetically coupled spins. Nat. Commun. 2015, 6, 7061. [Google Scholar] [CrossRef]
- Florek, W.; Kamieniarz, G.; Marlewski, A. Universal lowest energy configurations in a classical Heisenberg model describing frustrated systems with wheel geometry. Phys. Rev. B 2019, 100, 054434. [Google Scholar] [CrossRef]
- Adelnia, F.; Chiesa, A.; Bordignon, S.; Carretta, S.; Ghirri, A.; Candini, A.; Cervetti, C.; Evangelisti, M.; Affronte, M.; Sheikin, I.; et al. Low temperature magnetic properties and spin dynamics in single crystals of Cr8Zn antiferromagnetic molecular rings. J. Chem. Phys. 2015, 143, 244321. [Google Scholar] [CrossRef]
- Ghirri, A.; Chiesa, A.; Carretta, S.; Troiani, F.; van Tol, J.; Hill, S.; Vitorica-Yrezabal, I.; Timco, G.A.; Winpenny, R.E.P.; Affronte, M. Coherent Spin Dynamics in Molecular Cr8Zn Wheels. J. Phys. Chem. Lett. 2015, 6, 5062–5066. [Google Scholar] [CrossRef]
- Baker, M.L.; Lancaster, T.; Chiesa, A.; Amoretti, G.; Baker, P.J.; Barker, C.; Blundell, S.J.; Carretta, S.; Collison, D.; Güdel, H.U.; et al. Studies of a Large Odd-Numbered Odd-Electron Metal Ring: Inelastic Neutron Scattering and Muon Spin Relaxation Spectroscopy of Cr8Mn. Chem. Eur. J. 2016, 22, 1779–1788. [Google Scholar] [CrossRef] [PubMed]
- Baker, M.L.; Timco, G.A.; Piligkos, S.; Mathieson, J.S.; Mutka, H.; Tuna, F.; Kozłowski, P.; Antkowiak, M.; Guidi, T.; Gupta, T.; et al. A classification of spin frustration in molecular magnets from a physical study of large odd-numbered-metal, odd electron rings. Proc. Natl. Acad. Sci. USA 2012, 109, 19113–19118. [Google Scholar] [CrossRef] [PubMed]
- Woolfson, R.J.; Timco, G.A.; Chiesa, A.; Vitorica-Yrezabal, I.J.; Tuna, F.; Guidi, T.; Pavarini, E.; Santini, P.; Carretta, S.; Winpenny, R.E.P. [CrF(O2CtBu)2]9: Synthesis and Characterization of a Regular Homometallic Ring with an Odd Number of Metal Centers and Electrons. Angew. Chem. Int. Ed. 2016, 55, 8856–8859. [Google Scholar] [CrossRef]
- Bruzewicz, C.D.; Chiaverini, J.; McConnell, R.; Sage, J.M. Trapped-ion quantum computing: Progress and challenges. Appl. Phys. Lett. 2019, 6, 021314. [Google Scholar] [CrossRef]
- Preskill, J. Quantum Computing in the NISQ era and beyond. Quantum 2018, 2, 79. [Google Scholar] [CrossRef]
- Arute, F.; Arya, K.; Babbush, R.; Bacon, D.; Bardin, J.C.; Barends, R.; Biswas, R.; Boixo, S.; Brandao, F.G.S.L.; Buell, D.A.; et al. Quantum supremacy using a programmable superconducting processor. Nature 2019, 574, 505. [Google Scholar] [CrossRef] [PubMed]
- Feynman, R.P. Simulating physics with computers. Int. J. Theor. Phys. 1982, 21, 467–488. [Google Scholar] [CrossRef]
- Georgescu, I.M.; Ashhab, S.; Nori, F. Quantum simulation. Rev. Mod. Phys. 2014, 86, 153–185. [Google Scholar] [CrossRef]
- Tacchino, F.; Chiesa, A.; Carretta, S.; Gerace, D. Quantum Computers as Universal Quantum Simulators: State-of-the-Art and Perspectives. Adv. Quantum Technol. 2020, 3, 1900052. [Google Scholar] [CrossRef]
- Krantz, P.; Kjaergaard, M.; Yan, F.; Orlando, T.P.; Gustavsson, S.; Oliver, W.D. A quantum engineer’s guide to superconducting qubits. Appl. Phys. Rev. 2019, 6, 021318. [Google Scholar] [CrossRef]
- Córcoles, A.D.; Kandala, A.; Javadi-Abhari, A.; McClure, D.T.; Cross, A.W.; Temme, K.; Nation, P.D.; Steffen, M.; Gambetta, J.M. Challenges and Opportunities of Near-Term Quantum Computing Systems. Proc. IEEE 2020, 108, 1338–1352. [Google Scholar] [CrossRef]
- Cross, A.W.; Bishop, L.S.; Sheldon, S.; Nation, P.D.; Gambetta, J.M. Validating quantum computers using randomized model circuits. Phys. Rev. A 2019, 100, 032328. [Google Scholar] [CrossRef]
- Jurcevic, P.; Javadi-Abhari, A.; Bishop, L.S.; Lauer, I.; Bogorin, D.F.; Brink, M.; Capelluto, L.; Günlük, O.; Itoko, T.; Kanazawa, N.; et al. Demonstration of quantum volume 64 on a superconducting quantum computing system. arXiv 2020, arXiv:2008.08571. [Google Scholar]
- Li, Y.; Benjamin, S.C. Efficient Variational Quantum Simulator Incorporating Active Error Minimization. Phys. Rev. X 2017, 7, 021050. [Google Scholar] [CrossRef]
- Bonet-Monroig, X.; Sagastizabal, R.; Singh, M.; O’Brien, T.E. Low-cost error mitigation by symmetry verification. Phys. Rev. A 2018, 98, 062339. [Google Scholar] [CrossRef]
- Kandala, A.; Temme, K.; Córcoles, A.D.; Mezzacapo, A.; Chow, J.M.; Gambetta, J.M. Error mitigation extends the computational reach of a noisy quantum processor. Nature 2019, 567, 491–495. [Google Scholar] [CrossRef]
- McArdle, S.; Yuan, X.; Benjamin, S. Error-Mitigated Digital Quantum Simulation. Phys. Rev. Lett. 2019, 122, 180501. [Google Scholar] [CrossRef] [PubMed]
- Bravyi, S.; Sheldon, S.; Kandala, A.; Mckay, D.C.; Gambetta, J.M. Mitigating measurement errors in multiqubit experiments. Phys. Rev. A 2021, 103, 042605. [Google Scholar] [CrossRef]
- Suchsland, P.; Tacchino, F.; Fischer, M.H.; Neupert, T.; Barkoutsos, P.K.; Tavernelli, I. Algorithmic Error Mitigation Scheme for Current Quantum Processors. Quantum 2021, 5, 492. [Google Scholar] [CrossRef]
- Huggins, W.J.; McArdle, S.; O’Brien, T.E.; Lee, J.; Rubin, N.C.; Boixo, S.; Whaley, K.B.; Babbush, R.; McClean, J.R. Virtual Distillation for Quantum Error Mitigation. arXiv 2020, arXiv:2011.07064. [Google Scholar]
- Koczor, B. Exponential Error Suppression for Near-Term Quantum Devices. arXiv 2020, arXiv:2011.05942. [Google Scholar]
- McClean, J.R.; Jiang, Z.; Rubin, N.C.; Babbush, R.; Neven, H. Decoding quantum errors with subspace expansions. Nat. Commun. 2020, 11, 636. [Google Scholar] [CrossRef]
- Günther, J.M.; Tacchino, F.; Wootton, J.R.; Tavernelli, I.; Barkoutsos, P.K. Improving readout in quantum simulations with repetition codes. arXiv 2021, arXiv:2105.13377. [Google Scholar]
- Childs, A.M.; Maslov, D.; Nam, Y.; Ross, N.J.; Su, Y. Toward the first quantum simulation with quantum speedup. Proc. Natl. Acad. Sci. USA 2018, 115, 9456–9461. [Google Scholar] [CrossRef]
- Peruzzo, A.; McClean, J.; Shadbolt, P.; Yung, M.H.; Zhou, X.Q.; Love, P.J.; Aspuru-Guzik, A.; O’Brien, J.L. A variational eigenvalue solver on a photonic quantum processor. Nat. Commun. 2014, 5, 4213. [Google Scholar] [CrossRef]
- McClean, J.R.; Romero, J.; Babbush, R.; Aspuru-Guzik, A. The theory of variational hybrid quantum-classical algorithms. New J. Phys. 2016, 18, 023023. [Google Scholar] [CrossRef]
- Kandala, A.; Mezzacapo, A.; Temme, K.; Takita, M.; Brink, M.; Chow, J.M.; Gambetta, J.M. Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets. Nature 2017, 549, 242–246. [Google Scholar] [CrossRef] [PubMed]
- Moll, N.; Barkoutsos, P.; Bishop, L.S.; Chow, J.M.; Cross, A.; Egger, D.J.; Filipp, S.; Fuhrer, A.; Gambetta, J.M.; Ganzhorn, M.; et al. Quantum optimization using variational algorithms on near-term quantum devices. Quantum Sci. Technol. 2018, 3, 030503. [Google Scholar] [CrossRef]
- Cerezo, M.; Arrasmith, A.; Babbush, R.; Benjamin, S.C.; Endo, S.; Fujii, K.; McClean, J.R.; Mitarai, K.; Yuan, X.; Cincio, L.; et al. Variational Quantum Algorithms. arXiv 2020, arXiv:2012.09265. [Google Scholar]
- Bharti, K.; Cervera-Lierta, A.; Kyaw, T.H.; Haug, T.; Alperin-Lea, S.; Anand, A.; Degroote, M.; Heimonen, H.; Kottmann, J.S.; Menke, T.; et al. Noisy intermediate-scale quantum (NISQ) algorithms. arXiv 2021, arXiv:2101.08448. [Google Scholar]
- Barkoutsos, P.K.; Nannicini, G.; Robert, A.; Tavernelli, I.; Woerner, S. Improving Variational Quantum Optimization using CVaR. Quantum 2020, 4, 256. [Google Scholar] [CrossRef]
- Havlíček, V.; Córcoles, A.D.; Temme, K.; Harrow, A.W.; Kandala, A.; Chow, J.M.; Gambetta, J.M. Supervised learning with quantum-enhanced feature spaces. Nature 2019, 567, 209–212. [Google Scholar] [CrossRef]
- Mangini, S.; Tacchino, F.; Gerace, D.; Bajoni, D.; Macchiavello, C. Quantum computing models for artificial neural networks. EPL (Europhys. Lett.) 2021, 134, 10002. [Google Scholar] [CrossRef]
- Barkoutsos, P.K.; Gonthier, J.F.; Sokolov, I.; Moll, N.; Salis, G.; Fuhrer, A.; Ganzhorn, M.; Egger, D.J.; Troyer, M.; Mezzacapo, A.; et al. Quantum algorithms for electronic structure calculations: Particle-hole Hamiltonian and optimized wave-function expansions. Phys. Rev. A 2018, 98, 022322. [Google Scholar] [CrossRef]
- Parrish, R.M.; Hohenstein, E.G.; McMahon, P.L.; Martínez, T.J. Quantum Computation of Electronic Transitions Using a Variational Quantum Eigensolver. Phys. Rev. Lett. 2019, 122, 230401. [Google Scholar] [CrossRef]
- Ollitrault, P.J.; Kandala, A.; Chen, C.F.; Barkoutsos, P.K.; Mezzacapo, A.; Pistoia, M.; Sheldon, S.; Woerner, S.; Gambetta, J.M.; Tavernelli, I. Quantum equation of motion for computing molecular excitation energies on a noisy quantum processor. Phys. Rev. Res. 2020, 2, 043140. [Google Scholar] [CrossRef]
- Mazzola, G.; Ollitrault, P.J.; Barkoutsos, P.K.; Tavernelli, I. Nonunitary Operations for Ground-State Calculations in Near-Term Quantum Computers. Phys. Rev. Lett. 2019, 123, 130501. [Google Scholar] [CrossRef]
- Gard, B.T.; Zhu, L.; Barron, G.S.; Mayhall, N.J.; Economou, S.E.; Barnes, E. Efficient symmetry-preserving state preparation circuits for the variational quantum eigensolver algorithm. NPJ Quantum Inf. 2020, 6, 10. [Google Scholar] [CrossRef]
- Seki, K.; Shirakawa, T.; Yunoki, S. Symmetry-adapted variational quantum eigensolver. Phys. Rev. A 2020, 101, 052340. [Google Scholar] [CrossRef]
- Garlatti, E.; Chiesa, A.; Guidi, T.; Amoretti, G.; Santini, P.; Carretta, S. Unravelling the Spin Dynamics of Molecular Nanomagnets with Four-Dimensional Inelastic Neutron Scattering. Eur. J. Inorg. Chem. 2019, 2019, 1106–1118. [Google Scholar] [CrossRef]
- Chiesa, A.; Tacchino, F.; Grossi, M.; Santini, P.; Tavernelli, I.; Gerace, D.; Carretta, S. Quantum hardware simulating four-dimensional inelastic neutron scattering. Nat. Phys. 2019, 15, 455–459. [Google Scholar] [CrossRef]
- Choquette, A.; Di Paolo, A.; Barkoutsos, P.K.; Sénéchal, D.; Tavernelli, I.; Blais, A. Quantum-optimal-control-inspired ansatz for variational quantum algorithms. Phys. Rev. Res. 2021, 3, 023092. [Google Scholar] [CrossRef]
- Wecker, D.; Hastings, M.B.; Troyer, M. Progress towards practical quantum variational algorithms. Phys. Rev. A 2015, 92, 042303. [Google Scholar] [CrossRef]
- Di Paolo, A.; Barkoutsos, P.K.; Tavernelli, I.; Blais, A. Variational quantum simulation of ultrastrong light-matter coupling. Phys. Rev. Res. 2020, 2, 033364. [Google Scholar] [CrossRef]
- Tacchino, F.; Chiesa, A.; Sessoli, R.; Tavernelli, I.; Carretta, S. Molecular spin qudits for quantum simulation of light-matter interactions. arXiv 2021, arXiv:2103.09706. [Google Scholar]
- McClean, J.R.; Boixo, S.; Smelyanskiy, V.N.; Babbush, R.; Neven, H. Barren plateaus in quantum neural network training landscapes. Nat. Commun. 2018, 9, 4812. [Google Scholar] [CrossRef] [PubMed]
- Cerezo, M.; Sone, A.; Volkoff, T.; Cincio, L.; Coles, P.J. Cost function dependent barren plateaus in shallow parametrized quantum circuits. Nat. Commun. 2021, 12, 1791. [Google Scholar] [CrossRef] [PubMed]
- Powell, M.J.D. A Direct Search Optimization Method That Models the Objective and Constraint Functions by Linear Interpolation. In Advances in Optimization and Numerical Analysis; Gomez, S., Hennart, J.P., Eds.; Springer: Dordrecht, The Netherlands, 1994; pp. 51–67. [Google Scholar]
- Sharma, K.; Khatri, S.; Cerezo, M.; Coles, P.J. Noise resilience of variational quantum compiling. New J. Phys. 2020, 22, 043006. [Google Scholar] [CrossRef]
- Wang, S.; Fontana, E.; Cerezo, M.; Sharma, K.; Sone, A.; Cincio, L.; Coles, P.J. Noise-Induced Barren Plateaus in Variational Quantum Algorithms. arXiv 2020, arXiv:2007.14384. [Google Scholar]
- Aleksandrowicz, G.; Alexander, T.; Barkoutsos, P.; Bello, L.; Ben-Haim, Y.; Bucher, D.; Cabrera-Hernández, F.J.; Carballo-Franquis, J.; Chen, A.; Chen, C.; et al. Qiskit: An Open-source Framework for Quantum Computing. Zenodo 2019. [Google Scholar] [CrossRef]
- Spall, J. An Overview of the Simultaneous Perturbation Method for Efficient Optimization. Johns Hopkins Apl Tech. Dig. 1998, 19, 482–492. [Google Scholar]
- Huggins, W.J.; McClean, J.R.; Rubin, N.C.; Jiang, Z.; Wiebe, N.; Whaley, K.B.; Babbush, R. Efficient and noise resilient measurements for quantum chemistry on near-term quantum computers. NPJ Quantum Inf. 2021, 7, 23. [Google Scholar] [CrossRef]
- Yuan, X.; Endo, S.; Zhao, Q.; Li, Y.; Benjamin, S.C. Theory of variational quantum simulation. Quantum 2019, 3, 191. [Google Scholar] [CrossRef]
- Barison, S.; Vicentini, F.; Carleo, G. An efficient quantum algorithm for the time evolution of parameterized circuits. arXiv 2021, arXiv:2101.04579. [Google Scholar]
- Chiesa, A.; Santini, P.; Gerace, D.; Raftery, J.; Houck, A.A.; Carretta, S. Digital quantum simulators in a scalable architecture of hybrid spin-photon qubits. Sci. Rep. 2015, 5, 16036. [Google Scholar] [CrossRef]
- Tacchino, F.; Chiesa, A.; LaHaye, M.D.; Carretta, S.; Gerace, D. Electromechanical quantum simulators. Phys. Rev. B 2018, 97, 214302. [Google Scholar] [CrossRef]
- Cao, Y.; Romero, J.; Olson, J.P.; Degroote, M.; Johnson, P.D.; Kieferová, M.; Kivlichan, I.D.; Menke, T.; Peropadre, B.; Sim, S.; et al. Quantum Chemistry in the Age of Quantum Computing. Chem. Rev. 2019, 119, 10856–10915. [Google Scholar] [CrossRef] [PubMed]
- Gambetta, J.M.; Chow, J.M.; Steffen, M. Building logical qubits in a superconducting quantum computing system. NPJ Quantum Inf. 2017, 3, 2. [Google Scholar] [CrossRef]
- Chow, J.M.; Córcoles, A.D.; Gambetta, J.M.; Rigetti, C.; Johnson, B.R.; Smolin, J.A.; Rozen, J.R.; Keefe, G.A.; Rothwell, M.B.; Ketchen, M.B.; et al. Simple All-Microwave Entangling Gate for Fixed-Frequency Superconducting Qubits. Phys. Rev. Lett. 2011, 107, 080502. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Crippa, L.; Tacchino, F.; Chizzini, M.; Aita, A.; Grossi, M.; Chiesa, A.; Santini, P.; Tavernelli, I.; Carretta, S. Simulating Static and Dynamic Properties of Magnetic Molecules with Prototype Quantum Computers. Magnetochemistry 2021, 7, 117. https://doi.org/10.3390/magnetochemistry7080117
Crippa L, Tacchino F, Chizzini M, Aita A, Grossi M, Chiesa A, Santini P, Tavernelli I, Carretta S. Simulating Static and Dynamic Properties of Magnetic Molecules with Prototype Quantum Computers. Magnetochemistry. 2021; 7(8):117. https://doi.org/10.3390/magnetochemistry7080117
Chicago/Turabian StyleCrippa, Luca, Francesco Tacchino, Mario Chizzini, Antonello Aita, Michele Grossi, Alessandro Chiesa, Paolo Santini, Ivano Tavernelli, and Stefano Carretta. 2021. "Simulating Static and Dynamic Properties of Magnetic Molecules with Prototype Quantum Computers" Magnetochemistry 7, no. 8: 117. https://doi.org/10.3390/magnetochemistry7080117
APA StyleCrippa, L., Tacchino, F., Chizzini, M., Aita, A., Grossi, M., Chiesa, A., Santini, P., Tavernelli, I., & Carretta, S. (2021). Simulating Static and Dynamic Properties of Magnetic Molecules with Prototype Quantum Computers. Magnetochemistry, 7(8), 117. https://doi.org/10.3390/magnetochemistry7080117






