Abstract
There is significant interest worldwide to identify new antiferromagnetic materials suitable for device applications. Key requirements for such materials are: relatively high magnetocrystalline anisotropy constant, low cost, high corrosion resistance and the ability to induce a large exchange bias, i.e., loop shift, when grown adjacent to a ferromagnetic layer. In this article, a review of recent developments on the novel antiferromagnetic material MnN is presented. This material shows potential as a replacement for the commonly used antiferromagnet of choice, i.e., IrMn. Although the results so far look promising, further work is required for the optimization of this material.
1. Introduction
In 2014, Zhang et al. [1] showed that nontrivial spin Hall effects occur in metallic antiferromagnets such as FeMn, PtMn and IrMn. These results provided evidence that significant spintronic phenomena occur in antiferromagnetic (AF) materials. More recently, Wadley et al. [2] showed that spin–orbit torque could be used to switch CuMnAs electrically. Similarly, Bodnar et al. [3] and Meinert et al. [4] used relativistic Néel spin–orbit torques to switch the Néel vector in Mn2Au. Spin–orbit torques in AF materials have also been used to switch the magnetization of an adjacent F layer, e.g., [5]. The ability to manipulate the orientation of the AF axes using a spin-polarized current is of huge importance, as AF materials have a relaxation time of ~10−12 s compared to 10−9 s for ferromagnetic (F) materials [6]. Hence, in principle, a switching device based on an AF material would be capable of being many times faster than a conventional Magnetic Random Access Memory (MRAM) device. Such devices would also offer the advantage of not being subject to the demagnetizing field effect present in conventional F devices. AF-based spintronic devices can also be deployed in unconventional computing architectures such as neuromorphic computing, where artificial synapses can be used to execute complex cognitive tasks, e.g., [7]. For these reasons, there has been a significant increase in the level of worldwide activity in the field of AF materials. For a recent review on the topic of AF spintronics, see Reference [8].
The most successful spintronic devices to date are those based on the Giant Magnetoresistance (GMR) effect, i.e., spin-valve, and Tunneling Magnetoresistance (TMR) effect, i.e., tunnel junction, which have formed the basis of the read-head sensor of a Hard Disk Drive (HDD) for decades. AF materials are used in these devices to pin the magnetization of an F (reference) layer via the exchange-bias effect. This effect manifests itself as a shift in the hysteresis loop of the pinned F layer along the field axis. That F layer serves as a magnetic reference in the stack, which is necessary for sensing and MRAM applications. In addition, an enhancement in the coercivity of the material is typically observed. The exchange bias originates from the interplay of interactions across the F/AF interface and the bulk magnetocrystalline anisotropy of the AF. For a review on the topic of exchange bias, see Reference [9]. The first AF material to be used in a GMR commercial device was NiO, which was soon replaced by the metallic alloy FeMn. Although the thermal stability of the devices was significantly improved by doing so, corrosion resistance issues led to the replacement of FeMn by IrMn in the mid-1990s. To this date, IrMn is the material of choice for most industrial applications. PtMn, a simple L10 alloy, has been used in a thermal MRAM device but not in read heads due to the need for it to be annealed into the L10 structure [10]. However, Ir is one of the scarcest materials on Earth, making it very expensive. Hence, there is great interest worldwide in the identification of new, usable AF materials that could replace IrMn. The main requirements for such a material are: relatively high anisotropy energy density, which controls its thermal stability; low cost; high corrosion resistance and the ability to induce a significant exchange bias, i.e., loop shift, when grown adjacent to an F layer.
Over the last several years, there have been a number of publications exploring the properties of the equiatomic AF alloy MnN. For instance, broadband ferromagnetic resonance and in-plane angle-dependent measurements have been used to determine the in-plane anisotropies and relaxation of MnN/CoFeB bilayers [11]. One of the attractive properties of this material is that scarcity is not an issue. While there are only ~10−5 atoms of Ir/million atoms of silicon, Mn is much more abundant (~103 atoms Mn/million atoms of silicon). Given that almost 80% of the air we breathe is nitrogen, low cost is a given for this compound. In this article, a review of the recent advances in the study of this material will be presented.
2. Manganese Nitride: The Material
Manganese nitride is a complex material that exists in a number of phases, as shown in Figure 1. Depending on the stoichiometry and growth temperature, this compound can exist in a paramagnetic, ferrimagnetic or antiferromagnetic state [12]. Of particular interest to this review article is the tetragonal slightly distorted rocksalt θ phase, θ-MnN, which is AF. From now on, this phase will be referred to simply as MnN. Polycrystalline MnN thin films can be grown by reactive sputtering in a mixed Ar and N2 atmosphere at temperatures below 673 K and a nitrogen concentration >40% [13]. A 50:50 mixture at a deposition pressure of 2.3 × 10−3 mbar has been proposed as the optimum deposition conditions, although the exact parameters are likely to depend on the deposition system and the details of the sputtering geometry [14].
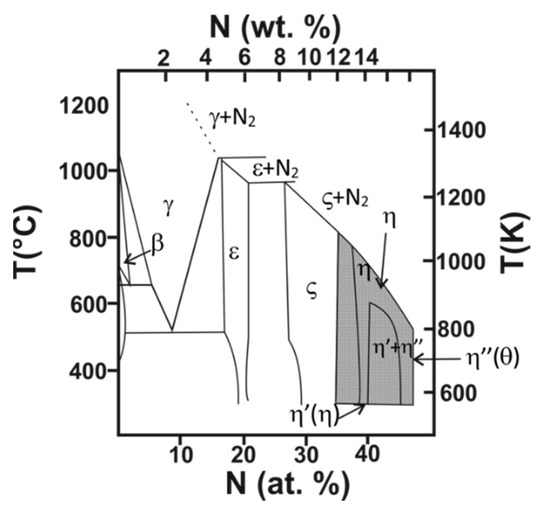
Figure 1.
Binary phase diagram of Mn-N. (Redrawn with permission from Journal of Materials Chemistry; published by the Royal Society of Chemistry, 2000) [13].
Neutron powder diffraction experiments have shown that the magnetic order of bulk MnN is collinear AF-I type, i.e., sheet structure with the Mn spins aligned parallel within the c planes [13]. In the same study, the spin orientation was observed to vary as a function of temperature. While at temperatures close to the Néel temperature (~650 K), the moments aligned along the c-axis, at room temperature, the spins were found to be tilted at 23° to the c-axis. These samples were nitrogen deficient. Similar studies on samples where the MnN was saturated suggested that the spin direction was along the c-axis [15]. In both cases, the Mn atoms had a magnetic moment of 3.3 μB at room temperature. More recently, a theoretical study has suggested that the spin alignment is along the c-axis [16]. The authors found that the first nearest-neighbor isotropic exchange interactions are AF, while the second nearest-neighbor interactions are strongly ferromagnetic. It was concluded that the interplay between these interactions leads to the AF-I-type ground state. The crystal structure for the θ-MnN phase is shown schematically in Figure 2. It has a tetragonal structure with a lattice constant of a = 4.256 Å and c = 4.189 Å at room temperature resulting in a c/a ratio of 0.984. Interestingly, the easy anisotropy axis lies perpendicular to the long axis of the crystal, as shown in Figure 2. Hence, it might be possible that slight variations in composition might result in modifications to the lattice constant (e.g., increasing the nitrogen content increases the lattice constant) and, potentially, the anisotropy constant of this material. The Néel temperature of this material is slightly higher than 650 K [13], so very similar to that of IrMn, which is ideal for device applications.
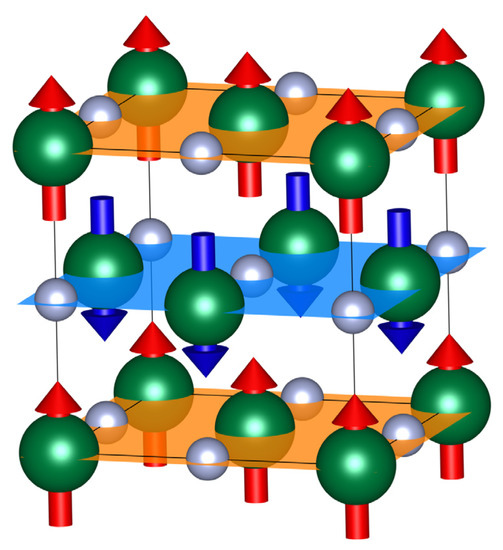
Figure 2.
Schematic crystal structure of MnN: green (bigger) spheres correspond to manganese atoms, while smaller, lighter spheres represent nitrogen atoms. The AF-I antiferromagnetic ground state with spin alignment along the c-axis is represented by the arrows (planes) of red and blue (orange and light blue) color.
3. Exchange Bias: In-Plane Studies
In an initial study, Meinert et al. [14] studied the dependence of the exchange bias in MnN/CoFe bilayers at room temperature as a function of the thickness and crystallinity of the AF layer. A typical hysteresis loop from this study is shown in Figure 3 [14].
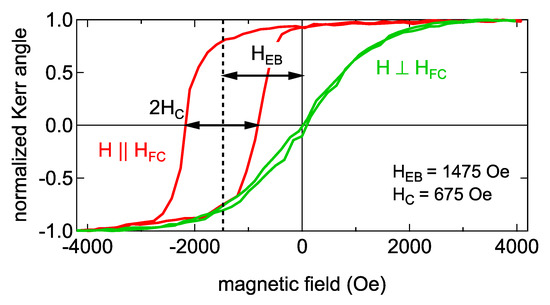
Figure 3.
Typical hysteresis loop for a MnN/CoFe exchange bias system. (Reproduced with permission from M. Meinert, Physical Review B; published by the American Physical Society, 2015) [14].
The crystallinity of the bilayers was controlled both during and after deposition. Samples with composition Ta(10 nm)/MnN(tAF)/Co70Fe30(tF)/Ta2O5(2 nm) were deposited on thermally oxidized Si wafers. The thickness of the AF layer, tAF, was varied in the range of 6 to 48 nm, while the CoFe thickness, tF, was varied in the range of 1 to 2.2 nm. After deposition, the samples were annealed at temperatures up to ~600 K in a 6.5 kOe magnetic field. The Ta seed layer grew with (011) orientation and very small grains (~1 nm). Before annealing, the lattice constant of MnN was larger than 4.256 Å, the bulk value reported in the literature. The lattice constant in the film plane was measured as a = 4.10 Å, resulting in a c/a ratio of 1.04. The variation of the loop shift as a function of tAF is shown in Figure 4 (solid red circles). The behavior is identical in shape to that observed for IrMn, whereby no loop shift is observed up to a given value of tAF. This is probably due to a combination of factors. As the thermal stability of the AF grains is increased via the increase in tAF, a sharp onset in the exchange bias is expected. The exchange bias then peaks around a value of tAF of 30 nm, decreasing following a ~1/tAF behavior for thicker films. Following the York model of exchange bias for polycrystalline films, this is a consequence of the shape of the energy barrier to reversal in the AF layer, which is controlled by the distribution of grain volumes, which is lognormal [9]. This is shown schematically in Figure 5. Below a critical volume, Vc, the grains are thermally unstable at the temperature of measurement and do not contribute towards the loop shift. At the higher end of the distribution, there is a second critical volume, Vset, above which the grains cannot be set and remain unaligned with the F layer upon annealing. Hence, it is only the grains with volumes between Vc and Vset that contribute to the loop shift. Ideally, both critical volumes will be outside the distribution so that the entire AF contributes towards the loop shift. In many cases, as the thickness of the AF layer is increased, a larger fraction of the AF grains cannot be set. Due to the shape of the tail in the lognormal distribution, the exchange bias decreases, mimicking a 1/tAF dependence as mentioned earlier.
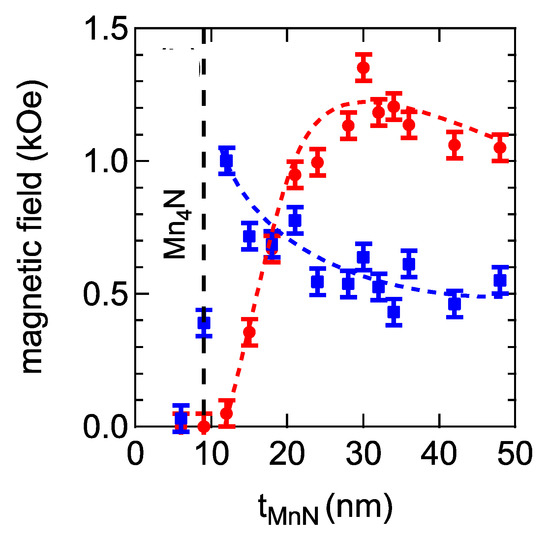
Figure 4.
Variation of the exchange bias (solid red circles) and coercive field (blue squares) as a function of MnN thickness. (Reproduced with permission from M. Meinert, Physical Review B; published by the American Physical Society, 2015) [14].
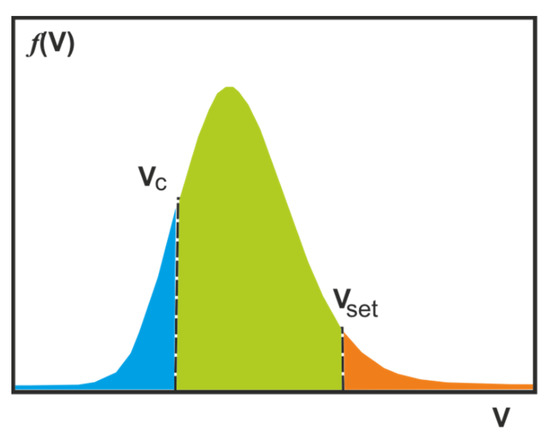
Figure 5.
Schematic diagram of the energy barrier to reversal in the AF layer.
A critical difference between the behavior of MnN and IrMn is that the peak in the loop shift as a function of tAF occurs at much lower thicknesses (~8 nm) for the latter. This is probably due to the lower magnetocrystalline anisotropy of MnN (~6 × 106 erg/cm3) compared to that of IrMn (up to ~3 × 107 erg/cm3). A second factor that controls the dependence of the loop shift on tAF is nitrogen desorption upon thermal annealing. In thinner films, nitrogen desorption can lead to a change in the MnN phase to Mn4N, which is not antiferromagnetic, as shown in Figure 4. Thicker films have sufficient nitrogen to withstand desorption effects to higher temperatures. This conclusion was supported by the annealing data, whereby samples with thicker AF layers could withstand higher annealing temperatures before the magnitude of the loop shift was observed to decrease. The dependence of the exchange bias on tF follows the expected ~1/tF behavior typical of exchange-bias systems.
The influence of the deposition pressure, annealing temperature and nitrogen content was also investigated [14]. The behavior was quite complex. For instance, while the coercivity was not found to depend greatly on the deposition pressure, the exchange bias was found to decrease almost linearly as the deposition pressure was increased. The annealing temperature dependence was even more complicated. A double ‘peak’ was observed in the magnitude of the loop shift as a function of the heating temperature. This trend was attributed to an irreversible structural or magnetic transition at the MnN/CoFe interface. In some cases, the annealing temperature was higher than the Néel temperature of the alloy at which point MnN undergoes a recrystallization process which might affect the coupling at the F/AF interface. Again, it is likely that these properties will be (deposition) system dependent.
The thermal stability of the bilayers was assessed via measurement of their median and maximum blocking temperature [14]. Although the thermal stability was lower than that of IrMn-based systems, especially when the thicknesses of the AF layers used in this study are taken into account, a median blocking temperature greater than 373 K was measured for tAF > 15 nm. Importantly, it was found that MnN is rather robust against oxidation, which is critical for device applications. This, coupled with the fact that large exchange-bias values of 1.8 kOe were measured, highlights the potential of MnN for spintronic applications. However, further work is required for the optimization of the growth conditions of this alloy. For instance, controlling the N/Ar mixture during deposition can result in loop shifts in excess of 2.7 kOe at room temperature and an enhanced thermal stability and median blocking temperature > 450 K for compositionally identical structures [17].
The effects of field annealing were further investigated as a function of the thickness of the MnN layer and the field annealing temperature in Ta/MnN/CoFeB exchange-bias systems in a more recent paper [18]. It was found that for thick (48 nm) MnN films, the exchange bias increased due to an improvement in the crystallinity of the films. However, for thinner films (30 nm), the exchange bias was found to decrease and even disappear due to nitrogen migration into the Ta buffer layer, which modified the antiferromagnetic state. Intermixing at the MnN/CoFeB interface was also observed, which was also attributed to the nitrogen deficiency in the MnN layer after annealing in a field. When not enough nitrogen was present, Co and Fe diffused into the MnN, resulting in the reduction of the measured exchange bias. It was suggested that the inclusion of a diffusion barrier layer between the Ta seed layer and the MnN layer might allow for higher annealing temperature to be used without degrading the properties of the films. This is critical if thinner layers were to be used.
Doping has been shown to enhance the thermal stability of MnN/CoFe exchange-bias systems [19]. Undoped samples with structure Ta(10 nm)/MnN(30 nm)/Co70Fe30/(1.6 nm)/Ta(0.5 nm)/Ta2 O5(5 nm) were deposited on thermally oxidized Si wafers. The samples were annealed at ~600 K in a 6.5 kOe for 15 min. Density Functional Theory (DFT) was used to calculate the defect energies for substitution of one Mn atom in the MnN lattice by a different element. Elements calculated to have both negative and positive defect energies were chosen for this experiment. In particular, Ti, Y, Si, Cr and Fe were selected. Doping elements were added by cosputtering from an RF source. A low power was used to ensure modest doping concentrations. After annealing the crystal structure of the samples was investigated by X-Ray diffraction. The position of the (002) MnN peak was found to shift towards lower angles, indicating a larger lattice constant when elements with a negative defect energy, i.e., Ti, Y, Si and Cr, were used, suggesting that low levels of nitrogen diffusion occurred. On the other hand, when elements with a positive defect energy, i.e., Fe, were used, the (002) peak was shifted towards higher angles when compared to the undoped samples. It was suggested that in this case, significant diffusion occurred because of the weaker binding of nitrogen.
The exchange bias and thermal stability of the doped/undoped samples were investigated as a function of the annealing temperature (273–825 K). The thermal stability of the samples doped with negative defect energies was increased. However, this enhancement was accompanied by a reduction in the magnitude of the loop shift. A similar trend has been observed in IrMn-based exchange-biased systems, whereby the choice of seed layer material has been shown to increase/decrease the anisotropy/loop shift [20]. Modest doping with Ti (3%) or Y (2%) resulted in a loop shift > 1 kOe for annealing temperatures up to ~750 K, as shown in Figure 6, and an enhancement in the thermal stability of 100 K when compared to the undoped sample. Doping with Fe, which has a positive defect energy, showed a negative effect on the thermal stability of MnN/CoFe in agreement with DFT calculations.
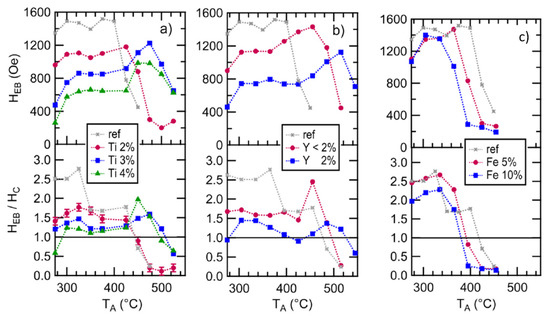
Figure 6.
Exchange bias as a function of annealing temperature for different dopant elements: (a) Ti, (b) Y, (c) Fe. The reference measurement (ref) refers to an undoped sample. (Adapted from M. Dunz, Büker and M. Meinert, Journal of Applied Physics 124, 203, 902 (2018); doi:10.1063/1.5051584) [19].
Over the last few years, it has become apparent that the Ta buffer layer is key to the performance of MnN-based exchange-bias systems, as it acts as a crystallographic seed layer for the MnN to grow on and a nitrogen sink during the annealing process. The effect of nitrogen diffusion in Ta/MnN/CoFeB stacks has been investigated as a function of the Ta layer thickness [21]. Samples with composition Ta(tTa)/MnN(30 nm)/Co40Fe40B20(1.6 nm)/Ta(0.5 nm)/Ta2O5(2 nm) were prepared on thermally oxidized Si wafers. The thickness of the Ta layer, tTa, was varied in the range of 1 to 15 nm. The samples were annealed at temperatures between 373 and 823 K. While increasing the thickness of the Ta layer improves the crystallinity of the MnN layer, thinner Ta layers provide a smaller nitrogen sink. This leads to a trade-off between thermal stability and large exchange bias. The effect of introducing a TaNx layer between the Ta seed and the MnN layers was also investigated in the same article [21]. Although the introduction of this extra layer can enhance the thermal stability of the bilayers, it has a negative effect on the magnitude of the loop shift. The data obtained highlighted the complicated nature of MnN, as many interconnected factors can result in structural/magnetic phase transitions. Hence, further work is required in this area to optimize the thermal stability and exchange bias properties of MnN-based exchange bias systems.
4. Exchange Bias: Out-of-Plane Studies
Magnetic multilayers with perpendicular magnetic anisotropy are also of great interest for spintronic applications given the lower critical current density needed for spin-transfer torque switching when compared to in-plane anisotropy systems, e.g., [22]. Hence, the possibility of achieving a large out-of-plane loop shift using MnN is of great interest. Zilske et al. [23] reported a giant perpendicular exchange bias of 3.6 kOe at room temperature in MnN/CoFeB bilayers. The samples had a similar composition and identical deposition conditions to some of the in-plane samples described earlier. The main difference was in the direction of the applied field used during the annealing process. In this case, the samples were annealed at temperatures in the range of ~400–700 K in a vacuum furnace in the presence of a 6.5 kOe out-of-plane field. This highlights the potential of MnN for integration into perpendicular magnetic tunnel junction/spin valves.
5. Anisotropy Constant
Another key requirement for a given AF material to be considered as a candidate for device applications is that it must have a relatively high magnetocrystalline anisotropy. Sinclair et al. [24] reported the first experimental measurement of the anisotropy constant of MnN in thin-film form from the measurement of the distribution of blocking temperatures in a MnN(tAF)/CoFe(2 nm) exchange-bias systems. A detailed description of the technique used can be found in Reference [25]. Briefly, in order to determine K, the samples are initially set at a temperature Tset in a positive saturating field for a period of time Tset. The samples are then cooled to a temperature, TNA, where the AF layer is free of thermal activation. The field is then reversed so that the F layer is now saturated in the opposite direction. By increasing the temperature of the sample to a temperature Tact for a period of time Tact, the AF grains are progressively reversed. The samples are then cooled to TNA, and the hysteresis loop is measured. By increasing the value of Tact, the energy barrier distribution within the AF is mapped. As a result, the hysteresis loop shifts from negative to positive field values. The critical point for the measurement of K is the value of Tact at which the exchange bias goes to 0. This is commonly known as the median blocking temperature as, at the point, half of the AF grains are oriented in the original setting direction and half of the grains in the opposite direction. Assuming the grain volume distribution within the sample is known, the value of K can be calculated using the median grain volume following that antiferromagnets are subject to thermal activation following a Néel–Arrhenius law. Figure 7 shows the blocking temperature distribution for samples of varying MnN thicknesses. From these data, it was concluded that MnN has an anisotropy energy density of 6.3 × 106 erg/cc as compared to a maximum anisotropy constant of 3.2 × 107 erg/cc for IrMn [20]. However, thicknesses > 20 nm appear to be necessary to achieve thermal stability above room temperature due to the small grain sizes (~5 nm). If the lateral grain size of the films could be increased by tuning the deposition conditions, it seems reasonable to suggest that the thickness of the MnN could be reduced, making it a very suitable candidate for device applications.
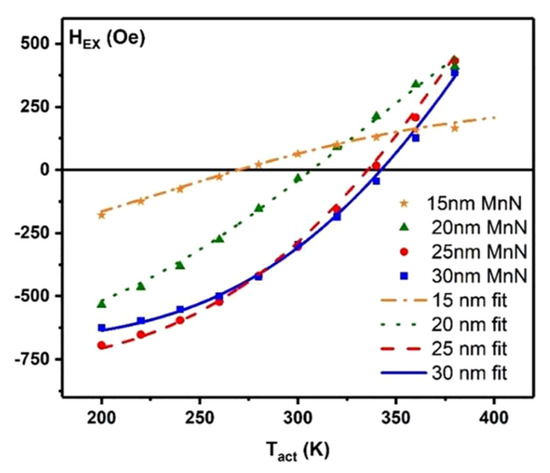
Figure 7.
Reverse field cooling experiment as a function of the MnN thickness. (Reproduced with permission from G. Vallejo-Fernandez, Journal of Magnetism and Magnetic Materials; published by Elsevier, 2019) [24].
6. Electrical Switching
The low anisotropy energy of MnN grains, especially at low thicknesses, can in some cases be seen as an advantage. The spin–orbit torque-induced electrical switching of polycrystalline MnN layers with the spin Hall effect of Pt has recently been studied [26]. The electrical manipulation of the magnetic order with current pulses was observed over a broad temperature range between 160 K and 260 K. With increasing temperature, a more efficient switching of the magnetic order was observed, with a simultaneous reduction in the relaxation time for randomization of the magnetic order. The analysis of the magnetocrystalline anisotropy in Reference [24] and the quantitative analysis of the temperature-dependent relaxation dynamics both consistently point to an energy barrier of 0.5 eV to 0.7 eV for the grains that participate in the observed switching. This renders the magnetic order of MnN easily switchable with the spin Hall effect but at the expense of a rapid thermal relaxation back to a disordered equilibrium. The same grains that are only weakly blocked or unblocked in the switching experiment do not contribute to exchange bias because of their relaxation dynamics.
7. Conclusions
Over the last few years, MnN has been demonstrated to show potential as a new AF material for spintronic applications. A summary of the properties of this compound compared to other Mn-based AFs is given in Table 1. This material can exist in a tetragonal structure, which by its very nature creates an anisotropy. One of the main advantages of this alloy compared to conventionally used AF materials is its low cost. Significant loop shifts, similar to values obtained for IrMn-based systems, have been achieved both for in-plane and out-of-plane MnN-based exchange-bias systems. However, the growth conditions and postdeposition treatment(s) for this compound are yet to be optimized. Large AF thicknesses are still required to observe the desired magnetic properties. It has also become apparent that the Ta buffer layer commonly used is critical to control the crystallinity of the MnN layer and the level of nitrogen diffusion observed upon thermal annealing. It might be possible that other materials offer better performance than Ta, and/or high-temperature deposition of the buffer layer might result in an increase in the crystallinity of the adjacent MnN layer. Tuning the deposition conditions of the MnN layer might result in an increase in the lateral grain size of the films, which would allow for a reduction in the thickness of the MnN layer. Furthermore, it is feasible that slight variations in composition might result in modifications to the lattice constant of the MnN films and, potentially, the anisotropy constant of the material. The mutually consistent results from the exchange bias and electrical switching studies corroborate our understanding of the importance of thermal activation in both phenomena in granular antiferromagnetic systems. While MnN is a novel but already well-studied antiferromagnet, open questions remain. How does the exchange bias behave in highly crystalline, epitaxial MnN thin films? What is the easy axis or easy plane of the polycrystalline MnN films, and how does it influence the observed exchange bias in detail? Thus, it seems like there is much more work to be done on MnN before our understanding of this intriguingly complex material is complete.

Table 1.
Summary of the main properties of Mn-based AF materials.
Author Contributions
Both authors have contributed to the preparation of this manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partly funded by the Royal Society No. INF\R1\180070.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data can be made available upon request.
Acknowledgments
G.V.F. would like to thank K. O’Grady for careful reading of the manuscript and insightful comments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhang, W.; Jungfleisch, M.B.; Jiang, W.; Pearson, J.E.; Hoffmann, A.; Freimuth, F.; Mokrousov, Y. Spin Hall effects in metallic antiferromagnets. Phys. Rev. Lett. 2014, 113, 196602. [Google Scholar] [CrossRef] [Green Version]
- Wadley, P.; Howells, B.; Elezny, J.; Andrews, C.; Hills, V.; Campion, R.P.; Novak, V.; Olejnik, K.; Maccherozzi, F.; Dhesi, S.S.; et al. Electrical switching of an antiferromagnet. Science 2016, 351, 587–590. [Google Scholar] [CrossRef] [Green Version]
- Bodnar, S.Y.; Mejkal, L.; Turek, I.; Gomonay, O.; Sinova, J.; Sapozhnik, A.A.; Elmers, H.-J.; Klaui, M.; Jourdan, M. Writing and reading antiferromagnetic Mn 2 Au by Néel spin-orbit torques and large anisotropic magnetoresistance. Nat. Commun. 2018, 9, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Meinert, M.; Graulich, D.; Matalla-Wagner, T. Electrical switching of antiferromagnetic Mn2Au and the role of thermal activation. Phys. Rev. Appl. 2018, 9, 064040. [Google Scholar] [CrossRef] [Green Version]
- Borders, W.A.; Akima, H.; Fukami, S.; Moriya, S.; Kurihara, S.; Horio, Y.; Sato, S.; Ohno, H. Analogue spin–orbit torque device for artificial-neural-network-based associative memory operation. Appl. Phys. Express 2017, 10, 013007. [Google Scholar] [CrossRef]
- Vallejo-Fernandez, G.; Aley, N.P.; Chapman, J.N.; O’Grady, K. Measurement of the attempt frequency in antiferromagnets. Appl. Phys. Lett. 2010, 97, 22505. [Google Scholar] [CrossRef]
- Fukami, S.; Ohno, H. Perspective: Spintronic synapse for artificial neural network. J. Appl. Phys. 2018, 124, 151904. [Google Scholar] [CrossRef] [Green Version]
- Baltz, V.; Manchon, A.; Tsoi, M.; Moriyama, T.; Ono, T.; Tserkovnyak, Y. Antiferromagnetic spintronics. Rev. Mod. Phys. 2018, 90, 015005. [Google Scholar] [CrossRef] [Green Version]
- O’Grady, K.; Fernandez-Outon, L.E.; Vallejo-Fernandez, G. A new paradigm for exchange bias in polycrystalline thin films. J. Magn. Magn. Mater. 2010, 322, 883–899. [Google Scholar] [CrossRef]
- Farrow, R.F.C.; Marks, R.F.; Gider, S.; Marley, A.C.; Parkin, S.S.P.; Mauri, D. MnxPt1−x: A new exchange bias material for Permalloy. J. Appl. Phys. 1997, 81, 4986–4988. [Google Scholar] [CrossRef]
- Rai, A.; Dunz, M.; Sapkota, A.; Zilske, P.; Mohammadi, J.B.; Meinert, M.; Mewes, C.; Mewes, T. Unidirectional and uniaxial anisotropies in the MnN/CoFeB exchange bias system. J. Magn. Magn. Mater. 2019, 485, 374–380. [Google Scholar] [CrossRef]
- Gokcen, N.A. The Mn-N (Manganese-Nitrogen) system. Bull. Alloy. Phase Diagr. 1990, 11, 33. [Google Scholar] [CrossRef]
- Leineweber, A.; Niewa, R.; Jacobs, H.; Kochelmann, W. The manganese nitrides η-Mn3N2 and θ-Mn6N5+ x: Nuclear and magnetic structures. J. Mater. Chem. 2000, 10, 2827–2834. [Google Scholar] [CrossRef]
- Meinert, M.; Büker, B.; Graulich, D.; Dunz, M. Large exchange bias in polycrystalline MnN/CoFe bilayers at room temperature. Phys. Rev. B 2015, 92, 144408. [Google Scholar] [CrossRef] [Green Version]
- Suzuki, K.; Yamaguchi, Y.; Kaneko, T.; Yoshida, H.; Obi, Y.; Fujimori, H.; Morita, H.J. Neutron diffraction studies of the compounds MnN and FeN. Phys. Soc. Jpn. 2001, 70, 1084–1089. [Google Scholar] [CrossRef]
- Simon, E.; Yanes, R.; Khmelevskyi, S.; Palotás, K.; Szunyogh, L.; Nowak, U. Magnetism and exchange-bias effect at the MnN/Fe interface. Phys. Rev. B 2018, 98, 094415. [Google Scholar] [CrossRef] [Green Version]
- Dunz, M.; Schmalhorst, J.; Meinert, M. Enhanced exchange bias in MnN/CoFe bilayers after high-temperature annealing. AIP Adv. 2018, 8, 056304. [Google Scholar] [CrossRef]
- Quaterman, P.; Hallsteinsen, J.; Dunz, M.; Meinert, M.; Arenholz, A.; Borchers, J.A.; Grutter, J. Effects of field annealing on MnN/CoFeB exchange bias systems. Phys. Rev. Mater. 2019, 3, 064413. [Google Scholar] [CrossRef]
- Dunz, M.; Büker, B.; Meinert, M. Improved thermal stability in doped MnN/CoFe exchange bias systems. J. Appl. Phys. 2018, 124, 203902. [Google Scholar] [CrossRef] [Green Version]
- Aley, N.P.; Vallejo-Fernandez, G.; Kroeger, R.; Lafferty, B.; Agnew, J.; Lu, Y.; O’Grady, K. Texture effects in IrMn/CoFe exchange bias systems. IEEE Trans. Magn. 2008, 44, 2820–2823. [Google Scholar] [CrossRef]
- Dunz, M.; Meinert, M. Role of the Ta buffer layer in Ta/MnN/CoFeB stacks for maximizing exchange bias. J. Appl. Phys. 2020, 128, 153902. [Google Scholar] [CrossRef]
- Nishimura, N.; Hirai, T.; Koganei, A.; Ikeda, T.; Okano, K.; Sekiguchi, Y.; Osada, Y. Magnetic tunnel junction device with perpendicular magnetization films for high-density magnetic random access memory. J. Appl. Phys. 2002, 91, 5246–5249. [Google Scholar] [CrossRef]
- Zilske, P.; Garulich, D.; Munz, D.; Meinert, M. Giant perpendicular exchange bias with antiferromagnetic MnN. Appl. Phys. Lett. 2017, 110, 192402. [Google Scholar] [CrossRef] [Green Version]
- Sinclair, J.; Hirohata, A.; Vallejo-Fernandez, G.; Meinert, M.; O’Grady, K. Thermal stability of exchange bias systems based on MnN. J. Magn. Magn. Mater. 2019, 476, 278–283. [Google Scholar] [CrossRef] [Green Version]
- Vallejo-Fernandez, G.; Fernandez-Outon, L.E.; O’Grady, K. Measurement of the anisotropy constant of antiferromagnets in metallic polycrystalline exchange biased systems. Appl. Phys. Lett. 2007, 91, 212503. [Google Scholar] [CrossRef]
- Dunz, M.; Matalla-Wagner, T.; Meinert, M. Spin-orbit torque induced electrical switching of antiferromagnetic MnN. Phys. Rev. Res. 2020, 2, 013347. [Google Scholar] [CrossRef] [Green Version]
- Fernandez-Outon, L.E.; Vallejo-Fernandez, G.; Manzoor, S.; Hillebrands, B.; O’Grady, K. Interfacial spin order in exchange biased systems. J. Appl. Phys. 2008, 104, 093907. [Google Scholar] [CrossRef]
- Kato, T.; Ito, H.; Sugihara, K.; Tsunashima, S.; Iwata, S. Magnetic anisotropy of MBE grown MnPt3 and CrPt3 ordered alloy films. J. Magn. Magn. Mater. 2004, 272, 778–779. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).