The Effect of pH and Viscosity on Magnetophoretic Separation of Iron Oxide Nanoparticles
Abstract
1. Introduction
- The aggregation behavior of BIONs in the gravity field is dependent on pH and viscosity, respectively. Therefore, the colloidal stability can be selectively controlled.
- During magnetophoresis, these effects directly influence the separation process. The aggregate size, as well as viscosity, result in different magnetophoretic velocities.
2. Results and Discussion
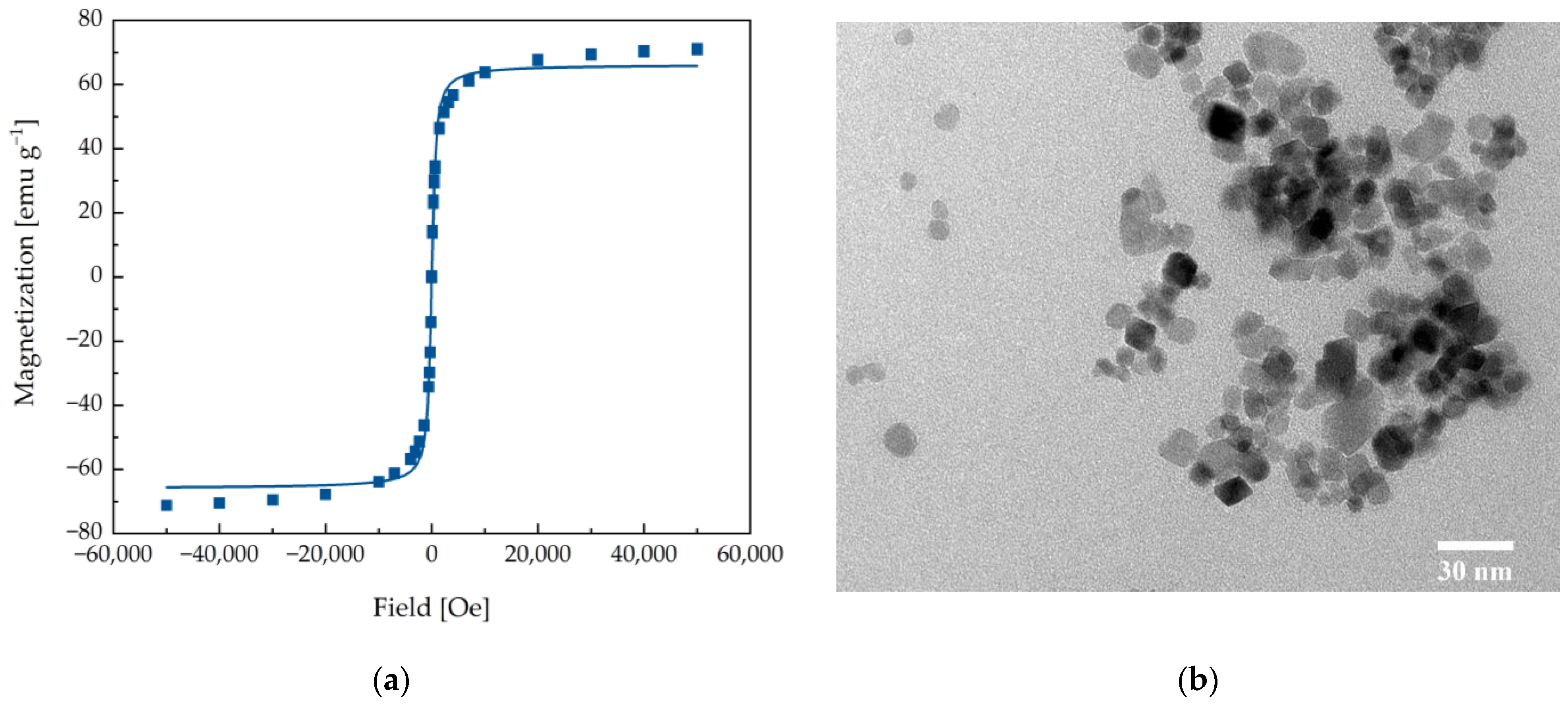
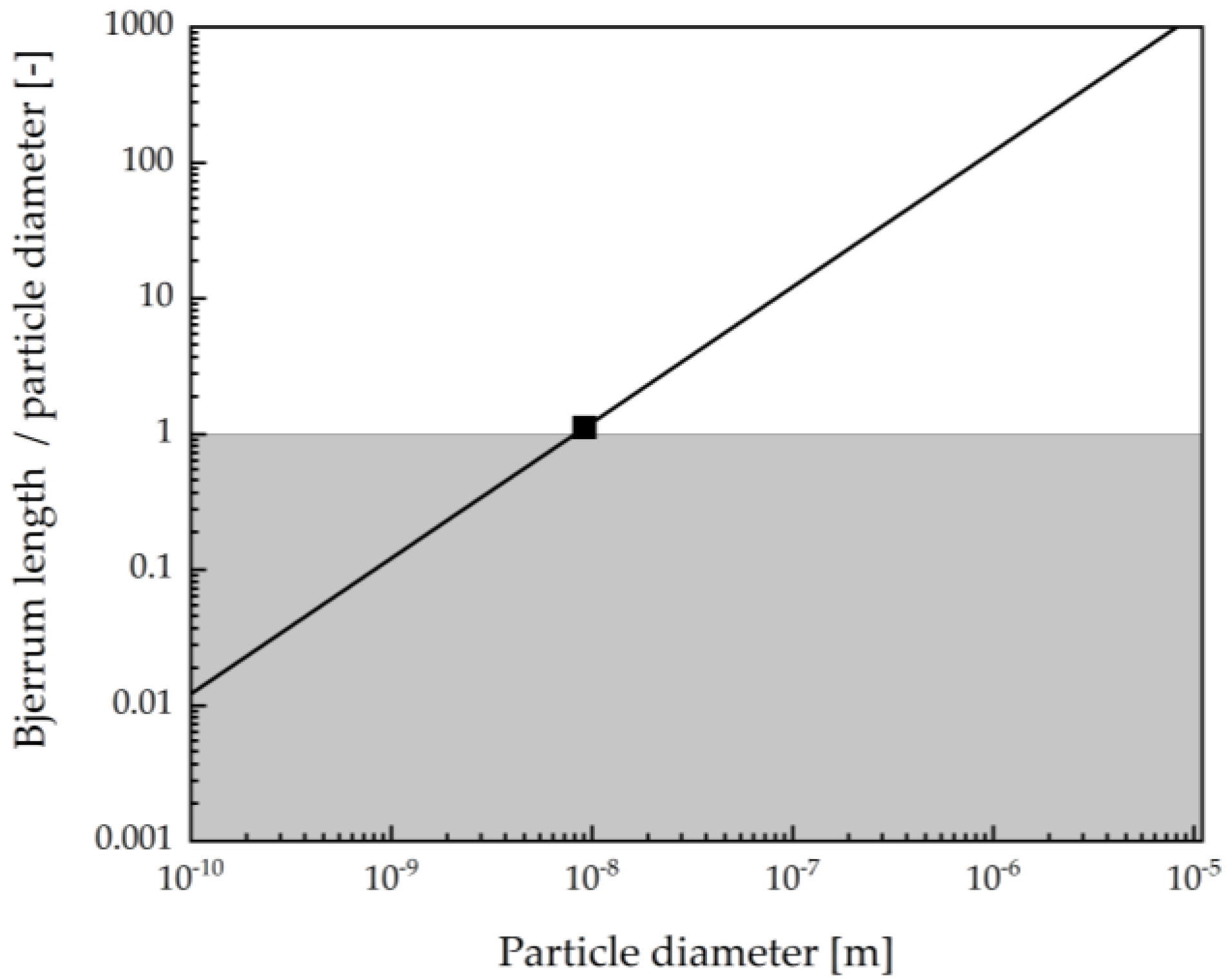
2.1. Particle Characterization
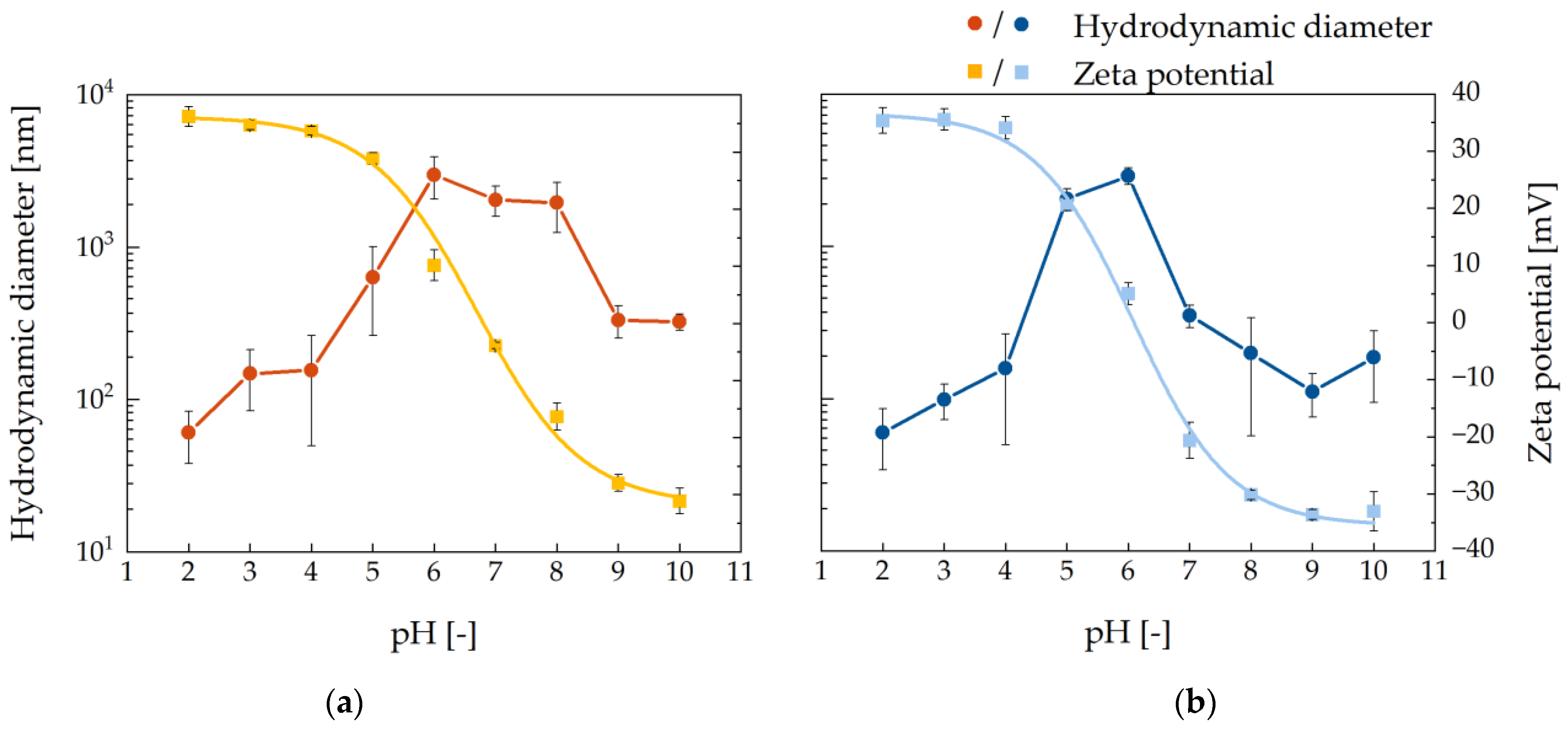
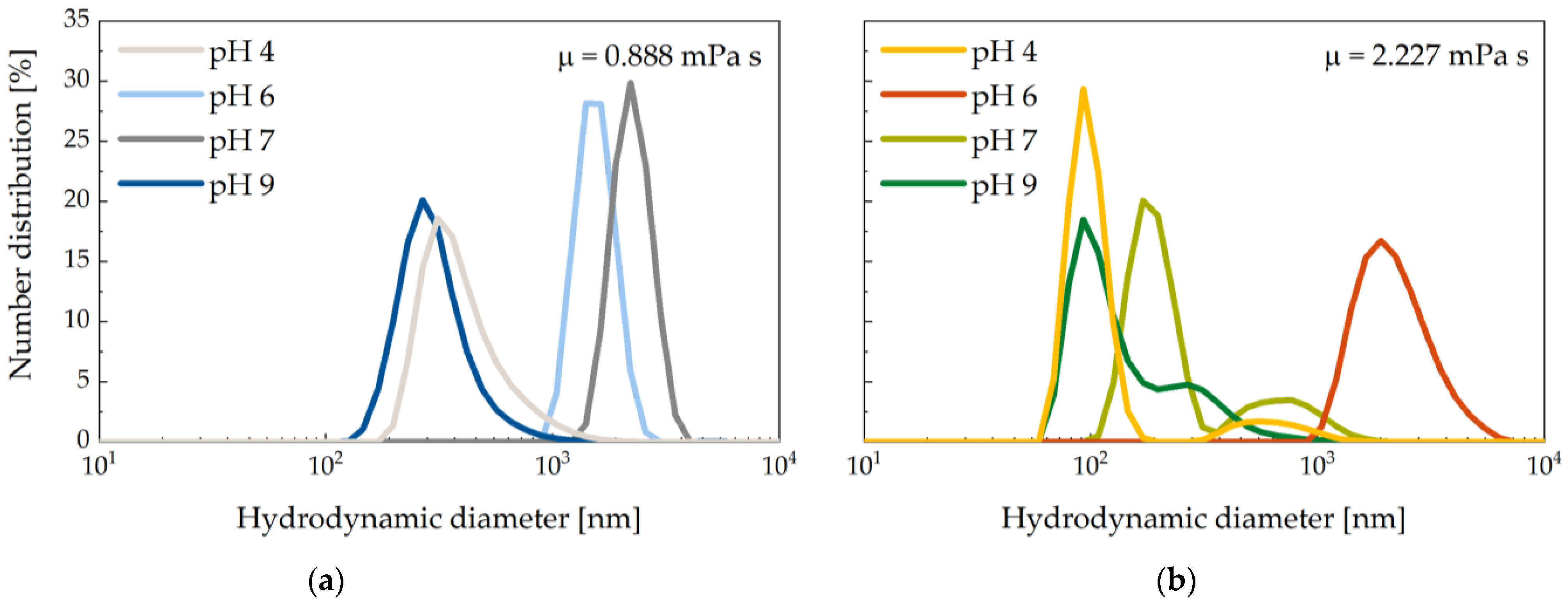
2.2. Influencing the Colloidal Stability of the BIONs due to Viscosity and pH
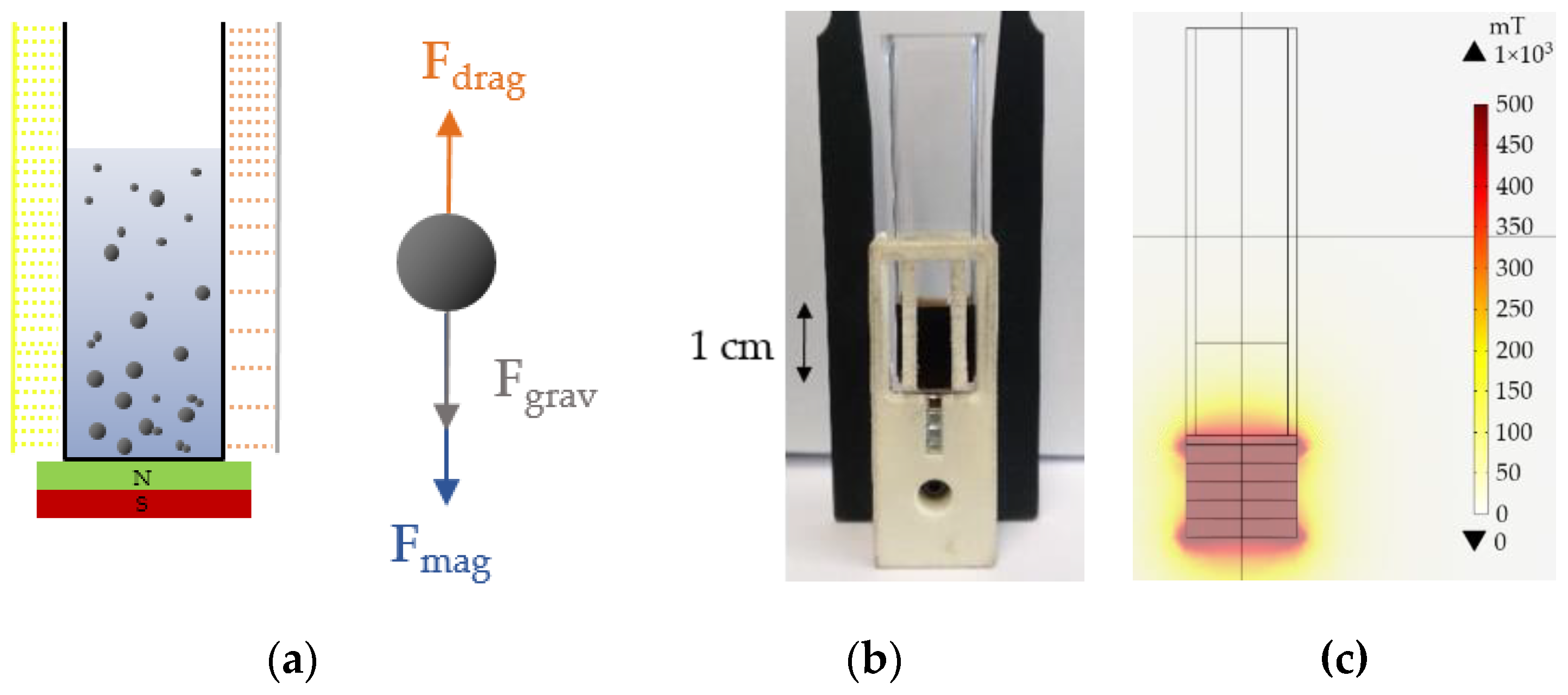
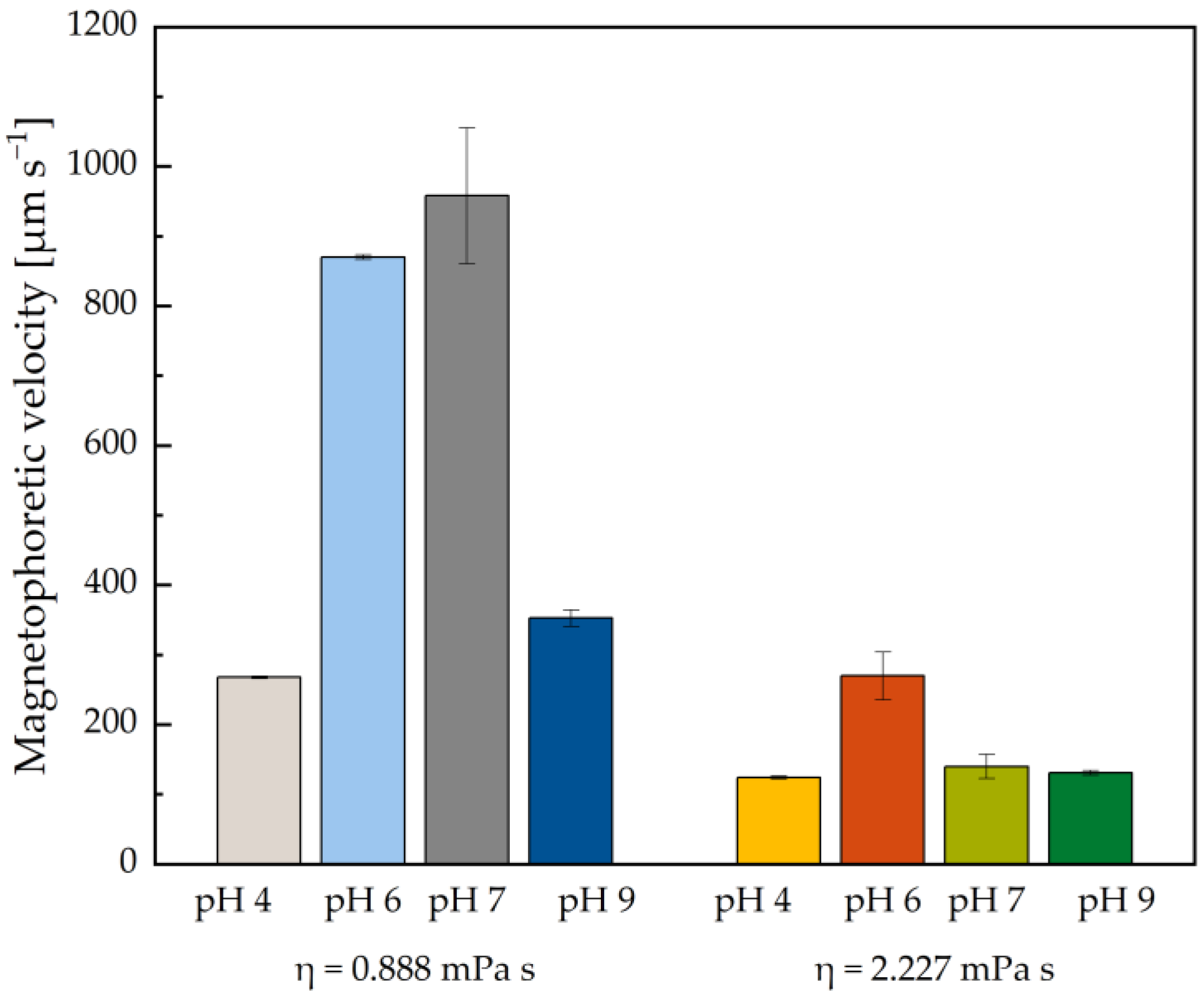
2.3. Dependence of the Magnetophoretic Velocity on Aggregate Size and Viscosity
3. Materials and Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fraga-García, P.; Kubbutat, P.; Brammen, M.; Schwaminger, S.; Berensmeier, S. Bare Iron Oxide Nanoparticles for Magnetic Harvesting of Microalgae: From Interaction Behavior to Process Realization. Nanomaterials 2018, 8, 292. [Google Scholar] [CrossRef]
- Schnell, F.; Kube, M.; Berensmeier, S.; Schwaminger, S.P. Magnetic Recovery of Cellulase from Cellulose Substrates with Bare Iron Oxide Nanoparticles. ChemNanoMat 2019, 5, 422–426. [Google Scholar] [CrossRef]
- Zhang, H.; Ding, W.; Li, S.; Ya, S.; Li, F.; Qiu, B. On-chip analysis of magnetically labeled cells with integrated cell sorting and counting techniques. Talanta 2020, 220, 121351. [Google Scholar] [CrossRef]
- Puddu, M.; Paunescu, D.; Stark, W.J.; Grass, R.N. Magnetically Recoverable, Thermostable, Hydrophobic DNA/Silica Encapsulates and Their Application as Invisible Oil Tags. ACS Nano 2014, 8, 2677–2685. [Google Scholar] [CrossRef]
- Ling, W.; Wang, M.; Xiong, C.; Xie, D.; Chen, Q.; Chu, X.; Qiu, X.; Li, Y.; Xiao, X. Synthesis, surface modification, and applications of magnetic iron oxide nanoparticles. J. Mater. Res. 2019, 34, 1828–1844. [Google Scholar] [CrossRef]
- Liu, S.; Yu, B.; Wang, S.; Shen, Y.; Cong, H. Preparation, surface functionalization and application of Fe3O4 magnetic nanoparticles. Adv. Colloid Interface Sci. 2020, 281, 102165. [Google Scholar] [CrossRef]
- Kodama, R. Magnetic nanoparticles. Magnetochemistry 2020, 6. [Google Scholar] [CrossRef]
- Massart, R. Preparation of aqueous magnetic liquids in alkaline and acidic media. IEEE Trans. Magn. 1981, 17, 1247–1248. [Google Scholar] [CrossRef]
- Leong, S.S.; Yeap, S.P.; Lim, J. Working principle and application of magnetic separation for biomedical diagnostic at high- and low-field gradients. Interface Focus 2016, 6, 20160048. [Google Scholar] [CrossRef]
- Lozar, T.; Jesenko, T.; Prevodnik, V.K.; Cemazar, M.; Hosta, V.; Jericevic, A.; Nolde, N.; Kuhar, C.G. Preclinical and Clinical Evaluation of Magnetic-Activated Cell Separation Technology for CTC Isolation in Breast Cancer. Front. Oncol. 2020, 10, 1–10. [Google Scholar] [CrossRef]
- Miltenyi, S.; Müller, W.; Weichel, W.; Radbruch, A. High gradient magnetic cell separation with MACS. Cytometry 1990, 11, 231–238. [Google Scholar] [CrossRef]
- Fratzl, M.; Delshadi, S.; Devillers, T.; Bruckert, F.; Cugat, O.; Dempsey, N.M.; Blaire, G. Magnetophoretic induced convective capture of highly diffusive superparamagnetic nanoparticles. Soft Matter 2018, 14, 2671–2681. [Google Scholar] [CrossRef]
- Corchero, J.L.; Villaverde, A. Biomedical applications of distally controlled magnetic nanoparticles. Trends Biotechnol. 2009, 27, 468–476. [Google Scholar] [CrossRef] [PubMed]
- Toh, P.Y.; Yeap, S.P.; Kong, L.P.; Ng, B.W.; Chan, D.J.C.; Ahmad, A.L.; Lim, J.K. Magnetophoretic removal of microalgae from fishpond water: Feasibility of high gradient and low gradient magnetic separation. Chem. Eng. J. 2012, 211-212, 22–30. [Google Scholar] [CrossRef]
- Alnaimat, F.; Karam, S.; Mathew, B.; Mathew, B. Magnetophoresis and Microfluidics: A Great Union. IEEE Nanotechnol. Mag. 2020, 14, 24–41. [Google Scholar] [CrossRef]
- Robert, D.; Pamme, N.; Conjeaud, H.; Gazeau, F.; Iles, A.; Wilhelm, C. Cell sorting by endocytotic capacity in a microfluidic magnetophoresis device. Lab. Chip 2011, 11, 1902–1910. [Google Scholar] [CrossRef] [PubMed]
- Kievit, F.M.; Zhang, M. Surface Engineering of Iron Oxide Nanoparticles for Targeted Cancer Therapy. Acc. Chem. Res. 2011, 44, 853–862. [Google Scholar] [CrossRef]
- Socoliuc, V.; Peddis, D.; Petrenko, V.I.; Avdeev, M.V.; Susan-Resiga, D.; Szabó, T.; Turcu, R.; Tombácz, E.; Vékás, L. Magnetic Nanoparticle Systems for Nanomedicine—A Materials Science Perspective. Magnetochemistry 2020, 6, 2. [Google Scholar] [CrossRef]
- Dulińska-Litewka, J.; Łazarczyk, A.; Hałubiec, P.; Szafrański, O.; Karnas, K.; Karewicz, A. Superparamagnetic Iron Oxide Nanoparticles—Current and Prospective Medical Applications. Materials 2019, 12, 617. [Google Scholar] [CrossRef]
- Ansari, S.A.M.K.; Ficiarà, E.; Ruffinatti, F.A.; Stura, I.; Argenziano, M.; Abollino, O.; Cavalli, R.; Guiot, C.; D’Agata, F. Magnetic Iron Oxide Nanoparticles: Synthesis, Characterization and Functionalization for Biomedical Applications in the Central Nervous System. Materials 2019, 12, 465. [Google Scholar] [CrossRef]
- Vangijzegem, T.; Stanicki, D.; Laurent, S. Magnetic iron oxide nanoparticles for drug delivery: Applications and characteristics. Expert Opin. Drug Deliv. 2019, 16, 69–78. [Google Scholar] [CrossRef]
- Soetaert, F.; Korangath, P.; Serantes, D.; Fiering, S.; Ivkov, R. Cancer therapy with iron oxide nanoparticles: Agents of thermal and immune therapies. Adv. Drug Deliv. Rev. 2020, 163-164, 65–83. [Google Scholar] [CrossRef] [PubMed]
- Belanova, A.A.; Gavalas, N.; Makarenko, Y.M.; Belousova, M.M.; Soldatov, A.V.; Zolotukhin, P.V. Physicochemical Properties of Magnetic Nanoparticles: Implications for Biomedical Applications In Vitro and In Vivo. Oncol. Res. Treat. 2018, 41, 139–143. [Google Scholar] [CrossRef]
- Nam, J.; Huang, H.; Lim, H.; Lim, C.; Shin, S. Magnetic Separation of Malaria-Infected Red Blood Cells in Various Developmental Stages. Anal. Chem. 2013, 85, 7316–7323. [Google Scholar] [CrossRef] [PubMed]
- Pamme, N.; Wilhelm, C. Continuous sorting of magnetic cells via on-chip free-flow magnetophoresis. Lab. Chip 2006, 6, 974–980. [Google Scholar] [CrossRef] [PubMed]
- Roth, H.-C.; Prams, A.; Lutz, M.; Ritscher, J.; Raab, M.; Berensmeier, S. A high-gradient magnetic separator for highly viscous process liquors in industrial biotechnology. Chem. Eng. Technol. 2016, 39, 469–476. [Google Scholar] [CrossRef]
- Mishima, F.; Hayashi, S.; Akiyama, Y.; Nishijima, S. Development of a Superconducting High Gradient Magnetic Separator for a Highly Viscous Fluid. IEEE Trans. Appl. Supercond. 2011, 22, 3700204. [Google Scholar] [CrossRef]
- Gupta, A.K.; Gupta, M. Synthesis and surface engineering of iron oxide nanoparticles for biomedical applications. Biomaterials 2005, 26, 3995–4021. [Google Scholar] [CrossRef]
- Coppola, L.; Caserta, F.; De Lucia, D.; Guastafierro, S.; Grassia, A.; Coppola, A.; Marfella, R.; Varricchio, M. Blood viscosity and aging. Arch. Gerontol. Geriatr. 2000, 31, 35–42. [Google Scholar] [CrossRef]
- Alphandéry, E. Bio-synthesized iron oxide nanoparticles for cancer treatment. Int. J. Pharm. 2020, 586, 119472. [Google Scholar] [CrossRef]
- Solsona, M.; Nieuwelink, A.-E.; Meirer, F.; Abelmann, L.; Odijk, M.; Olthuis, W.; Weckhuysen, B.M.; Berg, A.V.D. Magnetophoretic Sorting of Single Catalyst Particles. Angew. Chem. Int. Ed. 2018, 57, 10589–10594. [Google Scholar] [CrossRef] [PubMed]
- Faraudo, J.; Andreu, J.S.; Calero, C.; Camacho, J. Predicting the Self-Assembly of Superparamagnetic Colloids under Magnetic Fields. Adv. Funct. Mater. 2016, 26, 3837–3858. [Google Scholar] [CrossRef]
- Leong, S.S.; Ahmad, Z.; Low, S.C.; Camacho, J.; Faraudo, J.; Lim, J. Unified View of Magnetic Nanoparticle Separation under Magnetophoresis. Langmuir 2020, 36, 8033–8055. [Google Scholar] [CrossRef]
- Yavuz, C.T.; Mayo, J.T.; Yu, W.W.; Prakash, A.; Falkner, J.C.; Yean, S.; Cong, L.; Shipley, H.J.; Kan, A.; Tomson, M.; et al. Low-Field Magnetic Separation of Monodisperse Fe3O4 Nanocrystals. Science 2006, 314, 964–967. [Google Scholar] [CrossRef]
- Faraudo, J.; Camacho, J. Cooperative magnetophoresis of superparamagnetic colloids: Theoretical aspects. Colloid Polym. Sci. 2009, 288, 207–215. [Google Scholar] [CrossRef]
- Schwaminger, S.P.; Fraga-García, P.; Selbach, F.; Hein, F.G.; Fuß, E.C.; Surya, R.; Roth, H.-C.; Blank-Shim, S.A.; Wagner, F.E.; Heissler, S.; et al. Bio-nano interactions: Cellulase on iron oxide nanoparticle surfaces. Adsorption 2016, 23, 281–292. [Google Scholar] [CrossRef]
- Bean, C.P.; Livingston, J.D. Superparamagnetism. J. Appl. Phys. 1959, 30, S120–S129. [Google Scholar] [CrossRef]
- Turrina, C.; Berensmeier, S.; Schwaminger, S. Bare Iron Oxide Nanoparticles as Drug Delivery Carrier for the Short Cationic Peptide Lasioglossin. Pharmaceuticals 2021, 14, 405. [Google Scholar] [CrossRef]
- Schwaminger, S.; Syhr, C.; Berensmeier, S. Controlled Synthesis of Magnetic Iron Oxide Nanoparticles: Magnetite or Maghemite? Crystals 2020, 10, 214. [Google Scholar] [CrossRef]
- Schwaminger, S.P.; Bauer, D.; Fraga-García, P.; Wagner, F.E.; Berensmeier, S. Oxidation of magnetite nanoparticles: Impact on surface and crystal properties. CrystEngComm 2016, 19, 246–255. [Google Scholar] [CrossRef]
- Schwaminger, S.P.; Schwarzenberger, K.; Gatzemeier, J.; Lei, Z.; Eckert, K. Magnetically Induced Aggregation of Iron Oxide Nanoparticles for Carrier Flotation Strategies. ACS Appl. Mater. Interfaces 2021, 13, 20830–20844. [Google Scholar] [CrossRef] [PubMed]
- Schwaminger, S.P.; Blank-Shim, S.A.; Scheifele, I.; Fraga-García, P.; Berensmeier, S. Peptide binding to metal oxide nanoparticles. Faraday Discuss. 2017, 204, 233–250. [Google Scholar] [CrossRef] [PubMed]
- Stetefeld, J.; McKenna, S.; Patel, T.R. Dynamic light scattering: A practical guide and applications in biomedical sciences. Biophys. Rev. 2016, 8, 409–427. [Google Scholar] [CrossRef] [PubMed]
- Szalai, A.J.; Manivannan, N.; Kaptay, G. Super-paramagnetic magnetite nanoparticles obtained by different synthesis and separation methods stabilized by biocompatible coatings. Colloids Surfaces A Physicochem. Eng. Asp. 2019, 568, 113–122. [Google Scholar] [CrossRef]
- Sun, X.; Zheng, C.; Zhang, F.; Yang, Y.; Wu, G.; Yu, A.; Guan, N. Size-Controlled Synthesis of Magnetite (Fe3O4) Nanoparticles Coated with Glucose and Gluconic Acid from a Single Fe(III) Precursor by a Sucrose Bifunctional Hydrothermal Method. J. Phys. Chem. C 2009, 113, 16002–16008. [Google Scholar] [CrossRef]
- Cushing, B.L.; Kolesnichenko, V.; O’Connor, C.J. Recent Advances in the Liquid-Phase Syntheses of Inorganic Nanoparticles. Chem. Rev. 2004, 104, 3893–3946. [Google Scholar] [CrossRef] [PubMed]
- Benítez, E.I.; Genovese, D.B.; Lozano, J.E. Effect of typical sugars on the viscosity and colloidal stability of apple juice. Food Hydrocoll. 2009, 23, 519–525. [Google Scholar] [CrossRef]
- Chalikian, T.V. Ultrasonic and Densimetric Characterizations of the Hydration Properties of Polar Groups in Monosaccharides. J. Phys. Chem. B 1998, 102, 6921–6926. [Google Scholar] [CrossRef]
- Leong, S.S.; Ahmad, Z.; Lim, J. Magnetophoresis of superparamagnetic nanoparticles at low field gradient: Hydrodynamic effect. Soft Matter 2015, 11, 6968–6980. [Google Scholar] [CrossRef]
- Cuevas, G.D.L.; Faraudo, J.; Camacho, J. Low-Gradient Magnetophoresis through Field-Induced Reversible Aggregation. J. Phys. Chem. C 2008, 112, 945–950. [Google Scholar] [CrossRef]
- Einstein, A. Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen. Ann. Phys. 1905, 322, 549–560. [Google Scholar] [CrossRef]
- Furlani, E.P. Analysis of particle transport in a magnetophoretic microsystem. J. Appl. Phys. 2006, 99, 024912. [Google Scholar] [CrossRef]
- Mykhaylyk, O.; Lerche, D.; Vlaskou, D.; Schoemig, V.; Detloff, T.; Krause, D.; Wolff, M.; Joas, T.; Berensmeier, S.; Plank, C.; et al. Biomagnetic Particles Magnetophoretic Velocity Determined by Space- and Time-Resolved Extinction Profiles. IEEE Magn. Lett. 2015, 6, 1–4. [Google Scholar] [CrossRef]
- Laurent, S.; Forge, D.; Port, M.; Roch, A.; Robic, C.; Elst, L.V.; Muller, R.N. Erratum: Magnetic Iron Oxide Nanoparticles: Synthesis, Stabilization, Vectorization, Physicochemical Characterizations, and Biological Applications. Chem. Rev. 2008, 110, 2574. [Google Scholar] [CrossRef]
| η = 0.888 mPa s | η = 2.227 mPa s | |||
|---|---|---|---|---|
| pH | Sedimentation Velocity (µm s−1) | Hydrodynamic Diameter (nm) | Sedimentation Velocity (µm s−1) | Hydrodynamic Diameter (nm) |
| 4 | 1.57 ± 0.09 | 156 ± 106 | 0.88 ± 0.70 | 158 ± 108 |
| 6 | 3.82 ± 0.85 | 2986 ± 920 | 2.30 ± 0.01 | 2764 ± 446 |
| 7 | 3.69 ± 0.14 | 2047 ± 461 | 0.33 ± 0.28 | 351 ± 58 |
| 9 | 1.43 ± 0.37 | 331 ± 79 | 0.31 ± 0.06 | 111 ± 35 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wittmann, L.; Turrina, C.; Schwaminger, S.P. The Effect of pH and Viscosity on Magnetophoretic Separation of Iron Oxide Nanoparticles. Magnetochemistry 2021, 7, 80. https://doi.org/10.3390/magnetochemistry7060080
Wittmann L, Turrina C, Schwaminger SP. The Effect of pH and Viscosity on Magnetophoretic Separation of Iron Oxide Nanoparticles. Magnetochemistry. 2021; 7(6):80. https://doi.org/10.3390/magnetochemistry7060080
Chicago/Turabian StyleWittmann, Leonie, Chiara Turrina, and Sebastian P. Schwaminger. 2021. "The Effect of pH and Viscosity on Magnetophoretic Separation of Iron Oxide Nanoparticles" Magnetochemistry 7, no. 6: 80. https://doi.org/10.3390/magnetochemistry7060080
APA StyleWittmann, L., Turrina, C., & Schwaminger, S. P. (2021). The Effect of pH and Viscosity on Magnetophoretic Separation of Iron Oxide Nanoparticles. Magnetochemistry, 7(6), 80. https://doi.org/10.3390/magnetochemistry7060080