Magnetic Properties of Bi-Magnetic Core/Shell Nanoparticles: The Case of Thin Shells
Abstract
:1. Introduction
2. Materials and Methods
2.1. Synthesis of NPs
2.2. Morphostructural Properties
2.3. Magnetic Properties
3. Results
3.1. Morphostructural Properties
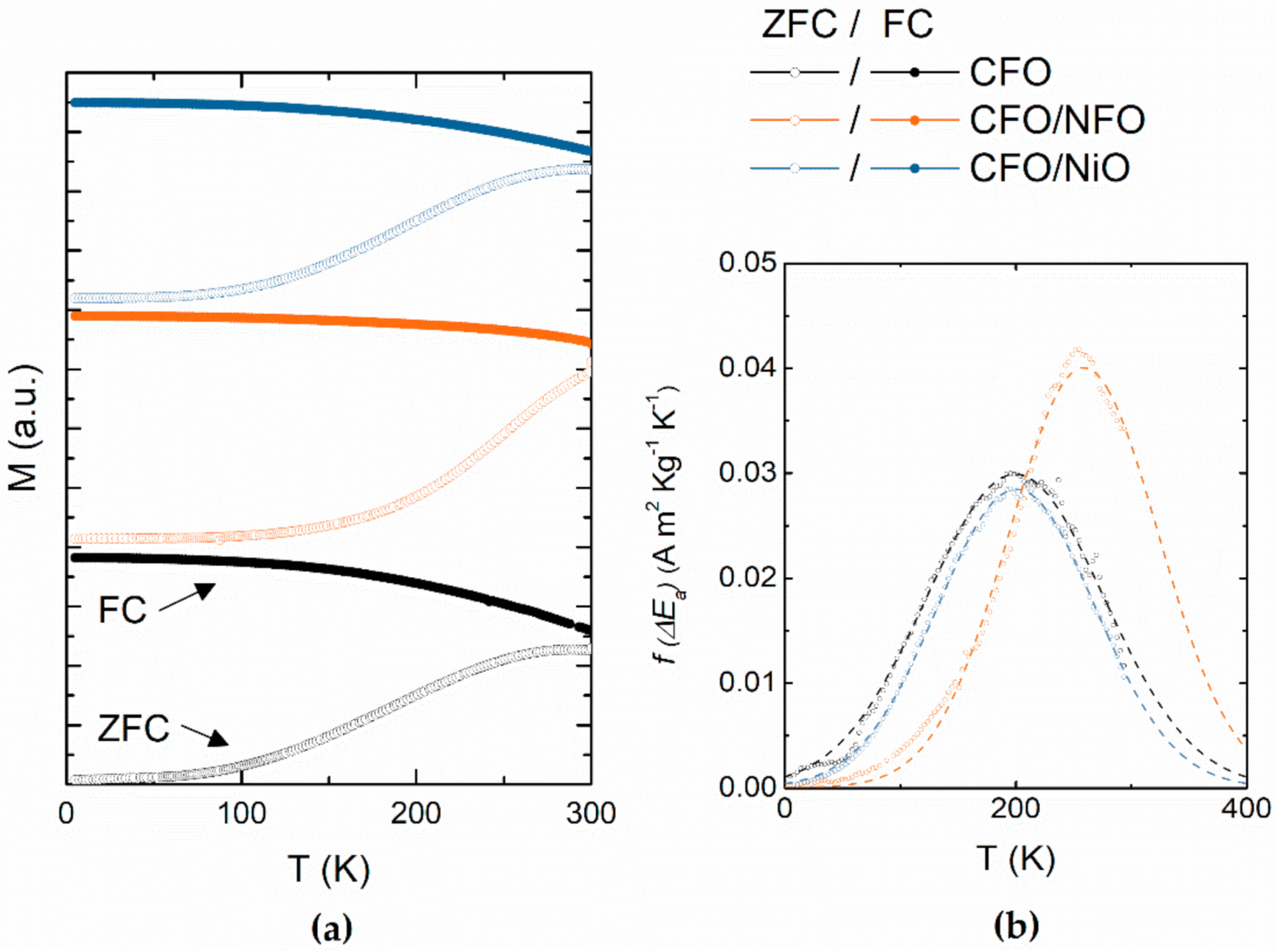
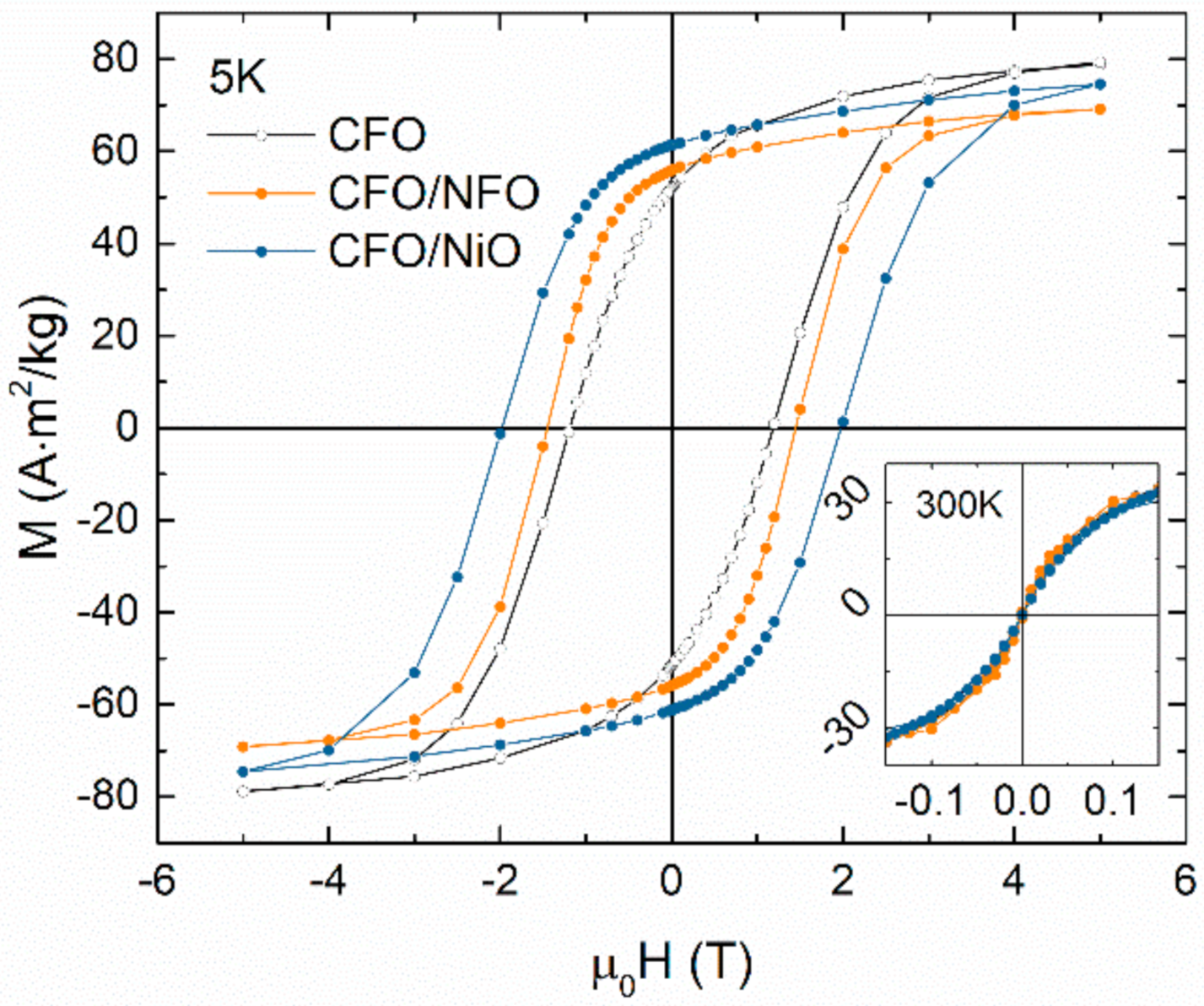
3.2. Magnetic Anisotropy
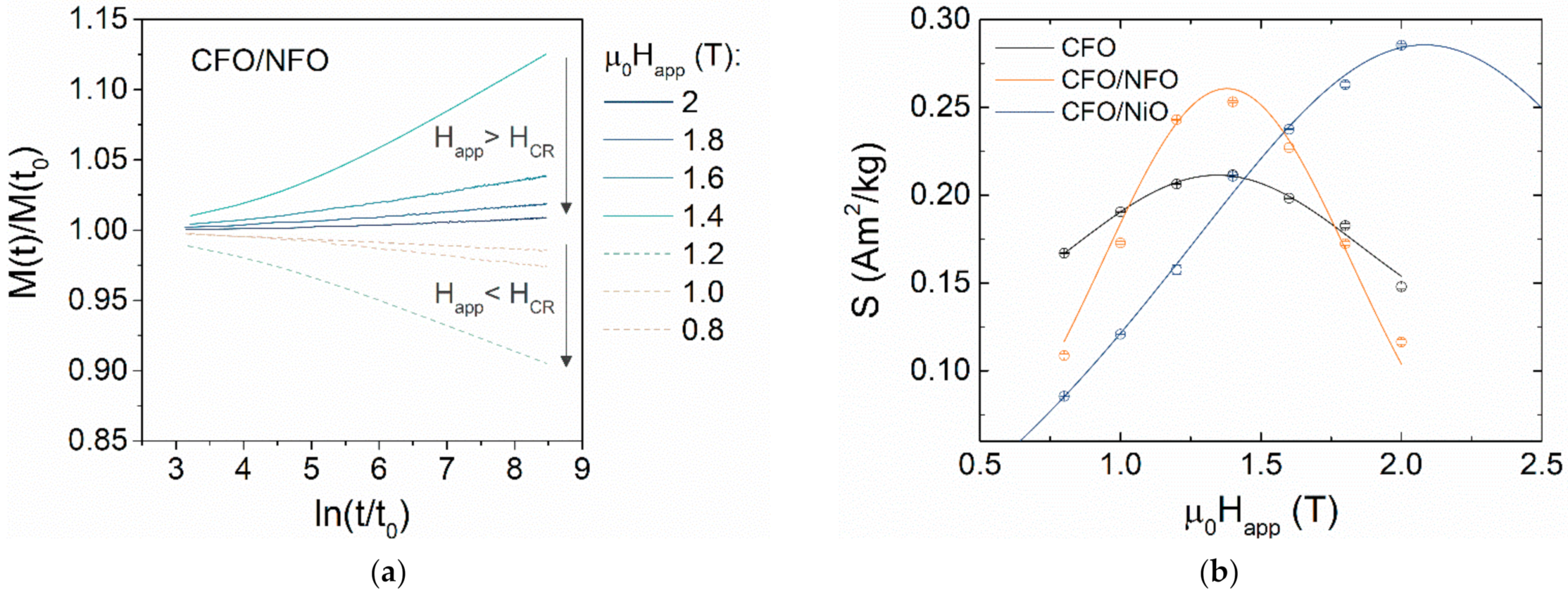
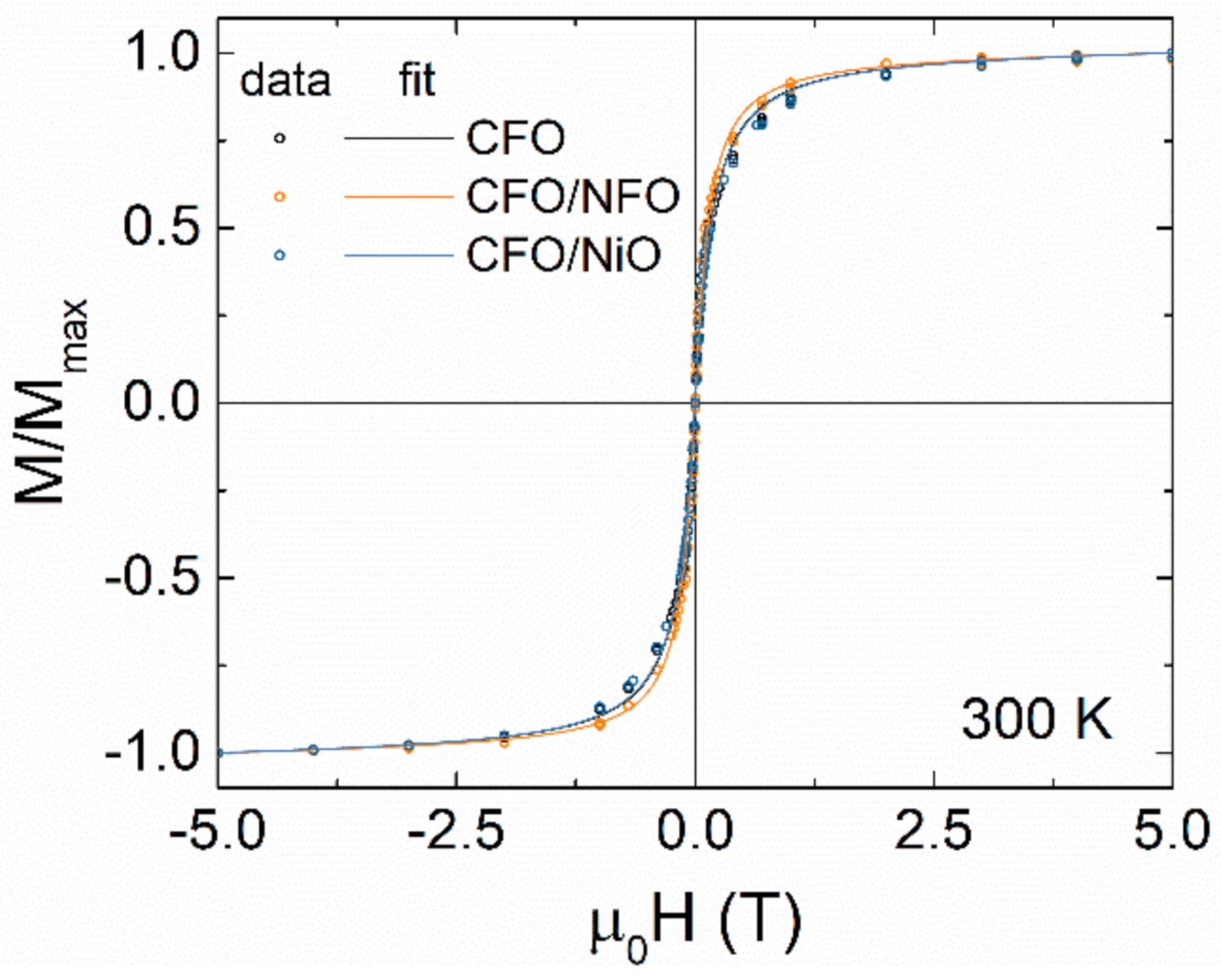
3.3. Intra- and Interparticle Interactions
- Fit of superparamagnetic M-H curve with Langevin–Chantrell method [47];
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lee, J.-H.; Jang, J.; Choi, J.; Moon, S.H.; Noh, S.; Kim, J.; Kim, J.-G.; Kim, I.-S.; Park, K.I.; Cheon, J. Exchange-coupled magnetic nanoparticles for efficient heat induction. Nat. Nanotechnol. 2011, 6, 418–422. [Google Scholar] [CrossRef] [PubMed]
- Noh, S.; Moon, S.H.; Shin, T.-H.; Lim, Y.; Cheon, J. Recent advances of magneto-thermal capabilities of nanoparticles: From design principles to biomedical applications. Nano Today 2017, 13, 61–76. [Google Scholar] [CrossRef]
- Vasilakaki, M.; Trohidou, K.N.; Nogués, J. Enhanced magnetic properties in antiferromagnetic-core/ferrimagnetic-shell nanoparticles. Sci. Rep. 2015, 5, 1–7. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sanna Angotzi, M.; Mameli, V.; Cara, C.; Musinu, A.; Sangregorio, C.; Niznansky, D.; Xin, H.L.; Vejpravova, J.; Cannas, C. Coupled hard–soft spinel ferrite-based core–shell nanoarchitectures: Magnetic properties and heating abilities. Nanoscale Adv. 2020, 2, 3191–3201. [Google Scholar] [CrossRef]
- López-Ortega, A.; Estrader, M.; Salazar-Alvarez, G.; Roca, A.G.; Nogués, J. Applications of exchange coupled bi-magnetic hard/soft and soft/hard magnetic core/shell nanoparticles. Phys. Rep. 2015, 553, 1–32. [Google Scholar] [CrossRef] [Green Version]
- Nogués, J.; Schuller, I.K. Exchange bias. J. Magn. Magn. Mater. 1999, 192, 203–232. [Google Scholar] [CrossRef]
- Lottini, E.; López-Ortega, A.; Bertoni, G.; Turner, S.; Meledina, M.; Van Tendeloo, G.; De Julián Fernández, C.; Sangregorio, C. Strongly Exchange Coupled Core|Shell Nanoparticles with High Magnetic Anisotropy: A Strategy toward Rare-Earth-Free Permanent Magnets. Chem. Mater. 2016, 28, 4214–4222. [Google Scholar] [CrossRef]
- Laureti, S.; Del Bianco, L.; Detlefs, B.; Agostinelli, E.; Foglietti, V.; Peddis, D.; Testa, A.M.; Varvaro, G.; Fiorani, D. Interface exchange coupling in a CoPt/NiO bilayer. Thin Solid Films 2013, 543, 162–166. [Google Scholar] [CrossRef]
- Meiklejohn, W.H.; Bean, C.P. New magnetic anisotropy. Phys. Rev. 1957, 105, 904–913. [Google Scholar] [CrossRef]
- Yang, M.; Ho, C.; Ruta, S.; Chantrell, R.; Krycka, K.; Hovorka, O.; Chen, F.; Lai, P.; Lai, C. Magnetic Interaction of Multifunctional Core–Shell Nanoparticles for Highly Effective Theranostics. Adv. Mater. 2018, 30, 1802444. [Google Scholar] [CrossRef] [Green Version]
- Socoliuc, V.; Peddis, D.; Petrenko, V.I.; Avdeev, M.V.; Susan-Resiga, D.; Szabó, T.; Turcu, R.; Tombácz, E.; Vékás, L. Magnetic Nanoparticle Systems for Nanomedicine—A Materials Science Perspective. Magetochemistry 2019, 6, 2. [Google Scholar] [CrossRef] [Green Version]
- Fabris, F.; Lohr, J.; Lima, E.; de Almeida, A.A.; Troiani, H.E.; Rodríguez, L.M.; Vásquez Mansilla, M.; Aguirre, M.H.; Goya, G.F.; Rinaldi, D.; et al. Adjusting the Néel relaxation time of Fe3O4/ZnxCo1−xFe2O4 core/shell nanoparticles for optimal heat generation in magnetic hyperthermia. Nanotechnology 2021, 32, 065703. [Google Scholar] [CrossRef] [PubMed]
- Estrader, M.; López-Ortega, A.; Golosovsky, I.V.; Estradé, S.; Roca, A.G.; Salazar-Alvarez, G.; López-Conesa, L.; Tobia, D.; Winkler, E.; Ardisson, J.D.; et al. Origin of the large dispersion of magnetic properties in nanostructured oxides: FexO/Fe3O4 nanoparticles as a case study. Nanoscale 2015, 7, 3002–3015. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Moon, S.H.; Noh, S.-H.; Lee, J.-H.; Shin, T.-H.; Lim, Y.; Cheon, J. Ultrathin Interface Regime of Core–Shell Magnetic Nanoparticles for Effective Magnetism Tailoring. Nano Lett. 2017, 17, 800–804. [Google Scholar] [CrossRef]
- Muzzi, B.; Albino, M.; Innocenti, C.; Petrecca, M.; Cortigiani, B.; de Julián Fernández, C.; Bertoni, G.; Fernández-Pacheco, R.; Ibarra, A.; Marquina, C.; et al. Unraveling the mechanism of the one-pot synthesis of exchange coupled Co-based nano-heterostructures with high energy product. Nanoscale 2020, 12, 14076–14086. [Google Scholar] [CrossRef]
- Quesada, A.; Granados-Miralles, C.; López-Ortega, A.; Erokhin, S.; Lottini, E.; Pedrosa, J.; Bollero, A.; Aragón, A.M.; Rubio-Marcos, F.; Stingaciu, M.; et al. Energy Product Enhancement in Imperfectly Exchange-Coupled Nanocomposite Magnets. Adv. Electron. Mater. 2016, 2, 1500365. [Google Scholar] [CrossRef]
- Sun, S.; Zeng, H.; Robinson, D.B.; Raoux, S.; Rice, P.M.; Wang, S.X.; Li, G. Monodisperse MFe2O4 (M=Fe, Co, Mn) Nanoparticles. J. Am. Chem. Soc. 2004, 126, 273–279. [Google Scholar] [CrossRef]
- Omelyanchik, A.; Villa, S.; Vasilakaki, M.; Singh, G.; Ferretti, A.M.; Ponti, A.; Canepa, F.; Margaris, G.; Trohidou, K.N.; Peddis, D. Interplay between inter- and intraparticle interactions in bi-magnetic core/shell nanoparticles. Nanoscale Adv. 2021. [Google Scholar] [CrossRef]
- Muscas, G.; Singh, G.; Glomm, W.; Mathieu, R.; Kumar, P.A.; Concas, G.; Agostinelli, E.; Peddis, D. Tuning the Size and Shape of Oxide Nanoparticles by Controlling Oxygen Content in the Reaction Environment: Morphological Analysis by Aspect Maps. Chem. Mater. 2015, 27, 1982–1990. [Google Scholar] [CrossRef]
- Bertotti, G. Hysteresis in Magnetism; Academic Press: Cambridge, MA, USA, 1998; pp. 3–30. [Google Scholar]
- Concas, G.; Congiu, F.; Muscas, G.; Peddis, D. Determination of Blocking Temperature in Magnetization and Mössbauer Time Scale: A Functional Form Approach. J. Phys. Chem. C 2017, 121, 16541–16548. [Google Scholar] [CrossRef]
- Micha, J.; Dieny, B.; Régnard, J.; Jacquot, J.; Sort, J. Estimation of the Co nanoparticles size by magnetic measurements in Co/SiO2 discontinuous multilayers. J. Magn. Magn. Mater. 2004, 272–276, E967–E968. [Google Scholar] [CrossRef]
- Knobel, M.; Nunes, W.C.; Socolovsky, L.M.; De Biasi, E.; Vargas, J.M.; DeNardin, J.C. Superparamagnetism and Other Magnetic Features in Granular Materials: A Review on Ideal and Real Systems. J. Nanosci. Nanotechnol. 2008, 8, 2836–2857. [Google Scholar] [CrossRef] [PubMed]
- Livesey, K.L.; Ruta, S.; Anderson, N.R.; Baldomir, D.; Chantrell, R.W.; Serantes, D. Beyond the blocking model to fit nanoparticle ZFC/FC magnetisation curves. Sci. Rep. 2018, 8, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Bruvera, I.J.; Zélis, P.M.; Calatayud, M.P.; Goya, G.F.; Sánchez, F.H. Determination of the blocking temperature of magnetic nanoparticles: The good, the bad, and the ugly. J. Appl. Phys. 2015, 118, 184304. [Google Scholar] [CrossRef]
- Omelyanchik, A.; Salvador, M.; D’orazio, F.; Mameli, V.; Cannas, C.; Fiorani, D.; Musinu, A.; Rivas, M.; Rodionova, V.; Varvaro, G.; et al. Magnetocrystalline and surface anisotropy in CoFe2O4 nanoparticles. Nanomaterials 2020, 10, 1288. [Google Scholar] [CrossRef]
- Peddis, D.; Orrù, F.; Ardu, A.; Cannas, C.; Musinu, A.; Piccaluga, G. Interparticle Interactions and Magnetic Anisotropy in Cobalt Ferrite Nanoparticles: Influence of Molecular Coating. Chem. Mater. 2012, 24, 1062–1071. [Google Scholar] [CrossRef]
- El-Hilo, M.; Chantrell, R. Rationalisation of distribution functions for models of nanoparticle magnetism. J. Magn. Magn. Mater. 2012, 324, 2593–2595. [Google Scholar] [CrossRef]
- Muscas, G.; Cobianchi, M.; Lascialfari, A.; Cannas, C.; Musinu, A.; Omelyanchik, A.; Rodionova, V.; Fiorani, D.; Mameli, V.; Peddis, D. Magnetic Interactions Versus Magnetic Anisotropy in Spinel Ferrite Nanoparticles. IEEE Magn. Lett. 2019, 10, 1–5. [Google Scholar] [CrossRef]
- Mameli, V.; Musinu, A.; Ardu, A.; Ennas, G.; Peddis, D.; Niznansky, D.; Sangregorio, C.; Innocenti, C.; Thanh, N.T.K.; Cannas, C. Studying the effect of Zn-substitution on the magnetic and hyperthermic properties of cobalt ferrite nanoparticles. Nanoscale 2016, 8, 10124–10137. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Peddis, D.; Laureti, S.; Mansilla, M.; Agostinelli, E.; Varvaro, G.; Cannas, C.; Fiorani, D. Exchange Bias in CoFe2O4/NiO nanocomposites. Superlattices Microstruct. 2009, 46, 125–129. [Google Scholar] [CrossRef]
- Peddis, D.; Cannas, C.; Piccaluga, G.; Agostinelli, E.; Fiorani, D. Spin-glass-like freezing and enhanced magnetization in ultra-small CoFe2O4 nanoparticles. Nanotechnology 2010, 21, 125705. [Google Scholar] [CrossRef]
- Kodama, R.H.; Berkowitz, A.E.; McNiff, E.J.; Foner, S. Surface spin disorder in NiFe2O4 nanoparticles. Phys. Rev. Lett. 1996, 77, 394–397. [Google Scholar] [CrossRef]
- Oyarzún, S.; Tamion, A.; Tournus, F.; Dupuis, V.; Hillenkamp, M. Size effects in the magnetic anisotropy of embedded cobalt nanoparticles: From shape to surface. Sci. Rep. 2015, 5, 14749. [Google Scholar] [CrossRef] [Green Version]
- Respaud, M.; Broto, J.M.; Rakoto, H.; Fert, A.R.; Thomas, L.; Barbara, B.; Verelst, M.; Snoeck, E.; Lecante, P.; Mosset, A.; et al. Surface effects on the magnetic properties of ultrafine cobalt particles. Phys. Rev. B 1998, 57, 2925–2935. [Google Scholar] [CrossRef]
- Cabreira Gomes, R.; G da Silva, F.; Silva, T.-Q.; Gomide, G.; Pilati, V.; Aquino, R.; Geshev, J.; Perzynski, R.; Depeyrot, J. Magnetic irreversibility and saturation criteria in ultrasmall bi-magnetic nanoparticles. J. Alloys Compd. 2020, 824, 153646. [Google Scholar] [CrossRef]
- Nogués, J.; Sort, J.; Langlais, V.; Skumryev, V.; Suriñach, S.; Muñoz, J.S.; Baró, M.D. Exchange bias in nanostructures. Phys. Rep. 2005, 422, 65–117. [Google Scholar] [CrossRef]
- Omelianchik, A.; Singh, G.; McDonagh, B.H.; Rodionova, V.; Fiorani, D.; Peddis, D.; Laureti, S.; Omelyanchik, A. From Mn3O4/MnO core–shell nanoparticles to hollow MnO: Evolution of magnetic properties. Nanotechnology 2017, 29, 055703. [Google Scholar] [CrossRef] [PubMed]
- Dai, J.; Feng, W.; Cheng, C.; Wen, X. The exchange bias effects of CoFe2O4@NiO nanofibers fabricated by electrospinning. Mater. Res. Express 2020, 7, 045009. [Google Scholar] [CrossRef]
- Mohan, R.; Ghosh, M.; Mukherjee, S. The exchange bias effect in CoFe2O4/NiO nanocomposites prepared by chemical co-precipitation method. Mater. Res. Express 2019, 6, 056105. [Google Scholar] [CrossRef]
- Chantrell, R.W.; O’Grady, K.; Search, H.; Journals, C.; Contact, A.; Iopscience, M.; Address, I.P. Magnetic characterization of recording media. J. Phys. D. Appl. Phys. 1992, 25, 1–23. [Google Scholar] [CrossRef]
- García-Otero, J.; Porto, M.; Rivas, J. Henkel plots of single-domain ferromagnetic particles. J. Appl. Phys. 2000, 87, 7376. [Google Scholar] [CrossRef] [Green Version]
- Wohlfarth, E.P. Relations between Different Modes of Acquisition of the Remanent Magnetization of Ferromagnetic Particles. J. Appl. Phys. 1958, 29, 595–596. [Google Scholar] [CrossRef]
- Kelly, P.E.; O’Grady, K.; Mayo, P.I. Switching mechanisms in cobalt phosphorus thin films. In Proceedings of the International Magnetics Conference; IEEE: New York, NY, USA, 1989; Volume 25, p. HA5. [Google Scholar]
- Wohlfarth, E.P. The coefficient of magnetic viscosity. J. Phys. F Met. Phys. 1984, 14, L155–L159. [Google Scholar] [CrossRef]
- Laureti, S.; Varvaro, G.; Testa, A.M.; Fiorani, D.; Agostinelli, E.; Piccaluga, G.; Musinu, A.; Ardu, A.; Peddis, D. Magnetic interactions in silica coated nanoporous assemblies of CoFe2O4 nanoparticles with cubic magnetic anisotropy. Nanotechnology 2010, 21, 315701. [Google Scholar] [CrossRef] [PubMed]
- Chantrell, R.; Popplewell, J.; Charles, S. Measurements of particle size distribution parameters in ferrofluids. IEEE Trans. Magn. 1978, 14, 975–977. [Google Scholar] [CrossRef]
- Bender, P.; Balceris, C.; Ludwig, F.; Posth, O.; Bogart, L.K.; Szczerba, W.; Castro, A.; Nilsson, L.; Costo, R.; Gavilán, H.; et al. Distribution functions of magnetic nanoparticles determined by a numerical inversion method. New J. Phys. 2017, 19, 073012. [Google Scholar] [CrossRef] [Green Version]
- van Rijssel, J.; Kuipers, B.W.; Erné, B.H. Non-regularized inversion method from light scattering applied to ferrofluid magnetization curves for magnetic size distribution analysis. J. Magn. Magn. Mater. 2014, 353, 110–115. [Google Scholar] [CrossRef]
- Huerta, J.M.M.; Medina, J.D.L.T.; Piraux, L.; Encinas, A. Self consistent measurement and removal of the dipolar interaction field in magnetic particle assemblies and the determination of their intrinsic switching field distribution. J. Appl. Phys. 2012, 111, 083914. [Google Scholar] [CrossRef] [Green Version]
- Néel, L. Théorie du traînage magnétique des substances massives dans le domaine de Rayleigh. J. Phys. Le Radium 1950, 11, 49–61. [Google Scholar] [CrossRef]
- Sandler, S.; Fellows, B.D.; Mefford, O.T. Best Practices for Characterization of Magnetic Nanoparticles for Biomedical Applications. Anal. Chem. 2019, 91, 14159–14169. [Google Scholar] [CrossRef] [Green Version]



| Sample | dXRD, nm | Normal | Log-Normal | ||
|---|---|---|---|---|---|
| dTEM, nm | σTEM | dTEM, nm | σTEM | ||
| CFO | 7.2 ± 0.4 | 8.3 ± 0.1 | 0.25 ± 0.03 | 8.3 ± 0.1 | 0.13 ± 0.02 |
| CFO/NFO | 8.9 ± 0.9 | 9.3 ± 0.1 | 0.31 ± 0.03 | 9.5 ± 0.1 | 0.15 ± 0.02 |
| CFO/NiO | 7.8 ± 0.7 | 9.3 ± 0.1 | 0.38 ± 0.03 | 9.6 ± 0.2 | 0.19 ± 0.02 |
| Sample | <TB>, K | σmag | MS, Am2kg−1 | MR/MS | µ0HC, T |
|---|---|---|---|---|---|
| CFO | 201 ± 8 | 0.76 ± 0.05 | 84 ± 4 | 0.61 ± 0.01 | 1.2 1 |
| CFO/NFO | 259 ± 10 | 0.50 ± 0.05 | 75 ± 4 | 0.76 ± 0.01 | 1.5 ± 0.1 |
| CFO/NiO | 200 ± 8 | 0.65 ± 0.05 | 80 ± 4 | 0.74 ± 0.01 | 2.0 ± 0.1 |
| Sample | dTEMlog, nm | dMAGI, nm | dMAGII, nm | dMAGIII, nm | σTEMlog | σmagII |
|---|---|---|---|---|---|---|
| CFO | 8.3 ± 0.1 | 6.9 ± 0.2 | 5.5 ± 0.2 | 6.9 | 0.13 ± 0.02 | 0.22 ± 0.02 |
| CFO/NFO | 9.5 ± 0.1 | 7.3 ± 0.2 | 6.0 ± 0.2 | 7.7 | 0.15 ± 0.02 | 0.20 ± 0.02 |
| CFO/NiO | 9.6 ± 0.2 | 6.5 ± 0.5 | 5.4 ± 0.2 | 6.9 | 0.19 ± 0.02 | 0.23 ± 0.02 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Omelyanchik, A.; Villa, S.; Singh, G.; Rodionova, V.; Laureti, S.; Canepa, F.; Peddis, D. Magnetic Properties of Bi-Magnetic Core/Shell Nanoparticles: The Case of Thin Shells. Magnetochemistry 2021, 7, 146. https://doi.org/10.3390/magnetochemistry7110146
Omelyanchik A, Villa S, Singh G, Rodionova V, Laureti S, Canepa F, Peddis D. Magnetic Properties of Bi-Magnetic Core/Shell Nanoparticles: The Case of Thin Shells. Magnetochemistry. 2021; 7(11):146. https://doi.org/10.3390/magnetochemistry7110146
Chicago/Turabian StyleOmelyanchik, Alexander, Silvia Villa, Gurvinder Singh, Valeria Rodionova, Sara Laureti, Fabio Canepa, and Davide Peddis. 2021. "Magnetic Properties of Bi-Magnetic Core/Shell Nanoparticles: The Case of Thin Shells" Magnetochemistry 7, no. 11: 146. https://doi.org/10.3390/magnetochemistry7110146
APA StyleOmelyanchik, A., Villa, S., Singh, G., Rodionova, V., Laureti, S., Canepa, F., & Peddis, D. (2021). Magnetic Properties of Bi-Magnetic Core/Shell Nanoparticles: The Case of Thin Shells. Magnetochemistry, 7(11), 146. https://doi.org/10.3390/magnetochemistry7110146










