A Quantum-Mechanical Study of Antiphase Boundaries in Ferromagnetic B2-Phase Fe₂CoAl Alloy

Abstract

In this study, we performed a quantum mechanical examination of thermodynamic, structural, elastic, and magnetic properties of single-phase ferromagnetic Fe${}_2$CoAl with a chemically disordered B2-type lattice with and without antiphase boundaries (APBs) with (001) crystallographic orientation. Fe${}_2$CoAl was modeled using two different 54-atom supercells with atoms on the two B2 sublattices distributed according to the special quasi-random structure (SQS) concept. Both computational models exhibited very similar formation energies (−0.243 and −0.244 eV/atom), B2 structure lattice parameters (2.849 and 2.850 Å), magnetic moments (1.266 and 1.274 ${\mu }_{\mathrm{B}}$/atom), practically identical single-crystal elastic constants ($C_{11}$ = 245 GPa, $C_{12}$ = 141 GPa, and similar $C_{44}$ = 132 GPa) and auxetic properties (the lowest Poisson ratio close to −0.1). The averaged APB interface energies were observed to be 199 and 310 mJ/m${}^2$ for the two models. The studied APBs increased the total magnetic moment by 6 and 8% due to a volumetric increase as well as local changes in the coordination of Fe atoms (their magnetic moments are reduced for increasing number of Al neighbors but increased by the presence of Co). The APBs also enhanced the auxetic properties.

1. Introduction

Ternary X${}_2$YZ materials with Heusler-type crystal lattice [1] include numerous combinations of different chemical elements. Their properties have been very intensively studied [2,3], including their magnetic properties [4,5,6], half-metallic features [7,8,9,10,11], magneto-optical properties [12], topological quantum properties [13,14], and shape memory features [15,16]. Regarding theoretical studies, there are two high-throughput studies conducted by Gilleßen and Dronskowski of 810 different ternary compounds with either the full [17] or inverse [18] Heusler structure.

Our study is focused on Fe${}_2$CoAl belonging to a very promising class of materials based on Fe and Al [19,20,21,22,23,24,25,26]. Earlier experimental studies [27,28,29,30,31,32,33,34,35,36,37] are currently complemented by research efforts related to applications in high-temperature coatings [38,39,40,41,42,43,44] and composites [45,46,47,48,49], new preparation techniques [50,51,52,53] and their material properties [54,55]. Theoretical studies of iron aluminides include ab initio calculations of single-phase materials [56,57,58,59,60,61,62,63,64,65] and nanocomposites [66,67], analyses of their magnetic characteristics [68,69], combined methodological approaches [70,71,72,73], and calculations of properties of defects [74,75,76,77,78,79]. We used a structural model based on the experimental work of Grover et al. [80], where a single-phase Fe${}_2$CoAl has a chemically disordered B2 lattice with one sublattice containing equal amounts of Fe and Co and the second sublattice equal amounts of Fe and Al. We employed ab initio calculations to study properties of both defect-free states and those containing antiphase boundaries (APBs) with (001) crystallographic orientation. APBs are extended defects commonly found in Fe-Al-based compounds [81,82,83,84,85,86] and have also been theoretically studied [87,88,89,90,91,92,93,94,95].

2. Methods

When modeling a partially disordered B2-phase of Fe${}_2$CoAl, we utilized two different 54-atom supercells (see Figure 1a,b) with the atoms on the two sublattices distributed according to the special quasi-random structure (SQS) concept [96] and generated using USPEX software [97,98,99]. The actual stoichiometry of our supercells Fe${}_{27}$Co${}_{14}$Al${}_{13}$ and Fe${}_2$Co${}_{1.037}$Al${}_{0.963}$ slightly deviates from the exact Fe${}_2$CoAl stoichiometry in favor of Co and at the expense of Al, because 54 is not divisible by 4. Cube-shaped 54-atom supercells were chosen as 3 × 3 × 3 multiples of a 2-atom B2 cell. The two models were then doubled along the [001] direction to obtain 108-atom supercells that we refer to as variant 1 and variant 2; see Figure 1c,d. In order to obtain supercells containing APBs, the atoms in the upper parts of these 108-atom supercells were shifted according to the APB-related 〈111〉 shift; see red arrows in Figure 1c,d. One atomic plane was cyclically relocated within the shifted parts of the supercells in order to preserve the stoichiometry; see Figure 1e,f. This construction leads to two different APBs per supercell, and, therefore, averaged APB-related characteristics, such as APB interface energy, are computed. One APB is located in the middle of the supercells shown in Figure 1e,f and the other at the top (its image also appears at the bottom due to the periodic boundary conditions). Both APBs differently change the local coordination of atoms (see below).

Our ab initio calculations were performed employing the Vienna Ab initio Simulation Package (VASP) [100,101] that implements density functional theory [102,103]. For parametrization, we used projector-augmented wave (PAW) pseudopotentials [104,105] and generalized gradient approximation (GGA) developed by Perdew and Wang [106] (PW91) with Vosko–Wilk–Nusair correction [107]. Our setup was chosen as it correctly predicts the ground state of Fe${}_3$Al (a binary variant of Fe${}_2$CoAl) to be the D0${}_3$ structure (its energy is lower than that of Fe${}_3$Al with the L1${}_2$ structure by about 5.5 meV/atom [108]). Our calculations were performed with a plane wave energy cut-off of 400 eV. The product of (i) the number of Monkhorst–Pack k-points and (ii) the number of atoms was equal to 27,648 (e.g., 8 × 8 × 4 k-point mesh in the case of 108-atom supercells in Figure 1c–f). We fully relaxed all studied supercells; i.e., the energy and forces were minimized with respect to atomic positions, cell shape, and volume (forces acting upon atoms were reduced under 0.01 eV/Å). All local magnetic moments of Fe and Co atoms were ferromagnetic. The formation energies discussed below were evaluated with respect to ferromagnetic bcc Fe, ferromagnetic hcp Co, and non-magnetic fcc Al, which were computed with the same cut-off energy and similar k-point densities.

3. Results

Regarding our two 54-atom computational models of B2-phase Fe${}_2$CoAl, their computed thermodynamic, structural, and magnetic properties are listed in

Table 1. Calculated formation energy $E_{\mathrm{f}}$, volume per atom V, a two-atom B2 lattice parameter $a^{\mathrm{B}2}$, tetragonality ratio $c/a$ (the lattice parameter c is perpendicular to the APB interfaces), magnetic moment $\mu$ per atom, and the averaged APB interface energy $\langle {\gamma }^{\mathrm{APB}}\rangle$ for supercells with APBs.

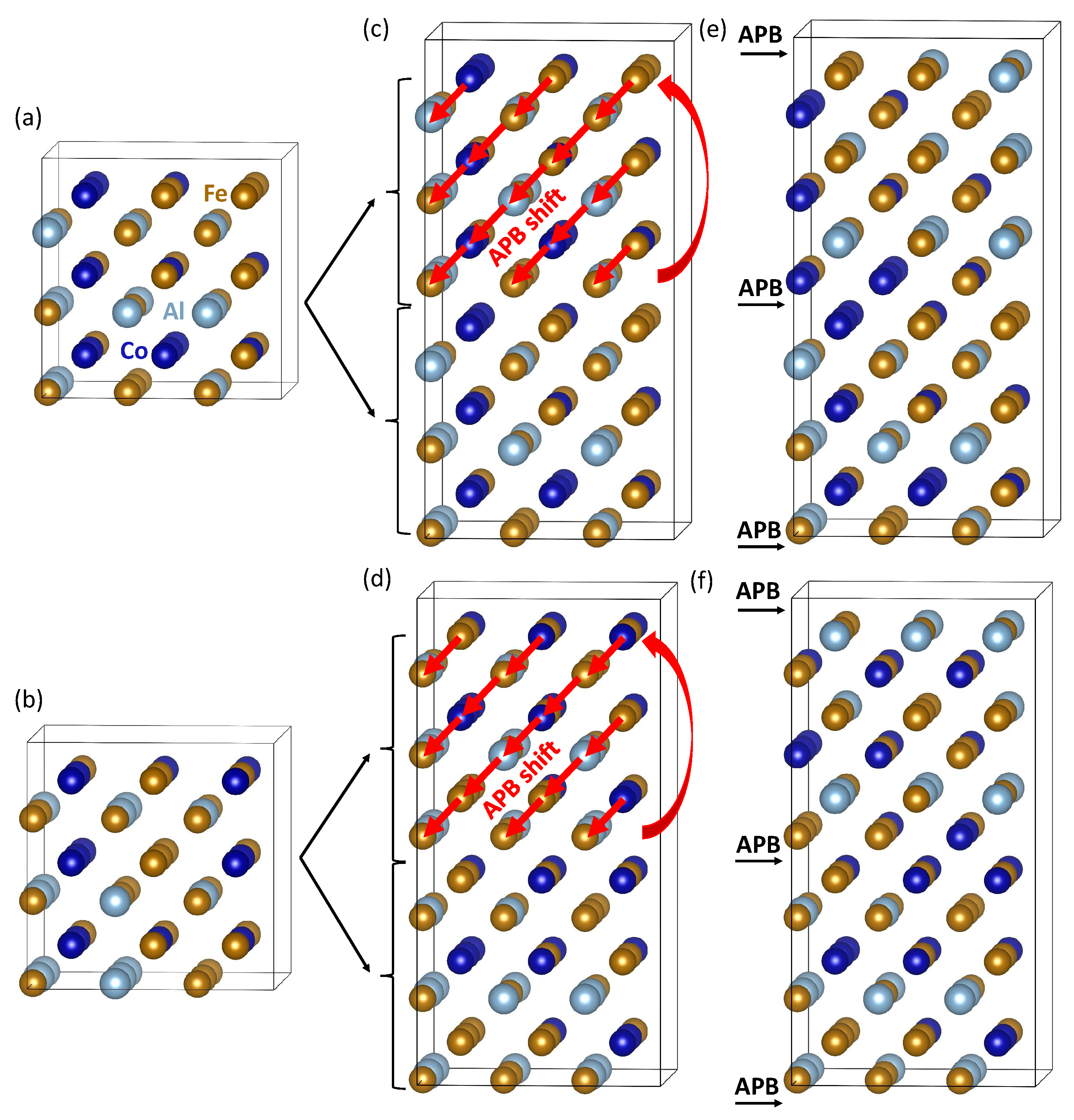
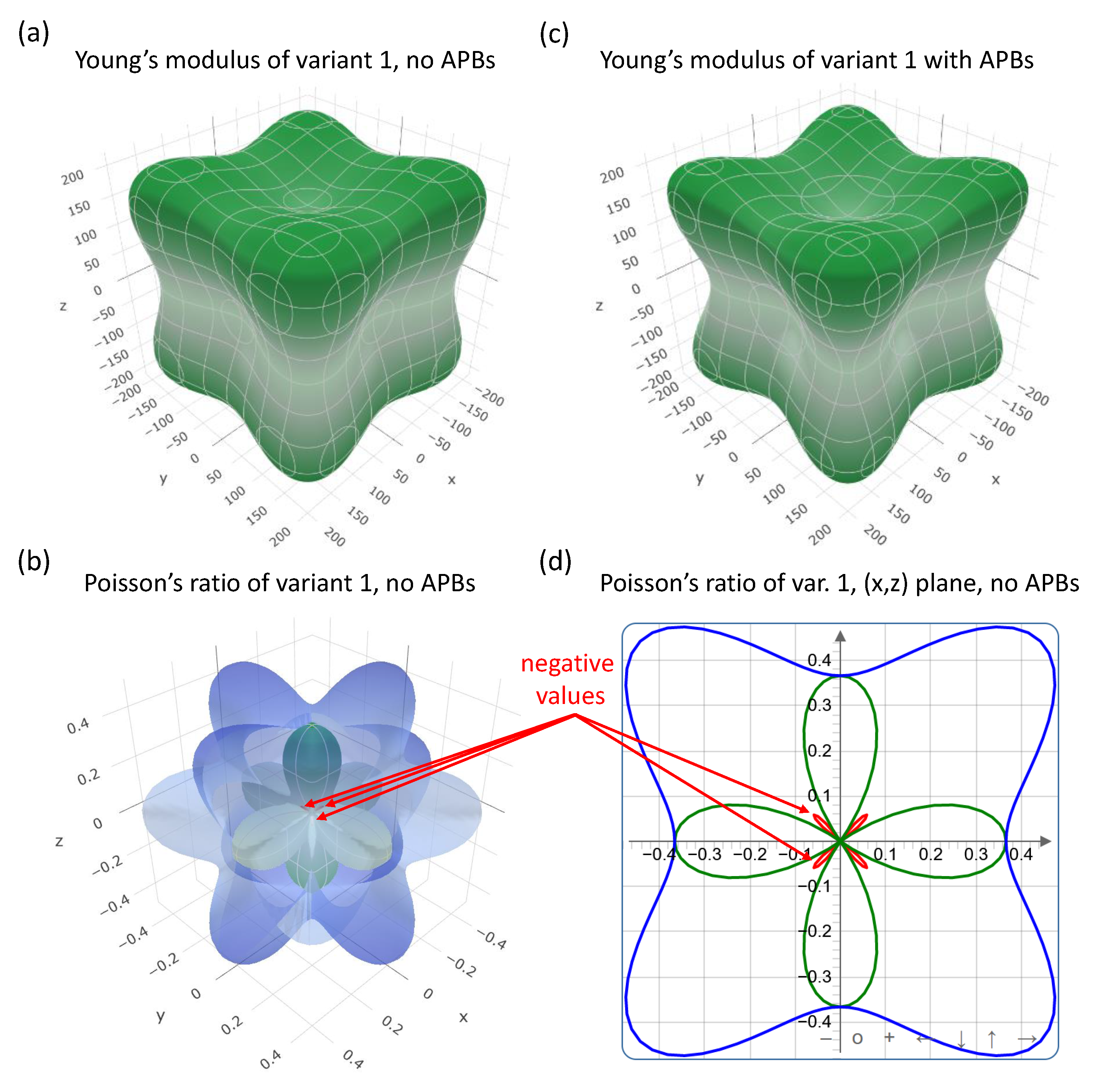
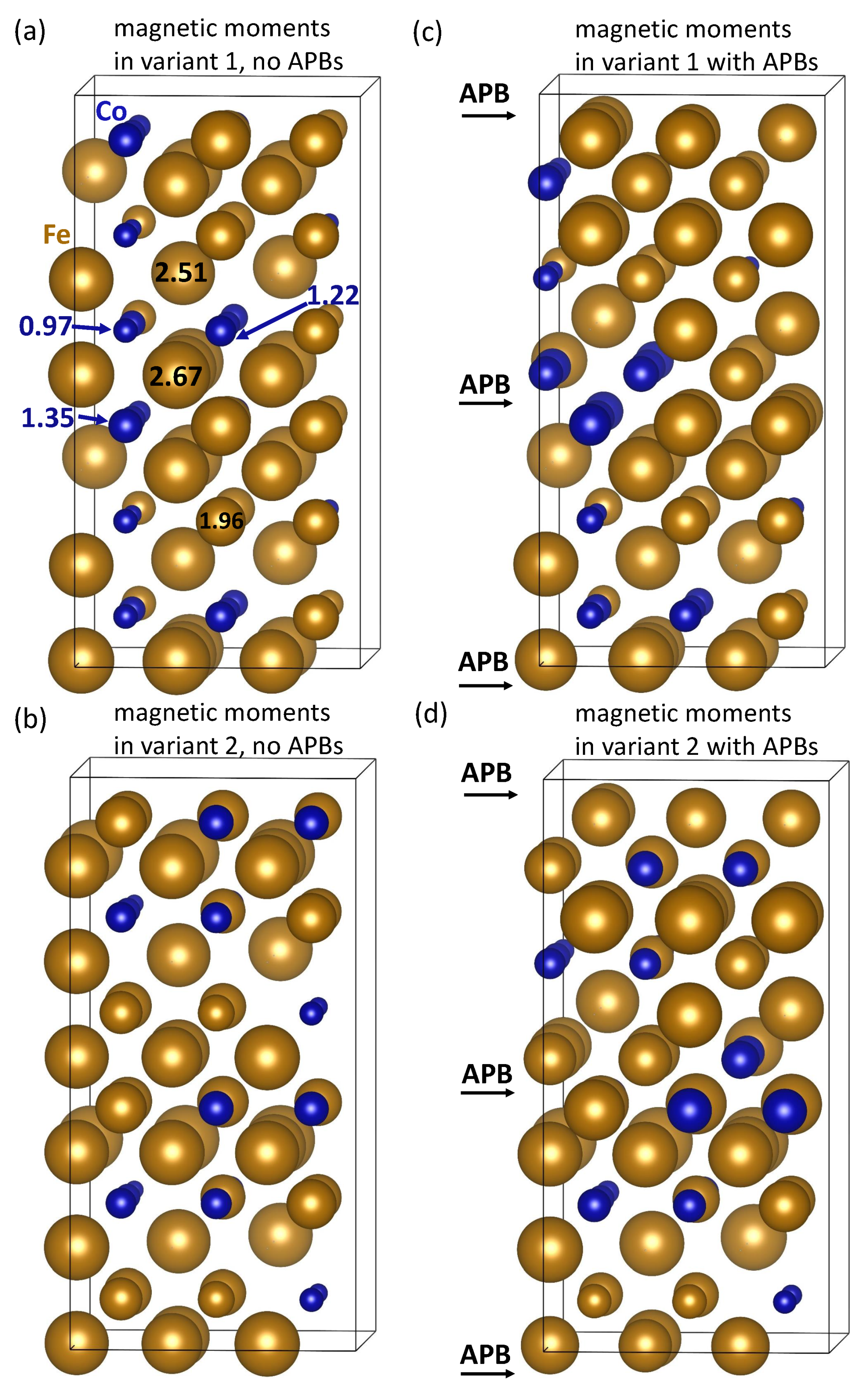
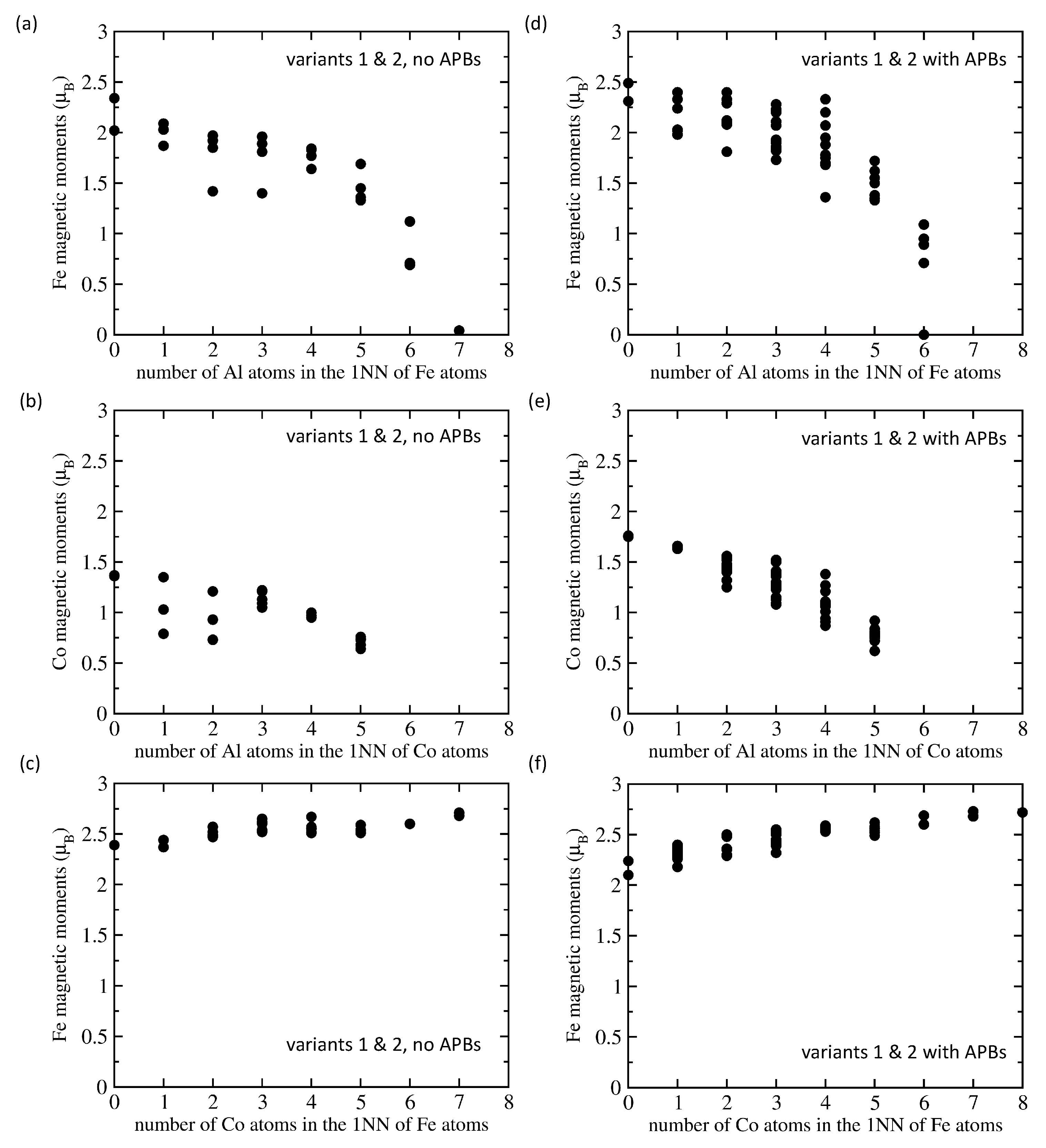
Structure	${\mathit{E}}_{\mathbf{f}}$	V	${\mathit{a}}^{\mathbf{B}2}$	$\mathit{c}/\mathit{a}$	$\mathit{\mu }$	$\langle {\mathit{\gamma }}^{\mathbf{APB}}\rangle$
	eV/atom	Å${}^3$/atom	Å		${\mathit{\mu }}_{\mathbf{B}}$/atom	mJ/m${}^2$
var. 1 no APBs	−0.243	11.56	2.849	1.000	1.266	—
var. 1 with APBs	−0.226	11.65	—	1.011	1.344	199
exp. A2-phase [112]	—	11.77	2.866	1.000	1.18–1.23	—
var. 2 no APBs	−0.244	11.58	2.850	1.000	1.274	—
var. 2 with APBs	−0.218	11.72	—	1.006	1.380	310

. The formation energies of both variants are very similar, −0.243 and −0.244 eV/atom, despite the apparently very different distribution of atoms (see Figure 1a,b), and we interpreted our findings as a proof of the quality of the used computational models. The above discussed formation energy is very close to that obtained in our previous study [109] (−0.269 eV/atom) for a smaller 16-atom supercell with partly disordered B2-phase sublattices. A small difference between the values is likely due to the fact that the 16-atom supercells used in our previous studies [109,110] allowed us to capture the exact Fe${}_2$CoAl stoichiometry, while the 54-atom supercells used in the current study are slightly off-stoichiometric Co-rich Fe${}_2$Co${}_{1.037}$Al${}_{0.963}$ materials as mentioned above. The 16-atom supercells are, on the other hand, quite small for proper modeling of disordered systems, their tensorial elastic properties in particular [111], and this is why we used larger supercells in our current study. B2 structure lattice parameters (2.849 and 2.850 Å), and magnetic moments (1.266 and 1.274 ${\mu }_{\mathrm{B}}$ per atom) of these two models are very similar and in agreement with experimental values (that are unfortunately available only for a completely disordered A2 phase). Table 1 also contains computed properties of systems with APBs. The APB interface energies (averaged over two different APB interfaces) for the two supercells, variants 1 and 2, are equal to 199 and 310 mJ/m${}^2$, respectively.

As far as the structure is concerned, the studied APBs have a multiple effect. First, the volume per atom is increased from 11.56 to 11.65 Å${}^3$ and from 11.58 to 11.72 Å${}^3$ for supercell variants 1 and 2, respectively. Second, the $c/a$ ratio of lattice parameters perpendicular and parallel to the APB interfaces slightly deviates from 1.000 (for a cubic-symmetry system) by 1.1% and 0.6% for variants 1 and 2, respectively.

As far as single-crystal elastic properties are concerned, the calculated values are summarized in

Table 2. Calculated single-crystal elastic constants of variants 1 and 2 as models of Fe${}_2$CoAl with and without APBs. The values of $C_{11}$, $C_{33}$, $C_{12}$, $C_{13}$, $C_{44}$, $C_{66}$, Young’s moduli $Y_{\min }$, $Y_{\max }$, and shear moduli $G_{\min }$ and $G_{\max }$ are given in GPa, and we expect their error bar to be 1–2 GPa. The minimum and maximum values of Y, G, and $\nu$ were obtained using ELATE software [114].

Single-Crystal	${\mathit{C}}_{11}$	${\mathit{C}}_{33}$	${\mathit{C}}_{12}$	${\mathit{C}}_{13}$	${\mathit{C}}_{44}$	${\mathit{C}}_{66}$
Elastic Constants	(GPa)	(GPa)	(GPa)	(GPa)	(GPa)	(GPa)
var. 1 without APBs	244	244	141	141	131	131
var. 1 with APBs	232	228	138	143	134	132
var. 2 without APBs	247	247	141	141	132	132
var. 2 with APBs	234	227	136	141	133	132
	${\mathit{Y}}_{\mathbf{min}}$	${\mathit{Y}}_{\mathbf{max}}$	${\mathit{G}}_{\mathbf{min}}$	${\mathit{G}}_{\mathbf{max}}$	${\mathit{\nu }}_{\mathbf{min}}$	${\mathit{\nu }}_{\mathbf{max}}$
	(GPa)	(GPa)	(GPa)	(GPa)
var. 1 without APBs	141	315	52	131	−0.083	0.626
var. 1 with APBs	117	318	43	134	−0.139	0.728
var. 2 without APBs	145	317	53	132	−0.075	0.614
var. 2 with APBs	120	316	45	133	−0.125	0.715

. It is worth mentioning that the anisotropic elastic properties of our computational supercells as models for a disordered state of Fe${}_2$CoAl are not exactly equal along certain directions, for example, [100], [010] and [001] crystallographic directions. The differences are small, about 1-2 GPa with respect to the values of about 150 GPa. Nevertheless, we used the rigorous mathematical treatment developed by Moakher and Norris [113] to determine the closest cubic-symmetry elastic tensor, and its components are listed in Table 2. As far as our two models for the B2-phase Fe${}_2$CoAl are concerned, the elastic constants $C_{11}$, $C_{12}$, and $C_{44}$ for the two supercells, variant 1 and variant 2, are practically identical (with differences within an expected error bar of our calculations, that is, about 1–2 GPa). The anisotropy of the elastic response is visualized in the form of directional dependencies of the single-crystal Young’s modulus in Figure 2a. Using ELATE software [114] to produce these figures, we also determined the minimum and maximum values of single-crystal Young’s modulus Y, shear modulus G, and Poisson’s ratio $\nu$. Interestingly, our analysis predicts that Fe${}_2$CoAl is an auxetic material; i.e., the Poisson ratio is negative for certain directions of loading—see the negative values of ${\nu }_{\min }$ in Table 2. Figure 2c shows directional dependences of the both maximum and minimum value of Poisson ratio (for details, see Ref. [114]), and Figure 2d visualizes these trends within the (x,z) plane with negative values marked by red colors (selected examples are highlighted by red arrows).

The impact of APBs on elastic properties is minimal. The elastic constant $C_{11}$, as well as $C_{33}$ due to the tetragonal symmetry of the APB-containing systems, is slightly lower (by a few percent), but other elastic constants are nearly unaffected. The impact of APBs on elastic properties is well demonstrated in the case of elastic characteristics of polycrystals. We evaluated them from the single-crystal elastic constants listed in Table 2, employing ELATE software [114] (open-access at http://progs.coudert.name/elate, accessed date 29 September 2021). The values obtained when using Voigt [115], Reuss [116] and Hill [117] homogenization methods are summarized in

Table 3. Polycrystalline bulk modulus B, Young’s modulus Y, shear modulus G, and Poisson’s ratio $\nu$ computed according to Voigt, Reuss, and Hill homogenization methods in the of variants 1 and 2 of Fe${}_2$CoAl with and without APBs as obtained using the ELATE software [114] (open-access at http://progs.coudert.name/elate, accessed date 29 September 2021). The expected error bar of the values of the three moduli (B, Y and G ) is 1–2 GPa.

Polycrystal	B	Y	G	$\mathit{\nu }$
Elasticity	Voigt/Reuss/Hill Values in GPa			Voigt/Reuss/Hill
APB-free var. 1	175/175/175	250/211/231	99/81/90	0.262/0.300/0281
var. 1 with APBs	171/171/171	247/194/221	98/74/86	0.260/0.311/0.285
APB-free var. 2	176/176/176	253/215/234	100/83/92	0.261/0.297/0.279
var. 2 with APBs	170/170/170	247/198/223	98/76/87	0.258/0.306/0.282

, and the APB-related changes are lower than 10%.

Importantly, the magnetic moments of APB-containing systems are higher by 6 and 8% for variants 1 and 2, respectively, when compared with their corresponding APB-free states; see Table 1. This increase in magnetism can be partly explained by the above-discussed increase in volume (magneto-volumetric effects), but there are other active mechanisms that require attention (see below).

4. Discussion

The enhancement of magnetism due to the studied APBs is significantly more complex at the level of individual atoms. It is schematically shown in Figure 3, where the atoms are represented by spheres with diameter scaling the magnitude of the local magnetic moments. In order to understand these complex states, it is worth discussing the impact of APBs on sublattices within the B2 phase of Fe${}_2$CoAl. This phase contains (according to Grover et al. [80]) one disordered sublattice with equal amounts of Fe and Co atoms and another disordered sublattice with equal amounts of Fe and Al atoms. Schematically we can decompose the chemical formula of Fe${}_2$CoAl into another one that reflects these sublattices, Fe${}_2$CoAl = (Fe,Co)(Fe,Al). In a state without APBs, the atoms at one sublattice represent the first nearest neighbors (1NN) of atoms from the other sublattice, but the studied APBs change it. At the APB interface in the middle of Figure 1e,f, the atoms at the (Fe,Co) sublattice have newly half of their 1NN atoms from the same (Fe,Co) sublattice.

Similarly, at the APB interface at the top/bottom of Figure 1e,f, the atoms at the (Fe,Al) sublattice are coordinated by the atoms from the same sublattice as one half of their 1NN shell. The change in the chemical composition of 1NN shell is essential for the magnetism of atoms. Figure 4 shows the local magnetic moments of either Fe or Co atoms as functions of the number of either Al or Co atoms in the 1NN shell. The local magnetic moments of Fe and Co atoms mostly decrease with an increasing number of Al atoms in their 1NN shell (see Refs. [69,75,94]). On the contrary, the magnetic moments of Fe atoms mostly increase with the increasing number of Co atoms in the 1NN shell of Fe atoms. While it is hard to extract clear trends from Figure 4, the visualized APB-related changes in the coordination of magnetic atoms also contribute into the increase in the total magnetic moment.

5. Conclusions

We performed a first-principles study on thermodynamic, structural, elastic, and magnetic properties of single-phase ferromagnetic Fe${}_2$CoAl with a chemically disordered B2-type lattice with and without antiphase boundaries (APBs). Following experimental work of Grover et al. [80], Fe${}_2$CoAl was modeled by two different 54-atom supercells with atoms on the two B2 sublattices distributed according to the special quasi-random structure (SQS) concept. Both models have very similar formation energies (−0.243 and −0.244 eV/atom), B2 structure lattice parameters (2.849 and 2.850 Å), magnetic moments (1.266 and 1.274 ${\mu }_{\mathrm{B}}$ per atom), practically identical elastic constants ($C_{11}$ = 245 GPa, $C_{12}$ = 141 GPa and $C_{44}$ = 132 GPa), and similar auxetic properties (the lowest Poisson ratio around −0.1). The APB interfaces have (001) crystallographic orientation and are characterized by a shift in the lattice along the 〈111〉 crystallographic direction. The averaged APB interface energies were found to be 199 and 310 mJ/m${}^2$ for the two models, and the difference between the two values clearly illustrates the sensitivity of the APB interface energy to the local atomic configuration at the interface. The studied APBs increased the total magnetic moment by 6 and 8% when compared with their corresponding APB-free states. This increase can be partly explained by differences in the volume and partly by rather complex APB-related changes in the coordination of magnetic atoms in the studied disordered system. In particular, we noted that the magnetic moment of Fe atoms was reduced by an increasing number of Al first nearest neighbors but was increased by the presence of Co first nearest neighbors. The APBs also enhanced the single-crystal auxetic properties when the minimum Poisson ratio was more negative due to the presence of APBs (changed from −0.083 to −0.139 and from −0.075 to −0.125 for variants 1 and 2, respectively).