Abstract
In this review, the technique of resonant soft X-ray reflectivity in the study of magnetic low-dimensional systems is discussed. This technique is particularly appealing in the study of magnetization at buried interfaces and to discriminate single elemental contributions to magnetism, even when this is ascribed to few atoms. The major fields of application are described, including magnetic proximity effects, thin films of transition metals and related oxides, and exchange-bias systems. The fundamental theoretical background leading to dichroism effects in reflectivity is also briefly outlined.
1. Introduction
X-ray reflectivity is typically applied in the hard X-ray regime to study the interface morphology of layered materials by exploiting the charge density contrast between adjacent layers [1]. Synchrotron X-ray sources have made it possible to scan the photon energy at resonance, in correspondence with specific elemental absorption edges, so as to add to the technique both additional layer-resolved selectivity and sensitivity to the chemical and electronic structure [2,3,4,5,6,7]. In particular, in the soft X-rays, the L2,3 edges of 3d transition metals and the M4,5 edges of rare earths become accessible, which carry fundamental information on the magnetic properties thanks to their pronounced magnetic circular dichroism effects [8].
Resonant soft X-ray magnetic scattering (or reflectivity) has advanced following the great success of X-ray magnetic circular dichroism (XMCD) in absorption, and permits one to disentangle the spin and orbital contributions to magnetism with elemental specificity [8]. XMCD in absorption is typically carried out on ultrathin films, since the information depth is limited to a few atomic layers. This limitation is due to the attainment of the magnetic-dependent absorption coefficient by measuring the electronic yield from the sample following its interaction with the X-ray beam. Therefore, the probed depth is limited by the inelastic mean free path of the outgoing electrons.
Basically, as the penetration depth of X-ray photons is much larger than that of the electrons, reflectivity contains all information at the origin of XMCD in absorption, but it also carries precious quantitative information on buried layers, buried interfaces, and morphology. In fact, in most typical cases, resonant soft X-ray magnetic reflectivity (RSXMR) is applied to derive magnetic depth profiles in layered materials. On the other hand, the intimate interplay between optical, magnetic, and structural properties may complicate considerably the experimental signal, especially across absorption edges where the optical constants present huge variations within photon ranges of a few eV. This may also be convenient in some cases, since by precise tuning of the photon energy one can emphasize (or mask) the information pertaining to selected layers or buried interfaces. In any case, in order to extract useful information from the experimental data, a simulation of the optical response is mandatory. This requires knowledge (or estimation) of the complex optical constants of the (anisotropic) materials, including magnetic effects and the layered structure of the system. These quantities are most often derived on the basis of best fits to the experimental data.
It should be noted that studies using RSXMR can be divided into two groups: (i) those that privilege angular scans at fixed, selected photon energies across and outside specific elemental absorption edges, and (ii) those that privilege energy scans across the edges at fixed, selected angles. These two visions typically reflect the ‘cultural’ origin of the experimental teams involved, with prominent expertise in either structural studies through diffraction techniques or in the investigation of electronic properties through spectroscopy. These two visions actually converge in exactly the same physics and phenomenology, and should simply be seen as two sides of the same coin.
The origin of the magneto-optical response can be ascribed to the different density of free states (holes) for spin-up and spin-down electrons in the valence-band due to Stoner splitting in a magnetized solid [9,10]. Absorption and resonant scattering of radiation depend on the polarization state and its relative orientation with respect to the direction of magnetic moments. Investigation of the ferromagnetic state of transition metals through XMCD and RSXMR measurements that use circularly polarized radiation with a photon energy tuned on absorption edge is most common [9]. In the analysis of resonant X-ray reflectivity measurements, the response of the system is conveniently described by a macroscopic (relative) dielectric tensor that connects the displacement vector and the electric field through the constitutive relation , with being the vacuum permittivity. If we look for a solution in the form , where is the complex wavevector and is the angular frequency of the radiation, the wave equation in the medium is written in matrix form [11,12,13,14]:
where is a 3×3 tensor of components and is the unitary matrix.
The investigated sample is usually a multilayer composed of slabs with different chemical compositions and/or different magnetic moments, each having thickness . Two adjacent slabs are separated by a horizontal plane interface with root-mean-square (rms) roughness . The electromagnetic fields propagating into the multilayer can be calculated imposing the boundary conditions at the interfaces for the electric and magnetic field of the electromagnetic radiation.
In order to simulate the reflectivity signal, a reasonable structural model—to later be refined through fitting—is a prerequisite. The propagation of the light beams in the layered system should then be simulated. The ‘simplest’ approach may be based on isotropic homogeneous layers with homogeneous magnetization. In this case, the Parrat formalism [15] is often used to simulate the reflectivity. Anisotropic materials can be treated and more refined results can be obtained applying the 4×4 matrix method [16,17,18,19,20,21,22,23,24,25,26], where each layer is considered anisotropic and described by a suitable dielectric tensor. Since the chemical (compositional) depth profile can be different from the magnetic profile, two independent structural models could be necessary in order to simulate the chemical contrast and magnetic responses.
In this review, we do not aim to be exhaustive but to give the interested reader a concise picture of the capabilities of the technique and its fields of application.
2. Methods
2.1. Experimental Setup
RSXMR requires photon tunability and circular (or elliptical) polarization of the light beam. This requires synchrotron radiation. RSXMR is typically carried out either on bending magnet beamlines, where elliptical polarization is obtained by selecting angular portions of the photon beam above or below the synchrotron ring orbital plane, or on beamlines equipped with insertion devices capable of circular polarization.
An example of the first type of beamline is shown in Figure 1a. This refers to the BEAR beamline [27,28,29] at the Elettra synchrotron radiation facility in Italy. The beamline operates in the photon energy range between 3 and 1600 eV. A polarization selector consisting of movable slits is positioned at the beginning of the beamline, just before the first optical element (parabolic mirror P1). It permits one to select the light polarization status: linear, by selecting the central portion of the beam, or left/right circular (elliptical), by moving the slit’s aperture above/below the orbital plane.
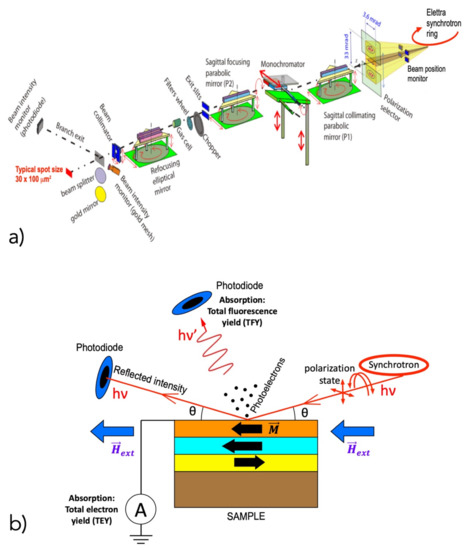
Figure 1.
(a) Layout of the BEAR bending magnet beamline at Elettra (Trieste, Italy) [27,28,29]; (b) scheme of a specular reflectivity experiment with indication of the external magnetic field and the magnetization in different layers. Note that the direction of may change from layer to layer.
A scheme of a typical (specular) reflectivity experiment is presented in Figure 1b: a magnetic field is applied parallel to the sample plane, inducing magnetization in the different layers/materials that compose the sample; the magnetizer is generally designed to permit experiments either in remanence magnetization or in applied field, depending on the specific type of investigation; the reflected intensity is measured with a photodiode; the sample and photodiode can be rotated independently around an axis perpendicular to the incoming beam and parallel to the sample surface to achieve θ–2θ scattering geometries; rotations of the sample and detector are typically realized through coaxial high-precision rotation stages (goniometers) equipped with differential pumping to guarantee UHV during measurements; and X-ray absorption experiments are often carried out at the same time by measuring the drain current or the emitted photoelectrons (total/partial electron yield mode) and/or by measuring the fluorescence photons (fluorescence yield mode) while the photon energy is scanned.
2.2. Origin of the Magnetic Dichorism Effect
The magnetization breaks the inversion symmetry of the system, introducing an antisymmetric term in the dielectric tensor . It is possible to demonstrate [11,30] that, for a system that should be optically isotropic in the absence of magnetization, if is directed along the axis, the dielectric tensor becomes:
In general, the elements of are complex numbers. If we consider a second-order expansion in for the elements of the tensor, the off-diagonal term is written as , while the diagonal terms are given as and , where is the electric permittivity with null magnetization and and are the first- and second-order magneto-optic coefficients, respectively. In X-ray spectroscopy, the antisymmetric and off-diagonal elements and are responsible for the XMCD effect and the dichroic reflectivity observed in RSXMR measurements when circular or elliptical polarization are employed. The additional terms of the diagonal depend on and are responsible for the X-ray magnetic linear dichroism (XMLD) that furnishes complementary information to XMCD and are used, in particular, in the study of antiferromagnetic materials [9] with . The second-order expansion in is exact for systems with spherical symmetry, whereas, in cubic crystals, higher-order terms are present. The off-diagonal and diagonal elements of are odd and even functions of , respectively [30].
When the radiation propagation direction is parallel to the magnetization direction (the axis), it can be shown that the wave equation has as solutions, i.e., polarization eigenstates, the left () and right () circularly-polarized radiation [11] corresponding to the values of refractive index given by:
This is intimately related to two different values of the absorption coefficient , which are responsible for dichroism in X-ray absorption, measured through XMCD. Dichroism is given, in this case, by:
Absorption measurements with opposite photon helicity provide the two absorption coefficients () and () as a function of the photon energy , or equivalently, the imaginary part of the two refractive indices . Defining the average and dichroic refractive index, from the experimentally measured imaginary parts and , the real parts and are calculated through Kramers–Krönig relations [31,32].
The real and imaginary parts of the refractive index can then be used to compute the dielectric tensor and to derive the specular reflectivity (and related dichroism) according to the procedure described by us in [25].
3. Applications
In this section, a series of examples of the main applications of RSXMR are presented. As indicated above, we do not aim to be exhaustive, but to give the interested reader a concise picture of the capabilities of this technique and its major fields of application.
3.1. First Studies
The first applications of RSXMR focused on metallic single crystals, thin films, and multilayers. The magneto-optical response was tested using circularly as well as linearly polarized light, identifying in both cases a marked difference in the reflectivity signal upon the reversal of the external magnetic field applied to the sample or after changing the polarization of the incident beam. Different approaches based on scattering theory or the Maxwell equations have been used in the interpretation of the experimental data. A substantial equivalence was obtained. The sensitivity of the technique to different atomic elements, together with the structural and morphological information provided by the interference effects, demonstrated the significant potential of resonant X-ray reflectivity in the study of complex magnetic heterostructures.
The sensitivity of X-ray resonant reflectivity with linearly polarized light was investigated by C. Kao and co-workers [33] on an Fe single crystal immersed in an external magnetic field (Figure 2a). A large asymmetry was observed at the L absorption edge upon switching the field polarity. The asymmetry signal was much larger compared with other conventional techniques based on the Kerr effect or photo-absorption with circularly polarized light, thus confirming the high potential of reflectivity in studying the magnetic properties of materials. C.-CX. Kao et al. applied RSXMR at Co L2,3 edges to a magnetic multilayer structure made of GaAs/ZnSe/Fe/Co/Al2O3 [34] (Figure 2b). The relevant changes in dichroic reflectivity observed by varying the angle of incidence were successfully interpreted in terms of interference effects due to the multilayer structure, using the classical electromagnetic theory. J.B. Kortright et al. [35] demonstrated the equivalence of the classical approach, based on the solution of the Maxwell equations, and the theory of resonant atomic scattering in the interpretation of the resonant X-ray magneto-optical transmission and absorption measurements; they applied their formalism to the study of Fe layers grown on SiNx membranes and capped with a SiC thin film. An Fe/C multilayer was extensively investigated by H-Ch Mertins and co-workers [36] by means of X-ray resonant reflectivity at Fe L2,3 edges using linearly and circularly polarized light, thereby obtaining the magnetic contribution to the Fe optical constants. M. Sacchi et al. [37] reported the complete determination of the Fe dielectric tensor, and in particular of its off-diagonal terms, by combining resonant X-ray absorption (Figure 2c). The same approach was also successfully adopted to study the magnetic properties of a Ni(110) single crystal using linear and circular polarized light [38]. The magnetic properties related to Fe and Mn atoms in Ir/Fe0.9Mn0.1/Ir and Ir/Fe0.7Mn0.3/Ir multilayers were investigated by J.M. Tonnere et al. [39] using RSXMR at the Fe and Mn L2,3 absorption edges, exploiting a transverse geometry; this allowed them to measure the very low magnetic moment of Mn, which was found to be equal to 0.2 µB.
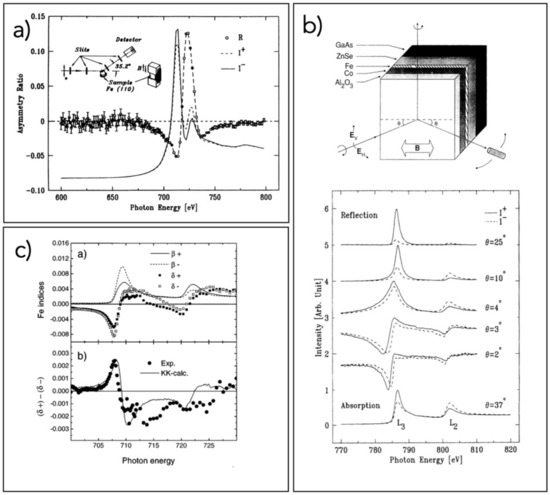
Figure 2.
(a) Specular reflectivity in p–polarized light on an Fe film of 35 Å, with magnetic field applied perpendicular to the scattering plane; the reflectivity curves obtained with opposite fields and the asymmetry ratio R are shown; the asymmetry ratio is particularly pronounced across the Fe 2p absorption edge (reprinted figure with permission from [33]. Copyright (1990) by the American Physical Society); (b) scattering geometry on a GeAs/ZnSe/Fe/Co/Al2O3 multilayer and dichroic reflectivity curves at different grazing angles; the dichroic absorption at the Co edge is also shown (reprinted figure with permission from [34]. Copyright (1994) by the American Physical Society); (c) imaginary part (β) and decrement of the real part (δ) of the complex refractive index at the Fe 2p edge obtained by coupling absorption and reflectivity at resonance and at the Bragg angle from a Fe/V superlattice (+ and − signs refer to opposite magnetizations) and comparison between δ+–δ- and the Kramers–Krönig (KK) transformation of β+−β− (reprinted figure with permission from [37]. Copyright (1998) by the American Physical Society).
3.2. Magnetic Proximity Effects
Circular dichroism revealed through X-ray reflectivity has been used extensively to study multilayers formed by the repetition of ferromagnetic and nonmagnetic thin films. These systems present relevant technological properties, with their electrical resistance being strongly affected by the relative magnetization of the adjacent layers. In particular, these heterostructures can exhibit the so-called tunnel magnetoresistance (TMR) and giant magnetoresistance (GMR) effects, exploited in the fabrication of compact high-performance digital memories and magnetic sensors. Specifically, when two magnetic layers separated by a nonmagnetic stratum present the same magnetization direction, the probability that an electron travels across the structure is maximum, whereas in the opposite configuration the probability is negligible. These multilayer systems show important interface effects related both to the modification of the bulk crystal structure, due to the lattice mismatch between layers of different composition, and to the direct role of the interface electronic orbitals. Due to its chemical specificity, RSXMR can be successfully used to study separately the magnetic behavior of the different elements. In addition, at grazing incidence, the interface effects can be strongly emphasized. In this way, it is possible to obtain information on the detailed magnetic profile, which provides a diagnostic tool for layer thickness optimization during growth. Magnetization due to the direct orbital hybridization at the interface between ferromagnetic and nonmagnetic layers has been widely observed.
M. Abes et al. [40] studied the magnetization of Mn and Cu in a [Co/Cu(x)/CuMn/Cu(x)] multilayer by varying the thickness, x, of the copper layer. Magnetization was induced in the CuMn diluted alloy due to its proximity to the ferromagnetic Co layer. It was found that the Mn spin polarization increased by decreasing the copper interlayer thickness, demonstrating the interfacial nature of the Mn and Cu magnetization. In particular, Mn changed its coupling with the Co magnetic moment from antiferromagnetic to ferromagnetic as a function of the distance from the Co layer.
A [Fe70Co30/Pd]n multilayer was characterized by N Awaji et al. [41], who found an enhancement of Fe and Co spin polarization in a region adjacent to the Pd layer with a thickness of about four atomic monolayers, in contrast to a reduction in the magnetization at the immediate interface, which was associated with atomic intermixing. RSXMR also evidenced magnetization proximity effects in Pt and Ir buffer layers that were used to study the interfacial Dzyaloshinskii–Moriya interaction (an antisymmetric exchange interaction between two neighboring magnetic spins, favoring spin canting [42,43]) in Co2FeAl thin films, as reported by M. Belmeguenai et al. [44]. A magnetization of Pt at the interface with Co in a Pt/Co bilayer was detected using angle resolved X-ray resonant magnetic reflectivity by J. Geissler et al. [45]. The resultant magnetic moment was mainly localized to within 1 nm of the Pt layer at the Pt/Co interface (Figure 3a). The magnetization of Pt grown on ferromagnetic Fe and Co33Fe67 layers was also studied by D. Graulich et al. [46]. An induced magnetization was even detected in Au films in contact with ferromagnetic materials: the magnetization in Au in a Fe/Au bilayer and in an Fe/Au/Fe trilayer was investigated by N. Hosoito et al. [47] at the Au L3 edge and a detailed magnetic depth profile was obtained. It was found that the induced magnetization in Au was pronounced close to Fe interfaces and reduced in the interior of the Au layer, with an attenuation length longer than 15 Å. Fe/Ce/La/Ce, Fe/La/Ce/La, and Fe/CeH2-δ multilayers were studied by N. Jaouen et al. [48] to highlight the magnetization inside the Ce layers. An antiferromagnetic coupling of α-like Ce with Fe was observed (Figure 3b) in Fe/Ce/La/Ce and Fe/La/Ce/La structures. Magnetization extended unexpectedly inside the Ce layer. This behavior was ascribed to the strain induced in Ce in the α-like phase. On the other hand, an Fe/CeH2-δ multilayer, where Ce was in the γ-like phase, revealed a strongly localized magnetization at the interface with Fe. In relation to spintronic devices, a Pd/Co/Pd trilayer was investigated by D.-O. Kim et al. [49] to measure the Pd magnetic polarization induced by Co. The main effects were localized at the two interfaces between Co and Pd, but the induced magnetization was strongly enhanced at the top Co/Pd interface with respect to the bottom Pd/Co interface. Interestingly, this anisotropic proximity effect was not found to be correlated to a different morphological or physical structure of the two interfaces. The behavior of spin polarization across a Pt layer coupled in a planar heterojunction with different ferromagnetic materials was studied using RSXMR by C. Klewe et al. [50]. Quantitative interpretation of the experimental data was given following an ab initio approach. Higher magnetization in Pt was found for Pt/Fe heterojunctions, while smaller values were obtained by coupling Pt with Ni. Using the ReMagX software [3,51], Krieft et al. [52] presented and discussed different strategies and iterative optimization approaches to fit X-ray reflectivity spectra of ferromagnet/Pt layered structures. If and represent the intensities of reflectivity collected with right and left circular polarization, respectively, the fitting of the average spectra provides the density depth profile of the different elements; therefore, the thickness and roughness of the various layers can be derived. This structural model is then used to fit the asymmetry ratio , which gives the spin polarization depth profile of the magnetic species. This scheme of analysis can be applied as a very general approach to fitting the spectra obtained in magnetic reflectivity experiments [49]. Proximity effects have also been observed in Pt/Fe bilayers [53] and were compared with Pt/NiFe2O4 to verify the presence of anomalous Nernst interfacial effects. The results obtained by fitting the RSXMR measurements were compared with ab initio calculations, revealing the presence of an enhancement of the interfacial magnetization only in the Pt/Fe system, which excluded a role of the interface in the Seebeck effect observed in Pt/NiFe2O4.
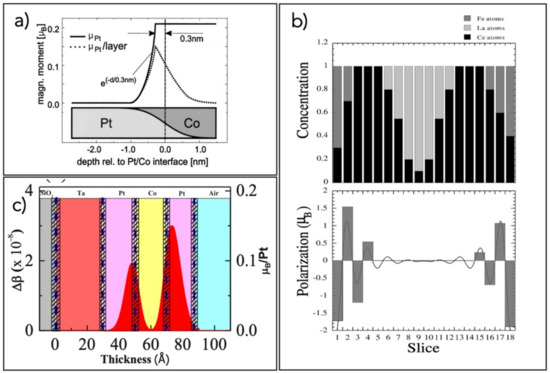
Figure 3.
(a) Profile of the magnetic polarization induced per Pt atom (straight line) and per layer (dotted), together with the chemical profile of a Pt/Co interface (at the bottom) (reprinted figure with permission from [45]. Copyright (2001) by the American Physical Society); (b) profile of the Ce atomic concentration (upper part) and of the Ce 5d induced polarization (lower part) in a CeLaCe/Fe multilayer (reprinted figure with permission from [48]. Copyright (2002) by the American Physical Society); (c) magneto–optic depth profile of a Ta/Pt/Co/Pt heterostructure; red curves denote the in-depth distribution of the spin–polarized Pt atoms; the dashed lines indicate the corresponding interface positions; and the dashed rectangles between the layers indicate the corresponding interlayer roughness (reprinted figure with permission from [55]. Copyright (2020) by the American Physical Society).
A Pt/Co/Ta trilayer was extensively studied by A. Moskaltsova et al. [54]. The magnetization profile of the Pt layer was extracted for different sequences of Pt, Co, and Ta films in the trilayer heterojunction. A spin polarization due to proximity was found only for those configurations in which Pt was in contact with Co, excluding a significant role of Ta. Ta was also used as a buffer layer to study the profile and entity of the magnetic coupling between Pt and Co by A. Mukhopadhyay et al. [55] and the induced magnetization profile in the Pt layer was quantitatively determined (Figure 3c). The role of proximity effects in the interfacial Dzyaloshinskii–Moriya interaction stabilizing Nèel domain walls in magnetic materials was investigated with RSXMR at the Pt L3 edge in a Pt/Co/Au,Ir/Pt structure, where Au and Ir played the role of spacers [56]. Results indicated a clear dependence of proximity-induced spin magnetization in Pt on the thickness of the spacer layers, together with a change in the organization of the magnetic domains, which was explained in terms of the interfacial Dzyaloshinskii–Moriya interaction. This last effect was also observed for greater thicknesses of the spacer layers, where the proximity effect was no longer present. R. M. Rowan-Robinson et al. [57] also used polar magneto-optical Kerr effect magnetometry to study the current-induced magnetization reversal in a Pt(5 nm)/Co(0.6 nm)/Pt(5 nm) trilayer designed to have weak perpendicular magnetic anisotropy. The magnetization reversal was observed for very low critical current density; this was related to the low anisotropy in perpendicular spin magnetization between the Co and Pt layers together with a low saturation value of magnetization. RSXMR was applied by L. Sève et al. [58] to investigate the magnetization of Ce and La in Ce/Fe and La/Fe multilayers as a function of the film thickness. The results obtained for La showed a clear proximity-induced magnetization localized mainly at the interface with the Fe film, while the amorphous structure of Ce grown on Fe induced a complex magnetic organization inside the Ce film: the magnetization extended across all of the Ce film with an oscillating behavior. Femtosecond laser pulses were applied by W. Szuszkiewicz et al. [59] to induce changes in the spin polarization at the interface in Pt/Co/Pt trilayers. X-ray reflectivity measurements indicated a rearrangement of interface magnetization from in-plane to out-of-plane after laser irradiation. This change was found to be irreversible and was related to the formation of a structural variation activated by the laser that produced a Pt-Co alloy at the Pt/Co interface.
3.3. Transition Metal Oxides
Due to the wide application possibilities in spintronic devices and the variety of compounds with specific magnetic properties, transition-metal oxides in the form of thin films or layered stacks likely represent the class of magnetic systems most studied with RSXMR. In particular, the interplay between electronic, magnetic, and structural properties—including interface effects—plays a fundamental role in different important, possibly interconnected, phenomena such as superconductivity, topological insulating phases, ferroelectricity, and ferromagnetism. Indeed, with its magnetic depth-, chemical depth-, and electronic state-profiling capabilities, RSXMR represents a unique instrument for the investigation of these systems.
Much work has been dedicated to manganites, whose magnetic properties are strictly related to their chemical composition and structural order, which in turn can be strongly influenced by lattice distortions, especially when the oxides are epitaxially grown on suitable crystalline templates. Coordination of oxygen sites can be varied thanks to epitaxial-growth strategies at the interfaces between materials in layered stacks, leading to a change of p-d hybridization, with strong influence on the magnetic behavior [60]. Rotation of the in-plane magnetic easy axis has been observed in manganite heterostructures by tailoring the interface oxygen network with a suitable choice of substrate [61] (Figure 4a). Complex magnetic structures have been detected (Figure 4b), such as the presence of a magnetic helix state in the LaNiO3 layers in manganite-nickelate superlattices [62], with Ni-O ligand hole states from LaNiO3 that are mostly filled due to electron transfer from interfacial Mn. Intermixing at the monolayer scale allows for control of charge transfer and induced magnetic moment in the nickelate layer [63], and antiferromagnetic order can be induced and stabilized in LaNiO3 by interfacial coupling [64]. Metal or insulator phases, or their coexistence, and temperature-induced transitions have been observed in perovskite manganite superlattices [65]. In bilayer manganites, it was demonstrated that only the outermost Mn–O bilayer exhibits no long-range ferromagnetic order, whereas the next bilayer displays the full spin polarization of the bulk [66]. A temperature-dependent magnetic dead layer was observed at air-exposed LSMO surfaces [67], which may be related to the reduced magnetization present at the junction of manganite-based magnetic tunnel junctions, deteriorating the performance of these devices.
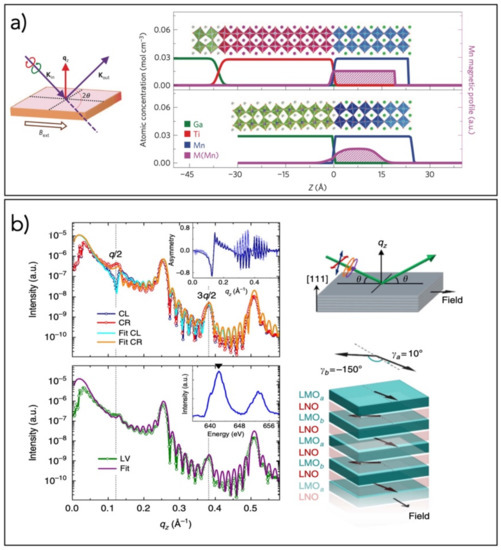
Figure 4.
(a) Atomic concentration depth profiles of Ga, Ti, Mn (green, red, and blue lines, respectively), and Mn magnetization (M, purple line with shaded area) obtained at 20 K on LSMO films with (top panel) and without (bottom panel) a STO buffer layer; the panel on the left shows the experimental geometry, where a 0.6 T magnetic field was applied in-plane along the magnetic easy axis during the measurement (reprinted with permission from Springer Nature, Nature Materials, [61], Copyright (2016)); (b) from [64]: top left, reflectivity for circularly left (CL, blue line) and right (CR, red line) polarized light taken on a LaNiO3/LaMnO3 superlattice; inset, extracted asymmetry ratio (CR−CL)/(CR + CL); bottom left, reflectivity with linearly vertical (LV) polarized light; inset, Mn L2,3 X-ray absorption spectrum, the arrow indicates the energy at which the reflectivity measurements were performed; top right, schematic of the scattering geometry for reflectivity measurements; bottom right, depiction of the extracted magnetic configuration.
Thickness-driven electronic phase transitions have been studied in perovskite heterostructures such as La2/3Sr1/3MnO3, with the observation of O 2p–Mn 3d hybridization coupled to layer-dependent octahedral tilts [68]. Magnetically diluted interface layers related to the chemical composition were detected in La0.67Sr0.33MnO3/multiferroic BiFeO3 bilayers [69]. RSXMR applied at LCMO/YBCO/STO trilayers revealed that the magnetization of the LCMO interface was controlled at low temperature by both the superconductor and the substrate [70]. Magnetic proximity effects in YBCO/LCMO multilayers have also been addressed by coupling RSXMR and neutron reflectometry [71]. Other interesting examples of applications of the technique include interface magnetization between the correlated metal CaRuO3 and the antiferromagnetic insulator CaMnO3 [72], the study of the interface between the half metallic Fe3O4 and the semiconductor ZnO [73], and the magnetization reversal of Cr at the CrO2/RuO2 interface [74].
Finally, it should be mentioned that RSXMR can be applied to obtain information on roughness, with the possibility of distinguishing between morphological roughness and magnetic roughness both at the surface and at buried interfaces. This has been applied and discussed [75] in reference to LSMO layers.
3.4. Exchange-Bias Systems
Exchange-bias [76] is the shift of the ferromagnetic hysteresis loop along the field axis that occurs in ferromagnet–antiferromagnet (FM–AF) systems as a consequence of the exchange coupling across an FM–AF interface. Due to the buried nature of the pinned and uncompensated moments at the interface between FM and AF materials, RSXMR appears to be particularly suitable for these type of studies.
In this context, S. Roy et al. [77] used specular reflectivity to measure the depth profile of the uncompensated spins at the FeF2/Co interface (Figure 5a), finding uncompensated magnetization in the antiferromagnetic FeF2 layer. Within 2–3.5 nm of the Co/FeF2 interface, the magnetization of uncompensated FeF2 was antiparallel to the spins of Co and rotated in conjunction with the Co spins. At distances greater than 3.5 nm from the interface, the uncompensated FeF2 magnetization was pinned, providing a means of establishing bias. In a different study, the depth-dependent charge and magnetization density on an absolute scale across a permalloy/CoO interface was determined via resonant soft X-ray magnetic reflectometry [78,79].
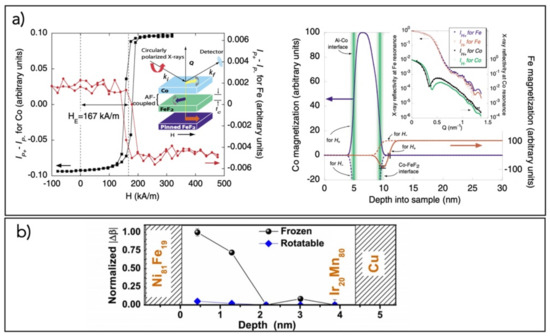
Figure 5.
(a) Left, hysteresis loops taken at Q = 0.49 and 0.38 nm−1 for Co (squares) and Fe (red dots), respectively, on the Co/FeF2 system: clear evidence of exchange bias is present; inset, representations of the X–ray experiment and sample structure; right, spin density depth profiles for Co (blue) and Fe (red) obtained by specular X–ray reflectivity (inset) at H± = ±796 kA/m (reprinted figure with permission from [77]. Copyright (2005) by the American Physical Society); (b) depth dependence of the frozen and rotating AF (Mn) uncompensated spins in a NiFe/IrMn exchange–biased bilayer (reprinted figure with permission from [85]. Copyright (2010) by the American Physical Society).
The layer structure of uncompensated spins in a CoFe/IrMn/NiFe trilayer system was studied as a function of temperature by J-S. Lee et al. [80]. Two distinct uncompensated spin layers were found due to the distinct Mn coupling to each of the FM materials.
The coupling between Fe and the uncompensated Mn moments in exchange-biased Fe/MnPd bilayers was obtained through investigation of the magnetization depth profile derived from RSXMR at Fe and Mn L edges [81]. A complex interfacial configuration was observed [81,82] consisting of a two-monolayer-thick FM region and pinned uncompensated Mn moments extending far deeper, with both located in the antiferromagnet. Element-resolved magnetization profiles were also obtained on Fe/CoO layers [83] and element-resolved hysteresis loops were recorded at different temperatures [84]. A dual behavior of the interfacial uncompensated spins was studied in the prototypical exchange-bias NiFe/IrMn system [85], where frozen uncompensated spins were found to be present deep in the AF film, whereas rotating ones were identified closer to the interface (Figure 5b). A sign change of the exchange-bias from negative to positive was also observed by S. K. Mishra et al. [86] in NiFe/IrMn with soft X-ray resonant magnetic scattering.
An Fe/NiO/Co trilayer system was investigated at the L edges of Fe, Co, and Ni [87] below the Néel temperature, simultaneously providing information on the chemical composition and the elemental-resolved magnetization behavior. Similarly, through RSXMR it was possible to derive the element-resolved magnetization profile of all-manganite La0.7Sr0.3MnO3/SrMnO3/La0.7Sr0.3MnO3 trilayers [88]. RSXMR also permitted the detection of a small but distinct magnetic moment, antiparallel to the Co moment, in the antiferromagnetic IrMn layer in a NiFe/Cu/Co/IrMn spin valve structure [89]. Frozen magnetic moments in NiFe/FeMn at the NiFe ferromagnet were observed by element- specific hysteresis loops [90]. A nearly pure orbital moment character was more recently inferred for the pinned moments in a Co/FeMn exchange-bias bilayer through the analysis of reflectivity [91]. Magnetization profiles were even derived from magnetic scattering in the hard X-rays, in particular at the Ir L edge in a MnIr/CoFe exchange-bias system [92].
3.5. Metallic Thin Films and Multilayers
The orientation of the magnetization in metallic thin films has been addressed with many techniques, including RSXMR. Metallic thin films, especially of transition metals, represent prototypical systems for the study of fundamental aspects of magnetism. Strain and epitaxy conditions may change the crystal structure of elemental metals, giving rise to artificially tailored magnetic properties that are not available in the corresponding bulk materials. RSXMR has been applied in prototypical studies: for example, to resolve the spin orientation structure of ultrathin fcc Fe films on Cu(001) [93,94]; to resolve the induced moment in uranium in U/Fe multilayers [95]; to probe the interlayer coupling in ferromagnetic/semiconductor multilayers [96]; and to measure the value of the magnetic moment, its orientation, and depth profiles in Fe/C [97], Gd/Fe [98,99,100], and Co/Mg [101] multilayers or in Cu/Fe/Cu trilayers on a semiconductor [102]. Carlomagno et al. [103] investigated, through resonant X-ray reflectivity, the structural and magnetic properties of a MgO/Co/MgO trilayer, evidencing difference in Co oxidation and roughness between the bottom (Co on MgO) and top (MgO on Co) interfaces, which was reflected in an asymmetric magnetization profile for the Co layer.
Vectorial analysis of magnetization has been performed through RSXMR to obtain information on the longitudinal and transverse components of the magnetization: transverse and longitudinal magnetic hysteresis loops have been determined in Co and FeCo films [104]. In- and out-of-plane magnetization and noncollinear profiles were determined with a subnanometer resolution in FePt multilayers [39] and in FeCo systems [105,106]. Perpendicular exchange coupling was measured at the interface between an antiferromagnet [NiO/CoO]3 and a Pt-Co ferromagnet film on Pt(111): a rotation of the easy magnetization axis of the ferromagnet was detected along the antiferromagnet spins [107]. Perpendicular anisotropy was also investigated by RSXMR in Co/Pt multilayers [108]. Magnetization profiles were recorded for bcc Fe films grown on a vicinal Ag(001) surface, but capped below a Au layer, revealing an enhancement of the magnetic moment at the interface [109].
3.6. Other Cases
RSXMR has been fruitfully applied in other relevant situations.
It has been used to derive the magnetic profile and to relate it to the chemical depth profile in organic-inorganic layered materials, which is of consequence to organic spintronics: A. Verna et al. [110] probed the structural and magnetic properties of a ferromagnetic/organic interface, consisting of a polycrystalline Co layer deposited on a fullerene thin film, and found a sharp interface with limited intermixing and a null remnant magnetization.
With regard to spintronics, diluted magnetic semiconductors have also indicated a possible ability to control the spin behavior in devices. As an example, Fe/(Ga,Mn)As heterointerfaces have been epitaxially grown and presented a robust ferromagnetism of the interfacial Mn atoms induced by the proximity effect [111].
It is worth mentioning that recent time-resolved experiments have been successfully carried out by applying X-ray magnetic circular dichroism in reflectivity: an ultrafast optically induced ferromagnetic alignment of antiferromagnetic Mn in Co/Mn multilayers has been observed probing the L3 edge of Mn in reflectivity after an ultrashort laser excitation [112]. Ultrafast, element-dependent demagnetization dynamics were studied in a Co/Pt multilayer with an X-ray-free electron laser by probing the Pt N6,7 and Co M2,3 edges [113]. Circularly polarized XUV light produced at the Fermi FEL at the Fe M2,3 edge was used to measure resonant magnetic reflectivities in a permalloy/Ta/permalloy trilayer film, permitting detection of ultrafast changes of spin and charge density profiles [114]. Pump-and-probe time-resolved resonant X-ray reflectivity was also applied at the Fe 2p edge to measure the electronic and magnetic dynamics of ferromagnetic insulating BaFeO3 thin films [115]: a transition into a metallic state induced by laser excitation was observed.
4. Conclusions
In this review, we have concisely described the basic concepts underlying resonant soft X-ray magnetic reflectivity. This technique is very powerful since it is able to discriminate and highlight the contribution to magnetism of single elemental species in a magnetic compound. It is also sensitive to the effect of few atomic magnetic moments, which may drive the macroscopic magnetic behavior in layered structures. We have described the general experimental requirements, the typical materials that are specifically investigated by this technique (thin films, buried interfaces, proximity effects, exchange-bias systems, and magnetic oxides) and the fundamental mechanisms that give rise to dichroism effects in reflectivity. This is always accompanied by references to the relevant literature so that the interested reader can readily expand her/his knowledge, if desired. The references also include a list of relevant studies where RSXMR has been successfully exploited with the aim of providing a wide but concise perspective of the different applicative fields.
Author Contributions
A.V., R.C. and L.P. contributed equally. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
We are indebted to S. Nannarone for having drawn our attention to the potentiality of reflectivity.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Als-Nielsen, J. Elements of Modern X-ray Physics; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Atwood, D. Soft X-rays and Extreme Ultraviolet Radiation; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Macke, S.; Radi, A.; Hamann-Borrero, J.E.; Verna, A.; Bluschke, M.; Brück, S.; Goering, E.; Sutarto, R.; He, F.; Cristiani, G.; et al. Element specific monolayer depth profiling. Adv. Mater. 2014, 26, 6554–6559. [Google Scholar] [CrossRef]
- Zwiebler, M.; Hamann-Borrero, J.E.; Vafaee, M.; Komissinskiy, P.; Macke, S.; Sutarto, R.; He, F.; Büchner, B.; Sawatzky, G.A.; Alff, L.; et al. Electronic depth profiles with atomic layer resolution from resonant soft X-ray reflectivity. New J. Phys. 2015, 17, 083046. [Google Scholar] [CrossRef]
- Ade, H. Characterization of organic thin films with resonant soft X-ray scattering and reflectivity near the carbon and fluorine absorption edges. Eur. Phys. J. Spec. Top. 2012, 208, 305–318. [Google Scholar] [CrossRef][Green Version]
- Mezger, M.; Ocko, B.M.; Reichert, H.; Deutsch, M. Surface layering and melting in an ionic liquid studied by resonant soft X-ray reflectivity. Proc. Natl. Acad. Sci. USA 2013, 110, 3733–3737. [Google Scholar] [CrossRef] [PubMed]
- Pasquali, L.; Mukherjee, S.; Terzi, F.; Giglia, A.; Mahne, N.; Koshmak, K.; Esaulov, V.; Toccafondi, C.; Canepa, M.; Nannarone, S. Structural and electronic properties of anisotropic ultrathin organic films from dichroic resonant soft X-ray reflectivity. Phys. Rev. B—Condens. Matter Mater. Phys. 2014, 89, 045401. [Google Scholar] [CrossRef]
- Stohr, J.; Siegmann, H.C. Magnetism: From Fundamentals to Nanoscale Dynamics; Springer: Berlin/Heidelberg, Germany, 2006; Volume 152. [Google Scholar]
- Stohr, J. X-ray Magnetic Circular Dichroism: Basic Concepts and Theory for 3D Transition Metal Atoms. In New Directions in Research with Third-Generation Soft X-ray Synchrotron Radiation Sources; Schlachter, A.S., Wuilleumier, F.J., Eds.; Springer: Dordrecht, The Netherlands, 1994; pp. 221–250. [Google Scholar]
- Mariot, J.-M.; Brouder, C. Spectroscopy and Magnetism: An Introduction. In Magnetism and Synchrotron Radiation; Beaurepaire, E., Scheurer, F., Krill, G., Kappler, J.-P., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; pp. 24–59. [Google Scholar]
- Paroli, P. An introduction to magneto-optics. In Magnetic Properties of Matter; Borsa, F., Tognetti, V., Eds.; World Scientific: Singapore, 1988; pp. 335–368. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Electrodynamics of Continous Media; Pergamon Press: Oxford, UK, 1984. [Google Scholar]
- Freiser, M.J. A Survey of Magnetooptic Effects. IEEE Trans. Magn. 1968, 4, 152–161. [Google Scholar] [CrossRef]
- Capelli, R.; Mahne, N.; Koshmak, K.; Giglia, A.; Doyle, B.P.; Mukherjee, S.; Nannarone, S.; Pasquali, L. Quantitative resonant soft X-ray reflectivity of ultrathin anisotropic organic layers: Simulation and experiment of PTCDA on Au. J. Chem. Phys. 2016, 145, 024201. [Google Scholar] [CrossRef]
- Parratt, L.G. Surface studies of solids by total reflection of X-rays. Phys. Rev. 1954, 95, 359–369. [Google Scholar] [CrossRef]
- Macke, S.; Goering, E. Magnetic reflectometry of heterostructures. J. Phys. Condens. Matter 2014, 26, 363201. [Google Scholar] [CrossRef]
- Yeh, P. Optical Waves in Layered Media; Wiley Series in Pure and Applied Optics; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Zak, J.; Moog, E.R.; Liu, C.; Bader, S.D. Magneto-optics of multilayers with arbitrary magnetization directions. Phys. Rev. B—Condens. Matter Mater. Phys. 1991, 43, 6423–6429. [Google Scholar] [CrossRef]
- Yeh, P. Optics of anisotropic layered media: A new 4 × 4 matrix algebra. Surf. Sci. 1980, 96, 41–53. [Google Scholar] [CrossRef]
- Yariv, A.; Yeh, P. Optical Waves in Crystals: Propagation and Control of Laser Radiation; Wiley Series in Pure and Applied Optics; Wiley: New York, NY, USA, 1984. [Google Scholar]
- Zak, J.; Moog, E.R.; Liu, C.; Bader, S.D. Universal approach to magneto-optics. J. Magn. Magn. Mater. 1990, 89, 107–123. [Google Scholar] [CrossRef]
- Yeh, P. Electromagnetic propagation in birefringent layered media. J. Opt. Soc. Am. 1979, 69, 742–756. [Google Scholar] [CrossRef]
- Berreman, D.W. Optics in Stratified and Anisotropic Media: 4×4-Matrix Formulation. J. Opt. Soc. Am. 1972, 62, 502. [Google Scholar] [CrossRef]
- Bertrand, P.; Hermann, C.; Lampel, G.; Peretti, J.; Safarov, V.I. General analytical treatment of optics in layered structures: Application to magneto-optics. Phys. Rev. B—Condens. Matter Mater. Phys. 2001, 64, 235421. [Google Scholar] [CrossRef]
- Pasquali, L.; Mahne, N.; Giglia, A.; Verna, A.; Sponza, L.; Capelli, R.; Bonfatti, M.; Mezzadri, F.; Galligani, E.; Nannarone, S. Analysis of Resonant Soft X-ray Reflectivity of Anisotropic Layered Materials. Surfaces 2021, 4, 18–30. [Google Scholar] [CrossRef]
- Smith, D.Y. Superconvergence and sum rules for the optical constants: Natural and magneto-optical activity. Phys. Rev. B 1976, 13, 5303–5315. [Google Scholar] [CrossRef]
- Nannarone, S.; Borgatti, F.; Deluisa, A.; Doyle, B.P.; Gazzadi, G.C.; Giglia, A.; Finetti, P.; Mahne, N.; Pasquali, L.; Pedio, M.; et al. The BEAR beamline at elettra. AIP Conf. Proc. 2004, 705, 450–453. [Google Scholar]
- BEAR beamline. 2021. Available online: www.elettra.trieste.it/elettra-beamlines/bear.html (accessed on 3 October 2021).
- Pasquali, L.; De Luisa, A.; Nannarone, S. The UHV experimental chamber for optical measurements (reflectivity and absorption) and angle resolved photoemission of the BEAR beamline at ELETTRA. AIP Conf. Proc. 2004, 705, 1142–1145. [Google Scholar]
- Haverkort, M.W.; Hollmann, N.; Krug, I.P.; Tanaka, A. Symmetry analysis of magneto-optical effects: The case of X-ray diffraction and X-ray absorption at the transition metal L2,3 edge. Phys. Rev. B—Condens. Matter Mater. Phys. 2010, 82, 094403. [Google Scholar] [CrossRef]
- Smith, D.Y. Dispersion relations and sum rules for magnetoreflectivity. J. Opt. Soc. Am. 1976, 66, 547–554. [Google Scholar] [CrossRef]
- Smith, D.Y. Comments on the dispersion relations for the complex refractive index of circularly and elliptically polarized light*. J. Opt. Soc. Am. 1976, 66, 454–460. [Google Scholar] [CrossRef]
- Kao, C.; Hastings, J.B.; Johnson, E.D.; Siddons, D.P.; Smith, G.C.; Prinz, G.A. Magnetic-resonance exchange scattering at the iron LII and LIII edges. Phys. Rev. Lett. 1990, 65, 373–376. [Google Scholar] [CrossRef]
- Kao, C.C.; Chen, C.T.; Johnson, E.D.; Hastings, J.B.; Lin, H.J.; Ho, G.H.; Meigs, G.; Brot, J.M.; Hulbert, S.L.; Idzerda, Y.U.; et al. Dichroic interference effects in circularly polarized soft-X-ray resonant magnetic scattering. Phys. Rev. B 1994, 50, 9599–9602. [Google Scholar] [CrossRef]
- Kortright, J.B.; Kim, S.K. Resonant magneto-optical properties of Fe near its 2p levels: Measurement and applications. Phys. Rev. B—Condens. Matter Mater. Phys. 2000, 62, 12216–12228. [Google Scholar] [CrossRef]
- Mertins, H.C.; Abramsohn, D.; Gaupp, A.; Schäfers, F.; Gudat, W.; Zaharko, O.; Grimmer, H.; Oppeneer, P.M. Resonant magnetic reflection coefficients at the Fe (formula presented) edge obtained with linearly and circularly polarized soft x rays. Phys. Rev. B—Condens. Matter Mater. Phys. 2002, 66, 1–8. [Google Scholar] [CrossRef]
- Sacchi, M.; Hague, C.F.; Pasquali, L.; Mirone, A.; Mariot, J.M.; Isberg, P.; Gullikson, E.M.; Underwood, J.H. Optical constants of ferromagnetic iron via 2p resonant magnetic scattering. Phys. Rev. Lett. 1998, 81, 1521–1524. [Google Scholar] [CrossRef]
- Sacchi, M.; Mirone, A. Resonant reflectivity from a Ni(110) crystal: Magnetic effects at the Ni 2p edges using linearly and circularly polarized photons. Phys. Rev. B—Condens. Matter Mater. Phys. 1998, 57, 8408–8415. [Google Scholar] [CrossRef]
- Tonnerre, J.M.; Jaouen, N.; Bontempi, E.; Carbone, D.; Babonneau, D.; De Santis, M.; Tolentino, N.; Grenier, S.; Garaudee, S.; Staub, U. Soft X-ray resonant magnetic reflectivity studies for in-and out-of-plane magnetization profile in ultra thin films. J. Phys. Conf. Ser. 2010, 211, 012015. [Google Scholar] [CrossRef]
- Abes, M.; Atkinson, D.; Tanner, B.K.; Charlton, T.R.; Langridge, S.; Hase, T.P.A.; Ali, M.; Marrows, C.H.; Hickey, B.J.; Neudert, A.; et al. Spin polarization and exchange coupling of Cu and Mn atoms in paramagnetic CuMn diluted alloys induced by a Co layer. Phys. Rev. B—Condens. Matter Mater. Phys. 2010, 82, 184412. [Google Scholar] [CrossRef]
- Awaji, N.; Noma, K.; Nomura, K.; Doi, S.; Hirono, T.; Kimura, H.; Nakamura, T. Soft X-ray resonant magnetic reflectivity study on induced magnetism in [Fe70Co30/Pd]nsuper-lattice films. J. Phys. Conf. Ser. 2007, 83, 012034. [Google Scholar] [CrossRef]
- Moriya, T. Anisotropic Superexchange Interaction and Weak Ferromagnetism. Phys. Rev. 1960, 120, 91–98. [Google Scholar] [CrossRef]
- Dzyaloshinsky, I. A thermodynamic theory of “weak” ferromagnetism of antiferromagnetics. J. Phys. Chem. Solids 1958, 4, 241–255. [Google Scholar] [CrossRef]
- Belmeguenai, M.; Roussigné, Y.; Bouloussa, H.; Chérif, S.M.; Stashkevich, A.; Nasui, M.; Gabor, M.S.; Mora-Hernández, A.; Nicholson, B.; Inyang, O.O.; et al. Thickness Dependence of the Dzyaloshinskii-Moriya Interaction in Co2FeAl Ultrathin Films: Effects of Annealing Temperature and Heavy-Metal Material. Phys. Rev. Appl. 2018, 9, 044044. [Google Scholar] [CrossRef]
- Geissler, J.; Goering, E.; Justen, M.; Weigand, F.; Schütz, G.; Langer, J.; Schmitz, D.; Maletta, H.; Mattheis, R. Pt magnetization profile in a Pt/Co bilayer studied by resonant magnetic X-ray reflectometry. Phys. Rev. B—Condens. Matter Mater. Phys. 2002, 65, 1–4. [Google Scholar] [CrossRef]
- Graulich, D.; Krieft, J.; Moskaltsova, A.; Demir, J.; Peters, T.; Pohlmann, T.; Bertram, F.; Wollschläger, J.; Jose, J.R.; Francoual, S.; et al. Quantitative comparison of the magnetic proximity effect in Pt detected by XRMR and XMCD. Appl. Phys. Lett. 2021, 118, 012407. [Google Scholar] [CrossRef]
- Hosoito, N.; Ohkochi, T.; Kodama, K.; Suzuki, M. Charge and induced magnetic structures of Au layers in Fe/Au bilayer and Fe/Au/Fe trilayer films by resonant X-ray magnetic reflectivity at the Au L 3 absorption edge. J. Phys. Soc. Japan 2014, 83. [Google Scholar] [CrossRef]
- Jaouen, N.; Tonnerre, J.M.; Raoux, D.; Bontempi, E.; Ortega, L.; Müenzenberg, M.; Felsch, W.; Rogalev, A.; Dürr, H.A.; Dudzik, E.; et al. Ce 5d magnetic profile in Fe/Ce multilayers for the (formula presented) and (formula presented) -like Ce phases by X-ray resonant magnetic scattering. Phys. Rev. B—Condens. Matter Mater. Phys. 2002, 66, 1–14. [Google Scholar] [CrossRef]
- Kim, D.O.; Song, K.M.; Choi, Y.; Min, B.C.; Kim, J.S.; Choi, J.W.; Lee, D.R. Asymmetric magnetic proximity effect in a Pd/Co/Pd trilayer system. Sci. Rep. 2016, 6, 1–8. [Google Scholar] [CrossRef]
- Klewe, C.; Kuschel, T.; Schmalhorst, J.M.; Bertram, F.; Kuschel, O.; Wollschläger, J.; Strempfer, J.; Meinert, M.; Reiss, G. Static magnetic proximity effect in Pt/ Ni1-x Fex bilayers investigated by X-ray resonant magnetic reflectivity. Phys. Rev. B 2016, 93, 214440. [Google Scholar] [CrossRef]
- Macke, S. ReMagX. 2018. Available online: https://www.remagx.org/wiki/doku.php (accessed on 3 October 2021).
- Krieft, J.; Graulich, D.; Moskaltsova, A.; Bouchenoire, L.; Francoual, S.; Kuschel, T. Advanced data analysis procedure for hard X-ray resonant magnetic reflectivity discussed for Pt thin film samples of various complexity. J. Phys. D Appl. Phys. 2020, 53, 375004. [Google Scholar] [CrossRef]
- Kuschel, T.; Klewe, C.; Schmalhorst, J.M.; Bertram, F.; Kuschel, O.; Schemme, T.; Wollschläger, J.; Francoual, S.; Strempfer, J.; Gupta, A.; et al. Static Magnetic Proximity Effect in Pt/NiFe2O4 and Pt/Fe Bilayers Investigated by X-ray Resonant Magnetic Reflectivity. Phys. Rev. Lett. 2015, 115, 097401. [Google Scholar] [CrossRef] [PubMed]
- Moskaltsova, A.; Krieft, J.; Graulich, D.; Matalla-Wagner, T.; Kuschel, T. Impact of the magnetic proximity effect in Pt on the total magnetic moment of Pt/Co/Ta trilayers studied by X-ray resonant magnetic reflectivity. AIP Adv. 2020, 10, 015154. [Google Scholar] [CrossRef]
- Mukhopadhyay, A.; Koyiloth Vayalil, S.; Graulich, D.; Ahamed, I.; Francoual, S.; Kashyap, A.; Kuschel, T.; Anil Kumar, P.S. Asymmetric modification of the magnetic proximity effect in Pt/Co/Pt trilayers by the insertion of a Ta buffer layer. Phys. Rev. B 2020, 102, 144435. [Google Scholar] [CrossRef]
- Rowan-Robinson, R.M.; Stashkevich, A.A.; Roussigné, Y.; Belmeguenai, M.; Chérif, S.M.; Thiaville, A.; Hase, T.P.A.; Hindmarch, A.T.; Atkinson, D. The interfacial nature of proximity-induced magnetism and the Dzyaloshinskii-Moriya interaction at the Pt/Co interface. Sci. Rep. 2017, 7, 1–11. [Google Scholar] [CrossRef]
- Rowan-Robinson, R.M.; Hindmarch, A.T.; Atkinson, D. Efficient current-induced magnetization reversal by spin-orbit torque in Pt/Co/Pt. J. Appl. Phys. 2018, 124, 183901. [Google Scholar] [CrossRef]
- Sève, L.; Jaouen, N.; Tonnerre, J.M.; Raoux, D.; Bartolomé, F.; Arend, M.; Felsch, W.; Rogalev, A.; Goulon, J.; Gautier, C.; et al. Profile of the induced 5d magnetic moments in Ce/Fe and La/Fe multilayers probed by X-ray magnetic-resonant scattering. Phys. Rev. B—Condens. Matter Mater. Phys. 1999, 60, 9662–9674. [Google Scholar] [CrossRef]
- Szuszkiewicz, W.; Ott, F.; Kisielewski, J.; Sveklo, I.; Dynowska, E.; Minikayev, R.; Kurant, Z.; Kuna, R.; Jakubowski, M.; Wawro, A.; et al. Polarized neutron reflectivity and X-ray scattering measurements as tools to study properties of Pt/Co/Pt ultrathin layers irradiated by femtosecond laser pulses. Phase Transit. 2016, 89, 328–340. [Google Scholar] [CrossRef]
- Huijben, M.; Koster, G.; Liao, Z.L.; Rijnders, G. Interface-engineered oxygen octahedral coupling in manganite heterostructures. Appl. Phys. Rev. 2017, 4, 041103. [Google Scholar] [CrossRef]
- Liao, Z.; Huijben, M.; Zhong, Z.; Gauquelin, N.; Macke, S.; Green, R.J.; Van Aert, S.; Verbeeck, J.; Van Tendeloo, G.; Held, K.; et al. Controlled lateral anisotropy in correlated manganite heterostructures by interface-engineered oxygen octahedral coupling. Nat. Mater. 2016, 15, 425–431. [Google Scholar] [CrossRef] [PubMed]
- Fabbris, G.; Jaouen, N.; Meyers, D.; Feng, J.; Hoffman, J.D.; Sutarto, R.; Chiuzbǎian, S.G.; Bhattacharya, A.; Dean, M.P.M. Emergent c-axis magnetic helix in manganite-nickelate superlattices. Phys. Rev. B. 2018, 98, 180401. [Google Scholar] [CrossRef]
- Gibert, M.; Viret, M.; Torres-Pardo, A.; Piamonteze, C.; Zubko, P.; Jaouen, N.; Tonnerre, J.M.; Mougin, A.; Fowlie, J.; Catalano, S.; et al. Interfacial Control of Magnetic Properties at LaMnO3/LaNiO3 Interfaces. Nano Lett. 2015, 15, 7355–7361. [Google Scholar] [CrossRef] [PubMed]
- Gibert, M.; Viret, M.; Zubko, P.; Jaouen, N.; Tonnerre, J.M.; Torres-Pardo, A.; Catalano, S.; Gloter, A.; Stéphan, O.; Triscone, J.M. Interlayer coupling through a dimensionality-induced magnetic state. Nat. Commun. 2016, 7, 1–7. [Google Scholar] [CrossRef]
- Hühn, S.; Jungbauer, M.; Michelmann, M.; Massel, F.; Koeth, F.; Ballani, C.; Moshnyaga, V. Modeling of colossal magnetoresistance in La0.67Ca0.33MnO3/Pr0.67Ca0.33MnO3 superlattices: Comparison with individual (La1−yPry)0.67Ca0.33MnO3 films. J. Appl. Phys. 2013, 113, 17–701. [Google Scholar] [CrossRef]
- Freeland, J.W.; Gray, K.E.; Ozyuzer, L.; Berghuis, P.; Badica, E.; Kavich, J.; Zheng, H.; Mitchell, J.F. Full bulk spin polarization and intrinsic tunnel barriers at the surface of layered manganites. Nat. Mater. 2005, 4, 62–67. [Google Scholar] [CrossRef][Green Version]
- Verna, A.; Davidson, B.A.; Szeto, Y.; Petrov, A.Y.; Mirone, A.; Giglia, A.; Mahne, N.; Nannarone, S. Measuring magnetic profiles at manganite surfaces with monolayer resolution. J. Magn. Magn. Mater. 2010, 322, 1212–1216. [Google Scholar] [CrossRef][Green Version]
- Liao, Z.; Gauquelin, N.; Green, R.J.; Macke, S.; Gonnissen, J.; Thomas, S.; Zhong, Z.; Li, L.; Si, L.; Van Aert, S.; et al. Thickness Dependent Properties in Oxide Heterostructures Driven by Structurally Induced Metal-Oxygen Hybridization Variations. Adv. Funct. Mater. 2017, 27, 1606717. [Google Scholar] [CrossRef]
- Bertinshaw, J.; Brück, S.; Lott, D.; Fritzsche, H.; Khaydukov, Y.; Soltwedel, O.; Keller, T.; Goering, E.; Audehm, P.; Cortie, D.L.; et al. Element-specific depth profile of magnetism and stoichiometry at the La0.67Sr0.33MnO3/BiFeO3 interface. Phys. Rev. B—Condens. Matter Mater. Phys. 2014, 90, 041113. [Google Scholar] [CrossRef]
- Brück, S.; Treiber, S.; MacKe, S.; Audehm, P.; Christiani, G.; Soltan, S.; Habermeier, H.U.; Goering, E.; Albrecht, J. The temperature-dependent magnetization profile across an epitaxial bilayer of ferromagnetic La2/3Ca1/3MnO3 and superconducting YBa2Cu3O7-δ. New J. Phys. 2011, 13, 033023. [Google Scholar] [CrossRef]
- Satapathy, D.K.; Uribe-Laverde, M.A.; Marozau, I.; Malik, V.K.; Das, S.; Wagner, T.; Marcelot, C.; Stahn, J.; Brück, S.; Rühm, A.; et al. Magnetic proximity effect in YBa 2Cu3O7/La2/3Ca1/3MnO3 and YBa2Cu3O7/LaMnO3+δ superlattices. Phys. Rev. Lett. 2012, 108, 197201. [Google Scholar] [CrossRef]
- Freeland, J.W.; Chakhalian, J.; Boris, A.V.; Tonnerre, J.M.; Kavich, J.J.; Yordanov, P.; Grenier, S.; Zschack, P.; Karapetrova, E.; Popovich, P.; et al. Charge transport and magnetization profile at the interface between the correlated metal CaRuO3 and the antiferromagnetic insulator CaMnO3. Phys. Rev. B—Condens. Matter Mater. Phys. 2010, 81, 094414. [Google Scholar] [CrossRef]
- Brück, S.; Paul, M.; Tian, H.; Müller, A.; Kufer, D.; Praetorius, C.; Fauth, K.; Audehm, P.; Goering, E.; Verbeeck, J.; et al. Magnetic and electronic properties of the interface between half metallic Fe3O4 and semiconducting ZnO. Appl. Phys. Lett. 2012, 100, 081603. [Google Scholar] [CrossRef]
- Zafar, K.; Audehm, P.; Schütz, G.; Goering, E.; Pathak, M.; Chetry, K.B.; Leclair, P.R.; Gupta, A. Cr magnetization reversal at the CrO2/RuO2 interface: Origin of the reduced GMR effect. Phys. Rev. B—Condens. Matter Mater. Phys. 2011, 84, 134412. [Google Scholar] [CrossRef]
- Verna, A.; Davidson, B.A.; Mirone, A.; Nannarone, S. The influence of surface roughness in X-ray resonant magnetic reflectivity experiments. Eur. Phys. J. Spec. Top. 2012, 208, 165–175. [Google Scholar] [CrossRef][Green Version]
- Nogués, J.; Schuller, I.K. Exchange bias. J. Magn. Magn. Mater. 1999, 192, 203–232. [Google Scholar] [CrossRef]
- Roy, S.; Fitzsimmons, M.R.; Park, S.; Dorn, M.; Petracic, O.; Roshchin, I.V.; Li, Z.P.; Batlle, X.; Morales, R.; Misra, A.; et al. Depth profile of uncompensated spins in an exchange bias system. Phys. Rev. Lett. 2005, 95, 047201. [Google Scholar] [CrossRef]
- Roy, S.; Sanchez-Hanke, C.; Park, S.; Fitzsimmons, M.R.; Tang, Y.J.; Hong, J.I.; Smith, D.J.; Taylor, B.J.; Liu, X.; Maple, M.B.; et al. Evidence of modified ferromagnetism at a buried Permalloy/CoO interface at room temperature. Phys. Rev. B—Condens. Matter Mater. Phys. 2007, 75, 014442. [Google Scholar] [CrossRef]
- Blackburn, E.; Sanchez-Hanke, C.; Roy, S.; Smith, D.J.; Hong, J.I.; Chan, K.T.; Berkowitz, A.E.; Sinha, S.K. Pinned Co moments in a polycrystalline permalloy/CoO exchange-biased bilayer. Phys. Rev. B—Condens. Matter Mater. Phys. 2008, 78, 180408. [Google Scholar] [CrossRef]
- Lee, J.S.; Kao, C.C.; Jang, H.; Ko, K.T.; Park, J.H.; Rhie, K.; Kim, J.Y. Uncompensated spins in trilayer CoFe/IrMn/NiFe exchange bias: Soft X-ray resonant magnetic scattering study. J. Phys. Condens. Matter 2011, 23, 256001. [Google Scholar] [CrossRef]
- Brück, S.; MacKe, S.; Goering, E.; Ji, X.; Zhan, Q.; Krishnan, K.M. Coupling of Fe and uncompensated Mn moments in exchange-biased Fe/MnPd. Phys. Rev. B—Condens. Matter Mater. Phys. 2010, 81, 134414. [Google Scholar] [CrossRef]
- Brück, S.; Schütz, G.; Goering, E.; Ji, X.; Krishnan, K.M. Uncompensated moments in the MnPd/Fe Exchange Bias System. Phys. Rev. Lett. 2008, 101, 126402. [Google Scholar] [CrossRef] [PubMed]
- Radu, F.; Nefedov, A.; Grabis, J.; Nowak, G.; Bergmann, A.; Zabel, H. Soft X-ray resonant magnetic scattering studies on Fe/CoO exchange bias system. J. Magn. Magn. Mater. 2006, 300, 206–210. [Google Scholar] [CrossRef][Green Version]
- Gruyters, M.; Schmitz, D. Microscopic nature of ferro- and antiferromagnetic interface coupling of uncompensated magnetic moments in exchange bias systems. Phys. Rev. Lett. 2008, 100, 077205. [Google Scholar] [CrossRef]
- Mishra, S.K.; Radu, F.; Valencia, S.; Schmitz, D.; Schierle, E.; Dürr, H.A.; Eberhardt, W. Dual behavior of antiferromagnetic uncompensated spins in NiFe/IrMn exchange biased bilayers. Phys. Rev. B—Condens. Matter Mater. Phys. 2010, 81, 212404. [Google Scholar] [CrossRef]
- Mishra, S.K.; Radu, F.; Dürr, H.A.; Eberhardt, W. Training-induced positive exchange bias in NiFe/IrMn bilayers. Phys. Rev. Lett. 2009, 102, 177208. [Google Scholar] [CrossRef] [PubMed]
- Zaharko, O.; Oppeneer, P.M.; Grimmer, H.; Horisberger, M.; Mertins, H.C.; Abramsohn, D.; Schäfers, F.; Bill, A.; Braun, H.B. Exchange coupling in Fe/NiO/Co film studied by soft X-ray resonant magnetic reflectivity. Phys. Rev. B—Condens. Matter Mater. Phys. 2002, 66, 1–10. [Google Scholar] [CrossRef]
- Jungbauer, M.; Hühn, S.; Michelmann, M.; Goering, E.; Moshnyaga, V. Exchange bias in La0.7Sr0.3MnO3/SrMnO3/La0.7Sr0.3MnO3 trilayers. J. Appl. Phys. 2013, 113, 17–709. [Google Scholar] [CrossRef]
- Hase, T.P.A.; Fulthorpe, B.D.; Wilkins, S.B.; Tanner, B.K.; Marrows, C.H.; Mickey, B.J. Weak magnetic moment on IrMn exchange bias pinning layers. Appl. Phys. Lett. 2001, 79, 985–987. [Google Scholar] [CrossRef][Green Version]
- Mohanty, J.; Persson, A.; Arvanitis, D.; Temst, K.; Van Haesendonck, C. Direct observation of frozen moments in the NiFe/FeMn exchange bias system. New J. Phys. 2013, 15, 033016. [Google Scholar] [CrossRef]
- Audehm, P.; Schmidt, M.; Bruck, S.; Tietze, T.; Grafe, J.; MacKe, S.; Schutz, G.; Goering, E. Pinned orbital moments—A new contribution to magnetic anisotropy. Sci. Rep. 2016, 6, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Doi, S.; Nomura, K.; Awaji, N.; Hosoito, N.; Yamagishi, R.; Suzuki, M. Magnetization profile of Ir in a MnIr/CoFe exchange bias system evaluated by hard X-ray resonant magnetic reflectivity. J. Appl. Phys. 2009, 106, 123919. [Google Scholar] [CrossRef]
- Violbarbosa, C.E.; Meyerheim, H.L.; Jal, E.; Tonnerre, J.M.; Przybylski, M.; Sandratskii, L.M.; Yildiz, F.; Staub, U.; Kirschner, J. Inhomogeneous temperature dependence of the magnetization in fcc-Fe on Cu(001). Phys. Rev. B—Condens. Matter Mater. Phys. 2012, 85, 184414. [Google Scholar] [CrossRef]
- Meyerheim, H.L.; Tonnerre, J.M.; Sandratskii, L.; Tolentino, H.C.N.; Przybylski, M.; Gabi, Y.; Yildiz, F.; Fu, X.L.; Bontempi, E.; Grenier, S.; et al. New model for magnetism in ultrathin fcc Fe on Cu(001). Phys. Rev. Lett. 2009, 103, 267202. [Google Scholar] [CrossRef]
- Brown, S.D.; Bouchenoire, L.; Thompson, P.; Springell, R.; Mirone, A.; Stirling, W.G.; Beesley, A.; Thomas, M.F.; Ward, R.C.C.; Wells, M.R.; et al. Profile of the U 5f magnetization in U/Fe multilayers. Phys. Rev. B—Condens. Matter Mater. Phys. 2008, 77, 014427. [Google Scholar] [CrossRef]
- Valvidares, S.M.; Quirós, C.; Mirone, A.; Tonnerre, J.M.; Stanescu, S.; Bencok, P.; Souche, Y.; Zárate, L.; Martín, J.I.; Vélez, M.; et al. Resolving antiferromagnetic states in magnetically coupled amorphous Co-Si-Si multilayers by soft X-ray resonant magnetic scattering. Phys. Rev. B—Condens. Matter Mater. Phys. 2008, 78, 064406. [Google Scholar] [CrossRef]
- Zaharko, O.; Mertins, H.C.; Grimmer, H.; Schäfers, F. Soft X-ray resonant magnetic reflectivity from Fe/C multilayers. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2001, 467–468, 1419–1422. [Google Scholar] [CrossRef]
- Meltchakov, E.; Mertins, H.C.; Scheer, M.; Di Fonzo, S.; Jark, W.; Schäfers, F. Soft X-ray resonant magnetic reflectivity of Gd/Fe multilayers. J. Magn. Magn. Mater. 2002, 240, 550–552. [Google Scholar] [CrossRef]
- Choi, Y.; Haskel, D.; Camley, R.E.; Lee, D.R.; Lang, J.C.; Srajer, G.; Jiang, J.S.; Bader, S.D. Temperature evolution of the Gd magnetization profile in strongly coupled Gd/Fe multilayers. Phys. Rev. B—Condens. Matter Mater. Phys. 2004, 70, 134420. [Google Scholar] [CrossRef]
- Haskel, D.; Srajer, G.; Lang, J.C.; Pollmann, J.; Nelson, C.S.; Jiang, J.S.; Bader, S.D. Enhanced interfacial magnetic coupling of Gd /Fe multilayers. Phys. Rev. Lett. 2001, 87, 207201. [Google Scholar] [CrossRef] [PubMed]
- Jonnard, P.; Le Guen, K.; André, J.M.; Delaunay, R.; Mahne, N.; Giglia, A.; Nannarone, S.; Verna, A.; Wang, Z.S.; Zhu, J.T.; et al. Determination of the magnetization profile of Co/Mg periodic multilayers by magneto-optic Kerr effect and X-ray magnetic resonant reflectivity. J. Phys. Conf. Ser. 2013, 417, 12025. [Google Scholar] [CrossRef]
- Sacchi, M.; Mirone, A.; Hague, C.F.; Hague, C.F.; Castrucci, P.; Gunnella, R.; De Crescenzi, M. Resonant magnetic scattering from fcc Cu/Fe/Cu/Si(111) heterostructures. Phys. Rev. B—Condens. Matter Mater. Phys. 2001, 64, 124031–124034. [Google Scholar] [CrossRef]
- Carlomagno, I.; Verna, A.; Forrest, T.; Meneghini, C. Structural Profile of a MgO/Co/MgO Trilayer Using Soft X-ray Resonant Magnetic Reflectivity. Springer Proc. Phys. 2021, 220, 155–167. [Google Scholar] [CrossRef]
- Lee, J.S.; Vescovo, E.; Arena, D.A.; Kao, C.C.; Beaujour, J.M.; Kent, A.D.; Jang, H.; Park, J.H.; Kim, J.Y. Longitudinal and transverse magnetization components in thin films: A resonant magnetic reflectivity investigation using circularly polarized soft X-rays. Appl. Phys. Lett. 2010, 96, 42507. [Google Scholar] [CrossRef]
- Tonnerre, J.M.; Przybylski, M.; Ragheb, M.; Yildiz, F.; Tolentino, H.C.N.; Ortega, L.; Kirschner, J. Direct in-depth determination of a complex magnetic configuration in an exchange-coupled bilayer with perpendicular and in-plane anisotropy. Phys. Rev. B—Condens. Matter Mater. Phys. 2011, 84, 100407. [Google Scholar] [CrossRef]
- Przybylski, M.; Tonnerre, J.M.; Yildiz, F.; Tolentino, H.C.N.; Kirschner, J. Non-collinear magnetic profile in (Rh/Fe1−xCox)2/Rh(001) bilayer probed by polarized soft X-ray resonant magnetic reflectivity. J. Appl. Phys. 2012, 111, 07C103. [Google Scholar] [CrossRef]
- Tonnerre, J.M.; De Santis, M.; Grenier, S.; Tolentino, H.C.N.; Langlais, V.; Bontempi, E.; García-Fernández, M.; Staub, U. Depth magnetization profile of a perpendicular exchange coupled system by soft-X-ray resonant magnetic reflectivity. Phys. Rev. Lett. 2008, 100, 157202. [Google Scholar] [CrossRef]
- Kortright, J.B.; Kim, S.K.; Denbeaux, G.P.; Zeltzer, G.; Takano, K.; Fullerton, E.E. Soft-X-ray small-angle scattering as a sensitive probe of magnetic and charge heterogeneity. Phys. Rev. B—Condens. Matter Mater. Phys. 2001, 64, 092401. [Google Scholar] [CrossRef]
- Jal, E.; Dąbrowski, M.; Tonnerre, J.M.; Przybylski, M.; Grenier, S.; Jaouen, N.; Kirschner, J. Magnetization profile across Au-covered bcc Fe films grown on a vicinal surface of Ag(001) as seen by X-ray resonant magnetic reflectivity. Phys. Rev. B—Condens. Matter Mater. Phys. 2013, 87, 224418. [Google Scholar] [CrossRef]
- Verna, A.; Bergenti, I.; Pasquali, L.; Giglia, A.; Albonetti, C.; Dediu, V.; Borgatti, F. Magnetic Depth Profiling of the Co/C60 Interface through Soft X-ray Resonant Magnetic Reflectivity. IEEE Trans. Magn. 2020, 56, 1–6. [Google Scholar] [CrossRef]
- Sperl, M.; MacCherozzi, F.; Borgatti, F.; Verna, A.; Rossi, G.; Soda, M.; Schuh, D.; Bayreuther, G.; Wegscheider, W.; Cezar, J.C.; et al. Identifying the character of ferromagnetic Mn in epitaxial Fe/(Ga,Mn)As heterostructures. Phys. Rev. B—Condens. Matter Mater. Phys. 2010, 81, 035211. [Google Scholar] [CrossRef]
- Golias, E.; Kumberg, I.; Gelen, I.; Thakur, S.; Gördes, J.; Hosseinifar, R.; Guillet, Q.; Dewhurst, J.K.; Sharma, S.; Schuler-Langeheine, C.; et al. Ultrafast Optically Induced Ferromagnetic State in an Elemental Antiferromagnet. Phys. Rev. Lett. 2021, 126, 107202. [Google Scholar] [CrossRef] [PubMed]
- Yamamoto, K.; El Moussaoui, S.; Hirata, Y.; Yamamoto, S.; Kubota, Y.; Owada, S.; Yabashi, M.; Seki, T.; Takanashi, K.; Matsuda, I.; et al. Element-selectively tracking ultrafast demagnetization process in Co/Pt multilayer thin films by the resonant magneto-optical Kerr effect. Appl. Phys. Lett. 2020, 116, 172406. [Google Scholar] [CrossRef]
- Gutt, C.; Sant, T.; Ksenzov, D.; Capotondi, F.; Pedersoli, E.; Raimondi, L.; Nikolov, I.P.; Kiskinova, M.; Jaiswal, S.; Jakob, G.; et al. Probing ultrafast changes of spin and charge density profiles with resonant XUV magnetic reflectivity at the free-electron laser FERMI. Struct. Dyn. 2017, 4, 55101. [Google Scholar] [CrossRef] [PubMed]
- Tsuyama, T.; Chakraverty, S.; Macke, S.; Pontius, N.; Schüßler-Langeheine, C.; Hwang, H.Y.; Tokura, Y.; Wadati, H. Photoinduced Demagnetization and Insulator-to-Metal Transition in Ferromagnetic Insulating BaFeO3 Thin Films. Phys. Rev. Lett. 2016, 116, 256402. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).