Next Article in Journal / Special Issue
Field-Induced Single-Ion Magnet Phenomenon in Hexabromo- and Hexaiodorhenate(IV) Complexes
Previous Article in Journal
Current Status of Magnetic Resonance on Saliva for Oral and Dental Health Early Diagnosis
Previous Article in Special Issue
Spontaneous Magnetization and Optical Activity in the Chiral Series {(L-proline)nV[Cr(CN)6]x} (0 < n < 3)
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Magnetochemistry
Volume 6
Issue 2
10.3390/magnetochemistry6020019
magnetochemistry-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Dysprosium Single-Molecule Magnets Involving 1,10-Phenantroline-5,6-dione Ligand

by
Olivier Galangau
,
Jessica Flores Gonzalez
,
Vincent Montigaud
,
Vincent Dorcet
,
Boris le Guennic
,
Olivier Cador
and
Fabrice Pointillart
*
Univ Rennes, CNRS, ISCR (Institut des Sciences Chimiques de Rennes) - UMR 6226, F-35000 Rennes, France
*
Author to whom correspondence should be addressed.
Magnetochemistry 2020, 6(2), 19; https://doi.org/10.3390/magnetochemistry6020019
Submission received: 3 April 2020 / Revised: 8 April 2020 / Accepted: 10 April 2020 / Published: 15 April 2020
(This article belongs to the Special Issue Feature Papers in Magnetochemistry)
Browse Figures
Versions Notes

Abstract

:
The two mononuclear complexes of the formula [Dy(tta)3(L)] (1) and [Dy(hfac)3(L)] (2) (where tta- = 2-thenoytrifluoroacetylacetonate and hfac- = 1,1,1,5,5,5-hexafluoroacetylacetonate) were obtained from the coordination reaction of the Dy(tta)3·2H2O or Dy(hfac)3·2H2O units with the 1,10-phenantroline-5,6-dione ligand (L). Their structures have been determined by X-ray diffraction studies on single crystals, and they revealed a supramolecular assembly of tetramers through σ-π interactions. Both complexes displayed a Single-Molecule Magnet (SMM) behavior without an external applied magnetic field. Magnetic relaxation happened through Orbach, Raman and Quantum Tunneling of the Magnetization (QTM). Wavefunction theory calculations were realized to rationalize the magnetic properties.

Graphical Abstract

1. Introduction

The design of lanthanide coordination complexes is crucial for the development of emitting materials [1,2] and molecular magnetism fields [3,4,5]. On the one hand, the specific characteristic of the lanthanide ions, such as intense, long-lived and sharp-line emissions, makes them ideal candidates for a plethora of applications ranging from luminescent- and bio-sensors [6,7], Organic Light-Emitting Diodes (OLEDs) [8], time-resolved fluoro-immunoassays [9] and imaging [10,11]. Nevertheless, the observation of such emissions needs to be sensitized by an indirect process, since the forbidden Laporte f-f transitions [12] have very weak absorption coefficients which lead to an inefficient direct excitation process. The indirect sensitization process is achieved using organic chromophores which possess adequate triplet and/or intra-ligand charge transfer excited states to efficiently perform an energy transfer to the spectroscopic levels of the lanthanide [13,14]. On the other hand, the strong magnetic anisotropy associated with a high magnetic moment makes lanthanide ions suitable for the observation of Single-Molecule Magnet (SMM) behavior [15]. Such magnetic bistability could find interest in potential applications such as high density storage devices [16], quantum computing [17] or spintronics [18]. In order to observe SMM behavior, the crucial parameter is the magnetic anisotropy, which must be uniaxial or planar depending on the electronic distribution of the f electrons, i.e., oblate or prolate [19]. The control of the magnetic anisotropy is driven by the nature and the position of the ligands around the metal center. Thus, recently, the use of cyclopentadienyl-based ligands has allowed for the design of mononuclear lanthanide SMMs with a high blocking temperature [20,21,22,23]. These two research fields highlight the important role of the organic ligands associated to the lanthanide ion.
To go one step forward, more complex ligands with multi-functionality, such as the combination of redox-activity with multi coordination sites, could be used. These kind of ligands can allow the observation of multi-emission or -SMM behavior [24,25,26,27]. In this context, the 1,10-phenantroline-5,6-dione (L) appears as a promising multifunctional ligand since it combines two potential coordination sites with electro-activity [28,29], leading to the design of potential multi-properties compounds, such as a combination of spin crossover and valence tautomerism, as has recently been proposed from a computational point of view [30]. Its electro-activity could be exploited to modulate the physical properties as a function of its oxidation state, i.e., to design redox magnetic and photo-emissive switches, as already published with other redox-active ligands [31,32,33]. The L ligand was employed to design both pure 4f [34,35,36,37,38,39] and hetero-bimetallic nd4f [40,41,42] coordination complexes to study their biological activities and photo-physical properties. It is worth noting that the elaboration of hetero-bimetallic compounds implies the reduction of the ligand in its 5,6-dihydroxy-1,10-phenantroline form. To the best of our knowledge, a magnetic study was not performed for lanthanide complexes involving the L ligand.
Thus, in the present article, we propose to analyze the magnetic properties of two mononuclear complexes of the formula [Dy(tta)3(L)] (1) and [Dy(hfac)3(L)] (2) (where tta- = 2-tenoytrifluoroacetylacetonate and hfac- = 1,1,1,5,5,5-hexafluoroacetylacetonate) from both experimental and computational points of view.

2. Results and Discussion

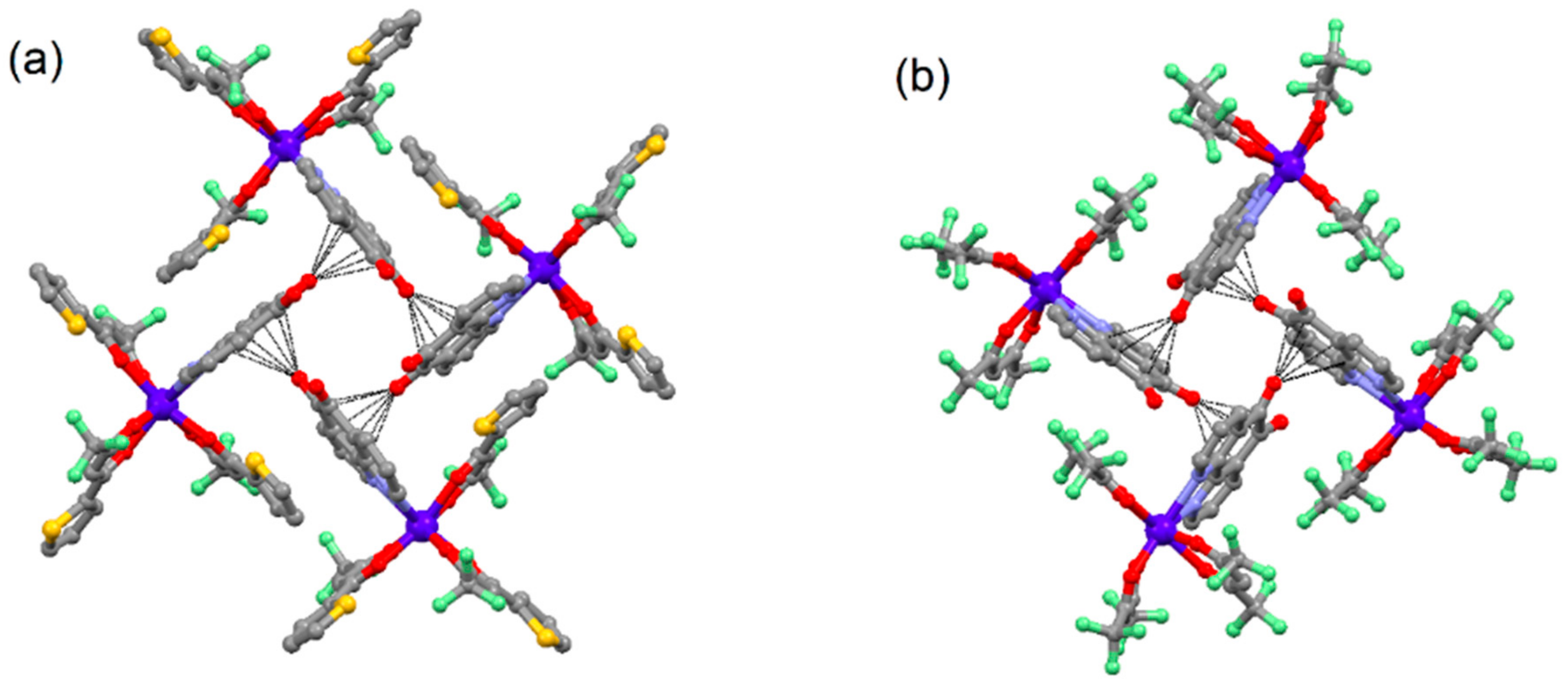
2.1. X-ray Structures

[Dy(tta)3(L)] (1). 1 crystallized in the tetragonal space group I4 (N°79) (Table S1). The asymmetric unit is composed of one complex of [Dy(tta)3(L)], and its Ortep view is depicted in Figure S1. The Dy(tta)3 unit is linked to the 1,10-phenantroline-5,6-dione ligand (L) through the nitrogen bidentate coordination site and to three tta- ancillary ligands (Figure 1a). The nature and the arrangement of these ligands led to a N2O6 environment with a slightly distorted triangular dodecahedron symmetry (TDD-8) (the distortion from the ideal symmetry CShMTDD−8 = 0.455 was determined using the SHAPE 2.1 program [43] with CShM = Continuous Shape Measures).
The average Dy-Otta and Dy-N distances are 2.321(8) Å and 2.572(10) Å, respectively. The 1,10-phenantroline-5,6-dione oxidation state of the ligand was confirmed by the carbonyl bond lengths of 1.194(16) and 1.228(17) Å.
The crystal packing revealed a supramolecular assembly leading to the formation of tetramers through π-σ interactions between one carbonyl group and the central aromatic ring of the phenantroline moiety (O1· · · Cπ distances range from 2.885 to 3.168 Å) (Figure 2a). π-π interactions between the thiophene ring of the tta- ligand and the same central aromatic ring of the phenantroline moiety participate to the stabilization of the tetramers. The shortest Dy-Dy intermolecular distance is 9.845 Å.
[Dy(hfac)3(L)] (2). The X-ray structure of 2 is similar to that of 1. It crystallized in the tetragonal I4 space group (N°82) (Figure S2 and Table S1). The DyIII ion is coordinated to three hfac- ligands and to L through the nitrogen bischelating coordination site (Figure 1b). The difference of the electron withdrawing between tta- and hfac- led to a slight variation of the Dy-Ohfac and Dy-N bond lengths with 2.333(8) and 2.535(8) Å, respectively. The N2O6 coordination sphere with a D2d triangular dodecahedron symmetry is slightly more distorted than the one determined for 1 (CShMTDD−8 = 0.726). The oxidation of the L ligand is retained with C=O bond lengths of 1.210(14) and 1.198(12) Å. The supramolecular tetramers are stabilized only by the π-σ interaction (O1· · · Cπ distances range from 2.802 to 3.148 Å) (Figure 2b), since the thiophene rings were replaced by CF3 groups. The shortest Dy-Dy intermolecular distance is 9.247 Å.
The two complexes 1 and 2 highlighted crystal packing which completes the different intermolecular arrangements that could be observed in the literature for compounds made from tris(β-diketonate) of lanthanide associated with phenanthroline derivatives. Indeed, non-substituted phenantroline or π-extended phenantroline led to parallel complex arrangements thanks to π-π interactions [44], phenantroline substituted with an electron donor group such as tetrathiafulvalene led to “head-to-tail” parallel dimers of complexes through donor-acceptor and π-π interaction [45], and phenantroline substituted by an electron rich atom with lone pairs led to perpendicular arrangements of complexes like for compounds 1 and 2.

2.2. Magnetic Properties

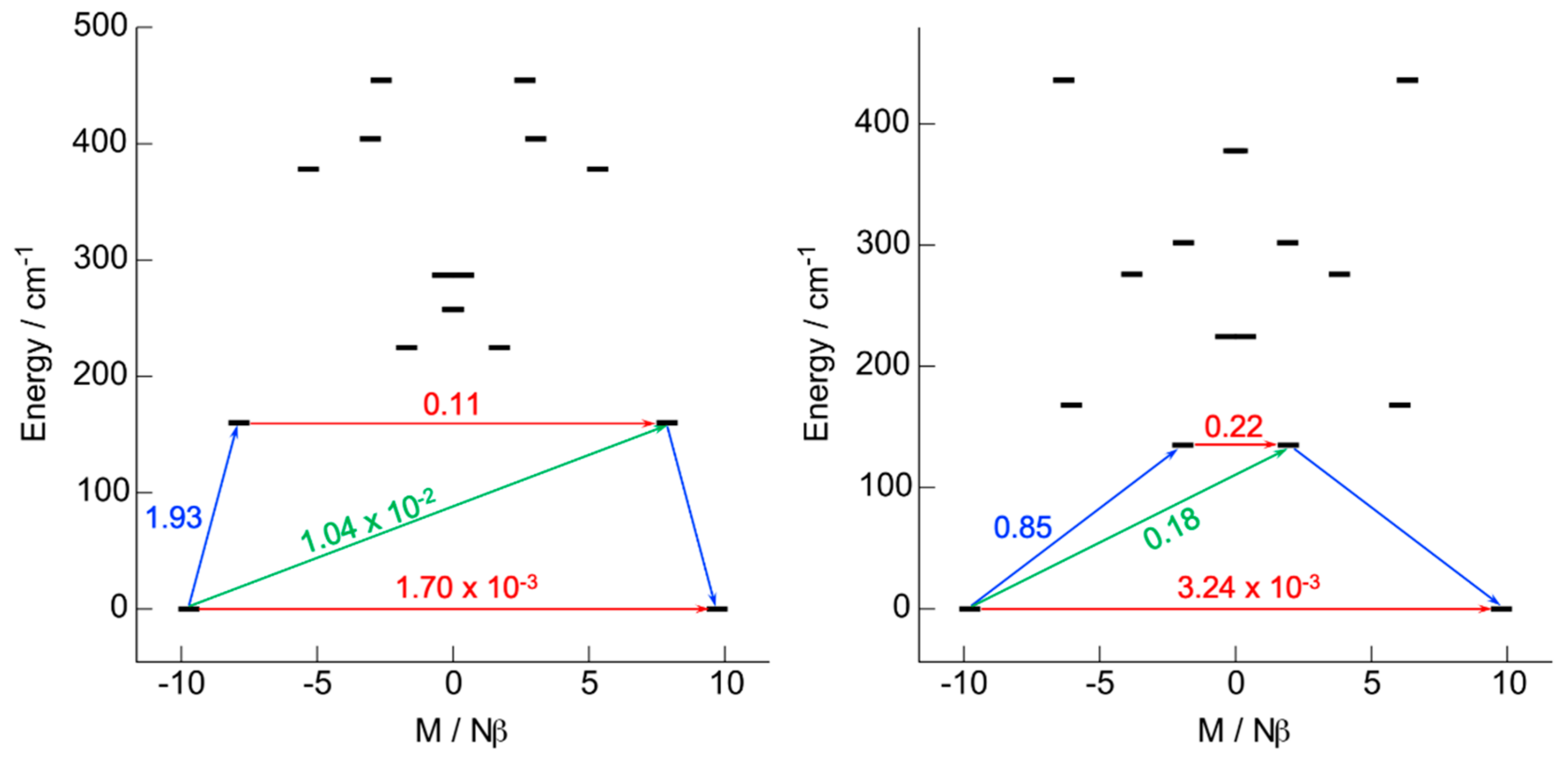
2.2.1. Ab Initio Calculations

State-Averaged-Complete Active Space Self-Consistent Field/Restricted Active Space State Interaction including Spin Orbit coupling (SA-CASSCF/RASSI-SO) calculations were performed for the two mononuclear complexes to extend the understanding and to rationalize the magnetic properties (see computational details). The computed energy splittings are depicted in Tables S2 and S3. For both systems, the DyIII center presents an almost pure Ising ground state, 92% MJ = | ± 15/2> for 1 and 95% MJ = | ± 15/2> for 2, defined by a g-tensor with a main component gZ = 19.43 for 1 and gZ = 19.56 for 2 and exhibiting negligible transversal components with gX = 0.00, gY = 0.01 for 1 and gX = 0.01, gY = 0.01 for 2. At this point, the Quantum Tunneling of the Magnetization (QTM) is expected weak, and a slow magnetic relaxation of the magnetization at zero field should be observable. One could observe that the weak difference of the uniaxial character of the magnetic anisotropy ground state follows the distortion trend of the coordination sphere. The main component of the ground state g-tensor of the DyIII center for each complex is represented in Figure 1. To give more insights on the orientation of the magnetic axis, the molecular electrostatic potential is investigated using the home-made Calculated Molecular Multipolar Electrostatics (CAMMEL) software which uses previously calculated Local Properties (LOPROP) charges to compute the electrostatic potential on a sphere centered on the lanthanide ion (see computational details). The resulting potential for both molecules is represented in Figure S3 along with the orientation of the ground state anisotropy. For both systems, the main magnetic component appears perpendicular to the plane containing the 1,10-phenantroline-5,6-dione ligand, i.e., the most charged direction as expected for an oblate ion [19]. The matrix elements of the transition magnetic moments between the Stark sub-levels for the Kramers ion of each complex have been computed in order to give more insights into the relaxation mechanisms (Figure 3). At the molecular scale, no major difference between the two compounds was identified except the higher energy gap between the ground and first excited state for 1 (230.4 K) than for 2 (194.3 K), as already observed when changing the hfac- ancillary ligands with tta- ones [45,46,47].

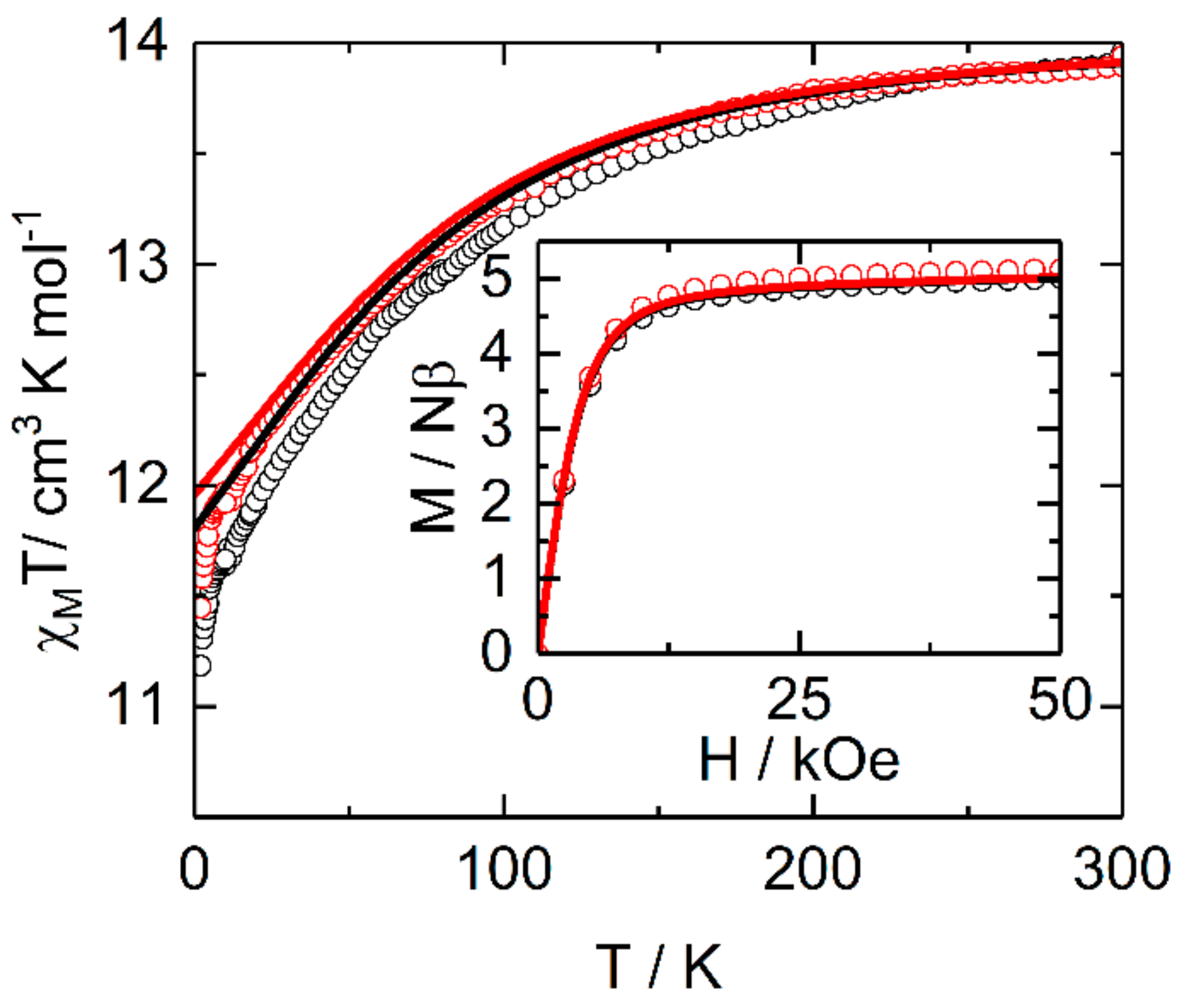
2.2.2. Static Magnetic Measurements

The dc magnetic properties of 1 and 2 were determined by measuring their thermal dependence on the magnetic susceptibility (Figure 4). The room temperature values are 13.90 cm3·K·mol−1 for compound 1 and 13.89 cm3·K·mol−1 for compound 2. These values are close to the expected one of 14.17 cm3·K·mol−1 for an isolated DyIII ion (6H15/2 ground state multiplet) [48]. Decreasing the temperature, χMT decreases monotonically down to 11.19 cm3·K·mol−1 for 1 and 11.45 cm3·K·mol−1 for 2 due to the thermal depopulation of the MJ states. Below 5 K, the decreasing is more pronounced, probably due to dominant antiferromagnetic intermolecular interactions (Figure 4).
The magnetization at 2 K displayed classical behavior for the isolated highly anisotropic DyIII ion. The simulated curves reproduced the experimental χMT(T) and M(H) measurements well, leading to the conclusions that the nature of the ground state and energy splitting are correctly computed and identified.

2.2.3. Dynamic Magnetic Measurements

The χM’ (in-phase) and χM’’ (out-of-phase) components of the ac susceptibility were measured for both compounds 1 and 2. For both compounds, a χM’’ was detected in the zero magnetic field, as suggested by ab initio calculations, with maxima localized at 310 Hz and 70 Hz at 2 K, respectively for 1 and 2. They highlighted a frequency dependence of the in-phase (Figure S4) and out-of-phase signal of the magnetization (Figure 5), allowing an analysis of the temperature variations (Tables S4 and S5) of the magnetic susceptibility in the framework of an extended Debye model (see SI) [49,50].
The out-of-phase component intensity of the magnetization is in agreement with the fact that almost 100% of the sample slowly relaxes, as shown by the normalized Argand (Figures S5 and S6). The Arrhenius plots of the relaxation time depicted in Figure 6 could be fitted in the zero field with a combination of two thermally activated regimes (Orbach and Raman) and one thermally independent regime (QTM): τ−1 = τ0−1exp(-Δ/kT) + CTn + τTI−1 (where τ is the relaxation time, Δ is the energy barrier, C is the Raman constant, n is the exponential constant describing the thermal dependence of the Raman and τTI is the relaxation time for the thermal independent regime). The best fits depicted in Figure 6 were obtained using the parameters of Table 1.
The involvement of the Raman process is supported by the discrepancy between the calculated energy barrier (Δ = 230.4 K for 1 and Δ = 194.3 K for 2) and the experimental barrier extracted from the high temperature region of the Arrhenius plot (Δ = 61(5) K for 1 and Δ = 83(5) K for 2) which can be explained by the operating under-barrier relaxation mechanism [51,52,53,54]. It is worth noting that a satisfying fit could only be obtained by fixing the energy gap to the computed value for each compound. The expected n value for Kramers ion should be 9 [48], but the presence of both acoustic and optical phonons could lead to lower values between 2 and 7 [55,56,57]. The anisotropy barrier values extracted for 1 and 2 are very close to those found for their analogues involving the 1,10-phenantroline ligand [58,59].
The application of an external magnetic field is efficient in cancelling the QTM. Thus, a field dependence of χM is studied (Figure 7 and Figure S7). For the two compounds, the presence of an external field led to a significant shift of the out-of-phase component to a lower frequency due to the cancelling of the fast relaxation of the magnetization through QTM.
1200 Oe and 1000 Oe have been chosen as optimal values of the applied magnetic field for 1 and 2, respectively. Under these applied fields, 1 and 2 highlighted a frequency dependence of the in-phase (Figure S8) and out-of-phase signals of the magnetization (Figure 8). An analysis of the framework of the extended Debye model allowed an extraction of the temperature dependence of the relaxation time (Figure 6, Tables S6 and S7). The out-of-phase component intensity of the magnetization and the normalized Argand indicated that almost the whole sample is slowly relaxing (Figures S9 and S10). The relaxation time follows two thermally dependent relaxation processes (Orbach and Raman) (Table 1). The best fit was obtained by fixing the Orbach process with the energy barrier (Δ) and relaxation time (τ0) determined for the corresponding compound for H = 0 Oe, since such a magnetic relaxation should be field-independent.
Replacing the tta- (compound 1) with hfac- (compound 2) led to a slowing down of the magnetic relaxation time, which is the inverse trend to that usually observed for such chemical engineering [45,46,47]. Indeed, from a molecular point of view, the replacement of hfac- by tta- led to a decrease of the coordination polyhedron distortion and an increase of the computed energy gap between the ground and first excited states (Tables S2 and S3). Thus, the explanation of the inverse trend might be of intermolecular origin with the presence of a significant antiferromagnetic interaction, as suggested by the quick decreasing of the χMT product at a very low temperature (Figure 4). Even if the σ-π interactions are similar in both compounds, the intermolecular distance between the DyIII ions, as well as the angles between the magnetic anisotropy vectors, change slightly, leading to a variation of the intermolecular magnetic interactions, which could modify the dynamic magnetic properties. Such a hypothesis is supported by the difference of the frequency dependence of χM’’ at 2 K under a 200 Oe applied field (Figure 7), which displayed a clear double contribution at frequencies of 2.5 and 400 Hz for 1 but not for 2. Such an observation should be an indication of stronger intermolecular dipolar interactions in 1 than in 2 [60].

3. Conclusions

In this article, two mononuclear DyIII complexes involving the 1,10-phenantroline-5,6-dione ligand (L) were structurally and magnetically studied. X-ray diffraction on a single crystal revealed a supramolecular assembly of four mononuclear compounds through σ-π interactions for the two [Dy(tta)3(L)] (1) and [Dy(hfac)3(L)] (2) derivatives. Both compounds behaved as a Single-Molecule Magnet in a zero applied magnetic field with the relaxation of the magnetization occurring through Orbach, Raman and QTM mechanisms. The latter could be efficiently cancelled under an optimal applied field, leading to the slowing of the magnetic relaxation. The experimental magnetic properties could be reproduced and rationalized by ab initio calculations. In zero and applied magnetic fields, 2 displayed better performances than 1, which is in contradiction to what is usually observed when changing the tta- ancillary ligand with hfac-. Such observations might be attributed to variations of the intermolecular dipolar interaction.

4. Materials and Methods

4.1. Synthesis General Procedures and Materials

The dysprosium complexes Dy(tta)3·2H2O (tta- = 2-thenoyltrifluoroacetonate anion) [61] and Dy(hfac)3·2H2O [62], as well as the 1,10-phenantroline-5,6-dione ligand [63] (L), were synthesized following previously reported methods. All other reagents were commercially available and used without further purification.

4.2. Synthesis of Complexes [Dy(tta)3(L)] (1) and [Dy(hfac)3(L)] (2)

[Dy(tta)3(L)] (1). 10.0 mg of L (0.048 mmol) were suspended in 10 mL of CH2Cl2, and then a solution of CH2Cl2 (9 mL) containing 41.0 mg of Dy(tta)3·2H2O (0.048 mmol) was added. The bright yellow suspension of L turned greenish with the addition of the DyIII salt. After 60 min of stirring at room temperature, 30 mL of n-hexane were layered. Suitable yellow single crystals for X-ray studies were obtained by slow diffusion. Yield (determined from isolated single crystals): 33 mg (67%). Anal. Calcd (%) for C36H18DyF9N2O8S3: C 41.69, H 1.74, N 2.70; found: C 41.74, H 1.83, N 2.66.
[Dy(hfac)3(L)] (2). The same experimental protocol was used replacing the Dy(tta)3·2H2O salt with 39.0 mg of Dy(hfac)3·2H2O. Yield: 28 mg (59%). Anal. Calcd (%) for C27H9DyF18N2O8: C 32.60, H 0.91, N 2.82; found: C 32.57, H 0.99, N 2.88.

4.3. Crystallography

Single crystals of 1 and 2 were mounted on an APEXIII D8 VENTURE Bruker-AXS diffractometer for data collection (MoKα radiation source, λ = 0.71073 Å), from the Centre de Diffractométrie (CDIFX), Université de Rennes 1, France (Table S1). The structure was solved and refined, respectively, with a direct method using the SHELXT program [64] and a full matrix least-squares method on F2 using the SHELXL-14/7 program [65]. The complete crystal structure results as a CIF file are deposited as Supporting Information. The CCDC number is 1,991,212 for 1 and 1,991,211 for 2.

4.4. Physical Measurements

The elemental analyses of the compounds were performed at the Centre Régional de Mesures Physiques de l’Ouest, Rennes. A Quantum Design MPMS-XL SQUID magnetometer was used to measure the dc magnetic susceptibility from solid polycrystalline samples. A 0.2 kOe, 2 kOe and 10 kOe magnetic field was applied respectively for the temperature ranges of 2–20 K, 20–80 K and 80–300 K. These measurements were all corrected for the diamagnetic contribution, as calculated with Pascal’s constants. The ac magnetic susceptibility measurements were performed on the same apparatus.

4.5. Computational Details

The atomic positions were extracted from the X-ray diffraction crystal structures of the 1 and 2 compounds. The wavefunction theory calculations (WFT) were carried out with the help of the OpenMolcas software package [66]. In these calculations, the complete active space self-consistent field [67] (CASSCF) approach was used to treat the static correlation effects arising from the partially filled 4f shell of the Dy(III) ion. The second-order Douglas-Kroll-Hess [68,69,70,71] scalar relativistic (SR) Hamiltonian was used to treat the scalar relativistic effects, in combination with the all-electron atomic natural orbital relativistically contracted (ANO-RCC) basis set from the Molcas library [72,73,74]. The basis sets were contracted to the triple-ζ plus polarization (TZP) quality for the Dy and O atoms bonded to the lanthanide (Dy = 25s22p15d11f4g2h/8s7p4d3f2g1h; O = 14s9p5d3f2g/4s3p2d1f), and to the double-ζ quality for H, C, F and S atoms (H = 8s4p3d1f/2s; C = 14s9p5d3f2g/3s2p, F = 14s9p5d3f2g/3s2p, S = 17s12p5d4f2g/4s3p1d). The calculations employed the state-averaged formalism at the SR level by taking into account the 21 sextet, the 224 quartet and the 490 doublet spin states arising from the 9 electrons spanning the seven 4f orbitals (i.e., CAS(9,7)). The spin-orbit coupling (SOC) was then introduced within a state interaction among the basis of calculated SR states using the restricted active space state interaction (RASSI) approach [75]. Herein the SOC matrix is diagonalized using the calculated 21 SR sextet, 224 SR quartet and the 98th lowest SR doublet spin states. The EPR g-factors were calculated according to [76], as implemented in the RASSI module of OpenMolcas, whereas the magnetic susceptibility and magnetization calculations were performed using the Single-Aniso of OpenMolcas, as detailed in [77].
The molecular electrostatic potential is calculated from the ab-initio LOPROP charge analysis [78]:
V r i = ∑ i N q i r i − r + p i ·   r i r i − r 3 + r i · Q i × r i r i − r 5
where q i , p , Q i and r i are respectively the charge, dipole, quadrupole moments and displacement vector of the i-th atom. The resulting molecular electrostatic potential is mapped and represented using the home-made CAMMEL code. The potential is drawn on a sphere defined by the user around the central lanthanide ion, for a given state (ground state in this case). For a clearer representation of the potential, the intensity can be directly related to both the color (red = high potential and blue = low potential) and the height of the irregularities. This program has already been used in previous works to give some hints on the orientation of magnetization axes [79,80].

Supplementary Materials

The following are available online at https://www.mdpi.com/2312-7481/6/2/19/s1, Figure S1. ORTEP view of 1. Thermal ellipsoids are drawn at 30% probability; Figure S2. ORTEP view of 2. Thermal ellipsoids are drawn at 30% probability; Figure S3. Molecular Electrostatic potential centered on the lanthanide ion for 1 (left) and 2 (right). The orientation of the ground state anisotropy axis is represented as a dark line. Figure S4. Frequency dependence of in-phase (χM’) and out-of-phase components (χM”) at 5 K for 1 in a zero applied magnetic field. Red lines are the best fitted curves; Figure S5. Frequency dependence of χM’ in the temperature range (a) 2–14 K for 1 and (b) 2–20 K for 2 in a zero applied magnetic field; Figure S6. Normalized Argand plot between 2 and 14 K for 1 in a zero applied magnetic field; Figure S7. Normalized Argand plot between 2 and 14 K for 2 in a zero applied magnetic field; Figure S8. Frequency dependence of χM’ at 2 K at various external fields for (a) 1 and (b) 2; Figure S9. Frequency dependence of χM’ in the temperature range 2–14 K for (a) 1 and for (b) 2 in a 1200 and 1000 Oe applied magnetic field, respectively; Figure S10. Normalized Argand plot between 2 and 14 K for 1 in a 1200 Oe applied magnetic field; Figure S11. Normalized Argand plot between 2 and 14 K for 2 in a 1000 Oe applied magnetic field; Table S1: X-ray crystallographic data for 1 and 2; Table S2: Computed energies, g-tensor and wavefunction composition of the ground state doublet in the effective spin ½ model for 1; Table S3: Computed energies, g-tensor and wavefunction composition of the ground state doublet in the effective spin ½ model for 2; Table S4: Best fitted parameters (χT, χS, τ and α) with the extended Debye model 1 at 0 Oe in the temperature range 2–13 K; Table S5: Best fitted parameters (χT, χS, τ and α) with the extended Debye model 2 at 0 Oe in the temperature range 2–13 K; Table S6: Best fitted parameters (χT, χS, τ and α) with the extended Debye model 1 at 1200 Oe in the temperature range 3.5–12 K; Table S7: Best fitted parameters (χT, χS, τ and α) with the extended Debye model 2 at 1000 Oe in the temperature range 3.5–14 K.

Author Contributions

O.G. performed the whole syntheses; V.D. realized the structure refinements; O.C. and J.F.G. performed and analyzed the magnetic data, V.M. and B.l.G. performed the ab initio calculations. F.P. conceived and designed the experiments and write the article with contributions of O.C and B.l.G. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by CNRS, Université de Rennes 1 and the European Commission through the ERC-CoG 725184 MULTIPROSMM (project n. 725184).

Acknowledgments

B.L.G. and V.M. thank the French GENCI/IDRIS-CINES center for high-performance computing resources.

Conflicts of Interest

The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.

Abbreviations

The following abbreviations are used in this manuscript:
SMMSingle Molecule Magnet
QTMQuantum Tunneling of the Magnetization
CH2Cl2dichloromethane
tta-2-thenoyltrifluoroacetonate
hfac-1,1,1,5,5,5-hexafluoroacetylacetonate
CASSCFComplete Active Space Self-Consistent Field
RASSI-SORestricted Active Space State Interaction – Spin-Orbit

References

  1. Bünzli, J.C.G.; Chauvin, A.-S.; Kim, H.K.; Deiters, E.; Eliseeva, S.V. Lanthanide luminescence efficiency in eight- and nine-coordinate complexes: Role of the radiative lifetime. Coord. Chem. Rev. 2010, 254, 2623–2633. [Google Scholar] [CrossRef]
  2. Bünzli, J.C.G. On the design of highly luminescent lanthanide complexes. Coord. Chem. Rev. 2015, 293–294, 19–47. [Google Scholar] [CrossRef]
  3. Woodruff, D.N.; Winpenny, R.E.P.; Layfield, R.A. Lanthanide Single-Molecule Magnets. Chem. Rev. 2013, 113, 5110–5148. [Google Scholar] [CrossRef]
  4. Sessoli, R.; Powell, A.K. Strategies towards single molecule magnets based on lanthanide ions. Coord. Chem. Rev. 2009, 253, 2328–2341. [Google Scholar] [CrossRef]
  5. Pointillart, F.; Cador, O.; Le Guennic, B.; Ouahab, L. Uncommon Lanthanide ions in purely 4f Single Molecule Magnets. Coord. Chem. Rev. 2017, 346, 150–175. [Google Scholar] [CrossRef]
  6. Bünzli, J.-C.G. Lanthanide Luminescence for Biomedical Analyses and Imaging. Chem. Rev. 2010, 110, 2729–2755. [Google Scholar] [CrossRef]
  7. Duke, R.M.; Veale, E.B.; Pfeffer, F.M.; Kruger, P.E.; Gunnlaugsson, T. Colorimetric and fluorescent anion sensors: An overview of recent developments in the use of 1,8-naphthalimide-based chemsensors. Chem. Soc. Rev. 2010, 39, 3936–3953. [Google Scholar] [CrossRef] [Green Version]
  8. Kuriki, K.; Koike, Y.; Okamoto, Y. Plastic Optical Fiber Lasers and Amplifiers Containing Lanthanide Complexes. Chem. Rev. 2002, 102, 2347–2356. [Google Scholar] [CrossRef]
  9. Moore, E.G.; Samuel, A.P.S.; Raymond, K.N. From Antenna to Assay: Lessons Learned in Lanthanide Luminescence. Acc. Chem. Res. 2009, 42, 542–552, and references therein. [Google Scholar] [CrossRef] [Green Version]
  10. Beeby, A.; Botchway, S.W.; Clarkson, I.M.; Faulkner, S.; Parker, A.M.; Parker, D.; Williams, J.A.G. Luminescence imaging microscopy and lifetime mapping using kinetically stable lanthanide(III) complexes. J. Photochem. Photobiol. B 2000, 57, 83–89. [Google Scholar] [CrossRef]
  11. Grichine, A.; Haefele, A.; Pascal, S.; Duperray, A.; Michel, R.; Andraud, C.; Maury, O. Millisecond lifetime imaging with a europium complex using a commercial confocal microscope under one or two-photon excitation. Chem. Sci. 2014, 5, 3475–3485. [Google Scholar] [CrossRef]
  12. Van Vleck, J.H. The Puzzle of Rare-earth Spectra in Solids. J. Phys. Chem. 1937, 41, 67–80. [Google Scholar] [CrossRef]
  13. D’Aléo, A.; Pointillart, F.; Ouahab, L.; Andraud, C.; Maury, O. Charge transfer excited states sensitization of lanthanide emitting from the visible to the near-infrared. Coord. Chem. Rev. 2012, 256, 1604–1620. [Google Scholar] [CrossRef]
  14. Pointillart, F.; Le Guennic, B.; Cador, O.; Maury, O.; Ouahab, L. Lanthanide Ion and Tetrathiafulvalene-Based Ligand as a “Magic” Couple toward Luminescence, Single Molecule Magnets, and Magnetostructural Correlations. Acc. Chem. Res. 2015, 48, 2834–2842. [Google Scholar] [CrossRef]
  15. Zhu, Z.; Guo, M.; Li, X.-L.; Tang, J. Molecular magnetism of lanthanide: Advances and perspectives. Coord. Chem. Rev. 2019, 378, 350–364. [Google Scholar] [CrossRef]
  16. Mannini, M.; Pineider, F.; Sainctavit, P.; Danieli, C.; Otero, E.; Sciancalepore, C.; Talarico, A.M.; Arrio, M.-A.; Cornia, A.; Gatteschi, D.; et al. Magnetic memory of a single-molecule quantum magnet wired to a gold surface. Nat. Mater. 2009, 8, 194–197. [Google Scholar] [CrossRef]
  17. Thiele, S.; Balestro, F.; Ballou, R.; Klyatskaya, S.; Ruben, M.; Wernsdorfer, W. Electrically driven nuclear spin resonance in single-molecule magnets. Science 2014, 344, 1135–1138. [Google Scholar] [CrossRef]
  18. Pedersen, K.S.; Ariciu, A.-M.; McAdams, S.; Weihe, H.; Bendix, J.; Tuna, F.; Piligkos, S. Toward Molecular 4f Single-Ion Magnet Qubits. J. Am. Chem. Soc. 2016, 138, 5801–5804. [Google Scholar] [CrossRef]
  19. Rinehart, J.D.; Long, J.R. Exploiting single-ion anisotropy in the design of f-element single-molecule magnets. Chem. Sci. 2011, 2, 2078–2085. [Google Scholar] [CrossRef]
  20. Guo, F.-S.; Day, B.-M.; Chen, Y.-C.; Tong, M.-L.; Mansikkamäki, A.; Layfield, R.A. A Dysprosium Metallocene Single-Molecule Magnet Functioning at the Axial Limit. Angew. Chem. Int. Ed. 2017, 56, 11445–11449. [Google Scholar] [CrossRef]
  21. Goodwin, C.A.P.; Ortu, F.; Reta, D.; Chilton, N.F.; Mills, D.P. Molecular magnetic hysteresis at 60 kelvin in dysprosocenium. Nature 2017, 548, 439–442. [Google Scholar] [CrossRef] [PubMed]
  22. McClain, K.R.; Gould, C.A.; Chakarawet, K.; Teat, S.J.; Groshens, T.J.; Long, J.R.; Harvey, B.G. High-temperature magnetic blocking and magneto-structural correlations in a series of dysprosium(III) metallocenium single-molecule magnets. Chem. Sci. 2018, 9, 8492–8503. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  23. Guo, F.-S.; Day, B.-M.; Chen, Y.-C.; Tong, M.-L.; Mansikkamäki, A.; Layfield, R.A. Magnetic hysteresis up to 80 kelvin in a dysprosium metallocene single-molecule magnet. Science 2018, 362, 1400–1403. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  24. Feng, M.; Pointillart, F.; Lefeuvre, B.; Dorcet, V.; Golhen, S.; Cador, O.; Ouahab, L. Multiple Single-Molecule Magnet Behaviors in Dysprosium Dinuclear Complexes Involving a Multiple Functionalized Tetrathiafulvalene-Based Ligand. Inorg. Chem. 2015, 54, 4021–4028. [Google Scholar] [CrossRef] [PubMed]
  25. Pointillart, F.; Guizouarn, T.; Lefeuvre, B.; Golhen, S.; Cador, O.; Ouahab, L. Rational Design of a Lanthanide-Based Complex Featuring Different Single-Molecule Magnets. Chem. Eur. J. 2015, 21, 16929–16934. [Google Scholar] [CrossRef] [PubMed]
  26. Speed, S.; Feng, M.; Fernandez Garcia, G.; Pointillart, F.; Lefeuvre, B.; Riobé, F.; Golhen, S.; Le Guennic, B.; Totti, F.; Guyot, Y.; et al. Lanthanide complexes involving multichelating TTF-based ligands. Inorg. Chem. Front. 2017, 4, 604–617. [Google Scholar] [CrossRef]
  27. Cador, O.; Le Guennic, B.; Ouahab, L.; Pointillart, F. Decorated Tetrathiafulvalene-Based Ligands: Powerful Chemical Tools for the Design of Single-Molecule Magnets. Eur. J. Inorg. Chem. 2020, 148–164. [Google Scholar] [CrossRef] [Green Version]
  28. Shukla, A.D.; Das, A. Redox responsive binuclear complexes using 5,6-dihydroxy-1,10-phenantroline as a bridging ligands: Synthesis, characterization and physicochemical studies. Polyhedron 2000, 19, 2605–2611. [Google Scholar] [CrossRef]
  29. Yuasa, J.; Suenobu, T.; Fukuzumi, S. Thermochromism of Metal Ion Complexes of Semiquinone Radical Anions. Control of Equilibria between Diamagnetic and Paramagnetic Species by Lewis Acids. J. Phys. Chem. A 2005, 109, 9356–9362. [Google Scholar] [CrossRef]
  30. Minkin, V.I.; Starikova, A.A.; Starikov, A.G. Quantum chemical modeling of magnetically bistable metal coordination compounds. Synchronization of spin crossover, valence tautomerism and charge transfer induced spin transition mechanisms. Dalton Trans. 2016, 45, 12103–12113. [Google Scholar] [CrossRef]
  31. Cador, O.; Le Guennic, B.; Pointillart, F. Electro-Activity and Magnetic Switching in Lanthanide-Based Single-Molecule Magnets. Inorg. Chem. Front. 2019, 6, 3398–3417. [Google Scholar] [CrossRef] [Green Version]
  32. Tropiano, M.; Kilah, N.L.; Morten, M.; Rahman, H.; Davis, J.J.; Beer, P.D.; Faulkner, S. Reversible Luminescence Switching of a Redox-Active Ferrocene-Europium Dyad. J. Am. Chem. Soc. 2011, 133, 11847–11849. [Google Scholar] [CrossRef] [PubMed]
  33. Molloy, J.K.; Jarjayes, O.; Philouze, C.; Fedele, L.; Imbert, D.; Thomas, F. A redox active switch for lanthanide luminescence in phenolate complexes. Chem. Commun. 2017, 53, 605–608. [Google Scholar] [CrossRef] [PubMed]
  34. Subhan, M.A.; Rahman, M.S.; Alam, K.; Hasan, M.M. Spectroscopic analysis, DNA binding and antimicrobial activities of metal complexes with phendione and its derivative. Spectrochim. Acta A 2014, 118, 944–950. [Google Scholar] [CrossRef] [PubMed]
  35. Li, Y.; Zhang, D.; Xu, H.; Tao, X.; Shen, Y. Preparation and Photoluminescent Properties of Doped Ternary Europium Complexes Bearing 1-(Naphthalen-2-yl)-3-phenylpropane-1,3-dione. Adv. Mater. Res. 2011, 239-242, 3161–3164. [Google Scholar] [CrossRef]
  36. Zhang, X.-F.; Xu, C.-J.; Wan, J. Mono- and dinuclear europium(III) complexes with thenoyltrifluoroacetone and 1,10-phenantroline-5,6-dione. Chem. Mon. 2014, 145, 1913–1917. [Google Scholar] [CrossRef]
  37. Song, Y.-M.; Xu, J.-P.; Ding, L.; Hou, Q.; Liu, J.-W.; Zhu, Z.-L. Syntheses, characterization and biological activities of rare earth metal complexes with curcumin and 1,10-phenantroline-5,6-dione. J. Inorg. Biochem. 2009, 103, 396–400. [Google Scholar] [CrossRef]
  38. Li, Y.; Li, Y.; Xu, H.; Tao, X.; Zhang, D.; Shen, Y. Synthesis and photoluminescent properties of doped ternary Eu1-xLnx(NPPD)3⋅DPQ complexes. J. Rare Earths 2010, 28, 654–659. [Google Scholar] [CrossRef]
  39. Li, Y.; Li, Y.; Chu, Y.; Tao, X.; Xu, H.; Shen, Y.; Zheng, A. An experimental and quantum mechanical study on luminescence properties of SM(β-Nbm)3⋅Pd. J. Lumin. 2012, 132, 1663–1667. [Google Scholar] [CrossRef]
  40. Shavaleev, N.M.; Moorcraft, L.P.; Pope, S.J.A.; Bell, Z.R.; Faulkner, S.; Ward, M.D. Sensitized near-infrared emission from lanthanides using a covalently-attached Pt(II) fragment as an antenna group. Chem. Commun. 2003, 1134–1135. [Google Scholar] [CrossRef]
  41. Shavaleev, N.M.; Moorcraft, L.P.; Pope, S.J.A.; Bell, Z.R.; Faulkner, S.; Ward, M.D. Sensitized Near-Infrared Emission from Complexes of YbIII, NdIII and ErIII by Energy-Transfer from Covalently Attached PtII-Based Antenna Units. Chem. Eur. J. 2013, 9, 5283–5291. [Google Scholar] [CrossRef] [PubMed]
  42. Hickson, J.R.; Horsewill, S.J.; Bamforth, C.; McGuire, J.; Wilson, C.; Sproules, S.; Farnaby, J.H. The modular synthesis of rare earth-transition metal heterobimetallic complexes utilizing a redox-active ligand. Dalton Trans. 2018, 47, 10692–10701. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  43. Llunell, M.; Casanova, D.; Cirera, J.; Alemany, P.; Alvarez, S. SHAPE Program for the Stereochemical Analysis of Molecular Fragments by Means of Continuous Shape Measures and Associated Tools; Departament de Quimica Fisica, Departament de Quimica Inorganica and Institut de Quimica Teorica i Computacional—Universitat de Barcelona: Barcelona, Spain, 2010. [Google Scholar]
  44. Chen, G.-J.; Guo, Y.-N.; Tian, J.-L.; Tang, J.; Gu, W.; Liu, X.; Yan, S.-P.; Cheng, P.; Liao, D.-Z. Enhancing Anisotropy Barriers of Dysprosium(III) Single-Ion Magnets. Chem. Eur. J. 2012, 18, 2484–2487. [Google Scholar] [CrossRef]
  45. Pointillart, F.; Jung, J.; Berraud-Pache, R.; Le Guennic, B.; Dorcet, V.; Golhen, S.; Cador, O.; Maury, O.; Guyot, Y.; Decurtins, S.; et al. Luminescence and Single-Molecule Magnet Behavior in Lanthanide Complexes Involving a Tetrathiafulvalene-Fused Dipyridophenazine Ligand. Inorg. Chem. 2015, 54, 5384–5397. [Google Scholar] [CrossRef]
  46. Da Cunha, T.T.; Jung, J.; Boulon, M.-E.; Campo, G.; Pointillart, F.; Pereira, C.L.M.; Le Guennic, B.; Cador, O.; Bernot, K.; Pineider, F.; et al. Magnetic Poles Determinations and Robustness of Memory Effect upon Solubilization in a DyIII-Based Single Ion Magnet. J. Am. Chem. Soc. 2013, 135, 16332–16335. [Google Scholar] [CrossRef] [Green Version]
  47. Fernandez-Garcia, G.; Flores Gonzalez, J.; Ou-Yang, J.-K.; Saleh, N.; Pointillart, F.; Cador, O.; Guizouarn, T.; Totti, F.; Ouahab, L.; Crassous, J.; et al. Slow Magnetic Relaxation in Chiral Helicene-Based Coordination Complex of Dysprosium. Magnetochemistry 2017, 3, 2. [Google Scholar] [CrossRef] [Green Version]
  48. Kahn, O. Molecular Magnetism; VCH: Weinhem, Germany, 1993. [Google Scholar]
  49. Dekker, C.; Arts, A.F.M.; Wijn, H.W.; van Duyneveldt, A.J.; Mydosh, J.A. Activated dynamics in a two-dimensional Ising spin glass: Rb2Cu1-xCoxF4. Phys. Rev. B 1989, 40, 11243–11251. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  50. Cole, K.S.; Cole, R.H. Dipersion and Absorption in Dielectrics I. Alternating Current Characteristics. J. Chem. Phys. 1941, 9, 341–351. [Google Scholar] [CrossRef] [Green Version]
  51. Zadrozny, J.M.; Atanasov, M.; Bryan, A.M.; Lin, C.-Y.; Rekken, B.D.; Power, P.P.; Neese, F.; Long, J.R. Slow magnetization dynamics in a series of two-coordinate iron(II) complexes. Chem. Sci. 2013, 4, 125–138. [Google Scholar] [CrossRef]
  52. Pedersen, K.S.; Dreiser, J.; Weihe, H.; Sibille, R.; Johannesen, H.V.; Sorensen, M.A.; Nielsen, B.E.; Sigrist, M.; Mutka, H.; Rols, S.; et al. Design of Single-Molecule Magnets: Insufficiency of the Anisotropy Barrier as the Sole Criterion. Inorg. Chem. 2015, 54, 7600–7606. [Google Scholar] [CrossRef]
  53. Chibotaru, L.F.; Ungur, L.; Soncini, A. The Origin of Nonmagnetic Kramers Doublets in the Ground State of Dysprosium Triangles: Evidence for a Toroidal Magnetic Moment. Angew. Chem. Int. Ed. 2008, 47, 4126–4129. [Google Scholar] [CrossRef] [Green Version]
  54. Lunghi, A.; Totti, F. The role of Anisotropic Exchange in Single Molecule Magnets: A CASSCF/NEVPT2 Study of the Fe4 SMM Building Block [Fe2(OCH3)2(dbm)4] Dimer. Inorganics 2016, 4, 28. [Google Scholar] [CrossRef] [Green Version]
  55. Singh, A.; Shrivastava, K.N. Optical-acoustic two-phonon relaxation in spin systems. Phys. Status Solidi B 1979, 95, 273–277. [Google Scholar] [CrossRef]
  56. Shirivastava, K.N. Theory of Spin-Lattice Relaxation. Phys. Status Solidi B 1983, 177, 437–458. [Google Scholar] [CrossRef]
  57. Goodwin, C.A.P.; Reta, D.; Ortu, F.; Chilton, N.F.; Mills, D.P. Synthesis and Electronic Structures of Heavy Lanthanide Metallocenium Cations. J. Am. Chem. Soc. 2017, 139, 18714–18724. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  58. Chen, G.-J.; Gao, C.-Y.; Tian, J.-L.; Tang, J.; Gu, W.; Liu, X.; Yan, S.-P.; Liao, D.-Z.; Cheng, P. Coordination-perturbed single-molecule magnet behavior of mononuclear dysprosium complexes. Dalton Trans. 2011, 40, 5579–5583. [Google Scholar] [CrossRef] [PubMed]
  59. Bi, Y.; Guo, Y.-N.; Zhao, L.; Guo, Y.; Lin, S.-Y.; Jiang, S.-D.; Tang, J.; Wang, B.-W.; Gao, S. Capping Ligand Perturbed Slow Magnetic Relaxation in Dysprosium Single-Ion Magnets. Chem. Eur. J. 2011, 17, 12476–12481. [Google Scholar] [CrossRef] [PubMed]
  60. Ho, L.T.A.; Chibotaru, L.F. Intermolecular mechanism for multiple maxima in molecular dynamic susceptibility. Phys. Rev. B 2018, 98, 174418. [Google Scholar] [CrossRef] [Green Version]
  61. Vooshin, A.I.; Shavaleev, N.M.; Kazakov, V.P. Chemiluminescence of praseodymium (III), neodymium (III) and ytterbium (III) β-diketonates in solution excited from 1,2-dioxetane decomposition and singlet-singlet energy transfer from ketone to rare-earth β-diketonates. J. Lumin. 2000, 91, 49–58. [Google Scholar] [CrossRef]
  62. Richardson, M.F.; Wagner, W.F.; Sands, D.E. Rare-earth trishexafluoroacetylacetonates and related compounds. J. Inorg. Nucl. Chem. 1968, 30, 1275–1289. [Google Scholar] [CrossRef]
  63. Wang, C.; Lystrom, L.; Yin, H.; Hetu, M.; Kilina, S.; McFarland, S.A.; Sun, W. Increasing the triplet lifetime and extending the ground-state absorption of bicyclometalated Ir(III) complexes for reverse saturable absorption and photodynamic therapy applications. Dalton Trans. 2016, 45, 16366–16378. [Google Scholar] [CrossRef] [PubMed]
  64. Sheldrick, G.L. SHELXT—Integrated space-group and crystal-structure determination. Acta Crystallogr. Sect. A Found Adv. 2015, 71, 3–8. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  65. Sheldrick, G.M. Crystal structure refinement with SHELXL. Acta Crystallogr. Sect. C Struct. Chem. 2015, 71, 3–8. [Google Scholar] [CrossRef] [PubMed]
  66. Aquilante, F.; Autschbach, J.; Carlson, R.K.; Chibotaru, L.F.; Delcey, M.G.; De Vico, L.; Galván, I.F.; Ferré, N.; Frutos, L.M.; Gagliardi, L.; et al. Molcas 8: New Capabilities for Multiconfigurational Quantum Chemical Calculations Across the Periodic Table. J. Comput. Chem. 2016, 37, 506–541. [Google Scholar] [CrossRef] [Green Version]
  67. Roos, B.O.; Taylor, P.R.; Siegbahn, P.E.M. A Complete Active Space SCF Method (CASSCF) Using a Density Matrix Formulated Super-CI Approach. Chem. Phys. 1980, 48, 157–173. [Google Scholar] [CrossRef]
  68. Douglas, M.; Kroll, N.M. Quantum electrodynamical corrections to the fine structure of helium. Ann. Phys. 1974, 82, 89–155. [Google Scholar] [CrossRef]
  69. Hess, B.A. Applicability of the no-pair equation with free-particle projection operators to atomic and molecular structure calculations. Phys. Rev. A 1985, 32, 756–763. [Google Scholar] [CrossRef]
  70. Hess, B.A. Relativistic electronic-structure calculations employing a two-component no-pair formalism with external-field projection operators. Phys. Rev. A 1986, 33, 3742–3748. [Google Scholar] [CrossRef] [Green Version]
  71. Wolf, A.; Reiher, M.; Hess, B.A. The generalized Douglas-Kroll transformation. J. Chem. Phys. 2002, 117, 9215–9226. [Google Scholar] [CrossRef] [Green Version]
  72. Widmark, P.-O.; Malmqvist, P.-A.; Roos, B.-O. Density matrix averaged atomic natural orbital (ANO) basis sets for correlated molecular wave functions. Theor. Chim. Acta 1990, 77, 291–306. [Google Scholar] [CrossRef]
  73. Roos, B.O.; Lindh, R.; Malmqvist, P.A.; Veryazov, V.; Widmark, P.O. Main Group Atoms and Dimers Studied with A New Relativistic ANO Basis Set. J. Phys. Chem. A. 2004, 108, 2851–2858. [Google Scholar] [CrossRef]
  74. Roos, B.O.; Lindh, R.; Malmqvist, P.-A.; Veryazov, V.; Widmark, P.-O. New Relativistic ANO Basis Sets for Transition Metal Atoms. J. Phys. Chem. A 2005, 109, 6575–6579. [Google Scholar] [CrossRef] [PubMed]
  75. Malmqvist, P.-A.; Roos, B.O.; Schimmelpfennig, B. The Restricted Active Space (RAS) state Interaction Approach with Spin-Orbit Coupling. Chem. Phys. Lett. 2002, 357, 230–240. [Google Scholar] [CrossRef]
  76. Bolvin, H. An alternative approach to the g-matrix: Theory and applications. ChemPhysChem 2006, 7, 1575–1589. [Google Scholar] [CrossRef]
  77. Chibotaru, L.F.; Ungur, L. Ab Initio Calculation of Anisotropic Magnetic Properties of Complexes. I. Unique Definition of Pseudospin Hamiltonians and Their Derivation. J. Chem. Phys. 2012, 137, 064112. [Google Scholar] [CrossRef]
  78. Gagliardi, L.; Lindh, R.; Karlström, G. Local properties of quantum chemical systems: The LoProp approach. J. Chem. Phys. 2004, 121, 4494–4500. [Google Scholar] [CrossRef] [Green Version]
  79. Zhang, K.; Montigaud, V.; Cador, O.; Li, G.-P.; Le Guennic, B.; Tang, J.; Wang, Y.-Y. Tuning Magnetic Interactions in Dy(III)4 Single-Molecule Magnets. Inorg. Chem. 2018, 57, 8550–8557. [Google Scholar] [CrossRef] [Green Version]
  80. Huang, G.; Fernandez-Garcia, G.; Badiane, I.; Camarra, M.; Freslon, S.; Guillou, O.; Daiguebonne, C.; Totti, F.; Cador, O.; Guizouarn, T.; et al. Magnetic Slow Relaxation in a Metal–Organic Framework Made of Chains of Ferromagnetically Coupled SingleMolecule Magnets. Chem. Eur. J. 2018, 24, 6983–6991. [Google Scholar] [CrossRef] [Green Version]
Magnetochemistry 06 00019 g001 550
Figure 1. Molecular structures of 1 (a) and 2 (b) with representation of the main component (gz) of the computed ground state anisotropy axis. Color code: gray: carbon, dark blue: nitrogen, red: oxygen, green: fluoride, yellow: sulfur, blue: dysprosium, white: hydrogen.
Figure 1. Molecular structures of 1 (a) and 2 (b) with representation of the main component (gz) of the computed ground state anisotropy axis. Color code: gray: carbon, dark blue: nitrogen, red: oxygen, green: fluoride, yellow: sulfur, blue: dysprosium, white: hydrogen.
Magnetochemistry 06 00019 g001
Magnetochemistry 06 00019 g002 550
Figure 2. Crystal packing of (a) 1 and (b) 2 with highlights of the π-σ interaction.
Figure 2. Crystal packing of (a) 1 and (b) 2 with highlights of the π-σ interaction.
Magnetochemistry 06 00019 g002
Magnetochemistry 06 00019 g003 550
Figure 3. Energies (in cm−1) and M (in Nβ) (where Nβ = Bohr Magnetons) values for the Kramers doublet states of 1 (Left) and 2 (Right). The values of the magnetic (i.e., isotropic Zeeman) transition moments between the states are given for comparison. The horizontal red values correspond to QTM (for the GS) and Thermal Activated (TA)-QTM (for the ESs) mechanisms of the magnetization relaxation, whereas the blue and green arrows correspond to thermal and Orbach mechanisms, respectively.
Figure 3. Energies (in cm−1) and M (in Nβ) (where Nβ = Bohr Magnetons) values for the Kramers doublet states of 1 (Left) and 2 (Right). The values of the magnetic (i.e., isotropic Zeeman) transition moments between the states are given for comparison. The horizontal red values correspond to QTM (for the GS) and Thermal Activated (TA)-QTM (for the ESs) mechanisms of the magnetization relaxation, whereas the blue and green arrows correspond to thermal and Orbach mechanisms, respectively.
Magnetochemistry 06 00019 g003
Magnetochemistry 06 00019 g004 550
Figure 4. Temperature dependence of χMT for 1 (black open circles) and 2 (red open circles). In the inset, the field variations of the magnetization at 2 K for 1 (black open circles) and 2 (red open circles). Full black and red lines correspond to the best computed curves.
Figure 4. Temperature dependence of χMT for 1 (black open circles) and 2 (red open circles). In the inset, the field variations of the magnetization at 2 K for 1 (black open circles) and 2 (red open circles). Full black and red lines correspond to the best computed curves.
Magnetochemistry 06 00019 g004
Magnetochemistry 06 00019 g005 550
Figure 5. Frequency dependence of χM’’ between 2 and 14 K for (a) 1 and for (b) 2 in the zero applied magnetic field.
Figure 5. Frequency dependence of χM’’ between 2 and 14 K for (a) 1 and for (b) 2 in the zero applied magnetic field.
Magnetochemistry 06 00019 g005
Magnetochemistry 06 00019 g006 550
Figure 6. Temperature dependences of the relaxation times (τ) at 0 Oe (full black circles) and 1200 Oe (open black circles) for 1 and at 0 Oe (full blue circles) and 1000 Oe (open blue circles) for 2. Full and dashed lines are the best fitted curves with the parameters given in the text.
Figure 6. Temperature dependences of the relaxation times (τ) at 0 Oe (full black circles) and 1200 Oe (open black circles) for 1 and at 0 Oe (full blue circles) and 1000 Oe (open blue circles) for 2. Full and dashed lines are the best fitted curves with the parameters given in the text.
Magnetochemistry 06 00019 g006
Magnetochemistry 06 00019 g007 550
Figure 7. Frequency dependence of χM’’ at 2 K at various external fields for (a) 1 and (b) 2.
Figure 7. Frequency dependence of χM’’ at 2 K at various external fields for (a) 1 and (b) 2.
Magnetochemistry 06 00019 g007
Magnetochemistry 06 00019 g008 550
Figure 8. Frequency dependence of χM’’ (a) between 2 and 12 K for 1 and (b) between 2 and 14 K for 2 in 1200 and 1000 Oe applied magnetic fields, respectively.
Figure 8. Frequency dependence of χM’’ (a) between 2 and 12 K for 1 and (b) between 2 and 14 K for 2 in 1200 and 1000 Oe applied magnetic fields, respectively.
Magnetochemistry 06 00019 g008
Table
Table 1. Dynamic parameters of the different relaxation mechanisms for 1 and 2.
Table 1. Dynamic parameters of the different relaxation mechanisms for 1 and 2.
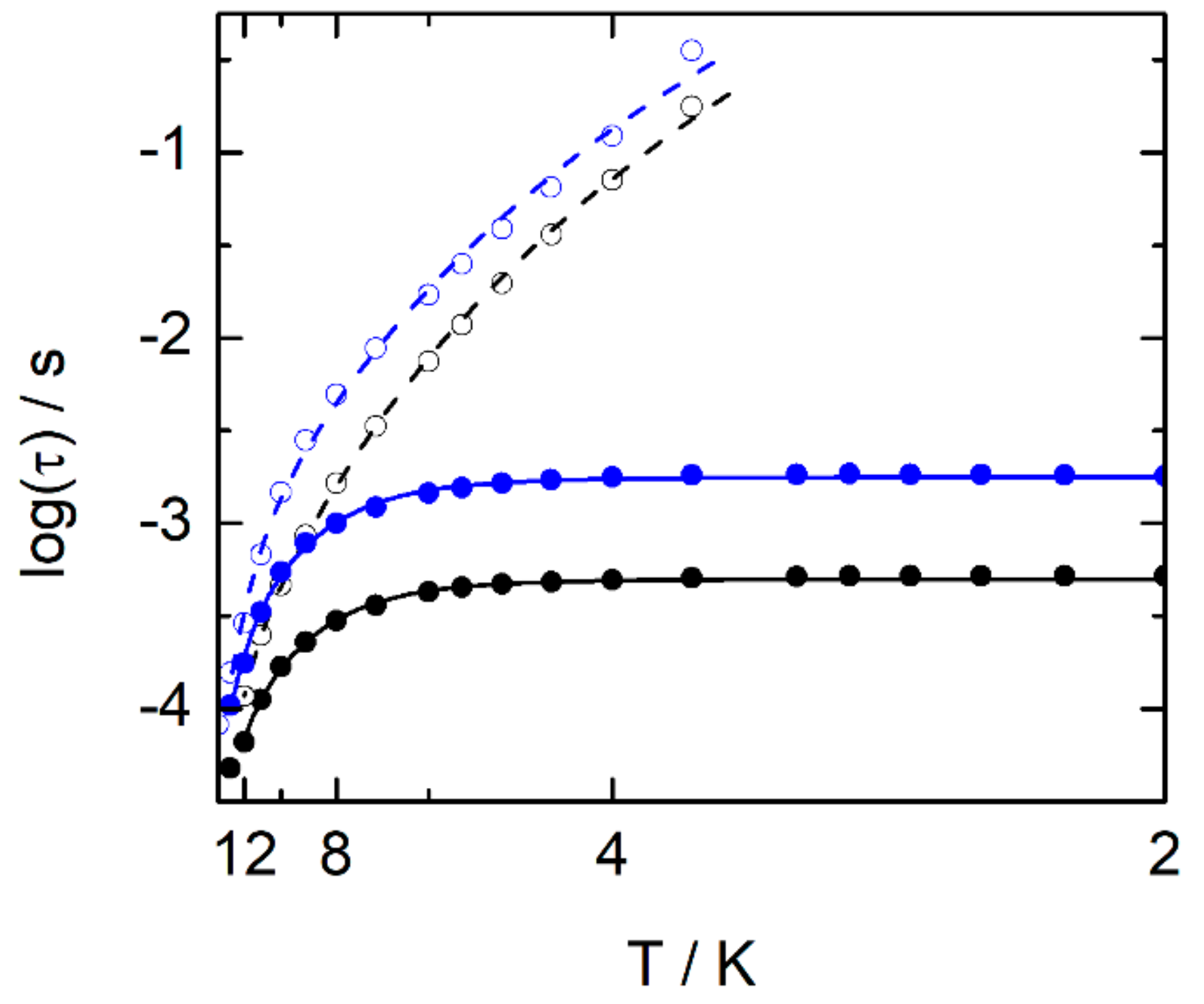
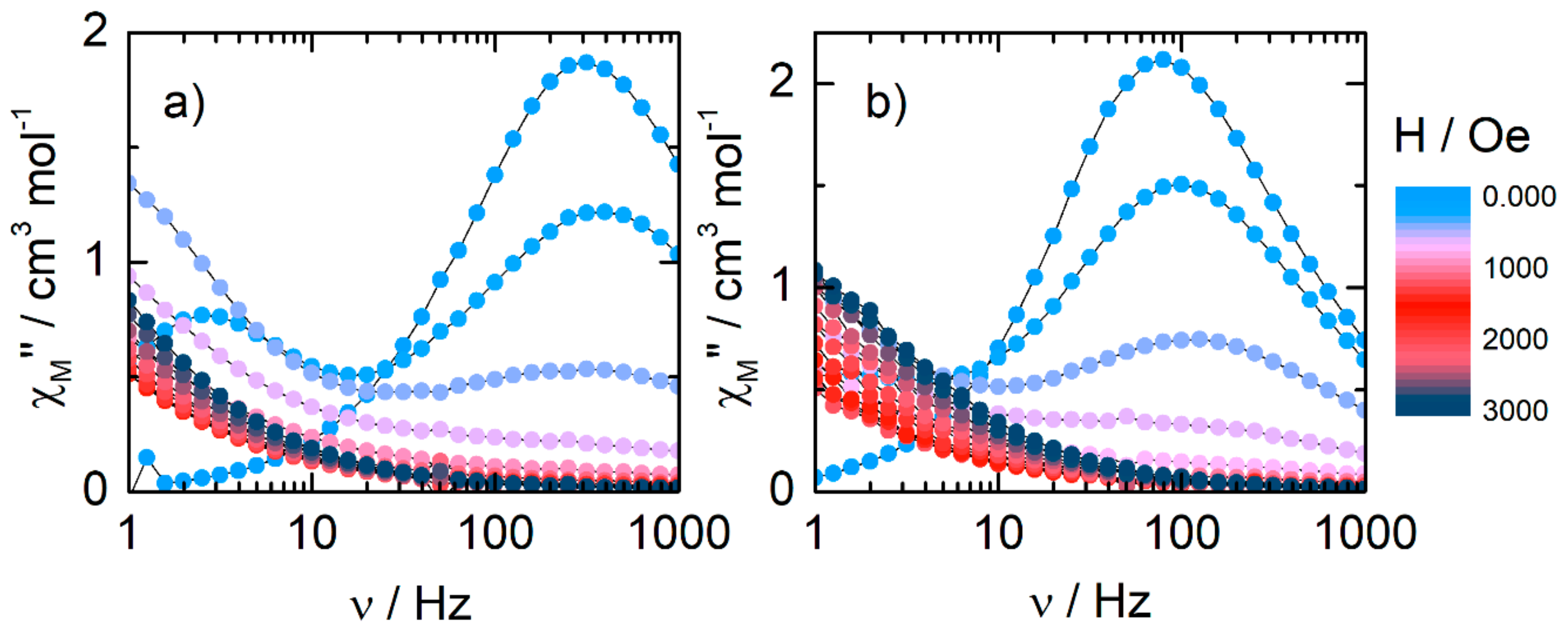
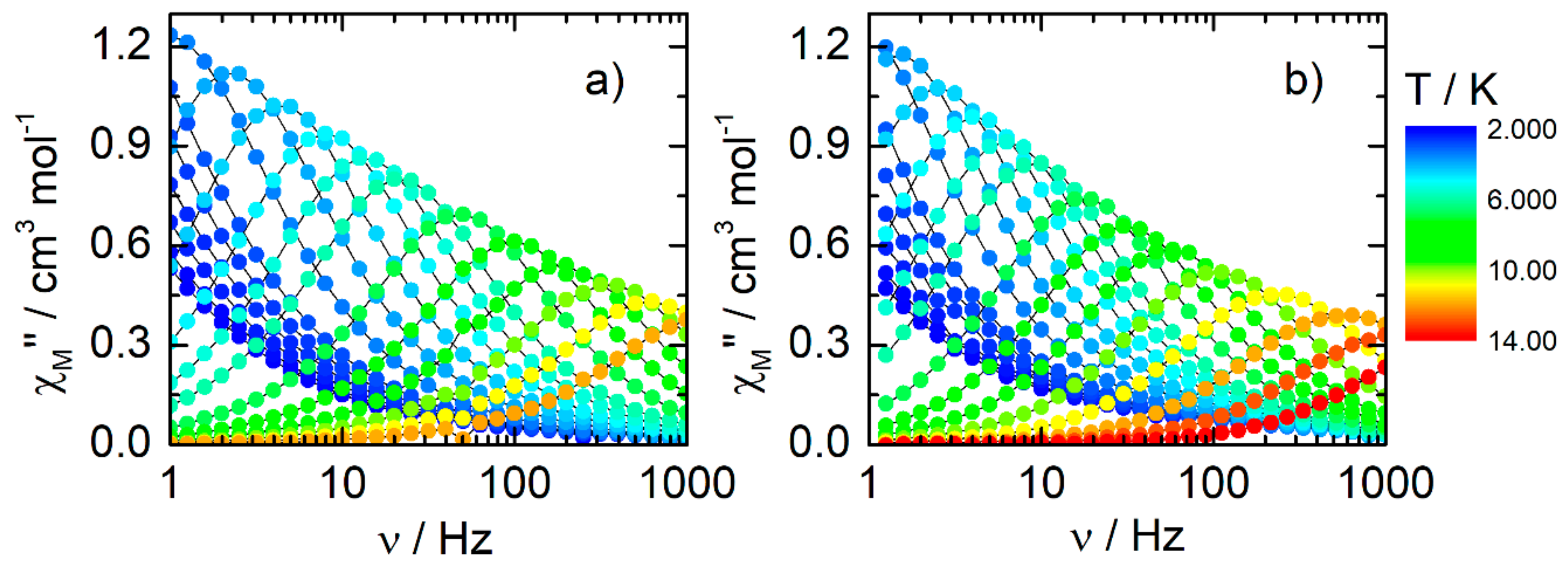
CompoundsField (Oe)OrbachRamanQTM
10Δ = 230.4 K (fixed)
τ0 = 1.66(29) × 10−12 s		C = 0.04(3) s−1K−n
n = 4.96(32)		τTI = 5.03(14) × 10−4 s
1000Δ = 230.5 K (fixed)
τ0 = 1.66(29) × 10−12 s (fixed)		C = 0.0068(6) s−1K−n
n = 5.50(7)
20Δ = 194.3 K (fixed)
τ0 = 6.80(11) × 10−11 s		C = 0.013(19) s−1K−n
n = 5.00(61)		τTI = 1.78(11) × 10−3 s
1000Δ = 194.3 K (fixed)
τ0 = 6.80(11) × 10−11 s (fixed)		C = 0.0084(16) s−1K−n
n = 4.90(11)

Share and Cite

MDPI and ACS Style

Galangau, O.; Flores Gonzalez, J.; Montigaud, V.; Dorcet, V.; le Guennic, B.; Cador, O.; Pointillart, F. Dysprosium Single-Molecule Magnets Involving 1,10-Phenantroline-5,6-dione Ligand. Magnetochemistry 2020, 6, 19. https://doi.org/10.3390/magnetochemistry6020019

AMA Style

Galangau O, Flores Gonzalez J, Montigaud V, Dorcet V, le Guennic B, Cador O, Pointillart F. Dysprosium Single-Molecule Magnets Involving 1,10-Phenantroline-5,6-dione Ligand. Magnetochemistry. 2020; 6(2):19. https://doi.org/10.3390/magnetochemistry6020019

Chicago/Turabian Style

Galangau, Olivier, Jessica Flores Gonzalez, Vincent Montigaud, Vincent Dorcet, Boris le Guennic, Olivier Cador, and Fabrice Pointillart. 2020. "Dysprosium Single-Molecule Magnets Involving 1,10-Phenantroline-5,6-dione Ligand" Magnetochemistry 6, no. 2: 19. https://doi.org/10.3390/magnetochemistry6020019

APA Style

Galangau, O., Flores Gonzalez, J., Montigaud, V., Dorcet, V., le Guennic, B., Cador, O., & Pointillart, F. (2020). Dysprosium Single-Molecule Magnets Involving 1,10-Phenantroline-5,6-dione Ligand. Magnetochemistry, 6(2), 19. https://doi.org/10.3390/magnetochemistry6020019

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop