Series of Chloranilate-Bridged Dinuclear Lanthanide Complexes: Kramers Systems Showing Field-Induced Slow Magnetic Relaxation †
Abstract
1. Introduction
2. Results and Discussions
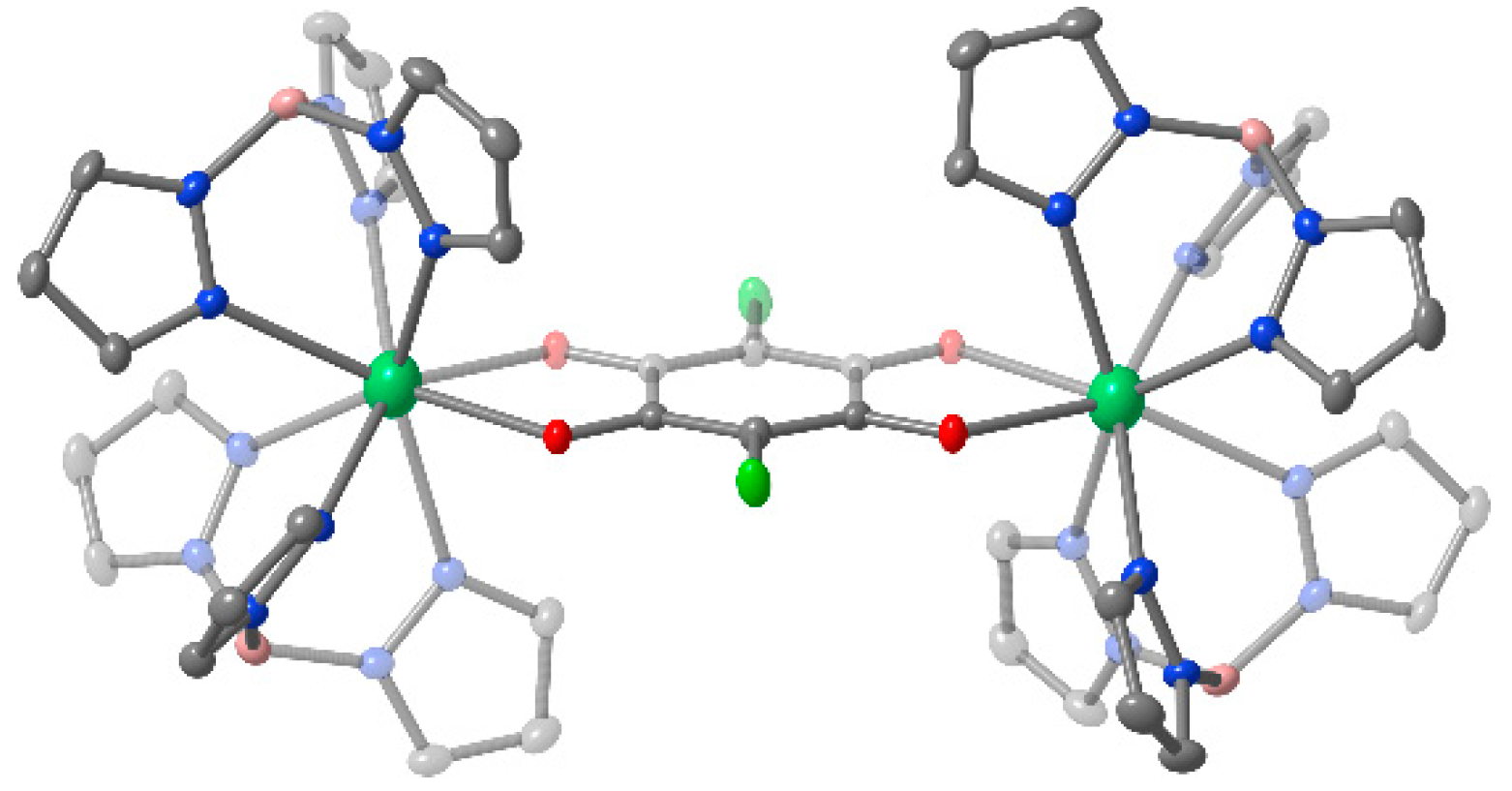
2.1. Structural Descriptions
2.2. Infrared Spectroscopy
2.3. Magnetic Properties
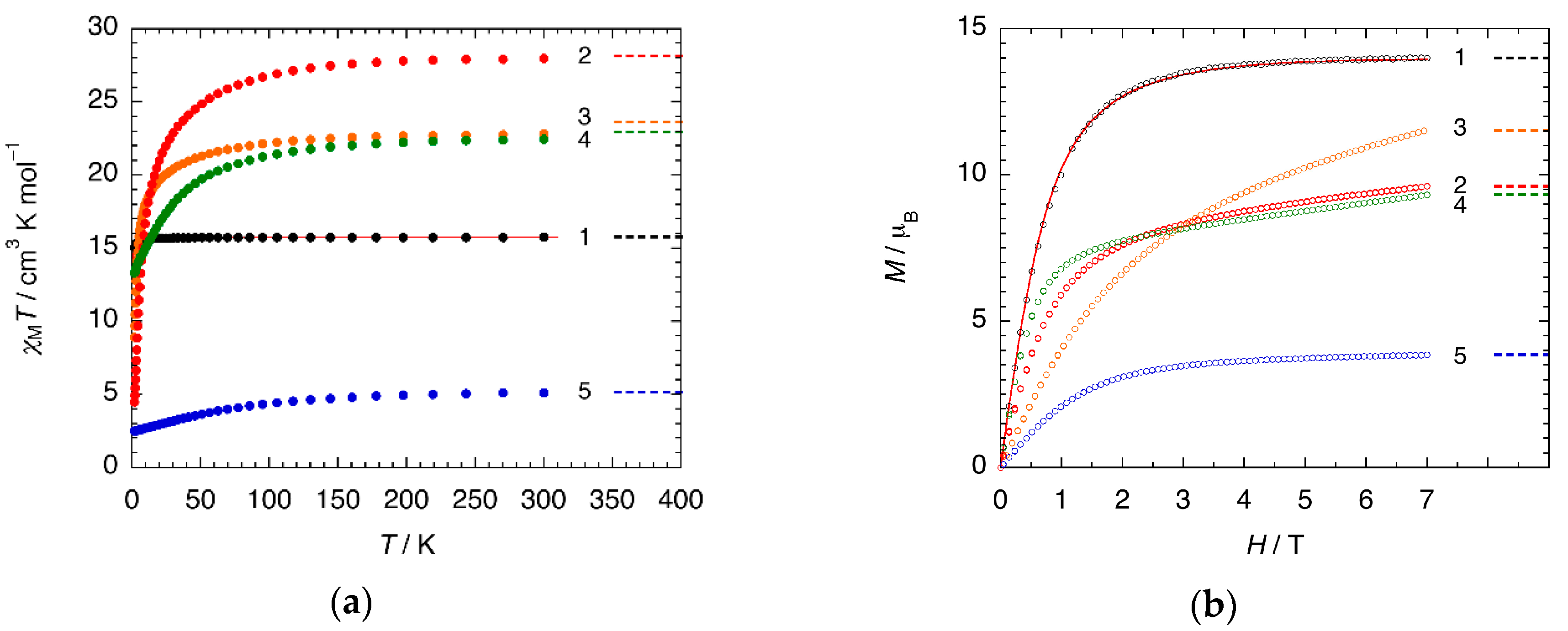
2.3.1. Static Magnetic Properties
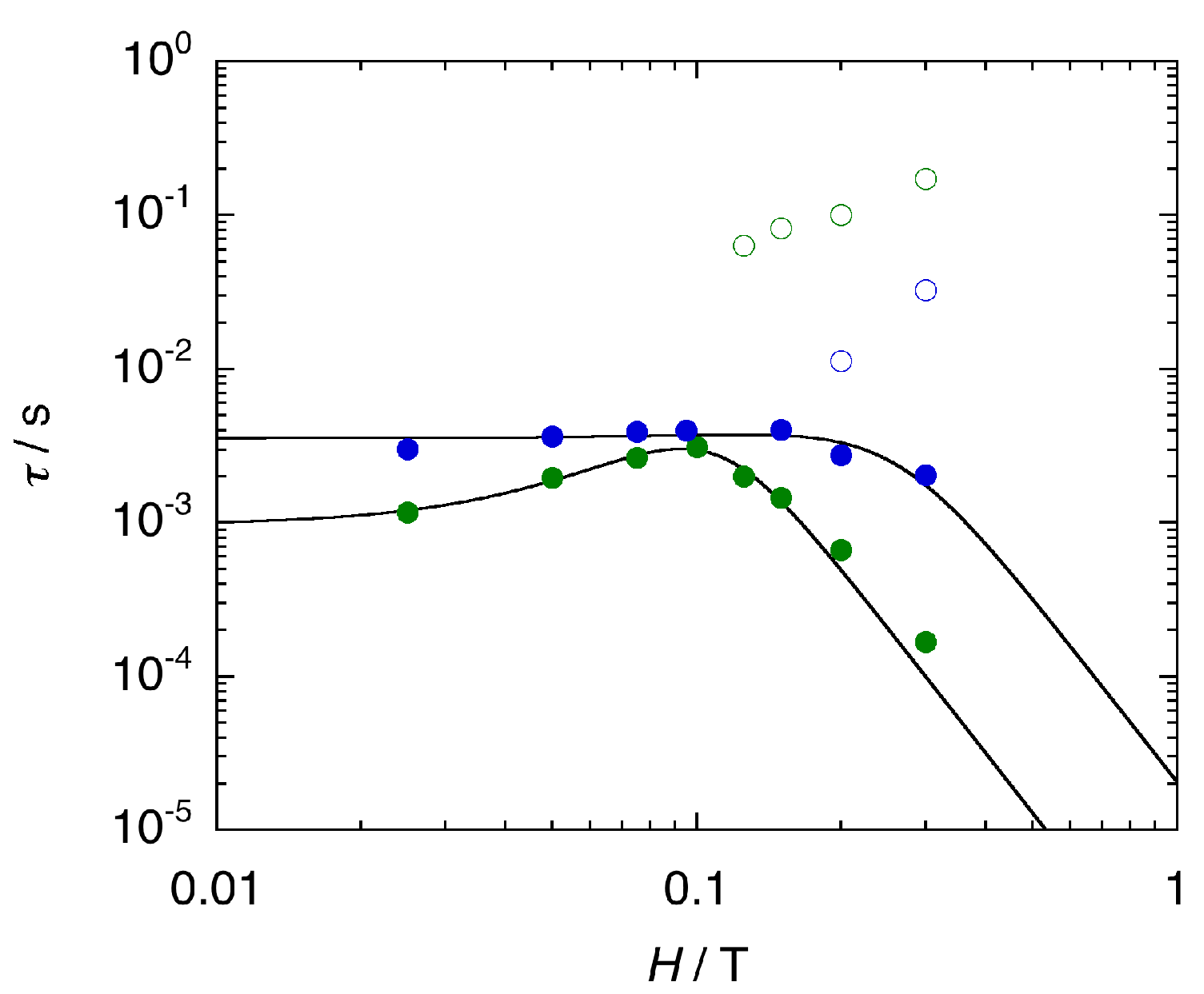
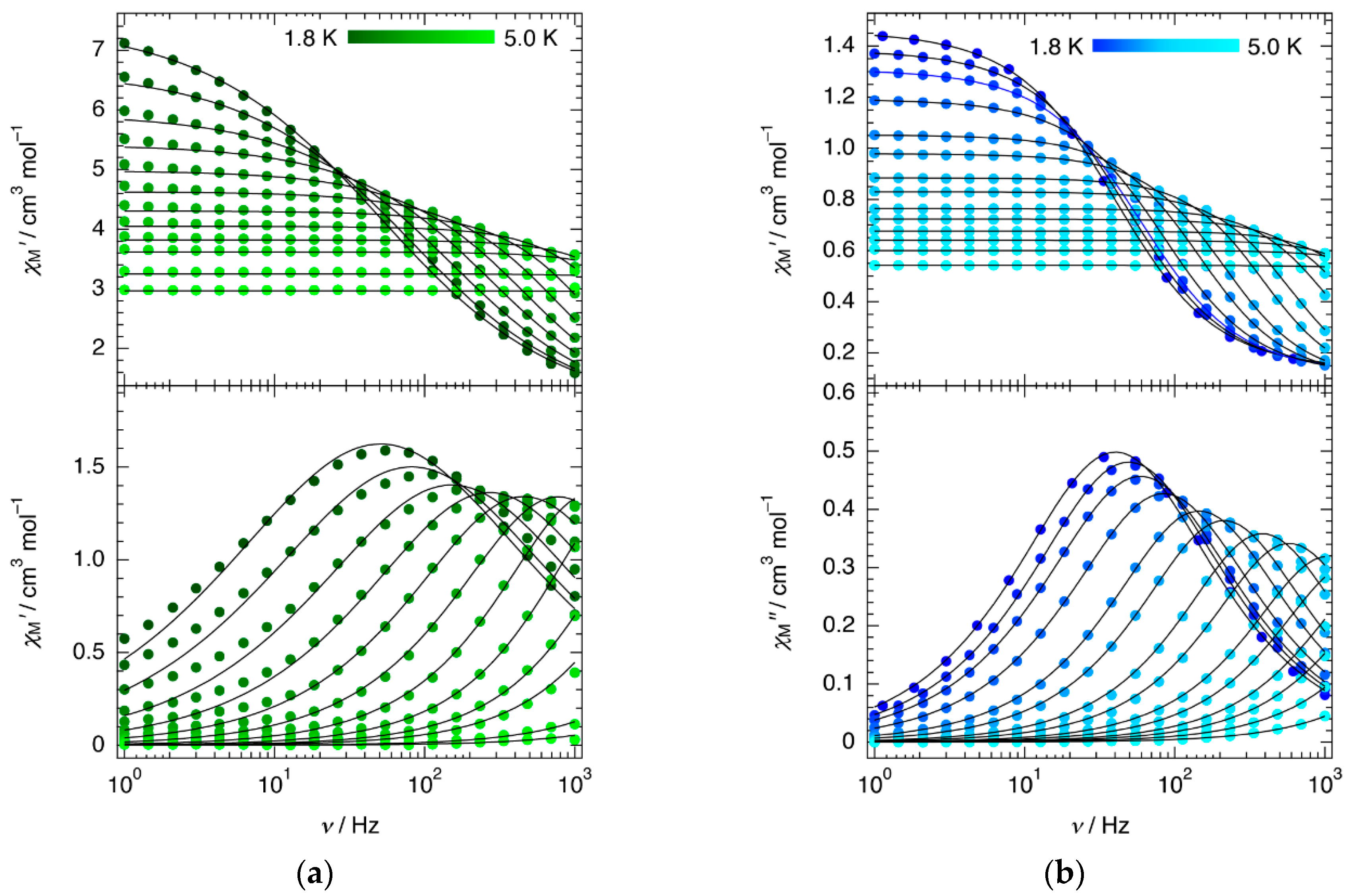
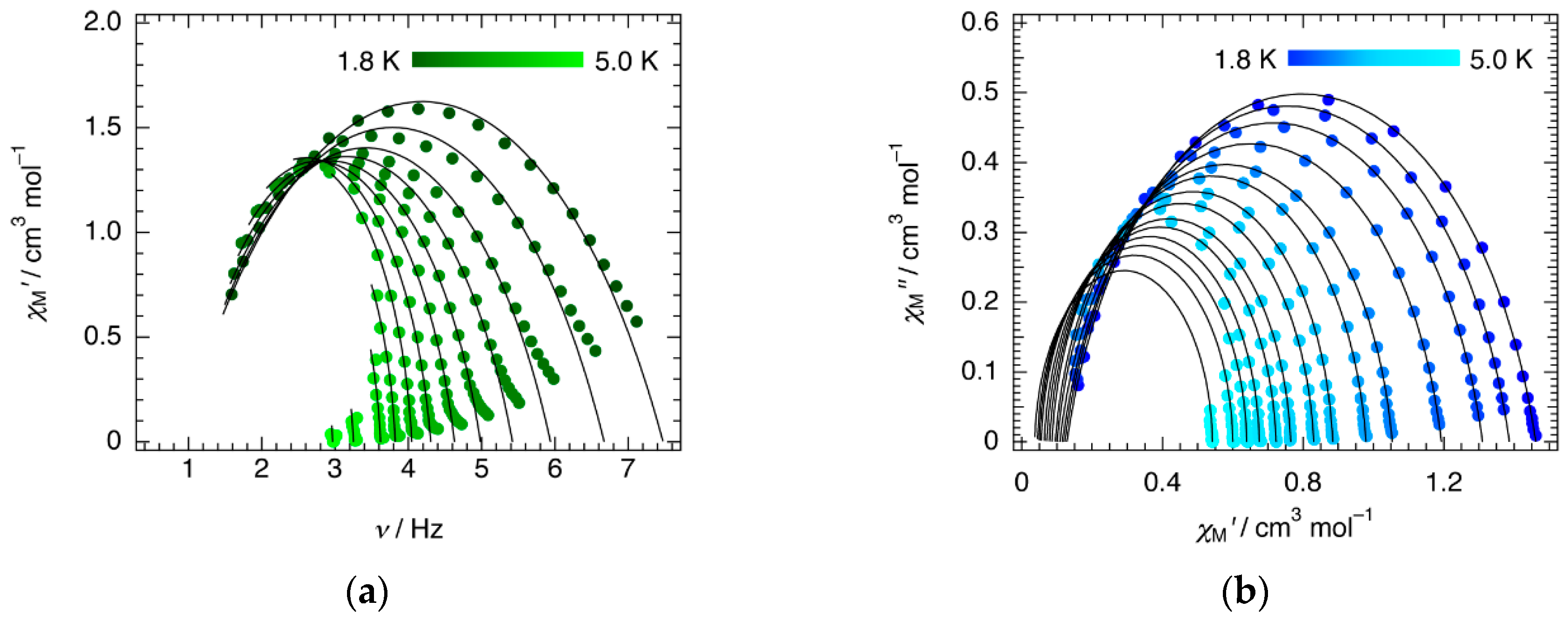
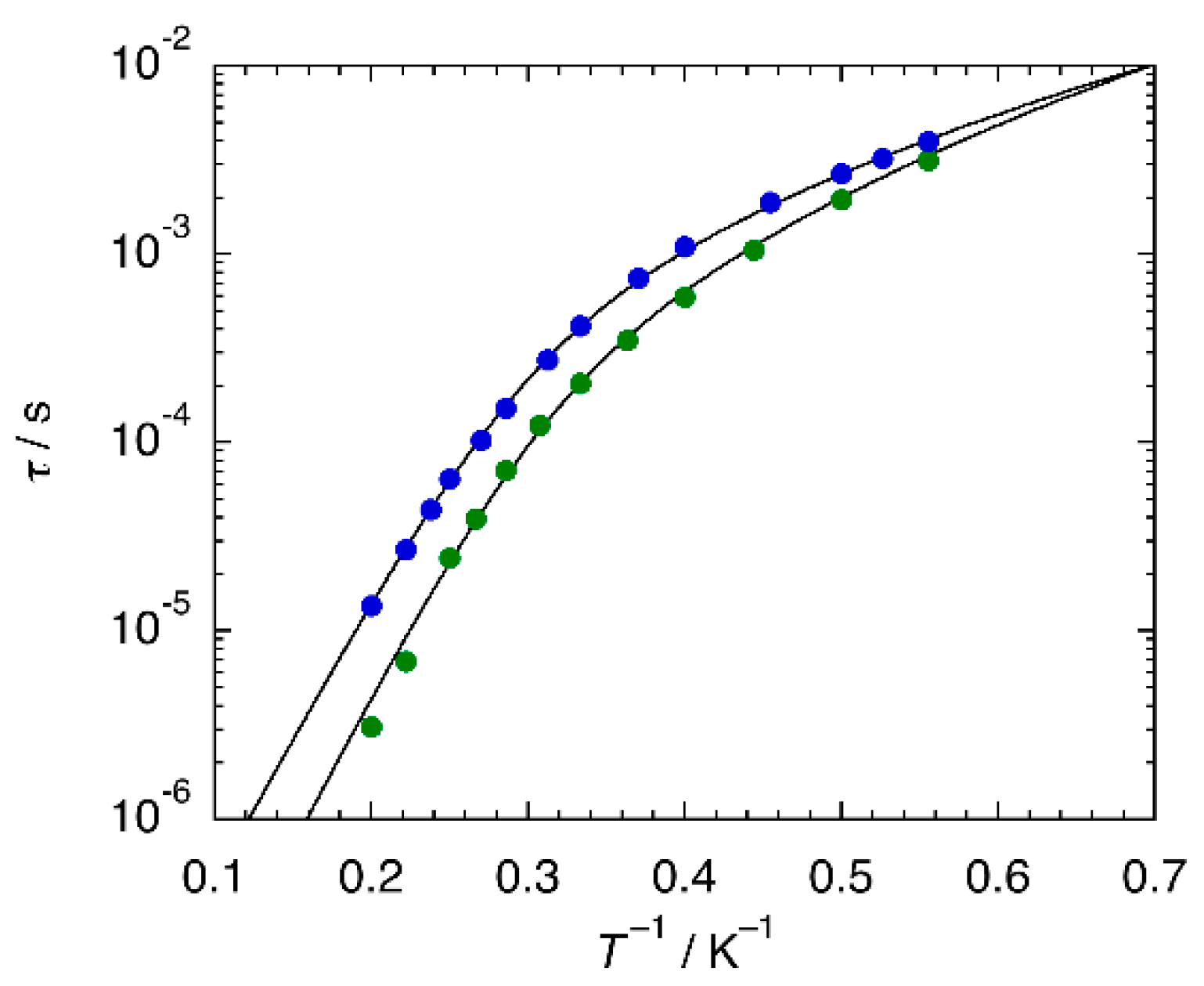
2.3.2. Dynamic Magnetic Properties
2.4. Electrochemistry
3. Experimental Section
3.1. Materials and Methods
3.2. Synthesis of [{Ln(Tp)2}2(μ-Cl2An)]·2CH2Cl2 (Ln = Gd (1), Tb (2), Ho (3), Er (4) and Yb (5))
3.3. Single Crystal X-ray Crystallography
3.4. Physical Measurements
4. Conclusions and Outlook
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mannini, M.; Pineider, F.; Sainctavit, P.; Danieli, C.; Otero, E.; Sciancalepore, C.; Talarico, A.M.; Arrio, M.-A.; Cornia, A.; Gatteschi, D.; et al. Magnetic memory of a single-molecule quantum magnet wired to a gold surface. Nat. Mater. 2009, 8, 194–197. [Google Scholar] [CrossRef]
- Leuenberger, M.N.; Loss, D. Quantum computing in molecular magnets. Nature 2001, 410, 789–793. [Google Scholar] [CrossRef]
- Meier, F.; Levy, J.; Loss, D. Quantum computing with spin cluster qubits. Phys. Rev. Lett. 2003, 90, 47901–47904. [Google Scholar] [CrossRef] [PubMed]
- Winpenny, R.E.P. Quantum information processing using molecular nanomagnets as qubits. Angew. Chem. Int. Ed. 2008, 47, 7992–7994. [Google Scholar] [CrossRef]
- Chiesa, A.; Whitehead, G.F.S.; Carretta, S.; Carthy, L.; Timco, G.A.; Teat, S.J.; Amoretti, G.; Pavarini, E.; Winpenny, R.E.P.; Santini, P. Molecular nanomagnets with switchable coupling for quantum simulation. Sci. Rep. 2014, 4, 7423. [Google Scholar] [CrossRef] [PubMed]
- Bogani, L.; Wernsdorfer, W. Molecular spintronics using single-molecule magnets. Nat. Mater. 2008, 7, 179–186. [Google Scholar] [CrossRef]
- Camarero, J.; Coronado, E. Molecular vs. inorganic spintronics: The role of molecular materials and single molecules. J. Mater. Chem. 2009, 19, 1678–1684. [Google Scholar] [CrossRef]
- Sanvito, S. Molecular spintronics. Chem. Soc. Rev. 2011, 40, 3336–3355. [Google Scholar] [CrossRef]
- Clemente-Juan, J.M.; Coronado, E.; Gaita-Ariño, A. Magnetic polyoxometalates: From molecular magnetism to molecular spintronics and quantum computing. Chem. Soc. Rev. 2012, 41, 7464–7478. [Google Scholar] [CrossRef]
- Rinehart, J.D.; Long, J.R. Exploiting single-ion anisotropy in the design of f-element single-molecule magnets. Chem. Sci. 2011, 2, 2078–2085. [Google Scholar] [CrossRef]
- Sorace, L.; Benelli, C.; Gatteschi, D. Lanthanides in molecular magnetism: Old tools in a new field. Chem. Soc. Rev. 2011, 40, 3092–3104. [Google Scholar] [CrossRef]
- Woodruff, D.N.; Winpenny, R.E.P.; Layfield, R.A. Lanthanide single-molecule magnets. Chem. Rev. 2013, 113, 5110–5148. [Google Scholar] [CrossRef] [PubMed]
- Habib, F.; Murugesu, M. Lessons learned from dinuclear lanthanide nano-magnets. Chem. Soc. Rev. 2013, 42, 3278–3288. [Google Scholar] [CrossRef]
- Liddle, S.T.; Van Slageren, J. Improving f-element single molecule magnets. Chem. Soc. Rev. 2015, 44, 6655–6669. [Google Scholar] [CrossRef] [PubMed]
- Pointillart, F.; Cador, O.; Le Guennic, B.; Ouahab, L. Uncommon lanthanide ions in purely 4f Single Molecule Magnets. Coord. Chem. Rev. 2017, 346, 150–175. [Google Scholar] [CrossRef]
- McAdams, S.G.; Ariciu, A.-M.; Kostopoulos, A.K.; Walsh, J.P.S.; Tuna, F. Molecular single-ion magnets based on lanthanides and actinides: Design considerations and new advances in the context of quantum technologies. Coord. Chem. Rev. 2017, 346, 216–239. [Google Scholar] [CrossRef]
- Dey, A.; Kalita, P.; Chandrasekhar, V. Lanthanide(III)-based single-ion magnets. ACS Omega 2018, 3, 9462–9475. [Google Scholar] [CrossRef]
- Zhu, Z.; Guo, M.; Li, X.-L.; Tang, J. Molecular magnetism of lanthanide: Advances and perspectives. Coord. Chem. Rev. 2019, 378, 350–364. [Google Scholar] [CrossRef]
- Sessoli, R.; Tsai, H.L.; Schake, A.R.; Wang, S.; Vincent, J.B.; Folting, K.; Gatteschi, D.; Christou, G.; Hendrickson, D.N. High-spin molecules: [Mn12O12(O2CR)16(H2O)4]. J. Am. Chem. Soc. 1993, 115, 1804–1816. [Google Scholar] [CrossRef]
- Sessoli, R.; Gatteschi, D.; Caneschi, A.; Novak, M.A. Magnetic bistability in a metal-ion cluster. Nature 1993, 365, 141–143. [Google Scholar] [CrossRef]
- Abdus Subhan, M.; Kawahata, R.; Nakata, H.; Fuyuhiro, A.; Tsukuda, T.; Kaizaki, S. Synthesis, structure and spectroscopic properties of chloranilate-bridged 4f-4f dinuclear complexes: A comparative study of the emission properties with Cr-Ln complexes. Inorg. Chim. Acta 2004, 357, 3139–3146. [Google Scholar] [CrossRef]
- Dunstan, M.A.; Rousset, E.; Boulon, M.-E.; Gable, R.W.; Sorace, L.; Boskovic, C. Slow magnetisation relaxation in tetraoxolene-bridged rare earth complexes. Dalton Trans 2017, 46, 13756–13767. [Google Scholar] [CrossRef] [PubMed]
- Ishikawa, R.; Michiwaki, S.; Noda, T.; Katoh, K.; Yamashita, M.; Matsubara, K.; Kawata, S. Field-induced slow magnetic relaxation of mono- and dinuclear dysprosium(III) complexes coordinated by a chloranilate with different resonance forms. Inorganics 2018, 6, 7. [Google Scholar] [CrossRef]
- Zhang, P.; Perfetti, M.; Kern, M.; Hallmen, P.P.; Ungur, L.; Lenz, S.; Ringenberg, M.R.; Frey, W.; Stoll, H.; Rauhut, G.; et al. Exchange coupling and single molecule magnetism in redox-active tetraoxolene-bridged dilanthanide complexes. Chem. Sci. 2018, 9, 1221–1230. [Google Scholar] [CrossRef] [PubMed]
- Flanagan, B.M.; Bernhardt, P.V.; Krausz, E.R.; Lüthi, S.R.; Riley, M.J. A ligand-field analysis of the trensal (H3trensal = 2,2’,2’’-Tris(salicylideneimino)triethylamine) ligand. An application of the angular overlap model to lanthanides. Inorg. Chem. 2002, 41, 5024–5033. [Google Scholar] [CrossRef]
- Quadrelli, E.A. Lanthanide contraction over the 4f series follows a quadratic decay. Inorg. Chem. 2002, 41, 167–169. [Google Scholar] [CrossRef] [PubMed]
- Seitz, M.; Oliver, A.G.; Raymond, K.N. The lanthanide contraction revisited. J. Am. Chem. Soc. 2007, 129, 11153–11160. [Google Scholar] [CrossRef]
- D’Angelo, P.; Zitolo, A.; Migliorati, V.; Chillemi, G.; Duvail, M.; Vitorge, P.; Abadie, S.; Spezia, R. Revised ionic radii of lanthanoid(III) ions in aqueous solution. Inorg. Chem. 2011, 50, 4572–4579. [Google Scholar] [CrossRef] [PubMed]
- Casanova, D.; Llunell, M.; Alemany, P.; Alvarez, S. The rich stereochemistry of eight-vertex polyhedra: A continuous shape measures study. Chem. Eur. J. 2005, 11, 1479–1494. [Google Scholar] [CrossRef] [PubMed]
- Llunell, M.; Casanova, D.; Cirera, J.; Bofill, J.M.; Alemany, P.; Alvarez, S. SHAPE; Version 2.1; University of Barcelona: Barcelona, Spain, 2013. [Google Scholar]
- Kitagawa, S.; Kawata, S. Coordination compounds of 1,4-dihydroxybenzoquinone and its homologues. Structures and properties. Coord. Chem. Rev. 2002, 224, 11–34. [Google Scholar] [CrossRef]
- Apostolidis, C.; Rebizant, J.; Kanellakopulos, B.; von Ammon, R.; Dornberger, E.; Müller, J.; Powietzka, B.; Nuber, B. Homoscorpionates (hydridotris(1-pyrazolyl)borato complexes) of the trivalent 4f ions. The crystal and molecular structure of [(HB(N2C3H3)3)3LnIII, (Ln = Pr, Nd). Polyhedron 1997, 16, 1057–1068. [Google Scholar] [CrossRef]
- Sears, V.F. Neutron scattering lengths and cross sections. Neutron News 1992, 3, 26–37. [Google Scholar] [CrossRef]
- Chen, Y.-C.; Liu, J.-L.; Wernsdorfer, W.; Liu, D.; Chibotaru, L.F.; Chen, X.-M.; Tong, M.-L. Hyperfine-interaction-driven suppression of quantum tunneling at zero field in a holmium(III) single-ion magnet. Angew. Chem. Int. Ed. 2017, 56, 4996–5000. [Google Scholar] [CrossRef]
- Moreno-Pineda, E.; Damjanović, M.; Fuhr, O.; Wernsdorfer, W.; Ruben, M. Nuclear spin isomers: Engineering a Et4N[DyPc2] spin qudit. Angew. Chem. Int. Ed. 2017, 56, 9915–9919. [Google Scholar] [CrossRef]
- Kishi, Y.; Pointillart, F.; Lefeuvre, B.; Riobé, F.; Le Guennic, B.; Golhen, S.; Cador, O.; Maury, O.; Fujiwara, H.; Ouahab, L. Isotopically enriched polymorphs of dysprosium single molecule magnets. Chem. Commun. 2017, 53, 3575–3578. [Google Scholar] [CrossRef]
- Flores Gonzalez, J.; Pointillart, F.; Cador, O. Hyperfine coupling and slow magnetic relaxation in isotopically enriched DyIII mononuclear single-molecule magnets. Inorg. Chem. Front. 2019. [Google Scholar] [CrossRef]
- Cole, K.S.; Cole, R.H. Dispersion and absorption in dielectrics, I. alternating current characteristics. J. Chem. Phys. 1941, 9, 341–351. [Google Scholar] [CrossRef]
- Guo, Y.-N.; Xu, G.-F.; Guo, Y.; Tang, J. Relaxation dynamics of dysprosium(iii) single molecule magnets. Dalton Trans. 2011, 40, 9953–9963. [Google Scholar] [CrossRef] [PubMed]
- Gatteschi, D.; Sessoli, R.; Villain, J. Molecular Nanomagnets; Oxford University Press: Oxford, UK, 2006. [Google Scholar] [CrossRef]
- CrystalClear-SM; Version 1.4.0 SP1; Rigaku and Rigaku/MSC: The Woodlands, TX, USA, 2008.
- CrystalStructure; Version 4.2.2; Rigaku and Rigaku/MSC: The Woodlands, TX, USA, 2017.
- Burla, M.C.; Caliandro, R.; Camalli, M.; Carrozzini, B.; Cascarano, G.L.; Giacovazzo, C.; Mallamo, M.; Mazzone, A.; Polidori, G.; Spagna, R. SIR2011: A new package for crystal structure determination and refinement. J. Appl. Crystallogr. 2012, 45, 357–361. [Google Scholar] [CrossRef]
- Sheldrick, G.M. Crystal structure refinement with SHELXL. Acta Crystallogr. Sect. C 2015, 71, 3–8. [Google Scholar] [CrossRef]
- Bain, G.A.; Berry, J.F. Diamagnetic corrections and Pascal’s constants. J. Chem. Educ. 2008, 85, 532–536. [Google Scholar] [CrossRef]
| Ln–O 2 | Ln–N 2 | Intramolecular Ln···Ln 3 | Intermolecular Ln···Ln 4 | |
|---|---|---|---|---|
| 1 | 2.398(3) | 2.514(3) | 8.7042(5) | 8.7420(5) |
| 2 | 2.375(3) | 2.492(3) | 8.661(2) | 8.703(2) |
| 3 | 2.363(2) | 2.482(2) | 8.6424(5) | 8.7308(4) |
| 4 | 2.348(2) | 2.465(2) | 8.6084(9) | 8.699(1) |
| 5 | 2.330(2) | 2.446(2) | 8.5599(9) | 8.671(1) |
| SAPR 2 | TDD 3 | BTBR 4 | |
|---|---|---|---|
| 1 | 2.320 | 0.831 | 1.788 |
| 2 | 2.291 | 0.809 | 1.774 |
| 3 | 2.199 | 0.764 | 1.728 |
| 4 | 2.215 | 0.749 | 1.732 |
| 5 | 2.189 | 0.722 | 1.707 |
| C–O 2 | C–C 2 | C–C 3 | |
|---|---|---|---|
| 1 | 1.259(4) | 1.391(5) | 1.537(4) |
| 2 | 1.252(4) | 1.390(5) | 1.542(4) |
| 3 | 1.258(3) | 1.394(3) | 1.537(3) |
| 4 | 1.256(3) | 1.392(4) | 1.534(4) |
| 5 | 1.253(3) | 1.393(4) | 1.532(4) |
| A (s−1 K−1 T−4) | B1 (s−1) | B2 (T−2) | |
|---|---|---|---|
| 4 | 6.80 × 105 | 1.03 × 103 | 3.85 × 102 |
| 5 | 2.70 × 104 | 2.82 × 102 | 6.42 |
| τ0 (s) | Δeff (cm−1) | C (s−1 K−n) | m | |
|---|---|---|---|---|
| 4 | 3.04 × 10−9 | 25.9 | 17.50 | 4.84 |
| 5 | 2.68 × 10−8 | 22.3 | 31.39 | 3.55 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ishikawa, R.; Michiwaki, S.; Noda, T.; Katoh, K.; Yamashita, M.; Kawata, S. Series of Chloranilate-Bridged Dinuclear Lanthanide Complexes: Kramers Systems Showing Field-Induced Slow Magnetic Relaxation. Magnetochemistry 2019, 5, 30. https://doi.org/10.3390/magnetochemistry5020030
Ishikawa R, Michiwaki S, Noda T, Katoh K, Yamashita M, Kawata S. Series of Chloranilate-Bridged Dinuclear Lanthanide Complexes: Kramers Systems Showing Field-Induced Slow Magnetic Relaxation. Magnetochemistry. 2019; 5(2):30. https://doi.org/10.3390/magnetochemistry5020030
Chicago/Turabian StyleIshikawa, Ryuta, Shoichi Michiwaki, Takeshi Noda, Keiichi Katoh, Masahiro Yamashita, and Satoshi Kawata. 2019. "Series of Chloranilate-Bridged Dinuclear Lanthanide Complexes: Kramers Systems Showing Field-Induced Slow Magnetic Relaxation" Magnetochemistry 5, no. 2: 30. https://doi.org/10.3390/magnetochemistry5020030
APA StyleIshikawa, R., Michiwaki, S., Noda, T., Katoh, K., Yamashita, M., & Kawata, S. (2019). Series of Chloranilate-Bridged Dinuclear Lanthanide Complexes: Kramers Systems Showing Field-Induced Slow Magnetic Relaxation. Magnetochemistry, 5(2), 30. https://doi.org/10.3390/magnetochemistry5020030







