Theory of Electron Spin Resonance in Ferromagnetically Correlated Heavy Fermion Compounds
Abstract
1. Introduction
2. The Kondo Lattice Model and the Transversal Dynamical Susceptibility
3. Special Cases
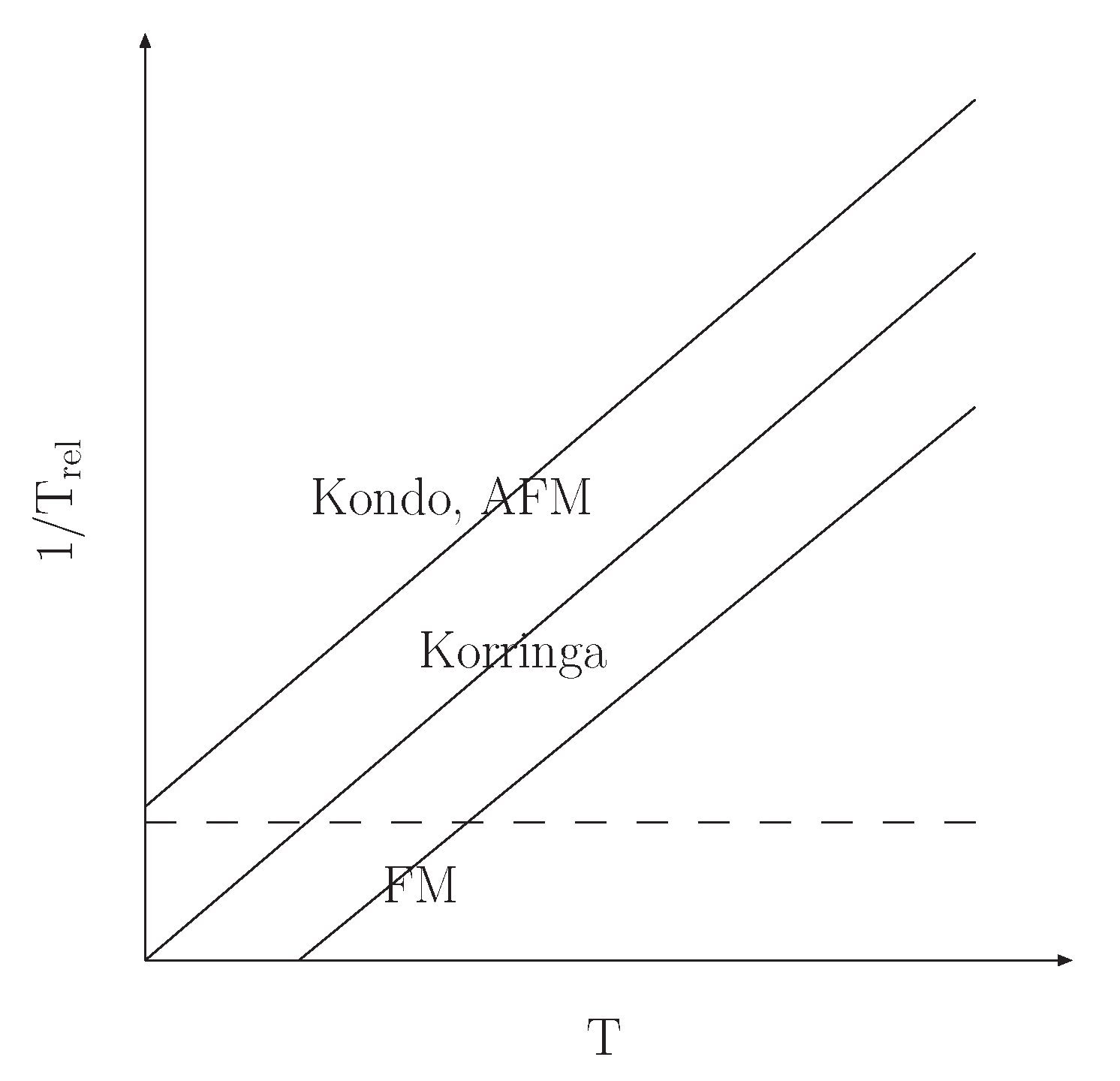
3.1. Korringa Relaxation
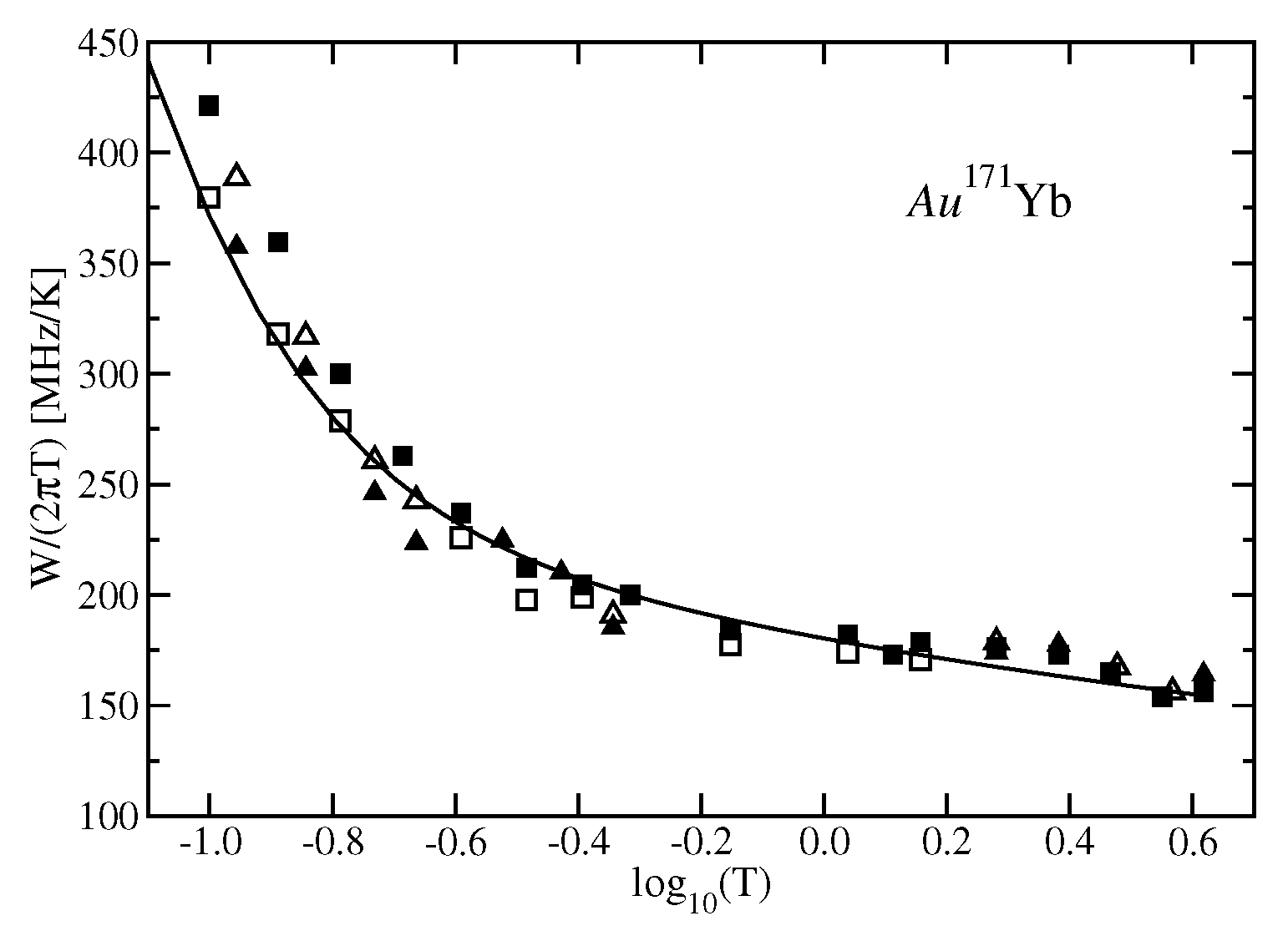
3.2. The Kondo Impurity
3.3. Paramagnetic Kondo lattice
3.4. Kondo Lattice with Antiferromagnetic Order
3.5. Kondo Lattice with Ferromagnetic Order
3.6. Summary
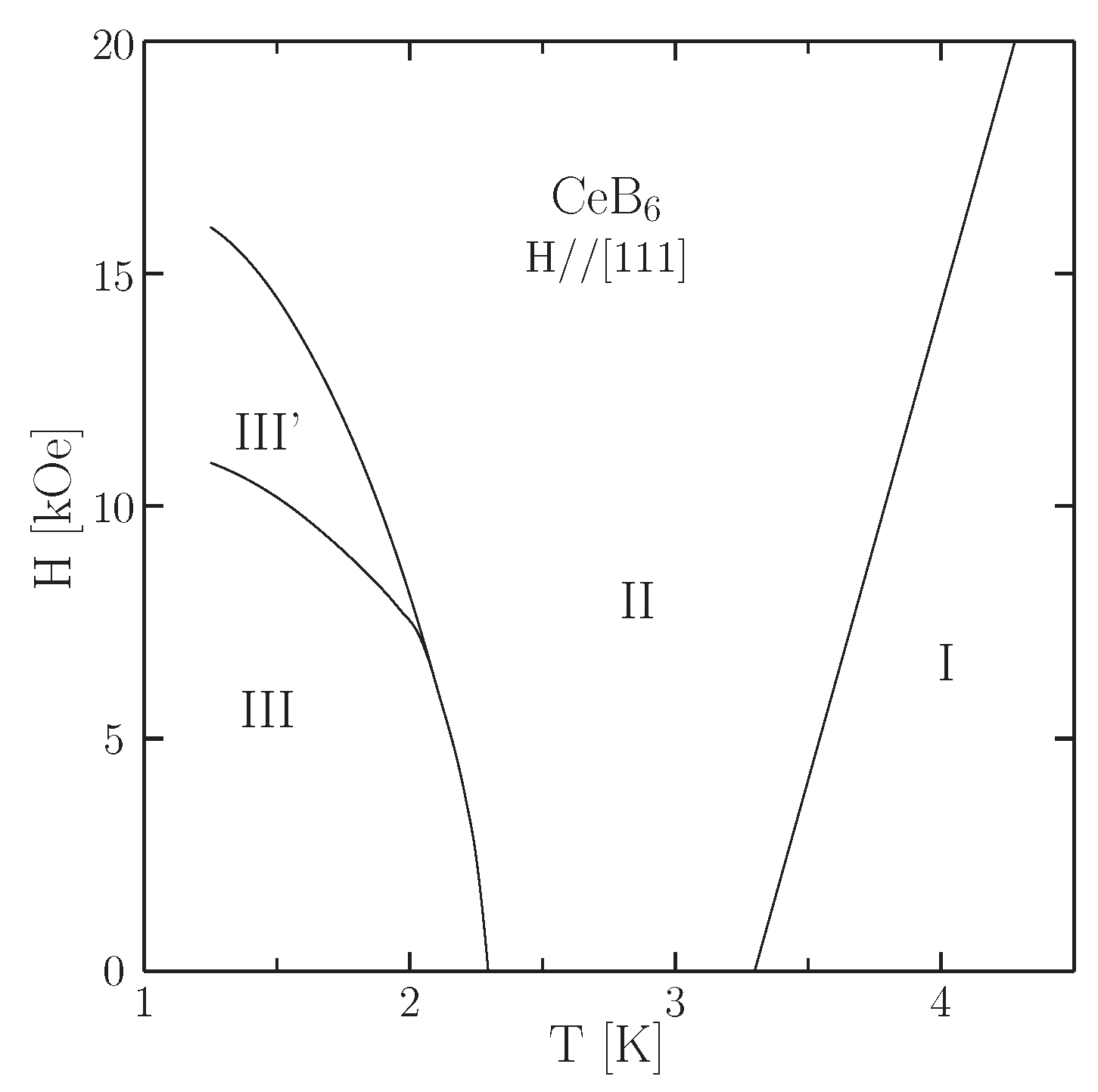
4. Antiferroquadrupolar Ordered CeB
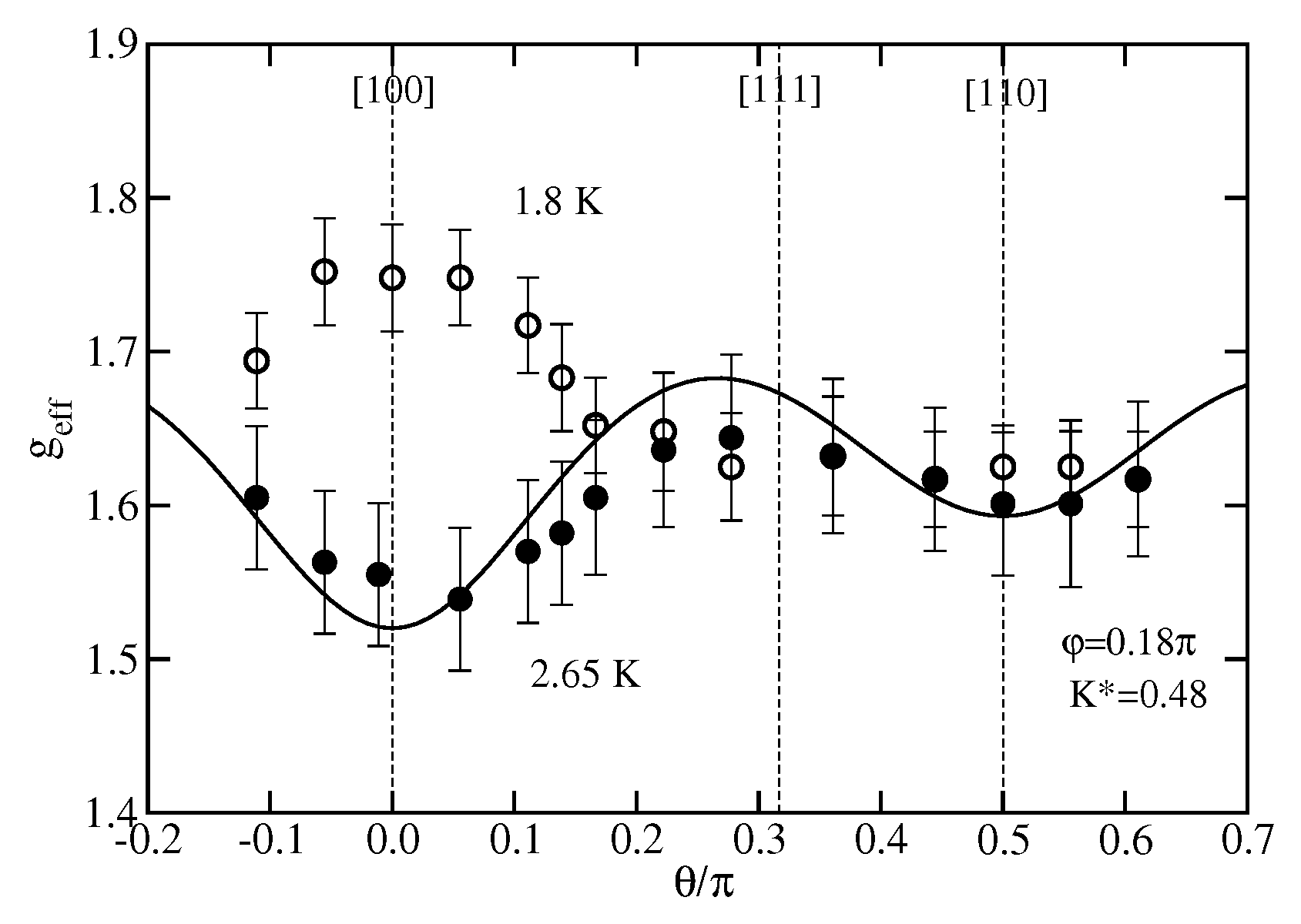
4.1. g-Factor for ESR in Phase II of CeB
4.2. Ferromagnetic Correlations in Phase II of CeB
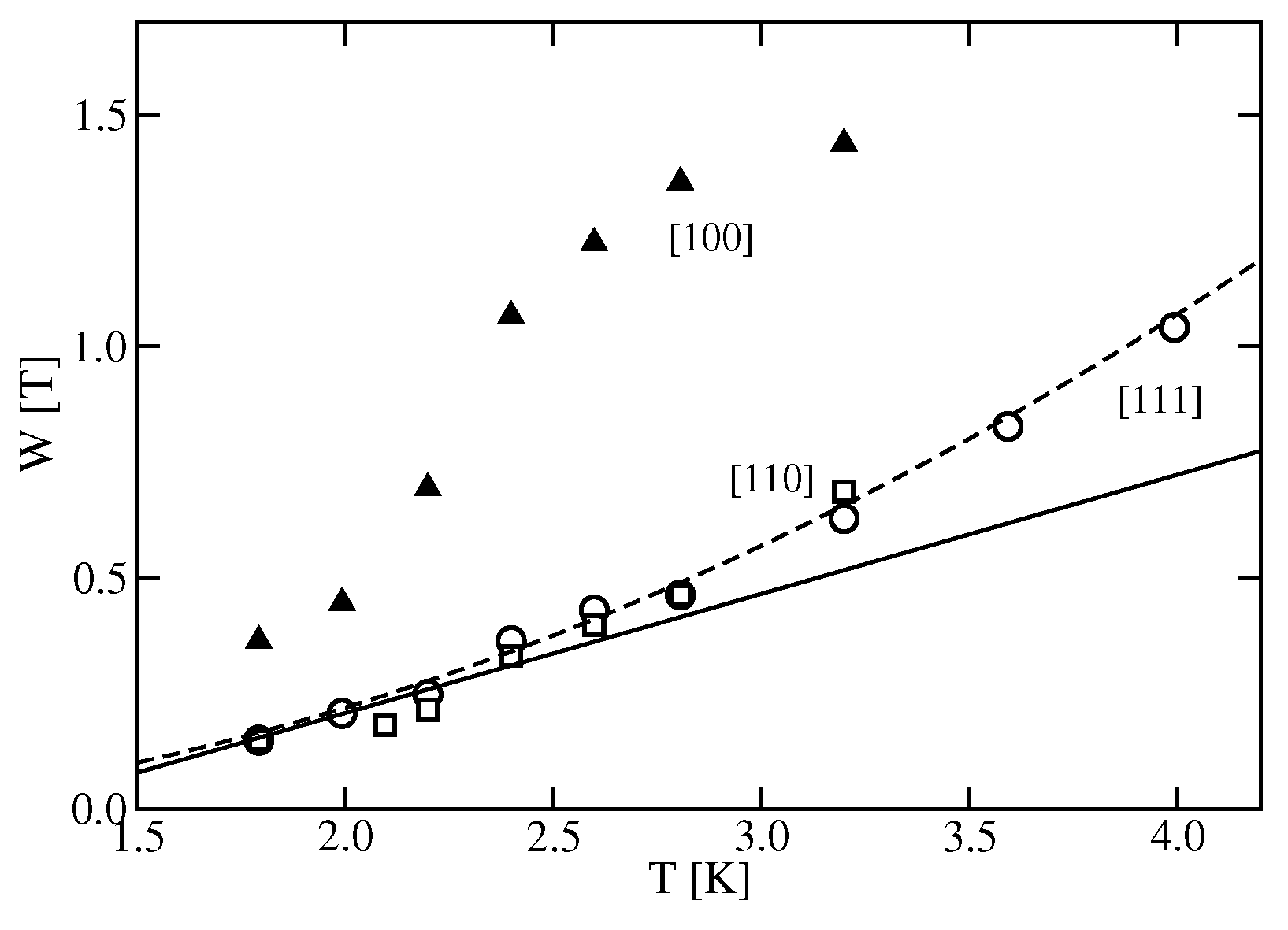
4.3. Line Width of ESR in Phase II of CeB
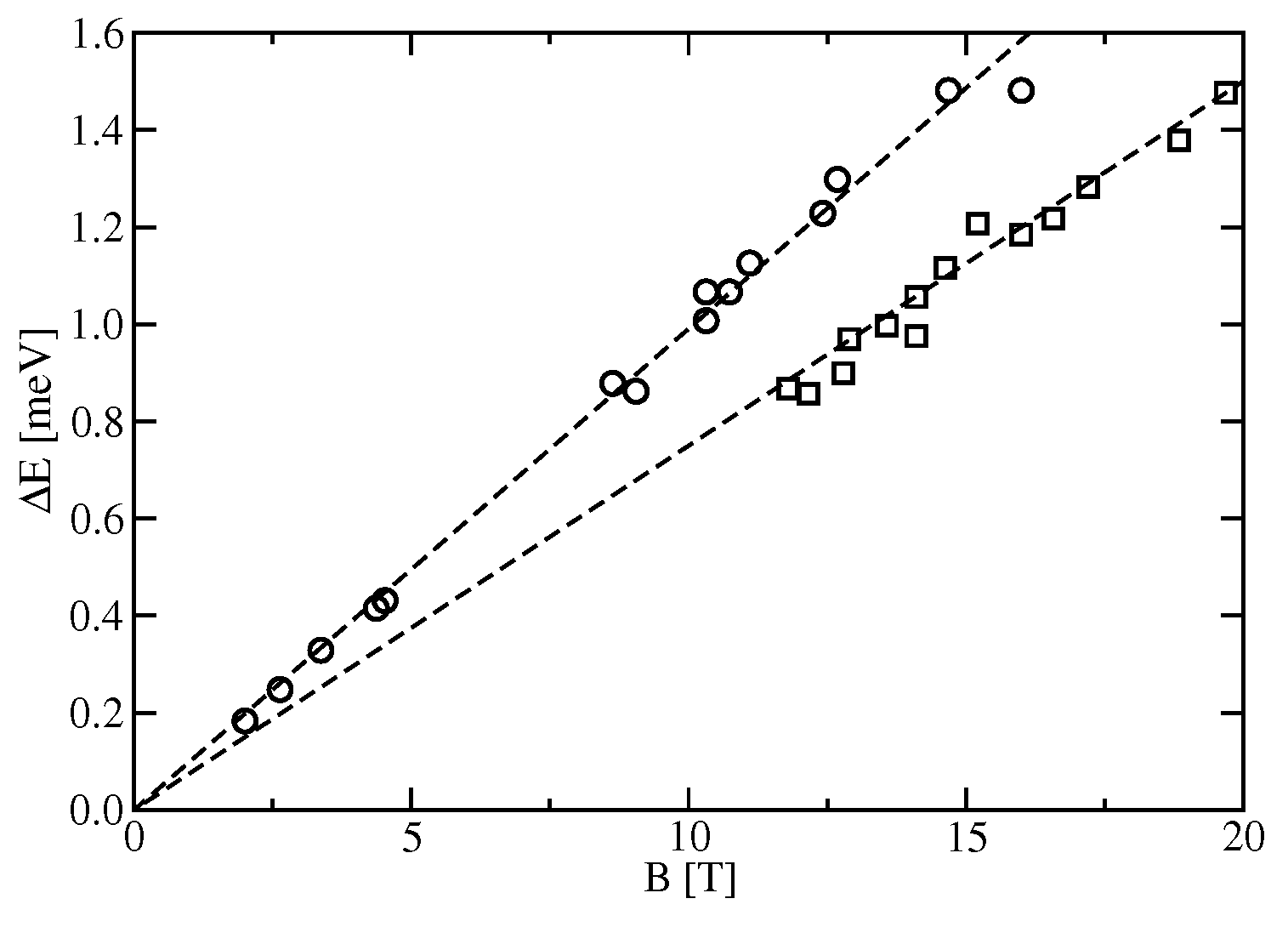
4.4. Second Resonance at High Fields in Phase II of CeB
4.5. Inelastic Neutron Scattering in CeB
- (1)
- A resonant magnetic exciton mode [59], similar to the ones found in unconventional superconductors [60], including heavy fermion superconductors (CeCuSi, CeCoIn, and CeRuAl) [61,62], was observed at , but in phase III. The mode is non-dispersive, sharply peaked and associated with the opening of a spin-gap at low energies. The spin-gap is the consequence of the magnetic order, since for the resonance peak shifts to and becomes the quasi-elastic peak of the paramagnetic state. A theoretical interpretation of the resonant exciton mode was provided by Akbari and Thalmeier [63].
- (2)
- At the -point (zone center), a strong FM soft mode was observed [64], These ferromagnetic fluctuations are large in phase III but also present (although weak) in phase II. However, no dispersive magnon excitations were found in the AFQ phase. The intensity of the magnetic excitations collapses into a broad central peak at zero energy (quasi-elastic peak) just above . The INS line width is smallest at the -point. The ferromagnetic fluctuations are expected to be enhanced in a magnetic field and are the reason for an accessible ESR signal in CeB.
- (3)
- Spin-wave modes emanate from the AFM wave-vectors and below . They display a spin-gap of about 0.3 to 0.4 meV and, at the zone boundary (M point), the modes reach up to 0.7 meV. Hence, the spin-gap and the band width are comparable.All the above excitations merge to form a continuous dispersive magnon band in a narrow energy range. The band is more dispersive in the AFQ phase.
- (4)
- In unconventional superconductors, a strong magnetic field splits the resonant magnetic exciton mode into two components. This is not the case for CeB, where a second field-induced magnon mode emerges whose energy increases with magnetic field [58]. At the FM zone center (-point) only a single mode is found with a non-monotonic field dependence in phase III. Inside the hidden order phase, it agrees well with the ESR resonance energy (Figure 6). INS measurements in the field range of the second (high-field) ESR resonance have not been carried out. It is interesting to point out that this secondary ISN response occurs also at the R-point, which is not accessible by ESR.
4.6. Summary
5. Longitudinal Dynamical Susceptibility
6. Conclusions
Conflicts of Interest
References
- Yamada, K. Perturbation Expansion for the Anderson Hamiltonian. II. Prog. Theor. Phys. 1975, 53, 970–986. [Google Scholar] [CrossRef]
- Shiba, H. The Korringa Relation for the Impurity Nuclear Spin-Lattice Relaxation in Dilute Kondo Alloys. Prog. Theor. Phys. 1975, 54, 967–981. [Google Scholar] [CrossRef]
- Von Spalden, Y.; Tsang, E.; Baberschke, K.; Schlottmann, P. ESR study of the Kondo effect in Au171Yb and Au174Yb. Phys. Rev. B 1983, 28, 24, 1984, 29, 487. [Google Scholar] [CrossRef]
- Sichelschmidt, J.; Ivan’shin, V.A.; Ferstl, J.; Geibel, C.; Steglich, F. Low Temperature Electron Spin Resonance of the Kondo Ion in a Heavy Fermion Metal: YbRh2Si2. Phys. Rev. Lett. 2003, 91, 156401. [Google Scholar] [CrossRef] [PubMed]
- Ivan’shin, V.A.; Aminov, L.K.; Kurkin, I.N.; Sichelschmidt, J.; Stockert, O.; Ferstl, J.; Geibel, C. Electron paramagnetic resonance of Yb3+ ions in a concentrated YbRh2Si2 compound with heavy fermions. Zh. Eksp. Teor. Fiz. Pis’ma Red. JETP Lett. 2003, 77, 526–529. [Google Scholar] [CrossRef]
- Duque, J.G.S.; Bittar, E.M.; Adriano, C.; Giles, C.; Holanda, L.M.; Lora-Serrano, R.; Pagliuso, P.G.; Rettori, C.; Pérez, C.A.; Wu, R.W.; et al. Magnetic field dependence and bottlenecklike behavior of the ESR spectra in YbRh2Si2. Phys. Rev. B 2009, 79, 035122. [Google Scholar] [CrossRef]
- Sichelschmidt, J.; Wykhoff, J.; von Nidda, H.-A.K.; Fazlishanov, I.I.; Hossain, Z.; Krellner, C.; Geibel, C.; Steglich, F. Electron spin resonance of YbIr2Si2 below the Kondo temperature. J. Phys. Condens. Matter 2007, 19, 016211. [Google Scholar] [CrossRef]
- Krellner, C.; Förster, T.; Jeevan, H.; Geibel, C.; Sichelschmidt, J. Relevance of Ferromagnetic Correlations for the Electron Spin Resonance in Kondo Lattice Systems. Phys. Rev. Lett. 2008, 100, 066401. [Google Scholar] [CrossRef] [PubMed]
- Ivan’shin, V.A.; Sukhanov, A.A.; Sokolov, D.A.; Aronson, M.C.; Jia, S.; Bud’ko, S.L.; Canfield, P.C. Electron spin resonance of dense Yb-based heavy-fermion compounds: New experimental data. J. Alloys Compd. 2009, 480, 126–127. [Google Scholar] [CrossRef]
- Bruning, E.M.; Krellner, C.; Baenitz, M.; Jesche, A.; Steglich, F.; Geibel, C. CeFePO: A heavy fermion metal with ferromagnetic correlations. Phys. Rev. Lett. 2008, 101, 117206. [Google Scholar] [CrossRef] [PubMed]
- Demishev, S.V.; Semeno, A.V.; Paderno, Y.B.; Shitsevalova, N.Y.; Sluchanko, N.E. Experimental evidence for magnetic resonance in the antiferro–Quadrupole phase. Phys. Status Solidi B 2005, 242, R27–R29. [Google Scholar] [CrossRef]
- Demishev, S.V.; Semeno, A.V.; Bogach, A.V.; Paderno, Y.B.; Shitsevalova, N.Y.; Sluchanko, N.E. Magnetic resonance in cerium hexaboride caused by quadrupolar ordering. J. Magn. Magn. Mater. 2006, 300, e534–e537. [Google Scholar] [CrossRef]
- Feher, G.; Kip, A.F. Electron spin resonance absorption in metals. I. Experimental. Phys. Rev. 1955, 98, 337. [Google Scholar] [CrossRef]
- Dyson, F. Electron spin resonance absorption in metals. II. Theory of electron diffusion and the skin effect. Phys. Rev. 1955, 98, 349. [Google Scholar] [CrossRef]
- Pake, G.E.; Purcell, E.M. Line shapes in nuclear paramagnetism. Phys. Rev. 1948, 74, 1184. [Google Scholar] [CrossRef]
- Rettori, C.; Davidov, D.; Orbach, R.; Chock, E.P.; Ricks, B. Electron-Spin Resonance of Rare Earths in Aluminum. Phys. Rev. B 1973, 7, 1. [Google Scholar] [CrossRef]
- Rettori, C.; Davidov, D.; Kim, H.M. Crystalline-field effects in the EPR of Er in various cubic metals. Phys. Rev. B 1973, 8, 5335. [Google Scholar] [CrossRef]
- Rettori, C.; Kim, H.M.; Chock, E.P.; Davidov, D. Dynamic behavior of paramagnetic ions and conduction electrons in intermetallic compounds: GdxLu1-xAl2. Phys. Rev. B 1974, 10, 1826. [Google Scholar] [CrossRef]
- Sichelschmidt, J.; Ivan’shin, V.A.; Ferstl, J.; Geibel, C.; Steglich, F.J. Suppression of the Kondo state in YbRh2Si2 by large magnetic fields. Magn. Magn. Mater. 2004, 42, 272–276. [Google Scholar]
- Schlottmann, P. Electron spin resonance in heavy-fermion systems. Phys. Rev. B 2009, 79, 045104. [Google Scholar] [CrossRef]
- Abrahams, E.; Wölfle, P. Electron spin resonance in Kondo systems. Phys. Rev. B 2008, 78, 104423. [Google Scholar] [CrossRef]
- Wölfle, P.; Abrahams, E. Phenomenology of ESR in heavy-fermion systems: Fermi-liquid and non-Fermi-liquid regimes. Phys. Rev. B 2009, 80, 235112. [Google Scholar] [CrossRef]
- Abrahams, E.; Wölfle, P. Critical quasiparticle theory applied to heavy fermion metals near an antiferromagnetic quantum phase transition. Proc. Natl. Aacd. Sci. USA 2012, 109, 3238. [Google Scholar] [CrossRef] [PubMed]
- Wölfle, P.; Abrahams, E. Quasiparticles beyond the Fermi liquid and heavy fermion criticality. Phys. Rev. B 2011, 84, 041101. [Google Scholar] [CrossRef]
- Zvyagin, A.A.; Kataev, V.; Büchner, B. Theory of the electron spin resonance in heavy fermion systems with non-Fermi-liquid behavior. Phys. Rev. B 2009, 80, 024412. [Google Scholar] [CrossRef]
- Huber, D.L. The effects of anisotropy and Yb–Yb interactions on the low-field electron spin resonance in YbRh2Si2 and YbIr2Si2. J. Phys. Condens. Matter 2009, 21, 322203. [Google Scholar] [CrossRef] [PubMed]
- Kochelaev, B.I.; Belov, S.I.; Skvortsova, A.M.; Kutuzov, A.S.; Sichelschmidt, J.; Wykhoff, J.; Geibel, C.; Steglich, F. Why could electron spin resonance be observed in a heavy fermion Kondo lattice? Eur. Phys. J. B 2009, 72, 485–489. [Google Scholar] [CrossRef]
- Bloch, F. Nuclear Induction. Phys. Rev. 1946, 70, 460. [Google Scholar] [CrossRef]
- Götze, W.; Wölfle, P. Dynamical impurity spin susceptibility in metals. J. Low Temp. Phys. 1971, 5, 575–589. [Google Scholar] [CrossRef]
- Götze, W.; Wölfle, P. Homogeneous dynamical susceptibilities of dilute magnetic alloys. J. Low Temp. Phys. 1972, 6, 455–471. [Google Scholar] [CrossRef]
- Götze, W.; Schlottmann, P. The zero field Kondo susceptibility at intermediate temperatures. Solid State Commun. 1973, 13, 17–20. [Google Scholar] [CrossRef]
- Götze, W.; Schlottmann, P. On the longitudinal static and dynamic susceptibility of spin-1/2 Kondo systems. J. Low Temp. Phys. 1974, 16, 87. [Google Scholar] [CrossRef]
- Fujita, T.; Suzuki, M.; Komatsubara, T.; Kunii, S.; Kasuya, T.; Ohtsuka, T. Anomalous specific heat of CeB6. Solid State Commun. 1980, 35, 569–572. [Google Scholar] [CrossRef]
- Zirngiebl, E.; Hillebrands, B.; Blumenröder, S.; Güntherodt, G.; Loewenhaupt, M.; Carpenter, J.M.; Winzer, K.; Fisk, Z. Crystal-field excitations in CeB6 studied by Raman and neutron spectroscopy. Phys. Rev. B 1984, 30, 4052. [Google Scholar] [CrossRef]
- Kunimori, K.; Kotani, M.; Funaki, H.; Tanida, H.; Sera, M.; Matsumura, T.; Iga, F. Theory of Electron Spin Resonance in Ferromagnetically Correlated Heavy Fermion Compounds. J. Phys. Soc. Jpn. 2011, 80, SA056. [Google Scholar] [CrossRef]
- Bierig, R.W.; Weber, M. Paramagnetic Resonance of Dysprosium in Cubic and Axial Fields in CaF2. Phys. Rev. 1963, 132, 164. [Google Scholar] [CrossRef]
- Davidov, D.; Orbach, R.; Rettori, C.; Tao, L.J.; Chock, E.P. Anisotropic Behavior of Dilute Au:Dy Alloys: Observation of the Γ8 (Quartet) Resonance. Phys. Rev. Lett. 1972, 28, 490. [Google Scholar] [CrossRef]
- Martins, G.B.; Rao, D.; Barberis, G.E.; Rettori, C.; Duro, R.J.; Sarrao, J.; Fisk, Z.; Oseroff, S.; Thompson, J.D. Electron spin resonance of Er3+ in YBiPt. Phys. Rev. B 1995, 52, 15062. [Google Scholar] [CrossRef]
- Lea, K.R.; Leask, M.J.M.; Wolf, W.P. The raising of angular momentum degeneracy of f-electron terms by cubic crystal fields. J. Phys. Chem. Solids 1962, 23, 1381–1405. [Google Scholar] [CrossRef]
- Schlottmann, P. Electron spin resonance in antiferro-quadrupolar-ordered CeB6. Phys. Rev. B 2012, 86, 075135. [Google Scholar] [CrossRef]
- Demishev, S.V.; Semeno, A.V.; Bogach, A.V.; Samarin, N.A.; Ishchenko, T.V.; Filipov, V.B.; Shitsevalova, N.Y.; Sluchanko, N.E. Magnetic spin resonance in CeB6. Phys. Rev. B 2009, 80, 245106. [Google Scholar] [CrossRef]
- Effantin, J.; Rossat-Mignod, J.; Burlet, P.; Bartholin, H.; Kunii, S.; Kasuya, T.J. Magnetic phase diagram of CeB6. Magn. Magn. Mater. 1985, 145, 47–48. [Google Scholar] [CrossRef]
- Schlottmann, P. Electron spin resonance in CeB6. J. Appl. Phys. 2013, 113, 17E109. [Google Scholar] [CrossRef]
- Semeno, A.V.; Gilmanov, M.I.; Bogach, A.V.; Krasnorussky, V.N.; Samarin, A.N.; Samarin, N.A.; Sluchanko, N.E.; Shitsevalova, N.Y.; Filipov, V.B.; Glushkov, V.V.; et al. Magnetic resonance anisotropy in CeB6: An entangled state of the art. Sci. Rep. 2016, 6, 39196. [Google Scholar] [CrossRef] [PubMed]
- Hall, D.; Fisk, Z.; Goodrich, R.G. Magnetic-field dependence of the paramagnetic to the high-temperature magnetically ordered phase transition in CeB6. Phys. Rev. B 2000, 62, 84. [Google Scholar] [CrossRef]
- Goodrich, R.G.; Young, D.P.; Hall, D.; Balicas, L.; Fisk, Z.; Harrison, N.; Betts, J.; Migliori, A.; Woodward, F.M.; Lynn, J.W. Extension of the temperature-magnetic field phase diagram of CeB6. Phys. Rev. B 2004, 69, 054415. [Google Scholar] [CrossRef]
- Terzioglu, C.; Browne, D.A.; Goodrich, R.G.; Hassan, A.; Fisk, Z. EPR and magnetic susceptibility measurements on CeB6. Phys. Rev. B 2001, 63, 235110. [Google Scholar] [CrossRef]
- Terzioglu, C.; Ozturk, O.; Kilic, A.; Goodrich, R.G.; Fisk, Z. Magnetic and electronic measurements in CeB6. J. Magn. Magn. Mater. 2006, 298, 33–37. [Google Scholar] [CrossRef]
- Stankiewicz, J.; Evangelisti, M.; Fisk, Z.; Schlottmann, P.; Gor’kov, L. Kondo Physics in a Rare Earth Ion with Well Localized 4f Electrons. Phys. Rev. Lett. 2012, 108, 257201. [Google Scholar] [CrossRef] [PubMed]
- Kubo, K.; Kuramoto, Y. Magnetic and quadrupolar interactions in NdB6. J. Phys. Condens. Matter 2003, 15, S2251. [Google Scholar] [CrossRef]
- Uimin, G.; Brenig, W. Crystal field, magnetic anisotropy, and excitations in rare-earth hexaborides. Phys. Rev. B 2000, 61, 60. [Google Scholar] [CrossRef]
- Uimin, G.; Kuramoto, Y.; Fukushima, N. Mode coupling effects on the quadrupolar ordering in CeB6. Solid State Commun. 1996, 97, 595–598. [Google Scholar] [CrossRef]
- Ohkawa, F.J. Orbital Antiferromagnetism in CeB6. J. Phys. Soc. Jpn. 1985, 54, 3909–3914. [Google Scholar] [CrossRef]
- Schlottmann, P. RKKY interaction between Ce ions in CexLa1-xB6. Phys. Rev. B 2000, 62, 10067. [Google Scholar] [CrossRef]
- Shiina, R.; Shiba, H.; Thalmeier, P.J. Magnetic-Field Effects on Quadrupolar Ordering in a Γ8-Quartet System CeB6. Phys. Soc. Jpn. 1997, 66, 1741. [Google Scholar] [CrossRef]
- Orbach, R. Spin-lattice relaxation in rare-earth salts. Proc. Royal Soc. A 1961, 264, 458. [Google Scholar] [CrossRef]
- Demishev, S.V.; Semeno, A.V.; Ohta, H.; Okubo, S.; Paderno, Y.B.; Shitsevalova, N.Y.; Sluchanko, N.E. High-frequency study of the orbital ordering resonance in the strongly correlated heavy fermion metal CeB6. Appl. Magn. Reson. 2008, 35, 319–326. [Google Scholar] [CrossRef]
- Portnichenko, F.Y.; Demishev, S.M.; Semeno, A.V.; Ohta, H.; Cameron, A.S.; Surmach, M.A.; Jang, H.; Friemel, G.; Dukhnenko, A.V.; Shitsevalova, N.Y.; et al. Magnetic field dependence of the neutron spin resonance in CeB6. Phys. Rev. B 2016, 94, 035114. [Google Scholar] [CrossRef]
- Friemel, G.; Li, Y.; Dukhnenko, A.V.; Shitsevalova, N.Y.; Sluchanko, N.E.; Ivanov, A.; Filipov, V.B.; Keimer, B.; Isonov, D.S. Resonant magnetic exciton mode in the heavy-fermion antiferromagnet CeB6. Nat. Commun. 2012, 3, 830. [Google Scholar] [CrossRef] [PubMed]
- Inosov, D.S.; Park, J.T.; Bourges, P.; Sun, D.L.; Sidis, Y.; Schneidewind, A.; Hradil, K.; Haug, D.; Lin, C.T.; Keimer, B.; et al. Normal-state spin dynamics and temperature-dependent spin-resonance energy in optimally doped BaFe1.85Co0.15As2. Nat. Phys. 2010, 6, 178–181. [Google Scholar] [CrossRef]
- Stock, C.; Broholm, C.; Hudis, J.; Kang, H.J.; Petrovic, C. Spin Resonance in the d-Wave Superconductor CeCoIn5. Phys. Rev. Lett. 2008, 100, 087001. [Google Scholar] [CrossRef] [PubMed]
- Stockert, O.; Arndt, J.; Faulhaber, E.; Geibel, C.; Jeevan, H.S.; Kirchner, S.; Loewenhaupt, M.; Schmalzl, K.; Schmidt, W.; Si, Q.; et al. Magnetically driven superconductivity in CeCu2Si2. Nat. Phys. 2011, 7, 119–124. [Google Scholar] [CrossRef]
- Akbari, A.; Thalmeier, P. Spin Exciton Formation inside the Hidden Order Phase of CeB6. Phys. Rev. Lett. 2012, 108, 146403. [Google Scholar] [CrossRef] [PubMed]
- Jang, H.; Friemel, G.; Ollivier, J.; Dukhnenko, A.V.; Shitsevalova, N.Y.; Filipov, V.B.; Keimer, B.; Inosov, D.S. Intense low-energy ferromagnetic fluctuations in the antiferromagnetic heavy-fermion metal CeB6. Nat. Mater. 2014, 13, 682–687. [Google Scholar] [CrossRef] [PubMed]
- Götze, W.; Schlottmann, P. Retardation Effects in the Longitudinal Spin Relaxation in Metals. II. J. Low Temp. Phys. 1973, 112, 149. [Google Scholar] [CrossRef]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schlottmann, P. Theory of Electron Spin Resonance in Ferromagnetically Correlated Heavy Fermion Compounds. Magnetochemistry 2018, 4, 27. https://doi.org/10.3390/magnetochemistry4020027
Schlottmann P. Theory of Electron Spin Resonance in Ferromagnetically Correlated Heavy Fermion Compounds. Magnetochemistry. 2018; 4(2):27. https://doi.org/10.3390/magnetochemistry4020027
Chicago/Turabian StyleSchlottmann, Pedro. 2018. "Theory of Electron Spin Resonance in Ferromagnetically Correlated Heavy Fermion Compounds" Magnetochemistry 4, no. 2: 27. https://doi.org/10.3390/magnetochemistry4020027
APA StyleSchlottmann, P. (2018). Theory of Electron Spin Resonance in Ferromagnetically Correlated Heavy Fermion Compounds. Magnetochemistry, 4(2), 27. https://doi.org/10.3390/magnetochemistry4020027



