Abstract
Magnons, recognized as the quanta of spin waves, offer a pathway for transmitting information without the need for electron motion, thus emerging as a leading candidate for the next generation of low-power electronics. Firstly, this study gives an overview by examining magnon modes possessing infinite wavelengths or zero wave numbers (known as ferromagnetic resonance) in classical ferromagnetic, antiferromagnetic, and synthetic antiferromagnetic systems. It delves into the dynamics of magnetization, particularly focusing on magnetic moments precession and the corresponding dispersion relationships under two distinct acoustic and optic eigenmodes. Furthermore, it elaborates on a novel hybrid quantum system termed magnon-magnon coupling. The study elucidates the mechanism behind the robust coupling between acoustic and optic magnon modes. Finally, we briefly discuss the current challenges and future research directions in this field.
1. Introduction
Magnonics [1,2,3,4,5,6,7,8,9,10] aims to use spin currents conveyed by spin waves (magnons) rather than electric currents for information processing and storage. By circumventing Joule heat losses, this approach emerges as an ideal candidate for the next generation of low-power electronic devices beyond conventional CMOS. As the primary research object of magnonics, magnons have attracted prominent interest since they were first introduced by F Bloch in 1932 [11]. Similar to phonons or photons, magnons are quasi-particles that exhibit a plethora of rich physical phenomena, such as magnonic crystals [12], spin-wave non-reciprocity [13,14], topological effects [15], and three-dimensional (3D) magnonic systems [16,17]. Among these, one of the most fundamental topics is magnon Bose-Einstein condensation (BEC), which has recently been demonstrated in room-temperature ferrimagnet yttrium iron garnet (YIG) [18,19]. And then numerous methods, including parametric pumping [20] and spin pumping effect [21], have been proposed for the formation of magnon BEC. Another great advantage in magnonics is the potential extension of the magnon spectrum into the highly promising terahertz (THz) range, holding significant implications for 6G communication technology [22,23,24,25]. For instance, Razdolski et al. [26] successfully excited THz magnon resonance modes in Fe/Au/Fe multilayers using ultrashort laser-induced spin currents, while several research groups have also demonstrated coherent THz excitation of antiferromagnets [27,28,29,30,31,32]. The discovery of these novel physical phenomena has significantly propelled the advancement of magnonics.
It is worth mentioning that the first direct observations of spin waves were achieved by using the ferromagnetic resonance (FMR) technique [33]. The physical mechanism that gives rise to the resonance phenomenon can be understood as follows. Typically, the magnetization vector M precesses around the effective field Heff, which includes the anisotropy field HK, the external bias magnetic field H0, the demagnetizing field Hd, the Dzyaloshinskii–Moriya interaction field HDMI etc., and can be calculated by , where F is the free magnetic energy. The corresponding magnetization precession is commonly described by the Landau-Lifshitz-Gilbert (LLG) equation [34]:
Here, is the gyromagnetic constant, Ms is the saturation magnetization, and is the Gilbert damping factor. The third and fourth terms in Equation (1) describe the corresponding spin-transfer torque, mp is the unit magnetization vectors of the spin polarizer, aJ and bJ are the damping-like and field-like torque factor, respectively. Generally, due to energy dissipation (damping), the amplitude of M precession gradually decreases. However, when a radio-frequency (rf) alternating magnetic field is applied, and its frequency aligns with the natural magnetization precession frequency, the energy dissipation is compensated. Consequently, the magnetization undergoes precession about its equilibrium direction of maximum amplitude without spatial variation, a phenomenon known as field-driven ferromagnetic resonance (FD-FMR), which results in the emergence of a distinct type of spin wave with an infinite wavelength (wave vector ) and serves as a valuable tool for investigating magnetic properties and high-frequency dynamics in various magnetic nanostructures [35,36,37]. And the FD-FMR tailored for detecting individual micron or nano-scale structures are of particular interest as they offer insights into fundamental physics and find applications in spintronic devices operating at microwave frequencies, such as microwave sources and resonators.
In contrast to FD-FMR, another method for exciting resonance modes involves utilizing spin-transfer torque (STT) generated by spin-polarized electrical currents [38,39]. By applying a rf charge current across a magnetic nanodevice that exhibits either tunneling magnetoresistance [40,41] or giant magnetoresistance [42,43], the magnetization of the free layer will be excited. Then, when the strength of STT induced by can coincidentally compensate the magnetic damping, the magnetization evolves into a steady-state oscillation, namely, spin-torque induced FMR(ST-FMR) [44,45,46,47,48,49,50]. The corresponding dynamic response of the magnetization in this method can then be inferred through magnetoresistance measurements and detected via the dc voltage output. The resonance state can be achieved using the frequency-swept method, the voltage signal is maximized when the excitation frequency approaches the FMR frequency. This method was firstly demonstrated in MgO-based MTJ devices by Tulapurkar et al. [40]. And then, Fuchs et al. [51] further reported the ST-FMR in an current-perpendicular-to-plane giant-magnetoresistance (CPP-GMR) device. Subsequently, the theoretical treatments of ST-FMR were presented by Kupferschmidt et al. [52] and Kovalev et al. [53]. An important finding arising from theoretical analysis was the reactive emission of spins from precessing ferromagnets into the nonmagnetic space, known as the spin pumping effect [54]. Various models have since been developed to describe ST-FMR behaviors [49,55,56,57,58]. Recently, the ST-FMR technique has emerged as a powerful tool for studying phenomena related to spin-orbit torque (SOT) [59,60,61] and assessing charge-to-spin conversion efficiency in diverse materials including normal heavy metals and alloys [62,63,64,65,66,67], topological insulator [68,69,70,71], antiferromagnetic materials [72,73,74,75] and so on.
In recent years, a number of experimental techniques have been developed to study the magnetization dynamics in magnetic nanostructures. Different from the above theoretical analysis, the FMR experiments are usually done with fixed frequency and scanning static field intensity. For macroscopic bulk samples, FMR can be measured by using standard microwave technology based on microwave cavities, where the appearance of the resonance can be observed by monitoring the reflected rectified microwave power from the microwave cavities and the resulting FMR signal has the shape of a Lorentzian derivative [76,77,78]. Time resolved magneto-optic Kerr effect (TR-MOKE) is another convenient technique to study the dynamics of the magnetization vector, where the sample can be periodically excited by an optical pulse. The optical pulse is split into two parts, namely, pump pulse and probe pulse. The pump pulse is used to trigger magnetic field pulses which excite magnetization dynamics in the sample, while the probe pulse is used to perform spatially resolved resonance measurements [79,80,81,82,83]. In addition, there are many other alternative techniques, such as photothermally modulated ferromagnetic resonance (PM-FMR) [84], scanning thermal microscopy ferromagnetic resonance (SThM-FMR) [85], and vector network analyzer ferromagnetic resonance (VNA-FMR) [86]. Each of these techniques has certain advantages for specific materials and applications.
As one of the most important characteristics of magnetic materials, FMR determines the operation speed of these magnetic materials in telecommunications and radar systems. With modern electronics progressing toward higher operation speed, higher FMR frequency is desperately needed [87]. Thus, it is very meaningful to study the FMR modes in different magnetic materials, such as ferromagnetic and antiferromagnetic systems. In this work, we firstly discuss the novel resonance phenomena caused by ST-FMR and then provide an overview of the recent progress of FMR modes in three classical magnetic systems: ferromagnets (FMs), antiferromagnets (AFMs), and synthetic antiferromagnets (SAFs). We delve into the precession characteristics of magnetic moments in acoustic mode (AM) and optic mode (OM), along with a detailed examination of the corresponding spin wave dispersion relationships. Notably, unlike previous studies focusing solely on the frequency and amplitude of magnons, we paid more attention to magnon polarization. On this basis, we further explored the coupling phenomena of magnon modes, which holds significant potential for hybrid magnonic systems aimed at advancing quantum information technologies and may pave the way for innovative applications and breakthroughs in the field of magnonics, particularly in the realm of quantum information processing.
2. Overview Magnetic Resonance Modes
2.1. Resonance Modes in Ferromagnets
For ferromagnetic samples, as shown in Figure 1a,b, the magnetic moments consistently align in the same direction under the action of the external magnetic field H0, resulting in a state of single domain state. For the homogeneously precessing magnetization described by Kittel (), only the effects of the external magnetic field H0, the anisotropy field HK and the demagnetizing field Hd need to be considered [88]. And for the convenience of derivation and discussion, the direction of M and H0 is represented in the spherical coordinates by the polar angle and the azimuthal angle , as shown in Figure 1b. In this scenario, the total free magnetic energy F can be expressed as:
where Kx and Ky are the in-plane anisotropy constant, Kz is the out-of-plane anisotropy constant, θH and φH represent the angles of the applied field H0, and θ and φ represent the angles of the magnetization M. We specify that the units used in the formula are CGS. The equilibrium direction of magnetization under a given H0 is obtained by minimizing the free magnetic energy F. And the resonance frequency can be written [89]:
for , with M and H0 parallel to [001], i.e., perpendicular to the film plane:
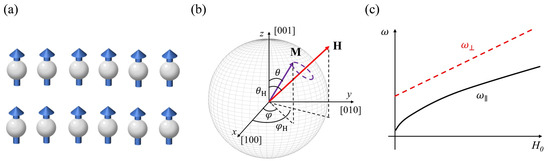
Figure 1.
(a) Classical spins arrangement of ferromagnets in the ground state. (b) Spherical coordinates used to express the field and magnetization vectors. The representative precession direction of the magnetization M in the schematic is counterclockwise (CCW), i.e., right-handed. (c) Illustrations of exemplary dispersion relations in two typical ferromagnetic samples, ferromagnets with in-plane (ω//) and perpendicular (ω⊥) magnetic anisotropy.
While for and , with M and H0 parallel to [010], i.e., parallel to the film plane:
Here, is the angular frequency of the uniform mode (FMR mode), Figure 1c shows the exemplary dispersion relations for in-plane and out-of-plane magnetized film, respectively. From Equation (5), we can conclude that in ferromagnets, only one resonance mode can be accommodated as determined by the LLG equation and the corresponding FMR frequency mainly depends on the applied field and the shape of the samples. Generally, the highest resonance frequency in ferromagnets is difficult to exceed 10 GHz without the application of the external magnetic field [90]. To meet the need for higher FMR frequencies, an extensive body of research has been conducted, investigating FMR in various geometries and material classes [87,91,92,93,94,95,96]. In particular, Oates et al. [97] achieved a resonant frequency nearing 100 GHz by applying external fields of around 5T in ferromagnetic thin films.
Another result we can get from the Kittel equation is that the spin waves excited in ferromagnets are always right-handed (RH), which has been confirmed by traditional FD-FMR experiments [79,86,87]. However, this conclusion may shift when considering the role of STT [38,39,98,99,100], as it introduced complexity to traditional FMR modes, giving rise to a variety of new spin wave phenomena, such as propagating spin waves [101,102], spin-wave Doppler shift [103], magnetic droplets [104,105,106,107,108] and spin-wave bullets [109,110]. Figure 2 shows two novel resonance phenomena caused by the ST-FMR technique. Zhou et al. [111] proved that stable left-handed (LH) polarized spin waves can be introduced into ferromagnets when a spin-polarized electrical current is presented. As shown in Figure 2a,b, the RH polarized spin waves and the LH polarized spin waves coexist in a ferromagnet when the spin current density is larger than a critical value, which is mainly due to the contribution of the coefficient of the nonadiabatic STT [112]. Interestingly, STT can not only change the polarization of the excited spin waves, but also induce additional magnon modes. Qin et al. [95,96] revealed that two resonance states with distinct resonance frequencies could appear in a nanoscale ring shape confined MTJs by launching the ST-FMR measurement, as illustrated in Figure 2c. The corresponding micromagnetic simulation results (see Figure 2d) distinctly depicted the magnetic moment precession of the two resonance states defined as mode-1 and mode-2, respectively. For mode-1, nearly all local magnetization precesses almost simultaneously in the same direction (acoustic-like). Conversely, for mode-2, local magnetizations in parts A and B precess in opposite directions (optic-like), suggesting that the two resonance states both originate from the in-phase and anti-phase localized magnetization oscillation. These studies undoubtedly prove the importance of ST-FMR in the measurement of spin dynamics in magnetic nanostructures. At present, the generation and regulation of spin waves by STT has become a research hotspot in the field of magnonics [113,114,115,116,117,118,119,120].
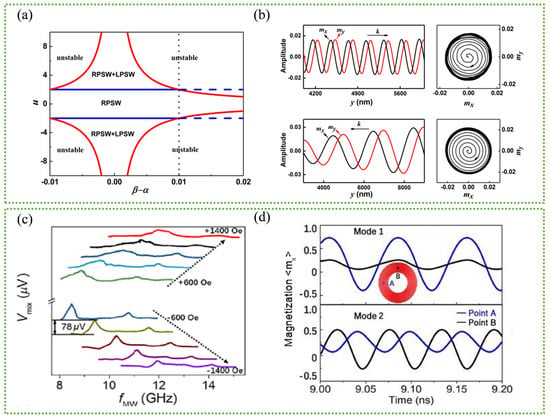
Figure 2.
Two novel resonance phenomena induced by STT-FMR technique. Top panel: STT induced left-handed polarized spin wave in ferromagnets. (a) Phase diagram for the right-handed polarized spin wave (RPSW) and left-handed polarized spin wave (LPSW). The two curves defined by u = ±2α/|α − β|, where α is the Gilbert damping parameter and β is the nonadiabatic STTs induced by the spin-polarized current. Outside the two curves, spin waves lose their stability. (b) Waveforms and the trajectory of the magnetization at a given position for the x-components mx and y-components my, clearly demonstrate the left-handed circular precession. (Reprinted with permission from Ref. [111]. Copyright 2019, American Physical Society.) Bottom panel: Additional resonance states induced by STT. (c) Typical ST-FMR spectra measured from ±600 Oe to ±1400 Oe, where two resonant peaks are clearly observed. fMW represents the frequency of the driving microwave change current, and the mixing voltage Vmix represents the corresponding ST-FMR signal. (d) Different types of local magnetization (mx) precessions taken at point A (blue curve) and point B (black curve). The two resonance modes exhibit obvious in-phase precession and anti-phase precession characteristics. (Reprinted with permission from Ref. [96]. Copyright 2018, American Physical Society).
2.2. Resonance Modes in Antiferromagnets
In comparison to ferromagnetic counterparts, the magnetizations of two adjacent magnetic sublattices in antiferromagnets point in exact opposite directions (), see Figure 3a, consequently, lacking a net macroscopic magnetization and making antiferromagnetic materials resistant to perturbation and free from stray fields. Moreover, the direct exchange or superexchange coupling field HE in crystal antiferromagnets even up to 107Oe, resulting in spin excitations occurring in the much higher THz frequency range [27,31,121]. Recent studies have also demonstrated THz excitations in AFMs using either a dc electric current or spin current, indicating the potential of AFMs for THz spintronic devices in generation, detection, and modulation [29,122,123,124,125]. All the above advantages lead to the increasing significance of AFMs and have spurred the development of antiferromagnetic spintronics [126,127,128,129,130,131,132,133,134,135]. In addition, Previous researches have indicated that magnons in collinear AFMs with easy-axis anisotropy could exhibit two different eigenmodes with opposite polarization (i.e., left-handed and right-handed) [30,125,136], as illustrated in Figure 3b. This property provides antiferromagnetic magnons a significant advantage in data processing by utilizing the chiralities of magnons as information carriers. On this basis, Cheng et al. [137,138,139,140] proposed to generate coherent magnon spin currents by inducing uniform spin precession at the antiferromagnetic resonance (AFMR). In this subsection, we select MnF2 as a typical antiferromagnetic material to delve into the AFMR modes in AFMs in detail.
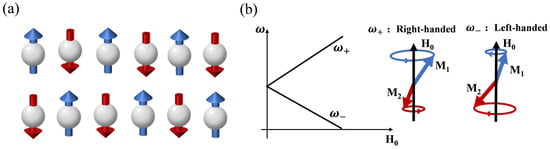
Figure 3.
(a) Classical spins arrangement of collinear antiferromagnets in the ground state. (b) Illustrations of the dispersion relations and resonance modes with right-handed and left-handed circular precession in collinear antiferromagnets.
To describe the intrinsic magnetic excitation of AFMs, we introduce an analytical theory extended from the classic coupled pendulum model, as illustrated in Figure 4a. Theoretically, two identical pendulums coupled with a weak spring could oscillate into two type of synchronization states: anti-phase asynchronous oscillation mode (optic mode) with a phase difference of δθ = |θ1 − θ2| = 180 or in-phase synchronous mode (acoustic mode) of δθ = 0. Similarly, spins in AFMs can also be modeled as a coupled pendulum system, see Figure 4b, the direct exchange field acting on two sublattices of spins M1 and M2 can be described as and , respectively ( is the antiferromagnetic coefficient). For simplicity, we consider two identical spins located in two sublattices, and the effective fields acting on the two spins. Thus, in the absence of the Gilbert damping, the equations of motion for these two sublattice magnetizations M1 and M2 can be governed by coupled Landau–Lifshitz (LL) equations:
where , , represents the anisotropy field. In the Cartesian coordinate system, Equation (6) can be written as a group of coupled equations [141]:
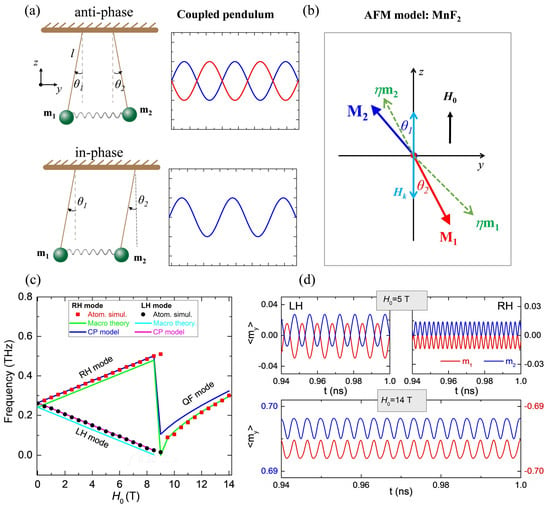
Figure 4.
(a) Classical mechanical model of coupled pendulums. (b) Sketch of magnetization oscillations of AFM sublattices. H0 is the external magnetic field, while HK denotes the uniaxial magnetic anisotropy. (c) Comparison of resonance spectra of MnF2 for the atomistic LLG simulations (red squares and black circles), along with the analytical results from the macrospin model (the green and cyan curves) as well as the coupled pendulum-like model (blue and magenta curves). (d) Anti-phase magnetization precession of the two sublattice m1 and m2 simulated at H0 = 5 T (<) for the left-handed and right-handed resonance modes, and the in-phase magnetization precession of m1 and m2 at H0 = 14 T (>) for the quasi-ferromagnetic resonance mode. (Reprinted with permission from Ref. [141]. Copyright 2023, Institute of Physics).
Then, the resonance frequencies can be easily derived as:
This result shows that there will be two eigenmodes in AFMs. In the absence of a magnetic field, these two resonance modes could degenerate into a single resonance state. Once a bias magnetic field is applied along the easy axis, two different resonance modes will be observed, and the resonance frequency increases (decreases) linearly with the increase of bias magnetic fields. Both qualitative and quantitative agreements are achieved between the atomistic LLG simulations and analytical models for the resonance modes (Figure 4c). Figure 4d shows the characteristics of magnetization precession under two typical external magnetic fields. For a relatively small external magnetic field (H0 < , spin-flop field ), two resonance modes coexist, and the magnetization precession of the two sublattices m1 and m2 under these two modes are both anti-phased, representing the LH and RH magnon modes, respectively. Once the bias magnetic field is increased over the spin-flop field, both the RH mode and LH mode are replaced by a single resonance mode, also known as the quasi-ferromagnetic (QF) resonance mode.
It should be emphasized that the above theory only applies to collinear AFMs with easy-axis anisotropy, but not to the case of easy-plane or biaxial antiferromagnets. Typical biaxial antiferromagnets, such as NiO, are characterized by two distinct anisotropies, a hard-axis anisotropy () and an in-plane easy-axis anisotropy (), as displayed in Figure 5a. Similar to collinear AFMs, there are also two resonance modes in biaxial AFMs, where the two eigenmodes are associated with the different anisotropy constants and referred to as out-of-plane mode () and in-plane mode (). The corresponding magnon dispersion spectrum are satisfied as and . It is worth noting that the resonance modes of biaxial AFMs exhibits completely different spin dynamic characteristics from that of easy-axis AFMs. For the out-of-plane mode (), precesses counterclockwise about the z-axis with elliptical trajectories, while precesses clockwise. The precessions in opposite directions give rise to an oscillating magnetization component in the y-direction, as illustrated in Figure 5b. For the in-plane mode (ω_), however, precesses clockwise while precesses counterclockwise, giving rise to an oscillating magnetization component in the x-direction. Based on this, Satoh et al. [142] found the coherent spin oscillations triggered nonthermally by a circularly polarized light in the fully compensated NiO, and the corresponding polarization rotation is shown in Figure 5c. Cheng et al. [29] further exploit the feedback mechanism in an AFM/heavy-metal heterostructure, see Figure 5d, when the spin current exceeds a threshold, the combined effect of spin pumping and current-induced torques introduces a steady-oscillation feedback with the oscillating frequency in the THz range. Immediately after that, Parthasarathy et al. [143] studied the precessional spin-torque dynamics in biaxial AFMs and proposed device setups for electrical control and detection of THz oscillations. And now, research on easy-plane AFMs has also become an important branch in the field of antiferromagnetic spintronics.
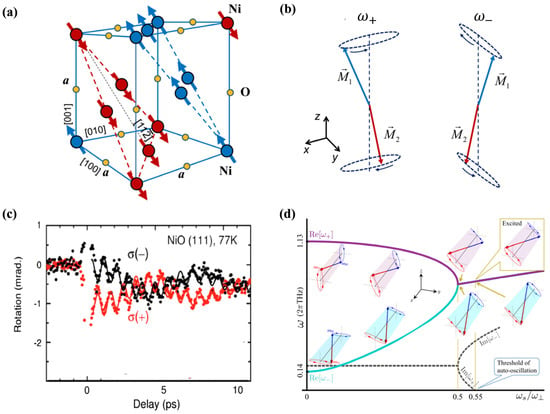
Figure 5.
(a) Crystal structure and spin arrangements in biaxial antiferromagnet NiO. (b) Illustration of the magnetization precessions of the two antiferromagnetic resonance modes, where represents the out-of-plane mode and represents the in-plane mode. (Reprinted with permission from Ref. [133]. Copyright 2019, American Institute of Physics.) (c) Temporal evolution of the two mixed spin wave modes in NiO. Spin wave polarization rotation after photoexcitation with different time delays is examined. The rapid oscillations correspond to the out-of-plane mode, while the slow oscillations correspond to the in-plane mode. (Reprinted with permission from Ref. [142]. Copyright 2010, American Physical Society.) (d) Evolutions of the eigenfrequencies and the eigenmodes of NiO as a function of the STT strength . In the region 0.5, Re[ and Re[ approach each other with the increasing STT. And the two sublattice magnetization precess elliptically with opposite chiralities. (Reprinted with permission from Ref. [29]. Copyright 2016, American Physical Society).
2.3. Resonance Modes in Synthetic Antiferromagnets
In the previous discussion, our focus primarily rested on naturally occurring crystal FMs and AFMs. However, advancements in nanofabrication techniques have enabled the engineering of thin layers of magnetic and non-magnetic materials, thereby unveiling a plethora of novel physical phenomena. One of such phenomenon is the coupling between two magnetic layers adjacent to the same non-magnetic spacer via the interlayer exchange coupling (IEC) [144,145,146,147,148]. The interlayer coupling results from the Ruderman-Kittel-Kasuya-Yosida (RKKY) interaction, whose strength is highly sensitive to the Fermi surface of the non-magnetic metal (such as Cr, Cu, Au, Ru) [149,150]. By modulating the thickness of the non-magnetic spacer, one can adjust the coupling from ferromagnetic (parallel alignment) to antiferromagnetic (antiparallel alignment). The multilayer structures (see Figure 6) composed of two ferromagnetic layers separated by a thin metallic spacer (FM/NM/FM) with an antiferromagnetic interaction between them, are commonly referred to as synthetic antiferromagnets (SAFs) [131,151]. As a synthetic material with both FMs and AFMs properties, SAFs can amalgamate the advantages of both materials. Firstly, the presence of IEC enables the resonance frequency to reach tens of gigahertz (GHz), surpassing that of FMs [35,152,153,154,155]. Secondly, the RKKY strength in SAFs is approximately 100 times weaker than the direct or super-exchange coupling in crystalline AFMs, facilitating easier detection and manipulation of magnetic alignments [151,156,157,158]. Moreover, there are two FMR modes that appear in SAFs. One is the acoustic mode (AM) with in-phase precession between the two FM layers, while the other is the optic mode (OM) with out-of-phase precession [159,160,161,162,163,164,165,166]. All of these advantages attribute SAFs as a prime candidate for next-generation spintronics. In this subsection, we delve into the diverse FMR modes in two distinct SAF structures, namely, in-plane magnetization and out-of-plane magnetization.
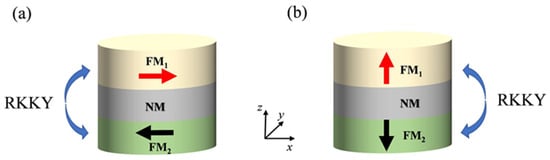
Figure 6.
Schematic of synthetic antiferromagnets. Bilayers with in-plane magnetization (a) and out-of-plane magnetization (b), respectively. The arrows within each ferromagnetic layer indicate the direction of magnetization.
2.3.1. FMR Modes in SAFs with In-Plane Uniaxial Anisotropy
The typical analytical model applicable to in-plane SAFs was developed by modifying the normal antiferromagnetic material as well as that of the single ferromagnetic layer. Firstly, the analytical expression of the corresponding dispersion relation of the corresponding FMR modes was given by Rezende et al. [160] and Wigen et al. [167], as shown in Figure 7. With the external field H0 I applied in the film plane parallel to the in-plane easy axis, the SAFs structure undergoes three unique equilibrium states: In region-I, where H0 is smaller than the critical spin flop field , the magnetizations of M1 and M2 opposite to each other along the easy axis direction, resulting in nearly zero net magnetization for the SAF system. Here, represents the saturation field, denotes the in-plane uniaxial anisotropy field, is the interlayer exchange field with exchange coupling constant . This region is also commonly referred to as the antiferromagnetic (AF) region. Two FMR modes emerge in this region, with the resonant frequencies given by [159]:
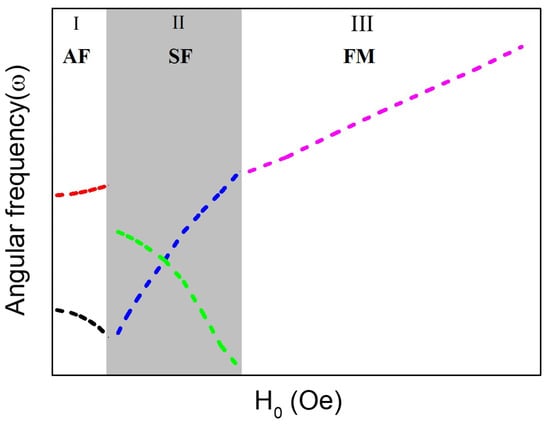
Figure 7.
Exemplary dispersion relation of frequency with the external bias magnetic field for SAFs with in-plane uniaxial anisotropy, obtained from the numerical calculation of Equations (3), (9), and (10).
In region-II, beyond the spin-flop (SF) field, the magnetizations of the two FM layers of M1 and M2 deviate from the complete antiparallel alignment, adopting a canted state. The FMR frequencies in this region are given by [159]:
when H0 > Hsat (region-III), both M1 and M2 align parallel to the easy axis. Consequently, the SAF trilayer system behaves akin to a single ferromagnetic layer, with the FMR frequency also expressible through Equation (3). Through the above analysis, we observe that the characteristics of the two FMR modes in SAFs exhibit obvious dependencies on external magnetic field and the anisotropy field . Interestingly, if the in-plane magnetic anisotropy is ignored, the first equilibrium state (region-I) does not exist with the application of the external magnetic field, and Equation (10) will simplify to [168]:
In this approximation, the two FMR modes (AM and OM) will exhibit even and odd parity properties. This phenomenon will be explained in detail in the next subsection.
We give a further detailed description of magnetization oscillation in the above three distinct equilibrium states. In region-I, the dynamic properties of the magnetizations between the two FM layers exhibit evident antiferromagnetic characteristics. Figure 8a shows two distinct resonance states at a small magnetic field. For the low-frequency mode (f1), as depicted in Figure 8b, the z-components of the magnetization and resonate in-phase, while and resonate out-of-phase. This result supports a periodic oscillation of the z-component sum of the two layers () and a canceled oscillation of the y-component sum (), identifying this resonance mode as the out-of-plane mode. In contrast, for the high-frequency mode (f2), it’s evident that and resonate out-of-phase, while and resonate in-phase, as shown in Figure 8c. This configuration results in a periodic oscillation signal of y-component sum (), identifying this resonance mode as the in-plane mode. It’s noteworthy that this feature resembles the behavior observed in NiO [142]. In region- II, magnetic resonances can also be observed twice at a given bias magnetic field H0, as shown in Figure 8d. However, the characteristics of the two resonance states are completely different. The magnetization vectors of the two FM layers display a scissor-like magnetization state due to the competition between the interlayer AF coupling and the bias magnetic field [169], as described in previous studies. More importantly, m1 and m2 will precess around their own effective fields, with the time evolutions of both the y- and z-components of m1 and m2 oscillating in-phase for the acoustic mode and anti-phase for the optic mode, as shown in Figure 8e and 8f, respectively. These two resonant modes occur only in SAFs with in-plane anisotropy and have been widely reported in the literature [164,165,170]. With the further increase of the magnetic field into the region-III, the magnetization vectors are forced to the direction of H0. In this case, the SAF trilayer system behaves as a single ferromagnetic layer. Theoretically, the optic mode will be hidden as the resonance intensity goes to zero, thus only the Kittel mode in the ferromagnetic phase can be observed [160].
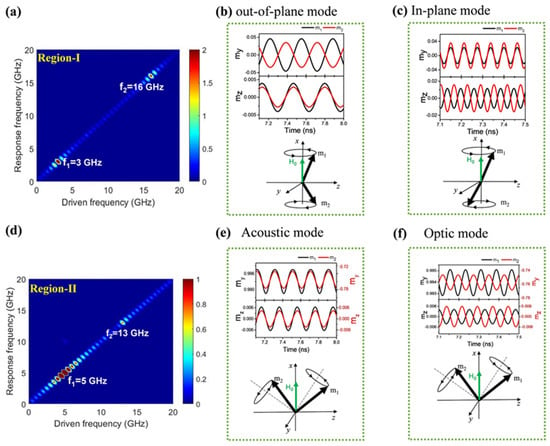
Figure 8.
The simulated FMR response signal for SAFs with in-plane uniaxial anisotropy in region-I (a) and region- II (d). The corresponding dynamic behavior of the two FM layers in the out-of-plane mode, (b) in-plane mode, (c) acoustic mode, (e) and optic mode (f). (Reprinted with permission from Ref. [36]. Copyright 2022, Institute of Physics).
2.3.2. FMR Modes in SAFs with Perpendicular Magnetic Anisotropy
Better than in-plane magnetized materials, magnetic thin films with perpendicular magnetic anisotropy (PMA) have attracted great interest due to their unique advantages such as greater information storage density, higher thermal stability, and faster response frequency [171,172,173,174,175,176]. Recent studies have shown that, similar to collinear AFMs, magnetic resonance modes with right-handed and left-handed precession can also be excited in PMA-SAFs [37,177]. In addition, conventional techniques employed for ferromagnetic materials, such as the magneto-optical Kerr effect and anomalous Hall effect, can be applied to detect the magnetic state or texture in SAFs, suggesting that PMA-SAFs structures can not only possess the characteristics of abundant polarization degrees of freedom of collinear AFMs, but also the spin dynamics is detectable by the same methods as FMs, which provide an attractive platform for designing the next generation of field-effect transistors based on magnon polarization. Here, we expand the description of the two resonance modes with opposite polarization in PMA-SAFs.
We first give a theoretical analysis of the FMR modes in ideal PMA-SAFs including two ferromagnetic layers with same thicknesses t and saturation magnetizations . The effective magnetic field acting on each FM sublayer can be written as:
where is the effective anisotropy field. In the absence of bias magnetic field or the bias field is smaller than the spin-flop field (), the magnetizations of the two FMs will align completely antiparallel. And the magnetization precessions of the two FMs are governed by Equation (1). By taking (i = 1, 2), Equation (1) can be re-written as a 4 × 4 matrix equation with the basis of (m1x, m1y, m2x, m2y). The matrix equation can be further simplified as:
The resonance frequencies are the eigenvalues of the resonance matrix [A]:
In the case of antiparallel state, the two resonance frequencies are given by:
Figure 9 shows the resonance frequency spectra (i.e., the dispersion relations) obtained by Equation (15). Here, and represent the resonance frequencies of the RH mode and LH mode, respectively. Note that for symmetry-breaking SAFs ( or ) the magnetic field are no longer equal and Equation (15) needs to be corrected accordingly [177]:
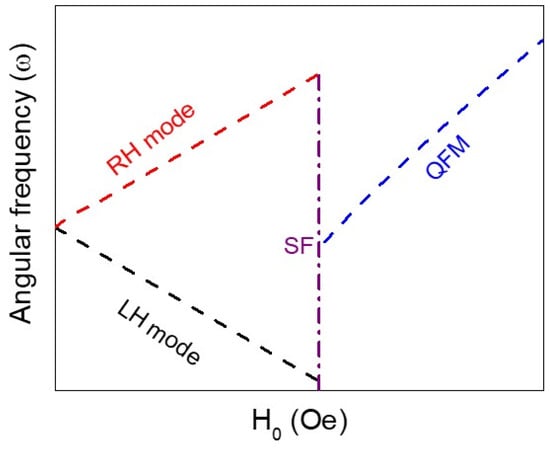
Figure 9.
Field-dependent dispersion relation of frequency with the external magnetic field applied along the easy-axis in PMA-SAFs. Obtained from the numerical calculation of Equation (15).
For symmetric SAFs, we can see that the resonance frequencies of the RH and LH precession modes are degenerate without a magnetic field, and they are split into high frequency and low frequency with an applied magnetic field. The frequency of RH (LH) branch linearly increases (decreases) with the increase of the applied magnetic field. While for symmetry-breaking SAFs, all the above conclusions are valid, the only difference is that the crossing fields in which the RH and LH modes degenerated are shifted from zero fields.
We then discuss the possible polarization under the condition of degeneracy between the two precession modes. Recent theoretical and experimental work show that the precession chirality of the magnon modes in the crossing field is directly dependent on the polarization of the rf microwave magnetic field [37,177]. Figure 10 shows the detailed trajectories of each magnetization under the application of four types of microwave fields. When the microwave field is taken as the counterclockwise (CCW) form of , see Figure 10a, the magnetization of the bottom layer mBL performs an active precession state (large circle) while the top layer mTL behaves as a forced precession state (small circle). In this case, the net magnetization precesses with a CCW rotation around the z-axis, i.e., RH polarization. But when the microwave driving field is taken as the clockwise (CW) form of , mTL will go to the active precession state while mBL will perform as the forced precession state, as shown in Figure 10b. And m performs a LH polarization procession. However, when the x-type microwave magnetic field is applied, the x-components of both mBL and mTL oscillate in-phase while the y-components oscillate out-of-phase with time, see Figure 10c. This type of magnetization resonance results in a periodic oscillation of the net magnetization in the x-direction and a constant value in y-direction (). In contrast, for a y-type microwave field , see Figure 10d, the x-components oscillate out-of-phase while the y-components oscillate in-phase, showing an oscillation in the y-direction and a constant value in the x-direction (). From the above phenomenon, we can conclude that when a linearly polarized microwave field is applied, the precession trajectory of the net magnetization becomes linear and oscillate in the direction of the corresponding microwave field. However, when a circularly polarized microwave field is applied, the precession trajectory of m will also become circular. These results reveal that arbitrary polarizations, including elliptically or linearly polarized magnons, can be achieved by the corresponding type of microwave magnetic field in PMA-SAFs, which provides a new road for us to exploit the polarization degree of freedom of the magnon to realize information transmission.
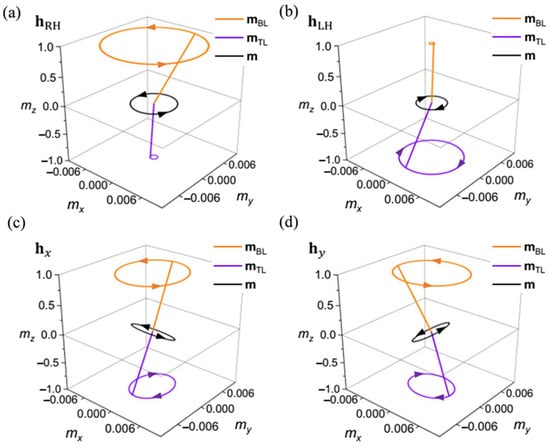
Figure 10.
Magnetization precession trajectories under four different forms of microwave driving fields : (a) CCW-type, (b) CW-type, (c) x-type, and (d) y-type, respectively. The volume-averaged magnetizations mBL (aurantium curve) and mTL (blue curve); the net magnetization vector m = (mBL + mTL)/2. (Reprinted with permission from Ref. [177]. Copyright 2022, American Physical Society).
2.3.3. Magnon-Magnon Coupling
In recent years, magnon–magnon hybrid systems have attracted significant attention due to their advancements in quantum information technologies [178,179,180,181]. SAFs serve as the most promising platforms for hybrid quantum systems. From the previous sections, we know that there are typically two distinct resonance modes in SAFs. For in-plane magnetized SAFs, the most well-known are the in-phase AM and anti-phase OM. Conversely, for perpendicularly magnetized SAFs, these eigenmodes exhibit clear LH and RH polarizations. In principle, the corresponding dispersion spectra will exhibit a degeneracy at their crossing field of in-plane SAFs or PMA-SAFs, meaning that the two orthogonal magnon modes cannot interact and are independent due to symmetrical protection [168]. An interesting question in the field of magnon spintronics is whether there exist additional magnon modes beyond the aforementioned four [2,182,183,184]. Recent studies have indicated that new magnon modes can indeed be excited by adjusting the coherent coupling of these two eigenmodes, a phenomenon known as the magnon-magnon coupling effect, which could be pivotal in the development of future magnonic devices [185,186,187,188,189,190,191,192,193]. MacNeill et al. [168] demonstrated that once the symmetry of the layered antiferromagnet CrCl3 is broken by tilting the external magnetic field H0, coupling between the AM and OM occurs, resulting in the formation of an anti-crossing gap. To describe these coupled resonance modes, the matrix formalism of the LLG equation is equivalent to solving the following two-by-two matrix, whose solutions capture the characteristics of the coupled magnon modes [168]:
where the angular frequency of the bare AM is given by:
and the angular frequency of the bare OM is given by:
HFM is the applied magnetic field required to fully align the two sublattices. The term represents the coupling of AM and OM:
Generally, the effect of the coupling term is negligible, and the solutions are approximately and . Only when the optic and acoustic modes become closer in frequency, are they hybridized by the coupling term, opening a gap. Figure 11a is the frequency-field dispersion relation obtained from the numerical calculation of Equation (17) and clearly displays an anti-crossing gap between the AM and OM in the spin-canted state. Interestingly, this coupling is zero for but becomes nonzero as the applied field H0 tilted out-of-plane. Similar experimental phenomena were reported by Kurebayashi et al. [164] in SAFs and Liensberger et al. [194] in YIG.
It has been demonstrated that the key to achieve the coupling between magnon modes is to break the rotational symmetry. In addition to the method of applying a tilted external magnetic field, there are other means to break the rotational symmetry and achieve the coupling phenomenon. Shiota et al. [163] demonstrated the magnon-magnon coupling between AM and OM can also be achieved with an in-plane magnetic field by utilizing magnons with nonuniform precession (), i.e., spin-wave resonance (SWR), see Figure 11b, the corresponding coupling strength can be tuned by the wave number k and the angle between the external magnetic field and the spin-wave propagation direction. Ma et al. [195] and He et al. [196,197,198] proved that the intrinsic symmetry breaking (i.e., different saturation magnetization or thickness of the two ferromagnetic sublayers of SAFs) will also lead to the coupling phenomena, as illustrated in Figure 11c. In addition, Wang et al. [199] and Comstock et al. [191] discovered the hybridization caused by Dzyaloshinskii–Moriya-Interaction (DMI), as shown in Figure 11d.
Figure 11.
Some novel mechanisms for inducing the coupling between acoustic and optic modes. (a) the coupling between acoustic mode and optic mode in SAFs achieved by the application of an out-of-plane tilted external magnetic field. (Reprinted with permission from Ref. [168]. Copyright 2019, American Physical Society.) (b) the magnon-magnon coupling mediated by the dynamic dipolar interaction. (Reprinted with permission from Ref. [163]. Copyright 2020, American Physical Society.) (c) intrinsic symmetry breaking induced magnon-magnon coupling. (Reprinted with permission from Ref. [196]. Copyright 2021, American Physical Society). (d) ultrastrong magnon–magnon coupling induced by the interlayer DMI. (Reprinted with permission from Ref. [199]. Copyright 2024, American Physical Society.)
Different from the coupling between the two different resonance modes of AM and OM mentioned above, a new coupling phenomenon called self-hybridizations has been attracting attention recently. By using micromagnetic simulation, Sklenar et al. [200] demonstrated that the number of optic and acoustic magnon modes are exquisitely sensitive to the number of layers, and self-hybridization occurs when more than two FM layers are present, as shown in Figure 12a. Unlike the bilayer SAF structure, two optic or acoustic mode branches can exist simultaneously in a four-layered SAF. The field-frequency relationships for the four-layered SAFs also show an anticrossing gap between the two branches, suggesting self-hybridization between magnons of the same character (optic or acoustic). Rong et al. [193] experimentally proved that the number of layers can not only determine the number of excitation modes, but also the mode hybridizations, see Figure 12b. They found that self-hybridizations of optic or acoustic modes appear in even-numbered layers (n = 4, 6 ) of SAFs, leading to an opening of gaps within the same type of modes. While for the odd-numbered layers (n = 3, 5 ), the self-hybridization phenomenon disappeared and was replaced by hybridization between different magnon modes. A global gap between AM and OM was generated and the corresponding coupling strength decreased with increasing layer number. All these studies greatly promoted the research of hybrid magnetic subsystems, which may invigorate the development of magnonics.
Figure 12.
(a) self-hybridization effect where pairs of either optic or acoustic magnons can interact in a SAF structure with four ferromagnetic layers. The field-frequency relationships for the four-layered SAFs also show an anticrossing gap between the two branches, suggesting self-hybridization between magnons of the same character. (Reprinted with permission from Ref. [200]. Copyright 2021, American Physical Society.) (b) self-hybridizations of acoustic or optic modes are achieved by changing the number of ferromagnet layers in SAFs. (Reprinted with permission from Ref. [193]. Copyright 2024, American Physical Society).
3. Conclusions and Perspectives
In recent years, there has been a growing interest in the utilization of magnon manipulation. Using the FMR technique, this article provided a concise review of the fundamental concepts and characteristics of the magnon modes in classical magnetic systems, encompassing both crystal magnetic materials (ferromagnets and antiferromagnets) and synthetic magnetic materials (synthetic antiferromagnets, or SAFs). Our focus has been on antiferromagnets with easy-axis anisotropy (such as MnF2 and Cr2O3), and SAFs with in-plane and perpendicular anisotropy. In ferromagnetic materials, the ferromagnetic resonance excitation is mainly influenced by the magnetic anisotropy field and the demagnetization field, resulting in resonance frequencies which are typically in the GHz range. In contrast, in antiferromagnets, the presence of two sublattices leads to a dominant antiferromagnetic coupling field, allowing antiferromagnetic resonance frequency (AFMR) to reach the THz range. This property holds significant potential for applications in high-frequency spintronic devices. Despite these promising prospects, the challenge of controlling and detecting magnetization in crystalline antiferromagnets lags behind expectations. SAFs offer a compelling solution by combining the high-frequency capabilities of antiferromagnets with the easy detection of ferromagnets. This amalgamation of advantages positions SAFs as potential candidates for future spintronic applications.
Furthermore, we delved into the polarization of magnon modes, highlighting the differences from ferromagnets. In collinear AFMs and PMA-SAFs, the presence of two magnon modes with opposite polarizations adds a novel degree of freedom for encoding and processing information. In AFMs with easy-axis anisotropy, applying a bias magnetic field along the easy-axis induces left-handed and right-handed polarization modes, whose resonance frequencies exhibit linear dependence on the applied field until reaching a critical spin-flop field. Similarly, in SAFs with perpendicular magnetic anisotropy, we observed analogous behavior. Interestingly, it was shown that small circularly polarized microwave fields can selectively excite magnon modes based on polarization, opening avenues for designing magnonic devices. Then, we further introduced the magnon-magnon hybrid systems, a novel approach to create new spin-wave states.
Author Contributions
Conceptualization, X.C., C.Z. and Y.L.; methodology, X.C., C.Z. and Y.L.; formal analysis, X.C., C.Z. and Y.L.; data curation, X.C.; writing—original draft preparation, X.C., writing—review and editing, C.Z. and Y.L.; supervision, Y.L.; project administration, Y.L.; funding acquisition, Y.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (NSFC) (Grant Nos. 12274322, 12304395, and 12347174) and the Opening Project of Shanghai Key Laboratory of Special Artificial Microstructure Materials and Technology.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Chumak, A.V.; Vasyuchka, V.I.; Serga, A.A.; Hillebrands, B. Magnon spintronics. Nat. Phys. 2015, 11, 453–461. [Google Scholar] [CrossRef]
- Barman, A.; Gubbiotti, G.; Ladak, S.; Adeyeye, A.O.; Krawczyk, M.; Gräfe, J.; Adelmann, C.; Cotofana, S.; Naeemi, A.; Vasyuchka, V.I.; et al. The 2021 Magnonics Roadmap. J. Phys. Condens. Matt. 2021, 33, 413001. [Google Scholar] [CrossRef] [PubMed]
- Yuan, H.Y.; Cao, Y.; Kamra, A.; Duine, R.A.; Yan, P. Quantum magnonics: When magnon spintronics meets quantum information science. Phys. Rep. 2022, 965, 1–74. [Google Scholar] [CrossRef]
- Li, Z.; Ma, M.; Chen, Z.; Xie, K.; Ma, F. Interaction between magnon and skyrmion: Toward quantum magnonics. J. Appl. Phys. 2022, 132, 210702. [Google Scholar] [CrossRef]
- Khitun, A.; Bao, M.; Wang, K.L. Magnonic logic circuits. J. Phys. D Appl. Phys. 2010, 43, 264005. [Google Scholar] [CrossRef]
- Lenk, B.; Ulrichs, H.; Garbs, F.; Münzenberg, M. The building blocks of magnonics. Phys. Rep. 2011, 507, 107–136. [Google Scholar] [CrossRef]
- Rezende, S.M. Fundamentals of Magnonics; Lecture notes in Physics; Springer: Berlin/Heidelberg, Germany, 2020; Volume 969. [Google Scholar]
- Rameshti, B.Z.; Kusminskiy, S.V.; Haigh, J.A.; Usami, K.; Lachance-Quirion, D.; Nakamura, Y.; Hu, C.M.; Tang, H.X.; Bauer, G.E.W.; Blanter, Y.M.; et al. Cavity magnonics. Phys. Rep. 2022, 979, 1–61. [Google Scholar] [CrossRef]
- Yu, H.; Xiao, J.; Schultheiss, H. Magnetic texture based magnonics. Phys. Rep. 2021, 905, 1–59. [Google Scholar] [CrossRef]
- Pirro, P.; Vasyuchka, V.I.; Serga, A.A.; Hillebrands, B. Advances in coherent magnonics. Nat. Rev. Mater. 2021, 6, 1114–1135. [Google Scholar] [CrossRef]
- Bloch, F. Zur Theorie des Austauschproblems und der Remanenzerscheinung der Ferromagnetika. Z. Phys. 1932, 74, 295–335. [Google Scholar] [CrossRef]
- Chumak, A.V.; Serga, A.A.; Hillebrands, B. Magnonic crystals for data processing. J. Phys. D Appl. Phys. 2017, 50, 244001. [Google Scholar] [CrossRef]
- Seki, S.; Okamura, Y.; Kondou, K.; Shibata, K.; Kubota, M.; Takagi, R.; Kagawa, F.; Kawasaki, M.; Tatara, G.; Otani, Y.; et al. Magnetochiral nonreciprocity of volume spin wave propagation in chiral-lattice ferromagnets. Phys. Rev. B 2016, 93, 235131. [Google Scholar] [CrossRef]
- Gallardo, R.A.; Alvarado-Seguel, P.; Schneider, T.; Gonzalez-Fuentes, C.; Roldán-Molina, A.; Lenz, K.; Lindner, J.; Landeros, P. Spin-wave non-reciprocity in magnetization-graded ferromagnetic films. New J. Phys. 2019, 21, 033026. [Google Scholar] [CrossRef]
- Wang, X.S.; Zhang, H.W.; Wang, X.R. Topological Magnonics: A Paradigm for Spin-Wave Manipulation and Device Design. Phys. Rev. Appl. 2018, 9, 024029. [Google Scholar] [CrossRef]
- Yao, W.; Li, C.; Wang, L.; Xue, S.; Dan, Y.; Iida, K.; Kamazawa, K.; Li, K.K.; Fang, C.; Li, Y. Topological spin excitations in a three-dimensional antiferromagnet. Nat. Phys. 2018, 14, 1011–1015. [Google Scholar] [CrossRef]
- Popov, P.A.; Sharaevskaya, A.Y.; Beginin, E.N.; Sadovnikov, A.V.; Stognij, A.I.; Kalyabin, D.V.; Nikitov, S.A. Spin wave propagation in three-dimensional magnonic crystals and coupled structures. J. Magn. Magn. Mater. 2019, 476, 423–427. [Google Scholar] [CrossRef]
- Demokritov, S.; Demidov, V.; Dzyapko, O.; Melkov, G.; Serga, A.A.; Hillebrands, B.; Slavin, A.N. Bose-Einstein condensation of quasi-equilibrium magnons at room temperature under pumping. Nature 2006, 443, 430–433. [Google Scholar] [CrossRef]
- Serga, A.A.; Tiberkevich, V.S.; Sandweg, C.W.; Vasyuchka, V.I.; Bozhko, D.A.; Chumak, A.V.; Neumann, T.; Obry, B.; Melkov, G.A.; Slavin, A.N.; et al. Bose–Einstein condensation in an ultra-hot gas of pumped magnons. Nat. Commun. 2014, 5, 3452. [Google Scholar] [CrossRef]
- Bozhko, D.A.; Serga, A.A.; Clausen, P.; Vasyuchka, V.I.; Heussner, F.; Melkov, G.A.; Pomyalov, A.; L’vov, V.S.; Hillebrands, B. Supercurrent in a room-temperature Bose–Einstein magnon condensate. Nat. Phys. 2016, 12, 1057–1062. [Google Scholar] [CrossRef]
- Safranski, C.; Barsukov, I.; Lee, H.K.; Schneider, T.; Jara, A.A.; Smith, A.; Chang, H.; Lenz, K.; Lindner, J.; Tserkovnyak, Y.; et al. Spin caloritronic nano-oscillator. Nat. Commun. 2017, 8, 117. [Google Scholar] [CrossRef]
- Walowski, J.; Münzenberg, M. Perspective: Ultrafast magnetism and THz spintronics. J. Appl. Phys. 2016, 120, 140901. [Google Scholar] [CrossRef]
- Baltz, V.; Manchon, A.; Tsoi, M.; Moriyama, T.; Ono, T.; Tserkovnyak, Y. Antiferromagnetic spintronics. Rev. Mod. Phys. 2018, 90, 015005. [Google Scholar] [CrossRef]
- Jungwirth, T.; Sinova, J.; Manchon, A.; Marti, X.; Wunderlich, J.; Felser, C. The multiple directions of antiferromagnetic spintronics. Nat. Phys. 2018, 14, 200–203. [Google Scholar] [CrossRef]
- Gomonay, O.; Baltz, V.; Brataas, A.; Tserkovnyak, Y. Antiferromagnetic spin textures and dynamics. Nat. Phys. 2018, 14, 213–216. [Google Scholar] [CrossRef]
- Razdolski, I.; Alekhin, A.; Ilin, N.; Meyburg, J.P.; Roddatis, V.; Diesing, D.; Bovensiepen, U.; Melnikov, A. Nanoscale interface confinement of ultrafast spin transfer torque driving non-uniform spin dynamics. Nat. Commun. 2017, 8, 15007. [Google Scholar] [CrossRef] [PubMed]
- Kampfrath, T.; Sell, A.; Klatt, G.; Pashkin, A.; Mährlein, S.; Dekorsy, T.; Wolf, M.; Fiebig, M.; Leitenstorfer, A.; Huber, R. Coherent terahertz control of antiferromagnetic spin waves. Nat. Photo. 2011, 5, 31–34. [Google Scholar] [CrossRef]
- Patil, R.A.; Su, C.-W.; Chuang, C.-J.; Lai, C.-C.; Liou, Y.; Ma, Y.R. Terahertz spin-wave waveguides and optical magnonics in one-dimensional NiO nanorods. Nanoscale 2016, 8, 12970–12976. [Google Scholar] [CrossRef] [PubMed]
- Cheng, R.; Xiao, D.; Brataas, A. Terahertz Antiferromagnetic Spin Hall Nano-Oscillator. Phys. Rev. Lett. 2016, 116, 207603. [Google Scholar] [CrossRef] [PubMed]
- Vaidya, P.; Morley, S.A.; van Tol, J.; Liu, Y.; Cheng, R.; Brataas, A.; Lederman, D.; del Barco, E. Subterahertz spin pumping from an insulating antiferromagnet. Science 2020, 368, 160. [Google Scholar] [CrossRef]
- Olejník, K.; Seifert, T.; Kašpar, Z.; Novák, V.; Wadley, P.; Campion, R.P.; Baumgartner, M.; Gambardella, P.; Nemec, P.; Wunderlich, J. Terahertz electrical writing speed in an antiferromagnetic memory. Sci. Adv. 2017, 4, eaar3566. [Google Scholar] [CrossRef]
- Yang, Y.; Wilson, R.B.; Gorchon, J.; Lambert, C.-H.; Salahuddin, S.; Bokor, J. Ultrafast magnetization reversal by picosecond electrical pulses. Sci. Adv. 2017, 3, 1603117. [Google Scholar] [CrossRef] [PubMed]
- Griffiths, J.H.E. Anomalous High-frequency Resistance of Ferromagnetic Metals. Nature 1946, 158, 670. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. On the theory of the dispersion of magnetic permeability in ferromagnetic bodies. Phys. Z. Sowjet 1935, 8, 153–169. [Google Scholar]
- Zhang, S.; Lin, J.; Miao, G.-X.; Li, S.; Zhao, G.; Wang, X.; Li, Q.; Cao, D.; Xu, J.; Yan, S. Ultrahigh Frequency and Anti-Interference Optical-Mode Resonance with Biquadratic Coupled FeCoB/Ru/FeCoB Trilayers. ACS Appl. Mater. Interfaces 2019, 11, 48230–48238. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Zheng, C.; Zhou, S.; Liu, Y.; Zhang, Z. Ferromagnetic resonance modes of a synthetic antiferromagnet at low magnetic fields. J. Phys. Condens. Matt. 2021, 34, 015802. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Zheng, C.; Zhang, Y.; Zhou, S.; Liu, Y.; Zhang, Z. Identification and manipulation of spin wave polarizations in perpendicularly magnetized synthetic antiferromagnets. New J. Phys. 2021, 23, 113029. [Google Scholar] [CrossRef]
- Slonczewski, J.C. Current-driven excitation of magnetic multilayers. J. Magn. Magn. Mater. 1996, 159, L1–L7. [Google Scholar] [CrossRef]
- Berger, L. Emission of spin waves by a magnetic multilayer traversed by a current. Phys. Rev. B 1996, 54, 9353–9358. [Google Scholar] [CrossRef]
- Tulapurkar, A.A.; Suzuki, Y.; Fukushima, A.; Kubota, H.; Maehara, H.; Tsunekawa, K.; Djayaprawira, D.D.; Watanabe, N.; Yuasa, S. Spin-torque diode effect in magnetic tunnel junctions. Nature 2005, 438, 339–342. [Google Scholar] [CrossRef]
- Yu, T.; Naganuma, H.; Oogane, M.; Ando, Y. DC Bias Reversal Behavior of Spin-Torque Ferromagnetic Resonance Spectra in CoFeB/MgO/CoFeB Perpendicular Magnetic Tunnel Junction. IEEE Trans. Magn. 2017, 53, 1–5. [Google Scholar] [CrossRef]
- Sankey, J.C.; Braganca, P.M.; Garcia, A.G.F.; Krivorotov, I.N.; Buhrman, R.A.; Ralph, D.C. Spin-Transfer-Driven Ferromagnetic Resonance of Individual Nanomagnets. Phys. Rev. Lett. 2006, 96, 227601. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Beaujour, J.M.L.; de Loubens, G.; Kent, A.D.; Sun, J.Z. Spin-torque driven ferromagnetic resonance of Co/Ni synthetic layers in spin valves. Appl. Phys. Lett. 2008, 92, 012507. [Google Scholar] [CrossRef]
- Tsoi, M.; Jansen, A.G.M.; Bass, J.; Chiang, W.C.; Seck, M.; Tsoi, V.; Wyder, P. Excitation of a Magnetic Multilayer by an Electric Current. Phys. Rev. Lett. 1998, 80, 4281–4284. [Google Scholar] [CrossRef]
- Kiselev, S.I.; Sankey, J.C.; Krivorotov, I.N.; Emley, N.C.; Schoelkopf, R.J.; Buhrman, R.A.; Ralph, D.C. Microwave oscillations of a nanomagnet driven by a spin-polarized current. Nature 2003, 425, 380–383. [Google Scholar] [CrossRef] [PubMed]
- Fuchs, G.D.; Emley, N.C.; Krivorotov, I.N.; Braganca, P.M.; Ryan, E.M.; Kiselev, S.I.; Sankey, J.C.; Ralph, D.C.; Buhrman, R.A.; Katine, J.A. Spin-transfer effects in nanoscale magnetic tunnel junctions. Appl. Phys. Lett. 2004, 85, 1205–1207. [Google Scholar] [CrossRef]
- Rippard, W.H.; Pufall, M.R.; Kaka, S.; Russek, S.E.; Silva, T.J. Direct-Current Induced Dynamics in Co90Fe10/Ni80Fe20 Point Contacts. Phys. Rev. Lett. 2004, 92, 027201. [Google Scholar] [CrossRef] [PubMed]
- Houssameddine, D.; Ebels, U.; Delaet, B.; Rodmacq, B.; Firastrau, I.; Ponthenier, F.; Brunet, M.; Thirion, C.; Michel, J.-P.; Prejbeanu-Buda, L.; et al. Spin-torque oscillator using a perpendicular polarizer and a planar free layer. Nat. Mater. 2007, 6, 447–453. [Google Scholar] [CrossRef] [PubMed]
- Kubota, H.; Fukushima, A.; Yakushiji, K.; Nagahama, T.; Yuasa, S.; Ando, K.; Maehara, H.; Nagamine, Y.; Tsunekawa, K.; Djayaprawira, D.D.; et al. Quantitative measurement of voltage dependence of spin-transfer torque in MgO-based magnetic tunnel junctions. Nat. Phys. 2008, 4, 37–41. [Google Scholar] [CrossRef]
- Zeng, Z.; Finocchio, G.; Zhang, B.; Amiri, P.K.; Katine, J.A.; Krivorotov, I.N.; Huai, Y.M.; Langer, J.; Azzerboni, B.; Wang, K.L.; et al. Ultralow-current-density and bias-field-free spin-transfer nano-oscillator. Sci. Rep. 2013, 3, 1426. [Google Scholar] [CrossRef]
- Fuchs, G.D.; Sankey, J.C.; Pribiag, V.S.; Qian, L.; Braganca, P.M.; Garcia, A.G.F.; Ryan, E.M.; Li, Z.P.; Ozatay, O.; Ralph, D.C.; et al. Spin-Torque Ferromagnetic Resonance Measurements of Damping in Nanomagnets. Appl. Phys. Lett. 2007, 91, 062507. [Google Scholar] [CrossRef]
- Kupferschmidt, J.N.; Adam, S.; Brouwer, P.W. Theory of the spin-torque-driven ferromagnetic resonance in a ferromagnet/normal-metal/ferromagnet structure. Phys. Rev. B 2006, 74, 134416. [Google Scholar] [CrossRef]
- Kovalev, A.A.; Bauer, G.E.W.; Brataas, A. Current-driven ferromagnetic resonance, mechanical torques, and rotary motion in magnetic nanostructures. Phys. Rev. B 2007, 75, 014430. [Google Scholar] [CrossRef]
- Tserkovnyak, Y.; Brataas, A.; Bauer, G.E.W. Spin pumping and magnetization dynamics in metallic multilayers. Phys. Rev. B 2002, 66, 224403. [Google Scholar] [CrossRef]
- Torres, L.; Finocchio, G.; Lopez-Diaz, L.; Martinez, E.; Carpentieri, M.; Consolo, G.; Azzerboni, B. Micromagnetic modal analysis of spin-transfer-driven ferromagnetic resonance of individual nanomagnets. J. Appl. Phys. 2007, 101, A502–A503. [Google Scholar] [CrossRef]
- Sankey, J.C.; Cui, Y.-T.; Sun, J.Z.; Slonczewski, J.C.; Buhrman, R.A.; Ralph, D.C. Measurement of the spin-transfer-torque vector in magnetic tunnel junctions. Nat. Phys. 2008, 4, 67–71. [Google Scholar] [CrossRef]
- Frankowski, M.; Chȩciński, J.; Skowroński, W.; Stobiecki, T. Perpendicular magnetic anisotropy influence on voltage-driven spin-diode effect in magnetic tunnel junctions: A micromagnetic study. J. Magn. Magn. Mater. 2017, 429, 11–15. [Google Scholar] [CrossRef]
- Borlenghi, S.; Mahani, M.R.; Fangohr, H.; Franchin, M.; Delin, A.; Fransson, J. Micromagnetic simulations of spin-torque driven magnetization dynamics with spatially resolved spin transport and magnetization texture. Phys. Rev. B 2017, 96, 094428. [Google Scholar] [CrossRef]
- Chernyshov, A.; Overby, M.; Liu, X.; Furdyna, J.K.; Lyanda-Geller, Y.; Rokhinson, L.P. Evidence for reversible control of magnetization in a ferromagnetic material by means of spin–orbit magnetic field. Nat. Phys. 2009, 5, 656. [Google Scholar] [CrossRef]
- Fang, D.; Kurebayashi, H.; Wunderlich, J.; Vyborny, K.; Zarbo, L.P.; Campion, R.P.; Casiraghi, A.; Gallagher, B.L.; Jungwirth, T.; Ferguson, A.J. Spin-orbit-driven ferromagnetic resonance. Nat. Nanotech. 2011, 6, 413–417. [Google Scholar] [CrossRef]
- Miron, I.M.; Garello, K.; Gaudin, G.; Zermatten, P.-J.; Costache, M.V.; Auffret, S.; Bandiera, S.; Rodmacq, B.; Schuhl, A.; Gambardella, P. Perpendicular switching of a single ferromagnetic layer induced by in-plane current injection. Nature 2011, 476, 189–193. [Google Scholar] [CrossRef]
- Hirsch, J.E. Spin Hall Effect. Phys. Rev. Lett. 1999, 83, 1834–1837. [Google Scholar] [CrossRef]
- Zhang, S. Spin Hall Effect in the Presence of Spin Diffusion. Phys. Rev. Lett. 2000, 85, 393–396. [Google Scholar] [CrossRef] [PubMed]
- Valenzuela, S.O.; Tinkham, M. Direct electronic measurement of the spin Hall effect. Nature 2006, 442, 176. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Moriyama, T.; Ralph, D.C.; Buhrman, R.A. Spin-Torque Ferromagnetic Resonance Induced by the Spin Hall Effect. Phys. Rev. Lett. 2011, 106, 036601. [Google Scholar] [CrossRef] [PubMed]
- Nan, T.; Emori, S.; Boone, C.T.; Wang, X.; Oxholm, T.M.; Jones, J.G.; Howe, B.M.; Brown, G.J.; Sun, N.X. Comparison of spin-orbit torques and spin pumping across NiFe/Pt and NiFe/Cu/Pt interfaces. Phys. Rev. B 2015, 91, 214416. [Google Scholar] [CrossRef]
- Sinova, J.; Valenzuela, S.O.; Wunderlich, J.; Back, C.H.; Jungwirth, T. Spin Hall effects. Rev. Mod. Phys. 2015, 87, 1213–1260. [Google Scholar] [CrossRef]
- Fan, Y.; Upadhyaya, P.; Kou, X.; Lang, M.; Takei, S.; Wang, Z.X.; Tang, J.S.; He, L.; Chang, L.T.; Montazeri, M.; et al. Magnetization switching through giant spin–orbit torque in a magnetically doped topological insulator heterostructure. Nat. Mater. 2014, 13, 699–704. [Google Scholar] [CrossRef]
- Shiomi, Y.; Nomura, K.; Kajiwara, Y.; Eto, K.; Novak, M.; Segawa, K.; Ando, Y.; Saitoh, E. Spin-electricity conversion induced by spin injection into topological insulators. Phys. Rev. Lett. 2014, 113, 196601. [Google Scholar] [CrossRef]
- Lee, J.S.; Richardella, A.; Hickey, D.R.; Mkhoyan, K.A.; Samarth, N. Mapping the chemical potential dependence of current-induced spin polarization in a topological insulator. Phys. Rev. B 2015, 92, 155312. [Google Scholar] [CrossRef]
- Kondou, K.; Yoshimi, R.; Tsukazaki, A.; Fukuma, Y.; Matsuno, J.; Takahashi, K.S.; Kawasaki, M.; Tokura, Y.; Otani, Y. Fermi-level-dependent charge-to-spin current conversion by Dirac surface states of topological insulators. Nat. Phys. 2016, 12, 1027–1031. [Google Scholar] [CrossRef]
- Zhang, W.; Jungfleisch, M.B.; Jiang, W.; Pearson, J.E.; Hoffmann, A.; Freimuth, F.; Mokrousov, Y. Spin Hall Effects in Metallic Antiferromagnets. Phys. Rev. Lett. 2014, 113, 196602. [Google Scholar] [CrossRef] [PubMed]
- Kimata, M.; Chen, H.; Kondou, K.; Sugimoto, S.; Muduli, P.K.; Ikhlas, M.; Omori, Y.; Tomita, T.; MacDonald, A.H.; Nakatsuji, S.; et al. Magnetic and magnetic inverse spin Hall effects in a non-collinear antiferromagnet. Nature 2019, 565, 627–630. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Shi, S.; Shi, G.; Fan, X.; Song, C.; Zhou, X.; Bai, H.; Liao, L.; Zhou, Y.; Zhang, H.; et al. Observation of the antiferromagnetic spin Hall effect. Nat. Mater. 2021, 20, 800–804. [Google Scholar] [CrossRef] [PubMed]
- Hu, S.; Shao, D.F.; Yang, H.; Pan, C.; Fu, Z.; Tang, M.; Yang, Y.; Fan, W.; Zhou, S.; Tsymbal, E.Y.; et al. Efficient perpendicular magnetization switching by a magnetic spin Hall effect in a noncollinear antiferromagnet. Nat. Commun. 2022, 13, 4447. [Google Scholar] [CrossRef] [PubMed]
- Kalarickal, S.S.; Krivosik, P.; Wu, M.; Patton, C.E.; Schneider, M.L.; Kabos, P.; Silva, T.J.; Nibarger, J.P. Ferromagnetic resonance linewidth in metallic thin films: Comparison of measurement methods. J. Appl. Phys. 2006, 99, 3060–3645. [Google Scholar] [CrossRef]
- Banholzer, A.; Narkowicz, R.; Hassel, C.; Meckenstock, R.; Stienen, S.; Posth, O.; Suter, D.; Farle, M.; Lindner, J. Visualization of spin dynamics in single nanosized magnetic elements. Nanotechnology 2011, 22, 295713. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Azevedo, A.; Santos, O.A.; Guerra, G.A.F.; Cunha, R.O.; Rodriguez-Suarez, R.; Rezende, S.M. Competing spin pumping effects in magnetic hybrid structures. Appl. Phys. Lett. 2014, 104, 117601. [Google Scholar] [CrossRef]
- Freeman, M.R.; Brady, M.J.; Smyth, J. Extremely high frequency pulse magnetic resonance by picosecond magneto-optic sampling. Appl. Phys. Lett. 1992, 60, 2555–2557. [Google Scholar] [CrossRef]
- Neudecker, I.; Perzlmaier, K.; Hoffmann, F.; Woltersdorf, G.; Buess, M.; Weiss, D.; Back, C.H. Modal spectrum of permalloy disks excited by in-plane magnetic fields. Phys. Rev. B 2006, 73, 134426. [Google Scholar] [CrossRef]
- Eschenlohr, A.; Battiato, M.; Maldonado, P.; Pontius, N.; Kachel, T.; Holldack, K.; Mitzner, R.; Foehlisch, A.; Oppeneer, P.M.; Stamm, C. Ultrafast spin transport as key to femtosecond demagnetization. Nat. Mater. 2013, 12, 332–336. [Google Scholar] [CrossRef]
- Boone, C.T.; Nembach, H.T.; Shaw, J.M.; Silva, T.J. Spin transport parameters in metallic multilayers determined by ferromagnetic resonance measurements of spin-pumping. J. Appl. Phys. 2013, 113, 1217–1226. [Google Scholar] [CrossRef]
- Capua, A.; Yang, S.-H.; Phung, T.; Parkin, S.S.P. Determination of intrinsic damping of perpendicularly magnetized ultrathin films from time-resolved precessional magnetization measurements. Phys. Rev. B 2015, 92, 224402. [Google Scholar] [CrossRef]
- Schreiber, F.; Hoffmann, M.; Geisau, O.; Pelzl, J. Investigation of the photothermally modulated ferromagnetic resonance signal from magnetostatic modes in yttrium iron garnet films. Appl. Phys. A 1993, 57, 545–551. [Google Scholar] [CrossRef]
- Meckenstock, R. Invited Review Article: Microwave spectroscopy based on scanning thermal microscopy: Resolution in the nanometer range. Rev. Sci. Instrum. 2008, 79, 041101. [Google Scholar] [CrossRef] [PubMed]
- Bilzer, C.; Devolder, T.; Crozat, P.; Chappert, C.; Cardoso, S.; Freitas, P.P. Vector network analyzer ferromagnetic resonance of thin films on coplanar waveguides: Comparison of different evaluation methods. J. Appl. Phys. 2007, 101, 074505. [Google Scholar] [CrossRef]
- Michael, F. Ferromagnetic resonance of ultrathin metallic layers. Rep. Prog. Phys. 1998, 61, 755. [Google Scholar]
- Kittel, C. On the Theory of Ferromagnetic Resonance Absorption. Phys. Rev. 1948, 73, 155–161. [Google Scholar] [CrossRef]
- Smit, J.; Beljers, H.G. Ferromagnetic resonance absorption in BaFe12O19, a highly anisotropic crystal. Philips Res. Rep. 1955, 10, 113. [Google Scholar]
- Phuoc, N.N.; Hung, L.T.; Ong, C.K. Ultra-high ferromagnetic resonance frequency in exchange-biased system. J. Alloys Compd. 2010, 506, 504–507. [Google Scholar] [CrossRef]
- Layadi, A. Ferromagnetic resonance modes in single and coupled layers with oblique anisotropy axis. Phys. Rev. B 2001, 63, 174410. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, S.; Qiao, S.; Du, H.; Liu, X.; Sun, R.; Chu, X.; Miao, G.; Dai, Y.; Kang, S.; et al. Dual-mode ferromagnetic resonance in an FeCoB/Ru/FeCoB synthetic antiferromagnet with uniaxial anisotropy. Appl. Phys. Lett. 2018, 112, 192401. [Google Scholar] [CrossRef]
- Castel, V.; Youssef, J.B.; Boust, F.; Weil, R.; Pigeau, B.; De Loubens, G.; Naletov, V.V.; Klein, O.; Vukadinovic, N. Perpendicular ferromagnetic resonance in soft cylindrical elements: Vortex and saturated states. Phys. Rev. B 2012, 85, 184419. [Google Scholar] [CrossRef]
- Nozaki, T.; Shiota, Y.; Miwa, S.; Murakami, S.; Bonell, F.; Ishibashi, S.; Kubota, H.; Yakushiji, K.; Saruya, T.; Fukushima, A. Electric-field-induced ferromagnetic resonance excitation in an ultrathin ferromagnetic metal layer. Nat. Phys. 2012, 8, 491–496. [Google Scholar] [CrossRef]
- Chen, X.; Qin, J.; Yu, T.; Han, X.-F.; Liu, Y. Micromagnetic simulation of spin torque ferromagnetic resonance in nano-ring-shape confined magnetic tunnel junctions. Appl. Phys. Lett. 2018, 113, 142406. [Google Scholar] [CrossRef]
- Qin, J.; Chen, X.; Yu, T.; Wang, X.; Guo, C.; Wan, C.; Feng, J.; Wei, H.; Liu, Y.; Han, X. Microwave Spin-Torque-Induced Magnetic Resonance in a Nanoring-Shape-Confined Magnetic Tunnel Junction. Phys. Rev. Appl. 2018, 10, 044067. [Google Scholar] [CrossRef]
- Oates, C.J.; Ogrin, F.Y.; Lee, S.L.; Riedi, P.C.; Smith, G.M.; Thomson, T. High field ferromagnetic resonance measurements of the anisotropy field of longitudinal recording thin-film media. J. Appl. Phys. 2002, 91, 1417–1422. [Google Scholar] [CrossRef]
- Stiles, M.D.; Miltat, J. Spin Transfer Torque and Dynamics. In Spin Dynamics in Confined Magnetic Structures III; Hillebrands, B., Thiaville, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Ralph, D.C.; Stiles, M.D. Spin transfer torques. J. Magn. Magn. Mater. 2008, 320, 1190–1216. [Google Scholar] [CrossRef]
- Ogrodnik, P.; Wilczyński, M.; Świrkowicz, R.; Barnaś, J. Spin transfer torque and magnetic dynamics in tunnel junctions. Phys. Rev. B 2010, 82, 134412. [Google Scholar] [CrossRef]
- Demidov, V.E.; Urazhdin, S.; Demokritov, S.O. Direct observation and mapping of spin waves emitted by spin-torque nano-oscillators. Nat. Mater. 2010, 9, 984–988. [Google Scholar] [CrossRef]
- Madami, M.; Bonetti, S.; Consolo, G.; Tacchi, S.; Carlotti, G.; Gubbiotti, G.; Mancoff, F.B.; Yar, M.A.; Akerman, J. Direct observation of a propagating spin wave induced by spin-transfer torque. Nat. Nanotech. 2011, 6, 635–638. [Google Scholar] [CrossRef]
- Bazaliy, Y.B.; Jones, B.A.; Zhang, S.-C. Modification of the Landau-Lifshitz equation in the presence of a spin-polarized current in colossal- and giant-magnetoresistive materials. Phys. Rev. B 1998, 57, R3213–R3216. [Google Scholar] [CrossRef]
- Hoefer, M.A.; Silva, T.J.; Keller, M.W. Theory for a dissipative droplet soliton excited by a spin torque nanocontact. Phys. Rev. B 2010, 82, 054432. [Google Scholar] [CrossRef]
- Mohseni, S.M.; Sani, S.R.; Persson, J.; Nguyen, T.N.A.; Chung, S.; Pogoryelov, Y.; Muduli, P.K.; Iacocca, E.; Eklund, A.; Dumas, R.K.; et al. Spin Torque–Generated Magnetic Droplet Solitons. Science 2013, 339, 1295–1298. [Google Scholar] [CrossRef] [PubMed]
- Macià, F.; Backes, D.; Kent, A.D. Stable magnetic droplet solitons in spin-transfer nanocontacts. Nat. Nanotech. 2014, 9, 992–996. [Google Scholar] [CrossRef]
- Xiao, D.; Liu, Y.; Zhou, Y.; Mohseni, S.M.; Chung, S.; Akerman, J. Merging droplets in double nanocontact spin torque oscillators. Phys. Rev. B 2016, 93, 094431. [Google Scholar] [CrossRef]
- Xiao, D.; Tiberkevich, V.; Liu, Y.H.; Liu, Y.W.; Mohseni, S.M.; Chung, S.; Ahlberg, M.; Slavin, A.N.; Akerman, J.; Zhou, Y. Parametric autoexcitation of magnetic droplet soliton perimeter modes. Phys. Rev. B 2017, 95, 024106. [Google Scholar] [CrossRef]
- Slavin, A.; Tiberkevich, V. Spin Wave Mode Excited by Spin-Polarized Current in a Magnetic Nanocontact is a Standing Self-Localized Wave Bullet. Phys. Rev. Lett. 2005, 95, 237201. [Google Scholar] [CrossRef]
- Bonetti, S.; Tiberkevich, V.; Consolo, G.; Finocchio, G.; Muduli, P.; Mancoff, F.; Slavin, A.; Akerman, J. Experimental Evidence of Self-Localized and Propagating Spin Wave Modes in Obliquely Magnetized Current-Driven Nanocontacts. Phys. Rev. Lett. 2010, 105, 217204. [Google Scholar] [CrossRef]
- Zhou, Z.W.; Wang, X.G.; Nie, Y.Z.; Xia, Q.L.; Zeng, Z.M.; Guo, G.H. Left-handed polarized spin waves in ferromagnets induced by spin-transfer torque. Phys. Rev. B 2019, 99, 014420. [Google Scholar] [CrossRef]
- Nishimura, N.; Hirai, T.; Koganei, A.; Ikeda, T.; Okano, K.; Sekiguchi, Y.; Osada, Y. Magnetic tunnel junction device with perpendicular magnetization films for high-density magnetic random access memory. J. Appl. Phys. 2002, 91, 5246–5249. [Google Scholar] [CrossRef]
- Falloon, P.E.; Jalabert, R.A.; Weinmann, D.; Stamps, R.L. Circuit model for domain walls in ferromagnetic nanowires: Application to conductance and spin transfer torques. Phys. Rev. B 2004, 70, 174424. [Google Scholar] [CrossRef]
- Xiao, J.; Bauer, G.E.W. Spin-Wave Excitation in Magnetic Insulators by Spin-Transfer Torque. Phys. Rev. Lett. 2012, 108, 217204. [Google Scholar] [CrossRef] [PubMed]
- Ulrichs, H.; Demidov, V.E.; Demokritov, S.O.; Urazhdin, S. Spin-torque nano-emitters for magnonic applications. Appl. Phys. Lett. 2012, 100, 162406. [Google Scholar] [CrossRef]
- Demidov, V.E.; Urazhdin, S.; Liu, R.; Divinskiy, B.; Telegin, A.; Demokritov, S.O. Excitation of coherent propagating spin waves by pure spin currents. Nat. Commun. 2016, 7, 10446. [Google Scholar] [CrossRef] [PubMed]
- Divinskiy, B.; Demidov, V.E.; Urazhdin, S.; Freeman, R.; Rinkevich, A.B.; Demokritov, S.O. Excitation and Amplification of Spin Waves by Spin–Orbit Torque. Adv. Mater. 2018, 30, 1802837. [Google Scholar] [CrossRef] [PubMed]
- Gurevich, A.G.; Melkov, G.A. Magnetization Oscillations and Waves; CRC Press: Boca Raton, FL, USA, 1996. [Google Scholar]
- Houshang, A.; Khymyn, R.; Fulara, H.; Gangwar, A.; Haidar, M.; Etesami, S.R.; Ferreira, R.; Freitas, P.P.; Dvornik, M.; Dumas, R.K.; et al. Spin transfer torque driven higher-order propagating spin waves in nano-contact magnetic tunnel junctions. Nat. Commun. 2018, 9, 4374. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, D.; Yang, Y.; Lee, K.; Mishra, R.; Go, G.; Oh, S.H.; Kim, D.H.; Cai, K.M.; Liu, E.L. Magnetization switching by magnon-mediated spin torque through an antiferromagnetic insulator. Science 2019, 366, 1125–1128. [Google Scholar] [CrossRef]
- Demidov, V.E.; Urazhdin, S.; Anane, A.; Cros, V.; Demokritov, S.O. Spin–orbit-torque magnonics. J. Appl. Phys. 2020, 127, 170901. [Google Scholar] [CrossRef]
- Wienholdt, S.; Hinzke, D.; Nowak, U. THz Switching of Antiferromagnets and Ferrimagnets. Phys. Rev. Lett. 2012, 108, 247207. [Google Scholar] [CrossRef]
- Wadley, P.; Howells, B.; Zelezny, J.; Andrews, C.; Hills, V.; Campion, R.P.; Novak, V.; Olejnik, K.; Maccherozzi, F.; Dhesi, S.S.; et al. Electrical switching of an antiferromagnet. Science 2016, 351, 587–590. [Google Scholar] [CrossRef]
- Khymyn, R.; Lisenkov, I.; Tiberkevich, V.; Ivanov, B.A.; Slavin, A. Antiferromagnetic THz-frequency Josephson-like Oscillator Driven by Spin Current. Sci. Rep. 2017, 7, 43705. [Google Scholar] [CrossRef]
- Li, J.; Wilson, C.B.; Cheng, R.; Lohmann, M.; Kavand, M.; Yuan, W.; Aldosary, M.; Agladze, N.; Wei, P.; Sherwin, M.S.; et al. Spin current from sub-terahertz-generated antiferromagnetic magnons. Nature 2020, 578, 70–74. [Google Scholar] [CrossRef]
- Gomonay, E.V.; Loktev, V.M. Spintronics of antiferromagnetic systems (Review Article). Low Temp. Phys. 2014, 40, 17–35. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, Y.; Ezawa, M. Antiferromagnetic Skyrmion: Stability, Creation and Manipulation. Sci. Rep. 2016, 6, 24795. [Google Scholar] [CrossRef]
- Gomonay, O.; Jungwirth, T.; Sinova, J. Concepts of antiferromagnetic spintronics. Phys. Status. Solidi-R 2017, 11, 1700022. [Google Scholar] [CrossRef]
- Šmejkal, L.; Mokrousov, Y.; Yan, B.; MacDonald, A.H. Topological antiferromagnetic spintronics. Nat. Phys. 2018, 14, 242–251. [Google Scholar] [CrossRef]
- Železný, J.; Wadley, P.; Olejník, K.; Hoffmann, A.; Ohno, H. Spin transport and spin torque in antiferromagnetic devices. Nat. Phys. 2018, 14, 220–228. [Google Scholar] [CrossRef]
- Duine, R.A.; Lee, K.-J.; Parkin, S.S.P.; Stiles, M.D. Synthetic antiferromagnetic spintronics. Nat. Phys. 2018, 14, 217–219. [Google Scholar] [CrossRef] [PubMed]
- Song, C.; You, Y.; Chen, X.; Zhou, X.; Wang, Y.; Pan, F. How to manipulate magnetic states of antiferromagnets. Nanotechnology 2018, 29, 112001. [Google Scholar] [CrossRef]
- Rezende, S.M.; Azevedo, A.; Rodríguez-Suárez, R.L. Introduction to antiferromagnetic magnons. J. Appl. Phys. 2019, 126, 151101. [Google Scholar] [CrossRef]
- Bai, H.; Zhang, Y.C.; Han, L.; Zhou, Y.J.; Pan, F.; Song, C. Antiferromagnetism: An efficient and controllable spin source. Appl. Phys. Rev. 2022, 9, 041316. [Google Scholar] [CrossRef]
- Šmejkal, L.; MacDonald, A.H.; Sinova, J.; Nakatsuji, S.; Jungwirth, T. Anomalous Hall antiferromagnets. Nat. Rev. Mater. 2022, 7, 482–496. [Google Scholar] [CrossRef]
- Keffer, F.; Kittel, C. Theory of Antiferromagnetic Resonance. Phys. Rev. 1952, 85, 329–337. [Google Scholar] [CrossRef]
- Cheng, R.; Xiao, J.; Niu, Q.; Brataas, A. Spin Pumping and Spin-Transfer Torques in Antiferromagnets. Phys. Rev. Lett. 2014, 113, 057601. [Google Scholar] [CrossRef] [PubMed]
- Cheng, R.; Niu, Q. Dynamics of antiferromagnets driven by spin current. Phys. Rev. B 2014, 89, 081105. [Google Scholar] [CrossRef]
- Cheng, R.; Daniels, M.W.; Zhu, J.G.; Xiao, D. Antiferromagnetic Spin Wave Field-Effect Transistor. Sci. Rep. 2016, 6, 24233. [Google Scholar] [CrossRef] [PubMed]
- Cheng, R.; Xiao, D.; Zhu, J.-G. Antiferromagnet-based magnonic spin-transfer torque. Phys. Rev. B 2018, 98, 020408. [Google Scholar] [CrossRef]
- Zheng, C.; Chen, X.; Zhou, S.; Liu, Y. Terahertz magnetic excitation in antiferromagnets: Atomistic spin simulations versus a coupled pendulum model. J. Phys. Condens. Matt. 2022, 35, 085801. [Google Scholar] [CrossRef] [PubMed]
- Satoh, T.; Cho, S.J.; Iida, R.; Shimura, T.; Kuroda, K.; Ueda, H.; Ueda, Y.; Ivanov, B.A.; Nori, F.; Fiebig, M. Spin Oscillations in Antiferromagnetic NiO Triggered by Circularly Polarized Light. Phys. Rev. Lett. 2010, 105, 077402. [Google Scholar] [CrossRef]
- Parthasarathy, A.; Cogulu, E.; Kent, A.D.; Rakheja, S. Precessional spin-torque dynamics in biaxial antiferromagnets. Phys. Rev. B 2021, 103, 024450. [Google Scholar] [CrossRef]
- Yosida, K. Magnetic Properties of Cu-Mn Alloys. Phys. Rev. 1957, 106, 893–898. [Google Scholar] [CrossRef]
- Grunberg, P.; Schreiber, R.; Pang, Y.; Brodsky, M.B.; Sowers, H. Layered magnetic structures: Evidence for antiferromagnetic coupling of Fe layers across Cr interlayers. Phys. Rev. Lett. 1986, 57, 2442–2445. [Google Scholar] [CrossRef] [PubMed]
- Binasch, G.; Grünberg, P.; Saurenbach, F.; Zinn, W. Enhanced magnetoresistance in layered magnetic structures with antiferromagnetic interlayer exchange. Phys. Rev. B 1989, 39, 4828–4830. [Google Scholar] [CrossRef] [PubMed]
- Parkin, S.S.P.; More, N.; Roche, K.P. Oscillations in exchange coupling and magnetoresistance in metallic superlattice structures: Co/Ru, Co/Cr, and Fe/Cr. Phys. Rev. Lett. 1990, 64, 2304–2307. [Google Scholar] [CrossRef] [PubMed]
- Lau, Y.C.; Betto, D.; Rode, K.; Coey, J.M.D.; Stamenov, P. Spin-orbit torque switching without an external field using interlayer exchange coupling. Nat. Nanotech. 2016, 11, 758–762. [Google Scholar] [CrossRef] [PubMed]
- Bruno, P.; Chappert, C. Oscillatory coupling between ferromagnetic layers separated by a nonmagnetic metal spacer. Phys. Rev. Lett. 1991, 67, 1602–1605. [Google Scholar] [CrossRef] [PubMed]
- Parkin, S.S.P.; Mauri, D. Spin engineering: Direct determination of the Ruderman-Kittel-Kasuya-Yosida far-field range function in ruthenium. Phys. Rev. B 1991, 44, 7131–7134. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.-H.; Ryu, K.-S.; Parkin, S. Domain-wall velocities of up to 750 m s−1 driven by exchange-coupling torque in synthetic antiferromagnets. Nat. Nanotech. 2015, 10, 221. [Google Scholar] [CrossRef] [PubMed]
- Devolder, T. Ferromagnetic resonance of exchange-coupled perpendicularly magnetized bilayers. J. Appl. Phys. 2016, 119, 153905. [Google Scholar] [CrossRef]
- Li, S.; Wang, C.; Chu, X.M.; Miao, G.X.; Xue, Q.; Zou, W.; Liu, M.; Xu, J.; Li, Q.; Dai, Y.; et al. Engineering optical mode ferromagnetic resonance in FeCoB films with ultrathin Ru insertion. Sci. Rep. 2016, 6, 33349. [Google Scholar] [CrossRef]
- Wu, G.; Chen, S.; Lou, S.; Liu, Y.; Jin, Q.Y.; Zhang, Z. Annealing effect on laser-induced magnetization dynamics in Co/Ni-based synthetic antiferromagnets with perpendicular magnetic anisotropy. Appl. Phys. Lett. 2019, 115, 142402. [Google Scholar] [CrossRef]
- Waring, H.J.; Johansson, N.A.B.; Vera-Marun, I.J.; Thomson, T. Zero-field Optic Mode Beyond 20 GHz in a Synthetic Antiferromagnet. Phys. Rev. Appl. 2020, 13, 034035. [Google Scholar] [CrossRef]
- Gusakova, D.; Houssameddine, D.; Ebels, U.; Dieny, B.; Buda-Prejbeanu, L.; Cyrille, M.C.; Delaet, B. Spin-polarized current-induced excitations in a coupled magnetic layer system. Phys. Rev. B 2009, 79, 104406. [Google Scholar] [CrossRef]
- Houssameddine, D.; Sierra, J.F.; Gusakova, D.; Delaet, B.; Ebels, U.; Buda-Prejbeanu, L.D.; Cyrille, M.C.; Dieny, B.; Ocker, B.; Langer, J.; et al. Spin torque driven excitations in a synthetic antiferromagnet. Appl. Phys. Lett. 2010, 96, 3149. [Google Scholar] [CrossRef]
- Baláž, P.; Barnaś, J. Current-induced dynamics of composite free layer with antiferromagnetic interlayer exchange coupling. Phys. Rev. B 2011, 83, 104422. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhou, L.; Wigen, P.E.; Ounadjela, K. Angular dependence of ferromagnetic resonance in exchange-coupled Co/Ru/Co trilayer structures. Phys. Rev. B 1994, 50, 6094–6112. [Google Scholar] [CrossRef] [PubMed]
- Rezende, S.M.; Chesman, C.; Lucena, M.A.; Azevedo, A.; de Aguiar, F.M.; Parkin, S.S.P. Studies of coupled metallic magnetic thin-film trilayers. J. Appl. Phys. 1998, 84, 958–972. [Google Scholar] [CrossRef]
- Zivieri, R.; Giovannini, L.; Nizzoli, F. Acoustical and optical spin modes of multilayers with ferromagnetic and antiferromagnetic coupling. Phys. Rev. B 2000, 62, 14950–14955. [Google Scholar] [CrossRef]
- Belmeguenai, M.; Martin, T.; Woltersdorf, G.; Maier, M.; Bayreuther, G. Frequency- and time-domain investigation of the dynamic properties of interlayer-exchange-coupled Ni81Fe19/Ru/Ni81Fe19 thin films. Phys. Rev. B 2007, 76, 104414. [Google Scholar] [CrossRef]
- Shiota, Y.; Taniguchi, T.; Ishibashi, M.; Moriyama, T.; Ono, T. Tunable Magnon-Magnon Coupling Mediated by Dynamic Dipolar Interaction in Synthetic Antiferromagnets. Phys. Rev. Lett. 2020, 125, 017203. [Google Scholar] [CrossRef]
- Sud, A.; Zollitsch, C.W.; Kamimaki, A.; Dion, T.; Khan, S.; Iihama, S.; Mizukami, S.; Kurebayashi, H. Tunable magnon-magnon coupling in synthetic antiferromagnets. Phys. Rev. B 2020, 102, 100403. [Google Scholar] [CrossRef]
- Kamimaki, A.; Iihama, S.; Suzuki, K.Z.; Yoshinaga, N.; Mizukami, S. Parametric Amplification of Magnons in Synthetic Antiferromagnets. Phys. Rev. Appl. 2020, 13, 044036. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, C.; Amin, V.P.; Zhang, Z.; Vogel, M.; Xiong, Y.; Sklenar, J.; Divan, R.; Pearson, J.; Stiles, M.D.; et al. Phase-resolved electrical detection of coherently coupled magnonic devices. Appl. Phys. Lett. 2021, 118, 202401. [Google Scholar] [CrossRef] [PubMed]
- Wigen, P.E.; Zhang, Z.; Zhou, L.; Ye, M.; Cowen, J.A. The dispersion relation in antiparallel coupled ferromagnetic films. J. Appl. Phys. 1993, 73, 6338–6340. [Google Scholar] [CrossRef]
- MacNeill, D.; Hou, J.T.; Klein, D.R.; Zhang, P.; Jarillo-Herrero, P.; Liu, L. Gigahertz Frequency Antiferromagnetic Resonance and Strong Magnon-Magnon Coupling in the Layered Crystal CrCl3. Phys. Rev. Lett. 2019, 123, 047204. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.-G. Spin valve and dual spin valve heads with synthetic antiferromagnets. IEEE Trans. Magn. 1999, 35, 655–660. [Google Scholar]
- Chen, X.; Zheng, C.; Zhou, S.; Liu, Y.; Zhang, Z. Manipulation of Time- and Frequency-Domain Dynamics by Magnon-Magnon Coupling in Synthetic Antiferromagnets. Magnetochemistry 2021, 8, 7. [Google Scholar] [CrossRef]
- Yakata, S.; Kubota, H.; Suzuki, Y.; Yakushiji, K.; Fukushima, A.; Yuasa, S.; Ando, K. Influence of perpendicular magnetic anisotropy on spin-transfer switching current in CoFeB/MgO/CoFeB magnetic tunnel junctions. J. Appl. Phys. 2009, 105, 103. [Google Scholar] [CrossRef]
- Schellekens, A.J.; Kuiper, K.C.; De Wit, R.R.J.C.; Koopmans, B. Ultrafast spin-transfer torque driven by femtosecond pulsed-laser excitation. Nat. Commun. 2014, 5, 4333. [Google Scholar] [CrossRef]
- Wu, D.; Zhang, Z.; Li, L.; Zhang, Z.; Zhao, H.B.; Wang, J.; Ma, B.; Jin, Q.Y. Perpendicular magnetic anisotropy and magnetization dynamics in oxidized CoFeAl films. Sci. Rep. 2015, 5, 12352. [Google Scholar] [CrossRef]
- Vemulkar, T.; Mansell, R.; Fernández-Pacheco, A.; Cowburn, R.P. Toward Flexible Spintronics: Perpendicularly Magnetized Synthetic Antiferromagnetic Thin Films and Nanowires on Polyimide Substrates. Adv. Funct. Mater. 2016, 26, 4704–4711. [Google Scholar] [CrossRef]
- Dieny, B.; Chshiev, M. Perpendicular magnetic anisotropy at transition metal/oxide interfaces and applications. Rev. Mod. Phys. 2017, 89, 025008. [Google Scholar] [CrossRef]
- Yi, L.; Yu, J.; Zhong, H.J.J.O.M.; Materials, M. Strong antiferromagnetic interlayer exchange coupling in [Co/Pt]6/Ru/[Co/Pt]4 structures with perpendicular magnetic anisotropy. J. Magn. Magn. Mater. 2018, 473, 381–386. [Google Scholar]
- Shiota, Y.; Arakawa, T.; Hisatomi, R.; Moriyama, T.; Ono, T. Polarization-Selective Excitation of Antiferromagnetic Resonance in Perpendicularly Magnetized Synthetic Antiferromagnets. Phys. Rev. Appl. 2022, 18, 014032. [Google Scholar] [CrossRef]
- Tabuchi, Y.; Ishino, S.; Ishikawa, T.; Yamazaki, R.; Usami, K.; Nakamura, Y. Hybridizing ferromagnetic magnons and microwave photons in the quantum limit. Phys. Rev. Lett. 2014, 113, 083603. [Google Scholar] [CrossRef]
- Lachance-Quirion, D.; Tabuchi, Y.; Gloppe, A.; Usami, K.; Nakamura, Y. Hybrid quantum systems based on magnonics. Appl. Phys. Express 2019, 12, 070101. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, W.; Tyberkevych, V.; Kwok, W.-K.; Hoffmann, A.; Novosad, V. Hybrid magnonics: Physics, circuits, and applications for coherent information processing. J. Appl. Phys. 2020, 128, 130902. [Google Scholar] [CrossRef]
- Hu, B.; Xie, Z.-K.; Lu, J.; He, W. Mapping the magnon–magnon hybrid state onto the Bloch sphere. Appl. Phys. Lett. 2024, 124, 232402. [Google Scholar] [CrossRef]
- Kruglyak, V.V.; Demokritov, S.O.; Grundler, D. Magnonics. J. Phys. D Appl. Phys. 2010, 43, 264001. [Google Scholar] [CrossRef]
- Zhang, X.; Zou, C.L.; Jiang, L.; Tang, H.X. Strongly Coupled Magnons and Cavity Microwave Photons. Phys. Rev. Lett. 2014, 113, 156401. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Y.; Li, C.; Wei, J.; He, B.; Xu, H.; Xia, J.; Luo, X.; Li, J.; Dong, J.; et al. Ultrastrong to nearly deep-strong magnon-magnon coupling with a high degree of freedom in synthetic antiferromagnets. Nat. Commun. 2024, 15, 2077. [Google Scholar] [CrossRef] [PubMed]
- Chumak, A.V.; Serga, A.A.; Hillebrands, B. Magnon transistor for all-magnon data processing. Nat. Commun. 2014, 5, 4700. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Liu, C.; Liu, T.; Xiao, Y.; Xia, K.; Bauer, G.E.W.; Wu, M.; Yu, H. Strong Interlayer Magnon-Magnon Coupling in Magnetic Metal-Insulator Hybrid Nanostructures. Phys. Rev. Lett. 2018, 120, 217202. [Google Scholar] [CrossRef] [PubMed]
- Dieny, B.; Prejbeanu, I.L.; Garello, K.; Gambardella, P.; Freitas, P.; Lehndorff, R.; Raberg, W.; Ebels, U.; Demokritov, S.O.; Akerman, J.; et al. Opportunities and challenges for spintronics in the microelectronics industry. Nat. Electron. 2020, 3, 446–459. [Google Scholar] [CrossRef]
- Mahmoud, A.; Ciubotaru, F.; Vanderveken, F.; Chumak, A.V.; Hamdioui, S.; Adelmann, C.; Cotofana, S. Introduction to spin wave computing. J. Appl. Phys. 2020, 128, 161101. [Google Scholar] [CrossRef]
- Xiao, X.; Chen, Z.; Dai, C.; Ma, F. Magnon mode transition in synthetic antiferromagnets induced by perpendicular magnetic anisotropy. J. Appl. Phys. 2022, 131, 093905. [Google Scholar] [CrossRef]
- Li, Z.; Sun, J.; Ma, F. Floquet engineering of selective magnon–magnon coupling in synthetic antiferromagnets. Appl. Phys. Lett. 2023, 123, 232406. [Google Scholar] [CrossRef]
- Comstock, A.H.; Chou, C.T.; Wang, Z.; Wang, T.; Song, R.; Sklenar, J.; Amassian, A.; Zhang, W.; Lu, H.; Liu, L.; et al. Hybrid magnonics in hybrid perovskite antiferromagnets. Nat. Commun. 2023, 14, 1834. [Google Scholar] [CrossRef]
- Hayashi, D.; Shiota, Y.; Ishibashi, M.; Hisatomi, R.; Moriyama, T.; Ono, T. Observation of mode splitting by magnon–magnon coupling in synthetic antiferromagnets. Appl. Phys. Express 2023, 16, 053004. [Google Scholar] [CrossRef]
- Rong, Y.; Jiang, C.; Wang, H.; Sun, L.; Liu, F.; Lu, J.; Wu, T.; Zhang, Y.; Zhao, Y.; Ma, F.; et al. Layer-dependent magnon-magnon coupling in a synthetic antiferromagnet. Phys. Rev. Appl. 2024, 21, 054050. [Google Scholar] [CrossRef]
- Liensberger, L.; Kamra, A.; Maier-Flaig, H.; Geprags, S.; Erb, A.; Goennenwein, S.T.B.; Gross, R.; Belzig, W.; Huebl, H.; Weiler, M. Exchange-Enhanced Ultrastrong Magnon-Magnon Coupling in a Compensated Ferrimagnet. Phys. Rev. Lett. 2019, 123, 117204. [Google Scholar] [CrossRef] [PubMed]
- Dai, C.; Ma, F. Strong magnon–magnon coupling in synthetic antiferromagnets. Appl. Phys. Lett. 2021, 118, 112405. [Google Scholar] [CrossRef]
- Li, M.; Lu, J.; He, W. Symmetry breaking induced magnon-magnon coupling in synthetic antiferromagnets. Phys. Rev. B 2021, 103, 064429. [Google Scholar] [CrossRef]
- He, W.; Xie, Z.K.; Sun, R.; Yang, M.; Li, Y.; Zhao, X.T.; Liu, W.; Zhang, Z.D.; Cai, J.W.; Cheng, Z.H.; et al. Anisotropic Magnon–Magnon Coupling in Synthetic Antiferromagnets. Chin. Phys. Lett. 2021, 38, 057502. [Google Scholar] [CrossRef]
- Hu, B.; He, W. Tunable magnon-magnon coupling mediated by in-plane magnetic anisotropy in synthetic antiferromagnets. J. Magn. Magn. Mater. 2023, 565, 170283. [Google Scholar] [CrossRef]
- Wang, Y.; Xia, J.; Wan, C.; Han, X.; Yu, G. Ultrastrong magnon-magnon coupling in synthetic antiferromagnets induced by interlayer Dzyaloshinskii-Moriya interaction. Phys. Rev. B 2024, 109, 054416. [Google Scholar] [CrossRef]
- Sklenar, J.; Zhang, W. Self-Hybridization and Tunable Magnon-Magnon Coupling in van der Waals Synthetic Magnets. Phys. Rev. Appl. 2021, 15, 044008. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).