Artificial Neural Network Based Apple Yield Prediction Using Morphological Characters
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Data Description
2.2. Development of Artificial Neural Network Model
2.3. Development of Multiple Linear Regression Model
2.4. Model Performance Measures
3. Results
3.1. Selection of Input Variables
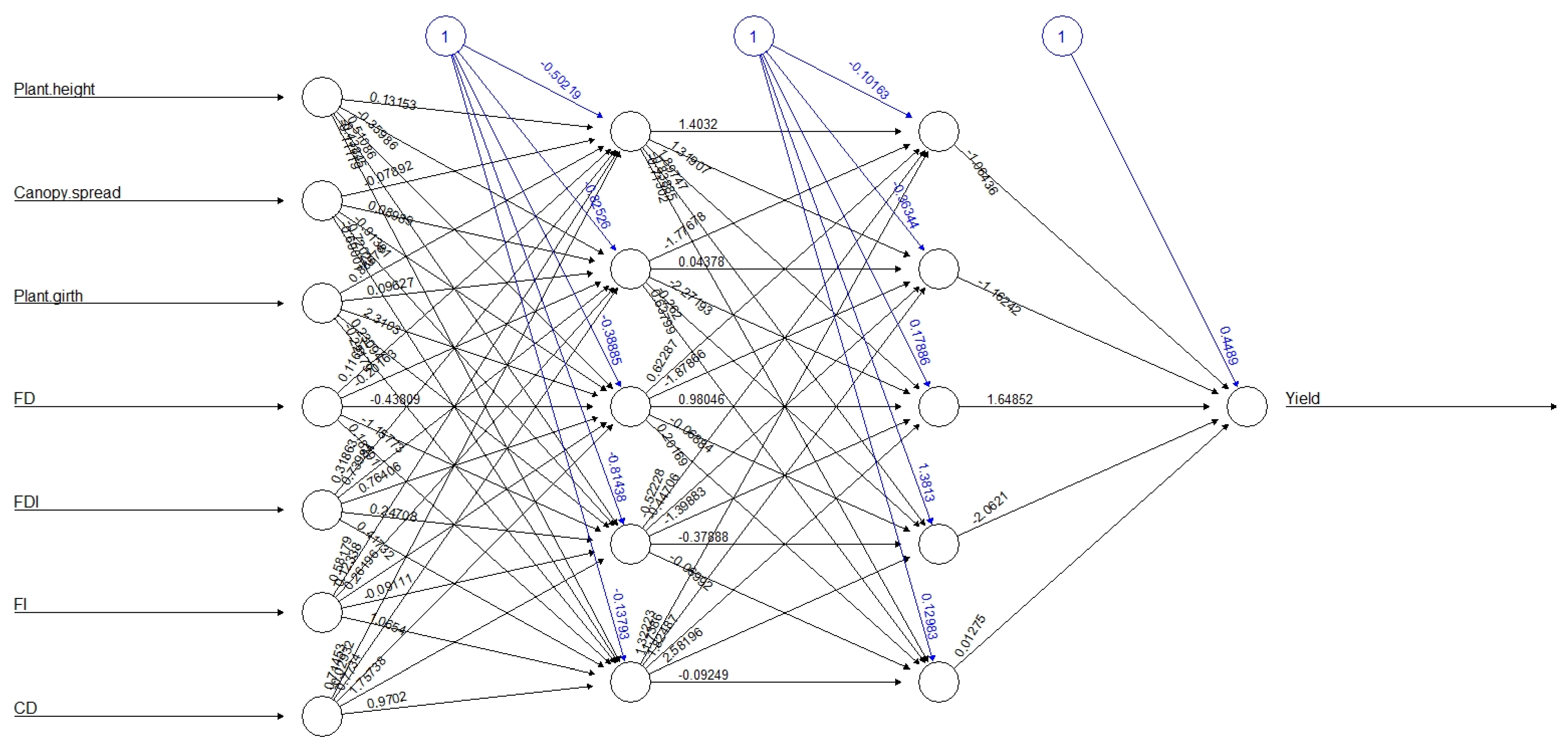
3.2. ANN Model Development
3.3. MLR Model Development
4. Discussion
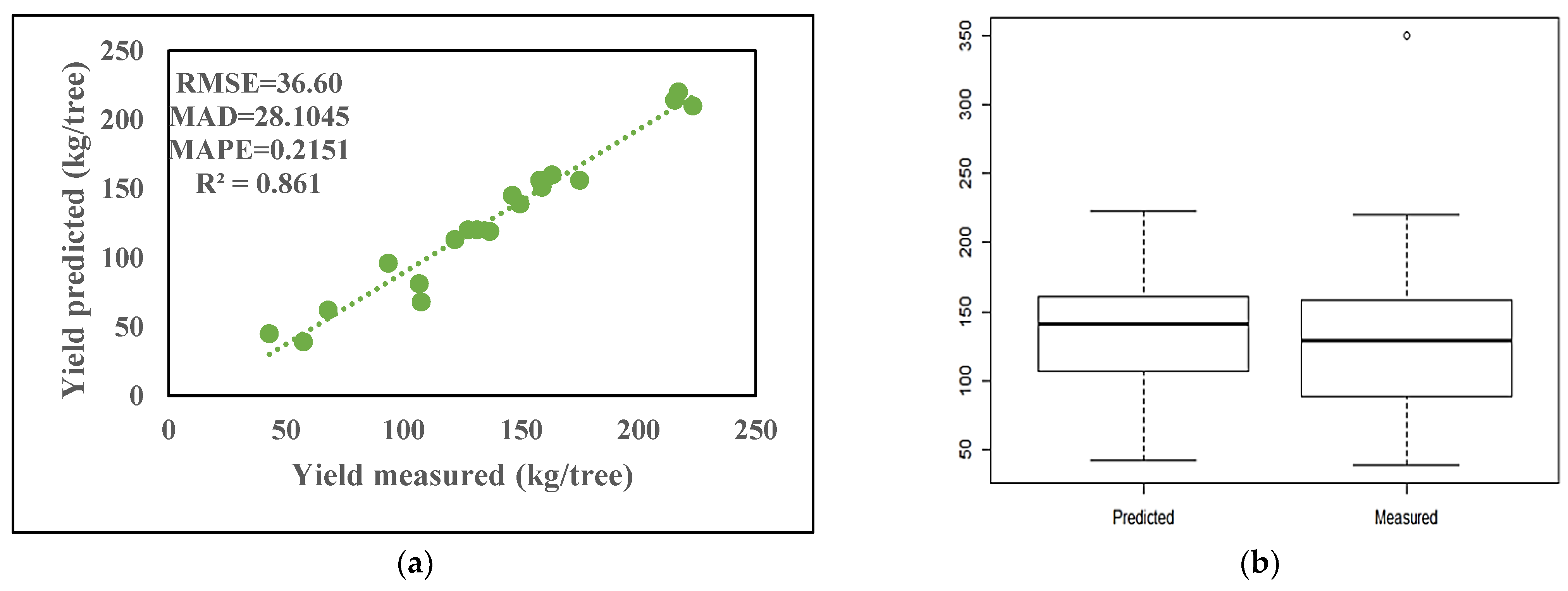
4.1. Comparison of Fitted Models
4.2. Sensitivity Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- FAO. FAOSTAT. Food and Agriculture Organization of the United Nations. 2020. Available online: https://www.fao.org/faostat/en/#home (accessed on 20 May 2022).
- Lezzoni, A.; Pritts, M.P. Application of principal component analysis to horticultural research. Hortic. Sci. 1991, 26, 334–338. [Google Scholar] [CrossRef]
- Guimarães, B.V.C.; Donato, S.L.R.; Aspiazú, I.; Azevedo, A.M. Yield prediction of ‘Prata Anã’ and ‘BRS Platina’ banana plants by artificial neural. Pesq. Agropec. Trop. Goiânia 2021, 51, 1–11. [Google Scholar] [CrossRef]
- Guimarães, B.V.C.; Donato, S.L.R.; Azevedo, A.M.; Aspiazú, I.; Silva Junior, A.A. Prediction of “Gigante” cactus pear yield by morphological characters and artificial neural networks. Rev. Bras. De Eng. Agrícola E Ambient. 2018, 22, 315–319. [Google Scholar] [CrossRef]
- Khazaei, J.F.; Shahbazi; Massah, J. Evaluation and modeling of physical and physiological damage to wheat seeds under successive impact loadings: Mathematical and neural networks modeling. Crop Sci. 2008, 48, 1532–1544. [Google Scholar] [CrossRef]
- Gutiérrez, P.A.; López-Granados, F.; Peña-Barragán, J.M.; Jurado-Expósito, M.; Hervás-Martínez, C. Logistic regression product-unit neural networks for mapping Ridolfia segetum infestations in sunflower crop using multitemporal remote sensed data. Comput. Electron. Agric. 2008, 64, 293–306. [Google Scholar] [CrossRef]
- Huang, Y.; Lan, Y.; Thomson, S.J.; Fang, A.; Hoffmann, W.C.; Lacey, R.E. Development of soft computing and applications in agricultural and biological engineering. Comput. Electron. Agric. 2010, 71, 107–127. [Google Scholar] [CrossRef]
- Kravchenko, A.N.; Bullock, D.G. Correlation of corn and soybean grain yield with topography and soil properties. Agron. J. 2000, 92, 75–83. [Google Scholar] [CrossRef]
- Park, S.J.; Hwang, C.S.; Vlek, P.L.G. Comparison of adaptive techniques to predict crop yield response under varying soil and land management conditions. Agric. Syst. 2005, 85, 59–81. [Google Scholar] [CrossRef]
- Kitchen, N.R.; Drummond, S.T.; Lund, E.D.; Sudduth, K.A.; Buchleiter, G.W. Soil electrical conductivity and topography related to yield for three contrasting soil-crop systems. Agron. J. 2003, 95, 483–495. [Google Scholar] [CrossRef]
- Miao, Y.; Mulla, D.J.; Robert, P.C. Identifying important factors influencing corn yield and grain quality variability using artificial neural networks. Precis. Agric. 2006, 7, 117–135. [Google Scholar] [CrossRef]
- Schultz, A.; Wieland, R.; Lutze, G. Neural networks in agroecological modeling-stylish application or helpful tool? Comput. Electron. Agric. 2000, 29, 73–97. [Google Scholar] [CrossRef]
- Fortin, J.G.; Anctil, F.; Parent, L.É.; Bolinder, M.A. A neural network experiment on the site-specific simulation of potato tuber growth in Eastern Canada. Comput. Electron. Agric. 2010, 73, 126–132. [Google Scholar] [CrossRef]
- Jiang, P.; Thelen, K.D. Effect of soil and topographic properties on crop yield in a north-central corn-soybean cropping system. Agron. J. 2004, 96, 252–258. [Google Scholar] [CrossRef]
- Das, P. Study on Machine Learning Techniques Based Hybrid Model for Forecasting in Agriculture. Ph.D. Thesis, PG-school IARI, New Delhi, India, 2019. [Google Scholar]
- Abdipour, M.; Younessi-Hmazekhanlu, M.; Ramazani, M.Y.H.; Omidi, A.H. Artificial neural networks and multiple linear regression as potential methods for modeling seed yield of safflower (Carthamus tinctorius L.). Ind. Crops Prod. 2019, 27, 185–194. [Google Scholar] [CrossRef]
- Mansouri, A.; Fadavi, A.; Mortazavian, S.M.M. An artificial intelligence approach for modeling volume and fresh weight of callus–A case study of cumin (Cuminum cyminum L.). J. Theor. Biol. 2016, 397, 199–205. [Google Scholar] [CrossRef]
- Hydrology. ASCE task committee on application of artificial neural networks in artificial neural networks in hydrology, I: Preliminary concepts. Hydrol. Eng. 2020, 5, 115–123. [Google Scholar] [CrossRef]
- Treder, W. Relationship between yield, crop density coefficient and average fruit weight of ‘gala’ apple. J. Fruit Ornam. Plant Res. 2008, 16, 53–63. [Google Scholar]
- Gholipoor, M.; Rohani, A.; Torani, S. Optimization of traits to increasing barley grain yield using an artificial neural network. Int. J. Plant Prod. 2013, 7, 1–17. [Google Scholar]
- Tiwari, M.K.; Chatterjee, C. Uncertainty assessment and ensemble flood forecasting using bootstrap based artificial neural networks (BANNs). J. Hydrol. 2010, 382, 20–33. [Google Scholar] [CrossRef]
- Tripathy, M. Power transformer differential protection using neural network principal component analysis and radial basis function neural network. Simul. Model. Pract. Theory 2010, 18, 600–611. [Google Scholar] [CrossRef]
- Abdipour, M.; Ramazani, S.H.R.; Younessi-Hmazekhanlu, M.; Niazian, M. Modeling oil content of sesame (Sesamum indicum L.) using artificial neural network and multiple linear regression approaches. J. Am. Oil Chem. Soc. 2018, 95, 283–297. [Google Scholar] [CrossRef]
- May, R.; Dandy, G.; Maier, H. Review of input variable selection methods for artificial neural networks. Artificial Neural Networks—Methodological Advances and Biomedical Applications. InTech 2011, 10, 16004. [Google Scholar] [CrossRef]
- Elhami, B.; Khanali, M.; Akram, A. Combined application of Artificial Neural Networks and life cycle assessment in lentil farming in Iran. Inform. Process. Agric. 2017, 4, 18–32. [Google Scholar] [CrossRef]
- Samarasinghe, S. Neural Networks for Applied Sciences and Engineering: From Fundamentals to Complex Pattern Recognition; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Hoskins, J.C.; Himmelblau, D.M. Artificial neural network models of knowledge representation in chemical engineering. Comput. Chem. Eng. 1988, 12, 881–890. [Google Scholar] [CrossRef]
- Sheela, K.G.; Deepa, S.N. Review on methods to fix number of hidden neurons in neural networks. Math. Probl. Eng. 2013, 2013, 425740. [Google Scholar] [CrossRef]
- Tufail, M.; Ormsbee, L.; Teegavarapu, R. Artificial intelligence-based inductive models for prediction and classification of fecal coliform in surface waters. J. Environ. Eng. 2008, 134, 789–799. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks: A Comprehensive Foundation; Prentice Hall: Ontario, CA, USA, 1999. [Google Scholar]
- Buyukozturk, S. Sosyal Bilimler Icin very Analizi el Kitabi; Pegem Yayincihk: Ankara, Turkey, 2002. [Google Scholar]
- Tabachnick, B.G.; Fidell, S.L. Using Multivariate Statistics; Harper Collins College Publishers: New York, NY, USA, 1996. [Google Scholar]
- Unver, O.; Gamgam, H. Uygulamah Istatistik Yontemleri; Siyasal Kitabevi: Ankara, Turkey, 1999. [Google Scholar]
- Das, P.; Paul, A.K.; Paul, R.K. Non-linear mixed effect models for estimation of growth parameters in Goats. J. Indian Soc. Agric. Stat. 2016, 70, 205–210. [Google Scholar]
- Emamgholizadeh, S.; Parsaeian, M.; Baradaran, M. Seed yield prediction of sesame using artificial neural network. Eur. J. Agron. 2015, 68, 89–96. [Google Scholar] [CrossRef]
- Forshey, C.G.; Elfving, D.C. Fruit numbers, fruit size and yield relationship in ‘McIntosh’ apple. J. Am. Soc. Hortic. 1977, 24, 399–402. [Google Scholar] [CrossRef]
- Treder, W.; Mike, A. Relationship between yield, crop density and average fruit weight in ‘lobo’ apple trees under various planting systems and irrigation treatments. Horttech 2001, 11, 248–254. [Google Scholar] [CrossRef]
- Westwood, M.N.; Roberts, A.N. The relationship between trunk cross-sectional area and weight of apple trees. J. Am. Soc. Hortic. 1970, 95, 28–30. [Google Scholar] [CrossRef]
- Ahmadi, S.H.; Sepaskhah, A.R.; Andersen, M.N.; Plauborg, F.; Jensen, C.R.; Hansen, S. Modeling root length density of field grown potatoes under different irrigation strategies and soil textures using artificial neural networks. Field Crops Res. 2014, 162, 99–107. [Google Scholar] [CrossRef]
- Hagan, M.T.; Demuth, H.B.; Beale, M. Neural Network Design; PWS Publishing, Co.: Boston, MA, USA, 1997. [Google Scholar]
- Balas, C.F.; Koc, M.L.; Tur, R. Artificial neural network based on principal component analysis, fuzzy systems and fuzzy neural networks for preliminary design of rubble mound breakwaters. Appl. Ocean Res. 2010, 32, 425–433. [Google Scholar] [CrossRef]
- Singh, T.N.; Kanchan, R.; Verma, A.K.; Singh, S. An intelligent approach for prediction of triaxial properties using unconfined uniaxial strength. Miner. Eng. 2003, 5, 12–16. [Google Scholar]





| Characters | Range | Mean | Std. Deviation |
|---|---|---|---|
| Plant height (m) | 3.05–11.89 | 7.22 | 2.21 |
| Canopy spread (m) | 1.32–9.48 | 5.57 | 2.03 |
| Plant girth (cm) | 0.15–0.91 | 0.61 | 0.18 |
| Flower density | 1.00–10.82 | 3.54 | 1.99 |
| Flower density index | 0.10–1.08 | 0.35 | 0.18 |
| Flowering intensity | 0.35–0.50 | 0.41 | 0.03 |
| Fruit set | 0.15–0.57 | 0.31 | 0.08 |
| Crop density | 0.30–4.40 | 1.09 | 0.66 |
| Length diameter ratio | 6.84–10.28 | 8.22 | 0.68 |
| Characters | PH | CS | PG | FD | FDI | FI | FS | CD | LDR | EV | CV |
|---|---|---|---|---|---|---|---|---|---|---|---|
| PC1 | −0.4223 | −0.4222 | −0.4178 | 0.3909 | 0.2924 | 0.1073 | 0.1183 | 0.4389 | 0.1108 | 3.07 | 34.15 |
| PC2 | 0.3905 | 0.3051 | 0.3672 | 0.3810 | 0.4114 | 0.4333 | −0.0969 | 0.3284 | −0.011 | 2.01 | 56.53 |
| Hidden Layer | Best Topology | RMSE | MAD | MAPE | R2 | Accuracy (%) | Error Rate | |
|---|---|---|---|---|---|---|---|---|
| Training | 1 | 7-3-1 | 36.3360 | 25.7337 | 0.2306 | 0.8121 | 90.36 | 0.2422 |
| 2 | 7-5-5-1 | 24.8300 | 18.2607 | 0.1523 | 0.9430 | 98.72 | 0.0736 | |
| 3 | 7-3-3-3-1 | 31.0590 | 22.3937 | 0.2053 | 0.8629 | 93.59 | 0.1769 | |
| 4 | 7-3-3-3-3-1 | 27.4964 | 21.2744 | 0.2136 | 0.8924 | 92.23 | 0.1386 | |
| 5 | 7-5-5-1-5-5-1 | 24.9840 | 19.8195 | 0.1556 | 0.9116 | 93.10 | 0.1140 | |
| 6 | 7-3-3-3-3-5-5-1 | 34.8300 | 17.81 | 0.2426 | 0.9113 | 95.10 | 0.11438 | |
| Testing | 1 | 7-3-1 | 63.2026 | 43.9649 | 0.3582 | 0.5622 | 93.01 | 0.2422 |
| 2 | 7-5-5-1 | 36.6078 | 28.1045 | 0.2151 | 0.8685 | 95.36 | 0.0736 | |
| 3 | 7-3-3-3-1 | 52.2906 | 38.2418 | 0.2974 | 0.7129 | 91.32 | 0.1769 | |
| 4 | 7-3-3-3-3-1 | 43.7711 | 28.2788 | 0.1900 | 0.7935 | 93.49 | 0.1386 | |
| 5 | 7-5-5-1-5-5-1 | 40.0703 | 28.2700 | 0.2111 | 0.8239 | 92.65 | 0.1140 | |
| 6 | 7-3-3-3-3-5-5-1 | 43.2684 | 32.92371 | 0.2360 | 0.8073 | 89.33 | 0.1144 |
| Model | RMSE | MAD | MAPE | R2 |
|---|---|---|---|---|
| ANN | 36.6078 | 28.1045 | 0.2151 | 0.8685 |
| MLR | 61.2501 | 39.7203 | 0.2620 | 0.7069 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bharti; Das, P.; Banerjee, R.; Ahmad, T.; Devi, S.; Verma, G. Artificial Neural Network Based Apple Yield Prediction Using Morphological Characters. Horticulturae 2023, 9, 436. https://doi.org/10.3390/horticulturae9040436
Bharti, Das P, Banerjee R, Ahmad T, Devi S, Verma G. Artificial Neural Network Based Apple Yield Prediction Using Morphological Characters. Horticulturae. 2023; 9(4):436. https://doi.org/10.3390/horticulturae9040436
Chicago/Turabian StyleBharti, Pankaj Das, Rahul Banerjee, Tauqueer Ahmad, Sarita Devi, and Geeta Verma. 2023. "Artificial Neural Network Based Apple Yield Prediction Using Morphological Characters" Horticulturae 9, no. 4: 436. https://doi.org/10.3390/horticulturae9040436
APA StyleBharti, Das, P., Banerjee, R., Ahmad, T., Devi, S., & Verma, G. (2023). Artificial Neural Network Based Apple Yield Prediction Using Morphological Characters. Horticulturae, 9(4), 436. https://doi.org/10.3390/horticulturae9040436








