Abstract
After automatic in-field picking, apple stem shortening requires fixing the apple position and maintaining a relatively stable posture, which puts high demands on the automatic apple-orienting structure. In this paper, a novel dual roller compact apple field orientation structure with dual rollers rotating in the same direction is proposed. It can realize the uniform orientation of apples after automatic picking in any attitude, and the apple auto-orientation phenomenon is theoretically analyzed based on the accurately established apple model, then the apple orientation test platform was set up and a monocular camera combined with YOLOv5m was used to determine the time of apple orientation. The results showed that 70.21% and 96.81% of the apples were respectively oriented within 7 s and 28 s with only two flexible rollers rotating in the corresponding direction. All the apples were oriented, and 95.24% of them moved along the axis toward the calyx end. The generalizability of the apple orientation device for different shapes of apples was then verified, and the relationship between the shape characteristics of apples and orientation speed was later illustrated. A structural basis was finally presented for automatic stem shortening and surface damage detection in the apple field.
1. Introduction
Aging increases the urgency of apple orchard picking automation [1]. It was deduced from a study in an orchard that the stems of the apples should be cut short after picking [2]. Moreover, the stem cannot be completely removed due to the fact that, according to the Chinese fresh apple grading standard, apples with missing stems are the worst fruit, regardless of whether their surface is smooth or not [3]. In addition, according to the Chinese standard for apple picking technology [4], some varieties with thin skin and prickly injury (e.g., Fuji) should be cut short after picking, so that the pedicel becomes lower than the fruit shoulder. The shortening of the apple stems can also reduce their puncturing the surface of other apples. According to the Inspection Instructions for Apple of the U.S. Department of Agriculture, the number of stems puncturing a single apple affects the apple’s grading standard [5]. For high-volume apple collection, shorter stems indicate more apples for the same weight for the fruit merchant, and the shortening of the apple stem has potential for a 5% increase in commercial value [6]. The current study on apple orchard machinery relied on stable and efficient apple orientation devices for surface damage detection and apple stem shortening in the orchard. However, no commercial automatic apple stem shortening devices are available, and the apple orientation is a key step in apple damage detection and apple grading [7]. Throop et al. [8] designed two wheels perpendicular to each other because the depressions at the calyx end cannot be acted upon by the rollers to orient the apples in the factory. Another way to orient apples consists in using a grooved ramp combined with the inertia of falling apples [9], as well as a set of concave mirrors to detect all the sides of the apple. Based on this method, Lefcourt proposes a method for repeated orientation of non-oriented apples to illustrate the feasibility of grooved ramp orientation in factory sorting [10]. Flemmer provided an accurate description of the angle during apple rotation, which provided a highly precise description of the position shift in the rotation of the apples, although it could not enable the inertia-based orientation of the apples [11]. Other quality inspection fields, such as seed visual inspection and fruit kernel removal, also require different degrees of orientation [12,13].
Apples should also be roughly sorted upon picking in the field [14,15], where their automatic sorting reduces the cost and increases the efficiency [14,16,17,18,19]. For instance, apples with no or minor damage can be graded and boxed according to their size, while those with major surface damage cannot be consumed as fresh apples and they are often recycled by factories for further processing into several products such as jam and juice [16,20]. In contrast to fine grading in factories, in field defect detection, missing apples or apples with obvious damage are separated from fresh apples to reduce the transportation costs [21,22,23,24]. Partially missing apples still have the maximum equatorial diameter, and thus it is difficult to separate the incomplete apples completely and apples with large black spots using traditional mechanical grading. The use of machine vision allows the bad apples to be distinguished from the fresh ones [25,26,27,28,29]. However, machine-vision-based apple surface damage detection requires a clear view of the entire circumference of the apple, and therefore a device that can make the apple rotate in a fixed direction and not obscure the space between the apple and the camera is required. Otherwise, the accuracy of the detection of the apple surface damage will be decreased [8]. Reese et al. [30] used only one camera with two concave mirrors to assist the detection of damage around the entire circumference of the apple, including its two end surfaces. However, an orientation device was necessary to improve the accuracy of the apple damage detection. Simple and effective apple-orienting structures are needed for both damage detection and stem shortening of apples in the field after harvest, and an orientation device for cutting short apple stems does not currently exist and the automatic shortening of apple stems theoretically places higher demands on the orientation effect. The central axis of the apple is oriented to coincide as much as possible with the actuator action point, which allows reduction in the accuracy requirements of the actuator. The apple orientation devices at the factory level are difficult to adapt to the size of the apple tree spacing, and complex devices are prone to failure on unstructured surfaces in the field [16].
Thus, it is a challenge to design simple and effective apple orientation devices to achieve a uniform direction of the central axis after apple picking. The axis of the apple can be kept parallel to the axis of the roller after orientation in any posture. In addition, the orientation device can make the apple rotate at a certain speed, so that all the circumferences of the apple can be captured with just one camera and the device does not block the surface of the captured apple [30]. Fortunately, the inertia-based orientation device for apples can satisfy the requirements of quick orientation of apples and observing their entire surface. In the experiment, the apples were placed on rollers made of TPU material. With a rotation speed of 10π rad s−1 (300 RPM) in the same direction as the double rollers, the apple placed in the detection device in any posture performs its automatic adjustment. That is, the center axis of the apple will be parallel to the center axis of the rollers.
In this paper, a theoretical analysis of apple orientation phenomenon is first conducted. An apple orientation experiment platform is then built to verify the universality of the apple orientation device. Finally, a relationship between the fruit shape index difference and apple orientation time is determined. The findings of this study provide structural and theoretical bases for damage detection in apple fields and automatic apple stem shortening.
2. Materials and Methods
2.1. Apple Shape Statistics and Modeling
The physical dimensions of Yantai Fuji apples were determined using a digital caliper gauge, and 15 dimensions of 152 randomly selected ripe apples were measured in a densely planted dwarfed orchard of fusiform apple trees. The measured dimensions are the left side distance (R1), right side distance (R2), stem end diameter (L1), calyx end diameter (L2), apple stem length (H3), stem end angle (θ1), calyx end angle (θ2), apple stem angle (θ3), minimum height (H1), maximum height (H2), stem end straight line diameter (L3), stem end depth (H5), calyx end straight line diameter (L4), calyx end depth (H4), and equatorial diameter (D) of the apple. A schematic diagram of the measured feature dimensions and their locations is shown in Figure 1a. To facilitate the subsequent experiments, the measured apples were individually numbered.
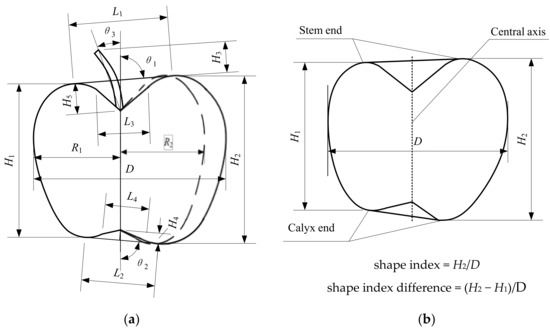
Figure 1.
Measurement feature data and sketching of apples: (a) positions of apple size measurements; (b) apple shape index difference and shape index.
To determine the general distribution of the location of the center of gravity of the apple, a 3D model was drawn in Solidworks (2020) according to the statistical average. As for the hierarchical modeling, this paper uses modeling in four equal parts along the longitudinal section of the apple. The maximum size and minimum size of the apple feature values were first used to obtain two 1/4 longitudinal sections of completely different sizes. The remaining two 1/4 models were then completed based on the sketches of the two sections with different sizes using the lofting command. The four parts of the apple were modeled as individual parts and assembled using assembly drawings.
The fruit shape index is the ratio obtained by dividing H2 by D [31], which can better describe the shape characteristics of an apple. It is a parameter used to describe the roundness of the apple. However, in the process of Yantai Fuji apple shape determination, it was deduced that the fruit shape index cannot accurately describe the shape of the apple, and the difference between H2 and H1 of some apples was relatively large. Therefore, this paper proposes to use H2 minus H1 divided by D to describe the height difference of apples per unit diameter, as shown in Figure 1b. The relationship between fruit shape index difference and orientation time is statistically presented in a later section.
2.2. Analysis of the Apple Rotational Orientation Theory
Assuming that the apple is placed at any position on a stationary flexible roller, it is subjected to different support forces in different positions due to the presence of depressions on the calyx and stem ends of its surface and the fact that its shape is not a standard sphere. The support forces in different directions constitute the tipping moment, which makes the apple tumble in the direction of the side view, where only one roller is visible. It is then driven in rotation by the friction of the roller. The motion of the apple after forces have balanced can be considered as a rigid body rotating at a fixed point, driven by the rotational friction of the roller.
To determine the size of the three principal axes of inertia of the apple, a 3D model of the average apple size is created in Solidworks (2020). The direction of the 3D model and the principal axis of inertia after using the mass evaluation command is shown Figure 2c. The static coordinate system is a right-handed system, as shown in Figure 2a,b. The directional cosine values of the angle between the inertia principal axis and the static coordinate system were Ix = (−0.68, −0.25, 0.69), Iy = (0.72, 0.00, 0.70), and Iz = (−0.18, 0.97, 0.18). The principal axes of inertia were PX = 154,988.78, PY = 159,690.16, and PZ = 167,648.14. When the flexible roller rotates in the same direction at 10π rad s−1 (300 RPM), the center axis of the apple will be parallel to the center axis of the roller. This indicates that the apple stably rotates around the Z-axis. Rigid body kinematics analysis is first used for the phenomenon of the apple rotating stably along the orientation of the main axis of maximum inertia.
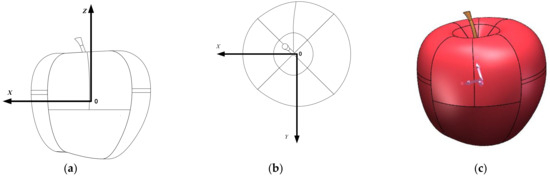
Figure 2.
Apple 3D modeling with static coordinates: (a) apple static coordinate system in the XZ-axis direction; (b) apple static coordinate system in the XY-axis direction; (c) 3D figure showing the position of the apple center of gravity and the direction of the main axis of inertia.
As the apple rotates around the Z-axis, due to the variable and unequal curvature of its shape, there will be small perturbations in the other two directions during the rotation, which makes it unstable. ω can then be expressed as:
where λ and μ represent the disturbances of rotation around the X- and Y-axes, respectively.
Assuming that the linear velocity of the apple rotation and the linear velocity of the roller are equal, the external torque is approximately zero. By substituting Equation (1) into the Eulerian kinematic equations, the following system of equations is obtained:
Based on the last two equations of Equation (2), the time derivative of the second equation and eliminating μ are introduced into the third equation and the following equation for the second order linear constant coefficient differential with respect to is obtained:
Based on the discriminant of the solution of the homogeneous linear differential equation, the general solution of Equation (3) can be determined as:
It can be deduced that the rotation around the Z-axis is a sinusoidal oscillation according to the initial state. That is, a small perturbation of the rigid body rotating around the apple Z-axis will not oscillate and disperse. However, if the apple is rotated around the Y-axis with a small perturbation, then:
Similarly, an equation for the second order linear constant coefficient differential with respect to λ can be obtained:
Based on the discriminant of the solution of the homogeneous linear differential equation, the general solution of Equation (6) can be determined as:
The perturbation grows exponentially with time and cannot converge. Therefore, it is unstable when rotating around the Y-axis. Since the perturbation does not cumulatively increase when rotating in the direction of the main axis of maximum inertia, the apple can stably rotate around it. The center axis of the apple is parallel to that of the roller after the orientation is completed. Since the gravitational force and the support force of the apple are still not in the same direction, the moments are not balanced, as shown in Figure 3a.
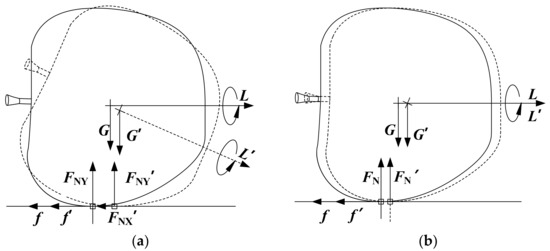
Figure 3.
Diagram explaining the phenomenon of the apple moving toward the calyx end: (a) apple tumbles due to unbalanced torque; (b) the inertia should be maintained so that the central axis returns to a position approximately parallel to the axis of the roller and creates relative sliding.
The frictional force of the roller is insufficient to balance the moment from gravity and support forces. The apple rotation nutation angle is affected by the unbalanced moment. The unbalanced torque causes the apple to roll clockwise along the surface of the roller with a certain angle, as shown in Figure 3a where the rolling apples and the applied forces are indicated by dashed lines. As the roller rotates, the apple will remain axially parallel to the roller axis under the influence of the moment of inertia, as shown by the dashed line in Figure 3b. Due to the weak friction between the roller and the apple, the apple exhibits sliding friction relative to the rollers. Therefore, there is a misalignment in successive positions as shown in Figure 3b. After the apple axis is rotated in the direction of the central axis of the roller, the apple rotation tends to be dynamically stable so that it moves along the central axis. The reason for this phenomenon is that the apple is pulled up by the upward rotational action of the moment of inertia and the frictional force of the roller is less than the roll torque, which causes the apple to move in the axial direction. The apple will keep moving horizontally along the axis until the thin plate provides a support force parallel to the axis of the roller. Theoretically, once the relative relationship between the position of the center of gravity of the apple and its equatorial position is determined, the direction of motion along the axis after its orientation is fixed. As shown in Figure 3b, if the center of gravity of the apple is to the right of the equatorial diameter, it moves in the direction of the axis of the roller towards the calyx end. The orientation can be accomplished with two rollers for a single apple, which theoretically explains the reason for the stable rotation. The generalizability of apple orientation still needs to be verified, and therefore an apple orientation test platform was built.
2.3. Construction of the Orientation Test Platform
2.3.1. Double Roller Installation and Restraint
The main body of the rotating device uses a double roller model with a minimum distance of 24 mm between the two rollers and a diameter of 49 mm, rotating in the same direction at 10π rad s−1 (300 RPM), as shown in Figure 4a. To guarantee the motor speed synchronization, the same A4988 and Arduino UNO are used for the two stepper motors. The two linear actuators are self-locking to ensure that the tilting angle is fixed during the roller rotation, as shown in Figure 4a. The self-locking feature of the screw is used to ensure that the rollers’ distance is fixed, as shown in Figure 4b. The PLA board is 3D printed and fixed with jackscrews, which are also used to ensure that the distance between the rollers is fixed during the rotation, and the PLA board is fixed to the transparent PMMA plate by hot melt adhesive, as shown in Figure 4c. The used TPU95A roller material has some elasticity to better protect the apple from damage during the rotation [32]. The 42 stepper motor is used to rotate the roller. The A4988 and Arduino UNO are used to control the rotation of the motor, with a 12 V mobile lithium battery as power supply.
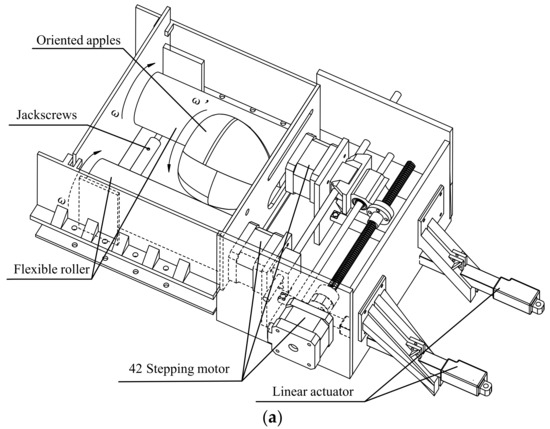

Figure 4.
Apple-orienting test platform construction: (a) test platform and control structure; (b) the self-locking screw guarantees a fixed roller distance; (c) the jackscrews guarantee a stable roller distance; (d) flexible roller made by 3D printing; (e) thickness of the flexible roller.
The flexible roller molding made with FDM3D printing is shown in Figure 4d. FDM3D printing is used as a flexible roller molding method with a conventional proximity extrusion 3D printer [33]. The end face of the roller is pre-drilled with holes for motor mating. The roller aperture size is 4.86 mm and the motor shaft diameter size is 5.01 mm, which presents an interference fit between the aperture and the motor. The print wire is black TPU95A made by ESUN, with a printhead temperature of 220 °C and a hot bed temperature of 60 °C. The print speed is 24 mm s−1 with 80% infill, shown in Figure 4d. In order to guarantee the softness of the material and to consider the stability of the structure, the thickness of the drum is 1.6 mm, as shown in Figure 4e.
2.3.2. Camera and Posture Determination Equipment
The test platform of the apple orientation and the camera shown in Figure 5a are used to determine the apple orientation time. Although the camera has low resolution, the timing requirements can be met with a low cost. The industrial camera has 1 million pixels, a sensing size of 1/4 inch COMS, a resolution of 720 p, and a focal length of 6 mm. The PyTorch-based YOLOv5m model is used as a training deep-learning framework to implement the determination of apple pose and to auxiliarily calculate the apple orientation time. The results from the study showed that YOLOv5 was easier to use under the same setting and could be chosen as the baseline network based on how well it detected things [34]. YOLOv5m was chosen for its rapid inference time and minimal hardware demands [35]. The determination is added for each frame of the apple pose while running the target detection code. The key frames of the apple orientation process are shown in Figure 5b, where the number below each image represents its current number of frames recorded by the camera.
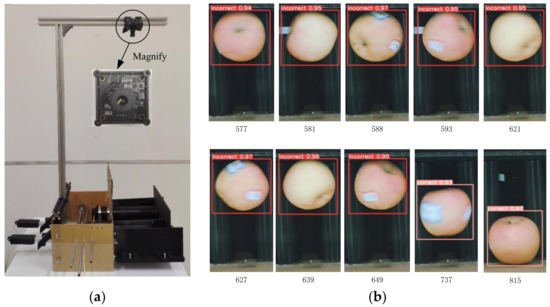
Figure 5.
Apple orientation process and its frame: (a) apple orientation test platform; (b) apple orientation process and its frame.
The apple pose is divided into two categories: incorrect and correct. In addition, the numbers of undirected and directed frames are separately counted. The total number of frames in which the apple changes from undirected to oriented is counted. The camera records the apple orientation process using 60 FPS, and the time of the apple orientation is calculated by dividing the number of frames by the video frame rate of 60. The dataset for model training is derived from the video captured by the monocular camera during the automatic orientation of the apple rotation. The video annotation of the images is performed on the CVAT.ai web page. The tags are set in two states: correct (apple oriented) and incorrect (apple non-oriented). The total number of datasets is 16,624, the validation set is 1845, the batch size is set to 6, and a total of 550 rounds are trained. It is important to mention that the apple will move along the axial direction after orientation. In the process of image training and labeling, the apple is judged to have completed orientation when it tends to move in the axial direction, instead of relying on sticking to the shell of the test platform. In order to ensure a high detection accuracy, this study does not perform the time calculation in real time but uses video recording, because the stable frame rate of video recording leads to more accurate calculation time.
2.4. Apple Orientation Experiment
The trained YOLOv5m model was used to measure the time required to orient 104 Yantai Fuji apples. All the apples were placed in a uniform pose, and they were all oriented vertically with the static coordinate system X-axis. The apples were rotated in the Y-axis direction, which indicates that the center axis of the apple is placed perpendicular to that of the roller. This is because the apples are theoretically unstable as they rotate around the second inertial axis. To determine if the apple can spontaneously rotate from an unstable state to a stable direction, orientation tests were also performed before the experiment with apple axis and roller axis of less than 90°. The obtained results showed that the longest orientation time was achieved by placing the apples in a posture with the central axes perpendicular to each other. The roller was continuously rotated at an angular speed of 10π rad−1 (300 RPM), and the apples were placed as close as possible to the surface of the roller to prevent them from spinning out of it. The camera recorded the entire process of rotating each apple in the direction of orientation, while naming the folder with the apple number. After saving the videos, their orientation times were calculated using the trained YOLOv5m.
3. Results and Discussion
Firstly, the apple statistics obtained from the shape characteristics are analyzed to show that there is not a complete overlap between the apple’s center of gravity and the equatorial diameter. Then, the relationship between apple orientation time and apple shape is analyzed, based on the statistical results of the speed of apple orientation time.
3.1. Apple Shape Characterization Results
Due to the apple shape, the overall center of gravity is at a certain distance from the equatorial diameter. The reason for the tipping of the apple is the distance that exists between the position of the center of gravity and the supporting force. The deviation between the two is also the reason for the phenomenon of axial movement of the apple after orientation. The shape parameters of 151 groups of Yantai Fuji varieties were randomly selected and the statistical results of the main dimensional parameters were obtained using vernier calipers, as shown in Figure 6a. The diameter of the end face of the fruit pedicel is larger than that of the end face of the calyx, leading to uneven distribution of mass on the two sides of the equatorial plane of the apple, which makes it hard to keep the central axis and the horizontal plane parallel when the apple is placed stationary on the plane without friction. Assuming the apple is a complete ellipsoid, its stem end and calyx end are cut in two opposite directions, but the volume cutoff at the stem end is larger than that at the calyx end, which causes its overall center of gravity to deviate from the equator.
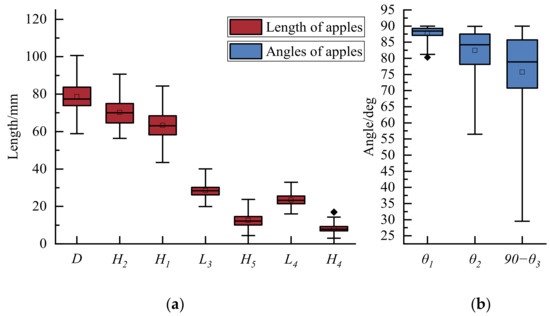
Figure 6.
Apple critical feature size statistics chart: (a) length of the apple measured using a vernier caliper; (b) angle measured using an angle ruler.
There is also a volume inequality between the depression at the end of the apple stem and that at the end of the calyx, which results in uneven mass distribution between the two sides of the apple. The greater the mass difference between the two, the more favorable it is for the apple to tumble toward the roller under the action of the rotational moment.
The statistics of other apple parameter size measurements are shown in Table 1. It can be noticed that all the size parameters above the equator are larger than the mean values of the parameters below the equator, which indicates the uneven distribution of apple mass. This leads to the appearance of orientation as well as movement towards the calyx end during apple rotation. The favorable orientation of apples is based on rotational inertia. The shape characteristics of the apple can be accurately described by the statistical results, where its center of gravity is located behind the equatorial diameter. The specific shape of the apple leads to the formation of a torque between its support force by the roller and its gravitational force, which is not sufficient to perform its force balance. Five of the one hundred and five apples moved in the direction of the calyx end. That is, 95.24% of the apples moved towards the calyx end in the direction of movement after orientation. It can be shown that the center of gravity of the apples is located more at the calyx end of their equatorial diameter, which is consistent with the location of their center of gravity in apple modeling.

Table 1.
Measurement results of other apple parameters.
3.2. Association Results between Apple Orientation Time and Apple Shape
After training, there were cases where the apple pose was not recognized during the actual calculation of the apple orientation time. For the experiments, recognition failed for 8 out of 104 apples. The small number of trained apples may be the reason for the unsuccessful recognitions. In total, 92.38% of the apples were effectively identified and oriented. The number of trained samples can be increased to solve the problem of remaining unidentified cases. The apple size was accurately determined by repeating measurement with 94 apples. The apples with stems and those with missing stems were distinguished. The relationship between the number of apples and the orientation time is shown in Figure 7. It can be seen that 74.07% and 97.53% of the apples with stems were oriented within 7 s, and 28 s, respectively. In total, 70.21% and 96.81% of the apples were oriented within 7 s and 28 s, respectively. With more apples orientated in a shorter time, this is consistent with the effect of long ramp orientation [9].
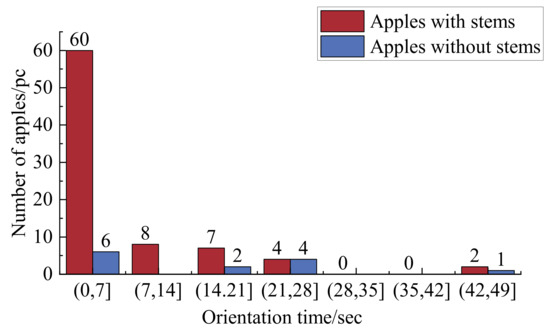
Figure 7.
Statistical graph of the apple orientation time.
The apples without stems were more likely to take longer time to orient. This is due to the fact that the apple stem can provide support force in different directions during the rotation process, which makes the orientation time shorter. On the other hand, the stem increases the overall height of the apple, which slows down the rotation speed at the two ends and accelerates its orientation.
It can be seen from the angle statistics of the apple in Figure 6b that the stem end angle (θ1) is close to 90°. The difference in the fruit shape index can characterize the degree of parallelism between the two ends of the apple per unit diameter when its stem end is used as the reference surface. In addition, the angle between the main axis of inertia of the apple and the static coordinate system also becomes larger due to the uneven distribution of the apple mass. The distribution of the fruit shape index difference by the number of apples observed by OrgininPro (2022) is shown in Figure 8, and it can be deduced that the fruit shape index difference is approximately normally distributed.
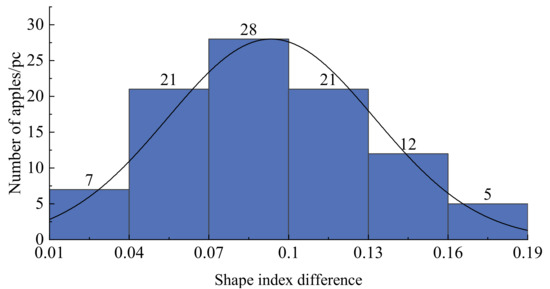
Figure 8.
Statistical distribution of the apple shape index difference and number of apples.
After removing the apples without stems, the relationship between the apple fruit shape index difference, height difference, and apple orientation frame number was found, as shown in Figure 9a. The frames were divided into four categories using the break in the number of frames with large gaps, and the fruit shape index difference was measured for different frames. The statistical plot between the fruit shape index difference and the number of apple-oriented frames is shown in red in Figure 9a. The mean t-test values between 70–260 frames and other categories were all less than 0.05. A graph of the relationship between the apple height difference and time change is shown in blue in Figure 9a. The latter also shows a strong relationship between the apple orientation time and the direction of apple height, with essentially the same trend of change.
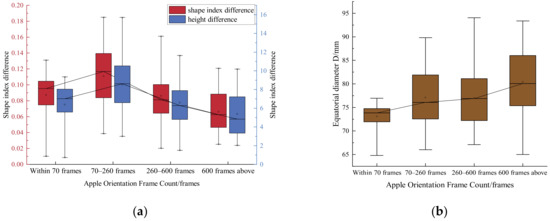
Figure 9.
Statistical graph of fruit shape and number of oriented frames of apples: (a) statistical graph of the relationship between the orientation time with index difference of fruit shape index and height difference; (b) statistical graph of orientation time function of the equatorial diameter.
Firstly, the fruit shape index difference is not the largest (it is relatively small) for the best effect of orientation, which should have some relationship with the direction of the apple principal axis of inertia. The asymmetry between the two sides of the height of the apple helps the direction of the support force to vary, and thus the greater the shape index difference, the shorter the orientation time, purely in the aspect that the variable support force helps the apple orientation. However, it is deduced that the shortest orientation time is not the one with the largest shape index difference, which is caused by the angle between the principal axis of inertia and the static coordinate axis of the apple also becoming larger. A small angle does not affect the stability of the apple rotation, and a larger angle affects the orientation time of the apple. Secondly, the orientation time of apples becomes longer as the difference of fruit shape index decreases. It can be observed from Figure 9a that the fastest orientation is not for the apple with the largest fruit shape index difference. In addition, after 70 frames, the apple orientation time becomes longer as the fruit shape index difference decreases. Moreover, it can be deduced that the speed of apple orientation can be roughly predicted by the maximum and minimum height difference of the apples. If the difference in apple height is large, then the orientation time is more concentrated in the relative middle.
It can also be seen from the mean t-test that the height difference and the fruit shape index difference do not significantly diverge between the minimum and maximum orientation frame ranges. Figure 9b shows the relationship between the equatorial diameter of the apple and the orientation frame, in which the mean t-test value is less than 0.05 between the two categories, under 70 and above 600 frames. Compared with the largest orientation time interval, the shortest orientation intervals tend to have smaller median diameters. This is because, for the same linear speed of the flexible roller, the apples with a smaller diameter can achieve a higher angular speed, which makes their orientation faster. There is still a significant difference in apple diameter between the maximum and minimum time, which indicates that the angular velocity is one of the key factors. Angular velocity is an important factor that affects the orientation time of apples, and this result is consistent with other materials oriented by the dual roller orientation method [36]. In other words, the apple orientation based on rotational inertia is still dominated by the angular velocity of the apple, and the different fruit shape indexes of the apple also have a secondary effect on its orientation. Thus, the size from the apple diameter can also be used as one of the factors to predict the time of apple orientation, which tends to be shorter when the apple size is smaller. When the apple size is larger, the larger the difference in the shape index and the shorter the orientation time of the apple.
Furthermore, based on the above theory, increasing the factor of changing the direction of the support force can accelerate the orientation of the apples, which is currently produced only by gravity and support forces. During the orientation process, the tilt angle of the roller can be changed or small non-smooth protrusions on the surface of the roller can be designed such that the direction of the support force on the apple is varied to speed up its tumbling. An additional rotating paddle wheel can be added to the roller axis orientation to provide a force parallel to its central axis in order to make the apples fall faster. Vibrations can also be artificially added to make the apples have axially unbalanced forces during rotation, which increases the likelihood of their tripping. Note that the use of this structure in the field should give better orientation results since the ground is an unstructured scene that can just cause vibrations and disturbances in the orientation device.
4. Conclusions
In this paper, a theoretical analysis of apple orientation is provided. The stability is determined according to rigid body kinematics and rotated around the direction of the main axis of maximum inertia, and thus the apple’s central axis can rotate parallel to the roller axis in a stable manner. A reasonable explanation is also given for the translations in the direction of the central axis when the apple is oriented. YOLOv5m combined with a low-cost monocular color camera is then used to calculate the orientation time of apples. The generalizability of the orientation structure to the Yantai Fuji apples is also verified. Finally, experiments are conducted to determine the relationship between the apple orientation and fruit shape index difference. The fruit shape index difference shows a trend of increasing and then decreasing with the increase in the orientation time. Valuable references on how to accelerate the apple orientation are also provided. For example, a suitable roller speed range can be selected to help shorten the apple orientation time, and shape changes and topology optimization of the surface of the roller should be beneficial in shortening the apple orientation time. There are some potential constraints, which can be modeled and analyzed using finite element modeling, such as dynamic properties and damage studies during the apple orientation process and the rigid–flexible coupling of the model [37].
The simple structure of automatic apple orientation can be useful for automatic sorting, automatic stem cutting, and field quality inspection. The automatic picking robot helps to perform the whole mechanization of apples in the field after picking. The phenomenon of apples moving to the calyx end is useful for factory high-throughput apple grading. Using the phenomenon of moving along the axis after the apples are oriented, multi-way rollers can be arranged in parallel to transport apples, which reduces the overall size and increases the efficiency. This allows for tighter rows than drive belts, enabling a greater throughput of mechanical apple grading and factory-level apple quality inspection.
Author Contributions
Conceptualization, S.Z. and J.C.; Funding acquisition, S.Z. and J.C.; Investigation, T.L., J.Z. and A.S.; Methodology, T.L. and J.Z.; Software, T.L. and J.Z.; Supervision, G.H. and S.Z.; Validation, G.H.; Writing—original draft, T.L.; Writing—review and editing, S.Z., G.H., J.Z. and A.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research and APC were funded by the National Natural Science Foundation of China (32201677), the Shaanxi Key Research Development Project (2023-ZDLNY-62), the Shaanxi Key Research and Development Project (2022NY-205), and the Qinchuangyuan Project of Shaanxi Province (2023KXJ-016).
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to laboratory policy.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ren, C.; Zhou, X.; Wang, C.; Guo, Y.; Diao, Y.; Shen, S.; Reis, S.; Li, W.; Xu, J.; Gu, B. Ageing threatens sustainability of smallholder farming in China. Nature 2023, 616, 96–103. [Google Scholar] [CrossRef] [PubMed]
- Yang, P.P.; Liang, H.L.; Wang, T.; Fan Wu, X.; Wu, H.Q. An apple picking tool that can cut short fruit stalks. Chinese patent CN110383988B, 14 May 2021. [Google Scholar]
- GB/T 10651-2008 Fresh Apples; General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China. China Standards Press: Beijing, China, 2008.
- NY/T 1086-2006; Technical Specification for Apple Harvestings. Sun, X. (Ed.) Ministry of Agriculture of the People’s Republic of China, China Agricultural Press: Beijing, China, 2006.
- United States Department of Agriculture. Apples Shipping Point and Market Inspection Instructions. Available online: https://www.ams.usda.gov/grades-standards/apple-grades-standards (accessed on 23 May 2023).
- Hanrahan, I. WA 38 Stem Punctures & Semi-Commercial Packout in the 2017–2018 Storage Season. 2018. Available online: https://treefruit.wsu.edu/wa-38-stem-punctures-packout/ (accessed on 15 April 2023).
- Wang, Z.; Jin, L.; Wang, S.; Xu, H. Apple stem/calyx real-time recognition using YOLO-v5 algorithm for fruit automatic loading system. Postharvest Biol. Technol. 2022, 185, 111808. [Google Scholar] [CrossRef]
- Throop, J.A.; Aneshansley, D.J.; Anger, W.C.; Peterson, D.L. Quality evaluation of apples based on surface defects: Development of an automated inspection system. Postharvest Biol. Technol. 2005, 36, 281–290. [Google Scholar] [CrossRef]
- Narayanan, P.; Lefcourt, A.A.; Tasch, U.; Rostamian, R.; Kim, M.S. Orientation of apples using their inertial properties. Trans. ASABE 2008, 51, 2073–2081. [Google Scholar] [CrossRef]
- Lefcourt, A.M.; Narayanan, P.; Tasch, U.; Kim, M.S.; Reese, D.; Rostamian, R.; Lo, Y.M. Orienting apples for imaging using their inertial properties and random apple loading. Biosyst. Eng. 2009, 104, 64–71. [Google Scholar] [CrossRef]
- Flemmer, C.; Bakker, H.; Flemmer, R. Analysis of the stochastic excursions of tumbling apples. Computers and Electronics in Agriculture 2021, 188, 106362. [Google Scholar] [CrossRef]
- Luo, T.; Zhao, J.; Gu, Y.; Zhang, S.; Qiao, X.; Tian, W.; Han, Y. Classification of Weed Seeds Based on Visual Images and Deep Learning. Inf. Process. Agric. 2021, 10, 40–51. [Google Scholar] [CrossRef]
- Kang, N.B.; Qiang, F.; Wu, L.G.; Wang, S.L.; He, J.G. Design and experiment of synchronization actuator system based on electromagnetism for fresh jujube classifier. Trans. Chin. Soc. Agric. Eng. (Trans. CSAE) 2017, 33, 254–260. [Google Scholar] [CrossRef]
- Pothula, A.K.; Zhang, Z.; Lu, R. Design features and bruise evaluation of an apple harvest and in-field presorting machine. Trans. ASABE 2018, 61, 1135–1144. [Google Scholar] [CrossRef]
- Lu, Y.Z.; Lu, R.F.; Zhang, Z. Development and preliminary evaluation of a new apple harvest assist and in-field sorting machine. Appl. Eng. Agric. 2022, 38, 23–35. [Google Scholar] [CrossRef]
- Zhang, Z.; Lu, Y.; Lu, R. Development and evaluation of an apple infield grading and sorting system. Postharvest Biol. Technol. 2021, 180, 111588. [Google Scholar] [CrossRef]
- Zhang, Z.; Pothula, A.K.; Lu, R. Economic analysis of a self-propelled apple harvest and infield sorting machine for the apple industry. In Proceedings of the 2016 ASABE Annual International Meeting, Orlando, FL, USA, 17–20 July 2016. [Google Scholar] [CrossRef]
- Bhargava, A.; Bansal, A. Classification and Grading of Multiple Varieties of Apple Fruit. Food Anal. Methods 2021, 14, 1359–1368. [Google Scholar] [CrossRef]
- Wei, X.; Song, W.; Fan, Y.; Sun, Y.; Li, Z.; Chen, S.; Shi, J.; Zhang, D.; Zou, X.; Xu, X. A SERS aptasensor based on a flexible substrate for interference-free detection of carbendazim in apple. Food Chem. 2024, 431, 137120. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez-Garcia, S.; Argiz, L.; Miguez, P.; Gullon, B. Exploring the production of bio-succinic acid from apple pomace using an environmental approach. Chem. Eng. J. 2018, 350, 982–991. [Google Scholar] [CrossRef]
- Zhang, Z.; Pothula, A.; Lu, R. Economic Evaluation of Apple Harvest and In-Field Sorting Technology. Trans. ASABE (Am. Soc. Agric. Biol. Eng.) 2017, 60, 1537–1550. [Google Scholar] [CrossRef]
- Tian, Y.N.; Yang, G.D.; Wang, Z.; Wang, H.; Li, E.; Liang, Z.Z. Apple detection during different growth stages in orchards using the improved YOLO-V3 model. Comput. Electron. Agric. 2019, 157, 417–426. [Google Scholar] [CrossRef]
- Ayaz, H.; Rodriguez-Esparza, E.; Ahmad, M.; Oliva, D.; Perez-Cisneros, M.; Sarkar, R. Classification of Apple Disease Based on Non-Linear Deep Features. Appl. Sci. 2021, 11, 6422. [Google Scholar] [CrossRef]
- Mizushima, A.; Lu, R. Development of a cost-effective machine vision system for infield sorting and grading of apples: Fruit orientation and size estimation. In Proceedings of the American Society of Agricultural and Biological Engineers Annual International Meeting 2011, Louisville, KY, USA, 7–10 August 2011; pp. 3193–3211. [Google Scholar]
- Sun, F.G.; Wang, Y.L.; Lan, P.; Zhang, X.D.; Chen, X.D.; Wang, Z.J. Identification of apple fruit diseases using improved YOLOv5s and transfer learning. Trans. Chin. Soc. Agric. Eng. (Trans. CSAE) 2022, 38, 171–179. [Google Scholar] [CrossRef]
- Thapa, R.; Zhang, K.; Snavely, N.; Belongie, S.; Khan, A. The Plant Pathology Challenge 2020 data set to classify foliar disease of apples. Appl. Plant Sci. 2020, 8, e11390. [Google Scholar] [CrossRef]
- Sabzi, S.; Nadimi, M.; Abbaspour-Gilandeh, Y.; Paliwal, J. Non-Destructive Estimation of Physicochemical Properties and Detection of Ripeness Level of Apples Using Machine Vision. Int. J. Fruit Sci. 2022, 22, 628–645. [Google Scholar] [CrossRef]
- Yuan, Y.; Yang, Z.; Liu, H.; Wang, H.; Li, J.; Zhao, L. Detection of early bruise in apple using near-infrared camera imaging technology combined with deep learning. Infrared Phys. Technol. 2022, 127, 104442. [Google Scholar] [CrossRef]
- Mamat, N.; Othman, M.F.; Abdulghafor, R.; Alwan, A.A.; Gulzar, Y. Enhancing Image Annotation Technique of Fruit Classification Using a Deep Learning Approach. Sustainability 2023, 15, 901. [Google Scholar] [CrossRef]
- Reese, D.; Lefcourt, A.M.; Kim, M.S.; Lo, Y.M. Using parabolic mirrors for complete imaging of apple surfaces. Bioresour. Technol. 2009, 100, 4499–4506. [Google Scholar] [CrossRef] [PubMed]
- Keshavarzpour, F.; Rashidi, M. Classification of Apple Size and Shape Based on Mass and Outer Dimensions. Am. Eurasian J. Agric. Environ. Sci. 2022, 9, 618–621. [Google Scholar]
- Liu, X.P.; Cao, Z.T.; Yang, L.; Chen, H.; Zhang, Y.L. Research on Damage Properties of Apples Based on Static Compression Combined with the Finite Element Method. Foods 2022, 11, 1851. [Google Scholar] [CrossRef]
- Christ, J.F.; Aliheidari, N.; Ameli, A.; Potschke, P. 3D printed highly elastic strain sensors of multiwalled carbon nanotube/thermoplastic polyurethane nanocomposites. Mater. Des. 2017, 131, 394–401. [Google Scholar] [CrossRef]
- Dhiman, P.; Kaur, A.; Balasaraswathi, V.R.; Gulzar, Y.; Alwan, A.A.; Hamid, Y. Image Acquisition, Preprocessing and Classification of Citrus Fruit Diseases: A Systematic Literature Review. Sustainability 2023, 15, 9643. [Google Scholar] [CrossRef]
- van Meekeren, A.; Gavari, M.A.; Dijkstra, K. Exploring the Effectiveness of Dataset Synthesis: An application of Apple Detection in Orchards. arXiv preprint 2023, arXiv:2306.11763v1. [Google Scholar]
- Cui, G.P.; Zheng, X.M.; Cui, Y.J.; Wang, J.Z.; Shi, Y.G.; Fu, L.S. Automatic Orientation Method for Postharvest Cabbage Based on Moment of Inertia. Trans. Chin. Soc. Agric. Mach. 2020, 51, 183–195. [Google Scholar] [CrossRef]
- Zhao, H.; Su, L.; Zhang, Y.; Cui, H.; Wang, J.; Ren, K. Analysis and Optimized Design of Rigid-Flexible Coupling Characteristics of Crab Apple Picking Machines and Crab Apple Trees. Appl. Sci. 2023, 13, 10502. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).