Wind-Induced Bending Characteristics of Crop Leaves and Their Potential Applications in Air-Assisted Spray Optimization
Abstract
1. Introduction
2. Materials and Methods
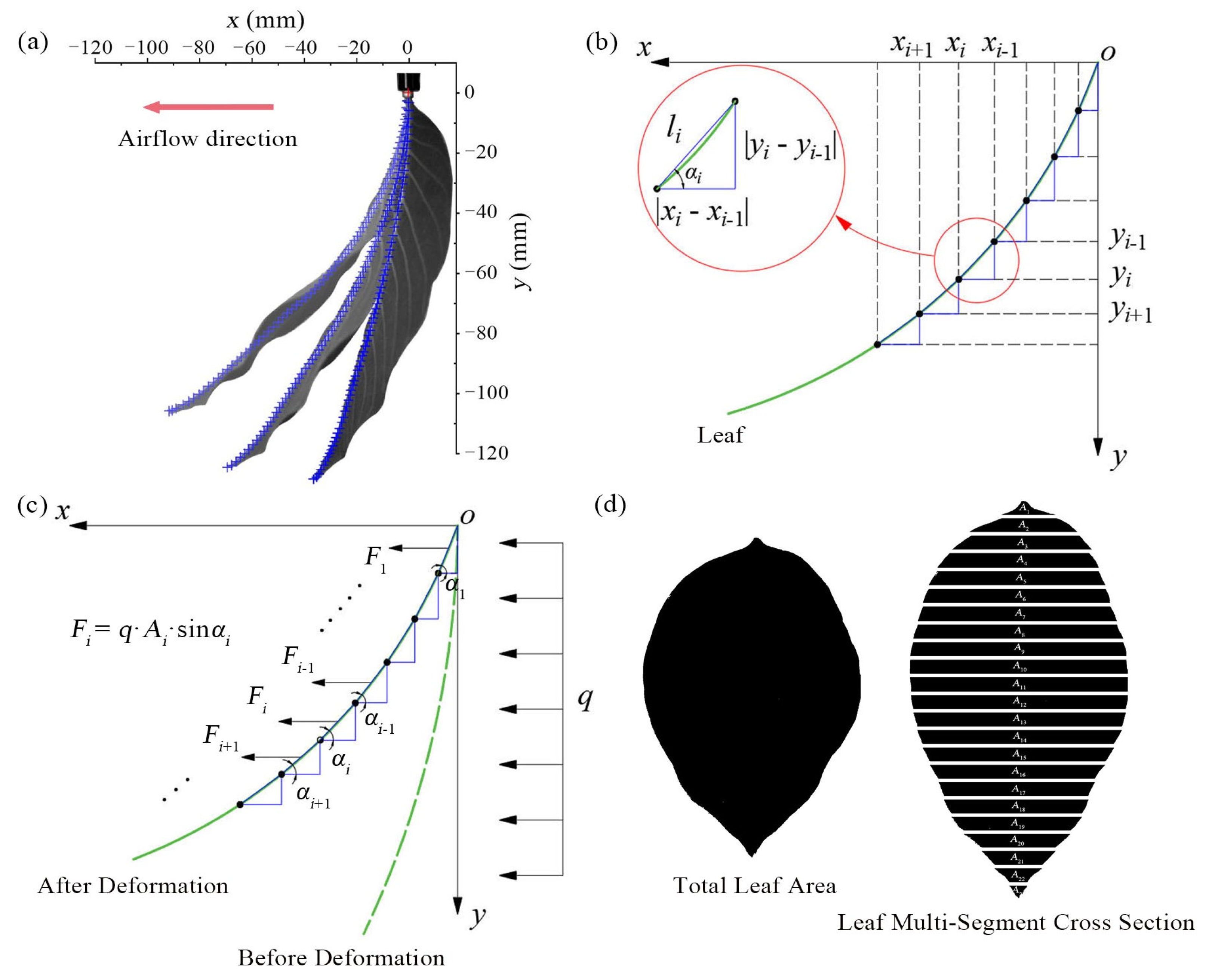
2.1. Experimental Materials
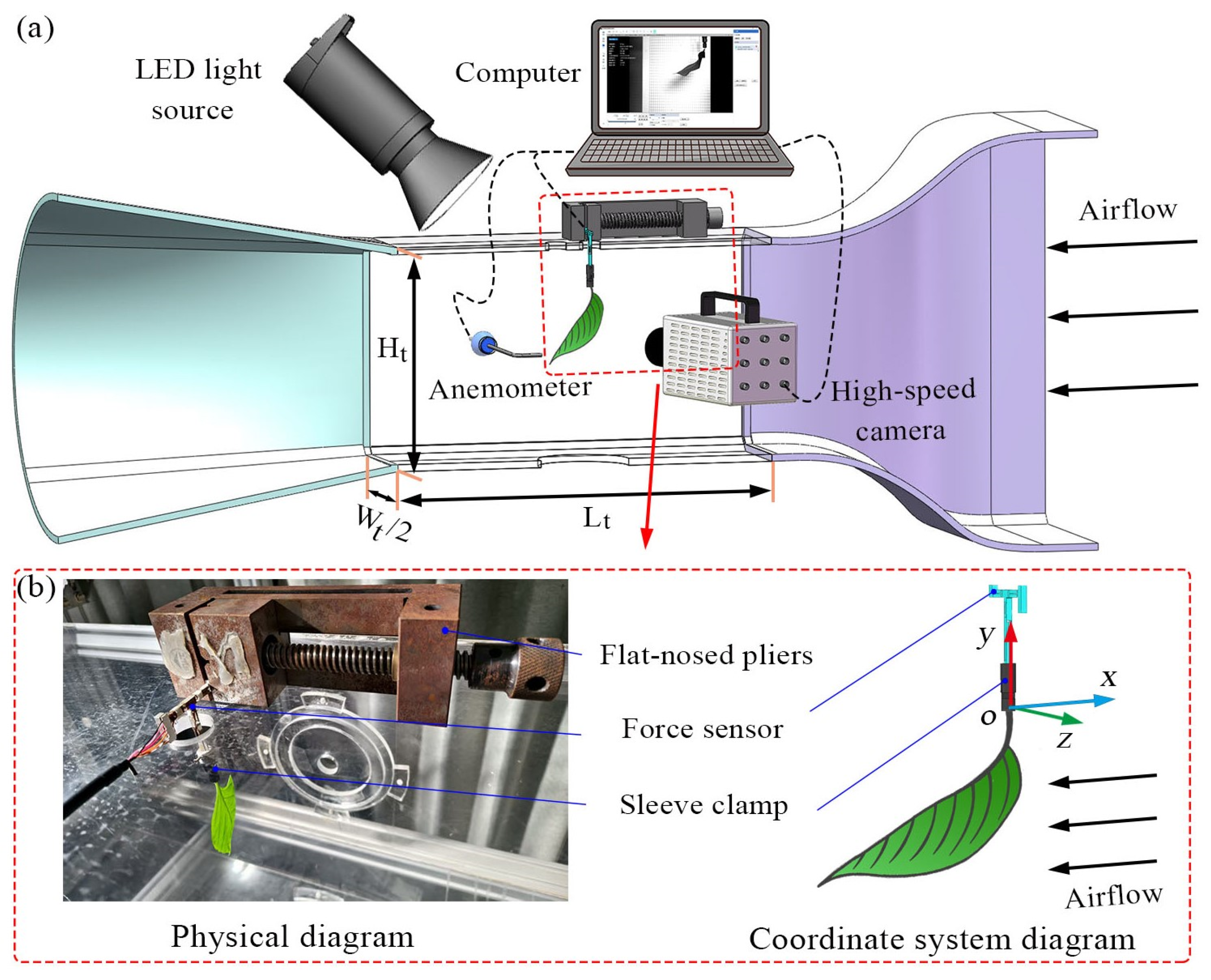
2.2. Experiment Setup
3. Results and Discussion
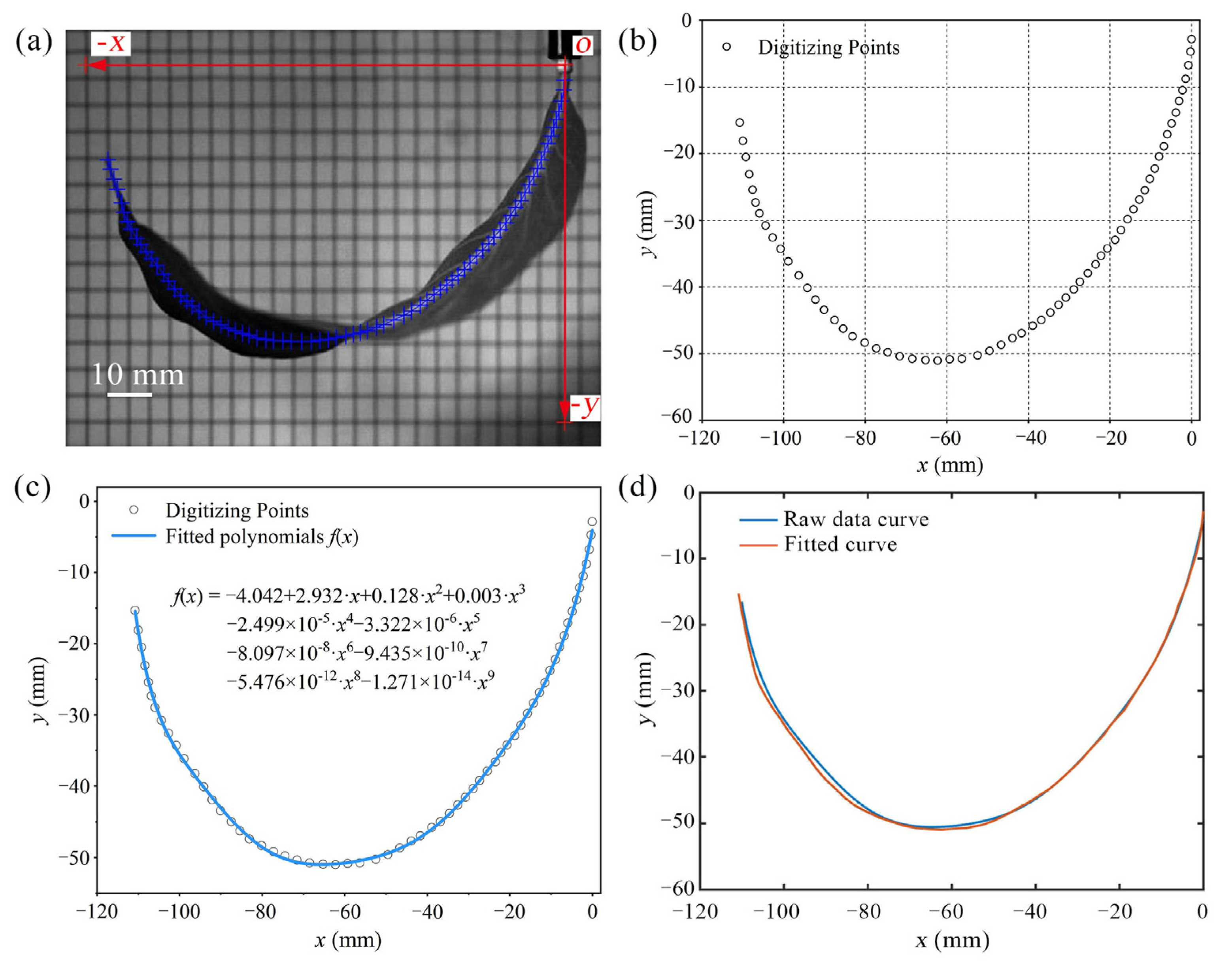
3.1. Aerodynamic Response of Crop Leaves
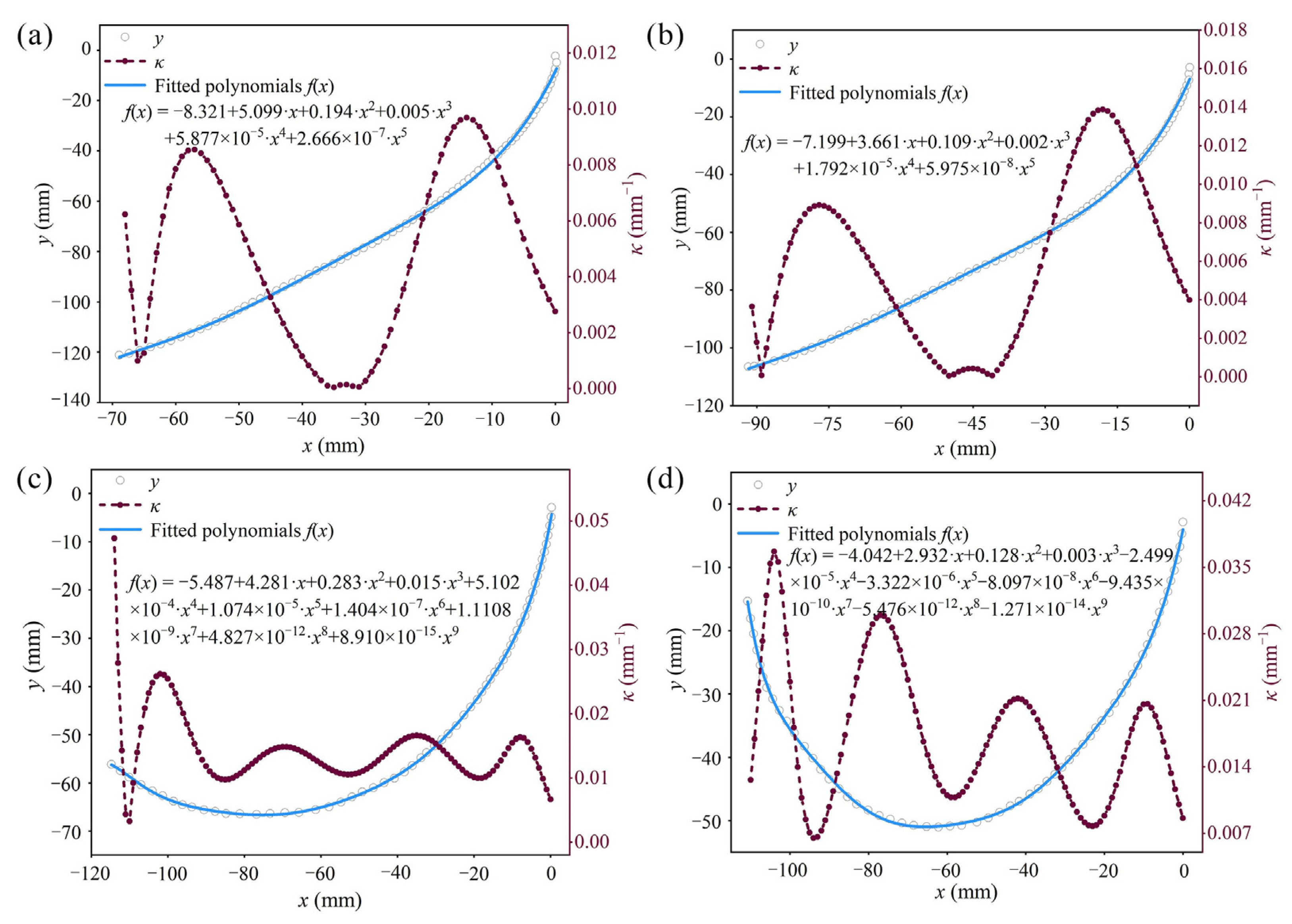
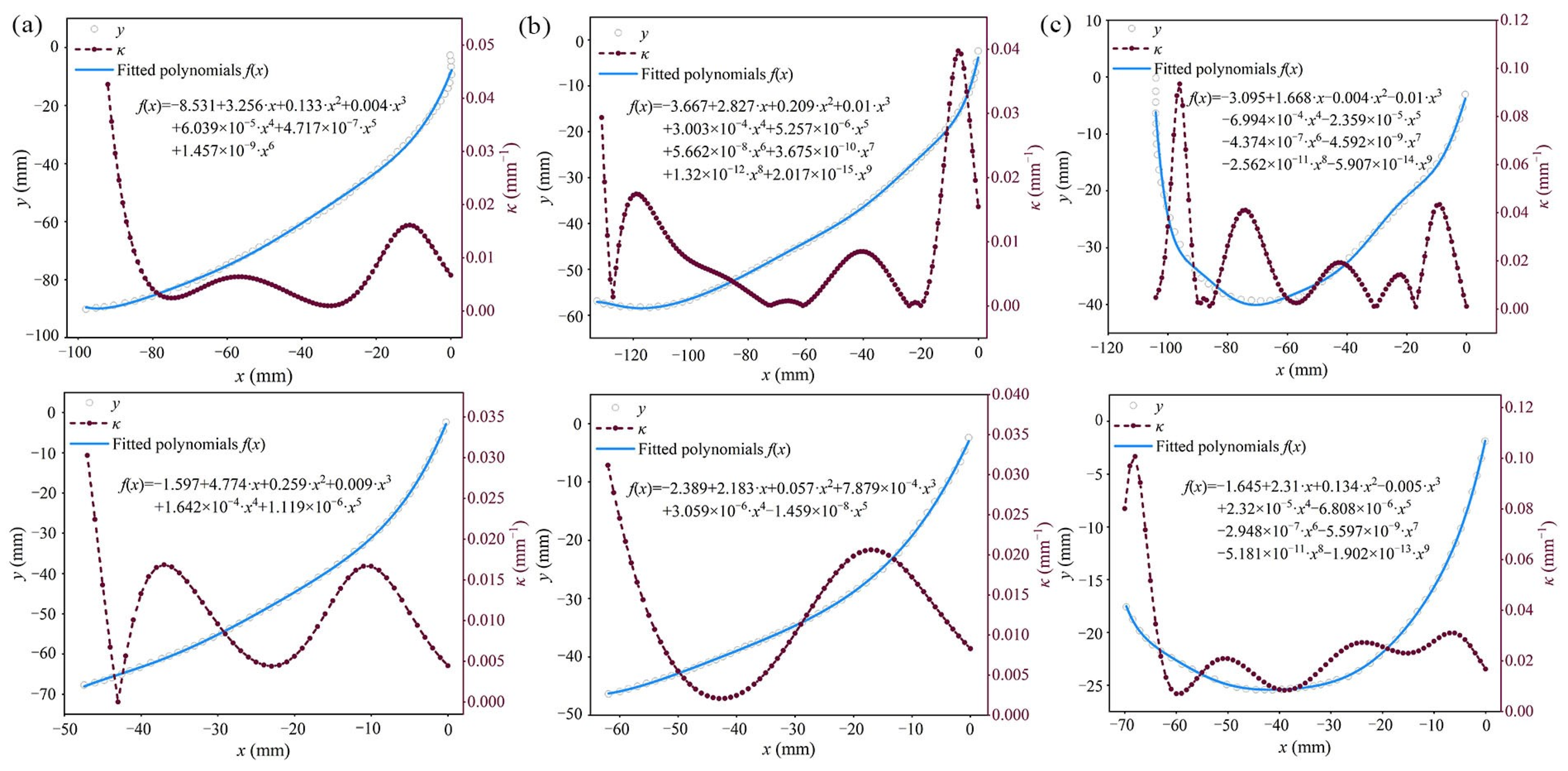
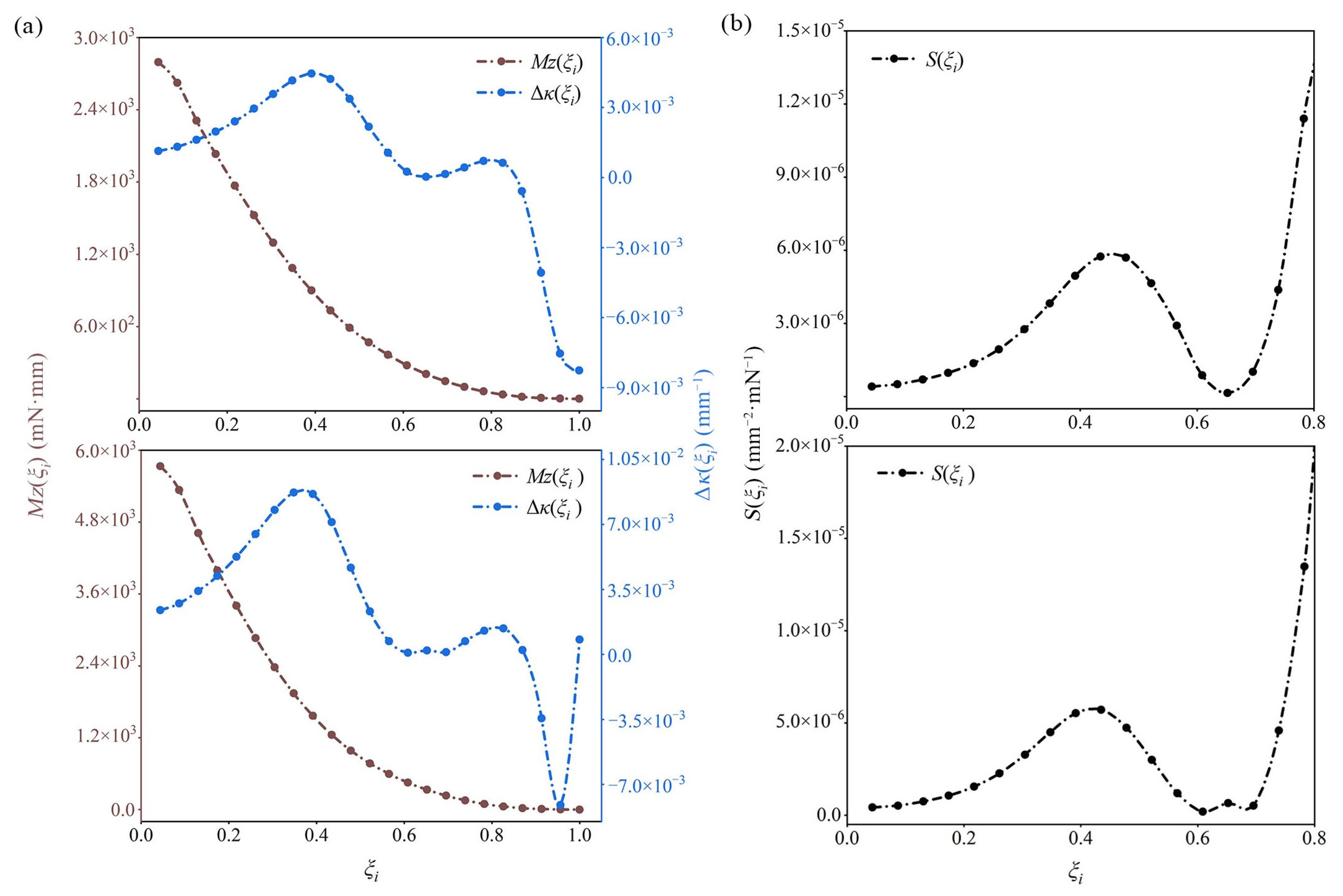
3.2. Distribution of Leaf Curvature
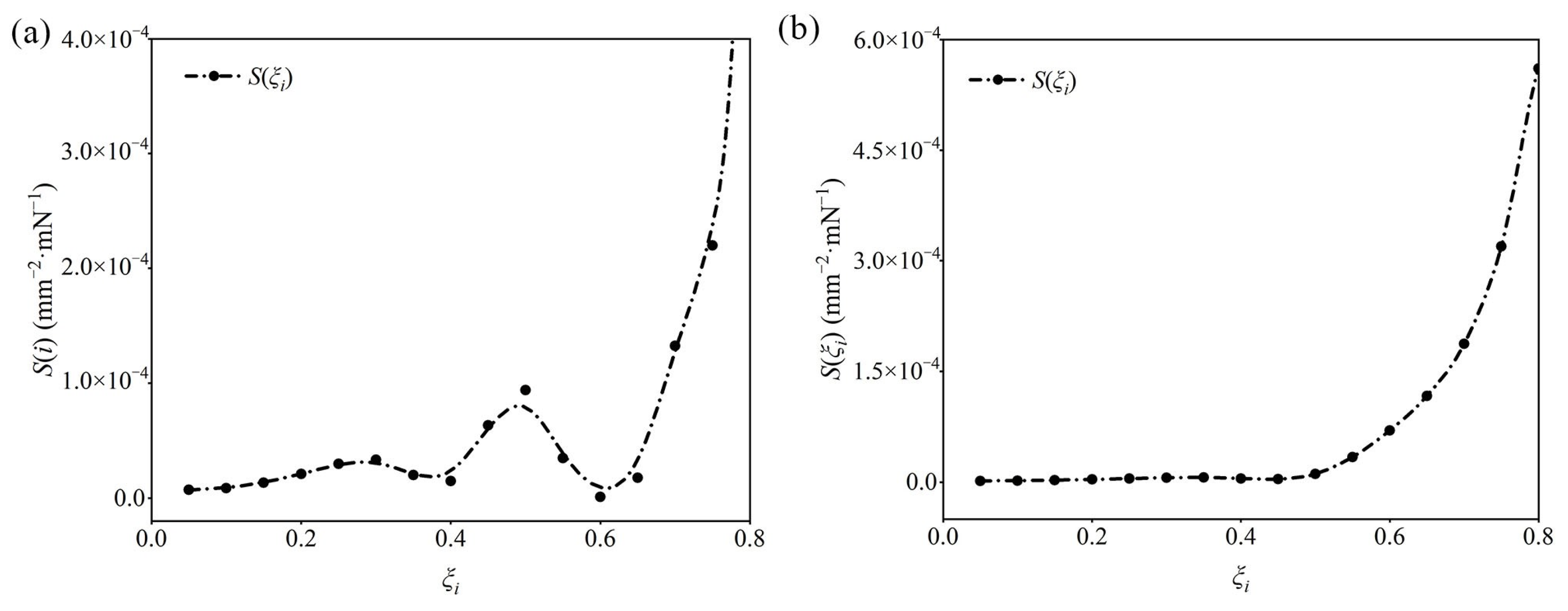
3.3. Distribution of Leaf Flexibility
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gao, J.; Tunio, M.; Chen, Y.; He, R. Design and experiment of low-frequency ultrasonic nozzle integrating air-assistant system and acoustic levitation mechanism. Int. J. Agric. Biol. Eng. 2020, 13, 25–33. [Google Scholar] [CrossRef]
- Hu, Y.; Chen, Y.; Wei, W.; Hu, Z.; Li, P. Optimization Design of Spray Cooling Fan Based on CFD Simulation and Field Experiment for Horticultural Crops. Agriculture 2021, 11, 566. [Google Scholar] [CrossRef]
- Li, G.; Chen, L.; Li, L.; Yi, T.; Ding, C.; Wang, J.; Zhao, C.; Zhang, R. Modeling and Experimental Validation of the Atomization Efficiency of a Rotary Atomizer for Aerial Spraying. Agronomy 2022, 12, 419. [Google Scholar] [CrossRef]
- Jing, L.; Wei, X. Spray Deposition and Distribution on Rice as Affected by a Boom Sprayer with a Canopy-Opening Device. Agriculture 2023, 13, 94. [Google Scholar] [CrossRef]
- Dai, S.; Zhang, J.; Jia, W.; Ou, M.; Zhou, H.; Dong, X.; Chen, H.; Wang, M.; Chen, Y.; Yang, S. Experimental Study on the Droplet Size and Charge-to-Mass Ratio of an Air-Assisted Electrostatic Nozzle. Agriculture 2022, 12, 889. [Google Scholar] [CrossRef]
- Ou, M.; Zhang, Y.; Wu, M.; Wang, C.; Dai, S.; Wang, M.; Dong, X.; Jiang, L. Development and Experiment of an Air-Assisted Sprayer for Vineyard Pesticide Application. Agriculture 2024, 14, 2279. [Google Scholar] [CrossRef]
- Tadrist, L.; Saudreau, M.; de Langre, E. Wind and gravity mechanical effects on leaf inclination angles. J. Theor. Biol. 2014, 341, 9–16. [Google Scholar] [CrossRef] [PubMed]
- Xi, T.; Li, C.; Qiu, W.; Wang, H.; Lv, X.; Han, C.; Ahmad, F. Droplet Deposition Behavior on a Pear Leaf Surface under Wind-Induced Vibration. Appl. Eng. Agric. 2020, 36, 913–926. [Google Scholar] [CrossRef]
- Wang, G.; Dong, X.; Jia, W.; Ou, M.; Yu, P.; Wu, M.; Zhang, Z.; Hu, X.; Huang, Y.; Lu, F. Influence of Wind Speed on the Motion Characteristics of Peach Leaves (Prunus persica). Agriculture 2024, 14, 2307. [Google Scholar] [CrossRef]
- Qiu, W.; Guo, H.; Cao, Y.; Li, X.; Wu, J.; Chen, Y.; Yu, H.; Zhang, Z. An electrical vortex air-assisted spraying system for improving droplet deposition on rice. Pest Manag. Sci. 2022, 78, 4037–4047. [Google Scholar] [CrossRef]
- Shi, Q.; Liu, D.; Mao, H.; Shen, B.; Li, M. Wind-induced response of rice under the action of the downwash flow field of a multi-rotor UAV. Biosyst. Eng. 2021, 203, 60–69. [Google Scholar] [CrossRef]
- Zhou, Q.; Xue, X.; Chen, C.; Cai, C.; Jiao, Y. Canopy deposition characteristics of different orchard pesticide dose models. Int. J. Agric. Biol. Eng. 2023, 16, 1–6. [Google Scholar] [CrossRef]
- Bhosale, Y.; Esmaili, E.; Bhar, K.; Jung, S. Bending, twisting and flapping leaf upon raindrop impact. Bioinspir. Biomim. 2020, 15, 036007. [Google Scholar] [CrossRef]
- Lauderbaugh, L.; Ginebra-Solanellas, R.; Holder, C.; Webb, R. A biomechanical model of leaf inclination angle oscillations after raindrop impact. Environ. Exp. Bot. 2021, 190, 104586. [Google Scholar] [CrossRef]
- Tadrist, L.; Julio, K.; Saudreau, M.; de Langre, E. Leaf flutter by torsional galloping: Experiments and model. J. Fluids Struct. 2015, 56, 1–10. [Google Scholar] [CrossRef]
- Zhang, C.; Zhou, H.; Xu, L.; Ru, Y.; Ju, H.; Chen, Q. Measurement of morphological changes of pear leaves in airflow based on high-speed photography. Front. Plant Sci. 2022, 13, 900427. [Google Scholar] [CrossRef]
- Liu, Y.; Andrew, M.; Li, J.; Yeomans, J.; Wang, Z. Symmetry breaking in drop bouncing on curved surfaces. Nat. Commun. 2015, 6, 10034. [Google Scholar] [CrossRef] [PubMed]
- Zheng, H.; Sun, H.; Cao, Y.; Lv, X.; Wang, C.; Chen, Y.; Yu, H.; Qiu, W. Computational fluid dynamics simulation analysis of the effect of curved rice leaves on the deposition behaviour of droplets. Plant Methods 2023, 19, 116. [Google Scholar] [CrossRef] [PubMed]
- Han, J.; Kim, W.; Bae, C.; Lee, D.; Shin, S.; Nam, Y.; Lee, C. Contact time on curved superhydrophobic surfaces. Phys. Rev. E 2020, 101, 043108. [Google Scholar] [CrossRef] [PubMed]
- Long, M.; Hasanyan, J.; Jung, S. Spreading dynamics of a droplet impacting a sphere. Phys. Fluids 2022, 34, 102115. [Google Scholar] [CrossRef]
- Niklas, K. Flexural stiffness allometries of angiosperm and fern petioles and rachises: Evidence for biomechanical convergence. Evolution 1991, 45, 734–750. [Google Scholar] [CrossRef] [PubMed]
- Moulia, B.; Fournier, M.; Guitard, D. Mechanics and form of the maize leaf: In vivo qualification of flexural behaviour. J. Mater. Sci. 1994, 29, 2359–2366. [Google Scholar] [CrossRef]
- Tang, L.; Shi, C.; Zhu, Y.; Jing, Q.; Cao, W. A quantitative analysis on leaf curvature characteristics in rice. In Crop Modeling and Decision Support; Springer: Berlin/Heidelberg, Germany, 2009; pp. 71–76. [Google Scholar] [CrossRef]
- Goodman, A.; Ennos, A. A comparative study of the response of the roots and shoots of sunflower and maize to mechanical stimulation. J. Exp. Bot. 1996, 47, 1499–1507. [Google Scholar] [CrossRef]
- Derksen, R.; Krause, C.; Fox, R.; Brazee, R.; Zondag, R. Effect of application variables on spray deposition, coverage, and ground losses in nursery tree applications. J. Environ. Hortic. 2006, 24, 45–52. [Google Scholar] [CrossRef]
- Wu, S.; Liu, J.; Wang, J.; Hao, D.; Wang, R. The Motion of Strawberry Leaves in an Air-Assisted Spray Field and Its Influence on Droplet Deposition. Trans. Asabe 2021, 64, 83–93. [Google Scholar] [CrossRef]
- Gao, Z.; Hu, W.; Dong, X.; Zhao, X.; Wang, S.; Chen, J.; Qiu, B. Motion behavior of droplets on curved leaf surfaces driven by airflow. Front. Plant Sci. 2024, 15, 1450831. [Google Scholar] [CrossRef]
- Shao, C.; Chen, Y.; Lin, J. Wind induced deformation and vibration of a Platanus acerifolia leaf. Acta Mech. Sin. 2012, 28, 583–594. [Google Scholar] [CrossRef]
- Jiang, H.; Xin, D.; Zhang, H. Wind-tunnel study of the aerodynamic characteristics and mechanical response of the leaves of Betula platyphylla Sukaczev. Biosyst. Eng. 2021, 207, 162–176. [Google Scholar] [CrossRef]
- Albayrak, I.; Nikora, V.; Miler, O.; O’Hare, M. Flow-plant interactions at a leaf scale: Effects of leaf shape, serration, roughness and flexural rigidity. Aquat. Sci. 2011, 74, 267–286. [Google Scholar] [CrossRef]
- Martone, P.; Denny, M. To bend a coralline: Effect of joint morphology on flexibility and stress amplification in an articulated calcified seaweed. J. Exp. Biol. 2008, 211, 3421–3432. [Google Scholar] [CrossRef] [PubMed]
- Martone, P.; Boller, M.; Burgert, I.; Dumais, J.; Edwards, J.; Mach, K.; Rowe, N.; Rueggeberg, M.; Seidel, R.; Speck, T. Mechanics without Muscle: Biomechanical Inspiration from the Plant World. Integr. Comp. Biol. 2010, 50, 888–907. [Google Scholar] [CrossRef]
- Niklas, K.J. The influence of gravity and wind on land plant evolution. Rev. Palaeobot. Palynol. 1998, 102, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Rosa, F.; Sutikno, P.; Suweca, I.; Moelyadi, M. Geometric morphometric banana leaf midrib as wind turbine airfoil profile. J. Mekanova: Mek. Inov. Dan Teknol. 2022, 8, 213. [Google Scholar] [CrossRef]
- Read, J.; Stokes, A. Plant biomechanics in an ecological context. Am. J. Bot. 2006, 93, 1546–1565. [Google Scholar] [CrossRef] [PubMed]
- Tu, Y.; Lin, Z.; Zhang, J. The effect of leaf shape on the deposition of spray droplets in rice. Crop Prot. 1986, 5, 3–7. [Google Scholar] [CrossRef]
- Wang, Z.; Zheng, C.; Li, T.; He, X. Analysing the preference for pesticide spray to be deposited at leaf-tips. Biosyst. Eng. 2021, 204, 247–256. [Google Scholar] [CrossRef]



| Crop Species | Walnut Leaf | Peach Leaf | Chili Pepper Leaf | |
|---|---|---|---|---|
| Parameter Value | ||||
| Geometric dimensions | Leaf length (mm) | 141.51 ± 8.93 | 128.39 ± 4.28 | 84.16 ± 3.87 |
| Leaf width (mm) | 97.57 ± 3.59 | 42.05 ± 1.99 | 55.88 ± 2.15 | |
| Leaf area (mm2) | 9872.71 ± 184.24 | 4226.56 ± 109.82 | 3441.42 ± 79.94 | |
| Bending stiffness | Leaf base region (N·mm2) | 33.64 ± 4.45 | 6.36 ± 3.17 | 4.39 ± 2.41 |
| Leaf tip region (N·mm2) | 0.43 ± 0.54 | 0.56 ± 0.28 | 0.68 ± 0.29 | |
| Leaf Curvature | Walnut Leaf (mm−1) | Peach Leaf (mm−1) | Chili Pepper Leaf (mm−1) |
|---|---|---|---|
| Wind Speed Value | |||
| 0 m/s | 0~0.018 | 0~0.061 | 0~0.027 |
| 3 m/s | 0~0.010 | 0~0.043 | 0~0.030 |
| 6 m/s | 0~0.014 | 0~0.047 | 0.002~0.031 |
| 9 m/s | 0.003~0.047 | 0~0.095 | 0.007~0.101 |
| 12 m/s | 0.007~0.037 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Z.; Ma, J.; Hu, W.; Wang, K.; Liu, K.; Chen, J.; Wang, T.; Dong, X.; Qiu, B. Wind-Induced Bending Characteristics of Crop Leaves and Their Potential Applications in Air-Assisted Spray Optimization. Horticulturae 2025, 11, 1002. https://doi.org/10.3390/horticulturae11091002
Gao Z, Ma J, Hu W, Wang K, Liu K, Chen J, Wang T, Dong X, Qiu B. Wind-Induced Bending Characteristics of Crop Leaves and Their Potential Applications in Air-Assisted Spray Optimization. Horticulturae. 2025; 11(9):1002. https://doi.org/10.3390/horticulturae11091002
Chicago/Turabian StyleGao, Zhouming, Jing Ma, Wei Hu, Kaiyuan Wang, Kuan Liu, Jian Chen, Tao Wang, Xiaoya Dong, and Baijing Qiu. 2025. "Wind-Induced Bending Characteristics of Crop Leaves and Their Potential Applications in Air-Assisted Spray Optimization" Horticulturae 11, no. 9: 1002. https://doi.org/10.3390/horticulturae11091002
APA StyleGao, Z., Ma, J., Hu, W., Wang, K., Liu, K., Chen, J., Wang, T., Dong, X., & Qiu, B. (2025). Wind-Induced Bending Characteristics of Crop Leaves and Their Potential Applications in Air-Assisted Spray Optimization. Horticulturae, 11(9), 1002. https://doi.org/10.3390/horticulturae11091002






