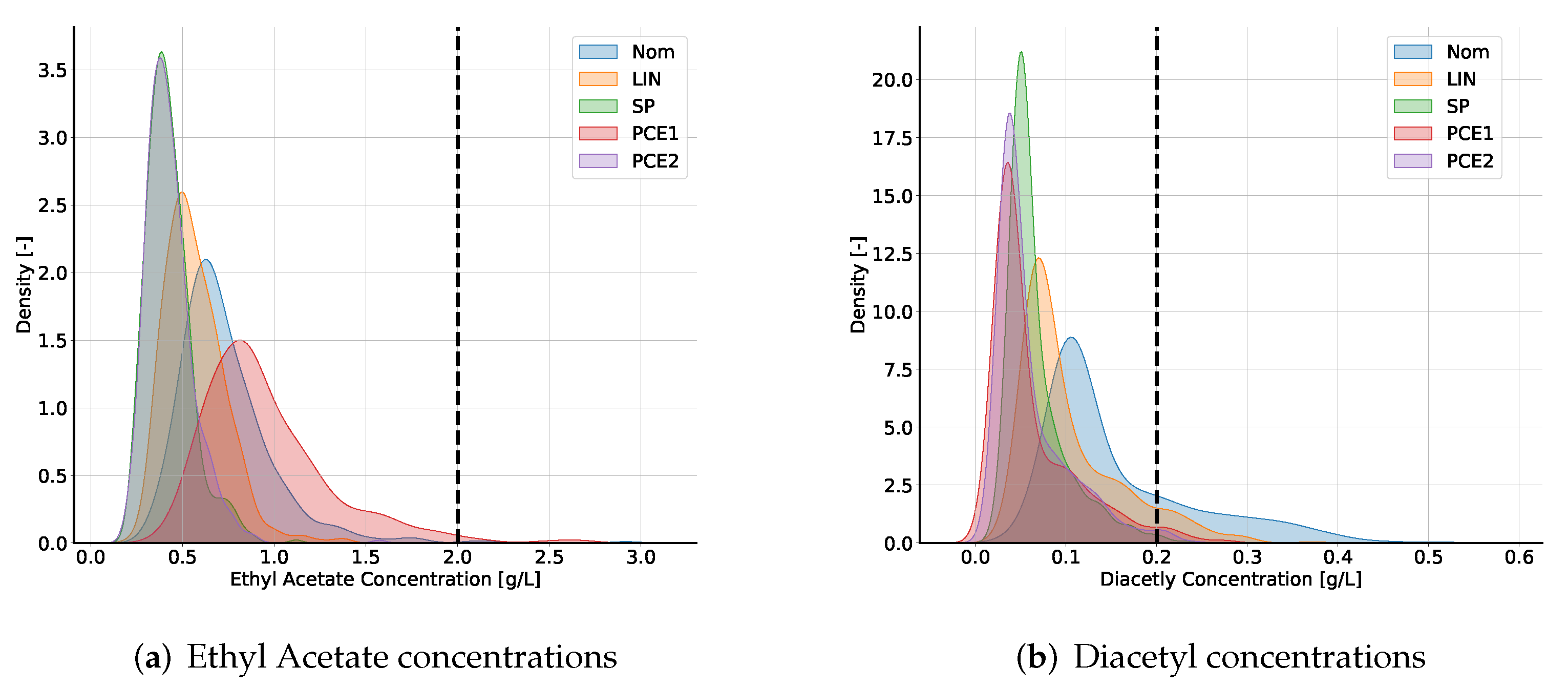
1. Introduction
Consumption of alcoholic beverages like beer, wine, and spirits has always played an important role in food security and health [
1]. With its history extending to more than 7 millennia [
2], beer is one of the most popular beverages in the world. The global beer consumption in 2019 was estimated at around 189.05 million kilolitres [
3]. The beer sector is a major contributor to the European Union’s economy with more than 10,300 active breweries providing over 130,000 jobs. In 2018, the beer sector contributed over €55 billion to the EU’s economic growth [
4]. With 340 breweries in Belgium producing over 1500 different beers [
5], the beer culture of Belgium has been inscribed on UNESCO’s Intangible Cultural Heritage of Humanity list [
6]. According to Belgian law [
7], beer is “
the beverage obtained after alcoholic fermentation of a wort prepared primarily from starch and sugary raw materials, of which at least 60% barley or wheat malt, as well as hops (possibly in processed form) and brewing water”. Thus, the main ingredients which form beer are only barley malt (i.e., a starch source), hops, yeast, and water.
Nevertheless, beer production is a complex process with a multitude of processing steps involved. The barley is converted into malt during the malting process. Malting converts the hard barley grains to friable malt by producing and activating various enzymes. The malt is then milled, and mixed with water to convert the starch and proteins into fermentable sugars through a process known as mashing. The mashed product, known as wort, is then boiled with hops (although hops can be added at different stages of the beer production). The residual hops and other products coagulated from the boiling process (called the trub) are removed from the wort. The clarified wort is cooled and transferred to a fermentation tank. There it is pitched with yeast and fermented to produce ethanol, carbon dioxide, and secondary metabolites.
Although the entire process involves only four ingredients, a plethora of chemical compounds are involved in the entire brewing process. The interaction of these chemical species gives each beer its characteristic flavour. According to Amerine et al. [
8], flavour is described as “
the sum of perceptions resulting from stimulation of the sense ends that are grouped together at the entrance of the alimentary and respiratory tracts”. Flavour comprises (i) odour: perception of volatile compounds in the nasal cavity, (ii) aroma: perception of volatiles which pass via the nasopharyngeal passage to the olfactory epithelium, (iii) taste: perception of soluble substances on the taste buds on the surface of the tongue, and (iv) mouthfeel: physical perception of beer in the mouth [
9]. Although only trace amounts of volatile esters are present in beer, they have a large influence on its flavour profile. Some common esters in beer are ethyl acetate, ethyl caprylate, ethyl octanoate, isoamyl acetate, etc. [
10,
11,
12,
13]. Apart from the esters, other volatile compounds include higher alcohols (e.g., amyl alcohol), carbonyl compounds (e.g., 2,3-butanedione, commonly called diacetyl), ketones, aldehydes, etc. [
11]. Although all these compounds are produced throughout the brewing process, a majority are produced as metabolic intermediates or by-products during the fermentation step [
12]. This makes fermentation a key process in the brewing chain.
Fermentation is an exothermic process in which the yeast converts the sugars in the wort to ethanol, carbon dioxide, and many other flavour-inducing compounds. The cooled wort is transferred to a cylindro-conical fermentation tank and the yeast is pitched. Along with the pitching rate and dissolved oxygen, fermentation is influenced by the temperature [
14]. Temperature has a strong effect on yeast metabolism. Most brewing yeasts have optimum growth temperatures between 30 and 34 °C. However, fermentation is carried out at much lower temperatures. Typically, lagers are fermented around 10 °C, while ales are fermented at 22 °C. At elevated temperatures, the fermentation is vigorous and leads to excessive loss of volatiles and formation of undesired by-products [
15]. However at higher temperatures, the time required for fermentations is reduced. Thus, the brewmaster must control the fermentation temperature such that fermentation is accelerated while still maintaining the beer quality profile. Traditionally, brewers have relied on their experience and traditional recipes for temperature control. In this paper, a computer-aided optimal control profile for the fermentation temperature is proposed.
Such an optimisation of the temperature profile is not novel. Several authors have proposed optimisation strategies to obtain a dynamic temperature profile by considering a variety of objectives. An objective describes the goal of the optimisation. In context of beer fermentation, some of the possible objectives are maximisation of ethanol concentration, minimisation of by-product formation, minimisation of batch time, or even a combination of these. Carrillo-Ureta et al. [
16] used genetic algorithms to determine the temperature profiles. Their objective was the combination of five different objectives: maximise ethanol concentration, minimise two by-products, minimise batch time, and minimise jumps in the temperature profile. Xiao et al. [
17] used a stochastic ant colony algorithm with similar objectives. In Rodman and Gerogiorgis [
18], a weighted objective of maximum ethanol and minimum batch time was optimised using a combination of simulated annealing and high fidelity simulations. Bosse and Griewank [
19] made use of forward–backward sweeping methods based on Pontryagin’s maximum principle to solve a modified version of the problem considered in Carrillo-Ureta et al. [
16]. Apart from the single objective studies, several multiobjective studies have also been reported. Andrés-Toro et al. [
20] also used genetic algorithms to solve the multiobjective optimisation problem by considering a variety of objectives. Rodman and Gerogiorgis [
14] used a simplified weighted-sum-type approach for multiobjective optimisation with two objectives: maximum ethanol and minimum batch time. In Rodman et al. [
21], a stochastic “
Strawberry” algorithm is used to determine the Pareto front between the contradicting objectives.
A common requirement for all the optimisation studies mentioned above is the process model. A process model is a mathematical abstraction of the reality. Describing the plethora of chemical species produced during fermentation [
12,
22] would lead to an extremely complex mathematical model. It is thus common to use reduced-order models which only consider key chemical compounds. A variety of process models have been proposed to describe the fermentation process [
23,
24,
25,
26]. The model developed in de Andrés-Toro et al. [
23] is based on extensive experimentation on industrial-scale fermentation and has been widely used in optimisation studies. All models contain parameters which have to estimate from experimental data.
As all experiments inherently have noise (either measurement noise, or in the case of yeast, biological variability), the parameters estimated from the data are uncertain. Although it is possible to reduce the uncertainty (i.e., improve the parameter accuracy) by performing more and better experiments, and by using better sensors, it is impossible to completely eliminate the uncertainty. Thus, any optimisation study based on a mathematical model must take this parametric uncertainty into consideration. Use of inaccurate parameters can lead to constraint violations, which in reality might affect the safety of the process or the quality of the product. In this paper, an optimisation strategy to determine the fermentation temperature profile by including the parametric uncertainty in the process model is presented. Following all the optimisation studies mentioned earlier, the model developed by de Andrés-Toro et al. [
23] is used.
In the following sections, the dynamic optimisation formulation under parametric uncertainty is presented. The concept and techniques of uncertainty propagation are introduced. This is followed by the description of the de Andres-Toro model for beer fermentation. The in-house tool used for the dynamic optimisation is briefly presented. The temperature profile obtained after the optimisation is then discussed in the results section. Finally, the conclusions section summarises the main findings of this paper.