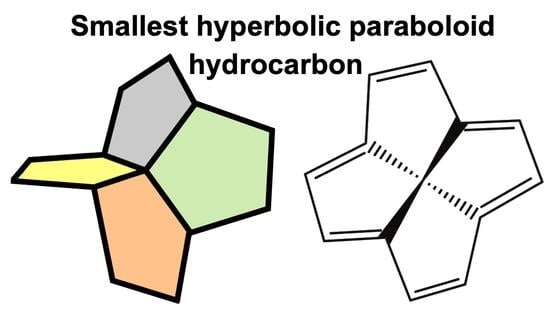
Thermochemistry of the Smallest Hyperbolic Paraboloid Hydrocarbon: A High-Level Quantum Chemical Perspective
Abstract
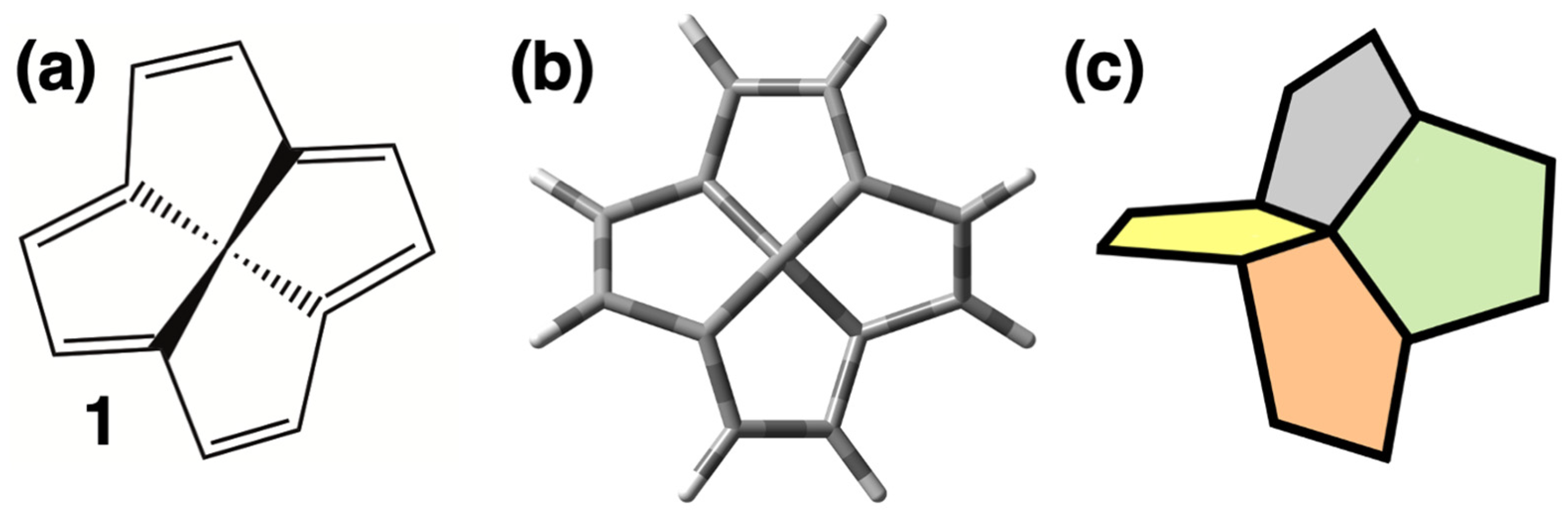
1. Introduction
2. Computational Details
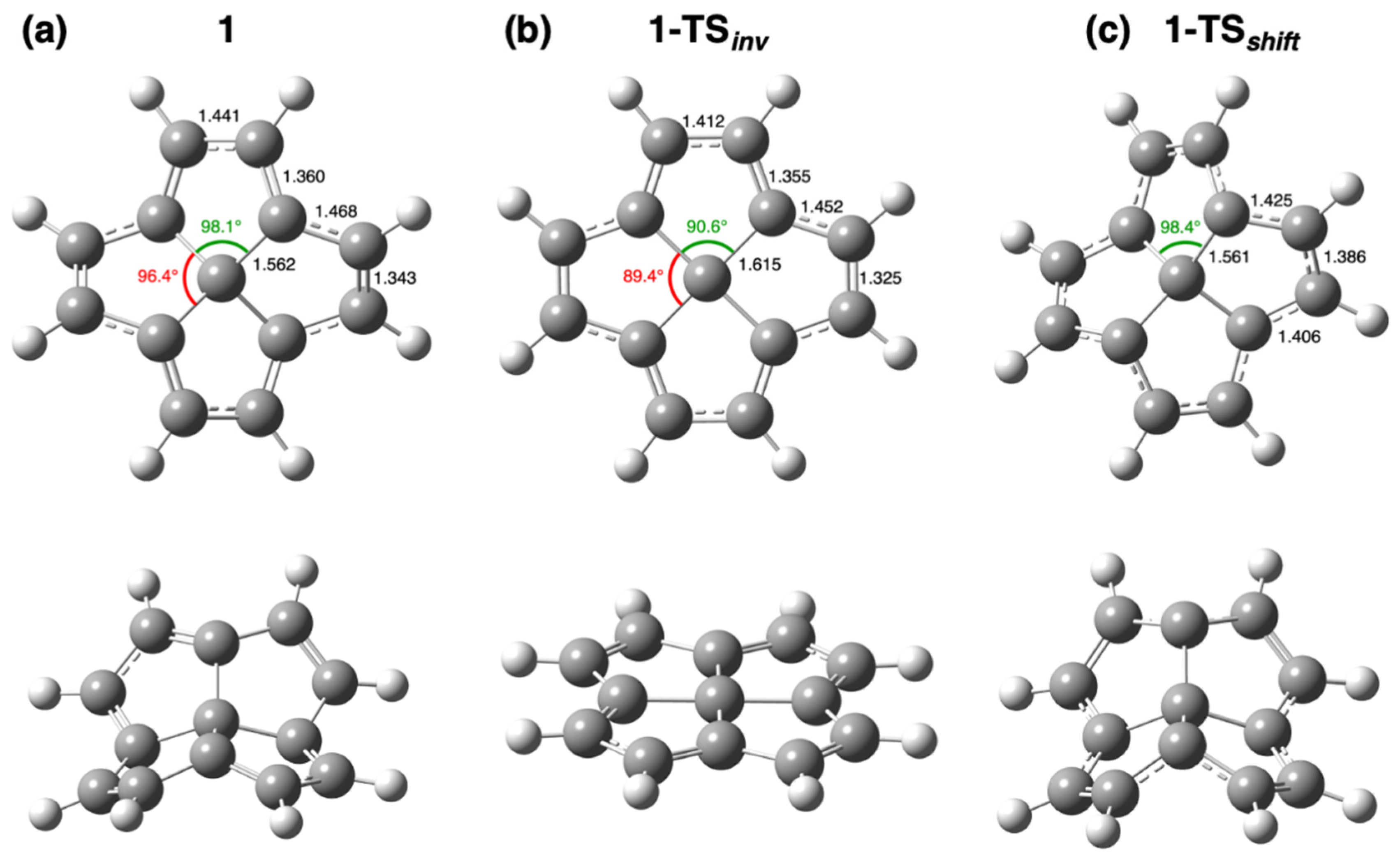
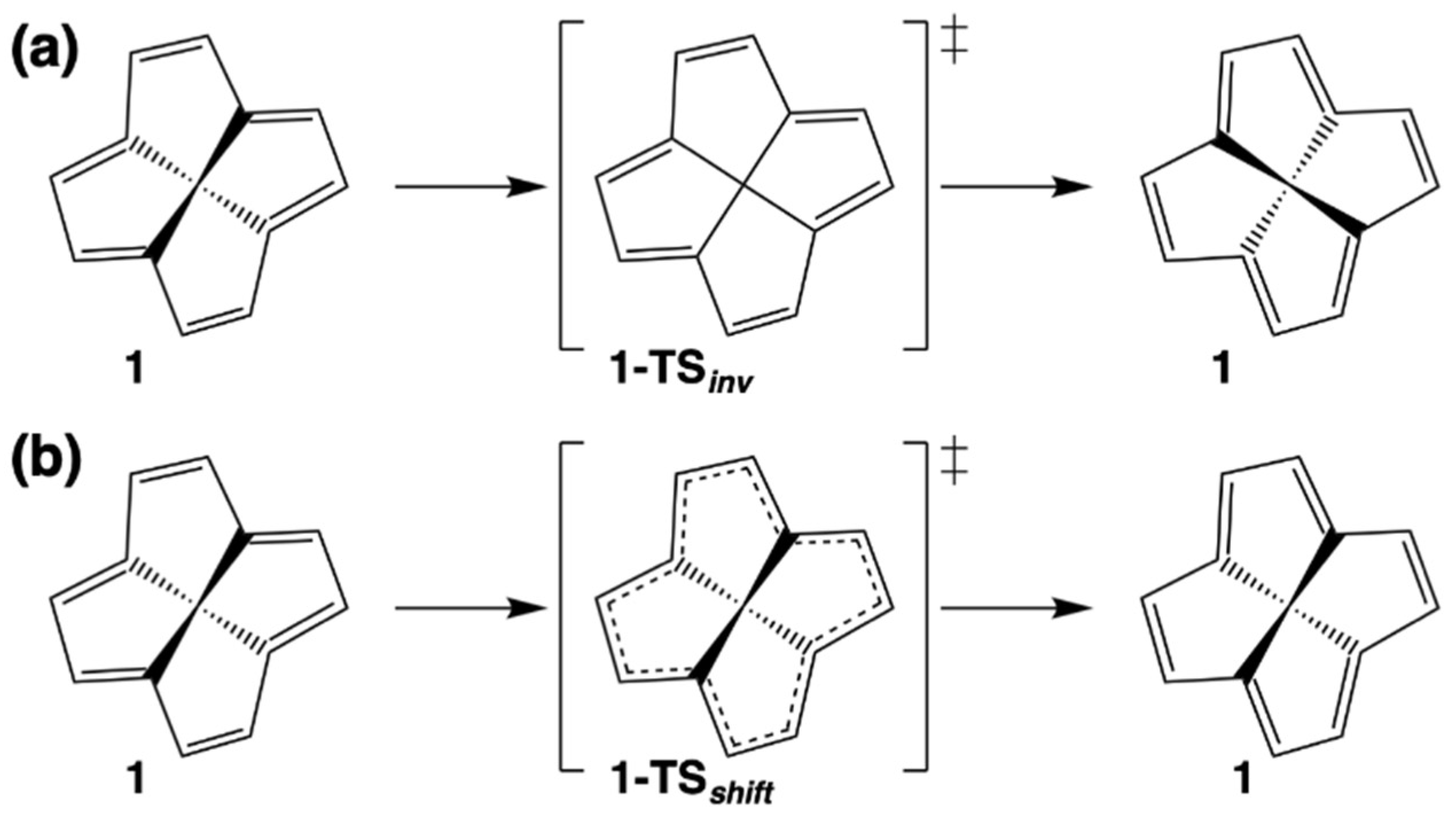
3. Results and Discussion
4. Conclusions
Supplementary Materials
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hoffmann, R.; Alder, R.W.; Wilcox, C.F. Planar tetracoordinate carbon. J. Am. Chem. Soc. 1970, 92, 4992. [Google Scholar] [CrossRef]
- Chandrasekhar, J.; Wurthwein, E.-U.; Schleyer, P.V.R. On the planarity of tetracoordinate carbon enclosed by annulene perimeters. Tetrahedron 1981, 37, 921. [Google Scholar] [CrossRef]
- Minkin, V.I.; Minyaev, R.M.; Hoffmann, R. Non-classical structures of organic compounds: Unusual stereochemistry and hypercoordination. Russ. Chem. Rev. 2002, 71, 869. [Google Scholar] [CrossRef]
- Keese, R. Carbon Flatland: Planar Tetracoordinate Carbon and Fenestranes. Chem. Rev. 2006, 106, 4787. [Google Scholar] [CrossRef] [PubMed]
- Spitler, E.L.; Johnson, C.A.; Haley, M.M. Renaissance of Annulene Chemistry. Chem. Rev. 2006, 106, 5344. [Google Scholar] [CrossRef] [PubMed]
- Pellegrino, S. On the Rigidity of Triangulated Hyperbolic Paraboloids. Proc. R. Soc. Land. A 1988, 418, 425. [Google Scholar]
- Ten, L.V. Rigidity of complete surfaces of negative curvature that coincide with a hyperbolic paraboloid outside a compact region. Russ. Math. Surv. 1980, 35, 111. [Google Scholar] [CrossRef]
- Nazir, M.A.; Hassan, A.; Shen, Y.; Wang, Q. Research progress on penta-graphene and its related materials: Properties and applications. Nano Today 2022, 44, 101501. [Google Scholar] [CrossRef]
- Zhang, S.; Zhou, J.; Wang, Q.; Chen, X.; Kawazoe, Y.; Jena, P. Penta-graphene: A new carbon allotrope. Proc. Natl. Acad. Sci. USA 2015, 112, 2372. [Google Scholar] [CrossRef]
- Cramer, C.J. Essentials of Computational Chemistry: Theories and Models, 2nd ed.; Wiley: Hoboken, NJ, USA, 2004. [Google Scholar]
- Levine, I.N. Quantum Chemistry, 7th ed.; Prentice Hall: New York, NY, USA, 2013. [Google Scholar]
- Karton, A. Quantum mechanical thermochemical predictions 100 years after the Schrödinger equation. Annu. Rep. Comput. Chem. 2022, 18, 123. [Google Scholar]
- Karton, A. A computational chemist’s guide to accurate thermochemistry for organic molecules. WIREs Comput. Mol. Sci. 2016, 6, 292. [Google Scholar] [CrossRef]
- Curtiss, L.A.; Redfern, P.C.; Raghavachari, K. Gaussian-4 theory. J. Chem. Phys. 2007, 126, 084108. [Google Scholar] [CrossRef] [PubMed]
- Curtiss, L.A.; Redfern, P.C.; Raghavachari, K. Gaussian-4 theory using reduced order perturbation theory. J. Chem. Phys. 2007, 127, 124105. [Google Scholar] [CrossRef] [PubMed]
- Curtiss, L.A.; Redfern, P.C.; Raghavachari, K. Gn Theory. WIREs Comput. Mol. Sci. 2011, 1, 810. [Google Scholar] [CrossRef]
- Zheng, J.; Zhao, Y.; Truhlar, D.G. The DBH24/08 Database and Its Use to Assess Electronic Structure Model Chemistries for Chemical Reaction Barrier Heights. J. Chem. Theory Comput. 2009, 5, 808. [Google Scholar] [CrossRef] [PubMed]
- Curtiss, L.A.; Redfern, P.C.; Raghavachari, K. Assessment of Gaussian-4 theory for energy barriers. Chem. Phys. Lett. 2010, 499, 168. [Google Scholar] [CrossRef]
- Karton, A.; O’Reilly, R.J.; Radom, L. Assessment of theoretical procedures for calculating barrier heights for a diverse set of water-catalyzed proton-transfer reactions. J. Phys. Chem. A 2012, 116, 4211. [Google Scholar] [CrossRef]
- Karton, A.; Martin, J.M.L. Explicitly correlated benchmark calculations on C8H8 isomer energy separations: How accurate are DFT, double-hybrid and composite ab initio procedures? Mol. Phys. 2012, 110, 2477. [Google Scholar] [CrossRef]
- Yu, L.-J.; Karton, A. Assessment of theoretical procedures for a diverse set of isomerization reactions involving double-bond migration in conjugated dienes. Chem. Phys. 2014, 441, 166. [Google Scholar] [CrossRef]
- Karton, A.; Goerigk, L. Accurate reaction barrier heights of pericyclic reactions: Surprisingly large deviations for the CBS-QB3 composite method and their consequences in DFT benchmark studies. J. Comput. Chem. 2015, 36, 622. [Google Scholar] [CrossRef]
- Yu, L.J.; Sarrami, F.; O’Reilly, R.J.; Karton, A. Reaction barrier heights for cycloreversion of heterocyclic rings: An Achilles’ heel for DFT and standard ab initio procedures. Chem. Phys. 2015, 458, 1–8. [Google Scholar] [CrossRef]
- Karton, A.; Schreiner, P.R.; Martin, J.M.L. Heats of formation of platonic hydrocarbon cages by means of high-level thermochemical procedures. J. Comput. Chem. 2016, 37, 49. [Google Scholar] [CrossRef] [PubMed]
- Karton, A. How reliable is DFT in predicting the relative energies of polycyclic aromatic hydrocarbon isomers? Comparison of functionals from different rungs of Jacob’s Ladder. J. Comput. Chem. 2017, 38, 370. [Google Scholar] [CrossRef]
- Karton, A.; Sylvetsky, N.; Martin, J.M.L. W4-17: A diverse and high-confidence dataset of atomization energies for benchmarking high-level electronic structure methods. J. Comput. Chem. 2017, 38, 2063. [Google Scholar] [CrossRef]
- Karton, A. Fullerenes Pose a Strain on Hybrid Density Functional Theory. J. Phys. Chem. A 2022, 126, 4709. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648. [Google Scholar] [CrossRef]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623. [Google Scholar] [CrossRef]
- Gonzalez, C.; Schlegel, H.B. An improved algorithm for reaction path following. J. Chem. Phys. 1989, 90, 2154. [Google Scholar] [CrossRef]
- Gonzalez, C.; Schlegel, H.B. Reaction path following in mass-weighted internal coordinates. J. Chem. Phys. 1990, 94, 5523. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 16, Revision E.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Perdew, J.P.; Schmidt, K. Jacob’s ladder of density functional approximations for the exchange-correlation energy. AIP Conf. Proc. 2000, 577, 1–20. [Google Scholar]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Perdew, J.P. Density-functional approximation for the correlation energy of the inhomogeneous electron gas. Phys. Rev. B 1986, 33, 8822. [Google Scholar] [CrossRef] [PubMed]
- Tao, J.M.; Perdew, J.P.; Staroverov, V.N.; Scuseria, G.E. Climbing the Density Functional Ladder: Nonempirical Meta–Generalized Gradient Approximation Designed for Molecules and Solids. Phys. Rev. Lett. 2003, 91, 146401. [Google Scholar] [CrossRef]
- Yu, H.S.; He, X.; Li, S.L.; Truhlar, D.G. MN15: A Kohn–Sham global-hybrid exchange–correlation density functional with broad accuracy for multi-reference and single-reference systems and noncovalent interactions. Chem. Sci. 2016, 7, 5032. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Chevary, J.A.; Vosko, S.H.; Jackson, K.A.; Pederson, M.R.; Singh, D.J.; Fiolhais, C. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 1992, 46, 6671. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158. [Google Scholar] [CrossRef]
- Yanai, T.; Tew, D.; Handy, N.C. A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51. [Google Scholar] [CrossRef]
- Zhao, Y.; Schultz, N.E.; Truhlar, D.G. Design of Density Functionals by Combining the Method of Constraint Satisfaction with Parametrization for Thermochemistry, Thermochemical Kinetics, and Noncovalent Interactions. J. Chem. Theory Comput. 2006, 2, 364. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215. [Google Scholar]
- Boese, A.D.; Martin, J.M.L. Development of density functionals for thermochemical kinetics. J. Chem. Phys. 2004, 121, 3405. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Truhlar, D.G. Design of Density Functionals That Are Broadly Accurate for Thermochemistry, Thermochemical Kinetics, and Nonbonded Interactions. J. Phys. Chem. A 2005, 109, 5656. [Google Scholar] [CrossRef] [PubMed]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D.; Johnson, E.R. A density-functional model of the dispersion interaction. J. Chem. Phys. 2005, 123, 154101. [Google Scholar] [CrossRef]
- The C13H8 Isomers Were Identified Using the ChemSpider Database. ChemSpider Is a Comprehensive Freely Available Database with over 100 Million Chemical Structures. Available online: http://www.chemspider.com (accessed on 1 January 2023).
- Sorensen, J.S.; Sorensen, N.A. Studies Related to Naturally Occurring Acetylene Compounds. XXII* Correctional Studies on the Constitution of the Polyacetylenes of some Annual Coreopsis Species. Acta Chem. Scand. 1958, 12, 756. [Google Scholar] [CrossRef]
- Akiyama, S.; Misumi, S.; Nakagawa, M. Cyclic Acetylenes. IX. Synthesis of a Cyclic Octaacetylene Containing Anthracene Nuclei. Bull. Chem. Soc. Jpn. 1962, 35, 1829. [Google Scholar] [CrossRef]
- Jones, E.R.H.; Skattebøl, L.; Whiting, M.C. Researches on acetylenic compounds. Part LX. The synthesis of three natural polyacetylenic hydrocarbons. J. Chem. Soc. 1958, 1054. [Google Scholar] [CrossRef]
- Keese, R.; Pfenninger, A.; Roesle, A. Planarization of Tetracoordinate Carbon Atom. Synthesis of 13-oxa-14-oxo-pentacyclo [5.5.2.1.04,15010,15]pentadecane, a bridged ‘tetraquinacane’. Helv. Chim. Acta 1979, 62, 326. [Google Scholar] [CrossRef]
- Bohm, M.C.; Gleiter, R.; Schang, P. On the planarity of tetracyclo [5.5.1.04,13o10,13] tridecahexaene. Tetrahedron Lett. 1979, 20, 2575. [Google Scholar] [CrossRef]
- Kubiak, G.G.I. Mechanistic and Synthetic Studies on the Scope of the Weiss Reaction. II. Studies Directed toward the Preparation of Staurane-1,3,5,7,9,11-Hexaene on the Route towards Tetracoordinate Planar Carbon. Ph.D. Thesis, The University of Wisconsin, Milwaukee, WI, USA, 1989. Available online: https://www.proquest.com/docview/303806144?pq-origsite=gscholar&fromopenview=true (accessed on 1 January 2023).
- Klärner, F.-G. About the Antiaromaticity of Planar Cyclooctatetraene. Angew. Chem. Int. Ed. 2001, 40, 3977. [Google Scholar] [CrossRef]
- Karton, A.; Tarnopolsky, A.; Martin, J.M.L. Atomization energies of the carbon clusters Cn (n = 2–10) revisited by means of W4 theory as well as density functional, Gn, and CBS methods. Mol. Phys. 2009, 107, 977. [Google Scholar] [CrossRef]

| Struct. | ∆Ee | ∆H0 | ∆H298 | Struct. | ∆Ee | ∆H0 | ∆H298 |
|---|---|---|---|---|---|---|---|
| 1 | 0.0 | 0.0 | 0.0 | 10 | 52.3 | 43.1 | 51.4 |
| 2 | 15.3 | 8.1 | 17.5 | 9 | 61.2 | 42.0 | 52.8 |
| 3 | 25.8 | 15.2 | 24.3 | 11 | 281.8 | 263.2 | 277.3 |
| 5 | 29.5 | 18.3 | 28.0 | 12 | 283.6 | 264.3 | 278.7 |
| 4 | 29.8 | 18.7 | 28.3 | 13 | 363.6 | 359.9 | 361.4 |
| 6 | 54.9 | 36.3 | 46.8 | 14 | 498.7 | 472.8 | 488.2 |
| 7 | 54.8 | 36.7 | 46.9 | 1-TSinv a | 262.7 | 247.5 | 249.2 |
| 8 | 57.4 | 38.5 | 48.9 | 1-TSshift b | 74.6 | 68.4 | 67.6 |
| RMSD | MAD | MSD | LD | |
|---|---|---|---|---|
| BLYP-D3BJ | 87.7 | 79.8 | −76.2 | −143.4 |
| BP86-D3BJ | 27.8 | 24.3 | −11.0 | −52.2 |
| PBE-D3BJ | 27.4 | 24.1 | −2.2 | −42.5 |
| BPBE-D3BJ | 23.6 | 19.9 | 1.8 | −34.2 |
| TPSS-D3BJ | 38.4 | 32.8 | −26.3 | −69.6 |
| MN15-L | 30.6 | 27.9 | −16.9 | −58.7 |
| B3LYP-D3BJ | 62.0 | 57.9 | −54.1 | −91.8 |
| CAM-B3LYP-D3BJ | 38.5 | 37.0 | −35.1 | −50.2 |
| PBE0-D3BJ | 23.1 | 17.8 | 17.4 | 38.8 |
| B3PW91-D3BJ | 14.9 | 13.3 | 2.7 | 22.0 |
| M06-2X | 47.9 | 45.7 | −45.7 | −61.3 |
| MN15 | 24.7 | 22.6 | −22.6 | −36.5 |
| PW6B95-D3BJ | 28.8 | 22.8 | −22.8 | −46.8 |
| M05-2X | 22.0 | 20.7 | −19.8 | −34.0 |
| BMK-D3BJ | 16.2 | 15.2 | 11.5 | −22.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karton, A. Thermochemistry of the Smallest Hyperbolic Paraboloid Hydrocarbon: A High-Level Quantum Chemical Perspective. C 2023, 9, 41. https://doi.org/10.3390/c9020041
Karton A. Thermochemistry of the Smallest Hyperbolic Paraboloid Hydrocarbon: A High-Level Quantum Chemical Perspective. C. 2023; 9(2):41. https://doi.org/10.3390/c9020041
Chicago/Turabian StyleKarton, Amir. 2023. "Thermochemistry of the Smallest Hyperbolic Paraboloid Hydrocarbon: A High-Level Quantum Chemical Perspective" C 9, no. 2: 41. https://doi.org/10.3390/c9020041
APA StyleKarton, A. (2023). Thermochemistry of the Smallest Hyperbolic Paraboloid Hydrocarbon: A High-Level Quantum Chemical Perspective. C, 9(2), 41. https://doi.org/10.3390/c9020041