Abstract
We investigated the IR absorption spectra of CVD diamond damaged by fast neutrons (>0.1 MeV) with high fluences ranging from 1 × 1018 to 2 × 1019 cm−2 and annealed at temperatures of 200 °C to 1680 °C. After annealing above 1000 °C, the formation of “amber-centers” (ACs), associated with multivacancy clusters, is detected as deduced from the appearance of a strong absorption line at 4100 cm−1. Moreover, the concentration of the ACs in the irradiated diamond can be an order of magnitude higher than that observed previously in the darkest brown natural diamonds. A number of other absorption lines, including the H1b center at 4936 cm−1 (0.612 eV) and new lines at ~5700 cm−1 (0.706 eV) and 9320 cm−1 (1.155 eV) not reported before in the literature, are observed, and their intensity evolutions at annealing temperatures are documented. At the highest fluences, all the lines show reduced intensities and broadening and spectral shifts due to a very high defect concentration and partial amorphization. The obtained experimental data can be used for the analysis of defect generation, transformations and healing in irradiated synthetic and natural diamonds.
Keywords:
diamond; fast neutrons; radiation damage; amorphization; defects; amber centers; FTIR spectra 1. Introduction
Diamond is a crystal with a very dense cubic lattice and extremely strong interatomic covalent bonds, which give it remarkable properties that are attractive for many applications in optics, electronics and mechanics. Particularly, this structure is the reason for the high radiation hardness of diamond, making it an excellent material for ionizing radiation detectors [1]. As the equilibrium solubility of impurities and their diffusion in diamond are very low, ion implantation has been used for doping for a long time [2]. Particularly, ion implantation is a common technique for the production of specific optically active defects and single photon emitters and for applications in electronics, photonics, quantum cryptography and biosensors [3,4]. Ion implantation allows the realization of a wide range of radiation damage, however, only within a shallow subsurface layer. The concentration of implantation-induced defects has quite a nonuniform spatial profile and may vary by orders of magnitude over the depth that hinders the study of the radiation damage’s nature, especially using optical spectroscopy methods, which inevitably have to analyze the material structure averaged over layers with different defect abundance.
In contrast, irradiation using fast neutrons allows similar levels of radiation damage to be achieved but uniformly over the crystal volume. As Raman spectroscopy analysis shows [5,6], the types of defects induced by ion implantation and neutron irradiation followed by high-temperature annealing are practically identical. As a consequence of a great variety of radiation-induced defects, not all of them have been comprehensively studied experimentally and theoretically up to now. Knowledge of the formation, modification and structure of the radiation defects is important for the assessment of the stability of diamond radiation detectors [7,8,9,10], first-order phase transition diamond–graphite under radiation damage, and diamond treatment (modification of color) in jewelry. Of special interest are defects both in untreated and irradiated diamonds, which show features in optical absorption and luminescence spectra.
Neutron collisions with carbon atoms create Frenkel pairs, and the displaced atom occupies an interstitial position, leaving a vacancy in the lattice site. Irradiation promotes the diffusion of the interstitial atoms, so a part of the closely positioned vacancies and interstitials recombine [11,12]. Depending on the radiation damage type and impurity abundance, this effect reduces the vacancy concentration by 20–60% [13,14], while a different fate awaits the vacancies in close proximity to the impurity atoms, primarily nitrogen. Nitrogen association with vacancy is energetically favorable [15], especially in the case of the C-defect, dispersed, single, substitutional atom N, characteristic of synthetic diamonds. As a result, the well-known defect NV has neutral and negatively charged states NV0 and NV− with zero-phonon lines (ZPLs) at 575 and 637 nm, respectively [16].
When the concentration of radiation-induced vacancies exceeds that of the N defects (it is this case we consider in the present work), another channel for vacancy annealing can be realized, namely aggregation in multivacancy complexes, whose properties are insufficiently studied far [17]. The presence of vacancy clusters along deformation-induced dislocations in diamonds was observed using transmission electron microscopy [18]; however, the structure of vacancy aggregates is difficult or even impossible to disclose using transmission electron microscopy [19]. The most reliable data on the vacancy complexes in diamond were obtained using positron annihilation spectroscopy (PAS), which uses a monochromatic positron beam directed on the specimen under study, where the positrons are thermalized and recombine with electrons. Using the PAS technique, it was established that the brown color in natural diamonds is due to multivacancy clusters [18,20,21]. The detailed classification of brown diamonds with a non-deformation-related and deformation-related color is given in [22,23], respectively. Most natural diamonds with a deformation-related brown color contain the so-called amber centers (ACs), which appear in the IR spectra as a ZPL near 4100 cm−1. Various ACs were found to be closely related defects, most likely involving multiple vacancies and nitrogen [23]. The term amber centers is also used to describe a series of broad bands related to diamonds with brown coloration and/or colored graining between approximately 3450 and 6000 cm−1 and structures that extend to approximately 10,500 cm−1, with the most prominent feature in the 4050–4200 cm−1 range [23,24]. Dangling bonds from sp2-bonded carbon on the inner walls of the cluster produce the necessary continuum of levels within the band gap [23]. The ACs produce absorption caused by electronic transitions—hence not vibrational absorptions—which exhibit their ZPLs with corresponding phonon side-bands.
There is a consensus that the majority of those lines originate from a variety of multivacancy complexes with or without impurities, such as nitrogen. The ACs in brown diamonds are unstable thermally and annealed during high-pressure, high-temperature (HPHT) treatments (T > 1800 °C and 6 GPa) [25]. This is believed to prevent the brown center formation in the extreme conditions of the Earth’s upper mantle [26]. Nevertheless, the destruction of ACs by HPHT treatment is unexplained at this time [27]. The AC defect was suggested to relate to A-defects in diamonds, but no linear correlation between ACs and the aggregation state and total nitrogen content was found [24]. It is assumed that the source of the generation of multivacancy centers in natural diamonds is plastic deformation, which creates high densities of dislocations and vacancies [19]. Plastic deformation can occur in nature under the effect of dynamic processes, followed by the disintegration of the deep-seated rocks and transportation of diamonds to the Earth’s surface by kimberlite magmas [28].
The absorption coefficients of AC bands commonly do not exceed a few tenths of cm−1 [23,24,25,29], which causes difficulties in the optical absorption measurement in thin layers. An additional problem is the inhomogeneous color of natural diamonds, as well as the sectorial distribution of impurities and defects over their volume [30,31,32,33]. This makes it much more difficult to establish a correspondence between the structure and properties of brown natural diamonds. Note that in CVD diamonds, in contrast to natural diamonds, nitrogen is present only in the form of single atoms in the substitution position and is distributed almost uniformly over the volume of the crystals.
One of most comprehensive studies of the optical properties of natural diamonds with ACs was performed in [23], where several hundred brown diamonds were measured, and the effects of annealing were described. It was suggested that ACs can be formed via radiation damage followed by annealing. However, due to the relatively low neutron fluence used (2 × 1017 cm−2), the amplitudes of radiation-induced AC absorption lines were rather low at a few hundredths of cm−1.
IR spectroscopy is a powerful technique to study radiative defects in neutron- and electron-irradiated diamonds, as the defects are uniformly distributed in the bulk. Radiation damage effects on the one-phonon absorption band [34,35,36,37,38] and hydrogen- [31,35,39] and nitrogen-related [35,37,38,40,41] local vibrational modes are among the most studied.
Here, we investigated IR spectra for diamond subjected to neutron irradiation at high doses, which is rarely explored (we can mention only [38] that deals with similar damage levels). We prepared samples with high AC concentrations using high-dose fast neutron irradiation, investigated the AC evolution upon annealing using IR spectroscopy, and studied the structural defect transformation in partially disordered diamond.
2. Materials and Methods
Translucent polycrystalline diamond films of thickness > 0.55 mm were grown on Si substrates of 57 mm in diameter using a microwave plasma CVD system (5 kW, 2.45 GHz) with methane–hydrogen mixtures [42]. The average grain size was 50–70 µm, as seen on growth surface [42]. CVD diamond as a burgeoning multifunctional material with tailored quality and characteristics fulfills the multifield application prospects with appropriate choice in terms of cost and quality [43]. Free-standing films were obtained using chemical removal of the substrate, cut with a laser to 5 × 3 mm2 chips, and mechanically polished on both sides.
Irradiation was carried out in the wet channel of the IVV-2M research nuclear reactor using fast neutrons (flux of 1014 cm−2 s−1, energies of over 0.1 MeV) to fluences of 1 × 1018 to 2 × 1019 cm−2, keeping the specimen temperature at 50 ± 10 °C [44].
We note that the fluences were 5, 15, 50 and 100 times higher compared to recent work on brown diamonds by Hainschwang et al. [23]; however, they were below critical fluence, after which annealing does not restore the diamond structure. It is known [44,45] that diamonds irradiated using fast neutrons with fluence as high as 5 × 1020 cm−2 still preserve their crystal lattice, are highly damaged, and restore the diamond peak in Raman spectrum after annealing.
The irradiated samples were annealed in steps in a vacuum oven with graphite walls to temperatures up to 1680 °C. Then, they were etched in acid mixture H2SO4 + K2Cr2O7 at 180 °C to remove graphitic contamination, which might appear on the external surface of the samples in course of the heat treatment.
After each annealing step, FT-IR spectra were recorded at room temperature with PerkinElmer Spectrum 100 FT-IR spectrometer (Waltham, MA, USA) in the spectral range of 400–7800 cm−1 and with Bruker 70v FT-IR spectrometer (Bruker Optik GmbH, Ettlingen, Germany) in a wider range of 370–25,000 cm−1. Raman and photoluminescence spectra were measured using Horiba Jobin Yvon Lab-RAM HR spectrometer (Lille, France) with excitation wavelength of 473 nm and resolution of 0.5 cm−1. The optical absorption spectra in the visible range were taken using Specord M400 (Carl Zeiss Industrielle Messtechnik GmbH, Jena, Germany) instrument. The samples after irradiation were opaque. The high-temperature annealing changed their color to dark-brown. Concentration of substitutional nitrogen in the samples before neutron irradiation was evaluated from UV-visible absorption spectra according to procedure described elsewhere [46]. The bounded hydrogen (CHx groups) concentration was determined from IR absorption spectra [39]. The properties of four investigated samples are summarized in Table 1. The index of the sample label indicates the value of respective fluence. The specimens D1, D3 and D20 were cut from the same mother wafer, while the specimen D10 was cut from another diamond wafer of a similar quality.

Table 1.
Neutron fluence, thickness and concentrations of substitutional nitrogen Nc and C-H bonds in the samples studied.
3. Results and Discussion
Diamond is transparent from UV to far IR spectral range. The only absorption bands in defect-free diamond are weak bands (absorption coefficient α below 14 cm−1) of two-phonon and three-phonon absorption in the range of 1400 to 4000 cm−1 [16]. The presence of impurities and defects lifts the restriction on one-phonon absorption with a band in the range of 400 to 1350 cm−1. Electron or neutron irradiation results in the formation of single defects or aggregates in the bulk [1,12,13,14,15,16]. Interestingly, the changes in the crystal structure with fluence are not monotonous. Upon low-radiation-induced damage, single vacancies and interstitials form, with the appearance of features, such as GR1, ND1 and 3H [16,40,41,47] in the optical spectra. In contrast, after electron irradiation with energies above 160 keV and fluences above 1.3 × 1020 cm−2, many lines, due to defect complexes, including being bounded to impurities, are observed in the photoluminescence (PL) spectra [48]. The nature of many of those centers is not elucidated [16,49]. For a comparable irradiation time, neutrons can result in a much higher damage level, even in diamond amorphization. The irradiated diamond loses transparency, and the PL yield reduces by orders of magnitude, making the PL and optical absorption spectroscopy in the visible range inefficient. In contrast, in Raman spectroscopy, the signal originates in thin subsurface layers, and their structure can be analyzed even in opaque samples. As we showed previously [6], trends in Raman spectra evolution with neutron fluence change at a threshold fluence of about 1 × 1019 cm−2 when the diamond peak no longer appears as a single distinct line but merges with a broad low-frequency band originating from a phonon confinement effect [50,51,52]. Similar observations were reported for Raman spectra in ion-implanted diamonds with dose increases [5,6,53,54]. Similar trends with neutron fluence could be expected for IR absorption spectra evolution, with specific changes around the critical fluence. Therefore, here, we investigated two specimens n-irradiated at moderate fluences of F = 1 × 1018 and F = 3 × 1018 cm−2 (samples D1 and D3) and two specimens irradiated at high fluences of 1 × 1019 and 2 × 1019 cm−2 (samples D10 and D20.).
3.1. Moderate Fluences (1 × 1018 and 3 × 1018 cm−2)
Figure 1 displays how the optical transmission spectrum evolves with annealing temperature Tan for the samples D1 and D3, which became opaque in the visible range after irradiation but partially transparent in the IR range. Particularly, for the sample D3, the transmission at 10,000 cm−1 (λ = 1000 nm) was 0.015% immediately after irradiation, and it increased to 0.035% after annealing at 200 °C (Figure 1b), corresponding to the absorption coefficients of 200 and 150 cm−1, respectively.
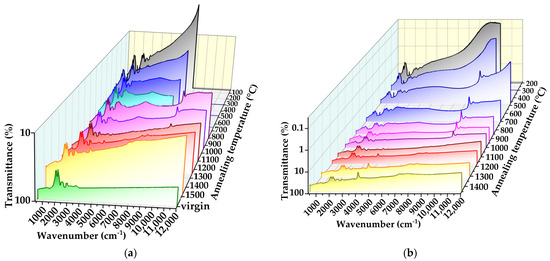
Figure 1.
Transformations of IR transmittance spectra vs. annealing temperature for samples D1 irradiated with neutrons with fluence F = 1 × 1018 cm−2 (a) and D3 with F = 3 × 1018 cm−2 (b).
After low-temperature annealing (Tan < 300 °C), the transmission spectra in the high-frequency range (with respect to the two-phonon band) have a monotonous shape without the appearance of ZPLs, while at low frequencies, they dominate the one-phonon absorption band and narrow local vibrational modes in the range of 1350–2000 °C [16,40]. The transmission for sample D3 after annealing at 300 °C and below remains lower than for sample D1 over the entire spectrum. Further annealing at Tan > 800–900°C results in improving the transmission primarily due to the reduction in the structureless monotonic absorption component. For instance, the transmission for sample D1 at λ > 600 nm (16,000 cm−1) is more than 10% after annealing at Tan ≥ 880 °C (Figure 1a).
Additional absorption bands in the range of 4000–12,000 cm−1 appear after heating to 300 °C and above, with the most prominent ones at 3100, 5900 and 9300 cm−1. The intensities of those three lines significantly reduce after annealing at 900–1000 °C, and simultaneously, a distinct band at 4100 cm−1 and a composite band at 7000–8500 cm−1 appear. For the sample D3, the 4100 cm−1 band magnitude exceeds that for the two-phonon band (Figure 1b). Based on the 4100 cm−1 band position, shape and evolution with annealing, it can be associated with AC defects [23,24,25,26,27,28,29,30,31,32,33,55]. In the virgin unirradiated samples, CHx bands (2800–3000 cm−1) of the bonded hydrogen, presumably located at the grain boundaries, are detected (see bottom spectrum in Figure 1a), as well as a structureless absorption due to the inclusion of amorphous carbon. The absorption coefficient α was calculated ignoring the effect of radiation-induced swelling [56,57,58], and the sample thickness was assumed to be equal to that of the virgin plate. The baseline in the IR absorption spectrum for each sample was determined by consideration of the changes in the spectrum after each run was performed with temperature steps of 50–100 °C.
The evolution of IR absorption spectra for samples D1 and D3 with annealing temperature are shown in Figure 2. The spectra exhibit a large number of lines, with positions shown by vertical lines. For sample D1, the following lines after the annealing are seen: 3100, 4100, 4650, 4925, 5700, 5900, 6420, 7420, 7880, 8495 cm−1 and band 9300 cm−1, while for sample D3, the lines are 3110, 4100, 4650, 5700, 7420, 7880, 8865 and band 9300 cm−1. Several lines in Figure 2 (their positions are marked by blue color) have not been observed in diamond before.
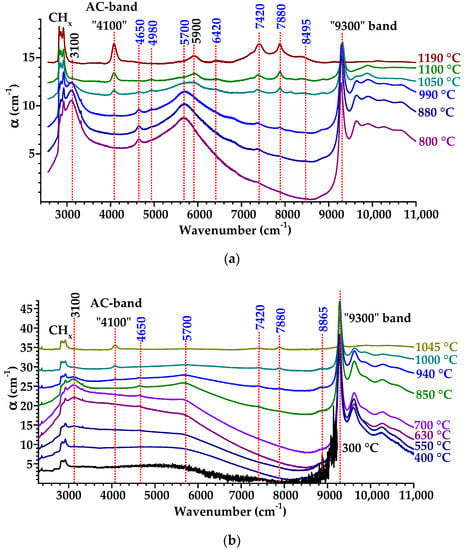
Figure 2.
Transformations of IR spectra of irradiated samples D1 (F = 1×1018 cm−2) (a) and D3 (F = 3 × 1018 cm−2) (b) with annealing temperatures. The intrinsic two- and three-phonon diamond absorption is subtracted. For clarity, the spectra are shifted vertically relative to each other. Positions of peaks in cm−1 are shown above the top spectrum, the black numbers refer to the lines reported in other works, and blue numbers indicate new lines not observed previously.
Intensive broad bands at 3100 cm−1 (0.384 eV) and 5700 cm−1 (0.707 eV) form after 300 °C annealing and strengthen with the temperature increase, reaching a maximum at 650–750 °C and disappearing at around 1050–1100 °C. The width of these two bands noticeably increases with fluence. A broad absorption band with a maximum of about 3100 cm−1 (Figure 2) was previously observed in heavily irradiated and annealed type IaA and type IaB natural diamonds [59], in which the position of the maximum of this band (3094–3110 cm−1) was specimen-dependent. In Ref. [59], the broad band at 3100 cm−1 was reported to appear immediately after irradiation and anneals out at 1000 °C. The 9300 cm−1 band is first detected at 300 °C, increases in intensity to its maximum (35 cm−1 for sample D1) at 550 °C, then decreases starting from about 900 °C, and eventually anneals out at 1150–1200 °C. Trends for other weaker lines can also be seen in Figure 2. The line at 4650 cm−1 (0.576 eV) appears at Tan = 500–550 °C, continues to increase at higher Tan, reaches a maximum at 670–850 °C, and disappears after annealing at 1050–1100 °C. The weak absorption at 8865 cm−1 (1.099 eV) in the spectrum for sample D3 (Figure 2b) appears at 700 °C and anneals out at 1050 °C. In general, the sets of the lines in samples D1 and D3 reveal a similarity; however, the intensities and FWHM of these lines vs. those of Tan may be slightly different.
The changes in the IR absorption spectra after annealing at temperatures above 1000 °C for samples D1 and D3 are shown in Figure 3a,b, respectively. The AC 4100 cm−1 absorption coefficient reaches α = 15 cm−1 for sample D3, which is an order of magnitude higher compared to that for the maximum AC absorption reported for natural diamonds [23,24,25,26,27,28,29,30,31,32,33]. The AC absorption for sample D1 is about three times lower than for D3; this ratio roughly corresponds with the neutron fluence ratio. As the temperature increases, the position of the 4100 cm−1 band for D1 shifts from 4075 cm−1 to 4101 cm−1 after annealing at 1480 °C and further to 4120 cm−1 after heating to 1590 °C. Furthermore, for sample D3, the AC band shifts from 4073 cm−1 to 4100 cm−1 after annealing at 1450 °C.
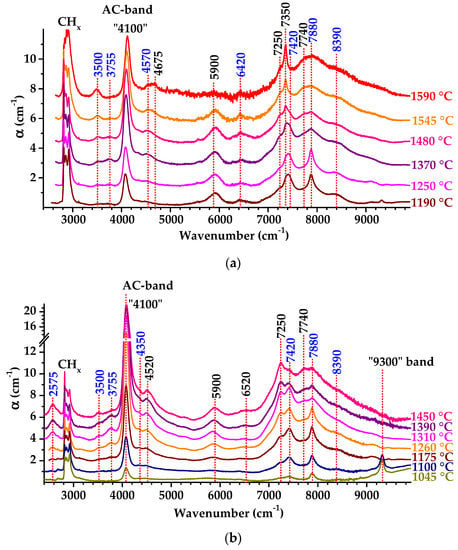
Figure 3.
Transformations of IR spectra of irradiated samples D1 (F = 1 × 1018 cm−2) (a) and D3 (F = 3 × 1018 cm−2) (b) with annealing temperature. The intrinsic two- and three-phonon diamond absorption is subtracted. For clarity, the spectra are shifted vertically relative to each other. Annealing temperatures are color-coded on panels on the right. Positions of peaks in cm−1 are shown above the top spectrum, the black numbers refer to the lines reported in other works, and blue numbers indicate new lines not observed previously.
The 9300 cm−1 band, another strong feature in the spectrum (Figure 3b), also demonstrates the annealing-induced blue shift from 9277 to 9318 cm−1 (Figure 2b). We note that a number of lines, with some of them being rather intensive, are detected in the spectra in the range of 7000 to 9000 cm−1 (as indicated in Figure 3a,b); however, we were not able to reveal meaningful trends in the intensity ratio between them or with respect to the 4100 and 9300 cm−1 bands with the annealing temperature.
3.1.1. 4100 cm−1 Band
The position of the 4100 cm−1 band associated with ACs varies with the annealing temperature as shown in Figure 4. The band maximum shifts to higher frequencies, which is better seen for sample D1 in Figure 4a. This shift seems to be too large (e.g., 26 and 11 cm−1 for samples D1 and D3 treated at 1480 °C and 1450 °C, correspondingly) to be caused by compressive stress, which does not exceed 2 GPa according to the Raman spectra analysis of the diamond peak position for sample D3 (not shown here). Alternatively, we estimated an even lower stress value from the shift of the two-phonon absorption band in the IR spectra of 1.0 and 0.5 cm−1 for D1 after annealing at 1200 and 1500 °C, respectively, which corresponds to the stress of ~1 GPa according to [60].
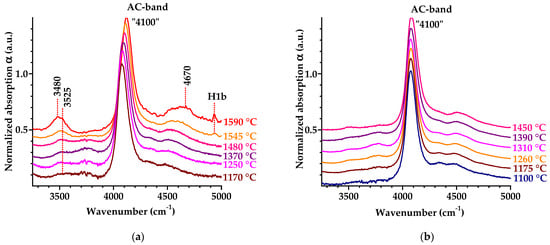
Figure 4.
A detailed view of amber center band in the IR spectra for crystals D1 (a) and D3 (b) at various annealing temperatures. The “4100 cm−1” band magnitude is normalized to unity. For clarity, the spectra are shifted vertically.
We deconvoluted the complex 4100 cm−1 band to components using Lorenzian profiles and derived two main lines peaking at 4065 cm−1 (0.504 eV) and 4112 cm−1 (0.510 eV) with FWHM of 65–70 and 100–110 cm−1, respectively. The high-frequency shift in the 4100 cm−1 band position with Tan occurs due to the relative amplification of the 4112 cm−1 component. These two components are well-known for diamonds with ACs [23,24,25,26,27,28,29,30,31,32,33].
The variations in the 4065 and 4112 cm−1 line positions with Tan for samples D1 and D3 are shown in more detail in Figure 5a. The 4112 cm−1 line enhances monotonically with Tan approaching saturation around 1400 °C. A decrease in the 4065 cm−1 line intensity above 1400 °C is in agreement with the literature data on the high-temperature annealing of natural diamond with ACs [23]. The 4065 cm−1 AC is clearly the least stable of all the ACs, so this line is considered to be a precursor of other ACs [33].
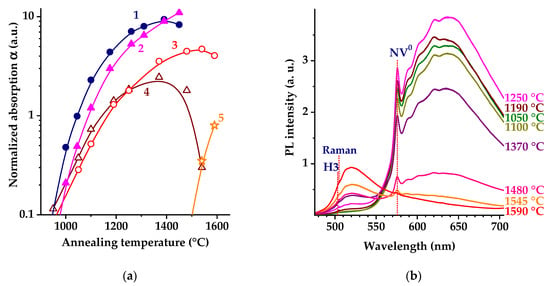
Figure 5.
(a) Evolution of intensities of 4112 cm−1 band (diamond and circles, curves 1 and 3) and 4065 cm−1 band (triangle down and triangle top, curves 2 and 4) with annealing temperature in IR absorption spectra for sample D1 (curves 2 and 4) and sample D3 (curves 1 and 3). Intensity of 4165 cm−1 band for sample D1 (stars, curve 5). (b) Normalized to Raman band PL spectra for sample D1 vs. Tan. The spectra were recorded with excitation at 473. Positions of H3 and NV0 ZPL are shown by vertical dashed lines.
The AC of the 4100 cm−1 band for sample D1 after annealing at 1545 and 1590 °C also contains a third component peaked at 4165 cm−1 (Figure 3a and Figure 4a), as found from the band deconvolution. The component of 4165 cm−1 (0.516 eV) is ascribed [23] to the AC, which includes A-centers in its structure. Synchronously with the 4165 cm−1 line, a band at 4936 cm−1 enhances with Tan (Figure 4a), which has FWHM of ~30 cm−1 and absorption of α ≈ 0.7 cm−1 after annealing at 1590 °C. The 4936 cm−1 (0.612 eV) band is caused by the H1b center, which is characteristic for diamonds with A-centers (two nitrogen atoms in neighboring sites in the diamond lattice) [61]. The H1b center has monoclinic-I symmetry, and it is characterized by a very weak vibronic side-band (S~0.1) [59,61].
The H1b center is believed to be formed by trapping the 2.086 eV (595 nm) center on the A-aggregate of nitrogen [16]. The 2.086 eV (595 nm) center relates to a (nitrogen and vacancy) defect and anneals out at temperatures of 1000 to 1100 °C [62]. According to [23], the H1b defects are standalone defects that consist of multiple vacancies and nitrogen, and they are—in the case of brown diamonds—a side product of the AC transformation of the 4063 cm−1 ACs into 4167 or 4111 cm−1 ACs. Our results (Figure 5a) are consistent with the model proposed in [23]. Note that the formation of H1b centers occurs simultaneously with the aggregation of single nitrogen into A-centers and the formation of H3 centers instead of NV0 centers in the PL spectra (Figure 5b).
The dynamics of the PL spectra of D1 with annealing (Figure 5b) confirm the formation of A-centers: the emission intensity of neutral nitrogen vacancy NV0 with a ZPL at 575 nm decreases, while the intensity of the H3 center (two nitrogen atoms coupled to a vacancy) with a ZPL at 503 nm increases, indicating nitrogen aggregation. In addition to the 4165 and 4941 cm−1 bands, there are other spectral features, such as the 4670 cm−1 (0.579 eV) band appearing at Tan = 1590 °C (Figure 4a); with similar trends with annealing, they appear synchronously with A-center formation. In this spectral range in natural diamond with a deformation-related color, a band at 4673 cm−1 is known, which was associated with ACs at 4165 cm−1 [23]. For sample D1, we observe the appearance and enhancement of the 7350 cm−1 (0.911 eV) band, again synchronously with A-center formation.
3.1.2. 9300 cm−1 Band
The frequency shift of the 9300 cm−1 band with the annealing temperature indicates the composite structure of the band. Figure 6 shows the shape of this band at different Tan (the spectra normalized to unity intensity) for samples D1 and D3. Assuming the 9320 cm−1 (1.155 eV) band is one of the components, as known from the literature [63,64,65], we deconvoluted the 9300 cm−1 band on two lines with Lorenzian profiles and determined the second line with a ZPL at 9320 cm−1. The interplay between the relative intensities of the components results in the observed shift of the integrated 9300 cm−1 band.
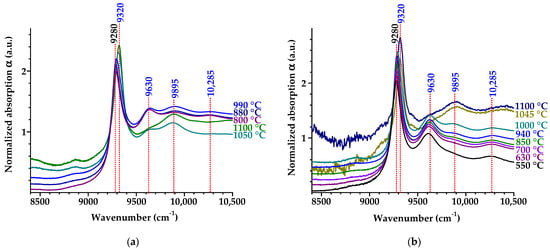
Figure 6.
IR absorption spectra around 9300 cm−1 band for samples D1 (a) and D3 (b) at different annealing temperatures. The band magnitude is normalized to unity. The spectra are shifted vertically for clarity.
The shift of the band maximum from 9280 to 9318 cm−1 (Figure 6b) is accompanied by changes in the high-frequency region, which might be phonon bands of 9280 and 9320 cm−1 ZPLs: 575 cm−1 phonon for the 9280 cm−1 (1.150 eV) band and 350 and 1005 cm−1 phonons for the 9320 cm−1 (1.155 eV) band (phonon frequencies are counted from ZPL positions). The frequencies of 1005 and 575 cm−1 in diamond coincide with LA and TA phonons in point L of the Brillouin zone, respectively [16].
The 9280 cm−1 (1.150 eV) band was observed earlier in the absorption spectra of diamonds irradiated using MeV electrons [63], fast neutrons [64] and helium ion-implanted diamond [65]. It was suggested [16] that this band is caused by multivacancy complexes, possibly including impurity nitrogen atoms [65]. Here, we observed the 9280 cm−1 band appearance after heating to 200 °C, and then it reaches a maximum at about 600 °C and vanishes at Tan > 1000°C. Possibly, the 9280 cm−1 center contains C=C groups, which, according to the Raman spectroscopy, annealed out at similar temperatures [66].
3.1.3. Defect Structure upon Moderate Radiation Damage
The electron irradiation of diamond with energies Eth < E < 2Eth, (Eth—threshold energy of displacement of a carbon atom) creates not more than one Frenkel pair per incident electron [48], where Eth ≈ 160 keV upon irradiation in a nonchanneling direction. This case is the most “clean” radiation damage with a simple defect structure, without amorphization regions or displacement spikes. Nevertheless, the PL spectra of such irradiated crystals reveal numerous optically active centers with narrow ZPLs; most of them still are not identified [67] in spite of the breadth of experience in diamond studies [16,49]. This diversity is considered to be due to the diffusion and reactions of the defects [12], especially in the case of high defect concentrations. Interstitials can be removed by annealing at about 400 °C [53]. It was found [68] that by annealing at 600 °C, single vacancies migrate and form divacancies, which anneal out at 800 °C, producing a series of electron paramagnetic resonance (EPR) active centers. Interstitials and vacancies have a tendency to aggregate into clusters to reduce their free energy. Various types of vacancy chains and clusters with different degrees of stability are produced by irradiation followed by annealing via the removal of atoms from the diamond lattice [69]. Eight EPR defects labelled O1, R5, R6, R7, R8, R9, R10 and R11 were detected after annealing between 700 and 1400 °C [70,71,72]. These centers are attributed to the ⟨110⟩-oriented multivacancy chains. The centers R7, R7a and R8 were tentatively associated with closed structures of eleven, nine and thirteen vacancies, respectively [71]. The concentration of the n-vacancy chains rapidly decreases with n [71]. At 1150 °C, all of these vacancy chains anneal out producing more stable vacancy clusters [71]. Until recent times, it remained unclear what happens to the vacancy clusters upon further temperature elevation. Here, observations of the absorption band around 4100 cm−1 in IR spectra on neutron-irradiated diamond (fluences (1 ÷ 3) × 1018 cm−2) after annealing at Tan > 1000 °C indicate the formation of ACs, namely large spherical aggregates consisting of 40 to 60 vacancies [20,21], either with nitrogen atoms (in presence of ZPLs at 4112 and 4165 cm−1) or without nitrogen atoms involved (ZPL at 4065 cm−1) [23]. An absorption band in the range of 7000–9000 cm−1 (Figure 3) is characteristic for the darkest brown natural diamonds, which have an absorption coefficient up to 0.7 cm−1 [23] (note that sample D3 shows several times higher absorption of that band).
The irradiation of synthetic and natural diamonds leads to the formation of several hundred different optically active defects, including intrinsic and impurity-related, point and extended ones [5,6,16,34,36,39,40,48,54,59,66]. In this regard, it is not surprising that, along with a group of AC bands near 4100 cm−1, other ZPLs are observed in the IR absorption spectra in a higher frequency range. It is important to note that the set of ZPL bands for samples D1 (Figure 2a and Figure 3a) and D3 (Figure 2b and Figure 3b) is approximately the same; however, their ratio and, to a lesser extent, the temperature dependences of the intensity bands differ. Based on the analysis of the IR spectra of natural diamonds, the absorption bands at 5875, 7265 and 9325 cm−1 are thought to be associated with ACs; the latter manifests itself by the 4112 cm−1 band (Table 2 in [23]). In addition, the 5920 cm−1 band was reported in the first publication on ACs [24]. Here, we observe (Figure 2 and Figure 3) the same lines at 5900, 7250 and 9320 cm−1 (0.731, 0.899 and 1.155 eV); however, one of them (9320 cm−1) shows a temperature dependence different from that for multivacancy AC complexes. The 4355 cm−1 band (4350 cm−1 (0.539 eV) in our spectra) was previously observed for annealed natural diamonds, which initially presented ACs; it changed synchronously with the 4065 cm−1 line [33]. However, most of the bands labelled in Figure 2 and Figure 3 have not been reported before [16,49].
A comparison of the temperature and fluence effects on the bands labelled in Figure 2 with the behavior of two major bands associated with ACs (Figure 4a) indicates that the former probably originated from centers different from the 4112 and 4065 cm−1 ones. We suppose that some of the observed bands are caused by other vacancy clusters of their precursors.
The annealing of ACs in natural diamonds requires high-pressure and high-temperature treatment at temperatures typically ranging from 2000 to 2500 °C and pressures between 55 and 85 kbar [23]. The specifics of such high-temperature annealing of brown CVD diamonds in graphite-stable and diamond-stable conditions is discussed in [73]. Accordingly, at least the same conditions are necessary for annealing ACs in diamonds irradiated using fast neutrons.
3.2. High Fluences (1 × 1019 and 2 × 1019 cm−2)
Figure 7 displays the panoramic transmission spectra for samples D10 and D 20 irradiated with high fluences of 1 × 1019 and 2 × 1019 cm−2, respectively. Such treatment is known to result in diamond amorphization [6]. The samples remained partially transparent only in the narrow spectral range of 1400–1700 cm−1 due to the significant enhancement of one-phonon absorption at a 400–1400 cm−1 range. The two-phonon absorption band broadens and practically is not seen at low annealing temperatures. The absorption at higher frequencies does not show the specific narrow lines observed for the low-fluence samples D1 and D3 (Figure 1, Figure 2 and Figure 3). With an increase in annealing temperature, the samples D10 and D20 become transparent in the range up to 10,000–11,000 cm−1, the intensity of the one-phonon absorption band reduces, and the shape of the two-phonon band partially restores (Figure 7).
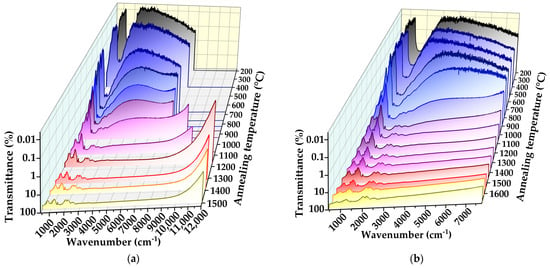
Figure 7.
Transformations of IR transmittance spectra vs. annealing temperature for samples D10 irradiated with neutrons with fluence F = 1 × 1019 cm−2 (a) and D20 with F= 2 × 1019 cm−2 (b).
The transmission spectra for D10 and D30 measured after annealing at not more than 700–800 °C show a clear maximum in the range of 3500–5000 cm−1, which shifts to shorter wavelengths upon further Tan increase (Figure 7). This shape of optical spectra for semiconducting crystals is characteristic of a transition defect (impurity), namely a valence or conductivity band for centers with low activation energy [74]. The formation of conductive layers with activation energy Ea of a few tenths of eV in irradiation-damaged (ion-implanted) diamonds was previously reported [75,76,77,78]. These values for Ea are in agreement with the spectra shape of our samples D10 and D20. The shift of the transmission spectra to longer wavelengths at high fluences corresponds to the formation of the defect (impurity) band within the band gap with an increase in the electrically active defects with low activation energy. This effect is well-known for boron-doped diamond (boron is an acceptor with Ea = 0.37 eV) [79].
Figure 8 shows how the absorption spectra for samples D10 and D20 vary with the annealing temperature. A band is present, which appears and shifts from 5970 to 5800 cm−1 after annealing between 1150 and 1550 °C. In contrast to samples D1 and D3, this band annealed out at 1550 °C. The bands at 7100 cm−1 (0.880 eV) (Figure 8a) and the broad band at 3900 cm−1 (0.483 eV) (Figure 8b) have not been reported before, to the best of our knowledge. We pay attention to the relative low absorption values for the observed bands in spectra for the heavily damaged samples D10 and D20; they are an order of magnitude lower compared to the moderate fluence-irradiated samples D1 and D3 (compared with Figure 2 and Figure 3). We suggest this is due to the amorphization effect in the former case [6], accompanied by a change in vacancy diffusion upon further annealing.
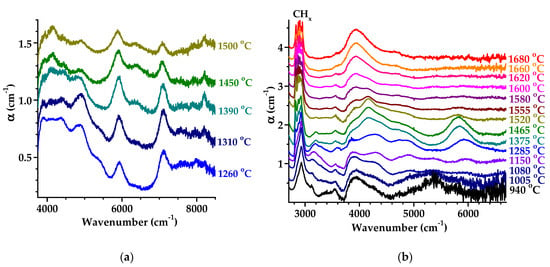
Figure 8.
Transformations of IR absorption spectra with annealing temperature for irradiated samples D10 (F = 1 × 1019 cm−2) (a) and D20 (F = 2 × 1019 cm−2) (b). The intrinsic two- and three-phonon absorption is subtracted. For clarity, the spectra are shifted vertically.
Other features in the IR spectra are related to bonded hydrogen. A transformation of the CHx band with Tan can be seen in Figure 8b. After annealing at temperatures not higher than 1200 °C, this band is structureless, but with a further increase in the annealing temperature, at least 15 relatively narrow bands of a Lorentzian shape in the range of 2800–3050 cm−1 are recorded due to the stretching vibrations of hydrogen chemically associated with various defects of radiation origin [39]. It was shown earlier [39] that neutrons act on grain boundaries in diamond, dislodging hydrogen into the grain bulk for distances of the order of a few micrometers. The changes in valence vibration of CHx groups in as-grown and neutron-irradiated CVD diamond were studied in detail elsewhere [39,80]. Finally, an absorption minimum between 3750 and 4000 cm−1 (Figure 8b) can be related to the effect of radiation damage on three-phonon absorption in diamond.
Figure 9 presents the evolution of absorption spectra with Tan for samples D10 and D20 in a spectral range where AC bands are detected. The weak band at 4160 cm−1 (0.516 eV) is close to the 4165 cm−1 band observed for sample D1 after annealing above 1500 °C (Figure 4a and Figure 5a). This band is usually associated with ACs incorporating two neighboring substitutional nitrogen atoms [23]. Broad low-intensity bands in the spectral range characteristic of ACs [24] with maxima at 3910 cm−1 (0.485 eV) and 4910 cm−1 (0.609 eV), which appear in the IR spectra of samples D10 and D20 in different annealing temperature ranges (Figure 9), were not previously observed in the spectra of diamonds. A further study is required for neutron-irradiated diamonds with highly pure crystals and, for comparison, samples with quantified nitrogen impurity.
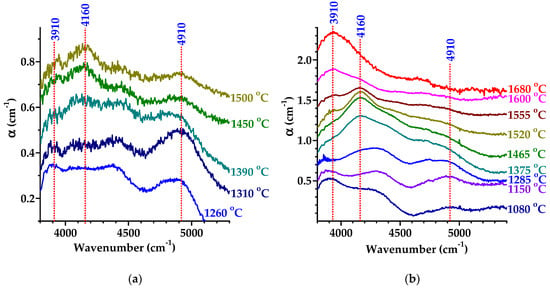
Figure 9.
Absorption spectra of irradiated samples D10 (a) and D20 (b) at different annealing temperatures in the spectral range where ACs are seen. The spectra are shifted vertically for clarity.
4. Conclusions
We used IR absorption spectroscopy to study the formation and modification of defects in CVD diamond irradiated using fast neutrons with moderate to high fluence in the range of 1 × 1018 to 2 × 1019 cm−2 and annealed at temperatures of up to 1680 °C. The advantage of IR spectroscopy in comparison with optical studies in the visible range is the ability to analyze the structures even of visually opaque diamonds strongly damaged by radiation. It is found that after annealing above 1000 °C, so-called amber centers, associated with multivacancy complexes, form, as evidenced by the appearance of absorption bands at 4100 and 5900 cm−1 and a group of lines in the range of 7000 to 9000 cm−1 in the spectra. The measured annealing temperature dependences of the detected bands are similar to those known amber centers in brown natural diamonds with deformation-related color centers, which are considered to consist of spherical vacancy aggregates (40–60 vacancies). Contrary to widespread opinion about ACs as indicators of the natural origin of diamonds to discriminate them from synthetic crystals, we observed in irradiated CVD diamonds ACs with concentration of an order of magnitude higher than that in the darkest brown natural diamond. It should be noted that other absorption bands that are not characteristic of natural diamonds are also present in irradiated CVD diamonds, which makes it possible to differentiate between natural and CVD diamonds.
In addition, after annealing below 1000 °C, a series of absorption bands were detected at 3100, 5700, 9280 and 9320 cm−1; two of them, the 5700 cm−1 and 9320 cm−1 bands, are reported here for irradiated diamond for the first time. From the temperature dependence of the characteristic AC band at 4100 cm−1, it is shown the band is a superposition of, at least, three components at 4065, 4112 and 4165 cm−1. Some new bands, which appeared after the highest temperature annealing above 1500 °C, are ascribed to the aggregation of nitrogen atoms, while several spectral features, which appeared at intermediate annealing (700–1400 °C), are presumably associated with ACs or could be AC precursors. At the highest fluences (~1019 cm−2), all absorption lines in the IR spectra show reduced intensities, broadening and spectral shifts ascribed to a very high defect concentration and partial amorphization, which affect the vacancies’ diffusion and aggregation. Our findings are important for the understanding of defect formation, transformation and healing in diamonds (for example, radiation detectors) subjected to high radiation doses.
Author Contributions
Conceptualization, A.A.K. and V.R.; methodology, A.A.K.; validation, A.V.K.; investigation, A.A.K., V.R., R.K. and M.K.; writing—original draft preparation, A.V.K. and V.R.; writing—review and editing, A.A.K. and R.K.; visualization, A.A.K. and M.K.; project administration, A.A.K. and V.R.; funding acquisition, A.A.K. and V.R. All authors have read and agreed to the published version of the manuscript.
Funding
The reported study was funded by the Russian Science Foundation, grant No. 22-72-10108 “Fundamental studies of structure transformations, optical and magnetic properties of diamond under the influence of fast neutron irradiation, ion implantation and femtosecond laser radiation” (in a part of spectroscopy study) and grant No. 23-42-00120 “Development of radiation-hard detectors based on low-dislocation single crystal chemical vapor deposition diamond with high charge collection efficiency” (in a part of diamond growth and samples preparation).
Data Availability Statement
Additional data are available upon request to the corresponding authors.
Acknowledgments
A.A.K. and M.K. (grant No. 22-72-10108) and V.R. (grant No. 23-42-00120) acknowledge the financial support from the Russian Science Foundation (grant No. 22-72-10108); R.K. and A.V.K. are thankful for the financial support provided within the framework of a state task from the Ministry of Science and Higher Education of the Russian Federation to the Kotelnikov Institute of Radio Engineering and Electronics of Russian Academy of Sciences.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shimaoka, T.; Koizumi, S.; Kaneko, J.H. Recent progress in diamond radiation detectors. Funct. Diam. 2022, 1, 205–220. [Google Scholar] [CrossRef]
- Prins, J.F. Ion implantation of diamond for electronic applications. Semicond. Sci. Technol. 2003, 18, S27–S33. [Google Scholar] [CrossRef]
- Lagomarsino, S.; Flatae, A.M.; Kambalathmana, H.; Sledz, F.; Hunold, L.; Soltani, N.; Reuschel, P.; Sciortino, S.; Gelli, N.; Massi, M.; et al. Creation of silicon-vacancy color centers in diamond by ion implantation. Front. Phys. 2021, 8, 601362. [Google Scholar] [CrossRef]
- Kobayashi, S.; Matsuzaki, Y.; Morishita, H.; Miwa, S.; Suzuki, Y.; Fujiwara, M.; Mizuochi, N. Electrical control for extending the Ramsey spin coherence time of ion-implanted nitrogen-vacancy centers in diamond. Phys. Rev. Appl. 2020, 14, 044033. [Google Scholar] [CrossRef]
- Poklonskaya, O.N.; Vyrko, S.A.; Khomich, A.A.; Averin, A.A.; Khomich, A.V.; Khmelnitsky, R.A.; Poklonski, N.A. Raman scattering in natural diamond crystals implanted with high-energy ions and irradiated with fast neutrons. J. Appl. Spectrosc. 2014, 81, 969–977. [Google Scholar] [CrossRef]
- Khomich, A.A.; Khmelnitsky, R.A.; Khomich, A.V. Probing the nanostructure of neutron-irradiated diamond using Raman spectroscopy. Nanomaterials 2019, 10, 1166. [Google Scholar] [CrossRef]
- Almaviva, S.; Angelone, M.; Marinelli, M.; Milani, E.; Pillon, M.; Prestopino, G.; Tucciarone, A.; Verona, C.; Verona-Rinati, G. Characterization of damage induced by heavy neutron irradiation on multilayered 6LiF-single crystal chemical vapor deposition diamond detectors. J. Appl. Phys. 2009, 106, 073501. [Google Scholar] [CrossRef]
- Angelone, M.; Verona, C. Properties of diamond-based neutron detectors operated in harsh environments. J. Nucl. Eng. 2021, 2, 422–470. [Google Scholar] [CrossRef]
- Passeri, M.; Pompili, F.; Esposito, B.; Pillon, M.; Angelone, M.; Marocco, D.; Pagano, G.; Podda, S.; Riva, M. Assessment of single crystal diamond detector radiation hardness to 14 MeV neutrons. Nucl. Inst. Methods Phys. Res. A 2021, 1010, 165574. [Google Scholar] [CrossRef]
- Liu, L.; Ouyang, X.; Gao, R.; Wan, P.; Ouyang, X. Latest developments in room-temperature semiconductor neutron detectors: Prospects and challenges. Sci. China-Phys. Mech. Astron. 2023, 66, 232001. [Google Scholar] [CrossRef]
- Prins, J.F. On the annihilation of vacancies by diffusing interstitial atoms in diamond. Diam. Relat. Mater. 2000, 9, 1835–1839. [Google Scholar] [CrossRef]
- Steeds, J.W.; Sullivan, W.; Wotherspoon, A.; Hayes, J.M. Long-range migration of intrinsic defects during irradiation or implantation. J. Phys. Condens. Matter. 2009, 21, 364219. [Google Scholar] [CrossRef] [PubMed]
- Newton, M.E.; Campbell, B.A.; Twitchen, D.J.; Baker, J.M.; Anthony, T.R. Recombination-enhanced diffusion of self-interstitial atoms and vacancy-interstitial recombination in diamond. Diam. Relat. Mater. 2002, 11, 618–622. [Google Scholar] [CrossRef]
- Dannefaer, S.; Pu, A.; Avalos, V.; Kerr, D. Annealing of monovacancies in electron and γ-irradiated diamonds. Physica B 2001, 308–310, 569–572. [Google Scholar] [CrossRef]
- Dannefaer, S. Defects in diamond. Phys. Stat. Sol. C 2007, 4, 3605–3613. [Google Scholar] [CrossRef]
- Zaitsev, A.M. Optical Properties of Diamond: A Data Handbook; Springer: Berlin, Germany, 2001. [Google Scholar]
- Hounsome, L.S.; Jones, R.; Martineau, P.M.; Fisher, D.; Shaw, M.J.; Briddon, P.R.; Öberg, S. Origin of brown coloration in diamond. Phys. Rev. B 2006, 73, 125203. [Google Scholar] [CrossRef]
- Bangert, U.; Barnes, R.; Gass, M.H.; Bleloch, A.L.; Godfrey, I.S. Vacancy clusters, dislocations and brown colouration in diamond. J. Phys. Condens. Matter. 2009, 21, 364208. [Google Scholar] [CrossRef]
- Laidlaw, F.H.J.; Diggle, P.L.; Breeze, B.G.; Dale, M.W.; Fisher, D.; Beanland, R. Spatial distribution of defects in a plastically deformed natural brown diamond. Diam. Relat. Mater. 2021, 117, 108465. [Google Scholar] [CrossRef]
- Jones, R. Dislocations, vacancies and the brown colour of CVD and natural diamond. Diam. Relat. Mater. 2009, 18, 820–826. [Google Scholar] [CrossRef]
- Mäki, J.M.; Tuomisto, F.; Kelly, C.J.; Fisher, D.; Martineau, P.M. Properties of optically active vacancy clusters in type IIa diamond. J. Physics: Cond. Matt. 2009, 21, 364216. [Google Scholar] [CrossRef]
- Hainschwang, T.; Notari, F.; Pamies, G. A defect study and classification of brown diamonds with non-deformation-related color. Minerals 2020, 10, 914. [Google Scholar] [CrossRef]
- Hainschwang, T.; Notari, F.; Pamies, G. A defect study and classification of brown diamonds with deformation-related color. Minerals 2020, 10, 903. [Google Scholar] [CrossRef]
- Massi, L.; Fritsch, E.; Collins, A.T.; Hainschwang, T.; Notari, F. The ‘‘amber centres’’ and their relation to the brown colour in diamond. Diam. Relat. Mater. 2005, 14, 1623–1629. [Google Scholar] [CrossRef]
- Reinitz, I.M.; Buerki, P.R.; Shigley, J.E.; McClure, S.F.; Moses, T.M. Identification of HPHT-Treated Yellow to Green Diamonds. Gems Gemol. 2000, 36, 128–137. [Google Scholar] [CrossRef]
- Collins, A.T.; Kanda, H.; Kitawaki, H. Colour changes produced in natural brown diamonds by high pressure, high-temperature treatment. Diam. Relat. Mater. 2000, 9, 113–122. [Google Scholar] [CrossRef]
- Kupriyanov, I.N.; Palyanov, Y.N.; Kalinin, A.A.; Shatsky, V.S. Effect of HPHT Treatment on Spectroscopic Features of Natural Type Ib-IaA Diamonds Containing Y Centers. Crystals 2020, 10, 378. [Google Scholar] [CrossRef]
- Wu, G.-C.; Yu, X.-Y.; Liu, F.; Li, H.-B.; Long, Z.-Y.; Wang, H. Color genesis of brown diamond from the Mengyin Kimberlite, China. Crystals 2022, 12, 449. [Google Scholar] [CrossRef]
- Mashkovtsev, R.I.; Rakhmanova, M.I.; Zedgenizov, D.A. Specific spectroscopic features of yellow cuboid diamonds from placers in the north-eastern Siberian Platform. J. Geosciences 2021, 66, 117–126. [Google Scholar] [CrossRef]
- Hainschwang, T.; Karampelas, S.; Fritsch, E.; Notari, F. Luminescence spectroscopy and microscopy applied to study gem materials: A case study of C centre containing diamonds. Miner. Petrol. 2013, 107, 393–413. [Google Scholar] [CrossRef]
- Zaitsev, A.M.; Wang, W.; Moe, K.S.; Johnson, P. Spectroscopic studies of yellow nitrogen-doped CVD diamonds. Diam. Relat. Mater. 2016, 68, 51–61. [Google Scholar] [CrossRef]
- Shiryaev, A.A.; Titkov, S.V. Spatial distribution of “Amber” defects in diamond: Results of IR mapping. New Data Miner. 2018, 52, 87–90. [Google Scholar]
- Eaton-Magaña, S.C.; Moe, K.S. Temperature effects on radiation stains in natural diamonds. Diam. Relat. Mater. 2016, 64, 130–142. [Google Scholar] [CrossRef]
- Morelli, D.T.; Perry, T.A.; Farmer, J.W. Phonon scattering in lightly neutron-irradiated diamond. Phys. Rev. B 1993, 47, 131. [Google Scholar] [CrossRef] [PubMed]
- Mita, Y.; Yamada, Y.; Nisida, Y.; Okada, M.; Nakashima, T. Infrared absorption studies of neutron-irradiated type Ib diamond. Phys. B 2006, 376–377, 288–291. [Google Scholar] [CrossRef]
- Khomich, A.V.; Khmelnitskii, R.A.; Hu, X.J.; Khomich, A.A.; Popovich, A.F.; Vlasov, I.I.; Dravin, V.A.; Chen, Y.G.; Karkin, A.E.; Ralchenko, V.G. Radiation damage effects on optical, electrical, and thermophysical properties of CVD diamond films. J. Appl. Spectrosc. 2013, 80, 707–714. [Google Scholar] [CrossRef]
- Mita, Y.; Nisida, Y.; Okada, M. Formation of the nitrogen aggregates in annealed diamond by neutron irradiation. AIP Adv. 2018, 8, 025106. [Google Scholar] [CrossRef]
- Dale, M.W. Colour Centres on Demand in Diamond. Ph.D. Thesis, University of Warwick, Warwick, UK, 2015. [Google Scholar]
- Khomich, A.A.; Dzeraviaha, A.N.; Poklonskaya, O.N.; Khomich, A.V.; Khmelnitsky, R.A.; Poklonski, N.A.; Ralchenko, V.G. Effect of neutron irradiation on the hydrogen state in CVD diamond films. J. Phys. Conf. Ser. 2018, 1135, 012019. [Google Scholar] [CrossRef]
- Woods, G.S. Infrared absorption studies of the annealing of irradiated diamonds. Philosoph. Magaz. B 1984, 50, 673–688. [Google Scholar] [CrossRef]
- Collins, A.T.; Dahwich, A. The annealing of interstitial-related optical centres in type Ib diamond. Diam. Relat. Mater. 2004, 13, 1959–1962. [Google Scholar] [CrossRef]
- Bolshakov, A.P.; Ralchenko, V.G.; Yurov, V.Y.; Shu, G.; Bushuev, E.V.; Khomich, A.A.; Ashkinazi, E.E.; Sovyk, D.N.; Antonova, I.A.; Savin, S.S.; et al. Enhanced deposition rate of polycrystalline CVD diamond at high microwave power densities. Diam. Relat. Mater. 2019, 97, 107466. [Google Scholar] [CrossRef]
- Zheng, Y.; Li, C.; Liu, J.; Wei, J.; Zhang, X.; Ye, H.; Ouyang, X. Chemical vapor deposited diamond with versatile grades: From gemstone to quantum electronics. Front. Mater. Sci. 2022, 16, 220590. [Google Scholar] [CrossRef]
- Karkin, A.E.; Voronin, V.I.; Berger, I.F.; Kazantsev, V.A.; Ponosov, Y.S.; Ralchenko, V.G.; Konov, V.I.; Goshchitskii, B.N. Neutron irradiation effects in chemical-vapor-deposited diamond. Phys. Rev. B 2008, 78, 033204. [Google Scholar] [CrossRef]
- Poklonski, N.A.; Khomich, A.A.; Svito, I.A.; Vyrko, S.A.; Poklonskaya, O.N.; Kovalev, A.I.; Kozlova, M.V.; Khmelnitskii, R.A.; Khomich, A.V. Magnetic and optical properties of natural diamonds with subcritical radiation damage induced by fast neutrons. Appl. Sci. 2023, 13, 6221. [Google Scholar] [CrossRef]
- Nistor, S.V.; Stefan, M.; Ralchenko, V.; Khomich, A.; Schoemaker, D. Nitrogen and hydrogen in thick diamond films grown by microwave plasma enhanced chemical vapor deposition at variable H2 flow rates. J. Appl. Phys. 2000, 87, 8741–8746. [Google Scholar] [CrossRef]
- Dobrinets, I.A.; Vins, V.G.; Zaitsev, A.M. HPHT-Treated Diamonds; Springer: Berlin, Germany, 2013. [Google Scholar]
- Steeds, J.W.; Charles, S.; Davis, T.J.; Gilmore, A.; Hayes, J.; Pickard, D.; Butler, J.E. Creation and mobility of self-interstitials in diamond by use of a transmission electron microscope and their subsequent study by photoluminescence microscopy. Diam. Relat. Mater. 1999, 8, 94–100. [Google Scholar] [CrossRef]
- Dischler, B. Handbook of Spectral Lines in Diamond: Volume 1: Tables and Interpretations; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Richter, H.; Wang, Z.P.; Ley, L. The one phonon Raman spectrum in microcrystalline silicon. Sol. Stat. Com. 1981, 39, 625–629. [Google Scholar] [CrossRef]
- Prawer, S.; Nugent, K.W.; Jamieson, D.N.; Orwa, J.O.; Bursill, L.A.; Peng, J.L. The Raman spectrum of nanocrystalline diamond. Chem. Phys. Lett. 2000, 332, 93–97. [Google Scholar] [CrossRef]
- Osswald, S.; Mochalin, V.N.; Havel, M.; Yushin, G.; Gogotsi, Y. Phonon confinement effects in the Raman spectrum of nanodiamond. Phys. Rev. B 2009, 80, 075419. [Google Scholar] [CrossRef]
- Orwa, J.O.; Nugent, K.W.; Jamieson, D.N.; Prawer, S. Raman investigation of damage caused by deep ion implantation in diamond. Phys. Rev. B. 2000, 62, 5461–5472. [Google Scholar] [CrossRef]
- Poklonskaya, O.N.; Khomich, A.A. Raman scattering in a diamond crystal implanted by high-energy nickel ions. J. Appl. Spectrosc. 2013, 80, 715–720. [Google Scholar] [CrossRef]
- Smit, K.V.; D’Haenens-Johansson, U.F.S.; Howell, D.; Loudin, L.C.; Wang, W. Deformation-related spectroscopic features in natural Type Ib-IaA diamonds from Zimmi (West African craton). Mineral. Petrol. 2018, 112, 243–257. [Google Scholar] [CrossRef]
- Khomich, A.V.; Khmelnitskiy, R.A.; Dravin, V.A.; Gippius, A.A.; Zavedeev, E.V.; Vlasov, I.I. Radiation damage in diamonds subjected to helium implantation. Phys. Sol. State 2007, 49, 1661–1665. [Google Scholar] [CrossRef]
- Kalish, R.; Reznik, A.; Nugent, K.W.; Prawer, S. The nature of damage in ion-implanted and annealed diamond. Nucl. Instr. Meth. Phys. Res. B 1999, 148, 626–633. [Google Scholar] [CrossRef]
- Khmelnitsky, R.A.; Dravin, V.A.; Tal, A.A.; Latushko, M.I.; Khomich, A.A.; Khomich, A.V.; Trushin, A.S.; Alekseev, A.A.; Terentiev, S.A. Mechanical stresses and amorphization of ion-implanted diamond. Nucl. Instr. Meth. Phys. Res. B 2013, 304, 5–10. [Google Scholar] [CrossRef]
- Kiflawi, G.D.; Fisher, D.; Kanda, H. New infrared absorption centres in electron irradiated and annealed type Ia diamonds. Diam. Relat. Mater. 1999, 8, 1576–1580. [Google Scholar] [CrossRef]
- Parsons, B.J. Spectroscopic Mode Grüneisen Parameters for Diamond. Proc. R. Soc. Lond. A 1977, 352, 397–417. [Google Scholar]
- Collins, A.T.; Stanley, M. Absorption and luminescence studies of synthetic diamond in which the nitrogen has been aggregated. J. Phys. D Appl. Phys. 1985, 18, 2537. [Google Scholar] [CrossRef]
- Gaillou, E.; Fritsch, E.; Notari, F. Photoinduced H1b and H1c centers in some natural treated diamonds. Diam. Relat. Mater. 2008, 17, 2029–2036. [Google Scholar] [CrossRef]
- Lomer, J.N.; Wild, A.M.A. Electron spin resonance in electron irradiated diamond annealed to high temperatures. Radiat. Eff. 1973, 17, 37–44. [Google Scholar] [CrossRef]
- Zhu, W.; Song, Z.; Lu, T.; Li, H. Pale yellow type IIa diamond coloured by H4 centres. J. Gemmol. 2020, 37, 350–352. [Google Scholar] [CrossRef]
- Nasdala, L.; Grambole, D.; Wildner, M.; Gigler, A.M.; Hainschwang, T.; Zaitsev, A.M.; Harris, J.W.; Milledge, J.; Schulze, D.J.; Hofmeister, W.; et al. Radio-colouration of diamond: A spectroscopic study. Contrib. Mineral. Petrol. 2013, 165, 843–861. [Google Scholar] [CrossRef]
- Khomich, A.A.; Averin, A.A.; Poklonskaya, O.N.; Bokova-Sirosh, S.N.; Dzeraviaha, A.N.; Khmelnitsky, R.A.; Vlasov, I.I.; Shenderova, O.; Poklonski, N.A.; Khomich, A.V. Features of the 1640 cm−1 band in the Raman spectra of radiation-damaged and nano-sized diamonds. J. Phys. Conf. Ser. 2019, 1400, 044017. [Google Scholar] [CrossRef]
- Steeds, J.W.; Kohn, S. Annealing of electron radiation damage in a wide range of Ib and IIa diamond samples. Diam. Relat. Mater. 2014, 50, 110–122. [Google Scholar] [CrossRef]
- Twitchen, D.J.; Newton, M.E.; Baker, J.M.; Anthony, T.R.; Banholzer, W.F. Electron-paramagnetic-resonance measurements on the divacancy defect center R 4/W 6 in diamond. Phys. Rev. B 1999, 59, 12900. [Google Scholar] [CrossRef]
- Hounsome, L.S.; Jones, R.; Martineau, P.M.; Shaw, M.J.; Briddon, P.R.; Öberg, S.; Blumenau, A.T.; Fujita, N. Optical properties of vacancy related defects in diamond. Phys. Status Solidi A 2005, 202, 2182–2187. [Google Scholar] [CrossRef]
- Iakoubovskii, K.; Stesmans, A. Dominant paramagnetic centers in 17 O-implanted diamond. Phys. Rev. B 2002, 66, 045406. [Google Scholar] [CrossRef]
- Iakoubovskii, K.; Stesmans, A. Vacancy clusters in diamond studied by electron spin resonance. Phys. Status Solidi A 2004, 201, 2509–2515. [Google Scholar] [CrossRef]
- Baker, J.M. Deducing atomic models for point defects in diamond: The relevance of their mechanism of formation. Diam. Relat. Mater. 2007, 16, 216–219. [Google Scholar] [CrossRef]
- Vins, V.; Yelisseyev, A.; Terentyev, S.; Nosukhin, S. Specifics of high-temperature annealing of brown CVD single crystal diamonds at graphite-stable and diamond-stable conditions. Diam. Relat. Mater. 2021, 118, 108511. [Google Scholar] [CrossRef]
- Dresselhaus, G.; Dresselhaus, M.S. The Optical Properties of Solids; Tauc, J., Ed.; Academic Press, Inc.: New York, NY, USA, 1966; p. 198. [Google Scholar]
- Kalish, R.; Reznik, A.; Prawer, S.; Saada, D.; Adler, J. Ion-implantation-induced defects in diamond and their annealing: Experiment and simulation. Phys. Status Solidi A 1999, 174, 83–99. [Google Scholar] [CrossRef]
- Prins, J.F. Electrical conduction in diamond after vacancy generation by means of carbon-ion implantation. Appl. Phys. Lett. 2000, 76, 2095–2097. [Google Scholar] [CrossRef]
- Trajkov, E.; Prawer, S. Conduction mechanisms in ion-implanted and annealed polycrystalline CVD diamond. Diam. Relat. Mater. 2006, 15, 1714–1719. [Google Scholar] [CrossRef]
- Xu, H.; Ye, H.; Coathup, D.; Mitrovic, I.Z.; Weerakkody, A.D.; Hu, X. An insight of p-type to n-type conductivity conversion in oxygen ion-implanted ultrananocrystalline diamond films by impedance spectroscopy. Appl. Phys. Lett. 2017, 110, 033102. [Google Scholar] [CrossRef]
- Thonke, K. The boron acceptor in diamond. Semicond. Sci. Technol. 2003, 18, S20. [Google Scholar] [CrossRef]
- Khomich, A.; Ralchenko, V.; Nistor, L.; Vlasov, I.; Khmelnitskiy, R. Optical properties and defect structure of CVD diamond films annealed at 900–1600 °C. Phys. Status Solidi A 2000, 181, 37–44. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).