Abstract
In theoretical studies of chemical reactions the reaction thermochemistry is usually reported for the stoichiometric reaction at standard conditions (ΔG°, ΔH°, ΔS°). We describe the computation of the equilibrium concentrations of the CO2-adducts for the general capture reaction CO2 + Capture System ⇆ CO2-adduct (GCR) and the rubisco-type capture reaction CO2 + Capture System ⇆ CO2-adduct + H2O (RCR) with consideration of the reaction CO2(g) ⇆ CO2(aq) via Henry’s law. The resulting equations are evaluated and graphically illustrated as a function of atmospheric CO2 concentration and as a function of temperature. The equations were applied to the thermochemistry of small molecule rubisco-model reactions and series of additional model reactions to illustrate the range of the Gibbs free enthalpy for the effective reversible capture and of the reaction entropy for economic CO2 release at elevated temperature. A favorable capture of free enthalpy is of course a design necessity, but not all exergonic reactions are suitable CO2 capture systems. Successful CO2 capture systems must allow for effective release as well, and this feature is controlled by the reaction entropy. The principle of using a two-pronged capture system to ensure a large negative capture entropy is explained and highlighted in the graphical abstract. It is hoped that the presentation of the numerical examples provides useful guidelines for the design of more efficient capture systems.
1. Introduction
Continuous atmospheric CO2 tracking started more than 50 years ago with CO2 measurement at Mauna Loa and resulted in the “Keeling Curve,” the iconic demonstration of the seasonal variations of CO2 concentrations and the steady rise of the annual average CO2 concentration [1,2]. NOAA’s (National Oceanic and Atmospheric Administration) CarbonTracker [3] employs a global network of CO2 mole fraction observations to study the CO2 exchange between the biosphere and the atmosphere as a function of time [4,5]. Comprehensive carbon inventories have been under development by the US Carbon Cycle Science Program [6] and include space-based CO2 observation (i.e., Orbiting Carbon Observatory, OCO-2 [7]). While considerable uncertainties remain with regard to accounting for all CO2, all reports consistently show that the global atmospheric CO2 concentrations have been growing steadily, and at Mauna Loa the average annual mean increased from 316.0 ppm in 1959 to its value of 404.83 ppm at the time of this writing [2]. The Intergovernmental Panel on Climate Change (IPCC [8]) reported in its fifth assessment report in 2014 (AR5 [9]) an average rate of increase in CO2 of 1.4 ppm/year. Data by the Energy Information Agency (EIA, [10]) show worldwide CO2 emissions from the consumption of coal were 13.8 billion metric tons in 2012, up from 8.0 billion metric tons two decades earlier, and there is no reason to expect this trend to stop any time soon. The need to communicate climate science and the urgency of addressing the CO2 problem have been recognized [11,12,13,14,15] but such efforts continue to meet with enormous obstacles [16].
CO2 scrubbing involves the capture of CO2 by a capture system (general capture reaction, GCR), the release of CO2 from the substrate and its collection, and the long-term CO2 sequestration [17]. CO2 capture from air has been demonstrated [18], it is the pertinent tool to address CO2 emissions from distributed sources [19,20,21], and CO2 capture from the air is the method of last resort to combat excessive atmospheric CO2 concentrations [22,23,24]. CO2 scrubbing relies on chemical systems for reversible CO2 capture [25,26] and usually involves carbamic acid formation (i.e., CO2 reaction with amines [27,28,29], polyamine-based solid adsorbents [30,31], alkylamine-appended metalorganic framework [32,33,34], or diamine-appended metal-organic frameworks [35], and alternative systems [36]). Biomimetic CO2 capture systems are of interest because they hold the promise to meet both the thermodynamic and the kinetic requirements for reversible CO2 capture.
CO2 + Capture System ⇆ CO2-adduct
CO2 + Carbonyl·H2N—(peptide)—MgL2·OH2 ⇆ CO2-adduct + H2O
CO2 + Capture System ⇆ CO2-adduct + H2O
We have been interested in the development of rubisco-based biomimetic systems for reversible CO2 capture from air. Our design of the chemical CO2 capture and release systems is informed by the understanding of the binding of the activator CO2 (ACO2) in rubisco (Figure 1) and the general strategy has been described [37,38]. Rubisco (ribulose 1,5-bisphosphate carboxylase/oxygenase, RuBisCO) catalyzes the addition of CO2 and water to RuBP (d-ribulose 1,5-bisphosphate) in the photosynthetic carbon assimilation via the Calvin-Bassham-Benson cycle, and results in two molecules of 3-PGA (3-phospho-d-glycerate) and 0.5 O2 [39,40]. Nearly all carbohydrate production in the biosphere depends on rubisco catalysis and rubisco is the most abundant protein on Earth. Form I rubisco contains eight large (L) and eight small (S) subunits, and the crystal structure of Spinacia oleracea [41,42] provided an early example of a hexa-decameric rubisco [43]. Form II rubisco lacks small subunits, generally occurs as L2, and is exemplified by the bacterial rubisco of Rhodospirillum rubrum [44]. The mechanism of rubisco catalysis has been studied in detail [45,46] and these studies have established that rubisco must be activated by carbamylation of active-site lysine (Lys) with an activator CO2 (ACO2). The carbamate formed is stabilized both by complexation to Mg2+ and by NH···OC hydrogen-bonding (Figure 1) and, importantly, the rubisco ACO2 capture (RCR) occurs with the release of a water molecule from the capture system.
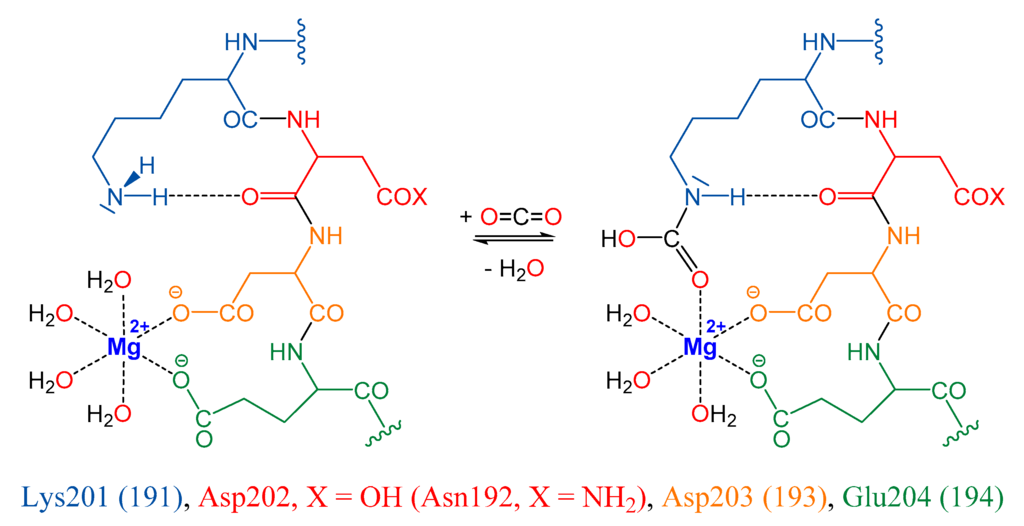
Figure 1.
CO2 capture in the active site of rubisco.
In theoretical studies of reaction thermochemistry one usually computes the reaction enthalpy ΔH° and the reaction entropy ΔS° for the stoichiometric reaction at standard conditions (1 atm, 25 °C) and determines the reaction Gibbs free enthalpy via ΔG° = ΔH° − T°·ΔS°. This knowledge then allows for the computation of equilibrium concentrations, although this step is not usually applied in theoretical studies. For reactions with a severely limited reagent, one needs to consider the consequences of the non-stoichiometry on product formation. With an atmospheric CO2 concentration of about 400 ppm, questions about the equilibrium concentration of CO2 capture reactions have been asked frequently and they are entirely warranted. Hence, in this paper, we describe the determination of CO2 capture equilibria as a function of CO2 concentration. In addition, we describe temperature dependence of the CO2 capture equilibria with a focus on the importance of the reaction entropy for effective CO2 release at elevated temperature.
2. Results and Discussion
2.1. Capture Reaction Systems Studied
We analyzed the thermochemistry of a rubisco-based small molecule model of the formation of N-methylcarbamic acid (NMCA) by addition of methylamine (CH3NH2) to CO2, considering substrate and product stabilization by an active-side carbonyl model and complexation by a model metal complex ML2 [37]. The model system is described by 14 reactions and the thermochemistry was determined at the B3LYP/6-31G* level for the natural case of magnesium M2+ = Mg2+. Reaction R1 is the formation of NMCA (H3C−NH−CO−OH) by addition of methylamine to CO2 in the gas phase. Three effects of the environment need to be considered in the active site of rubisco (Figure 1) and these are (A) the stabilization of the product by hydrogen-bonding between NMCA and a model carbonyl compound; (B) the complexation of NMCA by a model metal complex ML2; and (C) the forced replacement of ligand water by CO2 at the metal center.
Importantly, the complexation of CO2 to the metal cation M2+ requires the replacement of a water molecule, and our analysis showed that this H2O/CO2 replacement is an essential feature of rubisco thermochemistry. The exchange of a ligand water molecule by a CO2 molecule (reaction R10) is highly endergonic and this H2O/CO2 replacement penalty is required to lower the overall exergonicity of the CO2 capture reaction and to allow overall reversibility. Reaction R14 models the capture of CO2 and the addition of the Mg2+-complexed CO2 to a pre-positioned, carbonyl-aggregated methylamine CH3NH2·(A/K) to form the Mg2+-complexed and carbonyl-aggregated NMCA, (A/K)·NMCA·ML2.
CO2+ CH3NH2 ⇆ NMCA
H2O·MgL2+ CO2+ CH3NH2·FA ⇆ 17a + H2O
H2O·MgL2+ CO2+ CH3NH2·Ac ⇆ 21a + H2O
CO2(g) ⇆ CO2(aq)
We evaluated the RCR-reaction R14 with the model carbonyl formaldehyde (FA, R14a) and acetone (Ac, R14b), respectively. Molecular models of the CO2-adducts 17a (R14a) and 21a (R14b) are shown in Figure 2, and the associated thermochemical parameters are listed in Table 1.
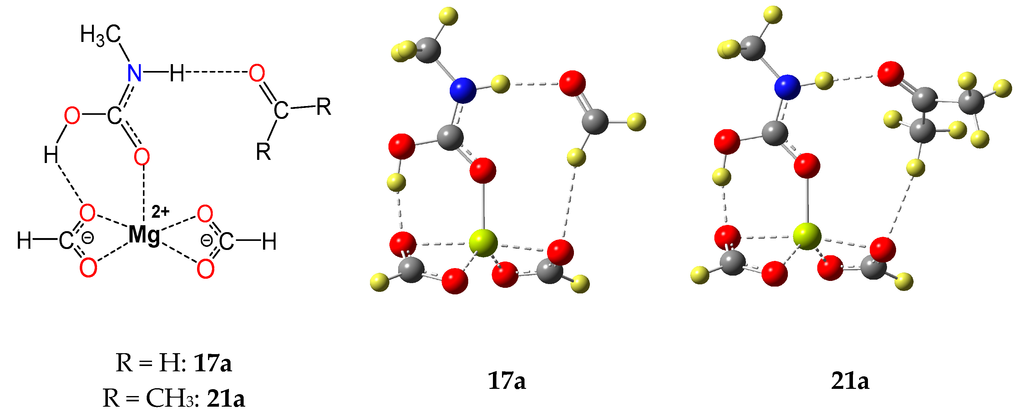
Figure 2.
Molecular model of aggregates 17a and 21a formed between the magnesium formate MgL2 complexed trans-trans isomer of N-methylcarbamic acid and model carbonyl formaldehyde (FA) or acetone (Ac), respectively. (Ball and Bond Type models are shown and color indicates elements: oxygen: red; nitrogen: blue; carbon: grey; hydrogen: yellow; magnesium: lime).

Table 1.
Thermochemical data for capture systems. 1
2.2. Equilibrium Concentrations with Non-Stoichiometric Conditions
The calculation of thermodynamic data for a given reaction with ab initio methods uses stoichiometric concentrations of the reagents. In the case of passive carbon capture, such an assumption does not accurately depict the relative concentrations of the reagents. Passive capture systems must operate at low pressures of CO2, including the current atmospheric concentration (~400 ppm) [47].
Also, Henry’s Law must be considered for aqueous carbon capture systems, because only dissolved CO2 is available for binding. Henry’s Law describes the proportion of gaseous CO2 that enters the aqueous phase at equilibrium, illustrated in reaction (R15) and described by Equation (1). KH(T) is constant for a given gas and a given temperature; for CO2 at room temperature this value has been experimentally determined to be KH(298.15) = = 0.034 [48]. Using Henry’s Law and the atmospheric pressure of CO2, it is then simple to determine an approximate concentration of CO2 in the aqueous phase of a passive capture system.
In this work, we primarily focus on the simple capture reactions (R1) and the rubisco capture reactions (R14). The product formation can be calculated using the equations for the equilibrium constants Keq for reactions (GCR) and (RCR), respectively. Defining the concentration of the capture system at equilibrium [CS] = [CS]0 − [CO2-CS], where [CO2-CS] is the concentration of the CO2-adduct formed and [CS]0 is the initial concentration of the capture system, we obtain equations (2-GCR) and (2-RCR).
The isotherms in Figure 3 show the concentration of the CO2-adduct formed [CO2-CS] as a function of the CO2 pressure. This relationship produces isothermal curves with their asymptotic boundaries determined by the initial concentration of the capture system.
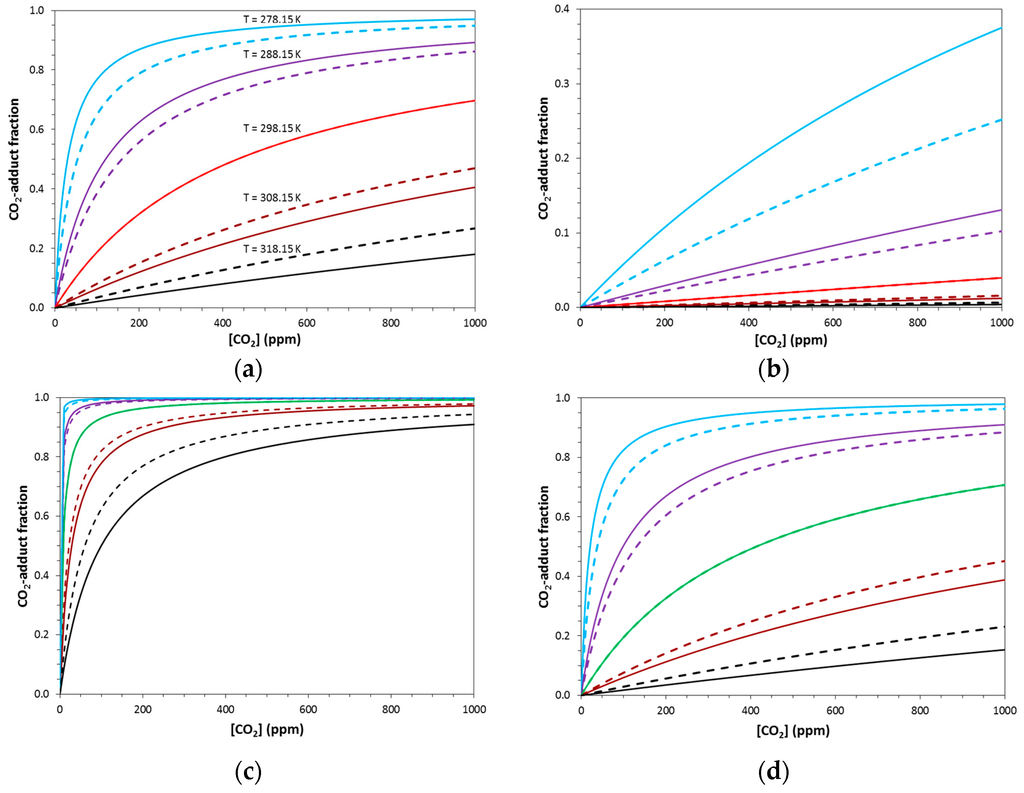
Figure 3.
Equilibrium concentrations of complexed product of a general capture reaction (GCR) (left) and a rubisco-type capture reaction (RCR) (right) at five temperatures from 278.15 to 318.15 K. The color of the central curve (298.15 K) corresponds to the same system in Figure 3 and Figure 4. Panels (a) and (b) describe the thermochemistry of R14a with ΔG° = −6.59 kcal/mol, ΔH° = −17.26 kcal/mol, and ΔS° = −35.81 cal/(mol·K). Panels (c) and (d) describe the thermochemistry of R14h with ΔG° = −9.00 kcal/mol, ΔH° = −19.67 kcal/mol, and ΔS° = −35.79 cal/(mol·K). Solid lines were computed with T-dependence of Henry’s Law and dashed lines were computed without.
The fraction of CO2-adduct differs greatly in magnitude depending on the application of the GCR or RCR equations. The same thermochemical parameters afford much higher fractions computed with the GCR equation than with the correct RCR equation (Figure 3). The fractions computed with the RCR equations for reactions R14a (red) and R14b (blue) at [CO2] = 400 ppm are listed in Table 1, and the respective values of 0.016 and 0.003 are very small. Obviously, our simplified theoretical model produces ΔG° values that are not exergonic enough. Hence, we also studied the hypothetical reaction R14h with ΔG° = −9 kcal/mol. For this model system, we set ΔS° (R14h) = ΔS° (R14a) and obtain ΔH° (R14h) = −19.67 kcal/mol. With R14h, we achieve a much more effective capture at room temperature (Figure 3d, green curve) and a very reasonable capture fraction of 0.492 (Table 1) at [CO2] = 400 ppm.
Temperature affects the curvature of the fraction (CO2-adduct) = f([CO2]) isotherms in Figure 3 and we will discuss the T-dependence in more detail below (see Section 2.3). Instead of the fraction (CO2-adduct), Figure 4 and Figure 5 show the ratios [CO2-CS]/[CS] as a function of [CO2]. The ratios were computed with equations 3-GCR and 3-RCR, where R is the gas constant (1.9858775 cal·mol−1·K−1), ΔG is the Gibbs Free Enthalpy of the capture reaction at T, and ΔG = ΔG° for the special case of T = T°. This ratio shows a linear dependence on the CO2 pressure, and temperature affects the slope (but not the curvature).

Figure 4.
Carbon capture at 298.15 K for two carbon capture systems at near atmospheric concentrations. Gibbs free enthalpies of ΔG° = −5.54 kcal/mol (R14b, blue), ΔG° = −6.59 kcal/mol (R14a, red), and ΔG° = −9.00 kcal/mol (R14h, green). Plots for GCR are shown in (a) and plots for the RCR are shown in (b). To achieve a significant capture ratio in the RCR system requires a significantly more exergonic capture reaction; i.e., green in (b). The secondary axis in (b) allows for the recognition of the much diminished capture ratios for the less exergonic reactions (blue and red). The linear functions are as follows: (a) Blue; y = 3.91 × 10−4x, Red; y = 2.30·× 10−3x; (b) Blue; y = 7.05 × 10−6x, Red; y = 4.15 × 10−5x, Green; y = 2.42 × 10−3x.
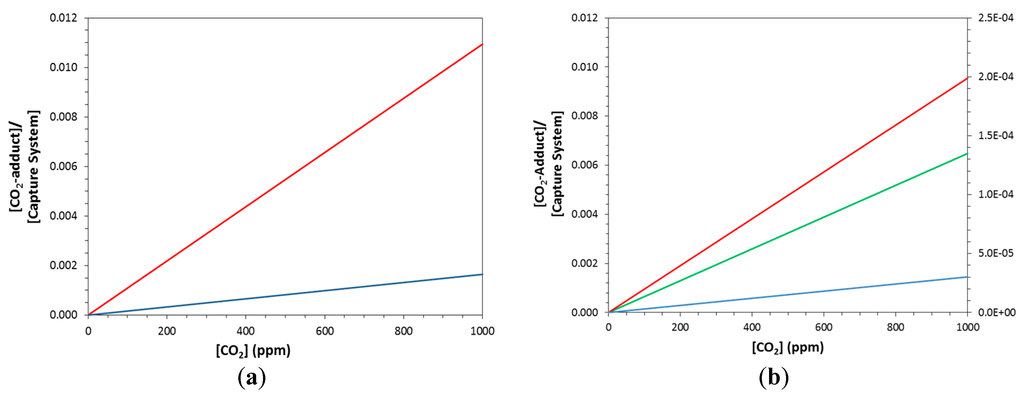
Figure 5.
Carbon release at 348.15 K (= T° + 50) for two carbon capture systems at near atmospheric concentrations. Color indicates reaction thermochemical parameters; blue curves (R14b), red curves (R14a), and green curves (R14h). The linear functions are as follows: (a) GCR: y = 1.66 × 10−6x (blue); 1.10 × 10−5x (red). (b) RCR: y = 3.02 × 10−8x (blue); 1.99 × 10−7x (red); 6.48 × 10−6x (green).
The Gibbs free enthalpy of the capture reaction obviously will vary with temperature because of the entropy term, ΔG = ΔH − T·ΔS. The reaction enthalpy ΔH(T) and reaction entropy ΔS(T) depend on temperature only modestly and, for the temperature variations considered here, they can be approximated very well by ΔH(T) = ΔH° and ΔS(T) = ΔS°. However, in our aqueous system temperature also significantly affects Henry’s constant. This variation is described by the van’t Hoff equation (Equation (4)), where the change in enthalpy of dissolution is a constant for a given gas. For CO2 the value is –ΔsolH/R = 2400 K. With this value, Equation (5) can be used to determine the value of the Henry’s constant at temperature T for CO2.
For –ΔsolH/R > 0, it is clear that CO2 will be better solvated at low temperatures and less solvated at temperatures higher than 298.15 K. This drives capture to be more effective at lower temperatures and release to be more effective at higher temperatures. The consequences of the T-dependence of Henry’s constant are illustrated for specific cases in Figure 3, where solid lines were computed with T-dependence of Henry’s Law and dashed lines without. In every panel, the dashed curves always are closer to the T°-curve than the solid curves, that is, the load difference will always be increased by the T-dependence of Henry’s constant.
2.3. Temperature Dependence of Capture Systems: Loading and Unloading
This illustration in Figure 6 is a rough schematic to consider the scale of the CO2 capture in a gedankenexperiment (German: thought experiment). This apparatus is comprised of several square trays containing thin layers of aqueous capture solution. In order to capture large amounts of CO2, the most important aspect is the volume of the capture system solution (CSS). To illustrate that a large volume is desired as well as a large surface area, a rack of shallow baths of solution was chosen to balance these two goals in a simple way. These thin layers are an attempt to acknowledge that the diffusion is a relevant and an important factor, but the schematic system is not optimized for diffusion because the main purpose of the gedankenexperiment is the thermodynamic analysis of slow processes. Because capture from ambient air occurs at very high dilutions of CO2, it will not be a fast capture regardless. Of course, for fast capture at concentrated sources, the amount of CO2 captured is controlled by kinetics and sophisticated chemical engineering solutions have been described that include more complicated gas/liquid contactor systems [49,50,51,52] and counter-current flow systems [53]. These systems vastly increase surface area-to-volume ratios and provide for surface renewal opportunities and facile gas diffusion. However, for passive capture from air the simplified apparatus of Figure 6 suffices to obtain a rough estimate of the amount of CO2 that would be collected per load cycle.
Load = FW(CO2) × [CO2-CS]400 × VCSS
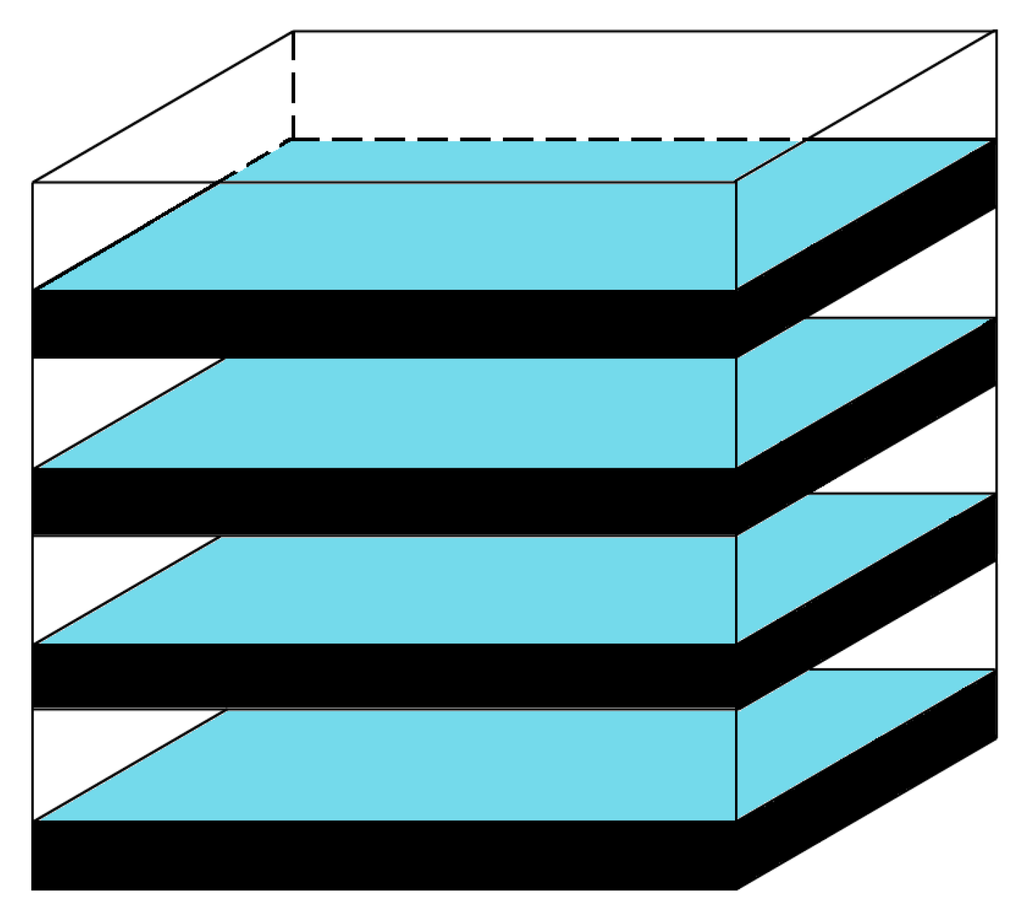
Figure 6.
Schematic diagram of the carbon capture apparatus.
The load is determined by the volume of the capture system solution, the initial concentration of the amine capture system, and the temperature of the aqueous capture system. The Load can be calculated simply using Equation (6), where Load is the mass of captured CO2 in g, FW(CO2) is the formula weight for CO2, 44.01 g/mol, [CO2-CS]400 is the equilibrium concentration of product (mol/L) when the partial pressure of CO2 is 400 ppm, and VCSS is the volume of the capture system solution (L). For an ideal capture system, the load should be highly dependent on the temperature so that T-variation may afford release under economic conditions. The fraction captured per cycle can be determined by comparison of the load data at capture and release temperatures (Table 1).
For a numerical illustration, we consider the trays of the apparatus to have a surface areas of 1 m2 and to hold a solution with a depth of 2.5 cm. For a standard system of 10 layers of these trays, this example results in a total solution volume of 250 L. Assuming an initial concentration of the capture system solution [CS]0 = 0.1 M, the load is calculated using Equation (6). To find the concentration of the product, the initial concentration of the capture system solution is multiplied by the fraction of CO2-adduct reported in Table 1. The amount of CO2 collected in one capture cycle, the cycle load, equals the difference of the loads at the capture and release temperatures. With apparatus parameters being equal, the cycle load parallels the difference in the CO2-adduct fractions at capture and release temperatures (cycle load fraction). In the case of capture system R14h, the free enthalpy is low enough to ensure binding at T° and the data in Table 1 show the fractions of CO2-adduct to be 0.492 (T°), 0.068 (T° + 20), and 0.007 (T° + 40). The fractions show that most CO2 will be released when the temperature is raised by 20°, and that nearly all of the CO2 will be released when the temperature is raised by 40°. The amount of CO2 collected per cycle for a capture temperature of T° and release temperatures of T° + 20 and T° + 40 are 0.47 kg and 0.53 kg, respectively.
2.4. Variations of Thermodynamic Parameters—Guidelines for Capture System Design
We modeled three sets of hypothetical reactions HR1−HR3 to explore the effectiveness of capture and release in dependence of the Gibbs free enthalpy and the capture reaction entropy (Table 1). The sets differ in the Gibbs free enthalpy with ΔG° = −6.59 kcal/mol for HR1 (as for R14a), ΔG° = −9 kcal/mol for HR2, and ΔG° = −11 kcal/mol for HR3. Within each set, we vary ΔH° in steps of 5 kcal/mol. For HR1 and HR2, we use ΔH° values of −15, −20, and −25 kcal/mol, respectively, and the ΔS° values follow. The systems HR3 were constructed to share the ΔS° values with HR2 and the ΔH° values follow. With these parameters, we used equation 2-RCR to compute the fractions of CO2-adduct at [CO2] = 400 ppm and T°, T° + 20, and T° + 40, and the results are listed in Table 1.
Reaction HR1 is not sufficiently exergonic to produce adequate capture and Table 1 shows that all fractions are relatively low. Reactions HR2 and HR3, with their higher binding free enthalpies, demonstrate adequate capture, and these systems are illustrated in Figure 7.
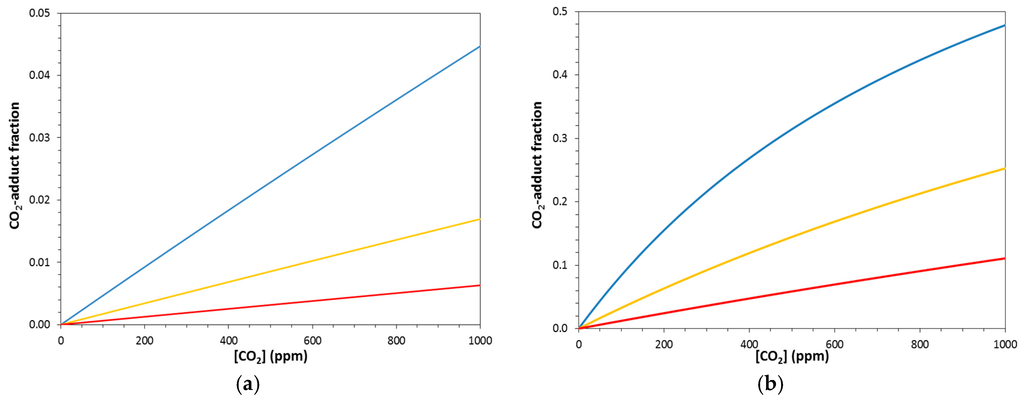
Figure 7.
Fraction of CO2-adduct remaining in capture solution at equilibrium at 338.15 K (= T° + 40) for the RCR-type reactions (a) HR2 with ΔG° = −9 kcal/mol and (b) HR3 with ΔG° = −11 kcal/mol. Reactions HR2 and HR3 are shown with entropies ΔS° of −20.12 (blue), −36.89 (yellow), and −53.66 cal/(mol·K) (red).
Figure 7 shows the fractions of CO2-adduct remaining bound at T° + 40 for the series of reactions HR2 and HR3, and this figure reveals the important role of entropy in the release process. As the reaction becomes more exentropic, the cycle yield improves in all cases, but the capture effectiveness is more complicated. For the most exentropic reaction of the HR2 series (HR2c), the fraction of CO2-adduct remaining at T° + 40 is 0.003 and the unloading is highly effective. Even for the system HR2a, with its exentropicity mirroring that of the GCR R1, the unloading remains efficient: the fraction remaining is only 0.018 and the cycle load difference relative to HR2c is small (3.3%). Comparison of the HR2 series (Figure 7a) shows that at atmospheric pressure, the difference in capture due to entropy is functionally low.
In the more exergonic series of hypothetical reactions (HR3), the cycle load efficiency increases as with HR2 as the system becomes more exentropic. However, with the more exergonic reaction HR3, the effect of entropy is drastically enhanced. Reaction HR3a is shown to have a fraction of CO2-adduct of 0.269 at T° + 40 compared to HR3b with a fraction of 0.119 remaining. This corresponds to a 21.5% increase in cycle load for the more exentropic reaction. Further, the fraction of CO2-adduct remaining for HR3c at the same temperature is 0.050. This is an 8.1% increase over HR3b and a 31.4% increase over HR3a. As illustrated by the increase in cycle load percentage across each series, the entropy effects for the more exergonic HR3 system are enhanced by a factor of nearly 10 over HR2.
After studying these hypothetical systems, it becomes pertinent to determine which would provide the best capture and the capture temperature plays an important role. We have already shown that ΔG° = −6.59 kcal/mol (R14a, HR1) is highly ineffective at T° and above, but as Figure 3b shows, at T° − 20 (278.15 K) the system will have a CO2-adduct fraction near 0.2. If we were to capture at T° − 20 and release at T°, the system will yield a relatively small but efficient cycle load. Even more useful at low temperatures would be a reaction with ΔG° = −9 kcal/mol (R14h, HR2). The most important feature of this hypothetical reaction is its variability around T°. The fraction of CO2-adduct captured of 0.492 at T° and [CO2] = 400 ppm by this reaction is almost exactly between the two asymptotes. Because of this, it will vary greatly in capture with even small differences in temperature, as can be seen in Figure 3d. This great variability causes these reactions to be useful for low temperatures while they are less useful for higher temperatures. Considering R14h at T° − 20 the fraction of CO2-adduct is greater than 0.9 at [CO2] = 400 ppm (Figure 3d). Raising the temperature to T° + 20 yields the fraction 0.068 (Table 1) and an excellent cycle load fraction of over 0.8. Even with a temperature variation from T° (CO2-adduct fraction = 0.492) to T° + 20, a cycle load fraction of 0.4 is obtained, a good collection that requires minimal heating.
However when considering a capture at T° + 20 (45 °C), and release at T° + 40, the cycle load fraction will fall to 0.06, a very poor collection. Thus for higher temperature climates, a system with a more robust exergonicity is desired, for example ΔG° = −11 kcal/mol (HR3). HR3b at T° + 20 has a CO2 capture fraction of 0.623, and increasing the temperature to T° + 40 (capture fraction of 0.119) yields a cycle load fraction of 0.504, a decent collection. Even better, for a capture at T° (capture fraction of 0.966) with release at T° + 40, the cycle load fraction is an excellent 0.847. At T° reaction HR3 already has a capture fraction of 0.966. Since the system cannot load significantly more CO2 during capture, there is no benefit to using this system in a climate with a temperature cooler than 25 °C; in fact, the efficiency would suffer because more heat would be required to liberate the CO2.
Our home state, Missouri, has great fluctuations in temperature through the seasons, so using a mixture of different capture systems may be most effective. In Columbia, Missouri, the average temperature in December is 0.78 °C which would indicate that a system with thermodynamic parameters similar to R14h would be best, while the average temperature in July is 25.4 °C, indicating that a reaction like HR3 would be considerably more effective [54]. For coastal or equatorial regions with less variation in temperature, the use of one capture system would be more feasible.
The considerations emphasize the significance of the magnitude of the entropy of the capture reaction. The large magnitude of reaction entropy of the capture reaction is a direct consequence of the presence of two capture moieties in the active site of rubisco and we offer an analogy with the illustration shown in Figure 8.
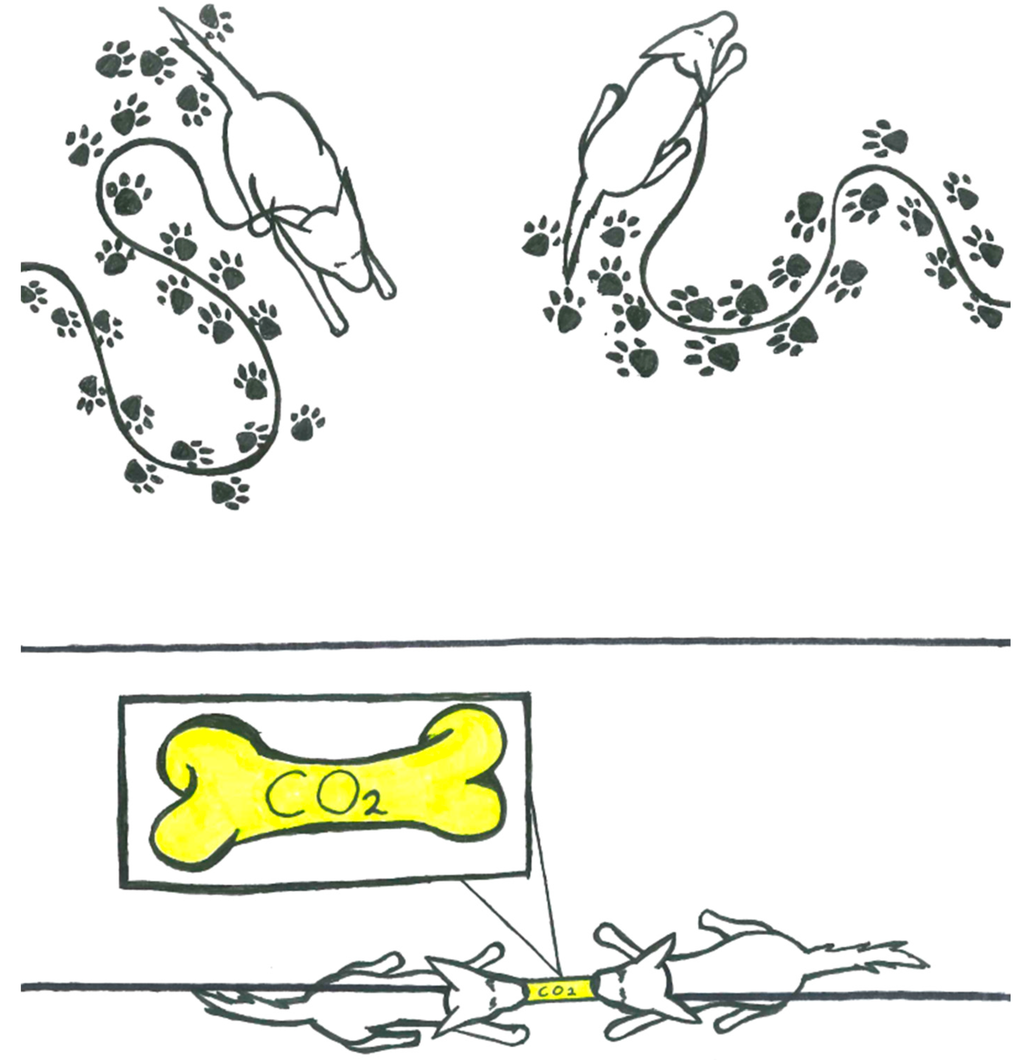
Figure 8.
The genius of the rubisco-capture system stems from the large reduction of system entropy associated with bringing the two tethered capture moieties (the Mg2+ site and the lysine amino group) together on CO2 capture. The principle is well exemplified by the image of two leashed dogs biting on the same bone. In the absence of the bone, each dog enjoys great freedom in their accessible range (illustration on top). Biting on the same bone curtails the accessible range and the freedom of the dogs’ mobilities (bottom).
3. Conclusions
In theoretical studies of chemical reactions with modern methods of electronic structure theory the reaction thermochemistry is usually reported for the stoichiometric reaction at standard conditions (1 atm, 25 °C) and the equilibrium constant Keq is related to the reaction Gibbs free enthalpy via ΔG° = ΔH° − T°·ΔS°. We described the computation of the equilibrium concentrations of the CO2-adducts for the general capture reaction GCR and the rubisco-type capture reaction (RCR) considering the atmospheric CO2 concentration via Henry’s law and as a function of temperature. The equations were applied to the thermochemistry of rubisco-based small molecule model reactions R1, R14a, and R14b, and three series of model reaction HR1–HR3 to illustrate the importance of the Gibbs free enthalpy for the effective capture and of the reaction entropy for economic CO2 release at elevated temperature. Having a favorable capture of free enthalpy is of course an absolute necessity, but not all exergonic reactions are suitable CO2 capture systems. Successful CO2 capture systems must allow for effective release as well, and this feature is controlled by the reaction entropy. It is hoped that the presentation of the numerical examples provides useful guidelines for the design of more efficient capture systems.
The active site of rubisco employs two capture moieties to trap the activator CO2. The metal site is attractive to any Lewis base, including water and CO2, and their exchanges will be fast. Eventually, a CO2 molecule will occupy a ligand site of Mg2+ and it will then be trapped by Lewis-acid assisted nucleophilic addition of the amino-group of lysine to the heterocumulene CO2. This two-pronged process allows for the capture of small amounts of CO2 in a huge excess of water, and the mechanism has two major consequences for the thermochemistry. The endergonicity of the H2O/CO2 replacement is required to reduce the overall exergonicity of the CO2 capture reaction and to allow overall reversibility. The second consequence for the RCR thermochemistry is the large reduction of system entropy which is associated with bringing the two tethered capture moieties (the Mg2+ site and the lysine NH2 group) together on CO2 capture. This entropy feature is crucial for the success of the rubisco-based capture and release system. While chemists have a good sense of binding enthalpies, it is usually more challenging to appreciate reaction entropies, and with this in mind we offer an analogy in Figure 8. The principle of using a two-pronged capture system to ensure a large negative capture entropy can be exemplified by two leashed dogs biting on the same bone. In the absence of the bone, each dog has a large accessible range and they will enjoy the freedom to access much of their accessible space (high mobility, high entropy). Biting on the same bone curtails the accessible range and reduces the dogs’ mobilities (low entropy). This principle also is highlighted by the graphical abstract.
Acknowledgments
Acknowledgment is made to the donors of the American Chemical Society Petroleum Research Fund for partial support of this research (#53415-ND4).
Author Contributions
Andrew Muelleman and Joseph Schell performed the research, computed the data, created Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7, and contributed to the writing. Spencer Glazer created the art work in the graphical abstract and Figure 8. Professor Rainer Glaser, Dipl.-Chem. guided the research and contributed to the writing.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Keeling, R.F. Recording Earth’s Vital Signs. Science 2008, 319, 1771–1772. [Google Scholar] [CrossRef] [PubMed]
- Trends in Atmospheric Carbon Dioxide, US Department of Commerce, National Oceanic & Atmospheric Administration (NOAA), Earth System Research Laboratory, Global Monitoring Division. Available online: http://www.esrl.noaa.gov/gmd/ccgg/trends (accessed on 28 April 2016).
- CarbonTracker CT2015, US Department of Commerce, National Oceanic & Atmospheric Administration (NOAA), Earth System Research Laboratory, Global Monitoring Division. Available online: http://www.esrl.noaa.gov/gmd/ccgg/carbontracker (accessed on 28 April 2016).
- Peters, W.; Jacobson, A.R.; Sweeney, C.; Andrews, A.E.; Conway, T.J.; Masarie, K.; Miller, J.B.; Bruhwiler, L.M.P.; Pétron, G.; Hirsch, A.I.; et al. An atmospheric perspective on North American carbon dioxide exchange: CarbonTracker. Proc. Natl. Acad. Sci. USA 2007, 104, 18925–18930. [Google Scholar] [CrossRef] [PubMed]
- CarbonTracker Documentation, CT2015 Release, CarbonTracker Team. 17 March 2016. Available online: http://www.esrl.noaa.gov/gmd/ccgg/carbontracker/CT2015_doc.pdf (accessed on 28 April 2016).
- United States Carbon Cycle Science Program. Available online: http://www.carbon cyclescience.gov (accessed on 28 April 2016).
- OCO-2, Orbiting Carbon Observatory, NASA, Jet Propulsion Laboratory. Available online: http://oco.jpl.nasa.gov (accessed on 28 April 2016).
- Intergovernmental Panel on Climate Change (IPCC). Available online: http://www.ipcc.ch (accessed on 28 April 2016).
- IPCC, 2014: Climate Change 2014: Synthesis Report. In Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Core Writing Team; Pachauri, R.K.; Meyer, L.A. (Eds.) IPCC: Geneva, Switzerland, 2016; p. 151. Available online: http://www.ipcc.ch/report/ar5 (accessed on 28 April 2016).
- Coal—Current Issues and Trends. EIA, U.S. Energy Information Agency. Available online: https://www.eia.gov (accessed on 28 April 2016).
- Gore, A. An Inconvenient Truth: The Planetary Emergency of Global Warming and What We Can Do about It; Rodale Books: Emmaus, PA, USA, 2006. [Google Scholar]
- Alliance for Climate Protection. Available online: https://www.change.org/organizations/climate_project (accessed on 28 April 2016).
- 350.org. Available online: https://350.org (accessed on 28 April 2016).
- The Carbon Bathtub. National Geographic Magazine. 2009. Available online: http://ngm.nationalgeographic.com/big-idea/05/carbon-bath (accessed on 28 April 2016).
- Bringing CO2 Monitoring to You: Communicating Atmospheric Chemistry. Available online: http://www.acs.org/content/acs/en/acs-webinars/professional-development/communicating-carbon.html (accessed on 28 April 2016).
- Victor, D.G. The Collapse of the Kyoto Protocol and the Struggle to Slow Global Warming; Princeton University Press: New Jersey, NJ, USA, 2004. [Google Scholar]
- IUPAC. Compendium of Chemical Terminology, 2nd ed.; Blackwell Scientific Publications: Oxford, UK, 1997; pp. 1342–1343. [Google Scholar]
- First Successful Demonstration of Carbon Dioxide Air Capture Technology Achieved. By Earth Institute, Columbia University. Available online: physorg.com/news96732819.html (accessed on 28 April 2016).
- Keith, D.W.; Ha-Duong, M.; Stolaroff, J.K. Climate strategy with CO2 capture from the air. Clim. Chang. 2006, 74, 17–45. [Google Scholar] [CrossRef]
- Lackner, K.S. Capture of carbon dioxide from ambient air. Eur. Phys. J. Special Topics 2009, 176, 93–106. [Google Scholar] [CrossRef]
- Socolow, R.; Desmond, M.; Aines, R.; Blackstock, J.; Bolland, O.; Kaarsberg, T.; Lewis, N.; Mazzotti, M.; Pfeffer, A.; Sawyer, K.; et al. Direct Air Capture of CO2 with Chemicals: A Technology Assessment for the APS Panel on Public Affairs; American Physical Society: Washington, DC, USA, 1 June 2011; Available online: http://www.aps.org/ policy/reports/assessments/upload/dac2011.pdf (accessed on 28 April 2016).
- Zeman, F.S.; Lackner, K.S. Capturing carbon dioxide directly from the atmosphere. World Resour. Rev. 2004, 16, 62–68. [Google Scholar]
- Lackner, K.S.; Brennan, S. Envisioning carbon capture and storage: Expanded possibilities due to air capture, leakage insurance, and C-14 monitoring. Clim. Chang. 2009, 96, 357–378. [Google Scholar] [CrossRef]
- Lackner, K.S.; Brennan, S.; Matter, J.M.; Alissa Park, A.H.; Wright, A.; van der Zwaan, B. The urgency of the development of CO2 capture from ambient air. Proc. Natl. Acad. Sci. USA 2012, 109, 13156–13162. [Google Scholar] [CrossRef] [PubMed]
- Boot-Handford, M.E.; Abanades, J.C.; Anthony, E.J.; Blunt, M.J.; Brandani, S.; MacDowell, N.; Fernandez, J.R.; Ferrari, M.C.; Gross, R.; Hallett, J.P.; et al. Carbon capture and storage update. Energy Environ. Sci. 2014, 7, 130–189. [Google Scholar] [CrossRef]
- Murphy, L.J.; Robertson, K.N.; Kemp, R.A.; Tuononen, H.M.; Clyburne, J.A.C. Structurally simple complexes of CO2. Chem. Commun. 2015, 51, 3942–3956. [Google Scholar] [CrossRef] [PubMed]
- Sun, Z.; Fan, M.; Argyle, M. Supported monoethanolamine for CO2 separation. Ind. Eng. Chem. Res. 2011, 50, 11343–11349. [Google Scholar] [CrossRef]
- Kuntz, J.; Aroonwilas, A. Performance of spray column for CO2 capture application. Ind. Eng. Chem. Res. 2008, 47, 145–153. [Google Scholar] [CrossRef]
- Idem, R.; Wilson, M.; Tontiwachwuthikul, P.; Chakma, A.; Veawab, A.; Aroonwilas, A.; Gelowitz, D. Pilot plant studies of the CO2 capture performance of aqueous MEA and mixed MEA/MDEA solvents at the University of Regina CO2 capture technology development plant and the Boundary Dam CO2 capture demonstration plant. Ind. Eng. Chem. Res. 2006, 45, 2414–2420. [Google Scholar] [CrossRef]
- Goeppert, A.; Czaun, M.; May, R.B.; Prakash, G.K.S.; Olah, G.A.; Narayanan, S.R. Carbon dioxide capture from the air using a polyamine based regenerable solid adsorbent. J. Am. Chem. Soc. 2011, 133, 20164–20167. [Google Scholar] [CrossRef] [PubMed]
- Andreoli, E.; Barron, A.R. Effect of spray-drying and cryo-milling on the CO2 absorption performance of C60 cross-linked polyethyleneimine. J. Mater. Chem. A 2015, 3, 4323–4329. [Google Scholar] [CrossRef]
- McDonald, T.; Lee, W.R.; Mason, J.A.; Wiers, B.M.; Hong, C.S.; Long, J.R. Capture of carbon dioxide from air and flue gas in the alkylamine-appended metal-organic framework mmen-Mg2(dobpdc). J. Am. Chem. Soc. 2012, 134, 7056–7065. [Google Scholar] [CrossRef] [PubMed]
- Sumida, K.; Rogow, D.L.; Mason, J.A.; McDonald, T.M.; Bloch, E.D.; Herm, Z.R.; Bae, T.-H.; Long, J.R. Carbon dioxide capture in metal-organic frameworks. Chem. Rev. 2012, 112, 724–781. [Google Scholar] [CrossRef] [PubMed]
- Poloni, R.; Smit, B.; Neaton, J.B. Ligand-assisted enhancement of CO2 capture in metal-organic frameworks. J. Am. Chem. Soc. 2012, 134, 6714–6719. [Google Scholar] [CrossRef] [PubMed]
- McDonald, T.M.; Mason, J.A.; Kong, X.; Bloch, E.D.; Gygi, D.; Dani, A.; Crocella, V.; Giordanino, F.; Odoh, S.O.; Drisdell, W.S.; et al. Cooperative insertion of CO2 in diamine-appended metal-organic frameworks. Nature 2015, 519, 303–319. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.-Z.; Song, Q.-W.; He, L.-N. Capture and Utilization of Carbon Dioxide with Poly-Ethylene Glycol, SpringerBriefs in Molecular Science; Springer: New York, NY, USA, 2012. [Google Scholar]
- Glaser, R.; Castello-Blindt, P.O.; Yin, J. Biomimetic Approaches to Reversible CO2 Capture from Air. N-Methylcarbaminic Acid Formation in Rubsico-Inspired Models. In New and Future Developments in Catalysis: Activation of Carbon Dioxide, 1st ed.; Suib, S.L., Ed.; Elsevier: Amsterdam, The Netherlands, 2013; pp. 501–534. [Google Scholar]
- Glaser, R. RuBisCO-Inspired Biomimetic Approaches to Reversible CO2 Capture from Air. Metal Dependence of the H2O/CO2 Replacement Penalty. In Advances in CO2 Capture, Sequestration and Conversion; Jin, F., He, L.-N., Hu, Y.H., Eds.; ACS Books: Washington, DC, USA, 2015; pp. 501–534. [Google Scholar]
- Shively, J.M.; Van Keulen, G.; Meijer, W.G. Something about almost nothing: CO2 fixation in chemautotrophs. Ann. Rev. Microbiol. 1998, 52, 191–230. [Google Scholar] [CrossRef] [PubMed]
- Hugler, M.; Sievert, S.M. Beyond the Calvin cycle: Autotrophic carbon fixation in the ocean. Ann. Rev. Marine Sci. 2011, 3, 89–261. [Google Scholar] [CrossRef] [PubMed]
- Taylor, T.C.; Andersson, I. Structure of a product complex of spinach ribulose-1,5-bisphosphate carboxylase/oxygenase. Biochemistry 1997, 36, 4041–4046. [Google Scholar] [CrossRef] [PubMed]
- Taylor, T.C.; Andersson, I. Structural transitions during activation and ligand binding in hexadecameric Rubisco inferred from the crystal structure of the activated unliganded spinach enzyme. Nat. Struct. Biol. 1996, 3, 95–101. [Google Scholar] [CrossRef] [PubMed]
- Gutteridge, S.; Newman, J.; Herrmann, C.; Rhoades, D. The crystal structures of Rubisco and opportunities for manipulating photosynthesis. J. Exp. Botany 1995, 46, 1261–1267. [Google Scholar] [CrossRef]
- Lundqvist, T.; Schneider, G. Structure of the ternary complex of ribulose 1,5-bisphosphate carboxylase, magnesium(II) and activator carbon dioxide at 2.3 Å resolution. Biochemistry 1991, 30, 904–908. [Google Scholar] [CrossRef] [PubMed]
- Hartman, F.C.; Harpel, M.R. Structure, function, regulation, and assembly of d-ribulose-1,5-bisphosphate carboxylase/oxygenase. Annu. Rev. Biochem. 1994, 63, 197–234. [Google Scholar] [CrossRef] [PubMed]
- Cleland, W.W.; Andrews, T.J.; Gutteridge, S.; Hartman, F.C.; Lorimer, G.H. Mechanism of Rubisco: The carbamate as general base. Chem. Rev. 1998, 98, 549–561. [Google Scholar] [CrossRef] [PubMed]
- Earth System Research Laboratory Global Monitoring Division. Available online: http://www.esrl.noaa.gov/gmd/ccgg/trends/ (accessed on 28 April 2016).
- Sander, R. Compilation of Henry’s law constants (version 4.0) for water as solvent. Atmos. Chem. Phys. 2015, 15, 4399–4981. [Google Scholar] [CrossRef]
- Kumar, P.S.; Hogendoorn, J.A.; Feron, P.H.M.; Versteeg, G.F. New absorption liquids for the removal of CO2 from dilute gas streams using membrane contactors. Chem. Eng. Sci. 2002, 57, 1639–1651. [Google Scholar] [CrossRef]
- Dindore, V.Y.; Brilman, D.W.F.; Geuzebroek, F.H.; Versteeg, G.F. Membrane-solvent selection for CO2 removal using membrane gas-liquid contactors. Sep. Purif. Technol. 2004, 40, 133–145. [Google Scholar] [CrossRef]
- Atchariyawut, S.; Feng, C.; Wang, R.; Jiraratananon, R.; Liang, D.T. Effect of membrane Structure on mass-transfer in the membrane gas-liquid contacting process using microporous PVDF hollow fibers. J. Membr. Sci. 2006, 285, 272–281. [Google Scholar] [CrossRef]
- Simons, K.; Nijmeijer, K.; Wessling, M. Gas-liquid membrane contactors for CO2 removal. J. Membr. Sci. 2009, 340, 214–220. [Google Scholar] [CrossRef]
- MacDowell, N.; Florin, N.; Buchard, A.; Hallett, J.; Galindo, A.; Jackson, G.; Adjiman, C.S.; Williams, C.K.; Shah, N.; Fennell, P. An overview of CO2 capture technologies. Energy Environ. Sci. 2010, 3, 1645–1669. [Google Scholar] [CrossRef]
- Climatological Data for St. Louis, Columbia, and Quincy—National Weather Service. Available online: http://www.weather.gov/lsx/cli_archive (accessed on 28 April 2016).
© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).