Next Article in Journal
Computational Fluid Dynamics Study on Bottom-Hole Multiphase Flow Fields Formed by Polycrystalline Diamond Compact Drill Bits in Foam Drilling
Next Article in Special Issue
Preliminary Results in the Investigation of In Vivo Iliac and Coronary Flow Collision, Vortex Formation, and Disorganized Flow Degeneration: Insights from Invasive Cardiology Based on Fluid Mechanics Principles and Practices
Previous Article in Journal
Soot and Flame Structures in Turbulent Partially Premixed Jet Flames of Pre-Evaporated Diesel Surrogates with Admixture of OMEn
Previous Article in Special Issue
Adjoint Solver-Based Analysis of Mouth–Tongue Morphologies on Vapor Deposition in the Upper Airway
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Fluids
Volume 9
Issue 9
10.3390/fluids9090209
fluids-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Numerical Simulation Studies on the Design of the Prosthetic Heart Valves Belly Curves

by
Jingyuan Zhou
1,†,
Yinkui Wu
2,†,
Lu Chen
1,
Tao Li
1,
Yan Xiong
3,* and
Yu Chen
1,*
1
Department of Applied Mechanics, Sichuan University, Chengdu 610065, China
2
Institute of Intelligent Manufacturing, Mianyang Polytechnic, Mianyang 621000, China
3
College of Mechanical Engineering, Sichuan University, Chengdu 610065, China
*
Authors to whom correspondence should be addressed.
†
These authors contributed equally to this project and are considered as the co-first authors.
Fluids 2024, 9(9), 209; https://doi.org/10.3390/fluids9090209
Submission received: 9 July 2024 / Revised: 29 August 2024 / Accepted: 3 September 2024 / Published: 10 September 2024
(This article belongs to the Special Issue Advances in Hemodynamics and Related Biological Flows)
Browse Figures
Review Reports Versions Notes

Abstract

Prosthetic heart valves (PHVs) are employed to replace the diseased native valve as a treatment of severe aortic valve disease. This study aimed to evaluate the effect of curvature of the belly curve on valve performance, so as to support a better comprehension of the relationship between valve design and its performance. Five PHV models with different curvatures of the belly curve were established. Iterative implicit fluid–structure interaction simulations were carried out, analyzing in detail the effect of belly curvature on the geometric orifice area (GOA), coaptation area (CA), regurgitant fraction (RF), leaflet kinematics and stress distribution on the leaflets. Overall, GOA and CA were negatively and positively related to the curvature of the belly curve, respectively. Nevertheless, an excessive increase in curvature can lead to incomplete sealing of free edges of the valve during its closure, which resulted in a decrease in CA and an increase in regurgitation. The moderate curvature of the belly curve contributed to reducing RF and fluttering frequency. Valves with small curvature experienced a significantly higher frequency of fluttering. Furthermore, all stress concentrations intensified with the increase in the curvature of the belly curve. The valve with moderate curvature of the belly curve strikes the best compromise between valve performance parameters, leaflet kinematics and mechanical stress. Considering the different effects of the curvature of belly curve on valve performance parameters, the PHV design with variable curvature of belly curve may be a direction towards valve performance optimization.

1. Introduction

Aortic valve disease (AVD) affects more than 60 million people worldwide [1]. Aortic valve replacement (AVR) remains the most effective treatment for severe AVD [2]. The ideal prosthetic heart valve (PHV) should have good biocompatibility, hemodynamics, and fatigue resistance at the same time. However, the two commonly used prostheses, mechanical heart valves and bioprosthetic heart valves, are susceptible to thrombosis and structural valve degeneration [3,4], respectively. Therefore, a valid alternative to the existing devices is expected to overcome the shortcomings of these two categories, which brings forward the requirements of PHV optimization.
The geometry of the PHV directly affects its performance and durability through altering its hemodynamics and stress [5]. It has been shown that using a geometry with more physiological flow contributes to improved hemodynamics [6,7,8], while abnormal flow patterns can promote blood cell damage to initiate thrombus formation [9]. ISO has developed a set of hemodynamic related standards for assessing PHV performance, making demands on the regurgitant fraction (RF) and effective orifice area (EOA) [10]. The PHV geometry also has an impact on leaflet stress, and high mechanical stresses are suggested to be the major causes of calcification and tearing [11,12,13]. Therefore, it is important to comprehensively understand the impact of PHV design parameters on its performance for the optimization of PHV.
Many research projects on such influence have been carried out from various perspectives. The effects of variable thickness on stresses of the valve have been pointed out, and the proposed methods showed potential for optimizing the stress distribution [14,15]. A novel mathematical approach for the construction of the whole AVR was proposed, and it was speculated that the wall shear stress of the new AVR model would reduce significantly, which could contribute to a small endothelial damage effect [16]. Computational frameworks were developed to improve the distribution of stress for PHV, and different designs could be obtained by varying parameters which controlled the shape of the attachment curve and the height of the free edge [12,13]. In addition, an automatic optimization framework using commercially available software packages was developed to consider a wider optimization design space. The results showed that increasing the ratio of valve height to leaflet coaptation height and the curvature of the attachment curve could potentially reduce von-Mises stress, but such a correlation was not observed for the belly curve [17]. However, this may result in sub-optimal TAV design because the user has no control over such optimization process [12]. The associated control points of the construction curves for the PHV surfaces were moved to investigate the influences of leaflet geometry on the EOA, the coaptation area (CA) and the geometric orifice area (GOA) [18,19].
In general, although progress in the optimization of leaflet geometry has been satisfactory, the influence of the curvature of the belly curve of PHV on its performance is not clarified. To solve this problem, in this study, 5 PHV models with different curvatures of the belly curve were established for fluid–structure interaction (FSI) simulations. Results were analyzed in terms of valve performance parameters, leaflets kinematics, mechanical stress and flow velocity distribution. This paper supports a better comprehension of the relationship between valve design and its performance, which would fit very well in future along with uncertainty quantification to obtain a continuous surface response.

2. Methods

2.1. Geometry and Mesh Generation

The 3D geometry of the valve and blood flow volume were created in Rhino 7.0 (Robert McNeel and Assoc, Seattle, WA, USA). Both the structure and fluid were meshed using ANSA 21.0.1 (BETA CAE Systems, Lucerne, Switzerland).
With reference to the geometry of the Sapien XT valve (Edwards Life Sciences, Irvine, CA, USA), the diameter was set to 23 mm and the height to 14.3 mm for all valves [20]. Uniformly distributed thicknesses of 0.4 mm was used for the valve leaflets [21]. The leaflets of PHV were generated by three basic curves: the attachment curve, the free edge and the belly curve (Figure 1a). Firstly, the attachment curve was the curve connecting the valve and the sinus. Secondly, the free edge referred to the curve that can move freely when the PHV remained open. Finally, the belly curve, which determined the curvature of the PHV, was located in the middle of the valve leaf surface.
The diameter and height of the PHV determined the fixed coordinates of point A and point E on the valve surface and two guidelines were generated according to the coordinates of the two points. Point A located at the center of the free edge was traced to show the kinematics of the leaflets. On the premise of ensuring a smooth curve, according to the distance between two guide lines, the height of three additional points B, C and D on the guide line1 remained unchanged, they were moved 5.1 mm, 7.8 mm and 6.6 mm to the right, respectively, to obtain the control points of the belly curve for valve 1, and the new control points obtained in the previous step were moved to the right in the same manner four times to obtain the control points for valve 2, valve 3, valve 4 and valve 5. A third-order curve was used to connect five control points in sequence in Rhino 7.0 to generate the belly curve of each valve, as shown in Figure 1b. While maintaining the shape of the free edge of each valve, the free edge was swept along the belly curve to generate the surface of the leaflet, which was then intersected by the wall of the fluid domain. One leaflet was rotated around the vertical axis to create three identical leaflets to generate the final valve model. Side views of all models are shown in Figure 1c.
The geometric relations of the aortic root in the current model were based on the measurements of the aortic root in adults [22]. Two straight-tube extensions were added to the inlet section (ventricular extension: 12.5 mm) and outlet section (aortic extension: 12.5 mm) of the aortic root for computational stability. The 3D geometry of the blood flow volume was created using 4 design parameters as shown in Figure 2a. The value of each design parameter is given in Table 1.
The valve leaflets were discretized into 1-Point Nodal Pressure tetrahedral solid elements, which are well suited for applications with incompressible material behavior [23,24]. The fluid domain was divided into 4-noded tetrahedral Eulerian elements with mesh refinement in the region of interest (fluid–structure interface). Taking valve 1 as an example, mesh independence studies were conducted for both domains with varying element sizes for one cardiac cycle (Table A1 in the Appendix A).
Consequently, the fine model had sufficient resolution, while two elements fitted through the thickness of the PHV reduced the possibility of shear locking in leaflets [25] and high density mesh specifically at high bending regions, offering certain accuracy for bending dominant problems [16]. The discretized solution fields for blood flow zone and valve leaflet structure are shown in Figure 2b. The other four models were discretized with the same mesh resolution, and the number of elements for all models are shown in Table A2 in Appendix A.

2.2. Materials

The density of the valve was 1100 kg/m3, which is typical for biological soft tissues [26]. Due to long clinical use in bioprosthetic heart valves and favorable hemodynamic performance [27], bovine pericardium was selected as material for the leaflets. The material is assumed to be isotropic and incompressible, adopting an Ogden’s equation to describe a hyper-elastic material model with nonlinear constitutive behavior, and the strain energy density function for an Ogden material is as follows:
W = ∑ p = 1 N μ p α p ( λ 1 α p + λ 2 α p + λ 3 α p − 3 )
where λ i , (i = 1, 2, 3) is the principal stretch ratio, and μ p and α p are material constants.
The material constants used in this analysis were taken from a previous study [28], which fitted the average stress–strain curve of glutaraldehyde fixed bovine pericardium using a 2nd order Ogden equation with μ 1 = 7.6 × 10 − 6   M P a ; μ 2 = 5.7 × 10 − 4     M P a ; α 1 = α 2 = 26.26 .
The fluid (blood) was assumed to be incompressible and Newtonian [29], with constant dynamic viscosity of 0.004 Pa∙s and a density of 1050 kg/m3.

2.3. FSI Approach

FSI modeling is the best approach capable of reproducing both the mechanics and hemodynamics of PHV [30,31]. In the present study, the FSI analysis was carried out by the strong coupling of the incompressible flow solver (ICFD) and the implicit mechanics solver in the LS-DYNA, Release 11.0 (Ansys, Canonsburg, PA, USA).
For FSI simulations, ICFD uses an Arbitrary Lagrangian–Eulerian (ALE) approach for mesh movement, and the interfaces between the solid and the fluid are Lagrangian and deform with the structure [32]. The solid and fluid geometry must match at the interface but not necessarily the meshes. Therefore, in the cases where FSI simulations result in large deformation of the leaflets, ICFD can automatically re-mesh to keep an acceptable mesh quality. Further, an interaction detection coefficient (IDC, IDC = 0.25) was set to ensure FSI interaction.
Corresponding to a constant time step of 0.1 ms, one cardiac cycle (0.8 s) was discretized in 8000-time steps. During the first time step, fluid dynamics were solved using the continuity and incompressible Navier–Stokes equations in ICFD. The forces computed would then be communicated to the implicit mechanics solver. The implicit mechanics solver returned the node displacements to the ICFD. The procedure was repeated until convergence has been reached. Once the convergence was reached, the next time step proceeded. The simulations were run over three cardiac cycles to achieve convergence and eliminate the effect of a sudden start during the 1st cardiac cycle. All results were extracted from the 3rd cycle.
A surface-to-surface contact with soft constraint was established and frictionless conditions were prescribed between adjacent leaflets [33]. These conditions were enforced each time the distance between two leaflets became smaller than 0.2 mm, effectively preventing a small orifice forming between the leaflets.

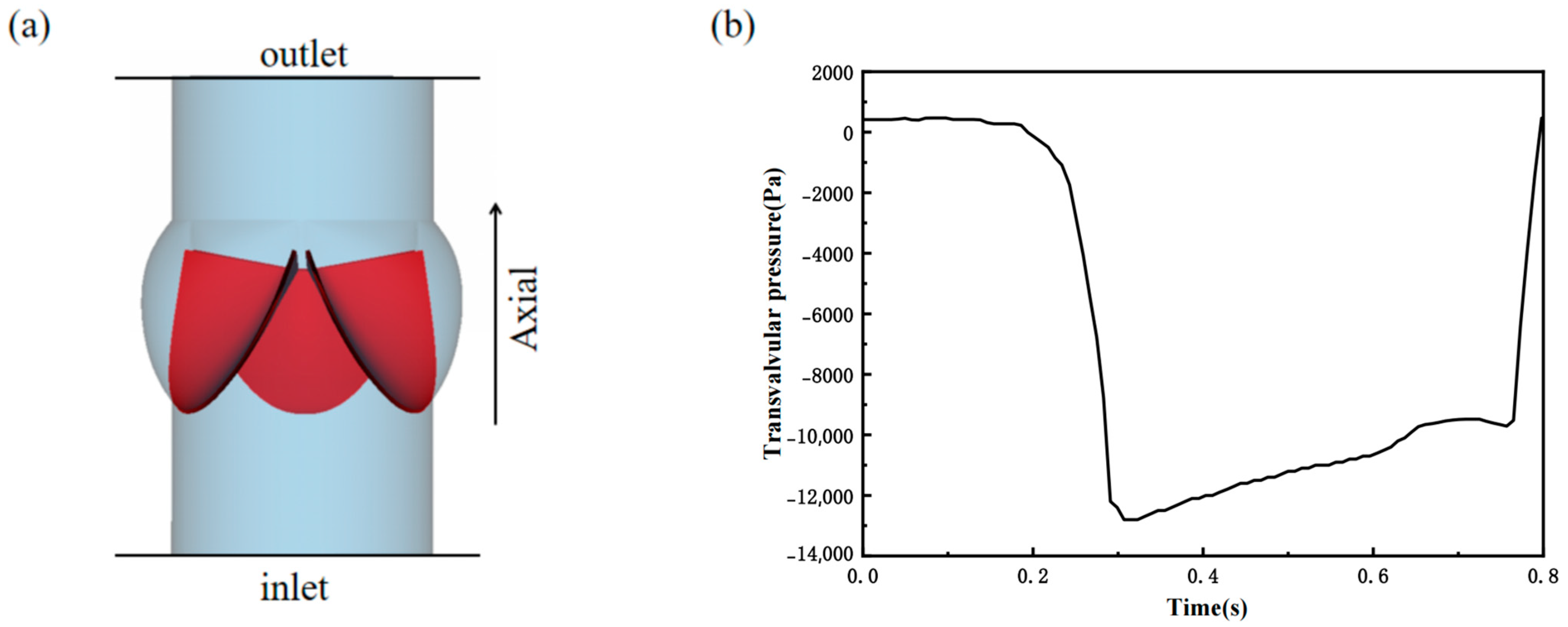
2.4. Flow and Boundary Conditions

In all models, the aortic wall was assumed to be rigid and a no-slip condition was employed at the wall–blood interface. Surfaces of valve leaflets in contact with blood flow were considered as fluid–structure interfaces, across which loads and displacements were transferred. All nodes along the attachment curves were considered to be fixed in the FSI simulations.
The inlet and outlet of the model are shown in Figure 3a. Taking into account that the regurgitation is a function of the valve properties, the flow boundary condition (BC) constrains the analysis as it enforces a specific regurgitant flow during valve closing [34,35]. Therefore, referring to physiological pressure pulses across the human aortic valve for the complete cardiac cycle [36], the transvalvular pressure waveform (Figure 3b) was applied at the inlet throughout the cardiac cycle, while maintaining a constant zero pressure at the outlet of the fluid domain.

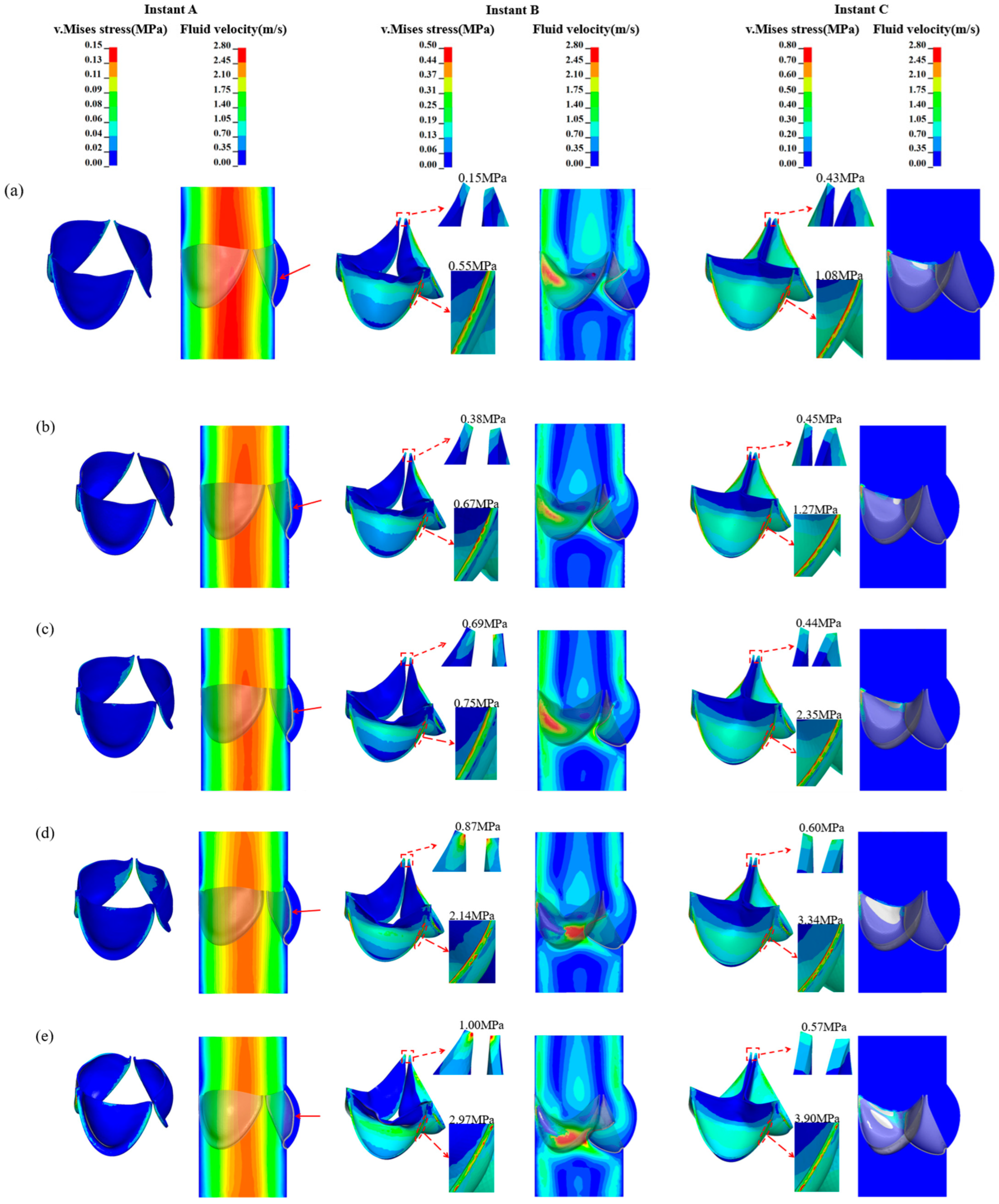
3. Results

3.1. Valve Performance Parameters

GOA (Geometric orifice area) represents the geometric area of the valve orifice [37]. It was measured with ImageJ 1.43 and obtained at the peak flow rate. CA (Coaptation area) indicates how much the three valve leaflets are in contact with each other during diastole [18]. CA was calculated by summing areas of all elements where contact occurred after the valve was fully closed.
Regurgitant fraction (RF) evaluates leakage after valve closure, and the equation from ISO 5840-3:2013 [10] was applied to calculate the RF:
R F = V R V F × 100 % V R = V C + V L
where VF is the volume of flow ejected through the test heart valve substitute during the forward flow period [10,38], and VR is the total volume of fluid through the valve per beat owing to the retrograde flow and is the sum of the closing volume (VC) and the leakage volume (VL) [21]. The calculation approaches and results of RF are summarized in Figure 4.
As shown in Table 2, increasing the curvature of the belly curve decreased GOA but improved CA. The highest GOA, 362.21 mm2, was exhibited by valve 1. The maximum CA, 365.73 mm2, was obtained in valve 4. Specially, it was observed that the free edges of valve 5 after its closure have almost no contact, resulting in a decrease in the CA of valve 5.
Figure 4a,c shows that valve 1–valve 3 exhibited similar magnitudes of VF and VR, while those of valve 4 and valve 5 were significantly smaller. Valve 4, with a moderate curvature of the belly curve, had the lowest RF.

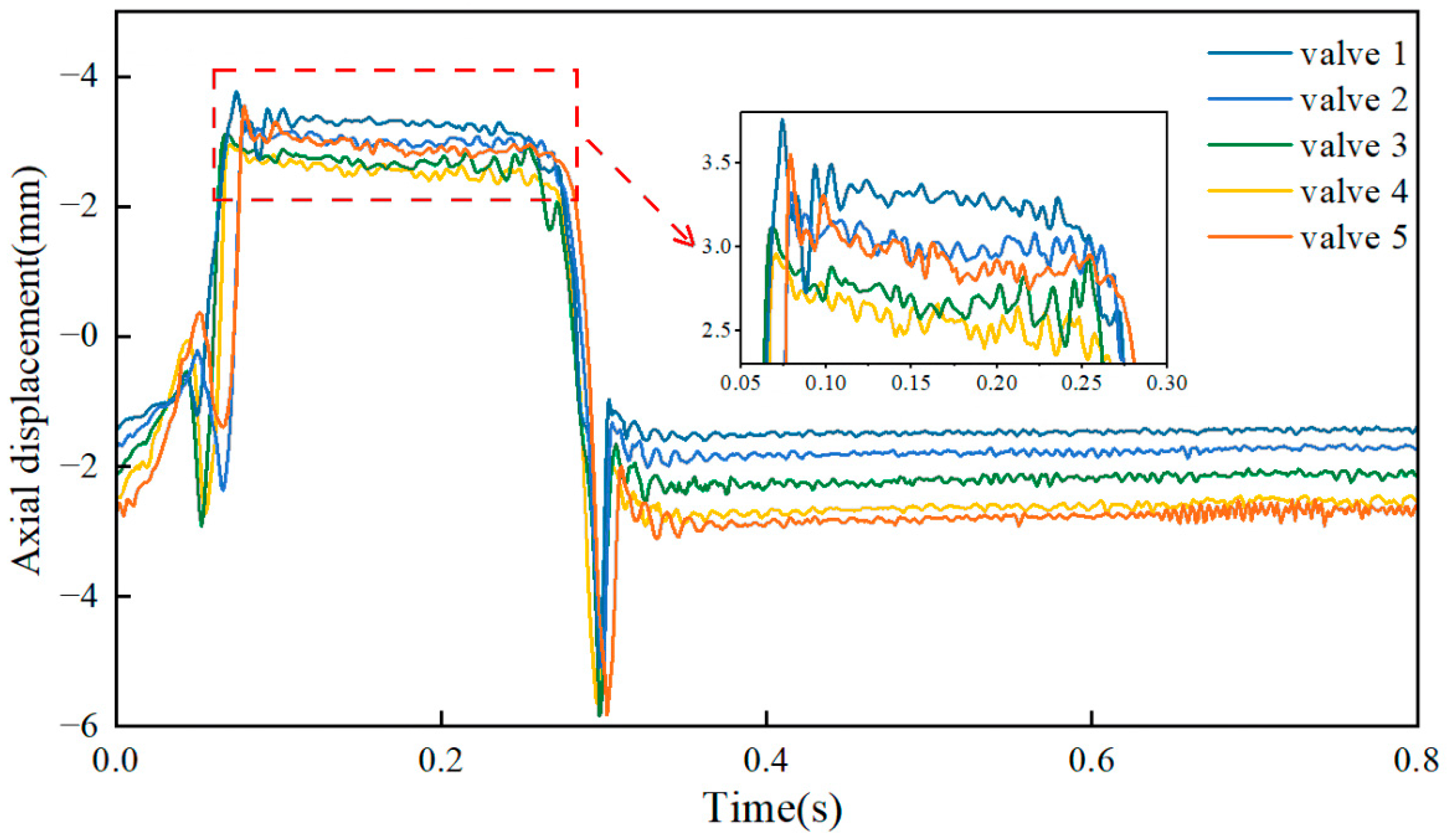
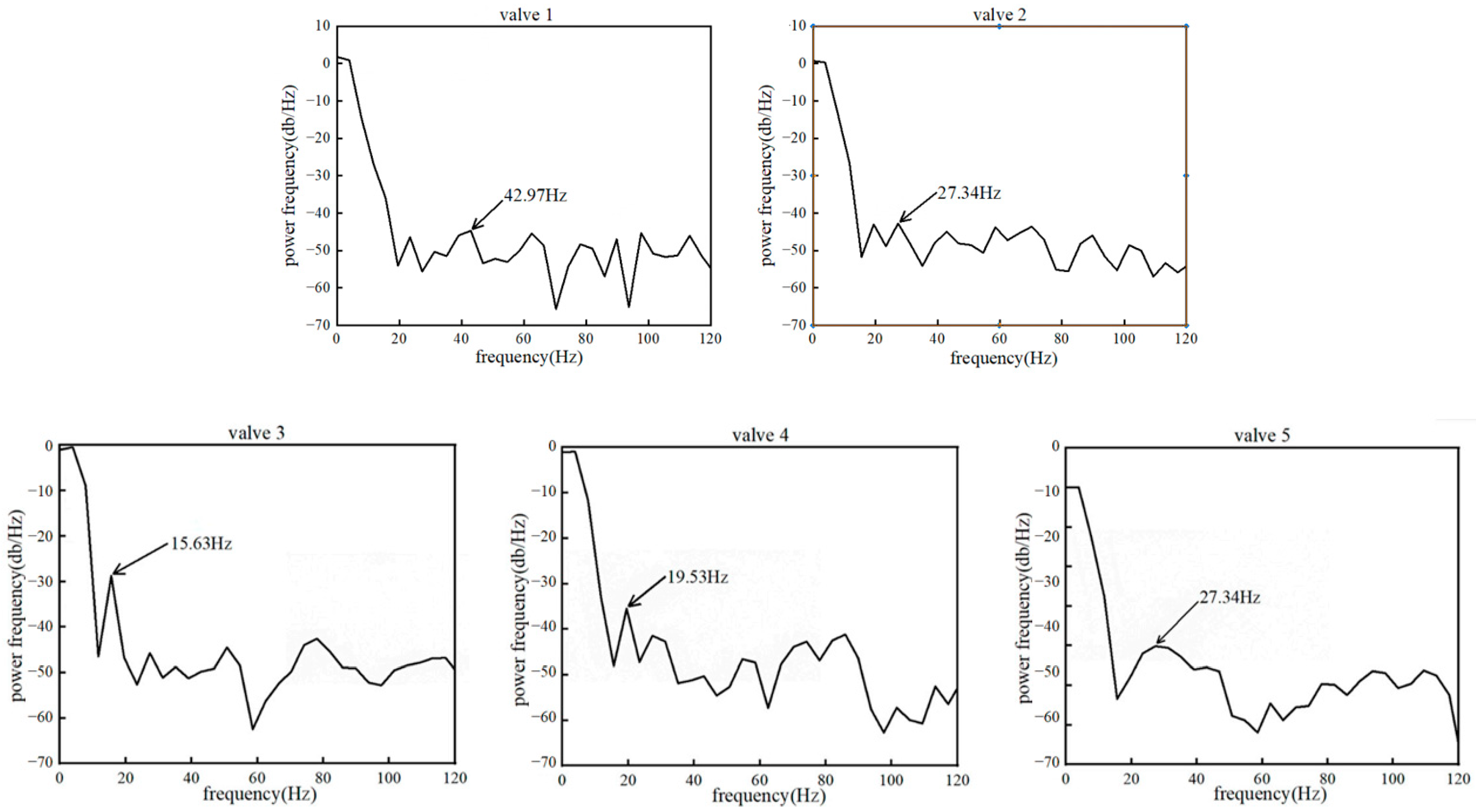
3.2. Leaflet Kinematics

Figure 5 shows the transient axial displacements of the traced marker located on the leaflets (i.e., point A in Figure 1a). The axis along which the displacement was evaluated is shown in Figure 3a.
The axial displacement of point A increased as the valve opened, followed by a minor fluttering motion. During the period of fluttering, the axial displacement of point A decreased with the increase in the curvature of the belly curve, except for valve 5. After the valves were fully closed, the greater the curvature of belly curve, the larger the absolute value of the axial displacement of point A. In addition, the axial displacement waveform of point A of valve 5 showed obvious oscillation at the end of diastole.
The waveforms of displacements in the inset of Figure 5 directly capture the fluttering dynamics of the valve during systole. The second highest peak in the power spectral density, calculated using MATLAB 2019a (MathWorks, Inc., Natick, MA, USA), was utilized to identify the dominant frequency characterizing leaflet fluttering [39]. As illustrated in Figure 6, the fluttering frequency of valve 1 (42.97 Hz) was notably higher than that of other valves. Valve 3 and valve 4 exhibited relatively lower fluttering frequencies (15.63 Hz and 19.53 Hz, respectively). With an increase in the curvature of the belly curve, valve 5 displayed higher fluttering frequencies (27.34 Hz).

3.3. Von-Mises Stress and Flow Velocity

Figure 4b shows the time instants used for analyzing the valve stress and flow velocity. The flow rate reached its peak at instant A, the flow rate of regurgitation was the maximum at instant B, and the instant C was taken from the fully closed phases of the valve.
At instant A (the first column of Figure 7), the stresses in the belly of all valves were close to 0 MPa and the stresses distributed upward along the attachment curve were considerably higher in valve 4 and valve 5 compared to the other three valves. Simultaneously, it was observed that the velocity profiles of valve 1–valve 3 were similar, and the magnitude of the velocity of the central flow was significantly greater than that of valve 4 and valve 5.
The belly region of the valve was subjected to flexure at instant B (the second column of Figure 7), leading to higher stress at that location. Additionally, high stresses were observed along the attachment curve and around the commissure tips. Through a comparison of the high stresses displayed by magnification (the maximum stresses marked on the side), it was found that the curvature of belly curve increased, local stress concentrations intensified and the peak stress also increased.
Valve 1 to valve 3 mainly exhibited regurgitation from the gap between the valve commissure tips, whereas valve 4 and valve 5 showed more obvious regurgitation through the valve orifice.
As depicted in the third column of Figure 7, stresses along the attachment curve at instant C were greater compared to instant B, while the stresses around the commissure tips of valve 3–valve 5 were reduced. In comparison to the first three valves, the velocity of regurgitation through the gap between the valve commissure tips was smaller in valve 4 and valve 5, and valve 5 exhibited a significant amount of low-speed regurgitation through the valve orifice.

4. Discussion

An ideal valve would have both large GOA, CA and small RF. Simulation results of GOA and CA conformed to the results reported by [18,40], and the results also demonstrate that GOA and CA were negatively and positively related to the curvature of the belly curve, respectively, which conforms to the previous FSI simulation [18] and further supports the FE result that the rounder the shape of the belly curve, the smaller the GOA [19]. However, as demonstrated by valve 5 in the third column of Figure 7, an excessive increase in curvature can result in incomplete sealing of free edges of the valve during closure. This outcome led to a series of results that appeared to be inconsistent with the aforementioned pattern. In comparison to valve 4, valve 5 exhibited a smaller CA (Table 2), a larger VR (Figure 4c) and more obvious oscillation in the axial displacement waveform of point A at the end of diastole (Figure 5).
In terms of peak flow rates, an average value of 500 mL/s of the five models was identified, consistently with other computational [41] and experimental work [42] using similar biomaterials. The results lead to the hypothesis that VR is in relation not only to the magnitude of CA but also to its spatial distribution. Specifically, a small VR can be achieved when CA is large and the free edges of the valve are effectively sealed. Valve 4 is a fine example of the fact that, although VF has decreased compared to the first three valves (Figure 4c), good closure, as shown in the third column of Figure 7, minimizes the VR of the valve, resulting in the lowest RF (Figure 4c).
The findings provide new insights into the design and optimization of PHV. For valves with small belly curvature, such as valve 1, a sufficient height of the free edges needs to be maintained to prevent further reduction in CA, which is already limited by the small curvature, because small CA is related to an increase in ventricular workload, which affects the service life of valves [18]. What is more, for valves with large belly curvature, such as valve 5, its complete sealing during closure can be accomplished by increasing the length of the free edges, so as to improve the CA and RF.
The deformation of the valve has an impact on its GOA and stress distribution. During the fully opened phase, the smaller the axial displacement of point A (Figure 5), the greater the bending deformation of the belly region of the valve (indicated by the red arrow in the velocity profile of the first column of Figure 7). This may be the reason why GOA and axial displacement generally decreased as the curvature of belly curve increased.
The influence of valve deformation on stress is mainly reflected in the closing phase. In the systolic phase, stresses in the belly regions of all valves were approximately 0 MPa (the first column of Figure 7), which were consistent with [40], meaning that low differential pressure is required for valve opening [43]. During the process of valve closure (the second column of Figure 7), it was observed that high stress in the belly region was associated with flexure that occurred there, and the increase in curvature of the belly curve would aggravate the bending deformation, thereby increasing the stress in the valve belly. In addition, stress concentrations could also be observed around the commissure tips, which were particularly obvious in valve 4 and valve 5, and the overall maximum von Mises stress value of the two valves and [36] were similar. The commissure tips endured the tension caused by the valve moving downwards along the axial direction and were sheared by the substantial amount of high-speed regurgitation. The stress concentrations reduced as the high-speed regurgitation through the gap between commissure tips also reduced after the valve was completely closed, as depicted by valve 4 and valve 5 in the third column of Figure 7. Therefore, it is our opinion that the stress concentration is in relation not only to the axial displacement of the valve, but also the regurgitation. Besides, the greater the downward displacement in the axial direction of point A (Figure 5), the more the valve was found to be pushed upstream toward the inlet, which generated higher stress along the attachment curve in the fully closed phase (the third column of Figure 7). Since the stress concentrations within the leaflets can accelerate tissue structural fatigue damage and initiate calcification by causing structural disintegration [12,44,45], special attention should be paid to valves with large belly curvature, as their stress concentrations were more obvious.
Prior studies noted that bioprosthetic heart valves can flutter in systole [39,46,47], which may contribute to leaflet fatigue and failure [48]. Therefore, it is necessary to examine the fluttering that occurs in such valves. Fluttering frequencies differ with valve geometry [39]. Taken together with prior results, the fluttering frequencies of bovine pericardial BHVs range from 26.32 Hz to 59.26 Hz [39,49,50,51]. In addition, a computational model indicates a significant low-frequency peak below 20 Hz for the bovine pericardial BHV with a thickness of 0.386 mm [47,49] What is more, the findings of this study suggest that moderate curvature of the belly curve contributes to reducing valve fluttering frequency. Curvature of belly curve that is either too small or too large can result in an elevated fluttering frequency, with the former having a more pronounced impact. Consequently, the durability of valves with small curvature of the belly curve are more susceptible to adverse effects caused by fluttering.

5. Limitation

This study analyzed the effect of only one of the design parameters qualitatively, therefore the adjustment range of the curvature of the belly curve of the valve was not given quantitatively, and possible interaction effects between the belly curve and the other geometrical parameters (e.g., the free edge, the dimension of the aortic root) were not captured. An isotropic nonlinear hyper-elastic material was assumed for the mechanical properties of the leaflets. The results of this article can provide certain reference for other isotropic materials. However, the reference provided for anisotropic materials, e.g., biomaterials used in real bioprosthetic valve leaflets, is limited. Regarding the fluid domain, a turbulence model was not used, which should be considered in future studies because it can model the effects of turbulence on the mean flow. However, turbulence models are not able to reproduce flow instabilities directly. The smoothness observed in the flow fields in Figure 7 may be due to the dissipative character of the numerical schemes used, rather than the absence of a turbulence model. Although this study did not capture flow instabilities, the results obtained still have general validity for the comparative purposes intended here. In this study, blood was modeled as an incompressible Newtonian fluid. Although blood is a complex fluid composed of approximately 45% highly deformable red blood cells suspended in a Newtonian fluid (plasma), the computational cost of resolving individual red blood cells in valve flow simulations is currently too high. Therefore, blood is treated as a Newtonian fluid in this context. This assumption is accurate in the left ventricle, where the size of red blood cells is several orders of magnitude smaller than the flow domain’s dimensions. Simplifying the blood to a Newtonian fluid reduces the computational complexity, especially in fluid–structure interaction (FSI) simulations involving complex geometries, like heart valves. While blood exhibits non-Newtonian behavior under certain conditions, such as shear thinning effects, these are less pronounced at the high flow velocities near heart valves, making the Newtonian assumption reasonable under high shear rate conditions. Previous studies have shown that assuming blood as a Newtonian fluid yields results that correlate well with experimental data in many cardiac valve simulations, suggesting that this simplification does not significantly affect the accuracy of the simulations.
In addition, the aortic wall was assumed as a rigid structure. Previous research indicates that the assumption of the rigid wall increases the level of the stresses and strain occurring at the point of the valve closure [52,53]. As this article is a qualitative study on the performance trends with respect to the curvature of the belly curve, it is expected that this impact will not change the trend of the results. Besides, several reports have shown that the flow rate oscillation based on the rigid artery hypothesis is observed to be much smaller in elastic-wall computations and human aortas [52,54,55], which has an impact on the magnitude of VR. Finally, the pressure BC avoids the defect of specifying regurgitation in advance but it is not enough to make comparisons between different PHVs. Independent of the condition of the valve, a fixed stroke volume is pumped by the heart for every cardiac cycle [56], but applying only a pressure BC did not ensure a fixed stroke volume between different valves. Consequently, the pressure BC had a certain influence on the findings. In this regard, a more precise BC that the flow controlled during systole and the pressure controlled during diastole will be adopted for FSI simulation of PHVs, and in-vitro studies will be carried out for the enhancement of simulation credibility in the future.

6. Conclusions

In this paper, FSI models were applied to simulate the performance of valves with different curvatures of belly curves. In general, GOA and CA are negatively and positively related to the curvature of the belly curve, respectively. Nevertheless, an excessive increase in the curvature can lead to incomplete sealing of free edges of the valve during its closure, which results in a decrease in CA and an increase in VR. Moderate curvature of the belly curve contributes to reduce RF and fluttering frequency. Valves with small curvature experienced a significantly higher frequency of fluttering. The peak stresses are distributed along the attachment curve and all stress concentrations intensify with the increase in the curvature of the belly curve. To sum up, the valve with moderate curvature of the belly curve strikes the best compromise between valve performance parameters, leaflets kinematics and mechanical stress. Considering the different effects of the curvature of belly curve on valve performance parameters, the PHV design with variable curvature of belly curve may be a direction of valve performance optimization.

Author Contributions

Conceptualization: T.L. and J.Z.; Methodology: J.Z. and Y.C.; Software: J.Z. and T.L.; Formal analysis: J.Z.; Investigation: J.Z.; Resources: Y.C. and Y.X.; Data curation: Y.W. and L.C.; Writing—original draft preparation: J.Z.; Writing—review and editing: Y.C. and L.C.; Visualization: Y.C. and Y.W.; Supervision: Y.C.; Project administration: Y.C. and Y.X.; Funding acquisition: Y.C. and Y.X. All authors have read and agreed to the published version of the manuscript.

Funding

This study was funded by the National Natural Science Foundation of China (Grant No. 12172239) under the project titled “Biomechanical Study of Synthetic Polymeric Heart Valves’ Flutter Behavior”.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors on request.

Conflicts of Interest

The authors declare no conflicts of interest.

Appendix A

Table A1. Mesh independence study of the fluid domain and solid domain.
Table A1. Mesh independence study of the fluid domain and solid domain.
Fluid DomainSolid Domain
Main Body
Min–Max Size (mm)		Fluid–Structure Interface
Min–Max Size (mm)		Total ElementsLeaflet Element
Size (mm)		Total Elements
Coarse0.4–10.4263,6620.435,051
Fine0.2–0.80.2–0.4469,8910.2–0.465,379
Finer0.15–0.60.15–0.31,194,9950.15–0.3130,773
Fluids 09 00209 g0a1
Figure A1. Mesh independence study was conducted by comparing (a) the GOA, (b) the von-Mises Stress during the complete closure phase of the valve, (c) the flow rate.
Figure A1. Mesh independence study was conducted by comparing (a) the GOA, (b) the von-Mises Stress during the complete closure phase of the valve, (c) the flow rate.
Fluids 09 00209 g0a1
Table A2. The number of elements for all models.
Table A2. The number of elements for all models.
Fluid ElementsSolid ElementsTotal Elements
valve 1469,89165,379535,270
valve 2467,63968,878536,517
valve 3468,86270,903539,765
valve 4448,66672,870521,536
valve 5438,43273,043511,475

References

  1. Salaun, E.; Clavel, M.A.; Rodes-Cabau, J.; Pibarot, P. Bioprosthetic aortic valve durability in the era of transcatheter aortic valve implantation. Heart 2018, 104, 1323–1332. [Google Scholar] [CrossRef] [PubMed]
  2. Butcher, J.T.; Mahler, G.J.; Hockaday, L.A. Aortic valve disease and treatment: The need for naturally engineered solutions. Adv. Drug Deliv. Rev. 2011, 63, 242–268. [Google Scholar] [CrossRef] [PubMed]
  3. Dvir, D.; Bourguignon, T.; Otto, C.M.; Hahn, R.T.; Rosenhek, R.; Webb, J.G.; Treede, H.; Sarano, M.E.; Feldman, T.; Wijeysundera, H.C.; et al. Standardized Definition of Structural Valve Degeneration for Surgical and Transcatheter Bioprosthetic Aortic Valves. Circulation 2018, 137, 388–399. [Google Scholar] [CrossRef] [PubMed]
  4. Iung, B.; Rodes-Cabau, J. The optimal management of ant thrombotic therapy after valve replacement: Certainties and uncertainties. Eur. Heart J. 2014, 35, 2942–2949. [Google Scholar] [CrossRef] [PubMed]
  5. Li, R.L.; Russ, J.; Paschalides, C.; Ferrari, G.; Waisman, H.; Kysar, J.W.; David, K. Mechanical considerations for polymeric heart valve development: Biomechanics, materials, design and manufacturing. Biomaterials 2019, 225, 119493. [Google Scholar] [CrossRef] [PubMed]
  6. Gharaie, S.H.; Morsi, Y. A novel design of a polymeric aortic valve. Int. J. Artif. Organs 2015, 38, 259–270. [Google Scholar] [CrossRef] [PubMed]
  7. Rahmani, B.; Tzamtzis, S.; Ghanbari, H.; Burriesci, G.; Seifalian, A.M. Manufacturing and hydrodynamic assessment of a novel aortic valve made of a new nanocomposite polymer. J. Biomech. 2012, 45, 1205–1211. [Google Scholar] [CrossRef]
  8. Rahmani, B.; Tzamtzis, S.; Sheridan, R.; Mullen, M.J.; Yap, J.; Seifalian, A.M.; Burriesci, G. A new transcatheter heart valve concept (the TRISKELE): Feasibility in an acute preclinical model. Eurointervention 2016, 12, 901–908. [Google Scholar] [CrossRef]
  9. Dasi, L.P.; Simon, H.A.; Sucosky, P.; Yoganathan, A.P. Fluid Mechanics of Artificial Heart Valves. Clin. Exp. Pharmacol. Physiol. 2009, 36, 225–237. [Google Scholar] [CrossRef]
  10. ISO 5840-3:2013; Cardiovascular Implants-Cardiac Valve Prostheses-Part 3: Heart Valve Substitutes Implanted by Transcatheter Techniques. The International Organization for Standardization: Geneva, Switzerland, 2013.
  11. Jiang, H.J.; Campbell, G.; Boughner, D.; Wan, W.K.; Quantz, M. Design and manufacture of a polyvinyl alcohol (PVA) cryogel tri-leaflet heart valve prosthesis. Med. Eng. Phys. 2004, 26, 269–277. [Google Scholar] [CrossRef]
  12. Travaglino, S.; Murdock, K.; Anh, T.; Martin, C.; Liang, L.; Wang, Y.; Sun, W. Computational Optimization Study of Transcatheter Aortic Valve Leaflet Design Using Porcine and Bovine Leaflets. J. Biomech. Eng.-Trans. ASME 2020, 142, 011007. [Google Scholar] [CrossRef] [PubMed]
  13. Li, K.; Sun, W. Simulated transcatheter aortic valve deformation: A parametric study on the impact of leaflet geometry on valve peak stress. Int. J. Numer. Methods Biomed. Eng. 2017, 33, e02814. [Google Scholar] [CrossRef] [PubMed]
  14. Tao, L.; Zhou, J.; Zhou, H.; Li, Y.; Yan, X.; Yu, C. Research on fatigue optimization simulation of polymeric heart valve based on the iterative sub-regional thickened method. Int. J. Numer. Methods Biomed. Eng. 2023, 39, e3717. [Google Scholar] [CrossRef] [PubMed]
  15. Claiborne, T.E.; Xenos, M.; Sheriff, J.; Chiu, W.-C.; Soares, J.; Alemu, Y.; Gupta, S.; Judex, S.; Slepian, M.J.; Bluestein, D. Toward Optimization of a Novel Trileaflet Polymeric Prosthetic Heart Valve via Device Thrombogenicity Emulation. Asaio J. 2013, 59, 275–283. [Google Scholar] [CrossRef]
  16. Kouhi, E.; Morsi, Y.S. A parametric study on mathematical formulation and geometrical construction of a stentless aortic heart valve. J. Artif. Organs 2013, 16, 425–442. [Google Scholar] [CrossRef]
  17. Abbasi, M.; Azadani, A.N. A geometry optimization framework for transcatheter heart valve leaflet design. J. Mech. Behav. Biomed. Mater. 2020, 102, 103491. [Google Scholar] [CrossRef]
  18. Xu, F.; Morganti, S.; Zakerzadeh, R.; Kamensky, D.; Auricchio, F.; Reali, A.; Hughes, T.J.R.; Sacks, M.S.; Hsu, M.-C. A framework for designing patient-specific bioprosthetic heart valves using immersogeometric fluid-structure interaction analysis. Int. J. Numer. Methods Biomed. Eng. 2018, 34, e2938. [Google Scholar] [CrossRef]
  19. Gulbulak, U.; Ertas, A.; Baturalp, T.B.; Pavelka, T. The effect of fundamental curves on geometric orifice and coaptation areas of polymeric heart valves. J. Mech. Behav. Biomed. Mater. 2020, 112, 104039. [Google Scholar] [CrossRef]
  20. Toggweiler, S.; Wood, D.A.; Rodes-Cabau, J.; Kapadia, S.; Willson, A.B.; Ye, J.; Cheung, A.; Leipsic, J.; Binder, R.K.; Gurvitch, R.; et al. Transcatheter Valve-In-Valve Implantation for Failed Balloon-Expandable Transcatheter Aortic Valves. JACC Cardiovasc. Interv. 2012, 5, 571–577. [Google Scholar] [CrossRef]
  21. Feng, W.; Yang, X.; Liu, Y.; Fan, Y. An In Vitro Feasibility Study of the Influence of Configurations and Leaflet Thickness on the Hydrodynamics of Deformed Transcatheter Aortic Valve. Artif. Organs 2017, 41, 735–743. [Google Scholar] [CrossRef]
  22. Roman, M.J.; Devereux, R.B.; Kramerfox, R.; Oloughlin, J.; Spitzer, M.; Robins, J. Two-Dimensional Echocardiographic Aortic Root Dimensions in Normal-Children and Adults. Am. J. Cardiol. 1989, 64, 507–512. [Google Scholar] [CrossRef] [PubMed]
  23. LS-DYNA_Manual_Volume_I_R11 LSTC. 2018. Available online: https://lsdyna.ansys.com/manuals/ (accessed on 2 September 2024).
  24. Bonet, J.; Burton, A.J. A simple average nodal pressure tetrahedral element for incompressible and nearly incompressible dynamic explicit applications. Commun. Numer. Methods Eng. 1998, 14, 437–449. [Google Scholar] [CrossRef]
  25. Amindari, A.; Kırkköprü, K.; Saltık, İ.l.; Sünbüloğlu, E. Effect of non-linear leaflet material properties on aortic valve dynamics—A coupled fluid-structure approach. Eng. Solid Mech. 2021, 9, 123–136. [Google Scholar] [CrossRef]
  26. Gnyaneshwar, R.; Kumar, R.K.; Balakrishnan, K.R. Dynamic analysis of the aortic valve using a finite element model. Ann. Thorac. Surg. 2002, 73, 1122–1129. [Google Scholar] [CrossRef]
  27. Huelsmann, J.; Gruen, K.; El Amouri, S.; Barth, M.; Hornung, K.; Holzfuss, C.; Lichtenberg, A.; Akhyari, P. Transplantation material bovine pericardium: Biomechanical and immunogenic characteristics after decellularization vs. glutaraldehyde-fixing. Xenotransplantation 2012, 19, 286–297. [Google Scholar] [CrossRef]
  28. Bozkurt, S.; Preston-Maher, G.L.; Torii, R.; Burriesci, G. Design, Analysis and Testing of a Novel Mitral Valve for Transcatheter Implantation. Ann. Biomed. Eng. 2017, 45, 1852–1864. [Google Scholar] [CrossRef]
  29. Wei, Z.A.; Sonntag, S.J.; Toma, M.; Singh-Gryzbon, S.; Sun, W. Computational Fluid Dynamics Assessment Associated with Transcatheter Heart Valve Prostheses: A Position Paper of the ISO Working Group. Cardiovasc. Eng. Technol. 2018, 9, 289–299. [Google Scholar] [CrossRef]
  30. Luraghi, G.; Wu, W.; De Gaetano, F.; Matas, J.F.R.; Moggridge, G.D.; Serrani, M.; Stasiak, J.; Costantino, M.L.; Migliavacca, F. Evaluation of an aortic valve prosthesis: Fluid-structure interaction or structural simulation? J. Biomech. 2017, 58, 45–51. [Google Scholar] [CrossRef]
  31. Marom, G.; Haj-Ali, R.; Raanani, E.; Schaefers, H.-J.; Rosenfeld, M. A fluid-structure interaction model of the aortic valve with coaptation and compliant aortic root. Med. Biol. Eng. Comput. 2012, 50, 173–182. [Google Scholar] [CrossRef]
  32. Caldichoury, I.; Paz, R.R.; Del Pin, F. ICFD Theory Manual Incompressible Fluid Solver in LS-DYNA; Livermore Software Technology Corp: Livermore, CA, USA, 2014. [Google Scholar]
  33. Cao, K.; Sucosky, P. Computational comparison of regional stress and deformation characteristics in tricuspid and bicuspid aortic valve leaflets. Int. J. Numer. Methods Biomed. Eng. 2017, 33, e02798. [Google Scholar] [CrossRef]
  34. De Hart, J.; Baaijens, F.P.T.; Peters, G.W.M.; Schreurs, P.J.G. A computational fluid-structure interaction analysis of a fiber-reinforced stentless aortic valve. J. Biomech. 2003, 36, 699–712. [Google Scholar] [CrossRef] [PubMed]
  35. de Tullio, M.D.; Afferrante, L.; Demelio, G.; Pascazio, G.; Verzicco, R. Fluid-structure interaction of deformable aortic prostheses with a bileaflet mechanical valve. J. Biomech. 2011, 44, 1684–1690. [Google Scholar] [CrossRef]
  36. Kim, H.; Lu, J.; Sacks, M.S.; Chandran, K.B. Dynamic simulation of bioprosthetic heart valves using a stress resultant shell model. Ann. Biomed. Eng. 2008, 36, 262–275. [Google Scholar] [CrossRef]
  37. Garcia, D.; Kadem, L. What do you mean by aortic valve area: Geometric orifice area, effective orifice area, or Gorlin area? J. Heart Valve Dis. 2006, 15, 601–608. [Google Scholar]
  38. Wu, C.; Saikrishnan, N.; Chalekian, A.J.; Fraser, R.; Ieropoli, O.; Retta, S.M.; Joseph, R.; Lee, S.; Marquez, S.; Mester, D.; et al. In-Vitro Pulsatile Flow Testing of Prosthetic Heart Valves: A Round-Robin Study by the ISO Cardiac Valves Working Group. Cardiovasc. Eng. Technol. 2019, 10, 397–422. [Google Scholar] [CrossRef]
  39. Lee, J.H.; Scotten, L.N.; Hunt, R.; Caranasos, T.G.; Vavalle, J.P.; Griffith, B.E. Bioprosthetic aortic valve diameter and thickness are directly related to leaflet fluttering: Results from a combined experimental and computational modeling study. JTCVS Open 2021, 6, 60–81. [Google Scholar] [CrossRef] [PubMed]
  40. Luraghi, G.; Migliavacca, F.; Matas, J.F.R. Study on the Accuracy of Structural and FSI Heart Valves Simulations. Cardiovasc. Eng. Technol. 2018, 9, 723–738. [Google Scholar] [CrossRef] [PubMed]
  41. Hsu, M.-C.; Kamensky, D.; Xu, F.; Kiendl, J.; Wang, C.; Wu, M.C.H.; Mineroff, J.; Reali, A.; Bazilevs, Y.; Sacks, M.S. Dynamic and fluid-structure interaction simulations of bioprosthetic heart valves using parametric design with T-splines and Fung-type material models. Comput. Mech. 2015, 55, 1211–1225. [Google Scholar] [CrossRef]
  42. Weinberg, E.J.; Kaazempur Mofrad, M.R. Transient, three-dimensional, multiscale simulations of the human aortic valve. Cardiovasc. Eng. 2007, 7, 140–155. [Google Scholar] [CrossRef]
  43. Rassoli, A.; Fatouraee, N.; Guidoin, R.; Zhang, Z.; Ravaghi, S. A comparative study of different tissue materials for bioprosthetic aortic valves using experimental assays and finite element analysis. Comput. Methods Programs Biomed. 2022, 220, 106813. [Google Scholar] [CrossRef]
  44. Applegate, P.M.; Boyd, W.D.; Applegate Ii, R.L.; Liu, H. Is it the time to reconsider the choice of valves for cardiac surgery: Mechanical or bioprosthetic? J. Biomed. Res. 2017, 31, 373–376. [Google Scholar] [CrossRef] [PubMed]
  45. Rodriguez-Gabella, T.; Voisine, P.; Puri, R.; Pibarot, P.; Rodes-Cabau, J. Aortic Bioprosthetic Valve Durability Incidence, Mechanisms, Predictors, and Management of Surgical and Transcatheter Valve Degeneration. J. Am. Coll. Cardiol. 2017, 70, 1013–1028. [Google Scholar] [CrossRef] [PubMed]
  46. Aljalloud, A.; Shoaib, M.; Egron, S.; Arias, J.; Tewarie, L.; Schnoering, H.; Lotfi, S.; Goetzenich, A.; Hatam, N.; Pott, D.; et al. The flutter-by effect: A comprehensive study of the fluttering cusps of the Perceval heart valve prosthesis. Interact. Cardiovasc. Thorac. Surg. 2018, 27, 664–670. [Google Scholar] [CrossRef] [PubMed]
  47. Johnson, E.L.; Wu, M.C.H.; Xu, F.; Wiese, N.M.; Rajanna, M.R.; Herrema, A.J.; Ganapathysubramanian, B.; Hughes, T.J.R.; Sacks, M.S.; Hsu, M.-C. Thinner biological tissues induce leaflet flutter in aortic heart valve replacements. Proc. Natl. Acad. Sci. USA 2020, 117, 19007–19016. [Google Scholar] [CrossRef] [PubMed]
  48. Peacock, J.A. An Invitro Study of the Onset of Turbulence in the Sinus of Valsalva. Circ. Res. 1990, 67, 448–460. [Google Scholar] [CrossRef]
  49. Becsek, B.; Pietrasanta, L.; Obrist, D. Turbulent Systolic Flow Downstream of a Bioprosthetic Aortic Valve: Velocity Spectra, Wall Shear Stresses, and Turbulent Dissipation Rates. Front. Physiol. 2020, 11, 577188. [Google Scholar] [CrossRef]
  50. Vennemann, B.; Roesgen, T.; Heinisch, P.P.; Obrist, D. Leaflet Kinematics of Mechanical and Bioprosthetic Aortic Valve Prostheses. ASAIO J. 2018, 64, 651–661. [Google Scholar] [CrossRef]
  51. Avelar, A.H.d.F.; Canestri, J.A.; Bim, C.; Silva, M.G.M.; Huebner, R.; Pinotti, M. Quantification and Analysis of Leaflet Flutter on Biological Prosthetic Cardiac Valves. Artif. Organs 2017, 41, 835–844. [Google Scholar] [CrossRef]
  52. Hsu, M.-C.; Kamensky, D.; Bazilevs, Y.; Sacks, M.S.; Hughes, T.J.R. Fluid-structure interaction analysis of bioprosthetic heart valves: Significance of arterial wall deformation. Comput. Mech. 2014, 54, 1055–1071. [Google Scholar] [CrossRef]
  53. Nestola, M.G.C.; Zulian, P.; Gaedke-Merzhauser, L.; Krause, R. Fully coupled dynamic simulations of bioprosthetic aortic valves based on an embedded strategy for fluid-structure interaction with contact. EUROPACE 2021, 23, I96–I104. [Google Scholar] [CrossRef]
  54. Kendall, M.E.; Rembert, J.C.; Greenfield, J.C. Pressure-Flow Studies in Man—Nature of Aortic Flow Pattern in both Valvular Mitral-Insufficiency and Prolapsing Mitral-Valve Syndrome. Am. Heart J. 1973, 86, 359–365. [Google Scholar] [CrossRef] [PubMed]
  55. Uther, J.B.; Peterson, K.L.; Shabetai, R.; Braunwal, E. Measurement of Ascending Aortic Flow Patterns in Man. J. Appl. Physiol. 1973, 34, 513–518. [Google Scholar] [CrossRef] [PubMed]
  56. Sundaram, G.B.K.; Balakrishnan, K.R.; Kumar, R.K. Aortic valve dynamics using a fluid structure interaction model—The physiology of opening and closing. J. Biomech. 2015, 48, 1737–1744. [Google Scholar] [CrossRef] [PubMed]
Fluids 09 00209 g001
Figure 1. (a) Three basic curves that generated the valve surface, (b) five belly curves and two guidelines generated based on five control points and (c) side views of valve 1, valve 2, valve 3, valve 4, and valve 5, from left to right.
Figure 1. (a) Three basic curves that generated the valve surface, (b) five belly curves and two guidelines generated based on five control points and (c) side views of valve 1, valve 2, valve 3, valve 4, and valve 5, from left to right.
Fluids 09 00209 g001
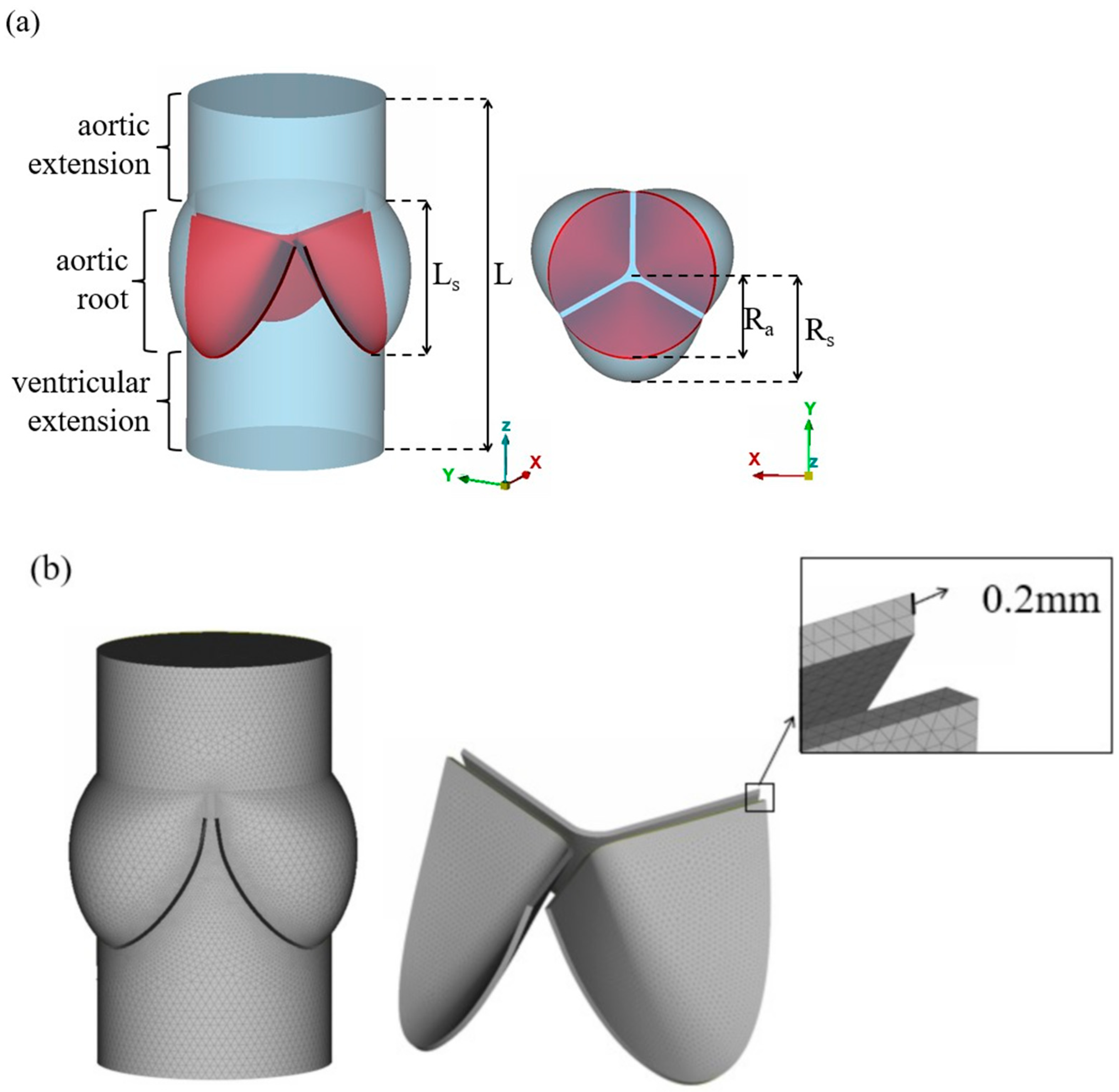
Fluids 09 00209 g002
Figure 2. (a) Geometry design of the fluid field using the modeling design parameters and (b) discretization of solution field by tetrahedral elements.
Figure 2. (a) Geometry design of the fluid field using the modeling design parameters and (b) discretization of solution field by tetrahedral elements.
Fluids 09 00209 g002
Fluids 09 00209 g003
Figure 3. (a) Inlet and outlet of the model and (b) transvalvular pressure difference between left ventricle and aorta.
Figure 3. (a) Inlet and outlet of the model and (b) transvalvular pressure difference between left ventricle and aorta.
Fluids 09 00209 g003
Fluids 09 00209 g004
Figure 4. The calculation approaches and results of RF. (a) Computed volumetric flow rate through the outlet of the tube throughout the cardiac cycle of 5 models, (b) Calculation methods of VF and VR; the three instants are used to analyze the valve stress and flow velocity (taking the volumetric flow rate of valve 1 for example), (c) The calculation results of 5 models.
Figure 4. The calculation approaches and results of RF. (a) Computed volumetric flow rate through the outlet of the tube throughout the cardiac cycle of 5 models, (b) Calculation methods of VF and VR; the three instants are used to analyze the valve stress and flow velocity (taking the volumetric flow rate of valve 1 for example), (c) The calculation results of 5 models.
Fluids 09 00209 g004
Fluids 09 00209 g005
Figure 5. Axial displacements of Point A on the leaflets for all models.
Figure 5. Axial displacements of Point A on the leaflets for all models.
Fluids 09 00209 g005
Fluids 09 00209 g006
Figure 6. Analysis of leaflet kinematics. Dominant fluttering frequencies from the axial displacement waveforms of point A during the systolic phase of the cardiac cycle in the inset of Figure 5.
Figure 6. Analysis of leaflet kinematics. Dominant fluttering frequencies from the axial displacement waveforms of point A during the systolic phase of the cardiac cycle in the inset of Figure 5.
Fluids 09 00209 g006
Fluids 09 00209 g007
Figure 7. The von-Mises stress distribution on the leaflets and flow velocity distribution of the valve cross-section for each valve. (a) Valve 1, (b) valve 2, (c) valve 3, (d) valve 4, (e) valve 5. The instants A, B and C are shown in Figure 4b, which are taken from the fully opened, partially closed, and fully closed phases of the valve, respectively. The red arrow at instant A indicates the deformation of the belly curve of the valve at the peak flow rate. The high stresses of the valve at instants B and C are displayed by magnification.
Figure 7. The von-Mises stress distribution on the leaflets and flow velocity distribution of the valve cross-section for each valve. (a) Valve 1, (b) valve 2, (c) valve 3, (d) valve 4, (e) valve 5. The instants A, B and C are shown in Figure 4b, which are taken from the fully opened, partially closed, and fully closed phases of the valve, respectively. The red arrow at instant A indicates the deformation of the belly curve of the valve at the peak flow rate. The high stresses of the valve at instants B and C are displayed by magnification.
Fluids 09 00209 g007
Table 1. Dimensions of design parameters used in modeling the AV.
Table 1. Dimensions of design parameters used in modeling the AV.
RaRsLsL
Dimension(mm)11.515.017.042.0
Ra: Radius of aorta, Rs: Radius of sinus, Ls: Sinus length, L: Model length.
Table 2. The GOA and the CA results from 5 FSI models. Contour plots indicates the total deformation of the valve; the measuring range of CA is circled with red dotted lines in the third column.
Table 2. The GOA and the CA results from 5 FSI models. Contour plots indicates the total deformation of the valve; the measuring range of CA is circled with red dotted lines in the third column.
GOA (mm2)CA (mm2)
valve 1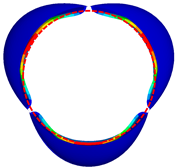Fluids 09 00209 i001
362.21		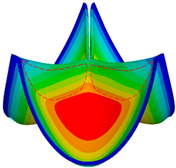Fluids 09 00209 i002
222.16
valve 2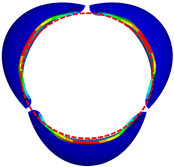Fluids 09 00209 i003
361.62		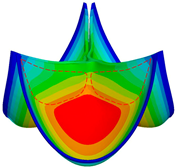Fluids 09 00209 i004
246.97
valve 3Fluids 09 00209 i005
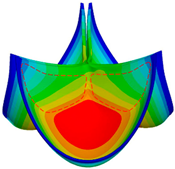361.51		Fluids 09 00209 i006
265.91
valve 4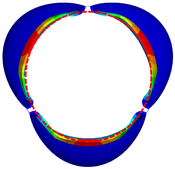Fluids 09 00209 i007
350.52		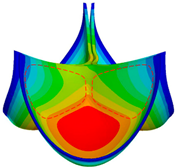Fluids 09 00209 i008
365.73
valve 5Fluids 09 00209 i009
349.52		Fluids 09 00209 i010
299.58
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Zhou, J.; Wu, Y.; Chen, L.; Li, T.; Xiong, Y.; Chen, Y. Numerical Simulation Studies on the Design of the Prosthetic Heart Valves Belly Curves. Fluids 2024, 9, 209. https://doi.org/10.3390/fluids9090209

AMA Style

Zhou J, Wu Y, Chen L, Li T, Xiong Y, Chen Y. Numerical Simulation Studies on the Design of the Prosthetic Heart Valves Belly Curves. Fluids. 2024; 9(9):209. https://doi.org/10.3390/fluids9090209

Chicago/Turabian Style

Zhou, Jingyuan, Yinkui Wu, Lu Chen, Tao Li, Yan Xiong, and Yu Chen. 2024. "Numerical Simulation Studies on the Design of the Prosthetic Heart Valves Belly Curves" Fluids 9, no. 9: 209. https://doi.org/10.3390/fluids9090209

APA Style

Zhou, J., Wu, Y., Chen, L., Li, T., Xiong, Y., & Chen, Y. (2024). Numerical Simulation Studies on the Design of the Prosthetic Heart Valves Belly Curves. Fluids, 9(9), 209. https://doi.org/10.3390/fluids9090209

Article Metrics

Back to TopTop