Aeroacoustic Coupling in Rectangular Deep Cavities: Passive Control and Flow Dynamics
Abstract
1. Introduction
2. Materials and Methods
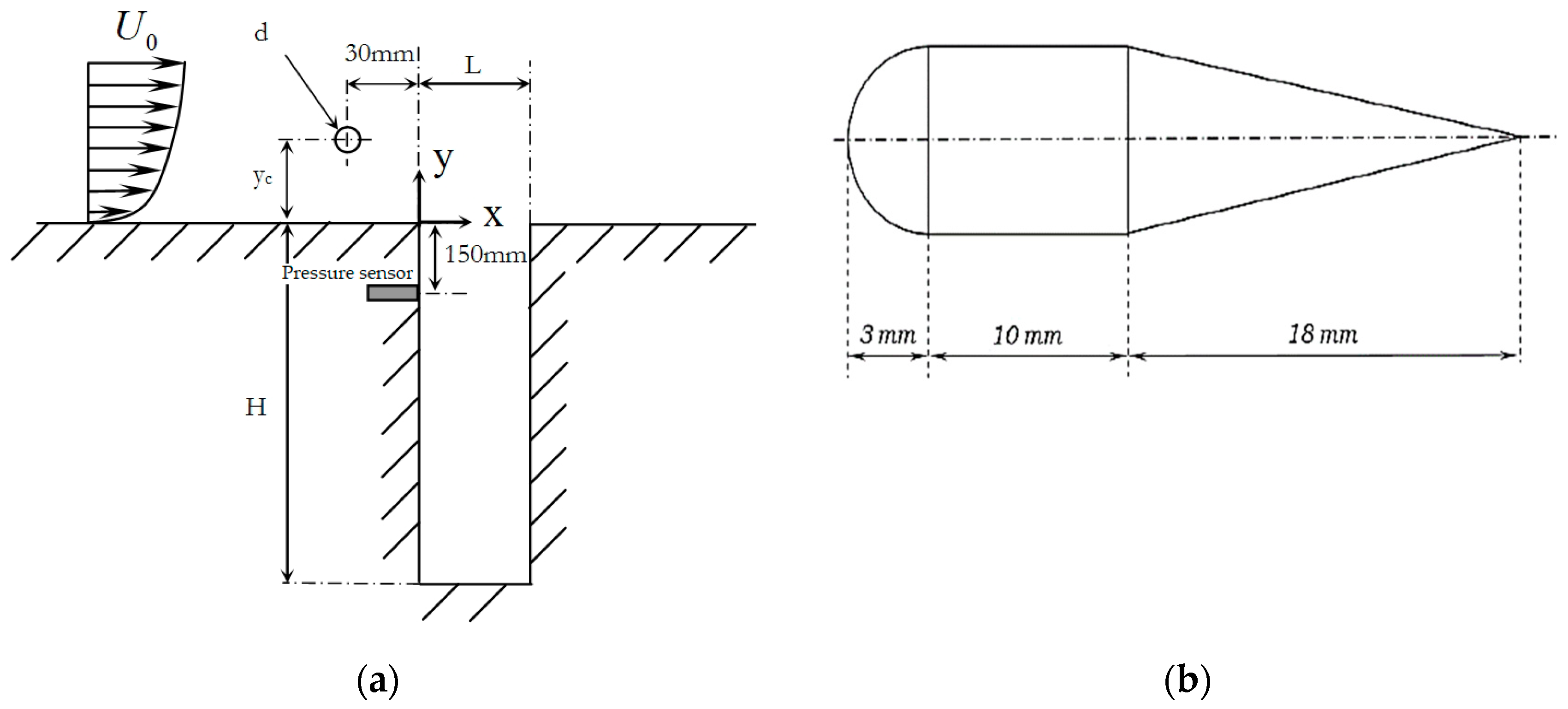
2.1. Cavity and Control Mechanism
2.2. Hot-Wire Measurements
2.3. Acoustic Measurements
2.4. PIV Velocity Measurements
3. Results
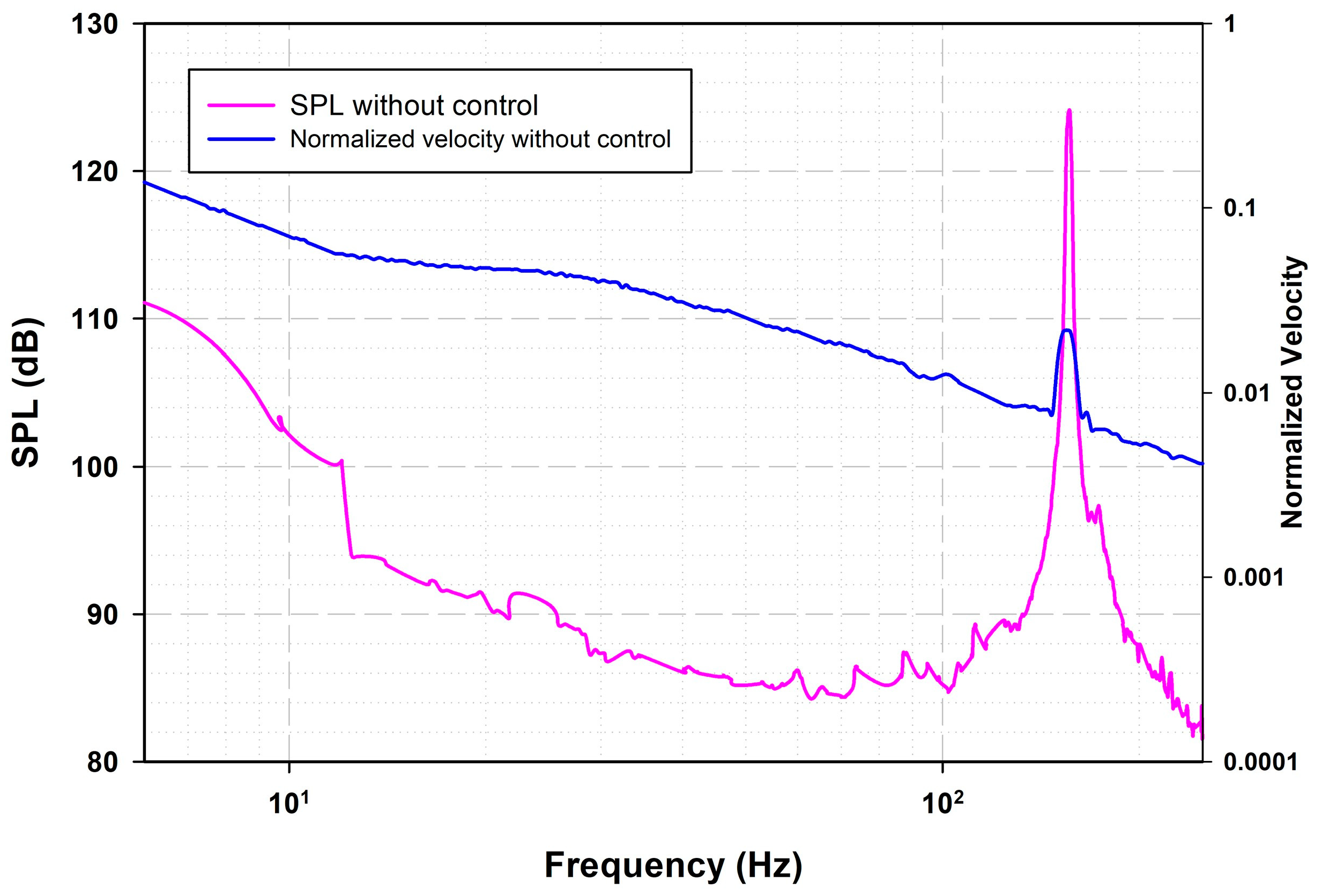
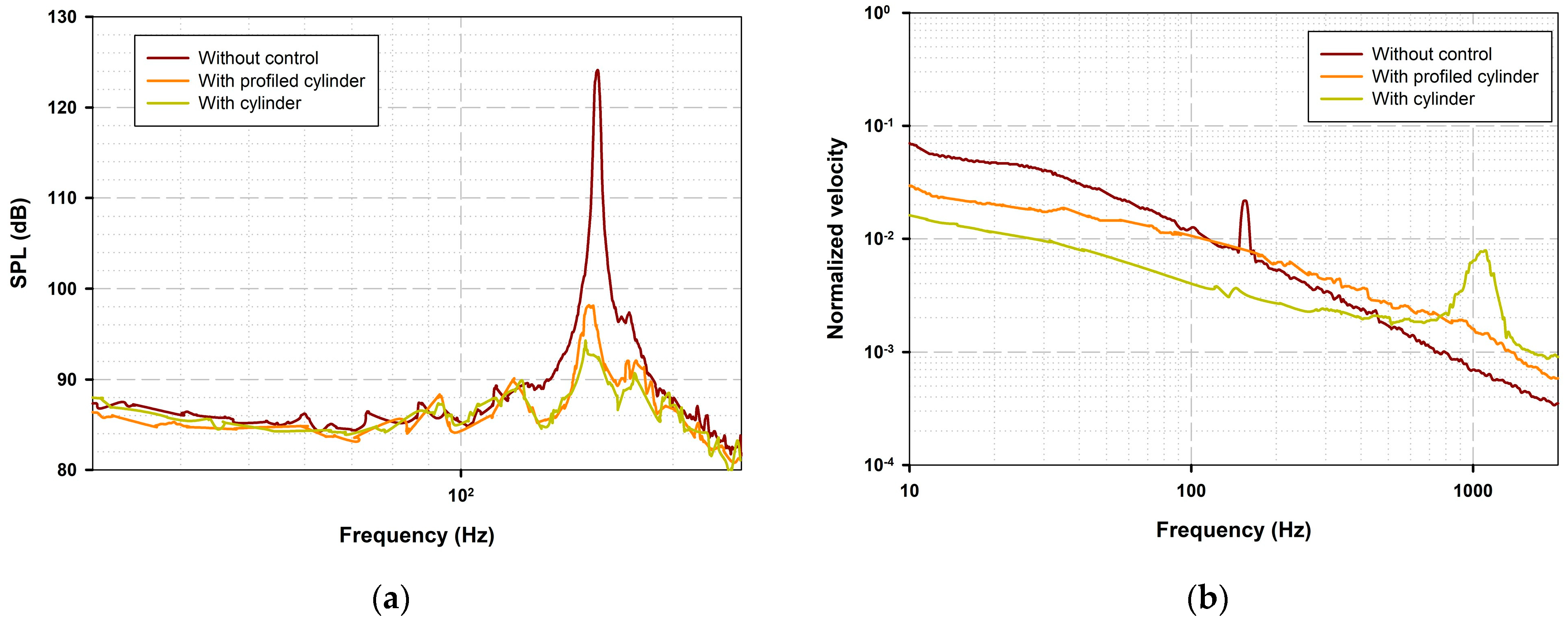
3.1. Acoustic Field
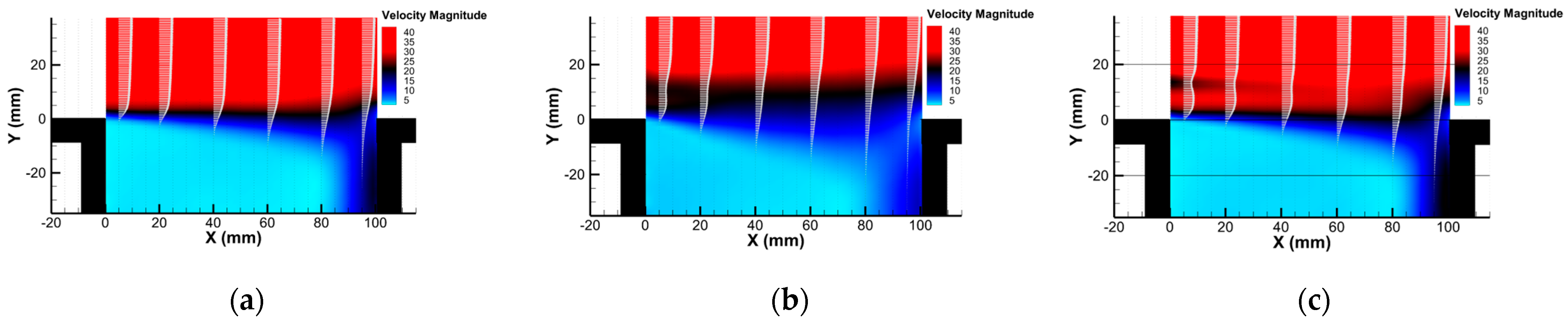
3.2. Kinematic Field
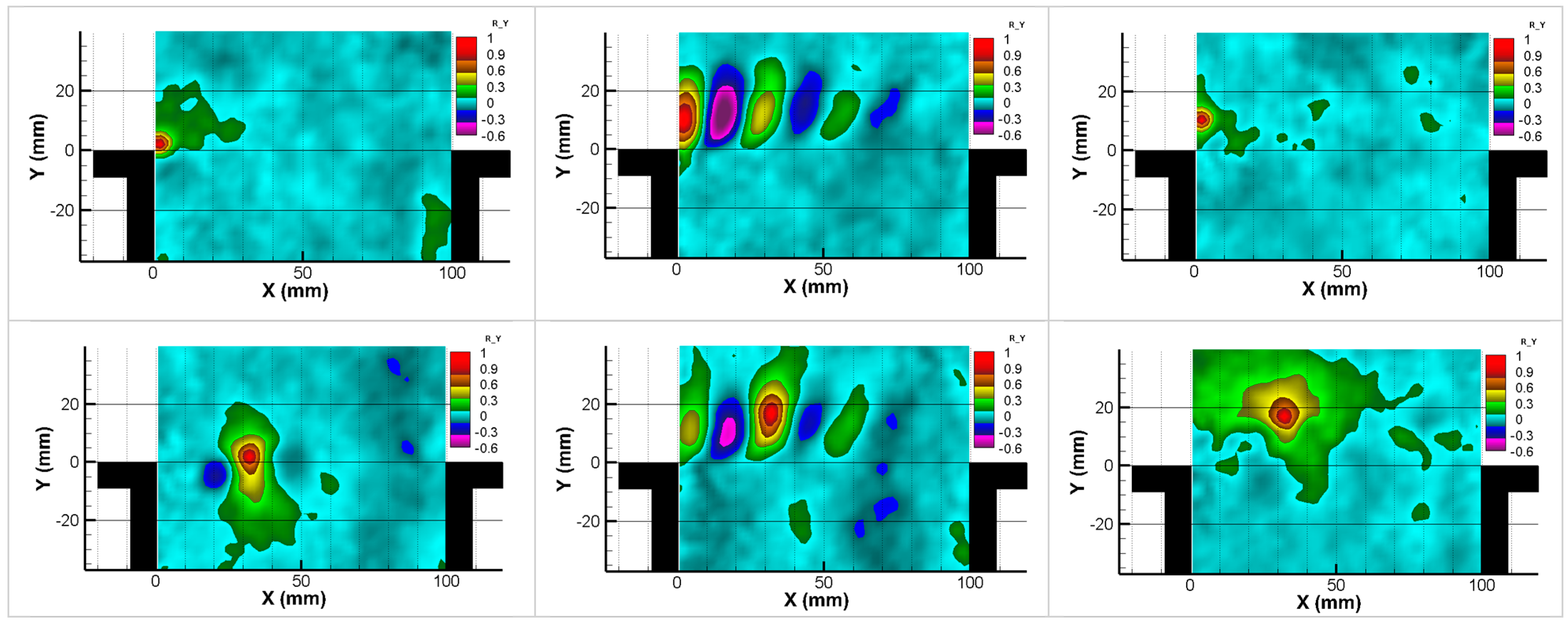
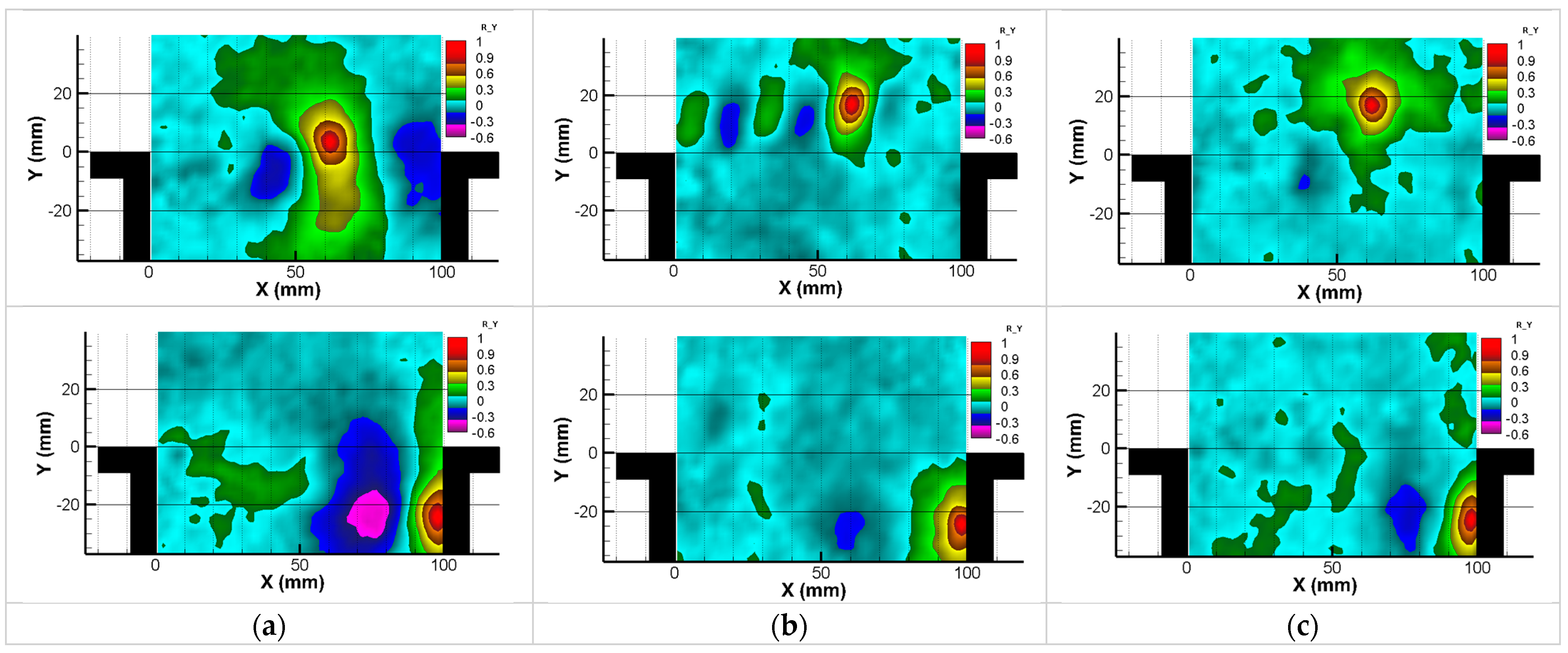
3.3. Cross-Correlation Maps
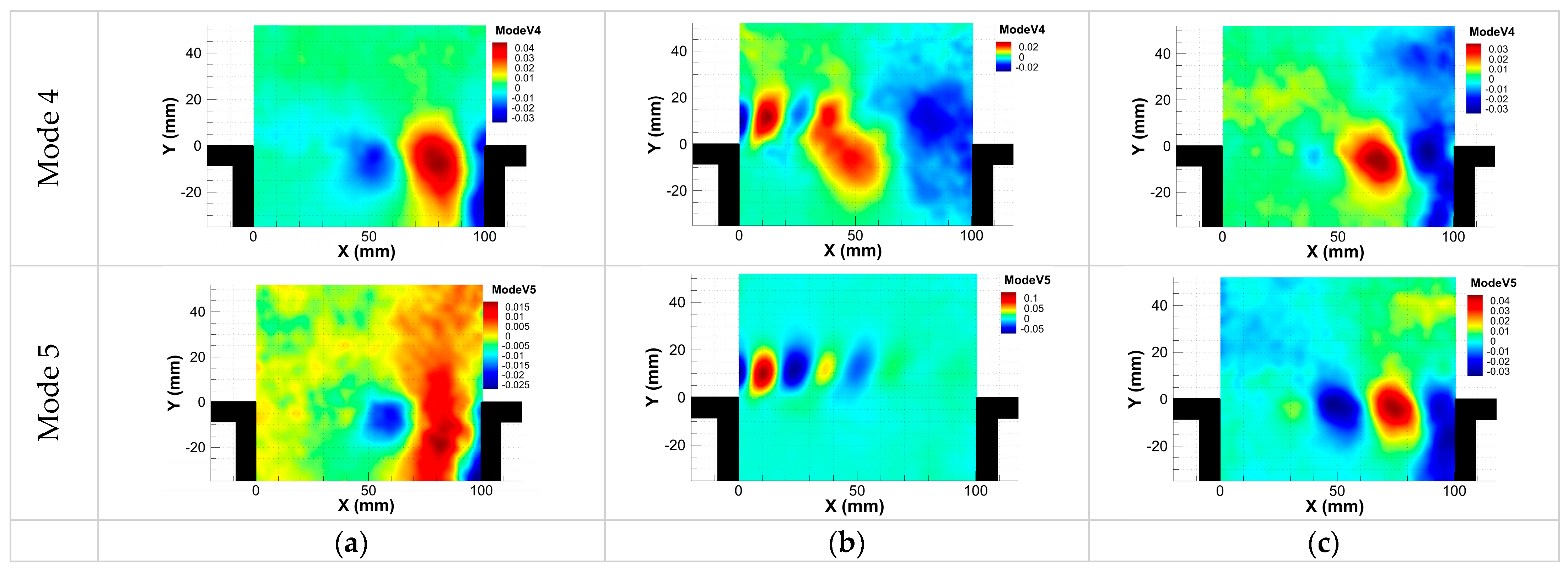
3.4. Proper Orthogonal Decomposition (POD)
4. Conclusions
- Achieving a similar significant reduction in noise with both the cylindrical and profiled cylindrical configurations confirms that this reduction is not attributable to high-frequency forcing.
- Vorticity distribution suggests that the presence of the profiled cylinder introduces minimal disturbance within the cavity shear layer compared to the circular cylinder;
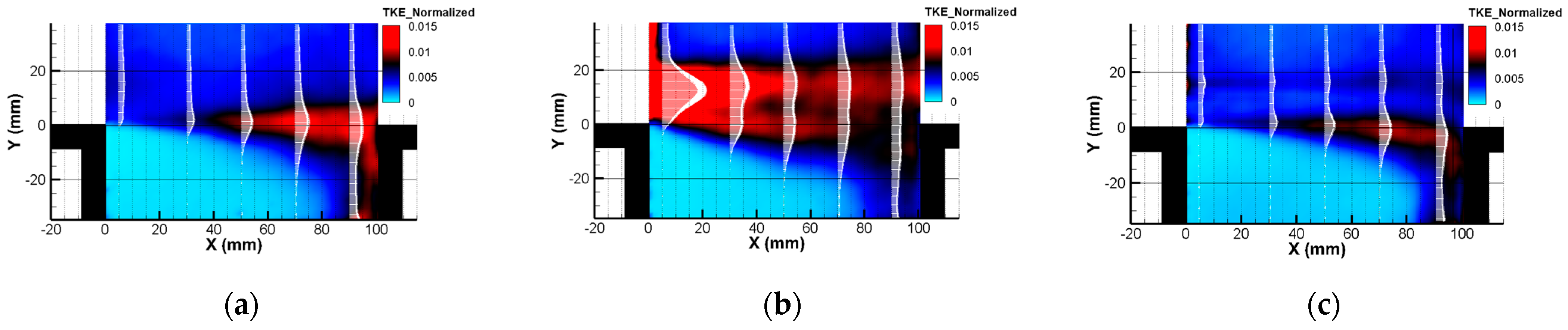
- The distribution of normalized turbulent kinetic energy (TKE) significantly decreases with the profiled cylinder, indicating lower TKE compared to the uncontrolled flow.
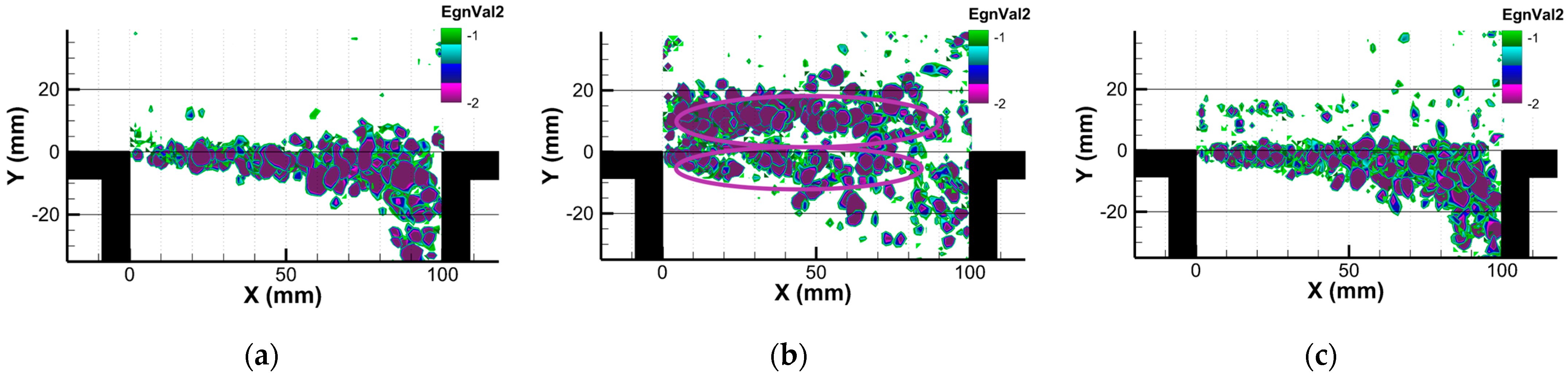
- Lambda-2 fields reveal two primary vortex paths in the case of control with a cylinder: one linked to vortices in the cavity shear layer and the other related to the cylinder shedding.
- Cross-correlation maps validate that effective control of aeroacoustic coupling does not necessitate high-frequency forcing.
- Snapshot POD analysis indicates that in the absence of control, and with control using a profiled cylinder, the first POD mode contains nearly 30% of the flow’s KE, while only 15% of the KE is contained in the first POD mode when using the standard cylinder. This aligns with the decreased vorticity distribution in the shear layer of the flow controlled with the cylinder, resulting in weakened vortical structures. Consequently, the POD projection attributes less energy to the first POD modes since they are associated with these coherent structures.
- Spatial modes reveal that the higher KE content shifts towards modes where vortical structures are oriented upward near the cavity trailing edge. This may partially explain the weak and less-organized pressure waves following the impingement of vortices with the controlled flow compared to the uncontrolled case.
- Many perspectives could be proposed:
- In this study, the focus was on reducing noise near deep cavities. It is worth noting that this noise reduction, achieved by adding a cylinder upstream of the cavity, may lead to an increase in drag and could therefore be detrimental to aerodynamic efficiency. Measurement of friction (estimation of drag) should be considered with the aim of optimizing both aerodynamic and aeroacoustic aspects.
- Investigating energetic transfers from the aerodynamic field towards the acoustic field with and without the control mechanisms would be of interest in a future investigation.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Powell, A. On Edge Tones and Associated Phenomena. 1953. Available online: https://www.ingentaconnect.com/search/article?option2=author&value2=Powell%2c+Alan&pageSize=10&index=7 (accessed on 28 February 2020).
- Krishnamurty, K. Acoustic Radiation from Two-Dimensional Rectangular Cutouts in Aerodynamic Surfaces; NTRS: Washington, DC, USA, 1955. [Google Scholar]
- Assoum, H.H.; Hamdi, J.; Hassan, M.; Abed-Meraim, K.; Kheir, M.E.; Mrach, T.; Asmar, S.E.; Sakout, A. Turbulent kinetic energy and self-sustaining tones: Experimental study of a rectangular impinging jet using high Speed 3D tomographic Particle Image Velocimetry. J. Mech. Eng. Sci. 2020, 14, 6322–6333. [Google Scholar] [CrossRef]
- Hamdi, J.; Assoum, H.H.; Abed-Meraïm, K.; Sakout, A. Volume reconstruction of a plane jet impinging on a slotted plate using the phase averaging technique. Energy Procedia 2017, 139, 404–409. [Google Scholar] [CrossRef]
- Assoum, H.H.; El Hassan, M.; Abed-Meraim, K.; Sakout, A. The vortex dynamics and the self sustained tones in a plane jet impinging on a slotted plate. Eur. J. Mech.-B/Fluids 2014, 48, 231–235. [Google Scholar] [CrossRef]
- El Zohbi, B.; Assoum, H.H.; Alkheir, M.; Afyouni, N.; Meraim, K.A.; Sakout, A.; El Hassan, M. Experimental investigation of the Aero-Acoustics of a rectangular jet impinging a slotted plate for different flow regimes. Alex. Eng. J. 2024, 87, 404–416. [Google Scholar] [CrossRef]
- Afyouni, N.E.; Alkheir, M.; Assoum, H.; El Zohbi, B.; Abed-Meraim, K.; Sakout, A.; El Hassan, M. Effect of a Control Mechanism on the Interaction between a Rectangular Jet and a Slotted Plate: Experimental Study of the Aeroacoustic Field. Fluids 2023, 8, 309. [Google Scholar] [CrossRef]
- Assoum, H.H.; El Kheir, M.; Afyouni, N.E.; El Zohbi, B.; Meraim, K.A.; Sakout, A.; El Hassan, M. Control of a rectangular impinging jet: Experimental investigation of the flow dynamics and the acoustic field. Alex. Eng. J. 2023, 79, 354–365. [Google Scholar] [CrossRef]
- Alkheir, M.; Assoum, H.H.; Hamdi, J.; Mrach, T.; Hassan, M.; Sakout, A. Experimental study of the vortex organization in a rectangular impinging jet in the presence of self-sustained tones. Energy Rep. 2021, 8, 1486–1492. [Google Scholar] [CrossRef]
- Assoum, H.H.; Hamdi, J.; Alkheir, M.; Meraim, K.A.; Sakout, A.; Obeid, B.; El Hassan, M. Tomographic Particle Image Ve-locimetry and Dynamic Mode Decomposition (DMD) in a Rectangular Impinging Jet: Vortex Dynamics and Acoustic Gen-eration. Fluids 2021, 6, 429. [Google Scholar] [CrossRef]
- Jabado, A.H.; Assoum, H.H.; Hammoud, A.; Meraim, K.A.; Sakout, A.; El Hassan, M. Review-Heat Transfer Inside Cavity Flows Trends. IOP Conf. Series Earth Environ. Sci. 2022, 1008, 012002. [Google Scholar] [CrossRef]
- Jabado, A.H.; El Hassan, M.; Assoum, H.H.; Hammoud, A.; Meraim, K.A.; Sakout, A. A review of cavity heat transfer under separated/reattached flow conditions. Energy Rep. 2021, 8, 949–956. [Google Scholar] [CrossRef]
- Charwat, A.; Roos, J.; Dewey, F., Jr.; Hitz, J. An investigation of separated flows-Part I: The pressure field. J. Aerosp. Sci. 1961, 28, 457–470. [Google Scholar] [CrossRef]
- Rossiter, J. The Effects of Cavities on the Buffeting of Aircraft. RAE Technical Memorandum No. Aero 754. 1962. Available online: https://www.semanticscholar.org/paper/The-effects-of-cavities-on-the-buffeting-of-Rossiter/6643bd3131210206868827364f0cb8cd5ecf40ae (accessed on 14 August 2024).
- East, L. Aerodynamically induced resonance in rectangular cavities. J. Sound Vib. 1966, 3, 277–287. [Google Scholar] [CrossRef]
- Plumblee, H.; Gibson, J.; Lassiter, L. A Theoretical and Experimental Investigation of the Acoustic Response of Cavities in an Aerodynamic Flow; Flight Dynamics Laboratory, Aeronautical Systems Division, Air Force Systems: Wright-Patterson AFB, OH, USA, 1962. [Google Scholar]
- Heller, H.; Holmes, D.; Covert, E. Flow-induced pressure oscillations in shallow cavities. J. Sound Vib. 1971, 18, 545–553. [Google Scholar] [CrossRef]
- Rockwell, D.; Naudascher, E. Review—Self-Sustaining Oscillations of Flow Past Cavities. J. Fluids Eng. 1978, 100, 152–165. [Google Scholar] [CrossRef]
- El Hassan, M.; Labraga, L.; Keirsbulck, L. Aero-Acoustic Oscillations inside Large Deep Cavities. 2007. Available online: https://espace.library.uq.edu.au/data/UQ_120829/Hassan_afmc_16_07.pdf?Expires=1723967529&Key-Pair-Id=APKAJKNBJ4MJBJNC6NLQ&Signature=GeOqc~Fgk-VhHIpIcKlbwYVBOvgOUEaGSVAleFBUb8Y-hXBY9EDHReUO8D0ifQH5lmgpI3XWPujvibc8P3MEtaHuogmkfxrP-jpntFHGom4bhc2bNeAxwFM9m2JUiJ9uDgQaA5-Hn6VOhvHcuYTgtvbe8nd4Ru2PbhMF-yJpGJalPybwbQRoVZVVcdVAUmS5tCSCW~wIcugfNJaMbczTxxPskxgJG0l~MOGl6dg6WclsKRGCDjG2xA0rkppW5jzK0NQbPpH0f0jVFvS1cd-k1vG4DvOT6Q5YQI80fPpGnkqAM1EDL9PJHCIn7QO5lvga3QvxRVZ9KaddBKiy2NeRQA__ (accessed on 15 August 2024).
- El Hassan, M.; Keirsbulck, L.; Labraga, L. Non-oscillating/Oscillating Shear Layer over a Large Deep Cavity at Low-Subsonic Speeds. Flow, Turbul. Combust. 2008, 82, 359–374. [Google Scholar] [CrossRef]
- El Hassan, M.; Keirsbulck, L.; Labraga, L. Aero-Acoustic Coupling Inside Large Deep Cavities at Low-Subsonic Speeds. J. Fluids Eng. 2008, 131, 011204. [Google Scholar] [CrossRef]
- Sinha, J.; Arora, K. Review of the flow-field analysis over cavities. In Proceedings of the 2017 International Conference on Infocom Technologies and Unmanned Systems (Trends and Future Directions) (ICTUS), Dubai, United Arab Emirates, 18–20 December 2017; pp. 870–876. [Google Scholar]
- Sarohia, V. Experimental investigation of oscillations in flows over shallow cavities. AIAA J. 1977, 15, 984–991. [Google Scholar] [CrossRef]
- Rossiter, J. Wind-Tunnel Experiments on the Flow over Rectangular Cavities at Subsonic and Transonic Speeds; Cranfield University: Bedford, UK, 1964. [Google Scholar]
- Lawson, S.; Barakos, G. Review of numerical simulations for high-speed, turbulent cavity flows. Prog. Aerosp. Sci. 2011, 47, 186–216. [Google Scholar] [CrossRef]
- Vikramaditya, N.; Kurian, J. Pressure oscillations from cavities with ramp. AIAA J. 2009, 47, 2974–2984. [Google Scholar] [CrossRef]
- Kok, J.C.; Soemarwoto, B.I.; van der Ven, H. X-LES simulations using a high-order finite-volume scheme. Notes Numer. Fluid Mech. Multidiscip. Des. 2008, 97, 87. [Google Scholar]
- El Hassan, M.; Keirsbulck, L. Passive control of deep cavity shear layer flow at subsonic speed. Can. J. Phys. 2017, 95, 894–899. [Google Scholar] [CrossRef]
- El Hassan, M.; Keirsbulck, L.; Labraga, L.; Lippert, M. Control of deep cavity tones using a spanwise cylinder at low-subsonic speeds. HEFAT 2008, 2008, 5. [Google Scholar]
- Cattafesta, L.N., III; Song, Q.; Williams, D.R.; Rowley, C.W.; Alvi, F.S. Active control of flow-induced cavity oscillations. Prog. Aerosp. Sci. 2008, 44, 479–502. [Google Scholar] [CrossRef]
- Stanek, M.; Ross, J.; Odedra, J.; Peto, J. High Frequency Acoustic Suppression-The Mystery of the Rod-in-Crossflow Revealed. In Proceedings of the 41st Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 2003. [Google Scholar]
- Stanek, M.; Raman, G.; Kibens, V.; Ross, J.; Odedra, J.; Peto, J. Control of cavity resonance through very high frequency forcing. In Proceedings of the 6th Aeroacoustics Conference and Exhibit, Hartford, CT, USA, 4–6 June 1980. [Google Scholar]
- Stanek, M.; Raman, G.; Ross, J.; Odedra, J.; Peto, J.; Alvi, F.; Kibens, V. High Frequency Acoustic Suppression—The Role of Mass Flow & The Notion of Superposition. In Proceedings of the 8th AIAA/CEAS Aeroacoustics Conference & Exhibit, Breckenridge, CO, USA, 17–19 June 2002. [Google Scholar]
- Shaw, L.; Clark, R.; Talmadge, D. F-111 generic weapons bay acoustic environment. J. Aircr. 1988, 25, 147–153. [Google Scholar] [CrossRef]
- Lumley, J.L. The structure of inhomogeneous turbulent flows. Atmos. Turbul. Radio Wave Propag. 1967, 166–178. [Google Scholar]
- Weiss, J. A Tutorial on the proper orthogonal decomposition. In Proceedings of the AIAA Aviation 2019 Forum, Dallas, TX, USA, 17–21 June 2019. [Google Scholar]
- Berkooz, G.; Holmes, P.; Lumley, J.L. The proper orthogonal decomposition in the analysis of turbulent flows. Annu. Rev. Fluid Mech. 1993, 25, 539–575. [Google Scholar] [CrossRef]
- Ribau, M.; Gonçalves, N.D.; Ferrás, L.L.; Afonso, A.M. Flow Structures Identification through Proper Orthogonal Decompo-sition: The Flow around Two Distinct Cylinders. Fluids 2021, 6, 384. [Google Scholar] [CrossRef]
- Delville, J. Characterization of the organization in shear layers via the Proper Orthogonal Decomposition. Flow, Turbul. Combust. 1994, 53, 263–281. [Google Scholar] [CrossRef]
- Hamdi, J.; Assoum, H.; Abed-Meraïm, K.; Sakout, A. Volume reconstruction of an impinging jet obtained from stereoscopic-PIV data using POD. Eur. J. Mech.-B/Fluids 2018, 67, 433–445. [Google Scholar] [CrossRef]
- Podvin, B.; Fraigneau, Y.; Lusseyran, F.; Gougat, P. A Reconstruction Method for the Flow Past an Open Cavity. J. Fluids Eng. 2005, 128, 531–540. [Google Scholar] [CrossRef]
- Rowley, C.; Colonius, T.; Murray, R. POD based models of self-sustained oscillations in the flow past an open cavity. In Proceedings of the 6th Aeroacoustics Conference and Exhibit, Hartford, CT, USA, 4–6 June 1980. [Google Scholar]
- Lawson, S.; Barakos, G.; Simpson, A. Understanding cavity flows using proper orthogonal decomposition and signal pro-cessing. J. Algorithms Comput. Technol. 2010, 4, 47–69. [Google Scholar] [CrossRef]
- Westerweel, J. Digital Particle Image Velocimetry; Delft University Press: Delft, The Netherlands, 1993. [Google Scholar]
- Prasad, A.; Adrian, R.; Landreth, C.; Offutt, P. Effect of resolution on the speed and accuracy of particle image ve-locimetry interrogation. Exp. Fluids 1992, 13, 105–116. [Google Scholar] [CrossRef]
- Raffel, M.; Willert, C.E.; Kompenhans, J. Particle Image Velocimetry: A Practical Guide; SPIE Optical Engineering Press: Bellingham, WA, USA, 1998. [Google Scholar]
- Illy, H.; Geffroy, P.; Jacquin, L. Control of cavity flow by means of a spanwise cylinder. In Proceedings of the 21th International Congress of Theoretical and Applied Mechanics, IUTAM, Warsaw, Poland, 15–21 August 2004. [Google Scholar]
- Illy, H.; Geffroy, P.; et Jacquin, L. Contrôle des oscillations de cavité au moyen d’un cylinder placé transversalement l’écoulement. In Proceedings of the 17me Congrès Français de mécanique, Troyes, France, 29 August–2 September 2005. [Google Scholar]
- Jeong, J.; Hussain, F. On the identification of a vortex. J. Fluid Mech. 1995, 285, 69–94. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jabado, A.H.; El Hassan, M.; Hammoud, A.; Sakout, A.; Assoum, H.H. Aeroacoustic Coupling in Rectangular Deep Cavities: Passive Control and Flow Dynamics. Fluids 2024, 9, 187. https://doi.org/10.3390/fluids9080187
Jabado AH, El Hassan M, Hammoud A, Sakout A, Assoum HH. Aeroacoustic Coupling in Rectangular Deep Cavities: Passive Control and Flow Dynamics. Fluids. 2024; 9(8):187. https://doi.org/10.3390/fluids9080187
Chicago/Turabian StyleJabado, Abdul Hamid, Mouhammad El Hassan, Ali Hammoud, Anas Sakout, and Hassan H. Assoum. 2024. "Aeroacoustic Coupling in Rectangular Deep Cavities: Passive Control and Flow Dynamics" Fluids 9, no. 8: 187. https://doi.org/10.3390/fluids9080187
APA StyleJabado, A. H., El Hassan, M., Hammoud, A., Sakout, A., & Assoum, H. H. (2024). Aeroacoustic Coupling in Rectangular Deep Cavities: Passive Control and Flow Dynamics. Fluids, 9(8), 187. https://doi.org/10.3390/fluids9080187





