Pressure and Velocity Profiles over a Weir Using Potential Flow Model
Abstract
1. Introduction
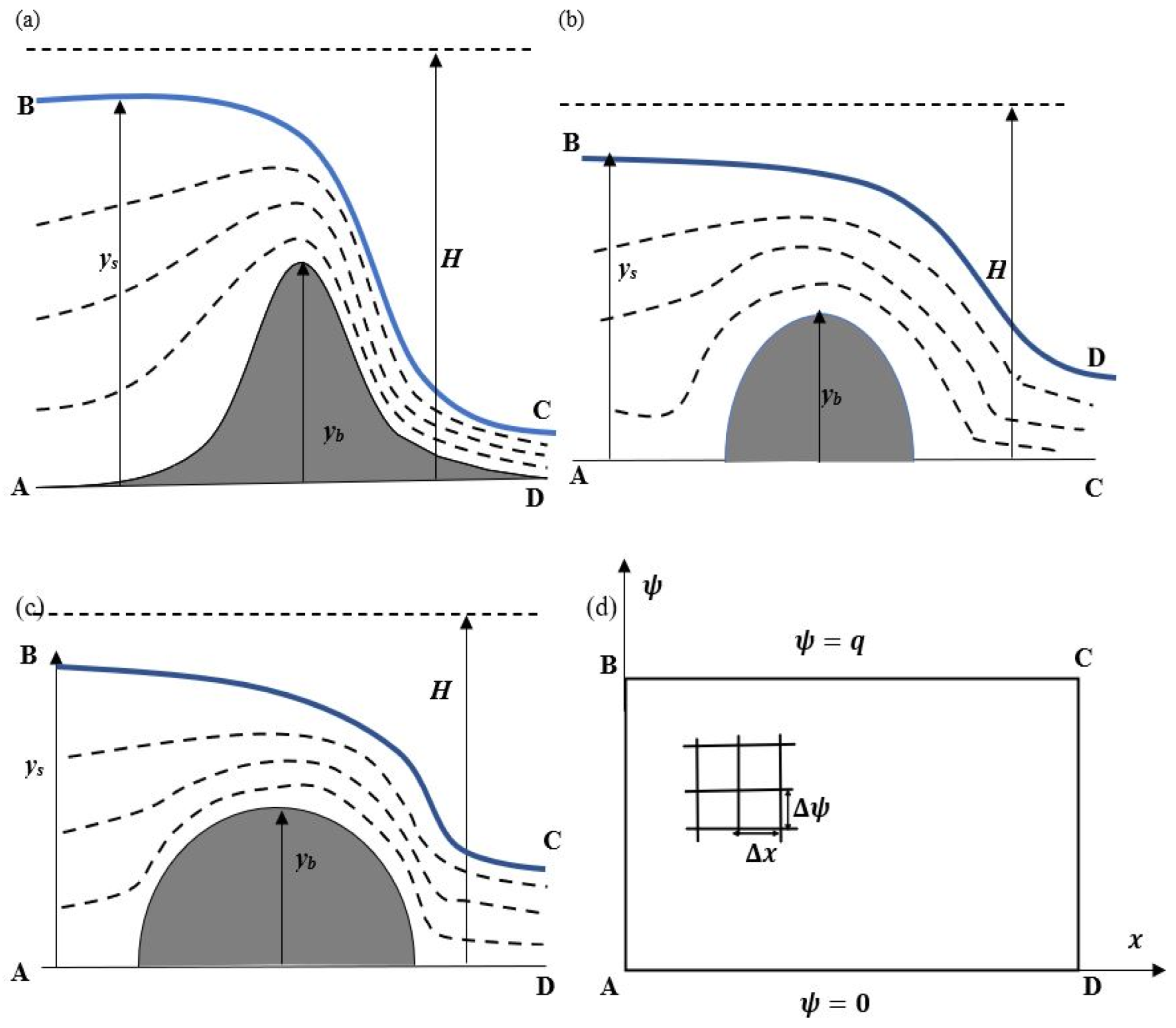
2. Governing Equation
2.1. The - Transformation
2.2. Boundary Conditions
2.2.1. Upstream and Downstream Boundaries
2.2.2. Free Surface Boundary
3. Solution Techniques
3.1. Solution of - Transformation of Laplace Equation
3.2. Velocity and Pressure Distributions
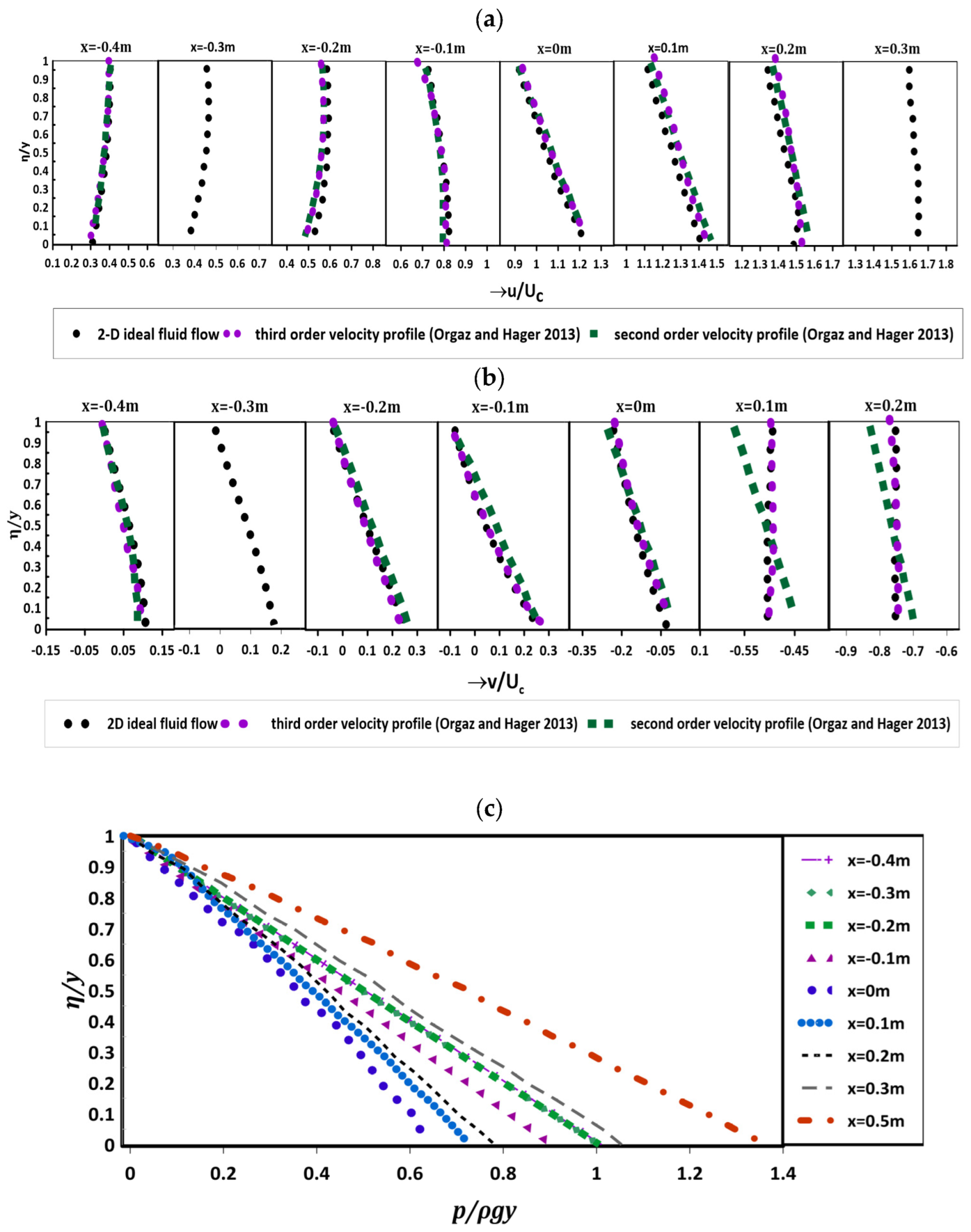
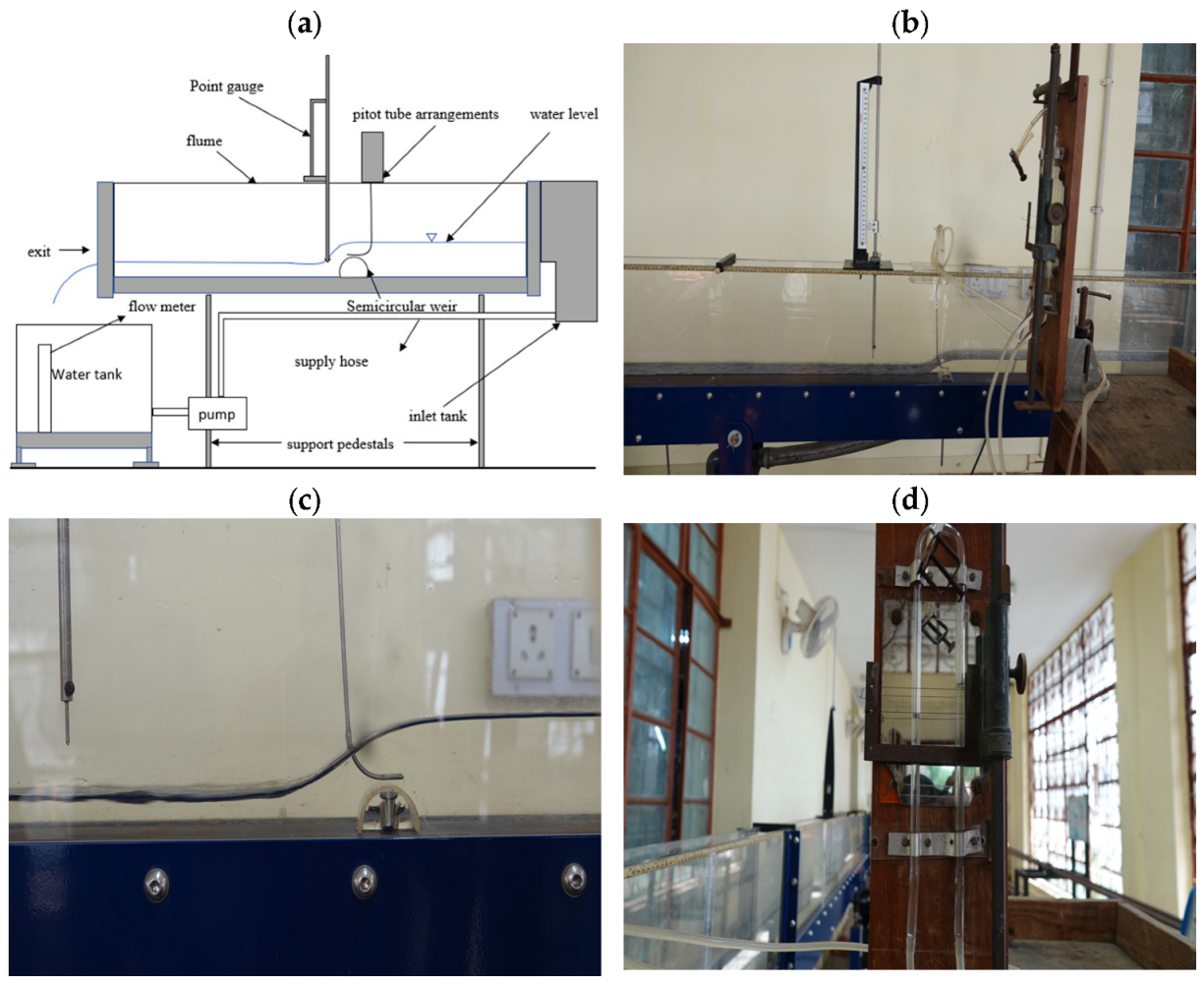
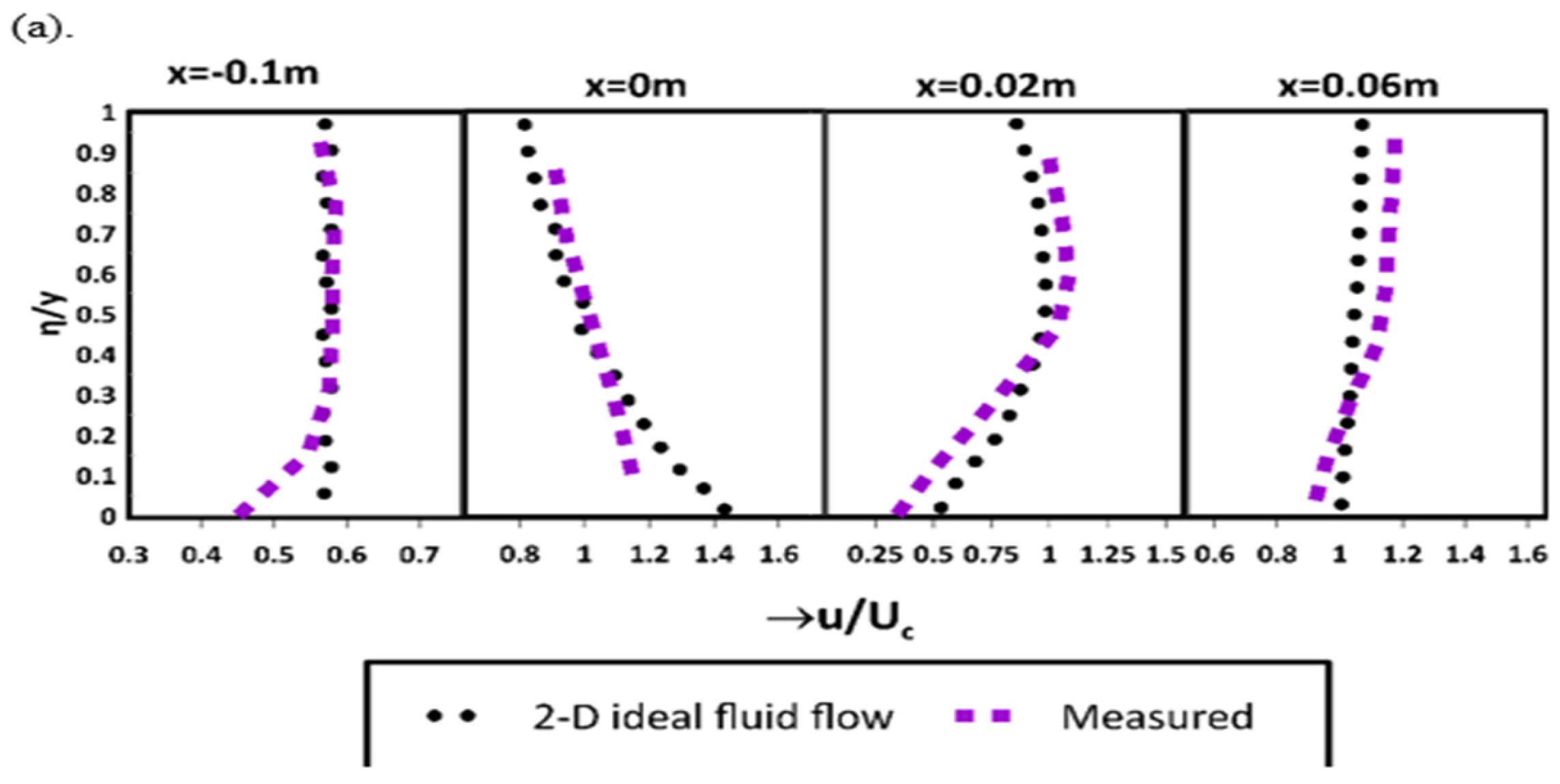
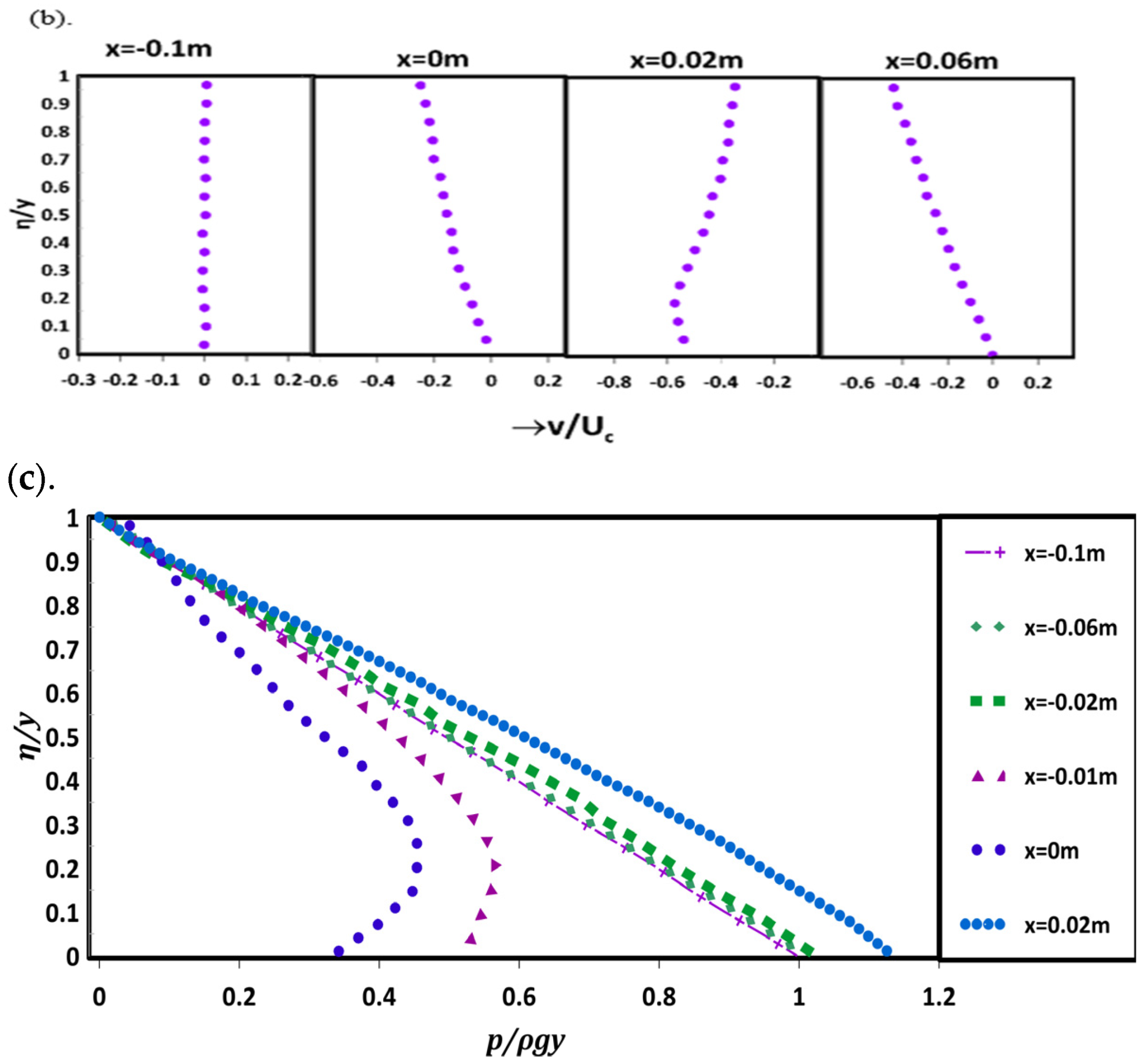
4. Results and Discussion
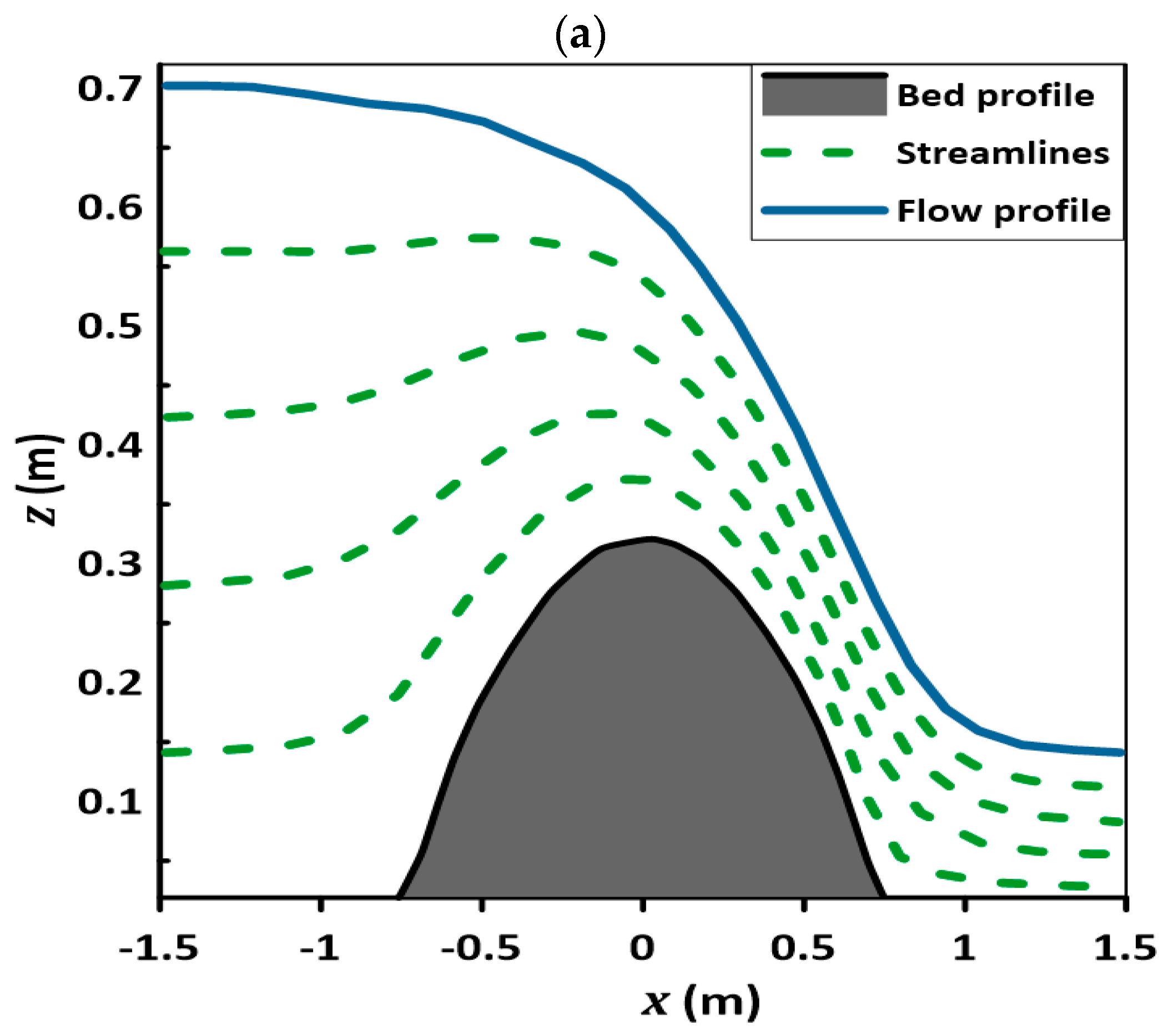
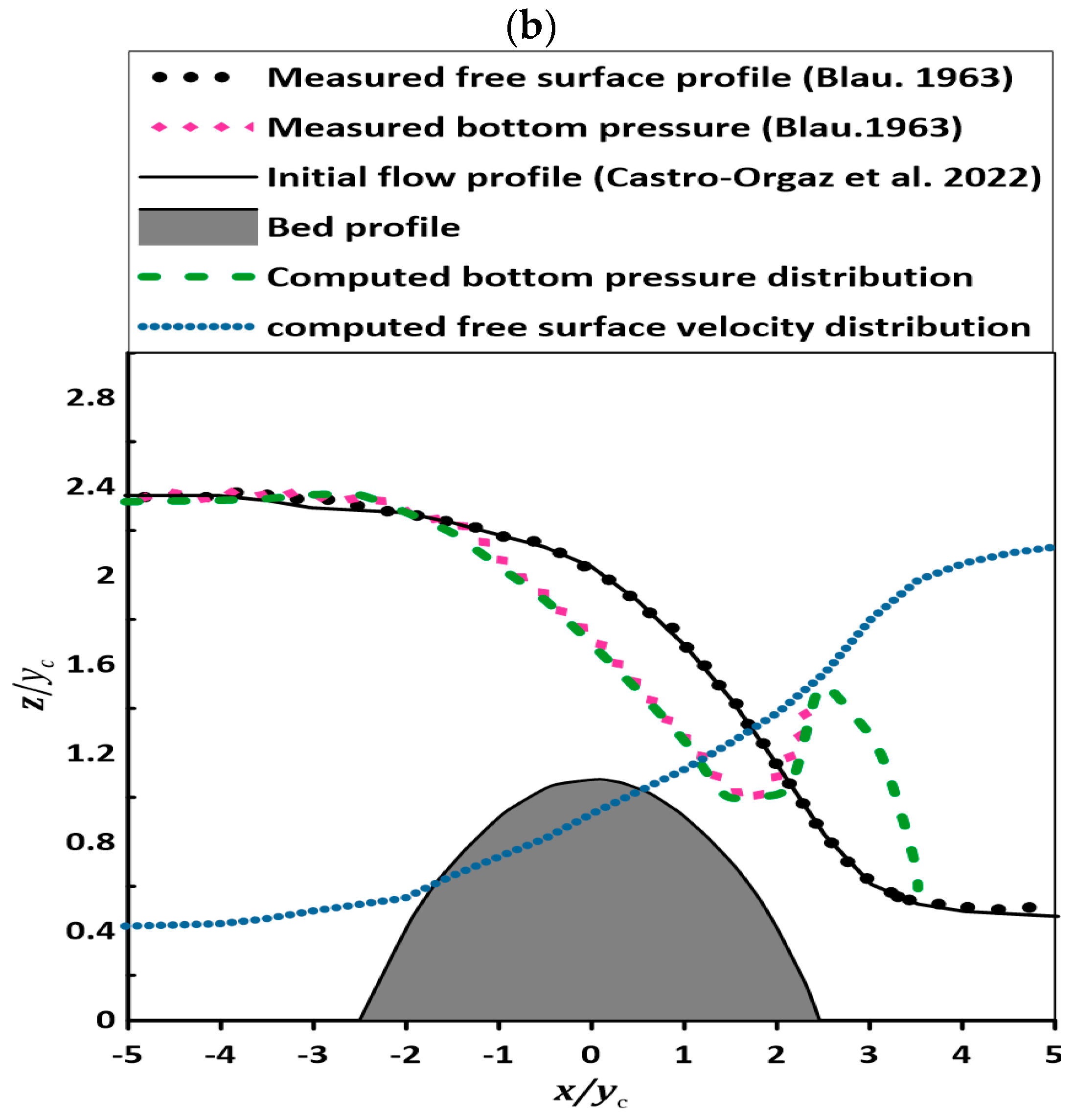
4.1. Flow over Gaussian Weir
4.2. Flow over Parabolic Weir
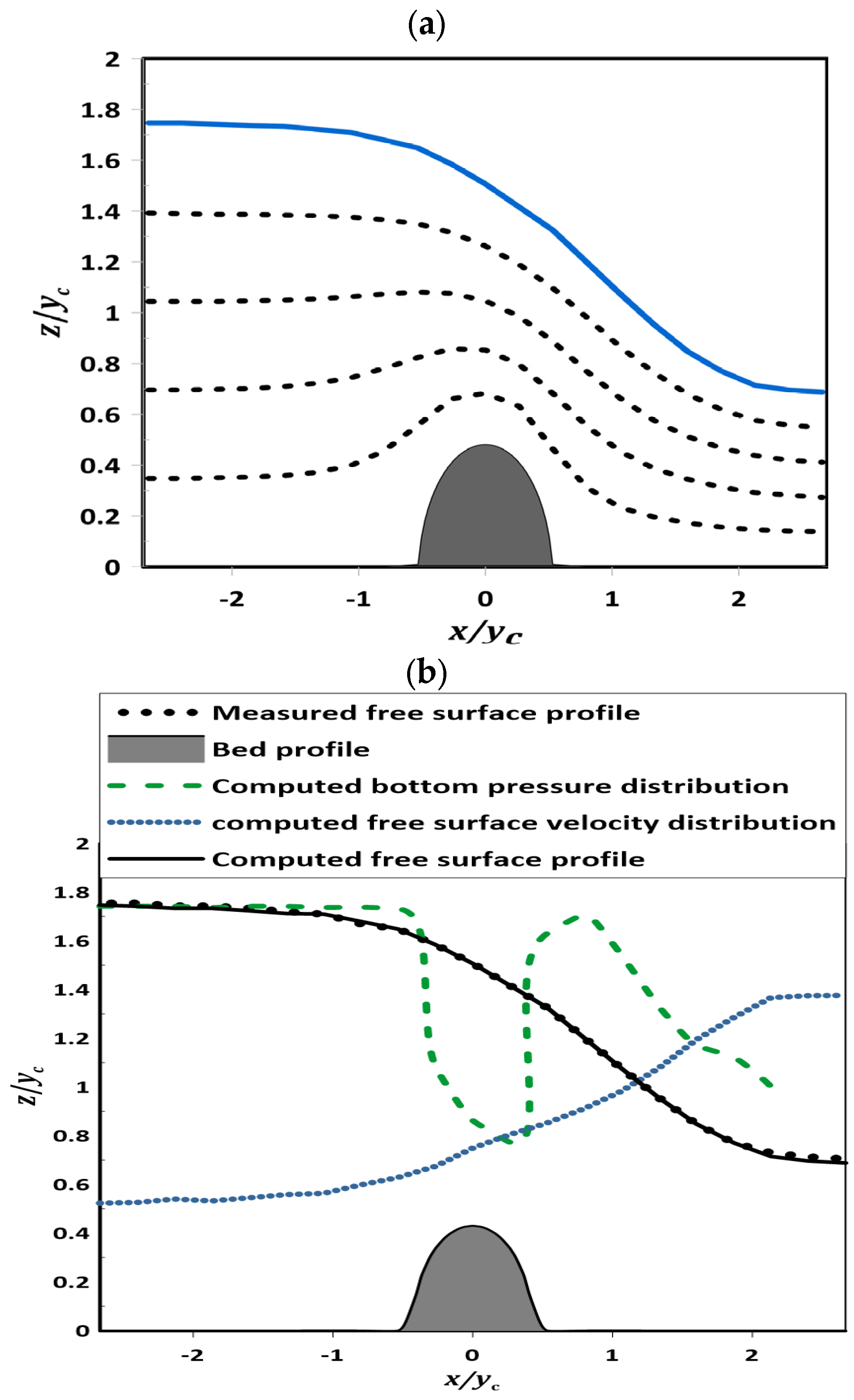
4.3. Flow over Semi-Circular Weir
5. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
Appendix C
Appendix C.1. Central Difference Approximation for First Derivative
Appendix C.2. Mixed Partial Derivative Approximation
References
- Vo, N.D. Characteristics of Curvilinear Flow Past Circular-Crested Weir; Concordia University: Montreal, QB, Canada, 1992. [Google Scholar]
- Vallentine, H.R. Applied Hydrodynamics; Butterworths Scientific Publications: London, UK, 1969. [Google Scholar]
- Chanson, H. Minimum Specific Energy and Critical Flow Conditions in Open Channels. J. Irrig. Drain. Eng. 2006, 132, 498–502. [Google Scholar] [CrossRef]
- Castro-Orgaz, O.; Chanson, H. Depth-Averaged Specific Energy in Open-Channel Flow and Analytical Solution for Critical Irrotational Flow over Weirs. J. Irrig. Drain. Eng. 2013, 140, 04013006. [Google Scholar] [CrossRef]
- Tadayon, R.; Ramamurthy, A.S. Turbulence Modeling of Flows over Circular Spillways. J. Irrig. Drain. Eng. 2009, 135, 493–498. [Google Scholar] [CrossRef]
- Rouse, H. Fluid Mechanics for Hydraulic Engineers; McGraw-Hill: New York, NY, USA, 1938. [Google Scholar]
- Pu, J.H.; Huang, Y.; Shao, S.; Hussain, K. Three-Gorges Dam Fine Sediment Pollutant Transport: Turbulence SPH Model Simulation of Multi-Fluid Flows. J. Appl. Fluid Mech. 2016, 9, 1–10. [Google Scholar] [CrossRef]
- Pu, J.H.; Cheng, N.S.; Tan, S.K.; Shao, S. Source Term Treatment of SWEs Using Surface Gradient Upwind Method. J. Hydraul. Res. 2012, 50, 145–153. [Google Scholar] [CrossRef]
- Pu, J.H. Turbulence Modelling of Shallow Water Flows Using Kolmogorov Approach. Comput. Fluids 2015, 115, 66–74. [Google Scholar] [CrossRef]
- Zheng, X.G.; Pu, J.H.; Chen, R.D.; Liu, X.N.; Shao, S.D. A Novel Explicit-Implicit Coupled Solution Method of SWE for Long-Term River Meandering Processinduced by Dambreak. J. Appl. Fluid Mech. 2016, 9, 2647–2660. [Google Scholar] [CrossRef]
- Messe, P. Ressaut et Ligne D’eau Dans Les Cours à Pente Variable [Hydraulic Jump and Free Surface Profile in Channels of Variable Slope]. Rev. Gén. Hydr. 1938, 4, 7–11. [Google Scholar]
- Andersen, V.M. Transition from Subcritical to Supercritical Flow. J. Hydraul. Res. 1975, 13, 227–238. [Google Scholar] [CrossRef]
- Southwell, R.V.; Vaisey, G. Relaxation Methods Applied to Engineering Problems XII: Fluid Motions Characterized by Free Streamlines. Philos. Trans. R. Soc. Lond. 1946, 240, 6. [Google Scholar] [CrossRef][Green Version]
- Markland, E. Calculation of Flow at a Free Overfall by Relaxation Methods. Proc. Inst. Civ. Eng. 1965, 31, 71–78. [Google Scholar] [CrossRef]
- Thom, A.; Apelt, C. Field Computations in Engineering and Physics; Van Nostrand: London, UK, 1961. [Google Scholar]
- Chan, S.T.; Larock, B.E.; Herrmann, L.R. Herrmann Free Surface Ideal Fluid Flows by Finite Element Methods. J. Hydraul. Div. 1973, 99, 959–974. [Google Scholar] [CrossRef]
- Cheng, A.H.; Liu, P.L.; Liggett, J.A. Liggett Boundary Calculations of Sluice and Spillway Flows. J. Hydraul. Div. 1981, 107, 1163–1178. [Google Scholar] [CrossRef]
- Chow, W.L.; Han, T. Inviscid Solution for the Problem of Free Overfall. ASME J. Appl. Mech. 1979, 46, 1–5. [Google Scholar] [CrossRef]
- Boadway, J.D. Transformation of Elliptical Partial Differential Equations for Solving Two-Dimensional Boundary Value Problems in Fluid Flow Overfall. Int. J. Numer. Methods Eng. 1976, 10, 527–533. [Google Scholar] [CrossRef]
- Montes, J.S. A Potential Flow Solution for the Free. Proc. Inst. Civ. Eng. 1992, 96, 259–266. [Google Scholar] [CrossRef]
- Cassidy, J.J. Irrotational Flow Over Spillways of Finite Height. J. Eng. Mech. Div. 1965, 91, 155–173. [Google Scholar] [CrossRef]
- Castro-Orgaz, O. Potential Flow Solution for Open-Channel Flows and Weir-Crest Overflow. J. Irrig. Drain. Eng. 2013, 139, 551–559. [Google Scholar] [CrossRef]
- Chanson, H.; Montes, J. Overflow Characteristics of Circular Weirs: Effect of Inflow Conditions. J. Irrig. Drain. Eng. 1998, 124, 152–162. [Google Scholar] [CrossRef]
- Castro-Orgaz, O.; Hager, W.H.; Cantero-Chinchilla, F.N. Shallow Flows over Curved Beds: Application of the Serre–Green–Naghdi Theory to Weir Flow. J. Hydraul. Eng. 2022, 148, 04021053. [Google Scholar] [CrossRef]
- Dressler, R.F. New Nonlinear Shallow-Flow Equations with Curvature. J. Hydraul. Res. 1978, 16, 205–222. [Google Scholar] [CrossRef]
- Boussinesq, J. Essai Sur La Theorie Des Eaux Courantes; Memoires Presentes Par Divers Savants a l’Academie Des Sciences; Imprimerie Nationale: Paris, France, 1877; pp. 1–680. Available online: https://gallica.bnf.fr/ark:/12148/bpt6k56673076 (accessed on 11 August 2024).
- Sivakumaran, N.S.; Tingsanchali, T.; Hosking, R.J. Steady Shallow Flow over Curved Beds. J. Fluid Mech. 1983, 127, 469–487. [Google Scholar] [CrossRef]
- Naghdi, P.M.; Vongsarnpigoon, L. The Downstream Flow beyond an Obstacle. J. Fluid Mech 1986, 162, 223–236. [Google Scholar] [CrossRef]
- Matthew, G.D. Higher Order, One-Dimensional Equations of Potential Flow in Open Channels. Proc.—Inst. Civ. Eng. Part 2 Res. Theory 1991, 91, 187–201. [Google Scholar] [CrossRef]
- Zhu, D.Z.; Lawrence, G.A. Non-Hydrostatic Effects in Layered Shallow Water Flows. J. Fluid Mech. 1998, 355, 1–16. [Google Scholar] [CrossRef]
- Castro-Orgaz, O.; Cantero-Chinchilla, F.N. Non-Linear Shallow Water Flow Modelling over Topography with Depth-Averaged Potential Equations; Springer: Amsterdam, The Netherlands, 2020; Volume 20, ISBN 0123456789. [Google Scholar]
- Montes, J.S. Potential-Flow Solution to 2D Transition from Mild to Steep Slope. J. Hydraul. Eng. 1994, 120, 601–621. [Google Scholar] [CrossRef]
- Wei, G.; Kirby, J.T.; Grilli, S.T.; Subramanya, R. A Fully Nonlinear Boussinesq Model for Surface Waves. Part 1. Highly Nonlinear Unsteady Waves. J. Fluid Mech. 1995, 294, 71–92. [Google Scholar] [CrossRef]
- Brocchini, M. A Reasoned Overview on Boussinesq-Type Models: The Interplay between Physics, Mathematics and Numerics. Proc. R. Soc. A Math. Phys. Eng. Sci. 2013, 469, 20130496. [Google Scholar] [CrossRef] [PubMed]
- Hosoda, T. Akhide Tada Free Surface Profile Analysis of Open Channel Flows by Means of 1-D Basic Equations with Effect of Vertical Acceleration. Proc. Hydraul. Eng. 1994, 38, 457–462. [Google Scholar] [CrossRef][Green Version]
- Onda, S.; Hosoda, T. Numerical Simulation on Development Process of Dunes and Flow Resistance. Proc. Hydraul. Eng. 2004, 48, 973–978. [Google Scholar] [CrossRef][Green Version]
- Komai, Y. Basic Characteristics on the Response of Water Surface Profiles of Open Channel Flows over an Obstacle. Bachelor’s Thesis, Undergraduate School of Kyoto University, Kyoto, Japan, 2006. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 10th ed.; Wiley: New York, NY, USA, 1972. [Google Scholar]
- Castro-Orgaz, O.; Hager, W.H. Velocity Profile Approximations for Two-Dimensional Potential Open Channel Flow. J. Hydraul. Res. 2013, 51, 645–655. [Google Scholar] [CrossRef][Green Version]
- Blau, E. Der Abfluss Und Die Hydraulische Energieverteilung Über Einer Parabelförmigen Wehrschwelle (Distributions of Discharge and Energy over a Parabolic-Shaped Weir); Mitteilungen der Forschungsanstalt für Schiffahrt, Wasser- und Grundbau: Berlin, Germany, 1963. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, M.R.A.; Hanmaiahgari, P.R.; Pu, J.H. Pressure and Velocity Profiles over a Weir Using Potential Flow Model. Fluids 2024, 9, 182. https://doi.org/10.3390/fluids9080182
Kumar MRA, Hanmaiahgari PR, Pu JH. Pressure and Velocity Profiles over a Weir Using Potential Flow Model. Fluids. 2024; 9(8):182. https://doi.org/10.3390/fluids9080182
Chicago/Turabian StyleKumar, M. R. Ajith, Prashanth R. Hanmaiahgari, and Jaan H. Pu. 2024. "Pressure and Velocity Profiles over a Weir Using Potential Flow Model" Fluids 9, no. 8: 182. https://doi.org/10.3390/fluids9080182
APA StyleKumar, M. R. A., Hanmaiahgari, P. R., & Pu, J. H. (2024). Pressure and Velocity Profiles over a Weir Using Potential Flow Model. Fluids, 9(8), 182. https://doi.org/10.3390/fluids9080182







